Abstract
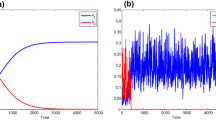
A mathematical model of growth and competitive interaction of microorganisms in the chemostat is analyzed. The growth-limiting nutrient is not in a form that can be directly assimilated by the microorganisms, and must first be transformed into an intermediate product by cell-bound extracellular enzymes. General monotone functions, including Michaelis-Menten and sigmoidal response functions, are used to describe nutrient conversion and growth due to consumption of the intermediate product. It is shown that the initial concentration of the species is an important determining factor for survival or washout. When there are two species whose growth is limited by the same nutrient, three different modes of competition are described. Competitive coexistence steady states are shown to be possible in two of them, but they are always unstable. In all of our numerical simulations, the system approaches a steady state corresponding to the washout of one or both of the species from the chemostat.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Bush, A. W., Cook, A. E.: The effect of time delay and growth rate inhibition in the bacterial treatment of wastewater. J. Theor. Biol. 63, 385–395 (1975)
Butler, G. J., Wolkowicz, G. S. K.: A mathematical model of the chemostat with a general class of functions describing nutrient uptake. SIAM J. Appl. Math. 45, 138–151 (1985)
Butler G. J., Wolkowicz, G. S. K.: Predator-mediated competition in the chemostat. J. Math. Biol. 24, 167–191 (1986)
Coppel, W. A.: Stability and Asymptotic Behavior of Differential Equations. Boston: D. C. Heath 1965
Chaloupka, J., Krumphanzl, V. (eds.): Extracellular Enzymes of Microorganisms. New York: Plenum 1987
Freedman, H. I., So, J. W.-H., Waltman, P.: Coexistence in a model of competition in the chemostat incorporating discrete delays. SIAM J. Appl. Math. 49, 859–870 (1989)
Herbert, D., Elsworth, R., Telling, R. C.: The continuous culture of bacteria: a theoretical and experimental study. J. Gen. Microb. 4, 601–622 (1956)
Hsu, S. B., Hubbell, S. P., Waltman, P.: A mathematical model for single-nutrient competition in continuous cultures of microorganisms. SIAM J. Appl. Math. 32, 366–383 (1977)
Hsu, S. B.: Limiting behavior for competing species. SIAM J. Appl. Math. 34, 760–763 (1978)
Nagata, Y., Yamaguchi, K., Maruo, B.: Genetic and biochemical studies on cell-bound α-amylase in Bacillus subtilis. Marburg J. Bacteriol. 119, 425–430 (1974)
Priest, F. G.: Extracellular Enzymes. Berkshire: Van Nostrand Reinhold 1984
Sargent, M. G., Ghosh, B. K., Lampen, J. O.: Localization of cell-bound penicillinase in Bacillus licheniformis. J. Bacteriol. 96, 1329–1338 (1968)
Smith, H. L.: Competing subcommunities of mutualists and a generalized Kamke theorem. SIAM J. Appl. Math. 46, 856–874 (1986)
Walker, G. J., Jacques, N. A.: Polysaccharides of oral streptococci, In: Raider, J., Peterkofsky, A, (eds.) Sugar Transport and Metabolism in Gram-positive Bacteria. Chichester: Ellis Horwood Limited 1987
Waltman, P., Hsu, S. B., Hubbell, S.: Theoretical and experimental investigations of microbial competition in continuous culture, In: Bjurton, T. (ed.) Modelling and Differential Equations in Biology. New York: Marcel Dekker 1980
Wolkowicz, G. S. K., Lu, Z.: Global dynamics of a mathematical model of competition in the chemostat: general response functions and differential death rates. SIAM J. Appl. Math. 52, 222–233 (1992)
Author information
Authors and Affiliations
Additional information
Research supported by NSF grant DMS-90-96279
Research supported by NSERC grant A-9358
Rights and permissions
About this article
Cite this article
Tang, B., Wolkowicz, G.S.K. Mathematical models of microbial growth and competition in the chemostat regulated by cell-bound extracellular enzymes. J. Math. Biol. 31, 1–23 (1992). https://doi.org/10.1007/BF00163841
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF00163841