1 Introduction

Various facets of real life are permeated by uncertain information [1,2,3,4,5]. The critical challenge of measuring uncertainty has prompted the advancement of numerous theories, including, but not confined to, probability theory [6], fuzzy sets [7, 8], Dempster–Shafer evidence theory [9], rough sets [10, 11], D numbers [12], Z numbers [13, 14], R numbers [15], entropy measure [16]. These theories, with their diverse foundations, find extensive applications in various real-life scenarios, bearing profound practical implications. Noteworthy applications include their valuable contributions to medical diagnosis [17, 18], target recognition [19], multi-attribute decision making [20,21,22], cluster analysis [23, 24], risk and reliability analysis [25].

Dempster–Shafer evidence theory is recognized as a highly effective tool for navigating uncertain information and reasoning based on evidence [26]. Numerous advantages characterize this theory, as it serves as a generalization of probability theory and provides a means to model uncertain information in real-life scenarios devoid of a priori probability. The pivotal role played by Dempster combination rules in fusing diverse information sources contributes to progressively mitigating information uncertainty through a step-by-step fusion process. From a geometric standpoint, the alignment of the Dempster combination rule with the commutative and combinative laws of multiplication enhances its widespread utilization across various domains, including information fusion, decision-making, image processing, and risk analysis. In the evolution of Dempster–Shafer evidence theory, scholarly attention has been drawn to three key aspects: enhancing the discrimination framework, generating BBA, and measuring conflicting evidence. The method for generating BBA is not standardized and necessitates tailored analysis based on specific situations. A method utilizing triangular fuzzy numbers to generate BBA was proposed in [27]. Boudraa et al. adopted a fuzzy membership degree derived from image histograms and utilized an unsupervised approach to calculate BBA [28]. Meanwhile, an algorithm for BBA generation based on the probability density function obtained through kernel density estimation and pairwise learning was introduced by Xiao et al. [29]. Applications in target recognition and cluster analysis are found for these generative methods. Nevertheless, the Dempster–Shafer evidence theory also has its limitations. In response, several alternative theories have been proposed to refine and extend its applicability. The theoretical landscape has witnessed the emergence of refined frameworks, such as the generalized evidence theory [30], D numbers [12], and the complex evidence theory advocated by Xiao and Deng [31] and Pan [32]. These advancements in theoretical frameworks are crafted to address specific challenges and, in turn, contribute to the overall enhancement of evidence reasoning.

In the domain of Dempster–Shafer evidence theory, the challenge of managing inherent uncertainty in the BBA is accentuated when encountering periodic data characterized by dynamic phase angles [31]. This limitation has been addressed by Xiao, who has adeptly introduced a complex Dempster–Shafer evidence theory. In this innovative variation, the BBA undergoes a transformation from being mapped in the power set to the real number domain (ranging from 0 to 1) to being mapped in the complex number domain, termed CBBA. This adaptation has been proven notably effective when handling data with multidimensional features [26]. Contributing to the progress in this field, a new CBBA that does not exactly consistent with Xiao’s CBBA is proposed in [32]. Pan and Deng’s CBBA adheres to the condition that the sum of the moduli of the CBBAs across all power sets equals 1 [32]. However, a significant distinction arises, as in Xiao’s complex Dempster–Shafer evidence theory, where the requirement is for the sum of CBBA across all power sets to equal 1. Despite these commendable theoretical advancements, the generation of CBBA remains a central challenge in complex Dempster–Shafer evidence theory. A method grounded in triangular fuzzy numbers for CBBA generation is proposed by Xiao, finding practical application in target recognition and showcasing a commendably high recognition rate. Nevertheless, there is still ample room for improvement in enhancing this recognition rate [33].

In this paper, an improved method for generating CBBA based on triangular fuzzy numbers is presented. The method is structured into four sequential steps: first of all, the division of the training set and test set; then, the modeling of triangular fuzzy numbers for different attributes; besides, the derivation of weights for different attributes; and finally, the generation of new CBBAs with associated weights. The consideration of objective weights for different attributes enhances the reasonability and reliability of the final generated CBBAs. For target recognition, the proposed method is employed, and a target recognition algorithm is formulated based on the developed CBBA generation approach. This algorithm is subsequently applied to various data sets, including the iris data set, banknote data set, and lense data set, to demonstrate its performance. Simulation results highlight that the recognition rate is improved significantly, leading to high-quality recognition outcomes.

The subsequent sections of the paper are organized as follows. In the second section, the fundamental concepts of Dempster–Shafer evidence theory, complex Dempster–Shafer evidence theory, and the definition of triangular fuzzy numbers are briefly introduced. The third section meticulously outlines the specific procedure for CBBA generation. Section four details and provides applications of the method to target recognition. Lastly, the fifth section encapsulates the paper with a summary.

2 Preliminary

2.1 Dempster–Shafer Evidence Theory

Definition 1

(Frame of discernment) The frame of discernment, denoted as \(\Omega \), comprises a set of mutually exclusive and non-empty elements: \(\Omega =\left\{ E _{1}, E _{2}, E_{3 }, \ldots , E_{N}\right\} \). This set, known as the frame of discrimination, serves as the basis for the context under consideration. The power set of \(\Omega \), represented as \(2^{\Omega }\), encompasses various subsets that can be constructed from its elements. This representation, cited from [34], is articulated as:

$$\begin{aligned} 2^{\Omega } =\left\{ \emptyset ,\left\{ E_{1} \right\} ,\left\{ E_{2} \right\} ,\cdots ,\left\{ E_{N} \right\} , \left\{ E_{1},E_{2} \right\} ,\cdots ,\Omega \right\} . \end{aligned}$$
(1)

Definition 2

(Mass function) The mass function, denoted as m, characterizes the basic belief assignment (BBA) within the discrimination framework \(\Omega \). As per the definition provided in [32], the BBA m is articulated as a mapping:

$$\begin{aligned} m: 2^{\Omega }\longrightarrow [0,1], \end{aligned}$$
(2)

this mapping adheres to two fundamental conditions:

$$\begin{aligned} m(\emptyset )= & {} 0, \end{aligned}$$
(3)
$$\begin{aligned} \sum _{B\in 2^{\Omega }}m(B)= & {} 1, \end{aligned}$$
(4)

in these expressions, when m(B) attains a value greater than zero, the corresponding set B is designated as the focus element within the discrimination framework \(\Omega \). The significance of m(B) lies in its indication of the support for proposition B. A higher value of m(B) signifies stronger support for the associated proposition.

Definition 3

(Dempster’s combination rule) The BBAs \(m_{1}\) and \(m_{2}\) operate on the discrimination frame \(\Omega \), with their respective focal elements denoted by B and C. The combination rule for these BBAs, represented as \(m=m_{1}\oplus m_{2}\), is defined as follows [32]:

$$\begin{aligned} m(A)=\left\{ \begin{array}{cc}\frac{\sum _{B\cap C=A}^{} m_{1}(B)m_{2}(C) }{1-K}, &{} A\ne \emptyset , \\ 0, &{} A=\emptyset ,\end{array}\right. \end{aligned}$$
(5)

in this formulation, the conflict coefficient K between the two BBAs is expressed passively:

$$\begin{aligned} K= \sum _{B\cap C=\emptyset }^{} m_{1}(B)m_{2}(C), \end{aligned}$$
(6)

it’s worth noting that, in general terms, \(0\le K< 1\).

2.2 Complex Dempster–Shafer Evidence Theory

The complex Dempster–Shafer evidence theory, adept at handling uncertain information, is equipped with a complex combinatorial rule that enhances information fusion. Widely applicable across various domains, this theory stands as a robust framework for dealing with uncertainty. In this subsection, fundamental concepts of the complex Dempster–Shafer evidence theory are presented.

Definition 4

(Frame of discernment) Let \(\Theta =\big \{\theta _{1}, \theta _{2}, \theta _{3 }, \ldots , \theta _{N}\big \}\) be a mutually exclusive and non-empty set, identified as a frame of discrimination. The power set of the frame of discrimination, denoted by \(2^{\Theta }\), is expressed as follows [34]:

$$\begin{aligned} 2^{\Theta } =\left\{ \emptyset ,\left\{ \theta _{1} \right\} ,\left\{ \theta _{2} \right\} ,\cdots ,\left\{ \theta _{N} \right\} , \left\{ \theta _{1},\theta _{2} \right\} , \cdots ,\Theta \right\} . \end{aligned}$$
(7)

Definition 5

(Complex mass function) The complex mass function, also known as the complex basic belief assignment (CBBA), represents a generalization of the BBA within the Dempster–Shafer evidence theory framework. It is a mapping from elements in the power set to complex domains [34]:

$$\begin{aligned} M: 2^{\Theta }\longrightarrow C, \end{aligned}$$
(8)

this mapping adheres to the following three conditions:

$$\begin{aligned} M(\emptyset )= & {} 0, \end{aligned}$$
(9)
$$\begin{aligned} M(B)= & {} m(B) e^{i \theta (B)}, B \in 2^{\Theta }, \end{aligned}$$
(10)
$$\begin{aligned} \sum _{B\in 2^{\Theta }}M(B)= & {} 1. \end{aligned}$$
(11)

Here, \(i=\sqrt{-1}\), and m(B) denotes the modulus of CBBA M(B), taking values in the range [0,1]. The term \(\theta (B)\) represents a phase term within the range \([-\pi ,\pi ]\). According to Euler’s formula, the CBBA M(B) may be presented in the following “rectangular” or “Cartesian” form:

$$\begin{aligned} M(B)=x+yi, \quad B\in 2^{\Theta }, \end{aligned}$$
(12)

this form satisfies \(\sqrt{x^{2}+ y^{2}} \in [0,1]\). Additionally, M(B) can be represented as:

$$\begin{aligned} \left| M(B) \right| =m(B)= \sqrt{x^{2}+ y^{2}}. \end{aligned}$$
(13)

When \(\left| M(B) \right| \) is greater than 0, proposition B is considered a focal element, and \(\left| M(B) \right| \) represents the degree of support for the proposition. A larger \(\left| M(B) \right| \) indicates stronger support, while a smaller value suggests weaker support. Notably, when \(y=0\), M(B) is a real number, causing the CBBA to degenerate into classical BBA.

Definition 6

(Complex Dempster’s combination rule) Two independent CBBAs, \(M_{1}\) and \(M_{2}\), within the discrimination frame \(\Theta \), with the focal element of \(M_{1}\) denoted as B and that of \(M_{2}\) denoted as C. The complex Dempster’s combination rule, symbolized as \(m=m_{1} \oplus m_{2}\), is articulated as follows [34]:

$$\begin{aligned} M(A)=\left\{ \begin{array}{cc}\frac{\sum _{B\cap C=A}^{} M_{1}(B)M_{2}(C) }{1-K}, &{} A\ne \emptyset , \\ 0, &{} A=\emptyset ,\end{array}\right. \end{aligned}$$
(14)

the conflict coefficient K of two CBBAs is expressed in terms of K as follows:

$$\begin{aligned} K= \sum _{B\cap C=\emptyset }^{} m_{1}(B)m_{2}(C). \end{aligned}$$
(15)

In decision-making scenarios, the CBBA may lack intuitiveness. Therefore, there arises a necessity to transform the CBBA. Xiao generalized the Pignistic probability transformation in Dempster–Shafer evidence theory and introduced the complex Pignistic probability transformation. This transformation facilitates the assignment of the CBBA of multiple subsets to a single subset, thereby enhancing the decision-making process.

Definition 7

(Complex Pignistic Probability Transformation) In the framework of discernment \(\Theta \), the complex Pignistic probability transformation is defined as follows, as presented by Xiao [35]:

$$\begin{aligned} CBet(B)=\sum _{A,B\in \Theta }^{}M(A) \frac{\left| A\cap B \right| }{\left| A\right| }, \end{aligned}$$
(16)

here, \(\left| A\cap B \right| \) denotes the cardinal number of the intersection of A and B, while \(\left| A\right| \) denotes the cardinal number of A.

2.3 Triangular Fuzzy Membership Function

Fuzzy sets, crucial for handling uncertainty, find extensive applications in decision-making. The concept of the degree of membership holds fundamental significance in fuzzy mathematics. Various fuzzy membership degree functions, such as triangular fuzzy distribution, trapezoidal fuzzy distribution, Gaussian fuzzy distribution, etc., have been explored [36]. In many instances, establishing a triangular fuzzy membership degree function proves more practical. The definition of the triangular fuzzy membership function is provided below.

Definition 8

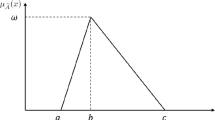
(Triangular fuzzy membership function) Suppose \(f _{B}\) denotes a triangular fuzzy membership function, and B is considered a focal element within the frame of discernment \(\Theta \). The trapezoidal fuzzy membership function is defined as follows [33]:

$$\begin{aligned} f_{B}(x)=\left\{ \begin{array}{cc} 0 &{} x<a, \\ \frac{x-a}{b-a} &{} a \le x<b, \\ \frac{c-x}{c-b} &{} b \le x<c, \\ 0 &{} c \le x, \end{array}\right. \end{aligned}$$
(17)

a denotes the lower bound of the fuzzy number, b signifies the most probable value of the fuzzy number, and c serves as the upper bound of the fuzzy number. The representation of the triangular fuzzy number is also possible in the form (a, b, c).

3 The Proposed Method for Generating CBBA

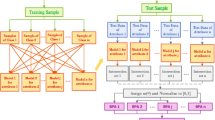
An approach is proposed in this paper to generate the CBBA for various attributes based on trapezoidal fuzzy numbers. The original data set comprises multiple classes of samples, each consisting of several attribute values. The process of generating the CBBA involves four distinct steps. Firstly, the original data set is partitioned into two classes: the training set and the test set. Subsequently, a model for each attribute is created using a triangular fuzzy number approach, leveraging the training set [33]. In the third step, the weights of each attribute are computed. Finally, test samples are chosen and inputted into the model derived in the previous step. The degrees of membership of focal elements for each attribute are determined based on the intersection points. This yields the proposed CBBA for different attributes. The flow chart of this method for generating the CBBA is depicted in Fig. 1. A more detailed process is outlined below.

Fig. 1
figure 1

Flow chart for generating CBBAs with weights

Full size image

The first step: Divide the original data set into a training set and a test set.

Assuming there are J classes of samples in the original data set, with each sample comprising I attribute values, and each class containing n test samples. Prior to experimentation, the original data set undergoes a division into two parts: a training set and a test set. Both sets are drawn in equal proportions from each class, with the training set to test set ratio being 3:2.

The second step: Triangular fuzzy numbers are modeled for different attributes based on the training set.

Within the training set, encompassing J classes, each sample is characterized by I attribute values, and there are S samples in each class. Let \(a_{ij}^{s}\) denote the i-th attribute value of the s-th training sample in class j (\(i=1,2,3,\dots ,I\); \(s=1,2,3,\dots ,S\); \(j=1,2,3,\dots ,J\)). The representation of \(a_{ij}^{s}\) is given by:

$$\begin{aligned} a_{ij}^{s} =x_{ij}^{s}+y_{ij}^{s}i. \end{aligned}$$
(18)

here, \(x_{ij}^{s}\) denotes the real part of the i-th attribute value for the s-th sample in class j, and \(y_{ij}^{s}\) represents the imaginary part. The modulus of a complex number is denoted by \(\left| \cdot \right| \).

The expression of the triangular fuzzy number stemming from attribute i within class j, denoted as \((a_{ij},b_{ij},c_{ij})\), is determined through the following computations:

$$\begin{aligned} \left| a_{ij} \right|= & {} \text {min}\sqrt{(x_{ij}^{s} )^{2} +(y_{ij}^{s} )^{2}},a_{ij}=x_{ij}^{s} +y_{ij}^{s} i, \end{aligned}$$
(19)
$$\begin{aligned} b_{ij}= & {} \frac{1}{S} \sum _{s=1}^{S} (x_{ij}^{s} +y_{ij}^{s}i), \end{aligned}$$
(20)
$$\begin{aligned} \left| c_{ij} \right|= & {} \text {max}\sqrt{(x_{ij}^{s} )^{2} +(y_{ij}^{s} )^{2}},c_{ij}=x_{ij}^{s} +y_{ij}^{s} i. \end{aligned}$$
(21)

Consequently, the formulation for the triangular fuzzy number originating from attribute i within class j is represented by the function \(f_{B}(x)\):

$$\begin{aligned} f_{B}(x)=\left\{ \begin{array}{cc} 0 &{} \left| x \right|<\left| a_{ij} \right| , \\ \frac{x-a_{ij}}{b_{ij}-a_{ij}} &{} \left| a_{ij} \right| \le \left| x \right|<\left| b_{ij} \right| , \\ \frac{c_{ij}-x}{c_{ij}-b_{ij}} &{} \left| b_{ij} \right| \le \left| x \right| <\left| c_{ij} \right| , \\ 0 &{} \left| c_{ij} \right| \le \left| x \right| . \end{array}\right. \end{aligned}$$
(22)

The triangular fuzzy number derived from the i-th attribute’s values across all samples within the j-th class in the training set can be denoted as \(TRI_{ij}\):

$$\begin{aligned} TRI_{ij} =(a_{ij}, b_{ij},c_{ij}). \end{aligned}$$
(23)

In order to generate the CBBA and obtain the degree of membership for focal elements, it is crucial to categorize the test sample into different classes of triangular fuzzy numbers. This necessitates the establishment of a triangular fuzzy number model comprising the triangular fuzzy numbers associated with attribute i. The representation of the triangular fuzzy number model for attribute i is denoted as \(TRI_{i}\) and can be expressed as follows:

$$\begin{aligned} TRI_{i}{} & {} =(TR_{i1},TR_{i2},TR_{i3},\cdots ,TR_{iJ}),\nonumber \\{} & {} \quad \ (i=1,2,3,\cdots ,I). \end{aligned}$$
(24)

Subsequently, the triangular fuzzy model for different attributes is collectively expressed as:

$$\begin{aligned} TRI_{1},TRI_{2},TRI_{3},\cdots ,TRI_{I}, \end{aligned}$$
(25)

the entire process is illustrated in Fig. 2.

To represent the triangular fuzzy number model of the different attributes of the sample inputs more intuitively, to be able to represent the triangular fuzzy numbers intuitively on the Cartesian coordinate system, the model of the established triangular fuzzy numbers needs to be processed, which means taking the modulus of the triangular fuzzy numbers.

Fig. 2
figure 2

The process of triangular fuzzy number models with different attributes

Full size image

The third step: Determine the weights of different attributes according to the recognition effect of different attributes on the sample.

As is widely recognized, diverse attributes exert distinct influences on sample recognition. In the context of the second step, the samples within the training set undergo sequential integration into the triangular fuzzy number model, each associated with specific attributes. Subsequent to multi-step computations, the recognition rates for the samples pertaining to different attributes are derived. The weights assigned to these attributes are then determined through the processing of the recognition rates. The following outlines the procedural steps involved in ascertaining the weights of the various attributes.

(1) Samples from the training set, with known classes, are randomly selected and, based on their attributes, incorporated into the triangular fuzzy number model established in the second step.

The model of the triangular fuzzy number for attribute i is employed to incorporate the value of attribute i from the training sample. This results in intersections with the triangular fuzzy numbers of various classes, denoted as \( \omega _{i1}, \omega _{i2},\cdots , \omega _{iJ} (i=1,2,\cdots , I)\) in sequential order. The corresponding vertical coordinates, \(\omega _{i1},\omega _{i2},\cdots ,\omega _{iJ}\) are then subjected to modulus operations, yielding \(\left| \omega _{i1} \right| ,\left| \omega _{i2} \right| ,\cdots ,\left| \omega _{iJ} \right| (i=1,2,\cdots , I)\).

(2) The samples are introduced into the model, resulting in intersections with various models. Subsequently, the degree of membership for different attributes of the focal element is determined based on these intersections.

The magnitudes \(\left| \omega _{i1} \right| ,\left| \omega _{i2} \right| ,\cdots ,\left| \omega _{iJ} \right| (i=1,2,\cdots , I)\) are arranged in descending order, assuming

$$\begin{aligned} \left| \omega _{i1} \right|>\left| \omega _{i2} \right| >\cdots \left| \omega _{iJ} \right| . \end{aligned}$$
(26)

Subsequently, the degree of membership for focal elements of attribute i is expressed as follows:

$$\begin{aligned} {} \begin{aligned}&G_{i} (\left\{ \theta _{1} \right\} )=\omega _{i1}, \\ {}&G_{i} (\left\{ \theta _{1},\theta _{2} \right\} )=\omega _{i2},\\ {}&G_{i} (\left\{ \theta _{1},\theta _{2}, \theta _{3} \right\} )=\omega _{i3},\\ {}&\dots \\ {}&G_{i} (\left\{ \theta _{1},\theta _{2},\theta _{3},\dots , \theta _{J} \right\} )=\omega _{iJ}, \end{aligned}\end{aligned}$$
(27)

where \(\theta _{1},\theta _{2},\dots , \theta _{J}\) represent class 1, class 2, \(\dots \), class J respectively.

(3) Discuss in separate cases to obtain CBBA for different attributes.

We first compute the sum of the degrees of membership \(SUM: SUM=\sum _{j=1}^{J} \omega _{ij} \) of the focal elements under different attributes and the sum of the degrees of membership for the modulus \(\left| SUM \right| =\left| \sum _{j=1}^{J} \omega _{ij} \right| \), \(\left| SUM \right| \) is divided into the following three cases:

Case 1:where \(\left| SUM \right| =\left| \sum _{j=1}^{J} \omega _{ij} \right| >1\), the value of \(1-\left| SUM \right| \) is indicative of uncertainty, and it is assigned to \(\Theta \). Consequently, the CBBA for attribute i is formulated as follows:

$$\begin{aligned}{} & {} M_{i} (\left\{ \theta _{1} \right\} ) =G(\left\{ \theta _{1} \right\} )=\omega _{i1}, \\ {}{} & {} M_{i}(\left\{ \theta _{1},\theta _{2} \right\} ) =G(\left\{ \theta _{1},\theta _{2} \right\} )=\omega _{i2},\\ {}{} & {} M_{i}(\left\{ \theta _{1},\theta _{2}, \theta _{3} \right\} ) =G(\left\{ \theta _{1},\theta _{2}, \theta _{3} \right\} )=\omega _{i3},\\ {}{} & {} \vdots \\ {}{} & {} M_{i}(\left\{ \theta _{1},\theta _{2},\theta _{3},\dots , \theta _{J} \right\} )=G(\left\{ \theta _{1},\theta _{2},\theta _{3},\dots , \theta _{J} \right\} )\\{} & {} +1-\left| SUM \right| =\omega _{iJ}+1-\left| SUM \right. |\end{aligned}$$

Case 2:when \(\left| SUM \right| =\left| \sum _{j=1}^{J} \omega _{ij} \right| =1\), the CBBA for attribute i is expressed as:

$$\begin{aligned}\begin{array}{c}M_{i}(\left\{ \theta _{1} \right\} )=G(\left\{ \theta _{1} \right\} )=\omega _{i1}, \\ M_{i}(\left\{ \theta _{1},\theta _{2} \right\} )=G(\left\{ \theta _{1},\theta _{2} \right\} )=\omega _{i2},\\ M_{i}(\left\{ \theta _{1},\theta _{2}, \theta _{3} \right\} )=G(\left\{ \theta _{1},\theta _{2}, \theta _{3} \right\} )=\omega _{i3},\\ \vdots \\ M_{i}(\left\{ \theta _{1},\theta _{2},\theta _{3},\dots , \theta _{J} \right\} )=G(\left\{ \theta _{1},\theta _{2},\dots , \theta _{J} \right\} ) =\omega _{iJ}.\end{array}\end{aligned}$$

Case 3:\(\left| SUM \right| =\left| \sum _{j=1}^{J} \omega _{ij} \right| >1\), so it needs to be normalized to \(\left| SUM \right| \). The CBBA for attribute i is:

$$\begin{aligned}\begin{array}{c}M_{i}(\left\{ \theta _{1} \right\} )=\frac{G(\left\{ \theta _{1} \right\} )}{\left| SUM \right| } =\frac{\omega _{i1}}{\left| SUM \right| }, \\ M_{i}(\left\{ \theta _{1},\theta _{2} \right\} )=\frac{G(\left\{ \theta _{1},\theta _{2} \right\} )}{\left| SUM \right| } =\frac{\omega _{i2}}{\left| SUM \right| },\\ M_{i}(\left\{ \theta _{1},\theta _{2},\theta _{3}\right\} )=\frac{G(\left\{ \theta _{1},\theta _{2},\theta _{3}\right\} )}{\left| SUM \right| } =\frac{\omega _{i3}}{\left| SUM \right| },\\ \vdots \\ M_{i}(\left\{ \theta _{1},\theta _{2},\theta _{3},\dots , \theta _{J}\right\} )=\frac{G(\left\{ \theta _{1},\theta _{2},\theta _{3},\dots , \theta _{J}\right\} )}{\left| SUM \right| } =\frac{\omega _{iJ}}{\left| SUM \right| }.\end{array}\end{aligned}$$

(4) By applying the complex Pignistic probabilistic transformation, the CBBA of multiple subsets in different attributes is assigned to single subsets.

The representation of the CBBA for a singleton set of attribute i is articulated as follows:

$$\begin{aligned} \overline{M^{i} } (\left\{ \theta _{1} \right\} ),\overline{M^{i} } (\left\{ \theta _{2} \right\} ),\overline{M^{i} } (\left\{ \theta _{3} \right\} ),\cdots ,\overline{M^{i} } (\left\{ \theta _{J} \right\} ). \end{aligned}$$

(5) Based on the modulus of the CBBA of the singleton set acquired earlier, the classes to which this sample belongs are determined.

The CBBA of a single subset of attribute i is ranked, and the class corresponding to the largest modulus is selected. Then, the sample is considered to belong to the class corresponding to the largest modulus within the triangular fuzzy number model of attribute i. If the calculated sample class matches the actual class of the sample, the sample can be correctly identified by the attribute. Conversely, if the calculated sample class differs from the actual class, the sample cannot be correctly identified by the attribute.

(6) Continuing the process, samples are consistently chosen from the training set and incorporated into the model, with steps 1 to 5 being iteratively executed to determine the recognition impact of different attributes on the samples, specifically, the recognition rate.

The recognition rate of a sample for attribute i is denoted as \(P_{i}\) \((i=1,2,3\ldots , I)\). The training set comprises m samples. It is assumed that among these m samples, the number of samples correctly identified by attribute i is \(m_{i}\). Consequently, the recognition rate of attribute i for the samples is expressed as follows:

$$\begin{aligned} P_{i} =\frac{m_{i} }{m},(i=1,2,3...,I). \end{aligned}$$

(7) The recognition rate is normalized to obtain the weights for different attributes.

The recognition rates for different attributes are:

$$\begin{aligned} P_{1}, P_{2}, P_{3}, \dots , P_{I}, \end{aligned}$$

the normalization of recognition rates for various attributes yields corresponding weights denoted as \(W_{1}, W_{2}, W_{3},\dots , W_{I}\). The recognition rates for different attributes are arranged in a ranking, and the attribute with the highest recognition rate is chosen, denoted as \(P_{k}\). Subsequently, the weights for different attributes can be formulated as follows, as described in [36]:

$$\begin{aligned} W_{1}=\frac{P_{1}}{P_{k}},W_{2}=\frac{P_{2}}{P_{k}},W_{3}=\frac{P_{3}}{P_{k}},\dots ,W_{I}=\frac{P_{I}}{P_{k}}. \end{aligned}$$

The fourth step: The test samples are put into a triangular fuzzy number model, and the CBBA for different attributes is obtained.

Random selection of test samples from the test set, which pertains to a particular class, is conducted. The test samples are then introduced into the triangular fuzzy number model for diverse attributes, and the procedure unfolds as follows:

(1) In the second step, the triangular fuzzy number model for different attributes is acquired, and the test samples are introduced into this model. Subsequently, the process (2) and (3) outlined in the third step is executed. Finally, the CBBA for different attributes is derived:

$$\begin{aligned} M_{i}(\left\{ \theta _{1} \right\} ),M_{i}(\left\{ \theta _{1},\theta _{2} \right\} ),M_{i}(\left\{ \theta _{1},\theta _{2}, \theta _{3} \right\} ),\dots ,M_{i}(\left\{ \theta _{1},\theta _{2},\theta _{3},\dots , \theta _{J} \right\} ). \end{aligned}$$

(2) The weights are used to amend the CBBA to obtain the weighted CBBA for different attributes:

$$\begin{aligned}\begin{array}{c}M_{i} (\left\{ \theta _{1} \right\} )=W_{i} *M_{i}(\left\{ \theta _{1} \right\} ),\\ M_{i} (\left\{ \theta _{1},\theta _{2} \right\} )=W_{i} *M_{i}(\left\{ \theta _{1}, \theta _{2} \right\} ),\\ M_{i} (\left\{ \theta _{1},\theta _{2},\theta _{3} \right\} )=W_{i} *M_{i}(\left\{ \theta _{1}, \theta _{2},\theta _{3} \right\} ),\\ M_{i} (\left\{ \theta _{1},\theta _{2},\theta _{3},\dots ,\theta _{J} \right\} )=W_{i} *M_{i}(\left\{ \theta _{1}, \theta _{2},\theta _{3},\theta _{3},\dots ,\theta _{J} \right\} ).\end{array}\end{aligned}$$

Consequently, the weighted CBBA, considered more reasonable than the unweighted CBBA, is achieved. Algorithm 1 corresponds to the aforementioned process.

Algorithm 1
figure a

Generation of a weight-fused CBBA

Full size image

4 Application

4.1 Application in Target Recognition

In this section, to demonstrate its applicability and effectiveness, the proposed method in this paper is employed for target recognition. The iris data set, the banknote data set and the lense data set are selected for the experiments, sourced from https://archive.ics.uci.edu/datasets. The subsequent table (Table 1) furnishes a concise description of the three data sets.

Table 1 Basic information about three data sets
Full size table

Given that the data in the iris data set, the banknote data set, and the lense data set comprises real numbers, it becomes necessary to map these real numbers onto the complex domain using the Fast Fourier Transform before the experiments are conducted. The process of target identification, formulated based on the proposed CBBA method, is outlined as follows:

Algorithm 2
figure b

The decision-making process in target recognition

Full size image

1. Select data sets, and identify power sets and discrimination frameworks.

2. Divide the selected data set into a training set and a test set.

3. Model the triangular fuzzy numbers with different attributes.

4. Determine the weights of different attributes based on the recognition effect.

5. Obtain the weighted CBBA.

6. Fuse weighted CBBA of different attributes by complex Demspter-Shafer combination rule.

7. Determine the class of the sample.

8. Repeat the above processes 3, 4, and 5 to calculate the recognition rate.

To showcase the effectiveness of the proposed method, a comparative analysis is conducted with Xiao [31] and classical Dempster–Shafer evidence theory. Xiao’s method relies on triangular fuzzy numbers to generate the CBBA, necessitating the application of the Fast Fourier Transform to the original data set before conducting experiments. In classical Dempster–Shafer evidence theory, the BBA is generated using triangular fuzzy numbers. The target recognition process associated with the proposed method is delineated by Algorithm 2. Results are presented in Tables 2, 3, and 4.

Table 2 Recognition rates obtained by different methods(Iris)
Full size table
Table 3 Recognition rates obtained by different methods(Banknote)
Full size table
Table 4 Recognition rates obtained by different methods(Lense)
Full size table
Fig. 3
figure 3

Comparison of target recognition rates of three methods for 10 experiments under the iris data set

Full size image
Fig. 4
figure 4

Comparison of target recognition rates of three methods for 10 experiments under the banknote data set

Full size image
Fig. 5
figure 5

Comparison of target recognition rates of three methods for 10 experiments under the lense data set

Full size image

The aforementioned target recognition process is iterated 1000 times to acquire recognition rates, and the results of every 100 experiments are averaged to yield ten sets of experimental recognition rates. Tables 2, 3, and 4 present the outcomes of ten sets of experiments conducted on the iris data set, banknote data set, and lenses data set, respectively. In these three tables, the second column denotes the target recognition rate obtained through the proposed method. The third column represents the target recognition rate based on Xiao’s method, and the fourth column displays the recognition rate based on the classical Dempster–Shafer evidence theory. As observed in Tables 2, 3, and 4, the values in the second column surpass those corresponding to both the third and fourth columns. For enhanced visualization of the results, Figs. 3, 4, and 5 correspond to Tables 2, 3, and 4, respectively.

In Fig. 3, the results obtained for the iris data set are presented. As observed in the Figure, the red line signifies the target recognition rate achieved through the proposed method, the blue line represents the recognition rate obtained through Xiao’s CBBA generation method, and the green line illustrates the target recognition rate obtained through the BBA generation method of classical Dempster–Shafer evidence theory. It can be noted that the value of the red line is approximately around 89.84\(\%\), the value of the blue line is roughly around 89.19\(\%\), and the value of the green line is roughly around 84.95\(\%\). Notably, the red line surpasses the blue line, and the blue line, in turn, surpasses the green line. Moving on to Fig. 4, the results obtained for the banknote data set are depicted. In this Figure, the value of the red line is approximately around 51.56\(\%\), the value of the blue line is approximately around 47.91\(\%\), and the value of the green line is approximately around 46.22\(\%\). Evidently, the red line stands out as the highest, indicating superior performance of the proposed method compared to the other two methods. Fig. 5 showcases the results obtained for the lens data set. Here, the value of the red line is approximately around 40.22\(\%\), the value of the blue line is approximately around 22.22\(\%\), and the value of the green line is approximately around 11.11\(\%\). Once again, the red line demonstrates the highest performance, signifying the superiority of the proposed method when compared to the other two methods.

Fig. 6
figure 6

Comparison of target recognition rates of three methods for 1000 experiments under the iris data set

Full size image
Fig. 7
figure 7

Comparison of target recognition rates of three methods for 1000 experiments under the banknote data set

Full size image
Fig. 8
figure 8

Comparison of target recognition rates of three methods for 1000 experiments under the lense data set

Full size image

The effectiveness of the proposed method was further illustrated by conducting another 1000 experiments on the iris data set, the banknote data set, and the lense data set, respectively. The recognition rates obtained from these data sets are displayed in Figs. 6, 7, and 8. As observed in these Figures, it’s noted that more than 80\(\%\) of the red dots surpass the blue dots, and similarly, more than 80\(\%\) of the blue dots exceed the green dots. This observation implies that the target recognition rate achieved by the proposed method stands as the highest, signifying that the proposed method is more effective and yields superior results in target recognition.

Fig. 9
figure 9

Comparison of target recognition rates of 1000 experiments conducted by three methods under the iris data set, each target recognition rate is obtained by sequential averaging

Full size image
Fig. 10
figure 10

Comparison of target recognition rates of 1000 experiments conducted by three methods under the banknote data set, each target recognition rate is obtained by sequential averaging

Full size image
Fig. 11
figure 11

Comparison of target recognition rates of 1000 experiments conducted by three methods under the lense data set, each target recognition rate is obtained by sequential averaging

Full size image

Having discussed the 1000 experiments above, the obtained recognition rates were sequentially averaged to generate another 1000 sets of data, as illustrated in Figs. 9, 10, and 11, respectively. As the number of experiments increased, the stabilization of the red line, the blue line, and the green line values became evident. The red line consistently surpassed the blue line, and in turn, the blue line consistently exceeded the green line. This phenomenon is attributed to the gradual increase in the number of proper recognitions achieved by the proposed method. With the growing number of experiments, the proposed method consistently outperforms Xiao’s method in correctly recognizing samples. Consequently, the averaged value of the red line surpasses that of the blue line. This underscores that the proposed method excels in recognizing more samples in target recognition, exhibiting superior performance.

The effectiveness of the proposed method was further emphasized through experiments conducted on the iris data set and the banknote data set, resulting in the generation of two graphs by varying the scale of the training set. Figure 12 represents the experimental outcomes derived from selecting different proportions of the training set in the iris data set, while Fig. 13 showcases the experimental results obtained by varying the proportions of the training set in the banknote data set. As observed from Figs. 12 and 13, the recognition rate achieved by the proposed method consistently surpasses that of the other two methods, irrespective of alterations in the proportion of the training set.

Fig. 12
figure 12

Experimental results obtained by taking different training sets in the iris data set

Full size image
Fig. 13
figure 13

Experimental results obtained by taking different training sets in the banknote data set

Full size image

4.2 Results Analysis and Discussion

In Figs. 3, 4, and 5, the red line’s value is observed to be higher than that of the blue line, indicating that the recognition rate achieved by the proposed method surpasses that of the method introduced by Xiao. This superiority arises from the consideration of weights assigned to different attributes of the sample within the proposed method. Distinct attributes exert varying degrees of influence on sample recognition, emphasizing the non-equivalency of these attributes. Attributes with robust recognition effects merit higher weights, while those with less impactful recognition effects are assigned lower weights. The weights serve to refine the obtained CBBA, resulting in a weighted CBBA that is more rational. The elevation of the blue line over the green line is attributed to the fact that the former represents the recognition rate based on the CBBA, while the latter represents the recognition rate based on the BBA. The CBBA inherently contains higher uncertainty information compared to the BBA, and its measurement of uncertainty is notably more accurate. The CBBA, derived by incorporating the test set into the triangular fuzzy number model with distinct attributes, is deemed more reasonable and suitable. This aspect proves advantageous for predicting the class of samples in subsequent analyses. In summary, a high recognition rate is achieved in target recognition by the proposed method, signifying its effectiveness.

5 Conclusion

In this paper, a new method for generating the CBBA is introduced. The method involves considering the weights of different attributes, which are determined based on the recognition effect of various attributes on the samples. These weights are employed to adjust the CBBA obtained from triangular fuzzy numbers, resulting in the derivation of the new CBBA. To validate the effectiveness of the proposed method, a target recognition algorithm is devised based on this approach. Experiments are conducted using the iris data set, the banknote data set, and the lense data set. In the iris data set, the recognition rate achieved through the proposed method reaches nearly 89.84\(\%\), surpassing both Xiao’s method and the classical Dempster-Shafer evidence theory method. For the banknote data set, the recognition rate based on the proposed method stands at about 51.56\(\%\), while in the lense data set, it reaches around 40.22\(\%\), both of which outperform the other two methods. Furthermore, in the majority of experiments, the proposed method consistently achieves the highest recognition rate. These results collectively demonstrate that the proposed method exhibits a high recognition rate and yields a superior recognition effect.

In future work, the investigation of the distance between CBBA is deemed essential, given that the conflict coefficient may not adeptly gauge the disparity between two bodies of evidence in certain scenarios. Additionally, a worthwhile research direction involves the application of CBBA to cluster analysis, decision-making, and other domains.