1 Introduction

Link prediction [1,2,3,4] is defined as predicting the connection possibility of any two disconnected nodes in an ordinary graph by utilizing the attributes of nodes, the topological information of the graph, and so on. Link prediction has essential applications in real life, such as predicting protein–protein interactions [5], predicting the possibility of people becoming friends in social networks [6, 7], predicting the possibility of two people publishing papers together [8, 9], recommender systems [10,11,12,13], drug discovery [14], knowledge acquisition [15], and label classification [16]. However, there are not only pairwise relationships, but also many higher-order relationships beyond pairwise interactions exist in real life. For example, in scientific collaboration networks [17], an article is often published by more than two authors, and in chemical reaction networks [18, 19], there are not only reactions between two compounds, but also reactions beyond two compounds. Hypergraph [20,21,22,23,24] is composed of nodes and hyperedges that can model the relationships beyond pairwise interactions. Unlike ordinary graphs, where edges can only connect two nodes, but hyperedges in hypergraphs can connect any number of nodes. Hyperlink prediction can be defined as predicting the possibility of any number of nodes forming hyperedges in the hypergraph by utilizing the hyperedge information, node attributes, hypergraph structure information, and so on. Hyperlink prediction can be used to predict the possibility of any number of authors collaborating to publish an article, as well as the possibility of any number of compounds producing chemical reactions.

Although hyperlink prediction is an important research problem, there are some difficulties to research it, for example, the problems of variable cardinality of hyperedges and prediction of directed hyperlink. In an ordinary graph (n nodes), the number of potential edges is only \(n^{2}\), but in a hypergraph (n nodes), the number of potential hyperedges is exponentially \(2^{n}\). If all possible hyperlinks are listed, there will be a total of \(2^{n}\) possibilities, so it is impractical to list, score and rank all hyperedges.

Currently, some researchers have also proposed hyperlink prediction methods. For example, Xu et al. [25] propose a hyperlink prediction method by using the hidden social feature information, and they solve the problem of predicting the relationship beyond pairwise interactions for the first time. Zhang et al. [26] consider that many potential hyperlinks are not consistent with the actual situation and the candidate hyperlink sets that satisfy the actual situation can be obtained by some special restrictive condition, and then utilize coordination matrix minimization (CMM) to propose a hyperlink prediction algorithm. Sharma et al. [27] propose a clique-closure hypothesis, and then utilize coordination matrix minimization to predict hyperlinks based on this hypothesis. Kumar et al. [28] propose a resource allocation-based hyperlink prediction algorithm with consulting the idea of hypergraph evolution model. Pan et al. [29] propose the loop structures based on nodes and hyperlinks, and then use modified logistic regression to transform the loop structure features into a hyperlink prediction method. Maurya and Ravindran [30] propose a hyperlink prediction algorithm based on k-uniform hypergraph by using tensor eigenvalue decomposition of hypergraph Laplacian. Fatemi et al. [31] propose two embedding methods for knowledge hypergraphs, named HsimplE and HypE, and solve the hyperlink prediction problem in knowledge hypergraphs for the first time. In addition, some researchers have proposed negative sampling methods [32, 33] to improve the hyperlink prediction process, and apply these negative sampling methods to hyperlink prediction algorithms to improve their hyperlink prediction performance.

Graph neural networks (GNNs) [34,35,36,37,38] have been growing at a very fast pace. Zhang and Chen [39] apply graph neural networks to link prediction based on binary relations in ordinary graphs, and then excellent results are obtained. However, there are few studies applying neural networks to hyperlink prediction. Yadati et al. [40] use graph convolutional network (GCN) to extract the node feature information, and then propose a GCN-based hyperlink prediction algorithm, abbreviated as NHP, and the experimental results show that the hyperlink prediction performance of NHP is better than the classic methods such as CMM [26] and SHC [41]. GCN is a model that can perform convolutional neural networks on graph structure data, and it extends convolution operation to irregular or non-Euclidean graph structure data such as metabolic networks, social networks, and telecommunication networks. Multi-layer GCN can be used to propagate the node feature information. However, the single layer GCN equation is stiffly used in the NHP method in the information propagation process, which does not achieve the effect of flexibly using GCN ideas to transfer the feature information of nodes.

Most of the hyperlink prediction methods introduced above focus on predicting hyperlinks in undirected hypergraphs. How to predict directed hyperlinks is a difficult and worthy problem. Especially in chemical reaction and metabolic reaction networks, the choice of reactants and products directly affects whether the chemical reaction will actually occur. For example, in the same hyperedge, the reaction between compounds Cu(OH)2 and HCl will produce compounds CuCl2 and H2O, but compounds CuCl2 and HCl will not react and produce compounds Cu(OH)2 and H2O. Therefore, it is urgent to solve the problem of how to predict hyperlink for directed hypergraphs.

Based on the above problems, A hyperlink prediction framework based on graph representation learning is proposed, which can apply different graph representation learning methods to obtain hypergraph structure data and predict the interaction between multiple targets. GCN and GAT focus on the influence of neighboring nodes on the central node, which can enhance the ability of models to perceive the neighborhood, thereby strengthening the joint spatial representation ability of models. The framework is then incubated with two methods, one is hyperlink prediction based on graph convolutional networks (GCN) and the other is hyperlink prediction based on graph attention networks (GAT). Finally, these two methods are extended to directed hyperlink prediction. Since GCN and GAT have strong ability to perceive the neighborhood, they can represent the characteristic attributes of nodes in the hyperedges effectively, which gives them a clear advantage in improving their performance in hyperlinks prediction. Hence, the main contributions of this article are as follows:

(1) A hyperlink prediction framework based on graph representation learning is proposed, which can be applied not only to hyperlink prediction in undirected hypergraphs but also in directed hypergraphs. (2) The any size of hyperlinks can be predicted by the proposed methods without the need of candidate hyperlink sets, and unseen hyperlinks also can be predicted under the problem of variable cardinality of hyperedges. (3) The proposed hyperlink prediction algorithm framework is applied to both the biological metabolic reaction network and the organic chemical reaction network, and experimental analysis show that the two proposed hyperlink prediction algorithms can effectively predict multivariate interactions in both undirected and directed hypergraphs with relatively low time complexity.

2 Preliminaries

2.1 Undirected Hypergraphs

The definition of hypergraph [24] was first proposed by Berge in 1970.

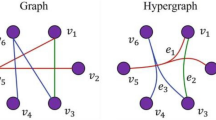
Suppose \(V = \{ v_{1} ,v_{2} , \ldots ,v_{n} \}\) is a finite set and \(E = \{ e_{1} ,e_{2} , \ldots ,e_{m} \}\), \(G = (V,E)\) is a hypergraph if (1) \(e_{i} \ne \emptyset \, (i = 1,2, \ldots ,m)\) and 2) \(\bigcup\nolimits_{i = 1}^{m} {e_{i} = V}\) are satisfied. The elements \(v_{1} ,v_{2} , \ldots ,v_{n}\) are the nodes of the undirected hypergraph \(G\), \(n = |V|\) denotes the number of nodes in \(G\), the elements \(e_{i} = \left\{ {v_{{i_{1} }} ,v_{{i_{2} }} , \ldots ,v_{{i_{j} }} } \right\}\left( {1 \le j \le n} \right)\) consisting of subsets of \(V\), is usually called the hyperedge of the hypergraph \(G\), \(|e_{i} |\) denotes the number of nodes contained in the hyperedge \(e_{i}\), and \(m = |E|\) denotes the number of hyperedges in the hypergraph.

A hypergraph is said to be a uniform hypergraph when the number of nodes in each hyperedge is equal, and a hypergraph is said to be a k-uniform hypergraph when the number of nodes in each hyperedge is equal to k. In an undirected hypergraph, each hyperedge contains a different set of nodes, and the total number of potential hyperedges is \(2^{n}\), and the set of unobserved hyperedges is \(E^{\prime} = 2^{n} - E\). Assuming that \(G\) is an incomplete undirected hypergraph, the hyperlink prediction of an undirected hypergraph can be defined as predicting the possibility of any number of nodes forming hyperedges in the hypergraph by utilizing the hyperedge information, node attributes, hypergraph structure information, and so on. As shown in Fig. 1, which represents the simplified process of hyperlink prediction for a synthetic undirected hypergraph, we need to predict the hyperlinks that are not currently observed but may be formed with time evolution by some hyperlink prediction methods.

Fig. 1
figure 1

Simplified process of hyperlink prediction for a synthetic undirected hypergraph. The hypergraph has 8 nodes, 3 hyperedges, and 28 potential hyperedges. We need to predict the nodes who may form hyperedges together in the future using some hyperlink prediction methods

Full size image

However, it is impractical to predict all possible hyperedges from an exponential hyperedge set. In fact, it is unnecessary to predict the set of all possible hyperedges. When given a particular dataset, many of the predicted hyperedges are not consistent with the actual situation. For example, in metabolic reactions, many predicted hyperedges do not have biological significance.

2.2 Directed Hypergraphs

A directed hypergraph [42] is denoted by unordered pair \(\vec{G} = (V,\vec{E})\), where \(V = \{ v_{1} ,v_{2} , \ldots ,v_{n} \}\), \(\vec{E} = \{ \vec{e}_{1} ,\vec{e}_{2} ,...,\vec{e}_{m} \}\), the elements \(v_{1} ,v_{2} , \ldots ,v_{n}\) are the nodes of the directed hypergraph \(\vec{G}\), the elements \(\vec{e}_{1} ,\vec{e}_{2} ,...,\vec{e}_{m}\) are the hyperedges of \(\vec{G}\). Specifically, the directed hyperedge consists of two parts, the head and tail of the hyperedge, respectively, that is, \(\vec{e}_{i} = (\vec{e}_{i}^{ + } ,\vec{e}_{i}^{ - } )\),where \(\vec{e}_{i}^{ + }\) is called the tail of the directed hyperedge, and \(\vec{e}_{i}^{ - }\) is called the head. Then, the hyperlink prediction of a directed hypergraph can be defined as using the observed directed hyperedges, node features, and hypergraph structure information to predict the possibility of any number of nodes in the hypergraph forming hyperedges and to predict the direction of the hyperedges. A simplified process of chemical reaction prediction for a synthetic directed hypergraph is shown in Fig. 2.

Fig. 2
figure 2

Simplified process for predicting hyperlinks in a synthetic directed chemical reaction hypergraph. The nodes in this hypergraph represent compounds and the hyperedges represent chemical reactions. The hypergraph has 9 nodes, 3 directed hyperedges, and 29 potential hyperedges, which means that there are 29–3 possibilities for future chemical reactions. We need to use hyperlink prediction methods to predict the compounds that are likely to react in the future, and then predict the direction of chemical reactions, that is, predict the head and tail of the directed hyperedges

Full size image

3 Proposed Methods

Graph Neural Networks (GNNs) are used to obtain graph structure data in this article, and then a GNNs-based hyperlink prediction framework is proposed. The framework is extended to two methods used for undirected hyperlink prediction and directed hyperlink prediction, which are the hyperlink prediction method based on GCN and the hyperlink prediction method based on GAT. These two proposed methods will be introduced in detail in the following.

3.1 Main Symbols Comparison Table

As shown in Table 1, the main comparison table of the symbols is provided for the convenience of the reader.

Table 1 Main symbols comparison
Full size table

3.2 Hyperlink Prediction for Undirected Hypergraphs: UGCN

Due to the particularity of graph structure data, the number of neighboring nodes of each node is not necessarily equal, it is not feasible to extract the features of nodes directly using convolution neural network model (CNN) [43], because operations such as convolution and pooling can only act on regular grids. GCN [34] is a model that can perform convolutional neural networks on graph structure data, and it extends convolution operation to irregular or non-Euclidean graph structure data such as metabolic networks, social networks, telecommunication networks, which can be described using graphs. Considering that the GCN model can extract graph data information effectively, an undirected hyperlink prediction method based on the GCN model is proposed, named UGCN for short. A schematic description of the UGCN framework is presented in Fig. 3.

Fig. 3
figure 3

Schematic description of UGCN framework

Full size image

The layer-wise information propagation rule of GCN is

$$H^{{(l + {1})}} = \sigma (\tilde{D}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \tilde{A}\tilde{D}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} H^{(l)} W^{(l)} ).$$
(1)

The feature information of the (l + 1)th layer of each node in the graph is obtained by aggregating the information of the node itself and its neighboring nodes in the lth layer. \(H^{(l)}\) is the activation matrix in the lth layer, if l = 0, \(H^{(0)}\) represents the initial node feature matrix X of the graph. \(W^{(l)}\) is the specific weight matrix of the l layer. \(\tilde{A} = A + I_{N}\), where \(A\) is an adjacency matrix which can be used to represent graph data, \(I_{N}\) is a identify matrix which denotes self-loops of nodes, therefore, \(\tilde{A}\) is the adjacency matrix after adding self-loops to all nodes. In the process of information propagation between layers, the neighboring information of the node can be obtained through the adjacency matrix. However, if we only use the adjacency matrix to transmit information, the information carried by the node itself will be lost. Therefore, it is necessary to retain the information of the nodes themselves by manually adding a self-loop to each node. \(\tilde{D}\) is a diagonal degree matrix, and \(\tilde{D}_{ii} = \sum\nolimits_{j} {\tilde{A}_{ij} }\) denotes the degree of nodes after adding self-loops. In the process of information propagation between layers, since matrix transformation needs to be continuously done, the node feature information matrix of the next layer obtained by aggregating the current information will continuously become larger. As the number of layers increases, the size of the output node feature information matrix will differ greatly from the initial feature matrix size, so this problem is avoided by normalizing the adjacency matrix in the process of information propagation. \(\tilde{D}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \tilde{A}\tilde{D}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}\) is the symmetric normalization of the adjacency matrix. \(\sigma ( \cdot )\) is a non-linear transformation activation function, such as ReLU function.

The feature of the node can be continuously propagated by multiple GCN layers. However, Since the receptive field will increase with the update of node features, if the network is deepened continuously and the number of GCN layers is too much, then each node will be affected by irrelevant nodes, and the obtained effect will decrease instead. Therefore, a two-layer GCN is used to propagate the node feature as follows:

$$\begin{aligned} Z &= f(X,A) \hfill \\ & = (\tilde{D}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \tilde{A}\tilde{D}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} ReLU(\tilde{D}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \tilde{A}\tilde{D}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} XW^{(0)} )W^{(1)} ), \hfill \\ \end{aligned}$$
(2)

where \(X = \{ x_{1} ,x_{2} ,...,x_{n} \} \in {\mathbb{R}}^{n \times d}\) is the initial node feature vector, n is the number of nodes, d is the dimension of node features, \(A\) is the adjacency matrix, and \(\tilde{D}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \tilde{A}\tilde{D}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}\) is the normalized adjacency matrix. Let \(\overline{A} = \tilde{D}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \tilde{A}\tilde{D}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}\), then Eq. (2) is changed to

$$Z = f(X,A) = (\overline{A}{\text{Re}} {\text{LU}}(\overline{A}XW^{(0)} )W^{(1)} ).$$
(3)

Suppose u is a node in hyperedge e, according to the above Eq. (3), node u not only aggregates the information from the neighboring nodes of node u but also the information originally carried by the node u, then the updated feature information of node u is as follows.

$$x_{u} = (\overline{A}{\text{ReLU}}(\overline{A}x_{u}^{(0)} W^{(0)} )W^{(1)} ),$$
(4)

where \(x_{u}^{(0)}\) is the initial feature vector of node u, \(x_{u}\) is the updated feature vector of node u after it passes through two GCN layers. After that, we preserve the higher-order relationships between nodes by aggregating the representation information of hyperedge e. The representation information of the hyperedge e is aggregated by using average function, that is the feature information of all nodes in the hyperedge e as follows:

$$h^{e} = \frac{1}{|e|}\sum\limits_{u \in e} {x_{u} } .$$
(5)

Considering that in some networks, the more similar the characteristics of the nodes, the higher the possibility of forming hyperedges. Such as the research collaboration network, if some authors have similar research directions, or are members of the same laboratory, or have the same collaborators, then these authors will be more likely to publish papers together. However, in some networks, the more different the characteristics of the nodes, the higher the possibility of forming hyperedges, such as the chemical reaction network in Fig. 2, the chemical reaction between Cu(OH)2 and HCl, where Cu(OH)2 is a base and HCl is an acid, and acids and bases are two kinds chemical substances with opposite properties. Therefore, Yadati et al. [40] propose a maxmin function to aggregate the representation information of the hyperedge e, that is

$$h^{e} = {\text{maxmin}}\{ x_{u} :u \in e\} = (\mathop {\max }\limits_{i \in e} x_{il} - \mathop {\min }\limits_{j \in e} x_{jl} ),$$
(6)

where \(l = 1,2,...,d\), d is the number of feature dimensions, \(\max_{i \in e} x_{il}\) is the maximum feature value of the nodes within the hyperedge e at the lth feature dimension, \(\min_{j \in e} x_{jl}\) is the minimum feature value of the nodes within the hyperedge e at the lth feature dimension, and \(\max_{i \in e} x_{il} - \min_{j \in e} x_{jl}\) denotes the difference between the maximum and minimum feature values of the nodes within the hyperedge e at the lth feature dimension.

Then, a fully connected layer and an activation layer are introduced to score the hyperedges. If the mean function will be used to aggregate the representation information of hyperedges, the scoring function is as follows:

$$s_{e} = \sigma (W \cdot h^{e} + b) = \sigma \left( {W \cdot \frac{1}{|e|}\sum\limits_{u \in e} {x_{u} } + b} \right).$$
(7)

If the maxmin function will be used to aggregate the representation information of hyperedges, the scoring function is as follows:

$$s_{e} = \sigma (W \cdot {\text{maxmin}}\{ x_{u} :u \in e\} + b),$$
(8)

where \(W\) and \(b\) are the weight matrix and bias of the fully connected layer, respectively, which are the hyperparameters need to be learned, and \(\sigma\) is the sigmoid activation function. Without loss of generality, it is possible to score the hyperedges using the above equation.

In order to ensure the accuracy of prediction, we need to ensure that the scores of hyperedges that can be observed in the hypergraph are more likely to be higher than the unobserved hyperedges in the hypergraph. Therefore, we can achieve the goal by optimizing the following objective function:

$$L_{U} = \frac{1}{|E|}\sum\limits_{e \in E} {g\left( {\left( {\frac{1}{|F|}\sum\limits_{f \in F} {s_{f} } } \right) - s_{e} } \right)} ,$$
(9)

where E is the set of observed hyperedges in the hypergraph, F is the set of hyperedges sampled from the set of unobserved hyperedges \(E^{\prime}\) in the hypergraph, \(|E^{\prime}| = 2^{n} - |E|\), and \(g(x) = \log (1 + e^{x} )\).

We continuously train the model and optimize the objective function so that the scores of the positive samples become higher and higher and the scores of the negative samples become lower and lower, thereby maximizing the difference in scores between the positive and negative samples.

3.3 Hyperlink Prediction for Undirected Hypergraphs: UGAT

GCN can effectively handle graph data information, but it also has some problems. For example, it cannot allocate the weights of neighboring nodes according to the node characteristic attributes, which lead to the GCN’s ability to capture the spatial information correlation is poor. GAT can allocate the weights of neighboring nodes according to the importance of associated nodes. Therefore, the graph attention network framework (GAT) [35] is introduced to propose an undirected hyperlink prediction method based on the GAT model, UGAT for short. A schematic description of the UGAT framework is presented in Fig. 4.

Fig. 4
figure 4

Schematic description of UGAT framework

Full size image

Suppose the input node feature vector is \(X = \{ x_{1} ,x_{2} ,...,x_{n} \} \in {\mathbb{R}}^{n \times d}\), where \(n\) is the number of nodes, d is the number of node feature dimensions, then the updated node feature vector after a GAT layer is \(X^{\prime} = \{ x^{\prime}_{1} ,x^{\prime}_{2} ,...,x^{\prime}_{n} \} \in {\mathbb{R}}^{{n \times d^{\prime}}}\). Firstly, a weight matrix W is used to act on each node, and then the self-attention mechanism is used to obtain the importance of neighboring nodes to the current center node, that is

$$e_{ij} = a(Wx_{i} ,Wx_{j} ),$$
(10)

where \(e_{ij}\) is the importance of node j to node i, and a is attention mechanism.

There are many ways to replace a. Here a single-layer feedforward neural network with parameter \(\vec{a} \in {\mathbb{R}}^{{2d^{\prime}}}\) is used to replace a, and then the LeakyReLU activation function is used to do nonlinearization. Hence \(e_{ij}\) is denoted as

$$e_{ij} = {\text{LeakyReLU}} (\vec{a}^{{\text{T}}} [Wx_{i} ||Wx_{j} ]),$$
(11)

where \(\vec{a}^{{\text{T}}}\) is the transposition of \(\vec{a}\), and \(||\) denotes the concatenation operation.

Then, the attention coefficient is obtained by normalizing the importance of neighboring nodes to the center node through the softmax function, we have

$$\begin{aligned} \alpha_{ij} &= {\text{softmax}}_{j} (e_{ij} ) \hfill \\ & = \frac{{\exp ({\text{LeakyReLU}} (\vec{a}^{{\text{T}}} [Wx_{i} ||Wx_{j} ]))}}{{\sum\nolimits_{{k \in \tau_{i} }} {exp({\text{LeakyReLU}} (\vec{a}^{{\text{T}}} [Wx_{i} ||Wx_{k} ]))} }}, \hfill \\ \end{aligned}$$
(12)

where \(j \in \tau_{i}\), and \(\tau_{i}\) is the set of nodes which adjacent to node i.

Finally, the attention coefficient of each neighbor node of the central node is multiplied with its node feature vector, then the product results are summed, and the final updated feature vector of the central node is

$$x^{\prime}_{i} = \sigma \left( {\sum\limits_{{j \in \tau_{i} }} {\alpha_{ij} } Wx_{j} } \right).$$
(13)

In order to improve the generalization ability of the attention mechanism, the multi-head graph attention mechanism is proposed, that is, K sets of independent single-head attention layers are concatenated together, then we have

$$x^{\prime}_{i} = \mathop {||}\limits_{k = 1}^{K} \sigma \left( {\sum\limits_{{j \in \tau_{i} }} {\alpha_{ij}^{k} W^{k} \vec{x}_{j} } } \right),$$
(14)

where \(||\) denotes the concatenation operation.

A two-layer GAT is used to propagate node feature information, the first layer is a 4-head GAT, and the second layer is a single-head GAT.

The node feature information propagation rule of the first GAT layer is

$$x_{i}^{(1)} = \mathop {||}\limits_{k = 1}^{4} \sigma \left( {\sum\limits_{{j \in \tau_{i} }} {\alpha_{ij}^{k} } W^{k} x_{j}^{(0)} } \right),$$
(15)

where \(x_{i}^{(1)}\) is the updated node feature through the first GAT layer, \(\sigma\) is non-linear activation function and an exponential linear unit (ELU) activation function is used here, \(\alpha_{ij}^{k} W^{k}\) is the attention coefficient of the kth head GAT in the first layer, and \(x_{j}^{(0)}\) is the initial node feature vector of any neighboring node of node i in the graph. Note that in order to retain the features of node i while obtaining the features of neighboring nodes, it is necessary to manually add a self-loop to each node to retain the information of the node itself. Therefore, when aggregating the feature information of nodes of the center node, the information of the center node itself is also included.

The node feature information propagation rule of the second GAT layer is

$$\begin{aligned} x_{i}^{(2)} & = \sigma \left( {\sum\limits_{{j \in \tau_{i} }} {\alpha_{ij}^{(1)} } W^{(1)} x_{j}^{(1)} } \right) \hfill \\ & = \sigma \left(\sum\limits_{{j \in \tau_{i} }} {\alpha_{ij}^{(1)} } W^{(1)} \left(\mathop {||}\limits_{k = 1}^{4} \sigma \left(\sum\limits_{{j \in \tau_{i} }} {\alpha_{ij}^{k} } W^{k} x_{j}^{(0)} \right)\right)\right), \hfill \\ \end{aligned}$$
(16)

where \(x_{i}^{(2)}\) is the updated node feature through the two-layer GAT, \(\sigma\) is the ELU activation function, and \(\alpha_{ij}^{(1)} W^{(1)}\) is the attention coefficient of the second GAT layer.

Then, the higher-order relationships between nodes are preserved by aggregating the representation information of the hyperedge e in the same way as the aggregation in Sect. 3.2.

The main pseudo-code of the UGCN and UGAT algorithms is provided to show more detail.

figure a

3.4 Hyperlink Prediction for Directed Hypergraphs

Directed hyperlink prediction not only needs to predict unobserved hyperlinks, but also needs to predict the direction of hyperlinks, that is, predict the head and tail of hyperlinks, which is a very difficult research problem. Therefore, the hyperlink prediction for directed hypergraph from the perspective of graph neural networks is explored in this article. Two kinds of directed hyperlink prediction algorithms are proposed, one is directed hyperlink prediction method based on GCN, which is called DGCN for short, and the other is directed hyperlink prediction method based on GAT, which is called DGAT for short. The difference between these two methods is only the pattern of obtaining the updated node feature information. One is to aggregate node feature information by using GCN, and the other is to aggregate node feature information by using GAT. Therefore, when introducing the two directed hyperlink prediction frameworks, we will introduce them together and do not introduce the two methods separately. As shown in Fig. 5, which is a schematic description of the hyperlink prediction framework for directed hypergraphs.

Fig. 5
figure 5

A schematic description of the hyperlink prediction framework for directed hypergraphs. The figure shows two hyperlink prediction algorithms for directed hypergraphs, DGCN and DGAT, respectively. The difference is the way of propagating node feature information, but the purpose is the same, which is to update the features of the nodes within the hyperedges

Full size image

Firstly, we utilize the proposed UGCN and UGAT in the previous two sections to propagate node features and aggregate hyperedge information, where the scoring function [40] used for a directed hyperlink \(e = (\vec{e}^{ + } ,\vec{e}^{ - } )\) is

$$s_{e} = \sigma (W \cdot {\text{maxmin}}_{D} \{ x_{u} :u \in e\} + b),$$
(17)

where \({\text{maxmin}}_{D} \{ x_{u} :u \in e\} = (\mathop {\max x_{il} }\limits_{{i \in \vec{e}^{ + } }} - \mathop {\min }\limits_{{j \in \vec{e}^{ - } }} x_{jl} )\) if \((\mathop {\max x_{il} }\limits_{{i \in \vec{e}^{ + } }} - \mathop {\min }\limits_{{j \in \vec{e}^{ - } }} x_{jl} ) > 0\), else \({\text{maxmin}}_{D} \{ x_{u} :u \in e\} = 0\), \(l = 1,2,...,d\), and d is the feature vector dimension.

Let \(e_{i}\) and \(e{}_{j}\) are two hyperlinks, this layer is utilized to determine the direction of the hyperlinks. In other words, we need to prediction the head and tail of the directed hyperlinks. Let \(o\) and \(r\) are the aggregated representation information of \(e_{i}\) and \(e{}_{j}\). The mean function is used to aggregate the feature information of hyperlinks \(e_{i}\) and \(e{}_{j}\) by averaging the feature information of all nodes in hyperlinks \(e_{i}\) and \(e{}_{j}\), respectively, that is

$$o = \frac{1}{{|e_{i} |}}\sum\limits_{{u \in e_{i} }} {x_{u} } ,\quad r = \frac{1}{{|e_{j} |}}\sum\limits_{{u \in e_{j} }} {x_{u} } .$$
(18)

Then, a fully connected layer and an activation layer are introduced to score the direction of the hyperedges, that is

$$D_{(o,r)} = \sigma (o^{{\text{T}}} W_{D} \cdot r + b_{D} ),$$
(19)

where \(\sigma\) is a sigmoid activation function, \(W_{D}\) and \(b_{D}\) are the weight matrix and bias of the linear layer, respectively. Without loss of generality, we need to ensure that the scores of the direction of observed directed hyperedges in the hypergraph are more likely to be higher than the direction of the unobserved directed hyperedges in the hypergraph. Therefore, we can achieve the goal by optimizing the following objective function:

$$L_{D} = \frac{1}{|E|}\sum\limits_{(p,q) \in E} {g\left( {\left( {\frac{1}{|F|}\sum\limits_{(o,r) \in F} {D_{(o,r)} } } \right) - D_{(p,q)} } \right)} ,$$
(20)

where E is the set of observed hyperedges in the hypergraph, F is the set of hyperedges sampled from the set of unobserved hyperedges \(E^{\prime}\) in the hypergraph, \(|E^{\prime}| = 2^{n} - |E|\), and \(g(x) = \log (1 + e^{x} )\).

In the process of predicting directed hyperlinks, we need to optimize not only the objective function (9) of the hyperlink prediction layer, but also the objective function (20) of the direction prediction layer, so that the final objective function of directed hyperlink prediction is

$$L = L_{U} + \lambda L_{D} ,$$
(21)

where \(\lambda\) is the parameter that needs to be learned.

The main pseudo-code of the DGCN and DGAT algorithms is provided to show more detail.

figure b

Hence, hyperlink prediction for undirected hypergraphs and directed hypergraphs can be realized by utilizing the content of this chapter. In addition, we will apply the proposed methods to real datasets to verify the effectiveness of the methods in the next chapter.

4 Experimental Results

4.1 Datasets

In order to verify the effectiveness of the proposed graph neural network-based undirected and directed hyperlink prediction, experimental validation on five real hypergraph datasets, which are iJO1366, iAF1260b, USPTO, DBLP, and Reverb45k [40], is performed. iJO1366 and iAF1260b are metabolic reaction datasets, USPTO is an organic chemical reaction dataset, DBLP is an undirected scientific collaboration dataset, and Reverb45k is a directed knowledge graph dataset. Note that USPTO, iJO1366 and iAF1260b are used not only for undirected hyperlink prediction, but also for directed hyperlink prediction. The details of the five real hypergraph datasets are presented in Table 2, where td denotes the dataset type, th denotes the hyperedge type, n denotes the number of nodes, m denotes the number of hyperedges, and d denotes the dimension of node features.

Table 2 The details of the five real hypergraph datasets
Full size table

4.2 Experimental Setup

Except for the experiments on the Reverb45k and USPTO datasets were performed in a workstation equipped with a 24-core Intel Xeon(R) Gold 5118 CPU @2.30 GHz processor and 64 GB RAM, the rest of experiments were run in a desktop pc equipped with an 8-core Intel Xeon(R) E-2244G CPU @3.80 GHz processor and 16 GB RAM. All the program code is run in Pycharm 2021.2.1.

The AUC and Recall@k (k is half of the number of unobserved hyperedges in the dataset) are used for assessing the prediction accuracy of the proposed hyperlink prediction methods. All experimental results are obtained with training rate of 20% and test rate of 80% for the datasets. Due to the large size of the Reverb45k dataset, the results on this dataset are obtained by randomly dividing this dataset once, and the results on the other datasets are obtained by randomly dividing the datasets three times.

We train the proposed methods for 50 iterations using Adam optimizer [44] with a learning rate of 0.0001 on all datasets. All weights are initialized using Glorot initialization [45]. The hidden size of each layer is 512. In addition, in the two-layer GCN model, dropout [46] = 0.5 is applied to the second layer’s inputs. In the two-layer GAT model, dropout = 0.5 is applied to both layers’ inputs and the process of normalized attention coefficients. The first layer consists of K = 4 attention heads, followed by an exponential linear unit (ELU) [47]. The second layer consists of a single attention head, followed by an ELU.

To avoid results deviation due to different size of the hyperlinks, for each observed hyperlink \(e \in E\), the same number of nodes are sampled as the negative hyperlink \(f \in F\), where half of the nodes in the negative hyperlink \(f\) are sampled from the observed hyperlink e, and the other half are sampled from node set \(V - e\) outside of the hyperlink e.

4.3 Experimental Results on Undirected Hyperlink Prediction

4.3.1 Baselines

To verify the feasibility of the proposed HGCA-UGCN and HGCA-UGAT undirected hyperlink prediction methods, the prediction performance of the following baselines applied to the hyperlink prediction task is compared.

HGNN [48]: Hypergraph neural network (HGNN) is a typical model that processes hypergraph data information after transforming hypergraphs into ordinary graphs. When the model is used for undirected hyperlink prediction task, its information propagation equation

$$X^{(l + 1)} = \sigma (D_{v}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} HWD_{e}^{ - 1} H^{{\text{T}}} D_{v}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} )X^{(l)} \Theta^{(l)} ,$$
(22)

and a linear layer are used to update the node features within the hyperedges.


Hyper-SAGNN [49]: The model utilizes the self-attention to aggregate the node features within the hyperedges. It can be directly used for undirected hyperlink prediction.


Node2Vec-mean: The Node2Vec [50] method is used to obtain the representation of the nodes in the hypergraph, and then the mean function is used to aggregate the information of the hyperedges.


Node2Vec-maxmin: The Node2Vec [50] method is used to obtain the representation of the nodes in the hypergraph, and then the maxmin function is used to aggregate the information of the hyperedges.


CMM [26]: The method predicts hyperlinks by alternately performing nonnegative matrix factorization and least square matching.


SHC [41]: The method transforms the hypergraph into a dual hypergraph, where the nodes in the original hypergraph become hyperedges and the hyperedges become nodes in its dual hypergraph, so that the hyperlink prediction becomes a problem of node classification.


NHP-U-mean [40]: This baseline simply uses the information propagation equation of GCN, that is Eq. (1), to update the features of the nodes, and then uses the mean function to aggregate the information of hyperedges, and finally scores the hyperedges.


NHP-U-maxmin [40]: This baseline simply uses the information propagation equation of GCN, that is Eq. (1), to update the features of the nodes, and then uses the maxmin function to aggregate the information of hyperedges, and finally scores the hyperedges.

4.3.2 Results

Tables 3 and 4 provide the results of the undirected hyperlink prediction of the proposed two models, UGCN and UGAT, with eight baselines. Table 3 presents the comparison of AUC and Recall@k values for all models on iJO1366, iAF1260b and USPTO datasets. Table 4 presents the comparison of AUC and Recall@k values for all models on the DBLP dataset. Note that -mean and -maxmin denote the information of the hyperedges aggregated with the mean and maxmin functions, respectively.

Table 3 Results comparison of undirected hyperlink prediction on iJO1366, iAF1260b and USPTO datasets
Full size table
Table 4 Results comparison of undirected hyperlink prediction on DBLP dataset
Full size table

As shown in Table 3, we find that the prediction performance of the two proposed undirected hyperlink prediction methods performs better on all three datasets. Compared with the eight baseline models, the two proposed methods have the best hyperlink prediction performance, where the AUC value increases by a minimum of 10% and a maximum of 40%, and the Recall@k value increases by a minimum of 3% and a maximum of 25%. CMM and SHC are hyperlink prediction methods based on candidate hyperlink sets. We find that the proposed methods can also predict hyperlinks efficiently without using candidate hyperlink sets from the experimental results. NHP-U-mean and NHP-U-maxmin use the information propagation equation of GCN to update the features of nodes, but the single layer GCN equation is stiffly used in the two methods in the information propagation process, which does not achieve the effect of flexibly using GCN ideas to transfer the feature information of nodes and is quite different from the convolution idea of GCN in essence. The convolution idea of GCN is used flexibly, so the performance of hyperlink prediction is greatly improved in this article. As shown in Table 4, it indicates that the hyperlink prediction performance of the proposed two methods is also better in the scientific collaboration hypergraph, which indicates that the proposed two methods can predict unseen hyperlinks effectively, where the AUC value increases by a minimum of 7% and a maximum of 43%, and the Recall@k value increases by a minimum of 1% and a maximum of 21%.

4.4 Experimental Results on Directed Hyperlink Prediction

4.4.1 Baselines

To verify the feasibility of the proposed DGCN and DGAT directed hyperlink prediction methods, we compare the prediction performance of the four baselines introduced in Sect. 4.4.1, which are HGNN, Hyper-SAGNN, Node2Vec-mean, and Node2Vec-maxmin, and the following two baselines.


NHP-D-mean [40]: This baseline simply uses the information propagation equation of GCN, that is Eq. (1), to update the features of the nodes, and then uses the mean function to aggregate the information of hyperedges, and finally scores the hyperedges and the direction of the hyperedges.


NHP-D-maxminD [40]: This baseline simply uses the information propagation equation of GCN, that is Eq. (1), to update the features of the nodes, and then uses the maxmin function to aggregate the information of hyperedges, and finally scores the hyperedges and the direction of the hyperedges.

4.4.2 Results

Tables 5 and 6 provide the results of the two proposed methods, DGCN and DGAT, with six Baselines for directed hyperlink prediction. Table 5 presents the comparison of AUC and Recall@k values of all methods on iJO1366, iAF1260b and USPTO datasets. Table 6 presents the comparison of AUC and Recall@k values of all methods on the Reverb45k dataset.

Table 5 Results comparison of directed hyperlink prediction on iJO1366, iAF1260b and USPTO datasets
Full size table
Table 6 Results comparison of directed hyperlink prediction on Reverb45k dataset
Full size table

As shown in Table 5, we find that the two proposed directed hyperlink prediction methods have better prediction performance on all three datasets. Compared with the six baseline models, the two proposed methods have the best directed hyperlink prediction performance, where the AUC value increases by a minimum of 29% and a maximum of 46%, and the Recall@k value increases by a minimum of 2% and a maximum of 32%. On all three datasets, most of the AUC values of these six baseline models are lower than 0.6, and the Recall@k values are lower than 0.3, while the AUC values of the proposed directed hyperlink prediction are more than 0.9, and the Recall@k values are more than 0.4. As shown in Table 6, it indicates that the hyperlink prediction performance of the two proposed directed hyperlink prediction methods also performs better in knowledge hypergraphs, where the AUC value increases by a minimum of 15% and a maximum of 35%, and the Recall@k value increases by a minimum of 7% and a maximum of 11%.

It can be found from Tables 2, 3, 4, 5 and 6 that the prediction results of the two proposed graph neural network-based hyperlink prediction are compared with those of other hyperlink prediction methods [26, 40, 41, 48,49,50], and it can be found that the prediction results of the proposed methods are better than those of the baselines on the undirected hyperlink prediction task and the directed hyperlink prediction task. GCN is a spectral domain-based GNNs, GAT is a spatial domain-based GNNs, and it can adjust neighbor weights according to the characteristic attributes of nodes. In order to compare the performance between the spectral domain-based and spatial domain-based GNNs on the hyperlink prediction task, a hyperlink prediction method based on GAT is proposed. Through the experimental results, it can be found that to some extent, GCN performs better on the undirected hyperlink prediction task, and GAT performs better on the directed hyperlink prediction task.

4.5 Hyperparameter Sensitivity Analysis

This section analyzes the influence of the hidden-layer size and the number of GAT heads on the experimental results in this article.

As shown in the line chart of Fig. 6, the influence of the hidden-layer size on the results of the proposed undirected and directed hyperlink prediction methods is shown on the iJO1366 and USPTO datasets, where the abscissa indicates the hidden-layer size and the ordinate indicates the AUC values. From Fig. 6, it can be found that although the AUC values decrease for a short duration when hidden size = 16, the overall trend is upward. In particular, when the hidden size = 512, the AUC values of DGCN-maxminD and DGAT-maxminD on the iJO1366 dataset reach steady state, and UGCN-maxmin, UGAT-maxmin and DGCN-maxminD show a moderate uptrend on the USPTO dataset. Therefore, the experimental results when hidden size = 512 are selected as the final experimental results of the proposed methods.

Fig. 6
figure 6

Influence of the hidden-layer size on the experimental results

Full size image

As shown in the thermodynamic chart of Fig. 7, the influence of the number of GAT heads on the results of the proposed UGAT and DGAT methods on the iJO1366 and iAF1260b datasets are presented. As shown in Fig. 7a, on the iJO1366 dataset, except for UGAT-maxmin which has different AUC results when the number of heads is different, the AUC results of the other three methods are basically equal. As shown in Fig. 7b, it can be found that these methods have the best AUC results when the number of GAT heads is equal to 4. Therefore, based on the above comparison, the results when GAT heads are equal to 4 are comprehensively selected as the final results.

Fig. 7
figure 7

Influence of the number of GAT heads on the results of the proposed UGAT and DGAT methods

Full size image

4.6 Time Complexity Analysis

As shown in Tables 7, 8, 9 and 10, the running time of the proposed methods are compared with the NHP algorithm on the iJO1366, iAF1260b and USPTO datasets. It can be found that the running time of the proposed UGCN and DGCN is lower than that of the NHP-U and NHP-D methods, whether using mean function or maxmin function to aggregate hyperedge feature information, and by comparing the experimental results in Tables 3, 4, 5 and 6, the prediction results of the proposed UGCN and DGCN are better than other algorithms, which indicates that the proposed UGCN and DGCN can predict hyperlinks efficiency with relatively low time complexity. Because the two-layer GAT is used in this article, and the first layer of GAT is 4-head, the running time of the proposed UGAT and DGAT methods is relatively higher than that of the NHP-U and NHP-D methods. However, compared with the NHP-U and NHP-D methods, the hyperlink prediction performance of the UGAT and DGAT methods has got a maximum improvement of 33%. Hence, it can be shown that the proposed methods can predict hyperlinks effectively.

Table 7 Comparison of running time of undirected hyperlink prediction using the mean function to aggregate hyperedge features
Full size table
Table 8 Comparison of running time of undirected hyperlink prediction using the maxmin function to aggregate hyperedge features
Full size table
Table 9 Comparison of running time of directed hyperlink prediction using the mean function to aggregate hyperedge features
Full size table
Table 10 Comparison of running time of undirected hyperlink prediction using the maxminD function to aggregate hyperedge features
Full size table

5 Conclusion

Hyperlink prediction is an important topic to explore the evolution of higher-order structures. GNNs can effectively extract graph data information, so a GNNs-based hyperlink prediction framework is proposed from the perspective of graph neural networks. We utilize this framework to propose two hyperlink prediction methods, GCN-based hyperlink prediction and GAT-based hyperlink prediction, respectively, and extend these two methods to predict directed hyperlinks. In this article, firstly, two-layer GCN and two-layer GAT are used to propagate the feature vector information of nodes in hyperlinks. Secondly, the hyperedge information is aggregated utilizing the updated node feature vector information. And then the scoring function is used to score the hyperlinks and the direction of the hyperlinks, Finally, through extensive experimental analysis, the any size of hyperlinks can be predicted by the proposed methods without the need of candidate hyperlink sets, and the hyperlinks can be efficiently predicted with relatively low time complexity. GCN is a spectral domain-based GNNs, GAT is a spatial domain-based GNNs. GCN and GAT focus on the influence of neighboring nodes on the central node, which can enhance the ability of models to perceive the neighborhood, thereby strengthening the joint spatial representation ability of models. It can also be found from the experimental results that GCN performs better on the undirected hyperlink prediction task, and GAT performs better on the directed hyperlink prediction task to some extent.

However, there are two problems with the two proposed methods. On the one hand, although the prediction performance of these two proposed methods is excellent, they lack interpretability, on the other hand, they do not consider the temporal information. Causal inference is a strong and effective tool in terms of interpretability. The hyperedges formed at different times are different in terms of the time series. Therefore, in the next work, we will tend to do research on explainable hyperlink prediction research while considering the factor of time.