Comparing quantum and classical machine learning for Vector Boson Scattering background reduction at the Large Hadron Collider

Abstract

We report on a consistent comparison between techniques of quantum and classical machine learning applied to the classification of signal and background events for the Vector Boson Scattering processes, studied at the Large Hadron Collider installed at the CERN laboratory. Quantum machine learning algorithms based on variational quantum circuits are run on freely available quantum computing hardware, showing very good performances as compared to deep neural networks run on classical computing facilities. In particular, we show that such kind of quantum neural networks is able to correctly classify the targeted signal with an Area Under the characteristic Curve (AUC) that is very close to the one obtained with the corresponding classical neural network, but employing a much lower number of resources, as well as less variable data in the training set. Albeit giving a proof-of-principle demonstration with limited quantum computing resources, this work represents one of the first steps towards the use of near term and noisy quantum hardware for practical event classification in High Energy Physics experiments.

1 Introduction

The Vector Boson Scattering (VBS) process (Anders et al. 2018; Covarelli et al. 2021) is one of the rarest occurrences stemming from the collision of the proton beams accelerated in the Large Hadron Collider (LHC) at the CERN laboratory in Genève. At the same time, it provides a unique test-bed to investigate the electro-weak sector of the Standard Model of particle physics, as for the scattering to be unitary it is necessary to invoke the presence of a spontaneous symmetry breaking, the mechanism theoretically originating the Higgs boson. Therefore, a precise measurement of the VBS will play a crucial role in the years to come at the LHC, as well as at its high-luminosity extension (HL-LHC). Here, the longitudinal component of the interaction will hopefully be statistically accessible (Ballestrero et al. 2018; CMS 2016). The specific process under investigation can be sketched with a generic Feynman diagram, as represented in Fig. 1. It is quite obvious from the representation that several particles are produced in the collision and originate from different sources in the kinematics of the process. Considering also that such a scattering event has a low probability to occur, it is evident that the data sets collected at the LHC by the ATLAS and CMS collaborations are and will be inevitably contaminated by a huge amount of events mimicking the signal of interest. It becomes crucial, then, to develop suitable methods to reduce the influence of background events that hinder the visibility of the VBS of interest. To this end, classical machine learning (ML) algorithms have been developed over the years allowing to perform trained event classification in high energy physics (Carleo et al. 2019). In particular, deep learning techniques have been applied to the problem of kinematic reconstruction for polarization discrimination in VBS (Grossi et al. 2020).

Fig. 1

A leading-order representation of the VBS between two generic vector bosons ($V_1$ and $V_2$) given in terms of Feynman diagrams; each boson is irradiated from a quark of one of the two protons participating in a LHC collision (the three valence quarks of each proton are represented as horizontal lines). The products are leptons (neutrinos, muons, electrons or tau particles) and quark jets. The two irradiating quarks ($q_3$ and $q_4$) get detected, while the remnant of each proton is lost in the LHC beam pipe

A new computational paradigm has been recently advancing, based on the merging of quantum computing and machine learning, namely Quantum Machine Learning (QML) (Biamonte et al. 2017). Initially thought as a theoretical playground, mostly inspired by the original proposals of simulating quantum physics with quantum mechanical devices (Feynman 1982), quantum computing has more recently become a reality thanks to fast progress in different technological platforms, which has allowed to realize working prototypes of programmable quantum processing units based on either superconducting circuits or trapped ions (Tacchino et al. 2020). In this context, the logical unit of information is the quantum bit (qubit), i.e., a quantum system with two internal basis states in which information can be encoded in an arbitrary superposition of the two, while operations are reduced to elementary single and two-qubit quantum gates (Nielsen and Chuang 2001). These computing machines allow to envision strong computational advantages over the classical paradigms of information processing. However, currently available quantum computers are limited in the number of qubits, as well as in the maximum number of allowed operations, due to the noisy character of the processing units (Moll et al. 2018). Nevertheless, even before fully fault tolerant quantum computation is developed,¹ the first use cases employing the so-called Noisy-Intermediate Scale Quantum (NISQ) computers (Preskill 2018) have started to be applied in various fields. In particular, applications of quantum machine learning to High Energy Physics have been proposed as one of the most promising playgrounds for such NISQ devices (Guan et al. 2021), and the first use cases have already been put forward (Terashi et al. 2021; Wu et al. 2021a, b).

In this work we report the first QML study of the VBS, specifically meant for the background reduction. We show a systematic comparison between the performances of classical deep learning algorithms and modern quantum neural networks developed on purpose for the present classification task. For the latter, we have performed numerical simulations employing the qasm_simulator of the IBM Quantum Experience,² as well as actual quantum computing runs launched on the ibmq_athens quantum device freely accessible through the cloud.³ Our study shows that available NISQ devices already reach performances comparable to classical ML computations, with the aim of discriminating the relevant signal from the unwanted noise in a large data set such as the one emerging from the LHC.

2 Methods

2.1 Simulation of VBS scattering events

In order to meaningfully benchmark the performances of the QML algorithm, we have performed a comparative study with a classical ML algorithm suitably trained on the same input data sets. The systematic study has been carried out on a set of simulated LHC collisions, as acquired from the CMS detector (Collaboration CMS et al. 2008): the VBS signal has been produced at leading order with the MadGraph5_aMC@NLO matrix-element Monte Carlo generator (Alwall et al. 2014), version 2.4.2. Non-perturbative effects such as parton showering and the underlying event have been simulated with the Pythia8 software (Sjöstrand et al. 2015), and minimum-bias pile-up events have been overlapped with a frequency comparable to the one expected during the LHC Run 2 of data taking. The simulation of the detector behavior is performed with a dedicated description of the CMS apparatus in the Geant4 package (Agostinelli et al. 2003). The backgrounds are simulated using Phantom and Madgraph. The largest contribution to the background comes from W+jets that consist in the production of a W boson in association with jets of particles initiated by quarks or gluons. Other minor background events were included as well, two vector bosons (VV), three vector bosons (VVV), Drell-Yan, single top and $t\bar{t}$, Vector Boson Fusion (VBF), vector boson with a real (V$\gamma$) or vitual (V$\gamma ^*$) photon (Tumasyan A et al. 2022).

The components of each event of interest are reconstructed with the software developed by the CMS Collaboration (Sirunyan et al. 2017), yielding electrons (Khachatryan et al. 2015), muons (Sirunyan et al. 2018), jets (Cacciari et al. 2012, 2008), and missing transverse energy. In the same software, the pile-up is subtracted as much as possible (Bertolini et al. 2014), the detector response is calibrated (Khachatryan et al. 2017), and jets classified according to their characteristics (Sirunyan et al. 2018; Thaler and Van Tilburg 2011; Larkoski et al. 2014; CMS 2013). Then, each event is characterized by a set of variables describing the VBS topology as well as the properties and kinematics of the final state particles. These features may at a first approximation be grouped in different categories, depending on whether they describe the features of each of the vector boson decays, or those of the two so-called tag-jets ($q_3$ and $q_4$ in Fig. 1), which are used to identify generic VBS-like topologies.

2.2 Classical ML analysis

Deep Neural Network (DNN) models have been trained to discriminate the signal from the background events in the VBS sample. The discriminator architecture consists of a feed forward neural network with $N_{l}$ hidden layers, having $N_{n}$ nodes each, connected to a single node output. The ReLu (Agarap 2019) activation function, defined as $\text {ReLu}(x>0) = x, \; \text {ReLu}(x\le 0) = 0$, is used for the hidden layers, and the sigmoid, $\sigma (x) =1 / (1+e^{-x})$, for the output node. For the results presented in this work, all the models have been optimized by minimizing the binary cross-entropy loss with the stochastic gradient descent technique, implemented with the Adam optimizer (Kingma and Ba 2014). Among the possible choices for classical ML algorithms to be employed as a benchmark, we opted for the most commonly chosen approach within the CMS collaboration, which is particularly suited in this case owing to the significant amount of jets and complicated variables set to be handled, for which DNNs turn out to be an optimal choice thanks to their expressivity.

The choice of the DNN input variables is implemented with an a posteriori optimization. Firstly, a model is trained with a large subset of the available variables. Then, a technique called SHAP (SHapley Additive exPlanations) (Lundberg and Lee 2017; Shapley 1953), developed in the field of explainable machine learning, is applied to rank the average contribution of each input variable to the discrimination power of the model. The variables of least impact are removed, and the procedure is repeated until a further reduction in the number of inputs worsens the model performance. This procedure is made possible by the fast and computationally cheap training procedure of simple DNNs. Among the most important variables, as identified by the SHAP technique and matching the physics expectations, are the $m_{jj}^{VBS}$ variable, the Zeppenfeld variable (Rainwater et al. 1996) of the lepton, and the number of jets in the event.

As an added information on the model complexity, we hereby mention the number of weights used in the DNN training, which is related to the number of nodes and layers. In our models the number of nodes ranged from around 5000 to 50,000. Hence, the runtime ranges from few milliseconds to few seconds on the available hardware (tests taken in February 2021). Further details are given in Appendix A.

Fig. 2

One-dimensional plot of the selected variables for the Variational Quantum Circuit

2.3 QML algorithm

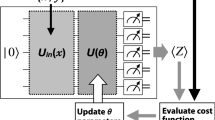
In gate-based quantum computers, such as the ones realized with superconducting qubits or ion traps, a computation is described by a quantum circuit representation that explicitly reports the single- and two-qubit operations. Different quantum computing learning models have been proposed, most of them mimicking the functionalities of artificial neural networks (Mangini et al. 2021). Among the different approaches, hybrid quantum-classical classifiers based on the kernel method, so-called quantum support vector machines (Schuld and Killoran 2019; Havlíček et al. 2019), have been successfully applied to differentiate signal and background events for the Higgs boson (Wu et al. 2021a, b). Here we rather exploit the general concept of Parametrized Quantum Circuits (PQC) as an effective model for a quantum neural network, similarly in spirit to a previous QML application in HEP (Terashi et al. 2021). In particular, the quantum algorithm used in this work is based on a variational quantum algorithm (McClean et al. 2016; Moll et al. 2018), belonging to the more general class of PQC (Benedetti et al. 2019), in which the algorithm is a function of a set of parameters (typically, rotation angles in single-qubit gates) to be optimized by classical minimization procedures, such as gradient descent-based learning.

The quantum circuits employed in this work are run on registers containing up to 5 qubits, depending on the available data set. Each qubit is associated to a variable describing the events under examination, selecting for each configuration the set of variables with the largest separating power between signal and background based on a cross-entropy test of each variable distribution (see Ref. Nielsen and Chuang (2001), Chapt. 11). Within the set of variables, the best five selected after the cross-entropy test are, respectively: (i) the invariant mass of the VBS jets pair, (ii) the energy of the leading VBS jet, i.e., the jet with the largest transverse momentum ($p_T$) among the two VBS jets, (iii) the transverse momentum of the leading VBS jet, (iv) the transverse momentum of the hadronic W boson, (v) the energy of the trailing VBS jet, i.e., the jet with the lowest P_T among the two VBS jets. In Fig. 2 we show the one-dimensional distributions of these variables. While the VBS topology is well represented by this choice, none of the selected variables contains information related to the detailed leptonic kinematics. As a possible extension of the present work, it would be interesting to include some of these excluded variables, employing more qubits in the register.

Fig. 3

(a) Global structure of the PQC built for the case of three input variables: starting from the idle configuration of the three qubits $q_{0,1,2}$ of the register (i.e., initialized in the state $|\Psi _0\rangle =|0\rangle ^{\otimes 3}$), represented by three horizontal lines, input variables $\textbf{x}$ are encoded in the quantum state through the $U_{map}$ operation. The latter is explicitly shown in (b), while variational parameters $\textbf{w}$ are given through the $U_{var}$ operation, explicitly shown in (c), in which $R_i(\textbf{w})$, with $i=x,y,z$, represent single-qubit rotations around a Cartesian axis in the Bloch sphere representation. Results are obtained through measurements of the qubits on the $\sigma _z$ basis, and saved as bits of information (i.e., 0 or 1) on a classical register, $c_{0,1}$, as represented in (a) for the first two qubits, $q_0$ and $q_1$. The entangling operation employed, $U_{ent}$, is a combination of Hadamard (H) and CNOT gates, as explicitly shown in (d) for the case of three qubits, and then generalized for larger registers

Fig. 4

Results from (a) classical DNN and (b) QML classification methods, respectively, reporting the AUC as a function of the number of variables associated to each event. Each classical result has been obtained varying the DNN architecture. Differently, the results corresponding to any fixed number of variables concern the same quantum circuit that was trained and tested different times. The best performance associated to each quantum circuit is explicitly highlighted in the plot

An example of the main structure of the whole PQC employed in this work is represented in Fig. 3a, specifically shown for the case of three input variables (i.e., three qubits used for the variables encoding). The input variables (i.e, the vector $\textbf{x}$ of elements $x_i$) are encoded into the quantum register through the unitary operation $U_{map}$, represented in Fig. 3b. The variational part of the algorithm is given by the operator $U_{var}({\textbf {w}})$, represented in Fig. 3c for completeness. These unitary operations are decomposed into basic elements, i.e., a combination of quantum gates that change the quantum state of each qubit (Nielsen and Chuang 2001). Single-qubit rotations are represented as $R_i (w)$ operations, for $i=x,y,z$ (e.g., a rotation by an angle $w_1$ around z is $R_z(w_1)$). Entangling operations, which allow to physically correlate different qubits, depend on the specific quantum hardware employed. In our case, the controlled-NOT (CNOT) gate (Nielsen and Chuang 2001) is the native entangling operation available on the IBM Quantum computers, and the corresponding unitary operation is generically indicated as $U_{ent}$, which is explicitly represented in Fig. 3d. Thanks to this entangling operation in the general circuit of Fig. 3a, the third qubit ($q_2$) affects the computation outcome even without being directly measured. We notice that the choice of qubit rotations used to give the input values to the circuit (Fig. 3c) was aimed at capturing any difference between signal and background probability density functions. Hence, the circuit behavior depends on the set of parameters $\textbf{w}$, which are updated during the training process, aimed at minimizing a loss function tuned to the circuit configuration to optimally discriminate the signal from background events. As an example, in a quantum circuit with two qubits, $q_0$ and $q_1$, the final values of their measurements, $z_0$ and $z_1$ (with values 0 or 1), are averaged 8192 times (which is the maximum allowed with the available quantum computing devices) to yield $\bar{z_0}$ and $\bar{z_1}$. These are then normalized by making use of the softmax function:

$$\begin{aligned} p_{signal}&\equiv {e^{\bar{z_0}}}/(e^{\bar{z_0}}+e^{\bar{z_1}})~, \\ p_{background}&\equiv {e^{\bar{z_1}}}/(e^{\bar{z_0}}+e^{\bar{z_1}})~. \end{aligned}$$

Fig. 5

Plot of the ROC curve (red line) whose associated AUC is the best ever obtained from QML training, as compared to the best ROC curve obtained from DNN training (green) and to the coin-flip curve (blue line)

Fig. 6

Results from (a) classical DNN and (b) QML classification methods, respectively, quantified using the AUC and obtained with different number of events during the training phase. Each color is associated to a different structure of the classical DNN or the QML approach. The best performance associated to each quantum circuit is explicitly highlighted in the plot

The latters are interpreted as the probability for each event to be of type signal or background respectively. To obtain the optimal parameters, $\textbf{w}_{\text {best}}$, the loss function is built as the distance between the output function $p_{signal}$ and the ideal classifier, whose evaluations give 1 for signal events and 0 for background events, based on the Kullback–Leibler (KL) divergence (S. Kullback 1951). For a generic number N of qubits, the variables are coupled starting from the previously established ordering. Namely, the variables mapped on qubits $q_0$ and $q_1$ are coupled, as well as the ones mapped on qubits $q_2$ and $q_3$, and so on. If N is an odd number, the last qubit is just not taken into account. Then, the same procedure described for the two-qubit case was applied on each pair of qubits, obtaining N $\textrm{mod}$ 2 results, which were analyzed with a weighted average, using the cross-entropy of the variables in each pair as weights.

The loss function minimization was performed with the Simultaneous Perturbation Stochastic Approximation (SPSA) algorithm (Spall 2012), since it conjugates fast performances (since the loss function is evaluated only twice per iteration) with stability against quantum errors (Spall et al. 1992). An example of the loss function minimization process for the PQC is explicitly reported in Fig. 7 in Appendix C.

3 Results

Both classical and quantum ML algorithm performances have been evaluated with two different tests, their efficiencies being quantified by use of the Area Under the Receiving Operating Characteristic (ROC) Curve (AUC). Typically, a binary classifier attributes a value between 0 and 1 to each event; the events with an assigned value larger than a fixed threshold will be then classified as signal, while the others as background. The Receiver Operating characteristic Curve (ROC) is the graph representing the relation between the False Positive Rate (FPR), on the horizontal axis, and the True Positive Rate (TPR), on the vertical axis, for different values of the threshold. The latter quantities are defined as follows:

• FPR: estimated probability of a negative event to be classified as positive.

• TPR: estimated probability of a positive event to be correctly classified.

The threshold variation between 0 and 1 allows to determine the TPR associated with any value of FPR. Since for any fixed value of the FPR a better classification requires a greater TPR, the Area Under ROC Curve (AUC) can be adopted as an index for the overall classification efficiency. A classifier is often applied in contexts where a particularly low FPR, or a particularly high TPR, are required. In such cases, a more specific study should be performed, with the threshold varied over limited ranges of values. Since this is not the case, the AUC general character is actually preferable. Alternative figures of merit are reported in Appendix B, giving consistent results.

The first test consists in varying the number of variables used in the classification. First, in Fig. 4a we show the results obtained from a classical DNN training including $10^4$ training events with a number of variables associated to each event ranging between 2 and 5. We test different DNN architectures (number of layers and number of nodes) for each number of variables, and we obtain a limited spreading of results (excluding the 2 variables case), as it is clearly seen in the Figure.

For the QML case, the same task has been performed by varying the number of qubits from 2 to 5. The corresponding results obtained for the AUC, as well as the best AUC value, are reported in Fig. 4b. For each number of variables, the training procedure has been repeated 5 times in order to check the spreading of results due both to the stochastic nature of SPSA and to the errors of the NISQ hardware, starting from the same training data set of 400 events and acting on a testing set of 4000 independent events. Interestingly, the best QML results are quantitatively close to the DNN ones. In addition, for small variables number, in particular for $n=2$, the QML AUC is larger than the corresponding DNN one, indicating a better efficiency of QML algorithms. As an example, in Fig. 5 we explicitly show a plot of the false positive rate against the true positive rate: the blue line represents the coin-flip case, the red curve is the calculated ROC, i.e., the best one obtained during the tests with the QML algorithm (corresponding to the 5 variables best AUC in Fig. 4b), and the green curve is the best ROC obtained with the DNN (corresponding to the 5 variables best AUC in Fig. 6a).

While several other evaluations have been performed (not shown here), no general conclusion can be drawn from these results since the AUC is larger in the QML approach as compared to the DNN for $n=2$, but it is lower for $n=3$, which was consistently obtained in all the evaluations performed. However, it can be conjectured that the main source of fluctuations observed in the tests for small numbers of events might be attributed to the SPSA, since hardware errors are less relevant. The latter do not depend on the number of training events, in particular they are not reduced on increasing the size of the training set. While the training has been performed on a simulator, the actual classification tests were performed by using a real quantum device (ibmq_athens). This implies that the parameters used to run the circuit on a real quantum device are set to the values obtained by optimizing them to perform a classification using a quantum computer simulator, not the quantum hardware itself. Whenever possible, it might be preferable in the future to directly optimize the training parameters on the real quantum computing device used for an optimal classification.

The second test performed in the present study consists in varying the number of training events, while keeping the number of variables fixed at either 3 or 5. First, we show the results obtained with the DNN training, in Fig. 6a, for different number of variables and hidden layers in the DNN. We also performed the classical training on networks of different sizes, i.e., with 64 or 128 hidden nodes. The number of training events considered ranges from a few hundreds to about hundred thousands. It is quite evident that the AUC value decreases on decreasing number of events, especially below 1000. This is particularly true when considering the training with 5 variables, less evident for the one considering 3 of them.

For what concerns the quantum algorithm, everything has been kept equal to the first test except for the number of variables, now fixed to 3 or 5, and the number of training events is varied over the interval (100, 700) with values distributed as Chebyshev nodes, such that they could be easily interpolated. Results are reported in Fig. 6b. There is an evident spread of results in terms of number of training events, for a fixed number of variables. With classical ML, the variance of the results is much smaller as compared to its quantum version. Considering the best AUC values determined with the QML algorithm, we notice that the 3 qubits circuit shows an increased AUC on increasing number of training events. On the other hand, the results for the 5 qubit circuit seem to have a much weaker dependence on the whole training events number range considered. In our opinion, this is an indication that the model saturates for a smaller number of training events. Moreover, the best AUC value is obtained with this QML algorithm by using less than 500 events for training to have AUC$>0.75$ (with 5 qubits), while the corresponding DNN requires a few thousand events to saturate at its best value. The AUC values of the QML results, even if calculated under the same conditions (e.g., the same number of qubits or training events), are quite spread, because of the stochastic nature of QML.

In summary, the QML algorithms developed in this study shows comparable results to classical ML ones operating in similar conditions, while using a smaller number of events during the training. At the same time, with the number of training events fixed at a number of the order of a few hundred, the QML algorithm outperforms its classical counterpart.

4 Conclusion

We have reported on a systematic comparison between classical and quantum machine learning approaches applied to a signal and background classification problem example from the collider physics domain, studying the Vector Boson Scattering processes. These kinds of interactions, occurring as a consequence of proton-proton collisions at the LHC, are a relevant benchmark of deep learning models because of the high multiplicity of particles produced with respect to other processes observed at particle colliders, and because of the overwhelming background they are usually mixed with. We have shown that a hybrid quantum-classical approach based on parametrized quantum circuits is able to reach performances similar to classically trained deep neural networks. As a relevant figure of merit we considered the area under the receiving operating characteristic curve, in relation to 5 kinematic variables simulated for the VBS process, suitably chosen to best describe all features of the elementary particles collision. The samples used have been generated with a realistic simulation based on Monte Carlo generators, including non-perturbative effects and a description of the detectors behavior. As a conclusion of the study, it has been shown that the QML algorithm requires a limited number of variables to be successfully trained, still giving good classification performances as compared to the fully classical approach. Hence, this hybrid algorithm can be envisioned for actual applications to the problem of HEP events classification already at the level of current noisy quantum hardware.

Appendices

Appendix A: Running time

The running complexity of a classical DNN can be measured in terms of the number of its parameters, which depends on the number of hidden layers and nodes for each layer. For example, in the models used for this study the number of parameters ranges from 65 (1 hidden layer, 16 nodes, 2 input features), to 50,433 (4 layers, 128 nodes, 5 input features). The running time of these models is negligible both on CPU and on GPU accelerators. Moreover, several independent events can be evaluated in parallel with batching to even decrease the time needed per event.

For what concerns the quantum algorithm, the quantum machine used is shared between IBMQ users through cloud quantum computing. This implies waiting lists whose duration strongly depends on the actual access to the cloud in a given moment. For this reason, we believe the running time is not a very significant parameter to characterize the quantum circuit. Instead, it is more relevant to quantify the number of single- ($n_S$) and two-qubit (i.e., CNOT) gates ($n_{CNOT}$) composing the parametrized quantum circuit. In the following, such numbers are estimated as a function of the number of variables ($n_{var}$).

$$\begin{aligned} n_{S} = 8 \cdot n_{var} + 2 \cdot \left( n_{var} \,\textrm{mod} \,2 \right) \end{aligned}$$

$$\begin{aligned} n_{CNOT} = n_{var} + 6 \cdot \left( n_{var} \,\textrm{mod} \,2 \right) \end{aligned}$$

Fig. 7

Loss function evaluated for a 5 qubits quantum circuit

Appendix B: Classification accuracy: figures of merit

Here we report a comparison between the best performing PQC and classical DNN, by explicitly showing the following figures of merit: accuracy rate, recall, precision, and F1 score. The values obtained for the two best algorithms are reported for both quantum and classical learning procedures in the Table, with the threshold fixed in order to set $FPR = 0.5$ in both cases. It is possible to give an explicit definition of these quantities starting from the following items

Index	DNN (5 variables, 3 layers, 32 nodes, $10^{3}$ training events)	PQC (5 variables, 400 training events)
Accuracy rate	0.67	0.66
Recall	0.84	0.81
Precision	0.63	0.62
F1 score	0.72	0.70

• Positive (P): number of signal events;

• Negative (N): background events;

• True Positive (TP): number of correctly classified signal events;

• True Negative (TN): number of correctly classified background events;

• False positive (FP): number of incorrectly classified background events;

• False Negative (FN): number of incorrectly classified signal events.

Then:

$$\begin{aligned} \mathrm {Accuracy\,rate}= & {} \frac{TP+TN}{P+N}\end{aligned}$$

(1)

$$\begin{aligned} \textrm{Recall}= & {} \frac{TP}{P}\end{aligned}$$

(2)

$$\begin{aligned} \textrm{Precision}= & {} \frac{TP}{TP+FP}\end{aligned}$$

(3)

$$\begin{aligned} \mathrm {F1\, score}= & {} \frac{2TP}{2TP+FP+FN} \end{aligned}$$

(4)

The values reported have been obtained from the testing data set. Overall, the QML accuracy is incredibly close to the classical DNN, in all the figures of merit considered, as a further confirmation of the main conclusions drawn in the present study.

Appendix C: Loss function for PQC

We hereby report an example of the training obtained from the loss function evaluation on a quantum circuit. We notice that, as the training process proceeds, the loss function value decreases until reaching a slowly converging plateau, which most probably corresponds to the best performance that can be reached from the quantum circuit. In fact, further application of the training procedure would not significantly improve the classification. The slow convergence towards zero means that even with an infinite training process this quantum circuit would not reach the performances of an ideal classifier.