Free vibration characteristics and wave propagation analysis in nonlocal functionally graded cylindrical nanoshell using wave-based method

Abstract

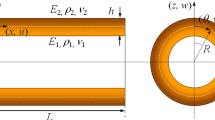
In this article, the free vibration characteristics and wave propagation analysis of functionally graded materials (FGM) cylindrical nanoshell is investigated by a semi-analytical method, wave-based method. The Eringen nonlocal theory and first-order shear deformation shell theory are adopted to establish the model of present systems. First, the calculation accuracy is verified which are compared with the solutions by the presented method with the results in the reported pieces of literature. Then, the free vibration characteristics concerning the nonlocal parameter, thickness to radius ratios, and length to radius ratios are derived, some parameter study examples are established, and some conclusions are obtained. Furthermore, the wave propagation characteristics related to the longitudinal wavenumber and circumferential wave number are proposed. Especially, the wave dispersion relations of wave frequency and phase velocity concerning the influence of nonlocal parameter, power-law exponent, thickness to radius ratios, and wavenumber in various directions are highlighted. The numerical examples conducted that these parameters have an important and obvious influence on the wave propagation characteristic for the wave frequency and phase velocity of nonlocal FGM cylindrical nanoshells.

Appendices

Appendix A

The detailed expression of the coefficients in Eq. (25) is shown as:

$$ \begin{array}{*{20}l} {L_{11} = A_{11} {\kern 1pt} \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{A_{66} }}{{R^{2} }}\frac{{\partial^{2} }}{{\partial \theta^{2} }},L_{12} = \frac{{A_{12} }}{R}\frac{{\partial^{2} }}{\partial x\partial \theta } + \frac{{A_{66} }}{R}\frac{{\partial^{2} }}{\partial x\partial \theta },L_{13} = \frac{{A_{12} }}{R}\frac{\partial }{\partial x}} \hfill \\ {L_{14} = B_{11} {\kern 1pt} \frac{{\partial^{2} }}{{\partial x^{2} }} + {\kern 1pt} \frac{{B_{66} }}{{R^{2} }}\frac{{\partial^{2} }}{{\partial \theta^{2} }},L_{15} = \frac{{B_{12} {\kern 1pt} }}{R}\frac{{\partial^{2} }}{\partial x\partial \theta } + \frac{{B_{66} }}{R}\frac{{\partial^{2} }}{\partial x\partial \theta },L_{21} = \frac{{\left( {A_{12} + A_{66} } \right)}}{R}\frac{{\partial^{2} }}{\partial x\partial \theta }} \hfill \\ {L_{22} = A_{66} {\kern 1pt} \frac{{\partial^{2} }}{{\partial x^{2} }} - \frac{{A_{11} }}{{R^{2} }}{\kern 1pt} \frac{{\partial^{2} }}{{\partial \theta^{2} }} - \frac{{K_{c} {\kern 1pt} A_{66} }}{{R^{2} }},L_{23} = \frac{{\left( {K_{{c{\kern 1pt} }} A_{66} + A_{11} } \right)}}{{R^{2} }}\frac{\partial }{\partial \theta }} \hfill \\ {L_{24} = \frac{{\left( {B_{66} + B_{12} } \right)}}{R}\frac{{\partial^{2} }}{\partial x\partial \theta },L_{25} = {\kern 1pt} \frac{{K_{c} {\kern 1pt} A_{66} }}{R} + \frac{{B_{11} }}{{R^{2} }}{\kern 1pt} \frac{{\partial^{2} }}{{\partial \theta^{2} }} + B_{{66{\kern 1pt} }} \frac{{\partial^{2} }}{{\partial x^{2} }}} \hfill \\ {L_{31} = - \frac{{A_{12} }}{R}\frac{\partial }{\partial x},L_{32} = \frac{{\left( { - K_{{c{\kern 1pt} }} A_{66} - A_{11} } \right)}}{{R^{2} }}\frac{\partial }{\partial \theta },L_{33} = - \frac{{A_{11} }}{{R^{2} }}{\kern 1pt} + \frac{{A_{66} {\kern 1pt} K_{c} }}{{R^{2} }}{\kern 1pt} \frac{{\partial^{2} }}{{\partial \theta^{2} }} + K_{c} {\kern 1pt} A_{66} \frac{{\partial^{2} }}{{\partial x^{2} }}} \hfill \\ {L_{34} = \left( {A_{66} {\kern 1pt} K_{c} {\kern 1pt} - \frac{{B_{12} }}{R}} \right)\frac{\partial }{\partial x},L_{35} = \left( {\frac{{A_{66} {\kern 1pt} K_{c} }}{R} - \frac{{B_{11} }}{{R^{2} }}} \right)\frac{\partial }{\partial \theta },L_{41} = B_{11} {\kern 1pt} \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{B_{66} }}{{R^{2} }}{\kern 1pt} \frac{{\partial^{2} }}{{\partial \theta^{2} }}} \hfill \\ {L_{42} = \frac{{\left( {B_{12} + B_{66} } \right)}}{R}\frac{{\partial^{2} }}{\partial x\partial \theta },L_{43} = \left( { - A_{66} {\kern 1pt} K_{c} {\kern 1pt} + \frac{{B_{12} }}{R}} \right)\frac{\partial }{\partial x},L_{44} = \frac{{D_{66} }}{{R^{2} }}{\kern 1pt} \frac{{\partial^{2} }}{{\partial \theta^{2} }} + D_{11} {\kern 1pt} \frac{{\partial^{2} }}{{\partial x^{2} }} - K_{c} {\kern 1pt} A_{66} {\kern 1pt} } \hfill \\ {L_{45} = \frac{{\left( {D_{12} + D_{66} } \right)}}{R}\frac{{\partial^{2} }}{\partial x\partial \theta },L_{51} = \frac{{\left( {B_{66} + B_{12} } \right)}}{R},L_{52} = \frac{{B_{22} }}{{R^{2} }}{\kern 1pt} \frac{{\partial^{2} }}{{\partial \theta^{2} }} + B{}_{66}{\kern 1pt} \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{K_{c} {\kern 1pt} A_{66} }}{R}} \hfill \\ {L_{53} = \left( {\frac{{ - A_{66} {\kern 1pt} K_{c} }}{R} + \frac{{B_{11} }}{{R^{2} }}} \right)\frac{\partial }{\partial \theta },L_{54} = \left( {\frac{{D_{12} + D_{66} }}{R}} \right)\frac{{\partial^{2} }}{\partial x\partial \theta },L_{55} = \frac{{D_{22} }}{{R^{2} }}{\kern 1pt} \frac{{\partial^{2} }}{{\partial \theta^{2} }} + D_{66} \frac{{\partial^{2} }}{{\partial x^{2} }} - {\kern 1pt} K_{c} {\kern 1pt} A_{66} } \hfill \\ \end{array} $$

The detailed expression of the coefficients in Eq. (27) is shown as:

$$ \begin{array}{*{20}l} {T_{11} = - k^{2} A_{11} - \frac{{n^{2} A_{66} }}{{R^{2} }}{\kern 1pt} + \omega^{2} I_{0} - \frac{{I_{0} {\kern 1pt} \omega^{2} \left( {R^{2} k^{2} + n^{2} } \right)}}{{R^{2} }},T_{12} = \frac{{ink\left( {A_{12} {\kern 1pt} + A_{66} {\kern 1pt} } \right)}}{R},T_{13} = \frac{{ikA_{12} {\kern 1pt} }}{R}} \hfill \\ {T_{14} = - k^{2} B_{11} {\kern 1pt} - \frac{{n^{2} B_{66} }}{{R^{2} }}{\kern 1pt} + \omega^{2} I_{1} - \frac{{I_{0} {\kern 1pt} \omega^{2} \left( {R^{2} k^{2} + n^{2} } \right)}}{{R^{2} }},T_{15} = \frac{{ink\left( {B_{12} + B_{66} } \right)}}{R}} \hfill \\ {T_{21} = \frac{{ink\left( {A_{12} + A_{66} } \right)}}{R},T_{22} = A_{66} k^{2} + {\kern 1pt} \frac{{n^{2} A_{11} }}{{R^{2} }} + \frac{{A_{66} {\kern 1pt} K_{c} }}{{R^{2} }}{\kern 1pt} - \omega^{2} I_{{0{\kern 1pt} }} { + }\frac{{I_{0} {\kern 1pt} \omega^{2} \left( {R^{2} k^{2} + n^{2} } \right)}}{{R^{2} }}} \hfill \\ {T_{23} = \frac{{nK_{{c{\kern 1pt} }} A_{66} + nA_{11} }}{{R^{2} }},T_{24} = \frac{{ink\left( {B_{12} {\kern 1pt} + B_{66} } \right)}}{R},T_{25} = B_{66} {\kern 1pt} k^{2} - \frac{{K_{c} {\kern 1pt} A_{66} }}{R}{\kern 1pt} + \frac{{n^{2} B_{11} }}{{R^{2} }} - \omega^{2} I_{1} { + }\frac{{I_{0} {\kern 1pt} \omega^{2} \left( {R^{2} k^{2} + n^{2} } \right)}}{{R^{2} }}} \hfill \\ {T_{31} = - \frac{{ikA_{12} }}{R},T_{32} = - {\kern 1pt} \frac{{nA_{11} }}{{R^{2} }} - \frac{{nA_{66} K_{{c{\kern 1pt} }} }}{{R^{2} }},T_{33} = - A_{{66{\kern 1pt} }} k^{2} K_{c} - \frac{{n^{2} A_{66} K_{{c{\kern 1pt} }} }}{{R^{2} }} - \frac{{A_{11} }}{{R^{2} }}{\kern 1pt} + I_{{0{\kern 1pt} }} \omega^{2} - \frac{{I_{0} {\kern 1pt} \omega^{2} \left( {R^{2} k^{2} + n^{2} } \right)}}{{R^{2} }}} \hfill \\ {T_{34} = ikA_{{66{\kern 1pt} }} K_{c} {\kern 1pt} - \frac{{ikB_{12} {\kern 1pt} }}{R},T_{35} = \frac{{nK_{c} {\kern 1pt} A_{66} }}{R} - \frac{{nB_{11} }}{{R^{2} }},T_{41} = k^{2} B_{11} + \frac{{n^{2} B_{66} }}{{R^{2} }} - I_{1} \omega^{2} { + }\frac{{I_{0} {\kern 1pt} \omega^{2} \left( {R^{2} k^{2} + n^{2} } \right)}}{{R^{2} }}} \hfill \\ {T_{42} = - \frac{{ink\left( {B_{{12{\kern 1pt} }} + B_{66} {\kern 1pt} } \right)}}{R},T_{43} = ikA_{66} {\kern 1pt} K_{c} {\kern 1pt} - \frac{{ikB_{12} }}{R},T_{44} = D_{11} k^{2} + A_{66} {\kern 1pt} K_{c} {\kern 1pt} + \frac{{n^{2} D_{66} }}{{R^{2} }}{\kern 1pt} - I_{2} \omega^{2} { + }\frac{{I_{0} {\kern 1pt} \omega^{2} \left( {R^{2} k^{2} + n^{2} } \right)}}{{R^{2} }}} \hfill \\ {T_{45} = - \frac{{ink{\kern 1pt} \left( {D_{12} + D_{66} } \right)}}{R},T_{51} = \frac{{ink\left( {B_{12} {\kern 1pt} + B_{66} {\kern 1pt} } \right)}}{R},T_{52} = k^{2} B_{{66{\kern 1pt} }} - {\kern 1pt} \frac{{A_{66} {\kern 1pt} K_{c} }}{R}{\kern 1pt} + \frac{{n^{2} B_{11} }}{{R^{2} }} - I_{1} \omega^{2} { + }\frac{{I_{0} {\kern 1pt} \omega^{2} \left( {R^{2} k^{2} + n^{2} } \right)}}{{R^{2} }}} \hfill \\ {T_{53} = \frac{{nB_{11} }}{{R^{2} }} - \frac{{nA_{{66{\kern 1pt} }} K_{c} }}{R},T_{54} = \frac{{ink\left( {D_{12} {\kern 1pt} + D_{66} } \right)}}{R},T_{55} = k^{2} {\kern 1pt} D_{66} + K_{c} {\kern 1pt} A_{66} + \frac{{n^{2} D_{11} }}{{R^{2} }}{\kern 1pt} - I_{2} w^{2} { + }\frac{{I_{0} {\kern 1pt} \omega^{2} \left( {R^{2} k^{2} + n^{2} } \right)}}{{R^{2} }}} \hfill \\ \end{array} $$

Appendix B

The detailed representation of the coefficients matrix in Eq. (29) is listed as:

$$ \begin{aligned} & \Delta_{\alpha } = \left| {\begin{array}{*{20}l} { - T_{13} } \hfill & {T_{12} } \hfill & {T_{14} } \hfill & {T_{15} } \hfill \\ { - T_{23} } \hfill & {T_{22} } \hfill & {T_{24} } \hfill & {T_{25} } \hfill \\ { - T_{43} } \hfill & {T_{42} } \hfill & {T_{44} } \hfill & {T_{45} } \hfill \\ { - T_{53} } \hfill & {T_{52} } \hfill & {T_{54} } \hfill & {T_{55} } \hfill \\ \end{array} } \right|_{{k_{n} = k_{n,ns} }} \quad \Delta_{\beta } = \left| {\begin{array}{*{20}l} {T_{11} } \hfill & { - T_{13} } \hfill & {T_{14} } \hfill & {T_{15} } \hfill \\ {T_{21} } \hfill & { - T_{23} } \hfill & {T_{24} } \hfill & {T_{25} } \hfill \\ {T_{41} } \hfill & { - T_{43} } \hfill & {T_{44} } \hfill & {T_{45} } \hfill \\ {T_{51} } \hfill & { - T_{53} } \hfill & {T_{54} } \hfill & {T_{55} } \hfill \\ \end{array} } \right|_{{k_{n} = k_{n,ns} }} \\ & \Delta_{\chi } = \left| {\begin{array}{*{20}l} {T_{11} } \hfill & {T_{12} } \hfill & { - T_{13} } \hfill & {T_{15} } \hfill \\ {T_{21} } \hfill & {T_{22} } \hfill & { - T_{23} } \hfill & {T_{25} } \hfill \\ {T_{41} } \hfill & {T_{42} } \hfill & { - T_{43} } \hfill & {T_{45} } \hfill \\ {T_{51} } \hfill & {T_{52} } \hfill & { - T_{53} } \hfill & {T_{55} } \hfill \\ \end{array} } \right|_{{k_{n} = k_{n,ns} }} \quad \Delta_{\delta } = \left| {\begin{array}{*{20}l} {T_{11} } \hfill & {T_{12} } \hfill & {T_{14} } \hfill & { - T_{13} } \hfill \\ {T_{21} } \hfill & {T_{22} } \hfill & {T_{24} } \hfill & { - T_{23} } \hfill \\ {T_{41} } \hfill & {T_{42} } \hfill & {T_{44} } \hfill & { - T_{43} } \hfill \\ {T_{51} } \hfill & {T_{52} } \hfill & {T_{54} } \hfill & { - T_{53} } \hfill \\ \end{array} } \right|_{{k_{n} = k_{n,ns} }} \\ \end{aligned} $$

$$ \Delta = \left| {\begin{array}{*{20}l} {T_{11} } \hfill & {T_{12} } \hfill & {T_{14} } \hfill & {T_{15} } \hfill \\ {T_{21} } \hfill & {T_{22} } \hfill & {T_{24} } \hfill & {T_{25} } \hfill \\ {T_{41} } \hfill & {T_{42} } \hfill & {T_{44} } \hfill & {T_{45} } \hfill \\ {T_{51} } \hfill & {T_{52} } \hfill & {T_{54} } \hfill & {T_{55} } \hfill \\ \end{array} } \right|_{{k_{n} = k_{n,ns} }} $$