Skip to main content
SpringerLink
Log in

Interval-valued q-rung orthopair fuzzy Aczel–Alsina operations-based Bonferroni mean aggregation operators and their applications

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

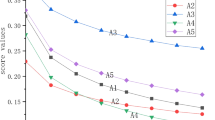
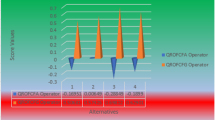
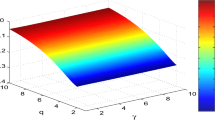
Abstract

As an extension of interval-valued intuitionistic fuzzy sets, the concept of interval-valued q-rung orthopair fuzzy (IVq-ROF) sets (IVq-ROFSs) represents an efficient tool for handling uncertain information in a more expansive context, owing to its utilization of the adjustable parameter \(\textit{q}\ge 1\). In the present article, we devise Aczel–Alsina (AA) operations to IVq-ROF numbers, employing the AA t-norm and t-conorm, and subsequently establish their inherent properties. Based on these operations, we originate a series of aggregation operators, including IVq-ROF AA weighted averaging (IVq-ROFAAWA) operator, IVq-ROF AA ordered weighted averaging (IVq-ROFAAOWA) operator, IVq-ROF AA hybrid averaging (IVq-ROFAAHA) operator, IVq-ROF AA weighted geometric (IVq-ROFAAWG) operator, IVq-ROF AA ordered weighted geometric (IVq-ROFAAOWG) operator, and IVq-ROF AA hybrid geometric (IVq-ROFAAHG) operator. Some required properties of the formulated operators are verified, and their interrelatedness is shown exhaustively. Meanwhile, we formulate the IVq-ROF weighted Bonferroni mean (IVq-ROFWBM) operator by leveraging AA operations, considering that the Bonferroni mean operator can capture the interrelationships among the input arguments. Based on these operators, a decision-making approach is framed for ranking the alternatives in the IVq-ROF environment. Further, we present an illustrative example concerning the distortion of the 2022 monsoon flood to showcase its practical applicability and to examine how various parameters impact the outcomes. Finally, the merits and originality of the presented methodology are underscored through a comprehensive comparison with prevailing approaches.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Data availability

No data sets have been used in this study.

References

  • Abbas F, Ali J, Mashwani WK, Syam MI (2023) q-rung orthopair fuzzy 2-tuple linguistic clustering algorithm and its applications to clustering analysis. Sci Rep 13(1):2789

    CAS  PubMed  PubMed Central  ADS  Google Scholar 

  • Aczél J, Alsina C (1982) Characterizations of some classes of quasilinear functions with applications to triangular norms and to synthesizing judgements. Aequ Math 25(1):313–315

    MathSciNet  Google Scholar 

  • Akram M, Sitara M (2022) Decision-making with q-rung orthopair fuzzy graph structures. Granul Comput 7(3):505–526

    Google Scholar 

  • Akram M, Bashir A, Edalatpanah S (2021) A hybrid decision-making analysis under complex q-rung picture fuzzy Einstein averaging operators. Comput Appl Math 40:305

    MathSciNet  Google Scholar 

  • Akram M, Shahzadi G, Alcantud JCR (2022) Multi-attribute decision-making with q-rung picture fuzzy information. Granul Comput 7:197–215

    Google Scholar 

  • Ali J (2023) Norm-based distance measure of q-rung orthopair fuzzy sets and its application in decision-making. Comput Appl Math 42(4):184

    MathSciNet  Google Scholar 

  • Ali J, Naeem M (2023) Multi-criteria decision-making method based on complex t-spherical fuzzy Aczel-Alsina aggregation operators and their application. Symmetry 15(1):85

    ADS  Google Scholar 

  • Alsina C, Schweizer B, Frank MJ (2006) Associative functions: triangular norms and copulas. World Scientific, Singapore

    Google Scholar 

  • Atanassov K (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96

    MathSciNet  Google Scholar 

  • Atanassov KT (1999) Interval valued intuitionistic fuzzy sets, in intuitionistic fuzzy sets. Springer, Berlin, pp 139–177

    Google Scholar 

  • Dombi J (1982) A general class of fuzzy operators, the De Morgan class of fuzzy operators and fuzziness measures induced by fuzzy operators. Fuzzy Sets Syst 8(2):149–163

    MathSciNet  Google Scholar 

  • Dutta B, Guha D (2015) Partitioned Bonferroni mean based on linguistic 2-tuple for dealing with multi-attribute group decision making. Appl Soft Comput 37:166–179

    Google Scholar 

  • Farahbod F, Eftekhari M (2012) Comparison of different t-norm operators in classification problems. arXiv preprint arXiv:1208.1955

  • Farid HMA, Riaz M (2021) Some generalized q-rung orthopair fuzzy Einstein interactive geometric aggregation operators with improved operational laws. Int J Intell Syst 36(12):7239–7273

    Google Scholar 

  • Gao J, Xu Z (2019) Differential calculus of interval-valued q-rung orthopair fuzzy functions and their applications. Int J Intell Syst 34(12):3190–3219

    Google Scholar 

  • Gao H, Ju Y, Zhang W, Ju D (2019) Multi-attribute decision-making method based on interval-valued \( q \)-rung orthopair fuzzy Archimedean Muirhead mean operators. IEEE Access 7:74300–74315

    Google Scholar 

  • Garg H (2017) A novel improved accuracy function for interval valued pythagorean fuzzy sets and its applications in the decision-making process. Int J Intell Syst 32(12):1247–1260

    Google Scholar 

  • Garg H (2019) Intuitionistic fuzzy Hamacher aggregation operators with entropy weight and their applications to multi-criteria decision-making problems. Iran J Sci Technol Trans Electr Eng 43(3):597–613

    Google Scholar 

  • Garg H (2021a) A new possibility degree measure for interval-valued q-rung orthopair fuzzy sets in decision-making. Int J Intell Syst 36(1):526–557

  • Garg H (2021b) New exponential operation laws and operators for interval-valued q-rung orthopair fuzzy sets in group decision making process. Neural Comput Appl 33(20):13937–13963

  • Garg H, Rani D (2022) An efficient intuitionistic fuzzy MULTIMOORA approach based on novel aggregation operators for the assessment of solid waste management techniques. Appl Intell 52(4):4330–4363

    Google Scholar 

  • Ghaleb AM, Kaid H, Alsamhan A, Mian SH, Hidri L (2020) Assessment and comparison of various MCDM approaches in the selection of manufacturing process. Adv Mater Sci Eng 2020:1–16

    Google Scholar 

  • Hussain A, Ullah K, Yang M-S, Pamucar D (2022) Aczel-Alsina aggregation operators on T-spherical fuzzy (T-SF) information with application to tsf multi-attribute decision making. IEEE Access 10:26011–26023

    Google Scholar 

  • Hussain A, Ullah K, Senapati T, Moslem S (2023) Complex spherical fuzzy Aczel Alsina aggregation operators and their application in assessment of electric cars. Heliyon 9(7):e18100

    PubMed  PubMed Central  Google Scholar 

  • Jabeen K, Khan Q, Ullah K, Senapati T, Moslem S (2023) An approach to MADM based on Aczel-Alsina power Bonferroni aggregation operators for q-rung orthopair fuzzy sets. IEEE Access. https://doi.org/10.1109/ACCESS.2023.3270267

    Article  Google Scholar 

  • Jana C, Senapati T, Pal M (2019a) Pythagorean fuzzy Dombi aggregation operators and its applications in multiple attribute decision-making. Int J Intell Syst 34(9):2019–2038

    Google Scholar 

  • Jana C, Muhiuddin G, Pal M (2019b) Some Dombi aggregation of q-rung orthopair fuzzy numbers in multiple-attribute decision making. Int J Intell Syst 34(12):3220–3240

    Google Scholar 

  • Jia X, Wang Y (2022) Choquet integral-based intuitionistic fuzzy arithmetic aggregation operators in multi-criteria decision-making. Expert Syst Appl 191:116242

    Google Scholar 

  • Jin C, Ran Y, Zhang G (2021) Interval-valued q-rung orthopair fuzzy fmea application to improve risk evaluation process of tool changing manipulator. Appl Soft Comput 104:107192

    Google Scholar 

  • Joshi BP, Singh A, Bhatt PK, Vaisla KS (2018) Interval valued q-rung orthopair fuzzy sets and their properties. J Intell Fuzzy Syst 35(5):5225–5230

    Google Scholar 

  • Ju Y, Luo C, Ma J, Gao H, Santibanez Gonzalez ED, Wang A (2019) Some interval-valued q-rung orthopair weighted averaging operators and their applications to multiple-attribute decision making. Int J Intell Syst 34(10):2584–2606

    Google Scholar 

  • Klement E, Mesiar R, Pap E (1997) Triangular norms. Tatra Mt Math Publ 13:169–193

    MathSciNet  Google Scholar 

  • Liang D, Darko AP, Xu Z, Quan W (2018) The linear assignment method for multicriteria group decision making based on interval-valued pythagorean fuzzy Bonferroni mean. Int J Intell Syst 33(11):2101–2138

    Google Scholar 

  • Liu P, Wang P (2018) Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. Int J Intell Syst 33(2):259–280

    Google Scholar 

  • Mahmood T, Rehman U, Ali Z (2023) Analysis and application of Aczel-Alsina aggregation operators based on bipolar complex fuzzy information in multiple attribute decision making. Inf Sci 619:817–833

    Google Scholar 

  • Mahnaz S, Ali J, Malik MA, Bashir Z (2021) T-spherical fuzzy Frank aggregation operators and their application to decision making with unknown weight information. IEEE Access 10:7408–7438

    Google Scholar 

  • Menger K (2003) Statistical metrics, in selecta mathematica. Springer, Berlin, pp 433–435

    Google Scholar 

  • Naeem M, Khan Y, Ashraf S, Weera W, Batool B (2022) A novel picture fuzzy Aczel-Alsina geometric aggregation information: application to determining the factors affecting mango crops. AIMS Math 7(7):12264–12288

    Google Scholar 

  • Peng X, Yang Y (2016) Fundamental properties of interval-valued pythagorean fuzzy aggregation operators. Int J Intell Syst 31(5):444–487

    Google Scholar 

  • Riaz M, Farid HMA, Karaaslan F, Hashmi MR (2020) Some q-rung orthopair fuzzy hybrid aggregation operators and TOPSIS method for multi-attribute decision-making. J Intell Fuzzy Syst 39(1):1227–1241

    Google Scholar 

  • Saha A, Senapati T, Yager RR (2021) Hybridizations of generalized Dombi operators and Bonferroni mean operators under dual probabilistic linguistic environment for group decision-making. Int J Intell Syst 36(11):6645–6679

    Google Scholar 

  • Seikh MR, Mandal U (2021) Intuitionistic fuzzy Dombi aggregation operators and their application to multiple attribute decision-making. Granul Comput 6(3):473–488

    Google Scholar 

  • Seker S, Bağlan FB, Aydin N, Deveci M, Ding W (2023) Risk assessment approach for analyzing risk factors to overcome pandemic using interval-valued q-rung orthopair fuzzy decision making method. Appl Soft Comput 132:109891

    PubMed  Google Scholar 

  • Senapati T (2022) Approaches to multi-attribute decision-making based on picture fuzzy Aczel-Alsina average aggregation operators. Comput Appl Math 41(1):40

    MathSciNet  Google Scholar 

  • Senapati T, Chen G, Yager RR (2022a) Aczel–Alsina aggregation operators and their application to intuitionistic fuzzy multiple attribute decision making. Int J Intell Syst 37(2):1529–1551

    Google Scholar 

  • Senapati T, Chen G, Mesiar R, Yager RR (2022b) Novel Aczel–Alsina operations-based interval-valued intuitionistic fuzzy aggregation operators and their applications in multiple attribute decision-making process. Int J Intell Syst 37(8):5059–5081

    Google Scholar 

  • Senapati T, Martínez L, Chen G (2023a) Selection of appropriate global partner for companies using q-rung orthopair fuzzy Aczel–Alsina average aggregation operators. Int J Fuzzy Syst 25(3):980–996

    Google Scholar 

  • Senapati T, Simic V, Saha A, Dobrodolac M, Rong Y, Tirkolaee EB (2023b) Intuitionistic fuzzy power Aczel–Alsina model for prioritization of sustainable transportation sharing practices. Eng Appl Artif Intell 119:105716

    Google Scholar 

  • Ullah K (2021) Picture fuzzy Maclaurin symmetric mean operators and their applications in solving multiattribute decision-making problems. Math Probl Eng 2021:1–31

    Google Scholar 

  • Wang W, Liu X (2011) Intuitionistic fuzzy geometric aggregation operators based on Einstein operations. Int J Intell Syst 26(11):1049–1075

    Google Scholar 

  • Wan B, Zhou S (2022) A integrating CRITIC-WASPAS group decision making method under interval-valued q-rung orthogonal fuzzy enviroment. arXiv preprint arXiv:2201.01027

  • Xing Y, Zhang R, Wang J, Zhu X (2018) Some new pythagorean fuzzy Choquet-Frank aggregation operators for multi-attribute decision making. Int J Intell Syst 33(11):2189–2215

    Google Scholar 

  • Xu Z, Chen Q (2011) A multi-criteria decision making procedure based on interval-valued intuitionistic fuzzy Bonferroni means. J Syst Sci Syst Eng 20(2):217–228

    Google Scholar 

  • Yager R (2013) Pythagorean fuzzy subsets. In: 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS)

  • Yager RR (2016) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25(5):1222–1230

    Google Scholar 

  • Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353

    Google Scholar 

  • Zedam L, Pehlivan NY, Ali Z, Mahmood T (2022) Novel Hamacher aggregation operators based on complex t-spherical fuzzy numbers for cleaner production evaluation in gold mines. Int J Fuzzy Syst 24(5):2333–2353

    Google Scholar 

  • Zhang Z (2017) Interval-valued intuitionistic fuzzy Frank aggregation operators and their applications to multiple attribute group decision making. Neural Comput Appl 28(6):1471–1501

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Numerical Sciences, Kohat University of Science and Technology, Kohat, KPK, Pakistan

    Jawad Ali & Wajid Rasool

Authors
  1. Jawad Ali
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wajid Rasool
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jawad Ali.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest regarding this study.

Additional information

Communicated by Junsheng Qiao.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ali, J., Rasool, W. Interval-valued q-rung orthopair fuzzy Aczel–Alsina operations-based Bonferroni mean aggregation operators and their applications. Comp. Appl. Math. 43, 7 (2024). https://doi.org/10.1007/s40314-023-02511-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-023-02511-7

Keywords

Search

Navigation