Closed-form pricing formulas for variance swaps in the Heston model with stochastic long-run mean of variance

Abstract

The Heston model is a popular stochastic volatility model in mathematical finance and it has been extended or modified in several ways by researchers to overcome the shortcomings of the model in the context of pricing derivatives. However, the extended models usually do not lead to a closed-form formula for the derivative prices. This paper is focused on a stochastic extension of the constant long-run mean of variance in the Heston model for the pricing of variance swaps. The extension is given by a positive function perturbed by an amplitude-modulated Brownian motion or Ito integral. We obtain two closed-form formulas for the fair strike prices of a variance swap under two corresponding underlying models. The formulas are explicitly given by elementary functions without any integral terms involved. Further, the two models show better performance than the Heston model when the market implied volatility has a concave-down pattern as shown in an unstable market circumstance caused by the COVID-19 pandemic.

1 Introduction

Volatility risk trading and management have been crucial issues more and more in financial market. In the past, volatility had been thought that it would be constant, for example, in the Black–Scholes world (1973). However, many evidences like volatility smile (Dumas et al. 1998) confirmed that the assumption would be false and it is prevailing that volatility also follows a stochastic process as risky assets do. Volatility has been recognized even as an asset now and trading volumes of financial derivatives related to volatility has increased rapidly. The classical methods to trade volatility are strangles or butterflies (cf. Hull 2009) which are composed of vanilla options. However, they have a drawback that their price could be affected by risks of other variables and it may lead to unsatisfactory hedges or speculations for market practitioners. So, volatility derivatives arose in the market. Variance swap is one of pure volatility derivatives and it is a forward contract that trades the spread between realized variance and strike $K_\text {var}$. The main advantage of variance swap is that it does not suffer from other risk exposures while traditional volatility trading strategies with options do. Refer to the book of Neftci (2008) for more details.

One of the most widely used stochastic volatility models is the Heston model (Heston 1993). The Heston model for underlying asset price $S_t$ and its variance $v_t$ is given by

$$\begin{aligned} \mathrm{d}S_t&=rS_t\mathrm{d}t+\sqrt{v_t}S_t \mathrm{d}W_t^1, \\ \mathrm{d}v_t&=\kappa (\theta -v_t)\mathrm{d}t + \sigma _v \sqrt{v_t}\mathrm{d}W_t^2 \end{aligned}$$

under a risk-neutral probability measure, where $W_t^1$ and $W_t^2$ are Brownian motions with $\mathrm{d}W_t^1 \mathrm{d}W_t^2=\rho \mathrm{d}t$, r is the risk-free rate, and $\kappa$, $\theta$ and $\sigma _v$ denote mean-reversion rate of variance, long-term mean of variance and volatility of variance (vol-of-vol), respectively, and they are all supposed to be positive. $\rho$ is correlation between the underlying asset and its variance process and it is assumed to be a constant between − 1 and 0. The Feller condition, $2\kappa \theta >\sigma _v^2$, is required. It is a sufficient condition for the variance to be always positive. There is a merit that an analytic form of the price formula for financial derivatives can be derived when the underlying dynamics is assumed to follow the Heston model. The reason is that the mean-reverting CIR process (Cox et al. 1985) of $v_t$ makes the characteristic function deduced by a partial differential equation related to the model be simple. There are lots of studies on variance swaps under the Heston model. For example, Swishchuk (2004) studied the pricing of volatility and variance swap by using a probabilistic approach. Broadie and Jain (2008) determined fair discrete and continuous variance strikes analytically. Zhu and Lian (2011) derived a closed-form solution for a discretely sampled variance swap with simple return using an additional variable introduced by Little and Pant (2001).

However, the Heston model has some weakness in that it may not fit well in market for short-term products and it may not give analytic solutions for SPX and VIX options prices simultaneously. It is true for all the single-factor stochastic volatility models. Thus the model have been extended or modified by researchers to overcome the shortcomings. For example, Zheng and Kwok (2014) extended the Heston model by adding simultaneous jumps and found closed form pricing formulas for exotic variance swaps. Elliott and Lian (2013) presented closed-form exact solutions for pricing discretely sampled variance and volatility swaps under the Heston model with regime switching. Kim and Kim (2020) obtained affine approximations for the generalized variance swaps based on the Heston model incorporated by stochastic interest rates by using the projection techniques of Grzelak and Oosterlee (2011). On the other hand, Christoffersen et al. (2009) proposed the so-called double Heston model, which has two different scale factors, for the fluctuation of the slope and the level of volatility smirk. Jeon et al. (2021) used a rescaled version of the double Heston model for consistent pricing SPX and VIX options. Fouque and Saporito (2018) proposed a multiscale volatility of volatility generalization of the Heston model and derived asymptotic solutions of SPX and VIX options using a perturbation theory. Also, there are some papers for pricing variance swaps based on the stochastic volatility models other than the Heston type models. For example, Yuen et al. (2015) derived quasi-closed form pricing formulas for the fair strike prices of exotic discrete variance swaps under the 3/2-stochastic volatility model. Kim and Kim (2019) used the moment generating function technique to find semi-analytic solutions for generalized variance swaps under the exponential Ornstein–Uhlenbeck (expOU) model and the double expOU model.

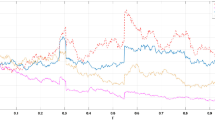
In this paper, we study the pricing of variance swaps under two stochastic volatility models extending the Heston model. First of all, we believe that the constant long-term mean level of variance in the Heston model does not reflect the time evolution of market volatility. Figure 1 presents the historical long-run variance calibrated from S &P 500 vanilla call and put options daily traded from 2013 to 2020 under the Heston model. The severely fluctuant part of the graph is due to the effect of COVID-19 pandemic. The figure clearly indicates that the long-run variance of the Heston model could not be considered as a constant. Simultaneously, we wish for a desired stochastic volatility model to maintain the analytical tractability of the Heston model for the pricing of variance swaps. So, based on stochastic long-run variance assumption, we adopt the model of He and Chen (2021) and a reduced version of the double mean-reverting model of Gatheral (2008). These are two-factor volatility models, where the long-term mean level of variance is given by a positive function perturbed by a small amplitude-modulated random process. A closed pricing formula for European options under the He–Chen model was derived as its characteristic function has a similar form to that of the Heston model. They exploited adaptive sample annealing (Ingber 1989) for empirical studies and showed their option pricing formula outperforms that of the Heston model. On the other hand, Gatheral’s double mean-reverting (DMR) model is also a two-factor volatility extension of the Heston model granting the mean-reverting property of the long-run variance. It has a strength that it fits both SPX and VIX option data well. See Bayer et al. (2013) for details. However, there is no closed-form formula for any types of financial derivatives yet under the original DMR model. Thus some researchers used a reduced version of the DMR model to find closed-form or approximate analytic solutions for the financial derivatives of their interest. For instance, Huh et al. (2018) presented closed-form approximate solutions for VIX derivatives under a rescaled version of the DMR model.

Fig. 1

Historical long-run variances calibrated from SPX vanilla options under the Heston model

In this paper, we obtain the fair strike value of discretely sampled variance swap under both the He–Chen model and a reduced version of the DMR model denoted by the rDMR model. All the adopted models have analytical tractability while they provide an improved performance on empirical data. To support these claims, the paper is organized as follows. The underlying models are specified in Sect. 2 and the fair strike value is given by a partial differential equation form in Sect. 3. Then we obtain the fair strike formulas of a discretely sampled variance swap under the two models in Sect. 4. Each formula is explicitly given by a closed-form solution expressed in terms of elementary functions (without any single integral involved). In Sect. 5, we check the validity of our formulas using Monte-Carlo simulation and investigate the sensitivity of the added parameters of the stochastic long-run variance process. Furthermore, the He–Chen model and the rDMR model are compared with the Heston model based on the VIX data in 2020.

2 Underlying dynamics

In this section, we describe two models, the He–Chen model and the rDMR model, whose long-run variance is driven by a stochastic process. First, the He–Chen model is given by

$$\begin{aligned} \mathrm{d}S_t&=rS_t\mathrm{d}t+\sqrt{v_t}S_t \mathrm{d}W_t^1, \nonumber \\ \mathrm{d}v_t&=\kappa (\theta _t-v_t)\mathrm{d}t + \sigma _v \sqrt{v_t}\mathrm{d}W_t^2, \nonumber \\ \mathrm{d}\theta _t&=\lambda \mathrm{d}t+\sigma _\theta \mathrm{d}W_t^3 \end{aligned}$$

(1)

under a risk-neutral probability measure, where $W_t^1$, $W_t^2$ and $W_t^3$ are standard Brownian motions with $\mathrm{d}W_t^1 \mathrm{d}W_t^2=\rho \mathrm{d}t$ and $\mathrm{d}W_t^1 \mathrm{d}W_t^3=\mathrm{d}W_t^2 \mathrm{d}W_t^3=0$. The parameters r, $\kappa$, $\sigma _v$ and $\lambda$ and the initial value $\theta _0$ of $\theta _t$ are non-negative constants. Here, $\sigma _{\theta }$ is assumed to be a small positive parameter so that $\theta _t$ can be a small perturbation around the non-negative function $\theta _0 + \lambda t$ in a weak (mean square) sense. Note that the model can be reduced to the Heston model when both $\lambda$ and $\sigma _\theta$ become zero.

On the other hand, the original DMR model is given by

$$\begin{aligned} \mathrm{d}S_t&=rS_t\mathrm{d}t+\sqrt{v_t}S_t \mathrm{d}W_t^1, \\ \mathrm{d}v_t&=\kappa (\theta _t-v_t)\mathrm{d}t + \sigma _v v_t^{\gamma _1}\mathrm{d}W_t^2, \\ \mathrm{d}\theta _t&=\alpha (\beta -\theta _t)\mathrm{d}t + \sigma _\theta \theta _t^{\gamma _2} \mathrm{d}W_t^3,\\ \mathrm{d}W_t^1 \mathrm{d}W_t^2&=\rho _{12} \mathrm{d}t, \quad \mathrm{d}W_t^1 \mathrm{d}W_t^3=\rho _{13}\mathrm{d}t, \quad \mathrm{d}W_t^2 \mathrm{d}W_t^3=\rho _{23}\mathrm{d}t \end{aligned}$$

under a risk-neutral probability measure, where r, $\kappa$, $\sigma _v$, $\sigma _{\theta }$, $\gamma _1$ and $\gamma _2$ are non-negative constants. $\alpha$ represents the mean reversion rate of $\theta _t$ and $\theta _t$ reverts to $\beta$ at the rate $\alpha$, where $\alpha <\kappa$ is assumed. This form of model could make it easy to catch the market movement effectively. However, it is onerous to find an analytic formula for the fair prices of derivatives because of the complexity of the model. So, to find an analytic solution for variance swaps, we reduce the DMR model to

$$\begin{aligned} \mathrm{d}S_t&=rS_t\mathrm{d}t+\sqrt{v_t}S_t \mathrm{d}W_t^1, \nonumber \\ \mathrm{d}v_t&=\kappa (\theta _t-v_t)\mathrm{d}t + \sigma _v \sqrt{v_t} \mathrm{d}W_t^2, \nonumber \\ \mathrm{d}\theta _t&=\alpha (\beta -\theta _t)\mathrm{d}t + \sigma _\theta \mathrm{d}W_t^3, \end{aligned}$$

(2)

which is called the rDMR model. Here, the initial value $\theta _0$ is assumed to be a non-negative constant. $\alpha$ and $\beta$ are non-negative parameters and $\sigma _{\theta }$ is a small positive parameter so that $\theta _t$ is a small perturbation around the non-negative function $\theta _0 \mathrm{e}^{-\alpha t}+\beta (1-\mathrm{e}^{-\alpha t})$. The difference between the original DMR model and the rDMR model is in the diffusion part of the variance $v_t$ and the long-term mean variance $\theta _t$ while the mean-reverting property of the original DMR model is still being kept. One can notice that the process $\theta _t$ is an Ornstein–Uhlenbeck process (Uhlenbeck and Ornstein 1930). The correlation structure $\mathrm{d}W_t^1 \mathrm{d}W_t^2=\rho \mathrm{d}t$ and $\mathrm{d}W_t^1 \mathrm{d}W_t^3=\mathrm{d}W_t^2 \mathrm{d}W_t^3=0$ is assumed to avoid the difficulty of obtaining an analytic solution formula for the fair strike of variance swaps while still keeping Heston’s correlation structure.

3 Problem formulation

Given the underlying asset price $S_t$, the discretely sampled realized variance of a variance swap over a time period [0, T] is defined by

$$\begin{aligned} \sigma ^2_{\text {RV}} = 100^{2}\times \frac{1}{T}\sum _{j=1}^N \left( \log \frac{S_{t_j}}{S_{t_{j-1}}}\right) ^{2}, \end{aligned}$$

(3)

where $\left[ 0,T\right]$ is divided into N periods of $[t_{j-1},t_{j}]$, $t_N=T$ and $j=1,\ldots ,N$. The fair strike, $K_{\text {var}}$, of the variance swap is given by the strike such that the expected value, under a risk-neutral probability measure, of the payoff $\sigma ^2_{\text {RV}}-K$ is equal to 0 at time $t=t_0=0$. Therefore, we have

$$\begin{aligned} K_{\text {var}}\left( t_{0},S_{t_{0}},v_{t_{0}},\theta _{t_{0}}\right)&={\mathbb {E}}^{0,*}\left[ \sigma _{\text {RV}}^{2}\right] =100^{2}\times \frac{1}{T}\sum _{j=1}^N {\mathbb {E}}^{0,*}\left( \log \frac{S_{t_j}}{S_{t_{j-1}}}\right) ^{2} \nonumber \\&=100^{2}\times \frac{1}{T}\sum _{j=1}^N {\mathbb {E}}^{0,*}\left[ {\mathbb {E}}^{t_{j-1},*}\left( \log \frac{S_{t_j}}{S_{t_{j-1}}}\right) ^{2}\right] , \end{aligned}$$

(4)

where the superscript $*$ denotes a risk-neutral probability measure. Here, the tower property of conditional expectation has been used. One could notice that the above realized variance is defined in terms of logarithmic return instead of simple return. The multi-period of simple return can be approximated by a product of the one-period simple returns, which may lead to a problem when the one-period values get close to zero. Meanwhile, the multi-period log return is a sum of the one-period log returns, being free of the computational problem. So, the preference for log return prevails in financial industry.

For convenience, let us use a new independent variable $I_t$, introduced by Little and Pant (2001), which is defined by

$$\begin{aligned} I_t=\int _0^t\delta \left( {t_{j-1}-s}\right) S_s \mathrm{d}s, \end{aligned}$$

where the $\delta (\cdot )$ means the generalized Dirac delta function. Note that $I_t=S_{t_{j-1}}$ if $t\ge t_{j-1}$ and $I_t=0$ if not.

Considering the time interval $[t_{j-1},t_j]$, let $U^j(t,S,v,\theta ;I)$ be the solution of the partial differential equation (PDE)

$$\begin{aligned}&\Bigg (\frac{\partial }{\partial t}+r S\frac{\partial }{\partial S}+\kappa (\theta -v)\frac{\partial }{\partial v}+\eta (\theta )\frac{\partial }{\partial \theta }+\frac{1}{2}S^2 v \frac{\partial ^2}{\partial S^2}+\frac{1}{2}\sigma _v^2 v \frac{\partial ^2}{\partial v^2} \nonumber \\&\quad +\frac{1}{2} \sigma _\theta ^2 \frac{\partial ^2}{\partial \theta ^2}+\rho \sigma _v v S \frac{\partial ^2}{\partial S \partial v}\Bigg )U^j=0 , \quad t_{j-1}\le t<t_{j}, \end{aligned}$$

(5)

with terminal condition $U^{j}(t,S,v,\theta ;I)|_{t=t_j}=\left( \log \frac{S_{t_j}}{I_{t_j}}\right) ^{2}$, where $\eta (\theta )$ is determined as $\eta (\theta )=\lambda$ under the He–Chen model and $\eta (\theta )=\alpha (\beta -\theta )$ under the rDMR model. Then, by applying the well-known Feynman-Kac theorem (cf. Oksendal 2000), we have

$$\begin{aligned} U^j\left( t_{j-1},S_{t_{j-1}},v_{t_{j-1}},\theta _{t_{j-1}};I_{t_{j}}\right) ={\mathbb {E}}^{t_{j-1},*}\left[ \left( \log \frac{S_{t_j}}{I_{t_j}}\right) ^{2}\right] . \end{aligned}$$

(6)

This is the value of the solution of (5) at time $t=t_{j-1}$. It is represented as a conditional expectation of the random variable $\left( \log \frac{S_{t_j}}{I_{t_j}}\right) ^2$ given the underlying value $S_{t_{j-1}}$ at time $t=t_{j-1}$.

The variable $I_t$ has a jump at each $t_{j-1}$ but the no-arbitrage pricing theory requires $U^{j}$ to be continuous (cf. Wilmott 2013). So, we have a jump condition expressed as

$$\begin{aligned} \lim _{t\ \uparrow \ t_{j-1}}^{ }U^j(t,S,v,\theta ;I)=\lim _{t\ \downarrow \ t_{j-1}}^{ }U^j(t,S,v,\theta ;I). \end{aligned}$$

(7)

Considering the time interval $[t_0,t_{j-1}]$ this time, let $W^j(t,S,v,\theta ;I)$ be the solution of the PDE

$$\begin{aligned}&\Big (\frac{\partial }{\partial t}+r S\frac{\partial }{\partial S}+\kappa (\theta -v)\frac{\partial }{\partial v}+\eta (\theta )\frac{\partial }{\partial \theta }+\frac{1}{2}S^2 v \frac{\partial ^2}{\partial S^2}+\frac{1}{2}\sigma _v^2 v \frac{\partial ^2}{\partial v^2} \nonumber \\&\quad +\frac{1}{2} \sigma _\theta ^2 \frac{\partial ^2}{\partial \theta ^2}+\rho \sigma _v v S \frac{\partial ^2}{\partial S \partial v}\Big )W^j=0, \qquad t_0 \le t < t_{j-1}, \end{aligned}$$

(8)

with terminal condition $W^{j}(t,S,v,\theta )|_{t=t_{j-1}}=U^{j}(t_{j-1},S,v,\theta ;S)$. Then the Feynman-Kac theorem gives

$$\begin{aligned} W^j(t_0,S_{t_0},v_{t_0},\theta _{t_0}) ={\mathbb {E}}^{0,*}\left[ U^{j}\left( t_{j-1},S_{t_{j-1}},v_{t_{j-1}},\theta _{t_{j-1}};S_{t_{j-1}}\right) \right] . \end{aligned}$$

(9)

Therefore, combining the above results (4), (6) and (9), the fair strike price (4) is expressed as

$$\begin{aligned} K_{\text {var}}(t_0,S_{t_0},v_{t_0},\theta _{t_0})=100^2\times \frac{1}{T}\sum _{j=1}^{N}W^j(t_0,S_{t_0},v_{t_0},\theta _{t_0}), \end{aligned}$$

(10)

where $W^j$ is given by the conditional expectation (9) and $U^{j}$ in (9) is given by the conditional expectation (6). So, to calculate the fair strike price $K_{\text {var}}$, we first need to solve the PDE problem (5) for $U^{j}$ (the inner expectation) and then compute the conditional expectation (9) (the outer expectation) for $W^{j}$.

4 Pricing variance swaps

In this section, we concretely solve the PDE problem (5) for the inner expectation $U^j$ for the He–Chen and rDMR models by using the Fourier transform and Green function methods. Then we calculate the outer expectation $W^{j}$ from the inner expectation result. The Fourier transform ${\hat{\phi }}$ of a given function $\phi$, which will be used from now on, is defined by

$$\begin{aligned} {\hat{\phi }}(\tau ,w,v,\theta ;I)=\int _{{\mathbb {R}}} \mathrm{e}^{-iwq} \phi (\tau ,q,v,\theta ;I)\mathrm{d}q. \end{aligned}$$

4.1 Preliminary results

Considering the payoff function $h(S;I)=\left( \log \frac{S}{I}\right) ^2$, using notation $\tau =t_{j}-t$ and $q=r\tau +\log (S)$ and taking the Fourier transform $\hat{U^j}$ of $U^j$, the PDE problem (5) becomes

$$\begin{aligned}&\Bigg (-\frac{\partial }{\partial \tau }+\kappa (\theta -v)\frac{\partial }{\partial v}+\eta (\theta )\frac{\partial }{\partial \theta }+\frac{1}{2} v^2 (-iw-w^2) \nonumber \\&\quad +\frac{1}{2}\sigma _v^2 v \frac{\partial ^2}{\partial v^2}+\frac{1}{2}\sigma _{\theta }^2\frac{\partial ^2}{\partial \theta ^2}+\rho \sigma _v iwv \frac{\partial }{\partial v}\Bigg )\hat{U^j}=0, \nonumber \\&\hat{U^j}(0,w,v,\theta ;I)={\hat{h}}(w;I), \quad 0<\tau \le t_{j}-t_{j-1}, \end{aligned}$$

(11)

where

$$\begin{aligned} {\hat{h}}(w;I)&:=\int _{{\mathbb {R}}} \mathrm{e}^{-iwq} h(\mathrm{e}^q;I)\mathrm{d}q. \end{aligned}$$

Let $G(\tau ,q,v,\theta ;I)$ be a function satisfying

$$\begin{aligned}&\Big (-\frac{\partial }{\partial \tau }+\kappa (\theta -v)\frac{\partial }{\partial v}+\eta (\theta )\frac{\partial }{\partial \theta }+\frac{1}{2} v^2 (-iw-w^2) \nonumber \\&\quad +\frac{1}{2}\sigma _v^2 v \frac{\partial ^2}{\partial v^2}+\frac{1}{2}\sigma _{\theta }^2\frac{\partial ^2}{\partial \theta ^2}+\rho \sigma _v iwv \frac{\partial }{\partial v}\Big ){\hat{G}}=0, \nonumber \\&G(0,w,v,\theta ;I)=\delta _0(q), \qquad 0<\tau \le t_{j}-t_{j-1}, \end{aligned}$$

(12)

where $\delta$ is the generalized Dirac-delta function. Then G is utilized as the Green function of (11). Following Heston’s procedure, we suppose that

$$\begin{aligned} {\hat{G}}(\tau ,w,v,\theta ;I)=\exp (A(\tau ,w)+vB(\tau ,w)+\theta C(\tau ,w)). \end{aligned}$$

(13)

Putting (13) into (12), one could get ordinary differential equations (ODEs) for $A(\tau ,w)$, $B(\tau ,w)$ and $C(\tau ,w)$. They will be obtained concretely for each of the He–Chen and rDMR models later. By the convolution property of Fourier transform, one can deduce

$$\begin{aligned} U^j(\tau ,q,v,\theta ;I)&=\frac{1}{2\pi }\int _{{\mathbb {R}}}\mathrm{e}^{iwq}{\hat{h}}(w;I){\hat{G}}(\tau ,w,v,\theta ;I)\mathrm{d}w. \end{aligned}$$

(14)

On the other hand, the Fourier transform of the payoff function h(S; I) can be expressed as

$$\begin{aligned} {\hat{h}}(w;I)=2\pi \left( -{\delta }_{0}''(w)-2i\left( \log I\right) {\delta }_{0}'(w)+\left( \log I \right) ^{2}{\delta }_{0}(w) \right) , \end{aligned}$$

where ${\delta }_{0}'(w)$ and ${\delta }_{0}''(w)$ are the first and second derivatives of Dirac delta function, respectively, defined in the sense of distribution and satisfy

$$\begin{aligned} {\delta }_{0}'(w)=\frac{-i}{2\pi }\int _{{\mathbb {R}}}q \mathrm{e}^{-iwq}\mathrm{d}q, \quad {\delta }_{0}''(w)=\frac{-1}{2\pi }\int _{{\mathbb {R}}}q^{2}\mathrm{e}^{-iwq}\mathrm{d}q, \end{aligned}$$

respectively. Therefore, from (13) and (14), one can deduce

$$\begin{aligned} U^j(\tau ,q,v,\theta ;I)&=\frac{1}{2\pi }\int _{{\mathbb {R}}}\mathrm{e}^{iwq}\cdot {\hat{h}}(w;I){\hat{G}}(\tau ,w,v,\theta ;I)\mathrm{d}w \nonumber \\&=\frac{1}{2\pi }\int _{{\mathbb {R}}}\mathrm{e}^{iwq}\cdot {\hat{h}}(w;I)\mathrm{e}^{A(\tau ,w)+vB(\tau ,w)+\theta C(\tau ,w)}\mathrm{d}w \nonumber \\&=\frac{\partial ^{2} \gamma }{\partial w^{2}}\Bigg |_{w=0}\cdot (-1)+\frac{\partial \gamma }{\partial w}\Bigg |_{w=0}\cdot \left( 2i \log I \right) +\gamma (\tau ,0,q) \cdot \left( \log I \right) ^{2}, \end{aligned}$$

(15)

where the function $\gamma (\tau ,w;q)$ is given by

$$\begin{aligned} \gamma (\tau ,w;q)=\exp (iwq+A(\tau ,w)+vB(\tau ,w)+\theta C(\tau ,w)). \end{aligned}$$

Based on the above preliminary results, we can derive closed-form formulas of the fair strike price under the He–Chen and rDMR models as shown in the following sections.

4.2 Inner expectation

First, we calculate concretely the inner expectation $U^j$ under the He–Chen model.

Proposition 1

Under the He–Chen model (1), $U^j(\tau ,S,v,\theta ;I)$ is given by

$$\begin{aligned} U^j(\tau ,S,v,\theta ;I)&=B_1^{2}v^2+C_{1}^{2}\theta ^2+2B_{1}C_{1}v\theta \nonumber \\&\quad +\left( 2B_{1}\log \frac{S}{I}+2A_{1}B_{1}+2B_{1}r\tau -B_{2}\right) v \nonumber \\&\quad +\left( 2C_{1}\log \frac{S}{I}+2A_{1}C_{1}+2C_{1}r\tau -C_{2}\right) \theta \nonumber \\&\quad -A_{2}+(r\tau +A_1+\log \frac{S}{I})^2, \end{aligned}$$

(16)

where

$$\begin{aligned} A_1(\tau )&=\frac{\lambda }{2}\left( \frac{\tau }{\kappa }-\frac{\tau ^2}{2}+\frac{1}{\kappa ^2}(\mathrm{e}^{-\kappa \tau -1})\right) , \\ B_1(\tau )&=\frac{1-\mathrm{e}^{\kappa \tau }}{2\kappa \mathrm{e}^{\kappa \tau }}, \quad C_1(\tau )=\frac{1}{2}\left( \frac{\mathrm{e}^{\kappa \tau }-1}{\kappa \mathrm{e}^{\kappa \tau }}-\tau \right) , \\ A_2(\tau )&=-\lambda \Bigg [\frac{1}{2}\left( 1+\frac{\sigma _v^2}{4\kappa ^2}-\frac{\rho \sigma _v}{\kappa }\right) \tau ^2+\left( -\frac{1}{\kappa }-\frac{5 \sigma _v^2}{8\kappa ^3}+\frac{2\rho \sigma _v}{\kappa ^2}\right) \tau \\&\quad \times \left( -\frac{1}{\kappa ^2}-\frac{\sigma _v^2}{2\kappa ^4}+\frac{2\rho \sigma _v}{\kappa ^3}\right) (\mathrm{e}^{-\kappa \tau }-1)-\frac{\sigma _v^2}{16c^4}(\mathrm{e}^{-2\kappa \tau }-1) \\&\quad +\left( \frac{\sigma _v^2}{2\kappa ^2}-\frac{\rho \sigma _v}{\kappa }\right) \left( \frac{1}{\kappa ^2}-\frac{\tau }{\kappa }\mathrm{e}^{-\kappa \tau }-\frac{1}{\kappa ^2}\mathrm{e}^{-\kappa \tau }\right) \Bigg ] \\&\quad +\frac{\sigma _\theta ^2}{4}\left( \frac{1}{2\kappa ^3}(\mathrm{e}^{-2\kappa \tau }-1)+\frac{2\tau \mathrm{e}^{-\kappa tau}}{\kappa ^2}-\frac{\tau }{\kappa ^2}+\frac{\tau ^2}{\kappa }-\frac{\tau ^2}{3}\right) ,\\ B_2(\tau )&=\frac{\sigma _v^2}{4\kappa ^3}\mathrm{e}^{-2\kappa \tau }+\frac{1}{\kappa }\left( 1-\frac{\rho \sigma _v }{\kappa }\right) \mathrm{e}^{-\kappa \tau }-\frac{1}{\kappa }-\frac{\sigma _v^2}{4\kappa ^3}+\frac{1}{\kappa ^2}\rho \sigma _v \\&\quad +\frac{\tau }{\kappa }\left( \frac{\sigma _v^2}{2\kappa }-\rho \sigma _v\right) \mathrm{e}^{-\kappa \tau },\\ C_2(\tau )&=-\frac{1}{2}\Bigg [\mathrm{e}^{-2\kappa \tau }\left( \frac{\sigma _v^2}{4\kappa ^2}\right) +\mathrm{e}^{-\kappa \tau }\left( \frac{2}{\kappa }+\frac{\sigma _v^2}{\kappa ^3}-\frac{4\rho \sigma _v}{\kappa ^2}\right) -\frac{2}{\kappa } \\&\quad -\frac{5\sigma _v^2}{4\kappa ^3}+\frac{4\rho \sigma _v}{\kappa ^2}+\tau \left( 2+\frac{\sigma _v^2}{2\kappa ^2}-\frac{2\rho \sigma _v}{\kappa }+2\mathrm{e}^{-\kappa \tau }\left( \frac{\sigma _v^2}{2\kappa ^2}-\frac{\rho \sigma _v}{\kappa }\right) \right) \Bigg ], \\ \tau&=t_j-t. \end{aligned}$$

Proof

Under the He–Chen model, we have $\eta (\theta )=\lambda$. Then, putting (13) into (12), one can get the following ODEs.

$$\begin{aligned} \frac{\partial A}{\partial \tau }(\tau ,w)&=\lambda C + \frac{1}{2}\sigma _\theta ^2 C^2, \\ A(0,w)&=0, \\ \frac{\partial B}{\partial \tau }(\tau ,w)&=\frac{1}{2}(-iw-w^2)+(\rho \sigma _{v}iw-\kappa )B+\frac{1}{2}\sigma _v^2 B^2, \\ B(0,w)&=0, \\ \frac{\partial C}{\partial \tau }(\tau ,w)&=\kappa B, \\ C(0,w)&=0. \end{aligned}$$

Since the ODE for $B(\tau ,w)$ is a Riccati type of equation with constant coefficients, B can be solved precisely. Then $A(\tau ,w)$ and $C(\tau ,w)$ can be solved by taking integration of the right side of their equation directly. The results are

$$\begin{aligned} A(\tau ,w)&=\lambda \int _{0}^{\tau }C(s,w)\mathrm{d}s+\frac{1}{2}\sigma _\theta ^2\int _{0}^{\tau }C^2(s,w)\mathrm{d}s, \\ B(\tau ,w)&=\frac{\kappa +a(w)}{\sigma _v^2}\cdot \frac{1-\mathrm{e}^{\tau a(w)}}{1-b(w)\mathrm{e}^{\tau a(w)}}, \\ C(\tau ,w)&=\frac{\kappa }{\sigma _v^2}\left( (\kappa +a(w))\tau -2\log \left( \frac{1-b(w)\mathrm{e}^{\tau a(w)}}{1-b(w)}\right) \right) , \\ a(w)&:=\sqrt{\kappa ^2+\sigma _v^2(w^2+iw)}, \quad b(w):=\frac{\kappa +a(w)}{\kappa -a(w)}. \end{aligned}$$

To calculate $U^j$, it is necessary to find the first and second derivatives of A, B and C with respect to w as can be seen in (15). Since the first derivative part in (15) is observed to be purely imaginary while the second derivative part is purely real, for convenience, we define $A_k$, $B_k$ and $C_k$ ($k=1,2$) as

$$\begin{aligned} A_{1}(\tau )&=\frac{1}{i}\cdot A_w(\tau ,0),\quad B_{1}(\tau )=\frac{1}{i}\cdot B_w(\tau ,0), \quad C_{1}(\tau )=\frac{1}{i}\cdot C_w(\tau ,0), \nonumber \\ A_{2}(\tau )&=A_{ww}(\tau ,0), \quad B_{2}(\tau )=B_{ww}(\tau ,0), \quad C_{2}(\tau )=C_{ww}(\tau ,0), \end{aligned}$$

(17)

where $A_w$, $B_w$, $C_w$, $A_{ww}$, $B_{ww}$ and $C_{ww}$ denote the first and second derivatives of A, B and C with respect to w, respectively. Since B and C are expressed by elementary functions only, $B_k$ and $C_k$ ($k=1,2$) can be obtained easily with a good deal of algebra. It looks like that numerical integration would be mandatory for calculating A. However, $A_k$’s can be calculated as closed-form solutions because of the characteristic of the payoff function. We have

$$\begin{aligned} A_w&=\lambda \int _{0}^{\tau } C_w(s,w) \mathrm{d}s + \sigma _\theta \int _{0}^{\tau } C_w(s,w) C(s,w) \mathrm{d}s, \\ A_{ww}&=\lambda \int _{0}^{\tau } C_{ww}(s,w) \mathrm{d}s +\sigma _\theta ^2 \int _{0}^{\tau }\left( C_{ww}(s,w) C(s,w)+\left( C_w(s,w) \right) ^{2}\right) \mathrm{d}s. \end{aligned}$$

Taking $w=0$ in the equations above, we get

$$\begin{aligned} A_w\Bigg |_{w=0}&=\lambda \int _{0}^{\tau }C_w(s,w)\Bigg |_{w=0}\mathrm{d}s, \\ A_{ww}\Bigg |_{w=0}&=\lambda \int _{0}^{\tau }C_{ww}(s,w)\Bigg |_{w=0}\mathrm{d}s + \sigma _\theta ^2\int _{0}^{\tau }\left( C_w(s,w)\Bigg |_{w=0}\right) ^{2} \mathrm{d}s \end{aligned}$$

since $C(\tau ,w)$ goes to zero as w goes to 0. Then we can obtain $A_1$ and $A_2$ by direct integration. Rearranging (15) with notations in (17), the desired result in (16) can be derived. $\square$

Next, we calculate concretely the inner expectation $U^j$ under the rDMR models.

Proposition 2

Under the rDMR model (2), $U^j(\tau ,S,v,\theta ;I)$ is given by

$$\begin{aligned} U^j(\tau ,S,v,\theta ;I)&= E_1^{2}v^2+F_{1}^{2}\theta ^2+2E_{1}F_{1}v\theta \nonumber \\&\quad +\left( 2E_{1}\log \frac{S}{I}+2D_{1}E_{1}+2E_{1}r\tau -E_{2}\right) v \nonumber \\&\quad +\left( 2F_{1}\log \frac{S}{I}+2D_{1}F_{1}+2F_{1}r\tau -F_{2}\right) \theta \nonumber \\&\quad -D_{2}+(r\tau +D_1+\log \frac{S}{I})^2, \end{aligned}$$

(18)

where

$$\begin{aligned} D_{1}(\tau )&=\frac{1}{2}\Bigg [\frac{\alpha \beta }{\alpha -\kappa }\left\{ \frac{(\mathrm{e}^{-\alpha \tau }-1)}{\alpha }-\frac{(\mathrm{e}^{-\kappa \tau }-1)}{\kappa }\right\} -\beta \left\{ \tau +\frac{(\mathrm{e}^{-\alpha \tau }-1)}{\alpha }\right\} \Bigg ],\\ E_{1}(\tau )&=\frac{1-\mathrm{e}^{\kappa \tau }}{2\kappa \mathrm{e}^{\kappa \tau }}, \quad F_{1}(\tau )=\frac{1}{2}\left\{ \frac{(\mathrm{e}^{-\kappa \tau }-\mathrm{e}^{-\alpha \tau })}{\alpha -\kappa }-\frac{(1-\mathrm{e}^{-\alpha \tau })}{\alpha }\right\} ,\\ D_{2}(\tau )&=\frac{\alpha \beta \sigma _v^2}{4\kappa ^2 (\alpha -2\kappa )}\left\{ \frac{(\mathrm{e}^{-\alpha \tau }-1)}{\alpha }-\frac{(\mathrm{e}^{-2\kappa \tau }-1)}{2\kappa }\right\} \\&\quad +\frac{\alpha \beta }{\alpha -\kappa }\left( 1-\frac{\rho \sigma _v}{\kappa }\right) \left\{ \frac{(\mathrm{e}^{-\alpha \tau }-1)}{\alpha }-\frac{(\mathrm{e}^{-\kappa \tau }-1)}{\kappa }\right\} \\&\quad +\beta \left( \frac{\rho \sigma _v}{\kappa }-\frac{\sigma _v^2}{4\kappa ^2}-1\right) \left\{ \tau +\frac{(\mathrm{e}^{-\alpha \tau }-1)}{\alpha }\right\} \\&\quad +\frac{\alpha \beta }{\alpha -\kappa }\left( \frac{\sigma _v^2}{2\kappa }-\rho \sigma _v\right) \left\{ \frac{-\tau \mathrm{e}^{-\kappa \tau }}{\kappa }-\frac{(\mathrm{e}^{-\kappa \tau }-1)}{\kappa ^2}\right\} \\&\quad +\frac{\alpha \beta }{(\alpha -\kappa )^2}\left( \frac{\sigma _v^2}{2\kappa }-\rho \sigma _v\right) \left\{ \frac{(\mathrm{e}^{-\kappa \tau }-1)}{\kappa }-\frac{(\mathrm{e}^{-\alpha \tau }-1)}{\alpha }\right\} \\&\quad +\frac{\sigma _\theta ^2}{4(\alpha -\kappa )^2}\left\{ \frac{(\mathrm{e}^{-2\kappa \tau }-1)}{2\kappa }-\frac{2(\mathrm{e}^{-(\alpha +\kappa )\tau }-1)}{\alpha +\kappa }+\frac{(\mathrm{e}^{-2\alpha \tau }-1)}{2\alpha }\right\} \\&\quad +\frac{\sigma _\theta ^2}{2\alpha (\alpha -\kappa )}\left\{ \frac{(\mathrm{e}^{-(\alpha +\kappa )\tau }-1)}{\alpha +\kappa }+\frac{(\mathrm{e}^{-\alpha \tau }-1)}{\alpha }-\frac{(\mathrm{e}^{-\kappa \tau }-1)}{\kappa }-\frac{(\mathrm{e}^{-2\alpha \tau }-1)}{2\alpha }\right\} \\&\quad +\frac{\sigma _\theta ^2}{4 \alpha ^2}\left\{ \frac{(\mathrm{e}^{-2\alpha \tau }-1)}{2\alpha }-\frac{2(\mathrm{e}^{-\alpha \tau }-1)}{\alpha }-\tau \right\} ,\\ E_{2}(\tau )&=\frac{\sigma _v^2}{4\kappa ^3}\mathrm{e}^{-2\kappa \tau }+\frac{1}{\kappa }\left( 1-\frac{\rho \sigma _v }{\kappa }\right) \mathrm{e}^{-\kappa \tau }-\frac{1}{\kappa }-\frac{\sigma _v^2}{4\kappa ^3}+\frac{1}{\kappa ^2}\rho \sigma _v \\&\quad +\frac{\tau }{\kappa }\left( \frac{\sigma _v^2}{2\kappa }-\rho \sigma _v\right) \mathrm{e}^{-\kappa \tau },\\ F_{2}(\tau )&=\frac{\sigma _v^2(\mathrm{e}^{-2\kappa \tau }-\mathrm{e}^{-\alpha \tau })}{4\kappa ^2(\alpha -2\kappa )}+\left( 1-\frac{\rho \sigma _v}{\kappa }\right) \left( \frac{\mathrm{e}^{-\kappa \tau }-\mathrm{e}^{-\alpha \tau }}{\alpha -\kappa }\right) \\&\quad +\left( \frac{\rho \sigma _v}{\kappa }-\frac{\sigma _v^2}{4\kappa ^2}-1\right) \left( \frac{1-\mathrm{e}^{-\alpha \tau }}{\alpha }\right) +\left( \frac{\sigma _v^2}{2\kappa }-\rho \sigma _v\right) \left( \frac{\tau \mathrm{e}^{-\kappa \tau }}{\alpha -\kappa }\right) \\&\quad -\left( \frac{\sigma _v^2}{2\kappa }-\rho \sigma _v\right) \frac{\mathrm{e}^{-\kappa \tau }-\mathrm{e}^{-\alpha \tau }}{(\alpha -\kappa )^2}. \end{aligned}$$

Proof

The inner expectation $U^j$ under the rDMR model can be derived by the analogous method as used in Proposition 1 for $U^j$ under the He–Chen model. Altering some symbols for $\gamma (\tau ,w;q)$ in (15), we define

$$\begin{aligned} \gamma (\tau ,w;q)=\exp (iwq+D(\tau ,w)+vE(\tau ,w)+\theta F(\tau ,w)) \end{aligned}$$

to make a difference between the solution in Proposition 2 and the solution (16) in Proposition 1. Since $\eta (\theta )=\alpha (\beta -\theta )$ in the rDMR model, the ODEs for D, E and F will be given by

$$\begin{aligned} \frac{\partial D}{\partial \tau }(\tau ,w)&=\alpha \beta F + \frac{1}{2}\sigma _\theta ^2 F^2, \\ D(0,w)&=0, \\ \frac{\partial E}{\partial \tau }(\tau ,w)&=\frac{1}{2}(-iw-w^2)+(\rho \sigma _{v}iw-\kappa )E+\frac{1}{2}\sigma _v^2 E^2, \\ E(0,w)&=0, \\ \frac{\partial F}{\partial \tau }(\tau ,w)&=\kappa E-\alpha F, \\ F(0,w)&=0, \end{aligned}$$

respectively. $D(\tau ,w)$ can be given as a form similar to $A(\tau ,w)$ in the proof of Proposition 1. $E(\tau ,w)$ is identical with $B(\tau ,w)$ as their equations are the same. $F(\tau ,w)$ can be expressed in terms of $E(\tau ,w)$. We have

$$\begin{aligned} D(\tau ,w)&=\alpha \beta \int _{0}^{\tau }F(s,w)\mathrm{d}s+\frac{1}{2}\sigma _\theta ^2\int _{0}^{\tau }F^2(s,w)\mathrm{d}s, \\ E(\tau ,w)&=B(\tau ,w), \\ F(\tau ,w)&=\kappa \mathrm{e}^{-\alpha \tau }\int _{0}^{\tau } \mathrm{e}^{\alpha s}E(s,w) \mathrm{d}s. \end{aligned}$$

Using the same logic as in the proof of Proposition 1, we define the corresponding terms $D_k$, $E_k$ and $F_k$ for $k=1,2$ and substitute them into (15). Then the same form as in (18) can be derived. What is left is finding analytic solutions of $D_k$, $E_k$ and $F_k$. $E_k$ is equal to $B_k$. $F_1$ and $F_2$ are expressed as

$$\begin{aligned} F_1(\tau )&=\frac{1}{i}\cdot F_w\Bigg |_{w=0}=\kappa \mathrm{e}^{-\alpha \tau }\int _{0}^{\tau } \mathrm{e}^{\alpha s}E_1(s) \mathrm{d}s, \\ F_2(\tau )&=F_{ww}\Bigg |_{w=0}=\kappa \mathrm{e}^{-\alpha \tau }\int _{0}^{\tau } \mathrm{e}^{\alpha s}E_2(s) \mathrm{d}s, \end{aligned}$$

respectively. Since $F(\tau ,w)$ goes to zero as $w\rightarrow 0$,

$$\begin{aligned} D_1(\tau )&=\frac{1}{i}\cdot D_{w}\Bigg |_{w=0}=\alpha \beta \int _{0}^{\tau } F_{w}(s,w)\Bigg |_{w=0}\mathrm{d}s, \\ D_2(\tau )&=D_{ww}\Bigg |_{w=0}=\alpha \beta \int _{0}^{\tau } F_{ww}(s,w)\Bigg |_{w=0} \mathrm{d}s+\sigma _\theta ^2\int _{0}^{\tau }\left( F_{w}(s,w)\Bigg |_{w=0}\right) ^{2} \mathrm{d}s. \end{aligned}$$

So, simple direct calculation starting with $E(\tau ,w)=B(\tau ,w)$ can lead to the desired result (18) in the proposition. $\square$

In the above Propositions 1 and  2, we have derived the inner expectations $U^j$ under the He–Chen and rDMR models, respectively. It is worthy to note that they have no integral terms whereas the characteristic functions contain integral terms. It is due to the payoff structure of variance swaps with log return. The characteristic function itself is not required to calculate $U^j$, whereas other financial derivatives like European options are in need of it.

4.3 Outer expectation

In this section, we obtain the outer expectations $W^j$ based on the result for the inner expectations $U^j$. Recall that the inner expectations $U^j$ at time $t=t_{j-1}$ under the He–Chen and rDMR models are given by

$$\begin{aligned} U^j(t_{j-1},S,v,\theta ;x)&=B_{1}^{2}(\varDelta \tau )v^2+C_{1}^{2}(\varDelta \tau )\theta ^2+2B_{1}(\varDelta \tau )C_{1}(\varDelta \tau )v\theta \nonumber \\&\quad +(2A_{1}(\varDelta \tau )B_{1}(\varDelta \tau )+2B_1(\varDelta \tau ) r \varDelta \tau -B_2(\varDelta \tau ))v \nonumber \\&\quad +(2A_{1}(\varDelta \tau )C_{1}(\varDelta \tau )+2C_1(\varDelta \tau ) r \varDelta \tau -C_2(\varDelta \tau ))\theta \nonumber \\&\quad +(r\varDelta \tau +A_{1}(\varDelta \tau ))^2-A_{2}(\varDelta \tau ) \;\;\; \text {(the He-Chen model)} \end{aligned}$$

(19)

and

$$\begin{aligned} U^j(t_{j-1},S,v,\theta ;x)&=E_{1}^{2}(\varDelta \tau )v^2+F_{1}^{2}(\varDelta \tau )\theta ^2+2E_{1}(\varDelta \tau )F_{1}(\varDelta \tau )v\theta \nonumber \\&\quad +(2D_{1}(\varDelta \tau )E_{1}(\varDelta \tau )+2E_1(\varDelta \tau ) r \varDelta \tau -E_2(\varDelta \tau ))v \nonumber \\&\quad +(2D_{1}(\varDelta \tau )F_{1}(\varDelta \tau )+2F_1(\varDelta \tau ) r \varDelta \tau -F_2(\varDelta \tau ))\theta \nonumber \\&\quad +(r\varDelta \tau +D_{1}(\varDelta \tau ))^2-D_{2}(\varDelta \tau ), \;\;\; \text {(the rDMR model)} \end{aligned}$$

(20)

respectively, where $\varDelta \tau =t_{j}-t_{j-1}=T/N$. Note that the variable S dependence of the inner expectations vanishes. The PDE (8) is reduced to

$$\begin{aligned} \Bigg (\frac{\partial }{\partial t}+\kappa (\theta -v)\frac{\partial }{\partial v}+\eta (\theta )\frac{\partial }{\partial \theta }+\frac{1}{2}\sigma _v^2 v \frac{\partial ^2}{\partial v^2}+\frac{1}{2} \sigma _\theta ^2 \frac{\partial ^2}{\partial \theta ^2} \Bigg )W^j=0 \end{aligned}$$

on the time interval $[t_0,t_{j-1})$. Then by the jump condition (7) and the Feynman-Kac theorem, the outer expectation $W^j$ can be represented as

$$\begin{aligned} W^j(t_0,v_{t_0},\theta _{t_0})= {\mathbb {E}}^{0,*}\left[ U^j(t_{j-1},S,v,\theta ;S) \Big | v_{t_0},\theta _{t_0} \right] . \end{aligned}$$

(21)

In the following propositions, we manipulate (21) and obtain explicit solutions for $W^j$ under the He–Chen and rDMR models.

Proposition 3

Under the He–Chen model (1), $W^j(t,v,\theta )$ is given by

$$\begin{aligned} W^j(t,v,\theta )&=B_{1}^{2}(\varDelta \tau ){\mathbb {E}}[v^2]+C_{1}^{2}(\varDelta \tau ){\mathbb {E}}[\theta ^2]+2B_{1}(\varDelta \tau )C_{1}(\varDelta \tau ){\mathbb {E}}[v\theta ] \nonumber \\&\quad +(2A_{1}(\varDelta \tau )B_{1}(\varDelta \tau )+2B_1(\varDelta \tau ) r \varDelta \tau -B_2(\varDelta \tau )){\mathbb {E}}[v] \nonumber \\&\quad +(2A_{1}(\varDelta \tau )C_{1}(\varDelta \tau )+2C_1(\varDelta \tau ) r \varDelta \tau -C_2(\varDelta \tau )){\mathbb {E}}[\theta ] \nonumber \\&\quad +(r\varDelta \tau +A_{1}(\varDelta \tau ))^2-A_{2}(\varDelta \tau ), \end{aligned}$$

(22)

where

$$\begin{aligned} {\mathbb {E}}[\theta ]&=\theta _{t} + \lambda \tau , \\ {\mathbb {E}}[\theta ^2]&=\theta _{t}^2+\lambda ^2\tau ^2+\sigma _\theta ^2\tau , \\ {\mathbb {E}}[v]&=v_{t}\mathrm{e}^{-\kappa \tau }-\theta _{t}(1-\mathrm{e}^{-\kappa \tau })+\lambda \tau -\frac{\lambda }{\kappa }(1-\mathrm{e}^{-\kappa \tau }), \\ {\mathbb {E}}[v\theta ]&=(v_{t}-\theta _{t})\mathrm{e}^{-\kappa \tau }-\frac{\lambda }{\kappa }(1-\mathrm{e}^{-\kappa \tau })(\theta _{t}+\lambda \tau )\\&\quad +(\theta _{t}+\lambda \tau )^2+\sigma _\theta ^2\tau -\frac{\sigma _\theta ^2}{\kappa }(1-\mathrm{e}^{-\kappa \tau }), \\ {\mathbb {E}}[v^2]&=\left( {\mathbb {E}}[v]\right) ^2+\frac{\sigma _\theta ^2}{2\kappa }(1-\mathrm{e}^{-2\kappa \tau })+\Lambda _1(\tau ), \\ \Lambda _1(\tau )&=\sigma _v^2(\mathrm{e}^{-\kappa \tau }-\mathrm{e}^{2-\kappa \tau })\left( \frac{v_{t}}{\kappa }-\frac{\theta _{t}}{\kappa }+\frac{\lambda }{\kappa ^2}\right) \\&\quad +\frac{\sigma _v^2}{2\kappa }(1-\mathrm{e}^{-2\kappa \tau })\left( \theta _{t}-\frac{3\lambda }{2\kappa }\right) + \lambda \frac{\sigma _v^2}{2\kappa }\tau , \\ \tau&:=t_{j-1}-t, \qquad \varDelta \tau :=t_{j}-t_{j-1}=T/N. \end{aligned}$$

Here, ${\mathbb {E}}[\ \cdot \ ]$ is a simple expression of ${\mathbb {E}}^{t,*}[\ \cdot \ |v_{t},\theta _{t}]$.

Proof

By the linear property of conditional expectation and Proposition 1, one can obtain (22), where the explicit calculations of the conditional expectations are given in Appendix A.1. $\square$

Proposition 4

Under the rDMR model (2), $W^j(t,v,\theta )$ is given by

$$\begin{aligned} W^j(t,v,\theta )&=E_{1}^{2}(\varDelta \tau ){\mathbb {E}}[v^2]+F_{1}^{2}(\varDelta \tau ){\mathbb {E}}[\theta ^2]+2E_{1}(\varDelta \tau )F_{1}(\varDelta \tau ){\mathbb {E}}[v\theta ] \nonumber \\&\quad +(2D_{1}(\varDelta \tau )E_{1}(\varDelta \tau )+2E_1(\varDelta \tau ) r \varDelta \tau -E_2(\varDelta \tau )){\mathbb {E}}[v] \nonumber \\&\quad +(2D_{1}(\varDelta \tau )F_{1}(\varDelta \tau )+2F_1(\varDelta \tau ) r \varDelta \tau -F_2(\varDelta \tau )){\mathbb {E}}[\theta ] \nonumber \\&\quad +(r\varDelta \tau +D_{1}(\varDelta \tau ))^2-D_{2}(\varDelta \tau ), \end{aligned}$$

(23)

where

$$\begin{aligned} {\mathbb {E}}[\theta ]&=\theta _{t}\mathrm{e}^{-\alpha \tau }+\beta (1-\mathrm{e}^{-\alpha \tau }),\\ {\mathbb {E}}[\theta ^2]&=\left\{ \theta _{t}\mathrm{e}^{-\alpha \tau }+\beta (1-\mathrm{e}^{-\alpha \tau })\right\} ^2 \\&\quad +\theta _{t}\frac{\sigma _\theta ^2}{\alpha }(\mathrm{e}^{-\alpha \tau }-\mathrm{e}^{-2\alpha \tau })+\frac{\beta \sigma _\theta ^2}{2\alpha }(1-\mathrm{e}^{-\alpha \tau })^2,\\ {\mathbb {E}}[v]&=v_{t}\mathrm{e}^{-\kappa \tau }+\beta (1-\mathrm{e}^{-\kappa \tau })+\frac{\kappa }{\kappa -\alpha }(\theta _{t}-\beta )(\mathrm{e}^{-\alpha \tau }-\mathrm{e}^{-\kappa \tau }), \\ {\mathbb {E}}[v\theta ]&={\mathbb {E}}[v]{\mathbb {E}}[\theta ]+\frac{\kappa \sigma _\theta ^2}{2\alpha (\kappa -\alpha )}(1-\mathrm{e}^{-2\alpha \tau }) \\&\quad -\frac{\kappa \sigma _\theta ^2}{(\kappa +\alpha )(\kappa -\alpha )}(1-\mathrm{e}^{-(\alpha +\kappa )\tau }),\\ {\mathbb {E}}[v^2]&=\left( {\mathbb {E}}[v]\right) ^2+\Lambda _2(\tau )+\left( \frac{\kappa \sigma _\theta }{\kappa -\alpha }\right) ^2\Big \{\frac{1}{2\kappa }(1-\mathrm{e}^{-2\kappa \tau })\\&\quad +\frac{1}{2\alpha }(1-\mathrm{e}^{-2\alpha \tau })-\frac{2}{\kappa +\alpha }(1-\mathrm{e}^{(-\alpha +\kappa )\tau })\Big \},\\ \Lambda _2(\tau )&=\sigma _v^2\Big [\frac{(v_{t}-\beta )}{\kappa }(\mathrm{e}^{-\kappa \tau }-\mathrm{e}^{-2\kappa \tau })+\frac{\beta }{2\kappa }(1-\mathrm{e}^{-2\kappa \tau })\\&\quad +\frac{\kappa (\theta _{t}-\beta )}{(\kappa -\alpha )(2\kappa -\alpha )}(\mathrm{e}^{-\alpha \tau }-\mathrm{e}^{-2\kappa \tau })-\frac{(\theta _{t}-\beta )}{\kappa -\alpha }(\mathrm{e}^{-\kappa \tau }-\mathrm{e}^{-2\kappa \tau })\Big ],\\ \tau&=t_{j-1}-t, \qquad \varDelta \tau =t_{j}-t_{j-1}=T/N. \end{aligned}$$

Proof

This proposition can be proved similarly to the proof of Proposition  3. The explicit calculations of the conditional expectations are given in Appendix A.2. $\square$

4.4 The fair strike value

Finally, the above propositions put together lead to the fair strike price $K_{\text {var}}$ of the variance swap as it is expressed as the sum of $\frac{100^2}{T}W^j$ for $1\le j \le N$, where N and T are sampling frequency and tenor of the variance swap, respectively.

Theorem 1

Under the He–Chen model (1) or the rDMR model (2), the fair strike $K_{\text {var}}$ at $t=t_0$ is

$$\begin{aligned} K_{\text {var}}=100^2\times \frac{1}{T}\sum _{j=1}^{N}W^j(t_0,v_{t_0},\theta _{t_0}), \end{aligned}$$

(24)

where $W^j$ is given by (22) under the He–Chen model or (23) under the rDMR model, respectively.

Proof

It is a direct result from (10) and Proposition  3 or Proposition  4. $\square$

We note that the pricing formulas for the He–Chen and rDMR models are all composed of elementary functions without any integral. If one sets $\lambda =\sigma _\theta =0$ in (22), the fair strike value $K_{\text {var}}$ in Theorem 1 is identical with the corresponding strike value under the Heston model.

5 Numerical results

5.1 Validity of the solutions

In this section, we use Monte-Carlo (MC) simulation to obtain the fair strikes of a discretely sampled variance swap under the He–Chen and rDMR models. Then we compare the results with the values calculated by the analytic formulas given in Theorem 1.

We use three kinds of samples, named as Sample 1, 2 and 3, in which the model parameters are given in Table 1, where r and T are fixed as $r=0.01$ and $T=1$, respectively.

Table 1 Sample parameters of the He–Chen and rDMR models for Monte-Carlo simulation

We use the well-known Euler–Maruyama scheme to generate sample paths up to maturity $T=1$ with N number of sub-intervals. The sample paths are given by

$$\begin{aligned} S_{t_j}&=S_{t_{j-1}}+rS_{t_{j-1}}\varDelta t+\sqrt{v_{t_{j-1}}}S_{t_{j-1}}\varDelta W_1(t_j), \\ v_{t_j}&=v_{t_{j-1}}+\kappa \left( \theta _{t_{j-1}}-v_{t_{j-1}}\right) \varDelta t+\sigma _v \sqrt{v_{t_{j-1}}}\left( \rho \varDelta W_1(t_j) + \sqrt{1-\rho ^2}\varDelta W_2(t_j)\right) ,\\ \theta _{t_j}&=\theta _{t_{j-1}}+\eta (\theta _{t_{j-1}})\varDelta t + \sigma _\theta \varDelta W_3(t_j), \end{aligned}$$

where $\varDelta t=T/N, \ t_j=j\varDelta t, \ \varDelta W_i(t_j)=W_i(t_j)-W_i(t_{j-1}), \ j=1,\dots ,N, \ i=1,2,3$. $\eta (\theta )=\lambda$ for the He–Chen model and $\eta (\theta )=\alpha (\beta -\theta _{t})$ for the rDMR model. We have taken 100,000 number of sample paths for each of different sampling frequency N. The prices given by the analytic formula in Theorem 1, the MC simulation results and the standard errors are shown in Table 2. In this table, $\text {AS}$, $\text {MC}$ and $\text {SE}$ stand for the analytic solution, the MC simulation result and the standard error, respectively. Table 2 demonstrates that our analytic result in Theorem 1 well agrees with the MC simulation result. Note that the error tends to increase as N decreases but it is mainly due to the discretization error caused by the Euler–Maruyama scheme.

Table 2 Fair strike prices $K_{\text {var}}$ obtained by the analytic formula in Theorem 1 and Monte-Carlo simulation results

5.2 Sensitivity analysis

In this section, we investigate the sensitivity of the fair strike value of a variance swap to the added parameters of the stochastic long-term mean of variance.

Fig. 2

Impact of the long-run mean $\theta _t$ of variance on the fair strike prices under the He–Chen model

5.2.1 The He–Chen model

First, under the He–Chen model, the impact of the long-term mean $\theta _t$ of variance on the fair strike $K_\text {var}$ is shown in Fig. 2. In Fig. 2a, b, we draw the time-to-maturity T dependence of the fair strike value $K_\text {var}$ for five different choices of $\lambda$ (the drift of $\theta _t$). It is expected that higher $\lambda$ leads to larger average value of volatility level. If $\lambda$ increases, then the fair strike value increases regardless of time-to-maturity as shown in Fig. 2a, b. If $\theta _0 > v_0$, then $K_\text {var}$ tends to increase with time-to-maturity as shown in Fig. 2a. If $\theta _0 < v_0$, then $K_\text {var}$ tends to decrease with time-to-maturity in a certain range of time-to-maturity as shown in Fig. 2b.

The sensitivity of the fair strike price to $\lambda$ is shown in Fig. 2c. It is clear that the fair strike value is an increasing function of $\lambda$. Also, we note that larger initial long-term mean of variance $\theta _0$ leads to higher fair strike price regardless of the initial value of $v_t$. In fact, all the cases in which $\theta _0$ is larger or smaller than or equal to $v_0(=0.1)$ are expressed in that graph.

In Fig. 2d, the impact of the volatility $\sigma _\theta$ of the long-run mean of variance is demonstrated for three choices of $\sigma _v$ (vol-of-vol). It is obvious that the fair strike price is also an increasing function of $\sigma _\theta$. Higher volatility of the long-run mean of variance gives rise to more volatile $\theta _t$ which makes the realized variance higher. We note from the figure that the fair strike is positively correlated with vol-of-vol as it should be.

Fig. 3

Impact of the long-run mean $\theta _t$ of variance on the fair strike prices under the rDMR model

5.2.2 The rDMR model

Figure 3 shows the impact of the long-run mean $\theta _t$ of variance on the fair strike prices under the rDMR model.

The fair strike prices against time-to-maturity T are depicted in Fig. 3a, where the parameters were given by $v_0=0.1$ and $\theta _0=0.2$. If the mean value $\beta$ of the long-run mean of variance is larger (smaller) than $v_0$, then the fair strike price increases (decreases) when T is sufficiently long enough. The relationship between the mean reversion rate $\alpha$ and the fair strike price is presented in Fig. 3b. If $\beta >\theta _0$, then the fair strike price increases with $\alpha$. Conversely, it decreases as $\alpha$ increases under the condition $\beta <\theta _0$. The expected value of $\theta _t$ would be closer to $\beta$ at the expiration as $\alpha$ gets larger. One more interesting thing is that when $\beta =\theta _0$, the impact of $\alpha$ on the fair strike is nearly negligible. From Fig. 3c, it is clear that the fair strike price is an increasing function of $\beta$. If $\alpha$ becomes larger, then the increasing speed increases. The sensitivity of $\sigma _\theta$ (the diffusion term of the long-run of variance) under the rDMR model is also expressed in Fig. 3d and the fair strike increases with it, which agrees with the expectation that the bigger the diffusion term is, the more volatile the long-run mean of variance is.

5.3 Model calibration

In this section, we carry out some empirical studies to verify how well the concept of stochastic long-run mean of variance matches the real market data related to variance swaps. There is no available market data of variance swaps itself as they are traded in the over-the-counter market. Fortunately, the value of the CBOE Volatility Index (VIX) is equivalent to the square root of the (strike) price of a variance swap. So, the VIX becomes an important tool for the calibration of the Heston type of stochastic volatility models considered in this paper. More specifically, given the underlying price (SPX) $S_t$, the VIX is given by

$$\begin{aligned} \text {VIX}_t(\tau )=100\times \sqrt{\frac{2}{\tau }{\mathbb {E}}^t\left[ \int _{t}^{t+\tau }\frac{\mathrm{d}S_s}{S_s}-{d}(\log (S_s))\right] }. \end{aligned}$$

Under the model (1) or (2), it can be reduced by the Ito formula to

$$\begin{aligned} \left( \text {VIX}_t (\tau )\right) ^2=100^2\times \frac{1}{\tau }\int _{t}^{t+\tau }{\mathbb {E}}^t[v_s] \mathrm{d}s. \end{aligned}$$

Thus we could use the VIX data as an instrument for calibration regarding the VIX as the square root of the strike of a variance swap as it is calculated with sufficiently high sampling frequency. One can check a study of details about VIX, for example, in Luo and Zhang (2012). We have exploited the Levenberg–Marquardt algorithm (Levenberg 1944) for the calibration in this paper. We adopt the Heston model as a benchmark and compare it with the He–Chen and rDMR models to investigate the influence of the parameters of the stochastic long-run mean of variance process.

Fig. 4

Calibration results of the Heston, He–Chen and rDMR models

Figure 4 presents the model fit after calibration under the Heston, He–Chen and rDMR models at four different dates. The estimated parameters are given in Table 3. Figure 4a depicts the VIX values in the ordinary market while Fig. 4b presents the results at the beginning of the financial crisis caused by COVID-19. One can notice that the market volatility of 2020-03-27 is much higher than that of 2020-01-03. The three models match well overall as shown in Fig. 4a, b. However, Fig. 4c, d indicate somewhat different results. The VIX values show a different pattern (concave-down behavior) in those figures. The Heston model does not capture the market behavior well when the expiration is long enough while the He–Chen and rDMR models fit them closely. This is because the fair strike prices under the original Heston model (constant long-run mean of variance) can represent only monotone increasing or decreasing behavior with respect to time-to-maturity. Note that Fig. 4c corresponds to an extremely turbulent environment caused by the COVID-19 pandemic.

Table 3 Parameters estimated by calibration to 2020-01-03, 2020-03-27, 2020-10-16 and 2020-11-27 VIX data quoted from CBOE

As shown in Table 4, the mean square errors (MSEs) between VIX values and theoretical values with the He–Chen or rDMR model are smaller than those with the Heston model, in particular, when the situation develops into a more unstable environment. It seems that there is no notable difference between the He–Chen model and the rDMR model in terms of market predictability.

Table 4 Mean square errors between VIX data and theoretical prices

6 Conclusion

In this paper, we use two stochastic long-run mean of variance models, called the He–Chen model and the rDMR model, extending the Heston model and follow the similar arguments to Heston’s original work and obtain successfully the closed-form formulas for the fair strike prices of the discretely sampled variance swaps with log return. Our solutions consist of elementary functions with no integral terms and thus they are very easy to calculate. The validity of our analytic formulas is confirmed by the Monte-Carlo simulation method. Some sensitivity analysis has been scrutinized to understand the effect of the newly added parameters of stochastic long-run mean of variance on the fair strike values of the variance swaps. A comparison analysis has been made between the VIX data and theoretical prices in the Heston, He–Chen, and rDMR models. The VIX data chosen in this paper covers not only a stable market situation but also a turbulent situation caused by the COVID-19 pandemic. The model fit results demonstrate that the stochastic long-run mean of variance has an vital impact on the fair strike prices of the variance swaps in the turbulent market condition. Subsequently, the He–Chen or rDMR model has better performance than the Heston model when the VIX market shows a concave-down pattern. There is no notable difference between the He–Chen model and the rDMR model in terms of market predictability. The choice between the two models may depend on the preference for the number of model parameters or the mean-reversion property of the stochastic long-run mean of variance. The He–Chen model requires fewer parameters than the rDMR model while the long-run mean of variance of the rDMR model reverts to the average level of the entire data set which is not the case in the He–Chen model.

There remain a quite number of open issues required to be considered apart from the problems discussed in this paper. For instance, hedging is an important topic required to be included. Considering the dynamic hedging of volatility swaps using variance swaps would make our paper more complete as done in the paper by Swishchuk and Vadori (2014) under the delayed Heston model. However, it doesn’t seem to be easy in the current exact analysis of this study. Also, both volatility and variance swaps calculations in one paper would be nice to be included in one paper. However, a closed-form exact solution of the price of volatility swaps is difficult to find even in the Heston model with constant long-run mean of variance due to the inherent difficulty associated with the nonlinearity in the pay-off function. So, inevitably, we would need to perform some approximate analysis for volatility swaps. Keeping the He–Chen and rDMR models as they are and considering the usage of continuously sampled swap prices as an approximation of the corresponding discretely sampled swap prices, we obtain closed-form approximate solution formulas in the case of continuously sampled volatility swaps and the results are shown in Appendix B. From the modeling point of view, it is possible to do an immediate extended research of this work as follows. For example, one may consider the same type of models as the He–Chen and rDMR models but with a more extended correlation structure than our choice in this paper. Then approximate solution formulas could be obtained by applying the same technique as used in Kim and Kim (2020). Also, other types of processes like the CIR process could be considered for the long-run mean of variance process.

Appendices

Appendix A: Expectations of $v_t$, $v_t\theta _t$ and $v_t^2$

1.1 A.1: The He–Chen model

The SDEs of $v_t$ and $\theta _t$ are given by

$$\begin{aligned} \mathrm{d}v_t&=\kappa (\theta _t-v_t)\mathrm{d}t + \sigma _v \sqrt{v_t}\mathrm{d}w_t^2, \\ \mathrm{d}\theta _t&=\lambda \mathrm{d}t+\sigma _\theta \mathrm{d}W_t^3, \end{aligned}$$

respectively, where $\mathrm{d}W_t^2 \mathrm{d}W_t^3=0$. The solution $\theta _t$ can be expressed as

$$\begin{aligned} \theta _t=\theta _{t_0} + \lambda (t-t_{0})+\sigma _\theta \int _{t_0}^{t}\mathrm{d}W_t^3 \end{aligned}$$

(25)

and thus

$$\begin{aligned} {\mathbb {E}}[\theta _t]&=\theta _{t_0} + \lambda (t-t_0), \\ {\mathbb {E}}[\theta _t^2]&=\theta _{t_0}^2+\lambda ^2(t-t_0)^2+\sigma _\theta ^2(t-t_0). \end{aligned}$$

By the Ito lemma, we have

$$\begin{aligned} d(\mathrm{e}^{\kappa s}v_s)&=\kappa \theta _s \mathrm{e}^{\kappa s}\mathrm{d}s+\sigma _v \mathrm{e}^{\kappa s}\sqrt{v_s}\mathrm{d}W_s^2, \end{aligned}$$

(26)

$$\begin{aligned} d(\mathrm{e}^{\kappa s}\theta _s)&=\kappa \theta _s \mathrm{e}^{\kappa s}\mathrm{d}s+\mathrm{e}^{\kappa s}(\lambda \mathrm{d}s + \sigma _\theta \mathrm{d}W_s^3). \end{aligned}$$

(27)

Integrating these equations, we have

$$\begin{aligned} \mathrm{e}^{\kappa t}v_t-\mathrm{e}^{\kappa t_0}v_{t_0}&=\int _{t_0}^{t}\kappa \theta _s \mathrm{e}^{\kappa s}\mathrm{d}s+\sigma _v \int _{t_0}^{t} \mathrm{e}^{\kappa s}\sqrt{v_s} \mathrm{d}W_s^2 , \end{aligned}$$

(28)

$$\begin{aligned} \mathrm{e}^{\kappa t}\theta _t-\mathrm{e}^{\kappa t_0}\theta _{t_0}&=\int _{t_0}^{t}\kappa \theta _s \mathrm{e}^{\kappa s}\mathrm{d}s+\lambda \int _{t_0}^{t} \mathrm{e}^{\kappa s}\mathrm{d}s+\sigma _\theta \int _{t_0}^{t} \mathrm{e}^{\kappa s}\mathrm{d}W_s^3. \end{aligned}$$

(29)

By eliminating $\int _{t_0}^t \kappa \theta _s \mathrm{e}^{\kappa s}\mathrm{d}s$ term, (28) and (29) lead to

$$\begin{aligned} v_t&=\theta _t+v_{t_0}\mathrm{e}^{\kappa (t_0-t)}-\theta _{t_0}\mathrm{e}^{\kappa (t_0-t)}-\frac{\lambda }{\kappa }(1-\mathrm{e}^{\kappa (t_0-t)}) \nonumber \\&\quad -\frac{\sigma _\theta }{\mathrm{e}^{\kappa t}}\int _{t_0}^{t} \mathrm{e}^{\kappa s}\mathrm{d}W_s^3+\frac{\sigma _v}{\mathrm{e}^{\kappa t}}\int _{t_0}^{t} \mathrm{e}^{\kappa s}\sqrt{v_s} \mathrm{d}W_s^2. \end{aligned}$$

(30)

and thus

$$\begin{aligned} {\mathbb {E}}[v_t]=v_{t_0}\mathrm{e}^{\kappa (t_0-t)}+\theta _{t_0}(1-\mathrm{e}^{\kappa (t_0-t)})+\lambda (t-t_0)-\frac{\lambda }{\kappa }(1-\mathrm{e}^{\kappa (t_0-t)}). \end{aligned}$$

Multiplying (25) and (30) and taking conditional expectation at $t_0$, we obtain

$$\begin{aligned} {\mathbb {E}}[v_t \theta _t]&={\mathbb {E}}[v_t]{\mathbb {E}}[\theta _t]-{\mathbb {E}}\left[ \frac{\sigma _\theta ^2}{\mathrm{e}^{\kappa t}}\int _{t_0}^{t}\mathrm{e}^{\kappa s}\mathrm{d}s\right] \\&=(v_{t_0}-\theta _{t_0})\mathrm{e}^{\kappa (t_0-t)}-\frac{\lambda }{\kappa }(1-\mathrm{e}^{\kappa (t_0-t)})(\theta _{t_0}+\lambda (t-t_0))\\&\quad +(\theta _{t_0}+\lambda (t-t_0))^2+\sigma _\theta ^2(t-t_0)-\frac{\sigma _\theta ^2}{\kappa }(1-\mathrm{e}^{\kappa (t_0-t)}), \end{aligned}$$

where the Ito isometry has been used. Similarly,

$$\begin{aligned} {\mathbb {E}}[v_t^2]&=\left( {\mathbb {E}}[v_t]\right) ^2+\frac{\sigma _\theta ^2}{\mathrm{e}^{2\kappa t}}\int _{t_0}^t \mathrm{e}^{2\kappa s}\mathrm{d}s+{\mathbb {E}}\left[ \frac{\sigma _v^2}{\mathrm{e}^{2\kappa t}}\int _{t_0}^t \mathrm{e}^{2\kappa s} v_s \mathrm{d}s\right] \\&=\left( {\mathbb {E}}[v_t]\right) ^2+\frac{\sigma _\theta ^2}{2\kappa \mathrm{e}^{2\kappa t}}(\mathrm{e}^{2\kappa t}-\mathrm{e}^{2\kappa t_0})+\Lambda _1(t;t_0) \end{aligned}$$

holds, where

$$\begin{aligned} \Lambda _1(t;t_0)&:={\mathbb {E}}\left[ \frac{\sigma _v^2}{\mathrm{e}^{2\kappa t}}\int _{t_0}^t \mathrm{e}^{2\kappa s} v_s \mathrm{d}s\right] =\frac{\sigma _v^2}{\mathrm{e}^{2\kappa t}}\int _{t_0}^t \mathrm{e}^{2\kappa s} {\mathbb {E}}[v_s] \mathrm{d}s \\&=\sigma _v^2(\mathrm{e}^{\kappa (t-t_0)}-\mathrm{e}^{2\kappa (t-t_0)})\left( \frac{v_{t_0}}{\kappa }-\frac{\theta _{t_0}}{\kappa }+\frac{\lambda }{\kappa ^2}\right) \\&\quad +\frac{\sigma _v^2}{2\kappa }(1-\mathrm{e}^{2\kappa (t-t_0)})\left( \theta _{t_0}-\frac{3\lambda }{2\kappa }\right) \\&\quad +\lambda \frac{\sigma _v^2}{2\kappa }(t-t_0) \end{aligned}$$

in which Fubini’s theorem has been used.

1.2 A.2: The rDMR model

The SDEs of $v_t$ and $\theta _t$ are given by

$$\begin{aligned} \mathrm{d}v_t&=\kappa (\theta _t-v_t)\mathrm{d}t + \sigma _v \sqrt{v_t}\mathrm{d}W_t^2, \\ \mathrm{d}\theta _t&=\alpha (\beta -\theta _t)\mathrm{d}t+\sigma _\theta \mathrm{d}W_t^3, \end{aligned}$$

where $\mathrm{d}W_t^2 \mathrm{d}W_t^3=0$. By Ito’s lemma, we have

$$\begin{aligned} d(\mathrm{e}^{\alpha s} \theta _s)&=\alpha \beta \mathrm{e}^{\alpha s}\mathrm{d}s+\mathrm{e}^{\alpha s}\sigma _\theta \mathrm{d}W_s^3, \end{aligned}$$

(31)

$$\begin{aligned} d(\mathrm{e}^{\kappa t}\theta _t)&=(\kappa -\alpha )\theta _t \mathrm{e}^{\kappa t}\mathrm{d}t+\alpha \beta \mathrm{e}^{\kappa t}\mathrm{d}t + \mathrm{e}^{\kappa t}\sigma _\theta \mathrm{d}W_t^3. \end{aligned}$$

(32)

Integrating (31) from $t_0$ to t, one can obtain

$$\begin{aligned} \theta _t=\mathrm{e}^{\alpha (t_0-t)}\theta _{t_0}+\beta (1-\mathrm{e}^{\alpha (t_0-t)})+\mathrm{e}^{-\alpha t}\int _{t_0}^t \mathrm{e}^{\alpha s}\sigma _\theta \mathrm{d}W_s^3. \end{aligned}$$

(33)

Integrating (26) and (32), we have

$$\begin{aligned} \mathrm{e}^{\kappa t}v_t-\mathrm{e}^{\kappa t_0}v_{t_0}&=\kappa \int _{t_0}^t\theta _s \mathrm{e}^{\kappa s}\mathrm{d}s+\sigma _v\int _{t_0}^t \mathrm{e}^{\kappa s}\sqrt{v_s}\mathrm{d}W_s^2, \end{aligned}$$

(34)

$$\begin{aligned} \mathrm{e}^{\kappa t}\theta _t-\mathrm{e}^{\kappa t_0}\theta _{t_0}&=(\kappa -\alpha )\int _{t_0}^t\theta _s \mathrm{e}^{\kappa s}\mathrm{d}s+\frac{\alpha \beta }{\kappa }(\mathrm{e}^{\kappa t}-\mathrm{e}^{\kappa t_0})+\sigma _\theta \int _{t_0}^t \mathrm{e}^{\kappa s} \mathrm{d}W_s^3. \end{aligned}$$

(35)

By eliminating $\int _{t_0}^t\theta _s \mathrm{e}^{\kappa s}\mathrm{d}s$ term from (34) and (35) and applying (33), we have

$$\begin{aligned} v_t&=v_{t_0}\mathrm{e}^{\kappa (t_0-t)}-\frac{\kappa }{\kappa -\alpha }\theta _{t_0}\mathrm{e}^{\kappa (t_0-t)}-\frac{\alpha \beta }{\kappa -\alpha }(1-\mathrm{e}^{\kappa (t_0-t)})+\frac{\kappa }{\kappa -\alpha }\theta _{t_0} \mathrm{e}^{\alpha (t_0-t)}\nonumber \\&\quad +\frac{\kappa \beta }{\kappa -\alpha }(1-\mathrm{e}^{\alpha (t_0-t)})+\frac{\kappa \sigma _\theta }{\kappa -\alpha }\mathrm{e}^{-\alpha t}\int _{t_0}^t \mathrm{e}^{\alpha s} \mathrm{d}W_s^3 \nonumber \\&\quad -\frac{\kappa \sigma _\theta }{\kappa -\alpha }\mathrm{e}^{-\kappa t}\int _{t_0}^t \mathrm{e}^{\kappa s} \mathrm{d}W_s^3 +\sigma _v \mathrm{e}^{-\kappa t}\int _{t_0}^t \mathrm{e}^{\kappa s}\sqrt{v_s}\mathrm{d}W_s^2 \end{aligned}$$

(36)

which leads to

$$\begin{aligned} v_t&={\mathbb {E}}[v_t]+\frac{\kappa \sigma _\theta }{\kappa -\alpha }\mathrm{e}^{-\alpha t}\int _{t_0}^t \mathrm{e}^{\alpha s} \mathrm{d}W_s^3 \\&\quad -\frac{\kappa \sigma _\theta }{\kappa -\alpha }\mathrm{e}^{-\kappa t}\int _{t_0}^t \mathrm{e}^{\kappa s} \mathrm{d}W_s^3 +\sigma _v \mathrm{e}^{-\kappa t}\int _{t_0}^t \mathrm{e}^{\kappa s}\sqrt{v_s}\mathrm{d}W_s^2 \end{aligned}$$

and

$$\begin{aligned} \theta _t={\mathbb {E}}[\theta _t]+\mathrm{e}^{-\alpha t}\int _{t_0}^t \mathrm{e}^{\alpha s}\sigma _\theta \mathrm{d}W_s^3, \end{aligned}$$

where

$$\begin{aligned} {\mathbb {E}}[v_t]&=v_{t_0}\mathrm{e}^{\kappa (t_0-t)}+\beta (1-\mathrm{e}^{\kappa (t_0-t)})+\frac{\kappa }{\kappa -\alpha }(\theta _{t_0}-\beta )(\mathrm{e}^{\alpha (t_0-t)}-\mathrm{e}^{\kappa (t_0-t)}), \\ {\mathbb {E}}[\theta _t]&=\theta _{t_0}\mathrm{e}^{\alpha (t_0-t)}+\beta (1-\mathrm{e}^{\alpha (t_0-t)}). \end{aligned}$$

Multiplying $v_t$ and $\theta _t$ and taking conditional expectation of the result, one can obtain

$$\begin{aligned} {\mathbb {E}}[v_t \theta _t]&={\mathbb {E}}[v_t]{\mathbb {E}}[\theta _t]+\frac{\kappa \mathrm{e}^{-2\alpha t}}{\kappa -\alpha }{\mathbb {E}}\left[ \int _{t_0}^t \mathrm{e}^{2\alpha s}\sigma _\theta ^2 \mathrm{d}s \right] \\&\quad -\frac{\kappa \mathrm{e}^{-(\alpha +\kappa ) t}}{\kappa -\alpha }{\mathbb {E}}\left[ \int _{t_0}^t \mathrm{e}^{(\alpha +\kappa ) s}\sigma _\theta ^2 \mathrm{d}s \right] \\&={\mathbb {E}}[v_t]{\mathbb {E}}[\theta _t]+\frac{\kappa \sigma _\theta ^2}{2\alpha (\kappa -\alpha )}(1-\mathrm{e}^{2\alpha (t_0-t)}) \\&\quad -\frac{\kappa \sigma _\theta ^2}{(\kappa +\alpha )(\kappa -\alpha )}(1-\mathrm{e}^{(\alpha +\kappa )(t_0-t)}). \end{aligned}$$

Also, the conditional expectation of the square of $v_t$ is calculated as

$$\begin{aligned} {\mathbb {E}}[v_t^2]&=\left( {\mathbb {E}}[v_t]\right) ^2+\left( \frac{\kappa }{\kappa -\alpha }\right) ^2 \mathrm{e}^{-2\alpha t}{\mathbb {E}}\left[ \int _{t_0}^t \mathrm{e}^{2\alpha s}\sigma _\theta ^2 \mathrm{d}s \right] \\&\quad +\left( \frac{\kappa }{\kappa -\alpha }\right) ^2 \mathrm{e}^{-2\kappa t}{\mathbb {E}}\left[ \int _{t_0}^t \mathrm{e}^{2\kappa s}\sigma _\theta ^2 \mathrm{d}s\right] \\&\quad -2\left( \frac{\kappa }{\kappa -\alpha }\right) ^2 \mathrm{e}^{-(\alpha +\kappa ) t}{\mathbb {E}}\left[ \int _{t_0}^t \mathrm{e}^{(\alpha +\kappa ) s}\sigma _\theta ^2 \mathrm{d}s \right] \\&\quad +\sigma _v^2 \mathrm{e}^{-2\kappa t}{\mathbb {E}}\left[ \int _{t_0}^t \mathrm{e}^{2\kappa s}v_s \mathrm{d}s\right] \\&=\left( {\mathbb {E}}[v_t]\right) ^2+\Lambda _2(t;t_0)+\left( \frac{\kappa \sigma _\theta }{\kappa -\alpha }\right) ^2\Bigg \{\frac{1}{2\kappa }(1-\mathrm{e}^{2\kappa (t_0-t)})\\&\quad +\frac{1}{2\alpha }(1-\mathrm{e}^{2\alpha (t_0-t)})-\frac{2}{\kappa +\alpha }(1-\mathrm{e}^{(\alpha +\kappa )(t_0-t)})\Bigg \}, \end{aligned}$$

where

$$\begin{aligned} \Lambda _2(t;t_0)&:=\sigma _v^2 \mathrm{e}^{-2\kappa t}{\mathbb {E}}\left[ \int _{t_0}^t \mathrm{e}^{2\kappa s}v_s \mathrm{d}s\right] \\&=\sigma _v^2\Big [\frac{(v_{t_0}-\beta )}{\kappa }(\mathrm{e}^{\kappa (t_0-t)}-\mathrm{e}^{2\kappa (t_0-t)})+\frac{\beta }{2\kappa }(1-\mathrm{e}^{2\kappa (t_0-t)})\\&\quad +\frac{\kappa (\theta _{t_0}-\beta )}{(\kappa -\alpha )(2\kappa -\alpha )}(\mathrm{e}^{\alpha (t_0-t)}-\mathrm{e}^{2\kappa (t_0-t)})\\&\quad -\frac{(\theta _{t_0}-\beta )}{\kappa -\alpha }(\mathrm{e}^{\kappa (t_0-t)}-\mathrm{e}^{2\kappa (t_0-t)})\Big ]. \end{aligned}$$

Appendix B: Continuously sampled variance and volatility swaps

The exact and approximate fair strike solution formulas for both variance and volatility swaps are derived, respectively, in the continuously sampled case as follows.

The fair strikes of continuously sampled variance and volatility swaps are defined by

$$\begin{aligned} K^c_{\text {var}}&= {\mathbb {E}}\left[ \frac{1}{T}\int _{0}^{T} v_{t}\mathrm{d}t\right] , \\ K^c_{\text {vol}}&= {\mathbb {E}}\left[ \sqrt{\frac{1}{T}\int _{0}^{T} v_{t}\mathrm{d}t}\right] , \end{aligned}$$

respectively, where $v_{t}$ is a stochastic variance process. The exact value of $K^c_{\text {var}}$ can be computed using the results of Appendix A.1 and A.2 directly. However, it is difficult to derive the exact formula of $K^c_{\text {vol}}$. Thus we manipulate the problem using the Brockhaus-Long (2000) approximation to obtain an approximate value of $K^c_{\text {vol}}$. Using a random variable V defined by

$$\begin{aligned} V = \frac{1}{T}\int _{0}^{T} v_{t}\mathrm{d}t, \end{aligned}$$

one can express $K^c_{\text {var}}$ and $K^c_{\text {vol}}$ as

$$\begin{aligned} K^c_{\text {var}}&= {\mathbb {E}}[V], \\ K^c_{\text {vol}}&= {\mathbb {E}}[\sqrt{V}] \thickapprox \sqrt{{\mathbb {E}}[V]} - \frac{\text {Var}[V]}{({\mathbb {E}}[V])^{3/2}}, \end{aligned}$$

respectively, where $\text {Var}[V]$ means the variance of V.

1.1 B.1: The He–Chen model

Using the expectation of $v_t$ given in Appendix A.1, the value of the fair strike $K^c_{\text {var}}$ under the He–Chen model is derived as

$$\begin{aligned} K^c_{\text {var}}&= {\mathbb {E}}[V] \nonumber \\&=\frac{1}{T}\int _{0}^{T} {\mathbb {E}}[v_{t}]\mathrm{d}t \nonumber \\&=\frac{1}{T}\int _{0}^{T} \left\{ \left( v_{0}-\theta _{0}+\frac{\lambda }{\kappa }\right) \mathrm{e}^{-\kappa t}+\lambda \kappa + \left( \theta _{0}-\frac{\lambda }{\kappa }\right) \right\} \mathrm{d}t \nonumber \\&= \frac{1}{\kappa T}\left( v_{0}-\theta _{0}+\frac{\lambda }{\kappa }\right) (1-\mathrm{e}^{-\kappa T})+\frac{1}{2}\lambda T + \left( \theta _{0}-\frac{\lambda }{\kappa }\right) . \end{aligned}$$

(37)

On the other hand, noting that the expectation of $V^{2}$ is expressed as

$$\begin{aligned} {\mathbb {E}}[V^2]&=\frac{1}{T^2}\int _{0}^{T}\int _{0}^{T}{\mathbb {E}}[v_s v_t ]\mathrm{d}s\mathrm{d}t, \end{aligned}$$

(38)

we use (30) and the property of Ito integral to obtain

$$\begin{aligned} {\mathbb {E}}[v_s v_t ]&={\mathbb {E}}[v_t]{\mathbb {E}}[v_s] + \frac{\sigma _\theta ^2}{\mathrm{e}^{k(t+s)}}{\mathbb {E}}\left[ \int _{0}^{s\wedge t} \mathrm{e}^{2\kappa \eta } \mathrm{d}\eta \right] +\frac{\sigma _v^2}{\mathrm{e}^{k(t+s)}}{\mathbb {E}}\left[ \int _{0}^{s\wedge t}\mathrm{e}^{2\kappa \eta } v_\eta \mathrm{d}\eta \right] \nonumber \\&=\left( {\mathbb {E}}[v_t]\right) ^{2}+\frac{\sigma _\theta ^2}{\mathrm{e}^{k(t+s)}}\int _{0}^{s\wedge t} \mathrm{e}^{2\kappa \eta } \mathrm{d}\eta + \frac{\sigma _v^2}{\mathrm{e}^{k(t+s)}}\int _{0}^{s\wedge t} \mathrm{e}^{2\kappa \eta } {\mathbb {E}}\left[ v_\eta \right] \mathrm{d}\eta \nonumber \\&=\left( {\mathbb {E}}[v_t]\right) ^{2}+\frac{\sigma _\theta ^2}{2\kappa \mathrm{e}^{k(t+s)}}\left( \mathrm{e}^{2k(s\wedge t))}-1\right) \nonumber \\&\quad +\frac{\sigma _v^2}{\kappa \mathrm{e}^{k(t+s)}}\left\{ \left( v_{0}-\theta _{0}+\frac{\lambda }{\kappa }\right) \left( \mathrm{e}^{k(s\wedge t)}-1\right) +\frac{\lambda }{2}(s \wedge t) \mathrm{e}^{2k(s\wedge t)}\right. \nonumber \\&\quad \left. +\left( \frac{\theta _0}{2}-\frac{3 \lambda ^2}{4\kappa }\right) \left( \mathrm{e}^{2k(s\wedge t))}-1\right) \right\} , \end{aligned}$$

(39)

where $s \wedge t := \text {min}(t,s)$. By (38) and (39), we have

$$\begin{aligned} {\mathbb {E}}[V^2]&=\left( E[V]\right) ^{2}+\frac{\sigma _{\theta }^2 }{2 \kappa ^3 T^2}\left( 4\mathrm{e}^{-\kappa T}-\mathrm{e}^{-2\kappa T}-3+2\kappa T\right) \\&\quad +\frac{\sigma _{v}^2}{\kappa ^3 T^2}\Bigg \{\left( v_{0}-\theta _{0}+\frac{\lambda }{\kappa }\right) \left( 1 - \mathrm{e}^{-2\kappa T} -2\kappa T \mathrm{e}^{-\kappa T}\right) \\&\quad +\frac{\lambda }{\kappa }\left( \frac{\kappa ^2 T^2}{2} - \kappa T - \mathrm{e}^{-\kappa T} + 1\right) +\left( \frac{\theta _0}{2}-\frac{3 \lambda ^2}{4\kappa }\right) \left( 4\mathrm{e}^{-\kappa T}-\mathrm{e}^{-2\kappa T}-3+2\kappa T\right) \Bigg \} \end{aligned}$$

and

$$\begin{aligned} \text {Var}[V]&= {\mathbb {E}}[V^2] - \left( E[V]\right) ^{2} \nonumber \\&=\frac{\sigma _{\theta }^2 }{2 \kappa ^3 T^2}\left( 4\mathrm{e}^{-\kappa T}-\mathrm{e}^{-2\kappa T}-3+2\kappa T\right) \nonumber \\&\quad +\frac{\sigma _{v}^2}{\kappa ^3 T^2}\Bigg \{\left( v_{0}-\theta _{0}+\frac{\lambda }{\kappa }\right) \left( 1 - \mathrm{e}^{-2\kappa T} -2\kappa T \mathrm{e}^{-\kappa T}\right) \nonumber \\&\quad +\frac{\lambda }{\kappa }\left( \frac{\kappa ^2 T^2}{2} - \kappa T - \mathrm{e}^{-\kappa T} + 1\right) +\left( \frac{\theta _0}{2}-\frac{3 \lambda ^2}{4\kappa }\right) \left( 4\mathrm{e}^{-\kappa T}-\mathrm{e}^{-2\kappa T}-3+2\kappa T\right) \Bigg \}. \end{aligned}$$

(40)

Therefore, the value of the fair strike $K^c_{\text {vol}}$ under the He–Chen model is approximated as

$$\begin{aligned} K^c_{\text {vol}}&\thickapprox \sqrt{K^c_{\text {var}}} - \frac{\text {Var}[V]}{({\mathbb {E}}[V])^{3/2}}, \end{aligned}$$

where $K^c_{\text {var}}$ and $\text {Var}[V]$ are given by (37) and (40), respectively.

1.2 B.2: The rDMR model

Using the expectation of $v_t$ in Appendix 1, the value of the fair strike $K^c_{\text {var}}$ under the rDMR model is derived as

$$\begin{aligned} K^c_{\text {var}}&= {\mathbb {E}}[V] \nonumber \\&=\frac{1}{T}\int _{0}^{T} {\mathbb {E}}[v_{t}]\mathrm{d}t \nonumber \\&=\frac{1}{T}\int _{0}^{T} \left\{ \left( v_{0}+\frac{\alpha \beta }{\kappa -\alpha }-\frac{\kappa \theta _{0}}{\kappa -\alpha }\right) \mathrm{e}^{-\kappa t}+\frac{\kappa }{\kappa -\alpha }\left( \theta _{0}-\beta \right) \mathrm{e}^{-\alpha t} + \beta \right\} \mathrm{d}t \nonumber \\&= \frac{1}{T}\left( \frac{v_{0}}{\kappa }+\frac{\alpha \beta }{\kappa (\kappa -\alpha )}-\frac{ \theta _{0}}{\kappa -\alpha }\right) (1-\mathrm{e}^{-\kappa T})+\frac{\kappa \left( \theta _{0}-\beta \right) }{T\alpha (\kappa -\alpha )}(1-\mathrm{e}^{-\alpha T})+\beta . \end{aligned}$$

(41)

On the other hand, from (36) we have

$$\begin{aligned} {\mathbb {E}}[v_s v_t ]&={\mathbb {E}}[v_t]{\mathbb {E}}[v_s] + \sigma _v^2\mathrm{e}^{-\kappa (t+s)}{\mathbb {E}}\left[ \int _{0}^{(s \wedge t)}\mathrm{e}^{2 \kappa \eta }v_\eta \mathrm{d}\eta \right] \nonumber \\&\quad +\left( \frac{\kappa \sigma _\theta }{\kappa -\alpha }\right) ^{2}\mathrm{e}^{-\alpha (t+s)}{\mathbb {E}}\left[ \int _{0}^{(s \wedge t)}\mathrm{e}^{2 \alpha \eta }\mathrm{d}\eta \right] \nonumber \\&\quad +\left( \frac{\kappa \sigma _\theta }{\kappa -\alpha }\right) ^{2}\mathrm{e}^{-\alpha (t+s)}{\mathbb {E}}\left[ \int _{0}^{(s \wedge t)}\mathrm{e}^{2 \kappa \eta }\mathrm{d}\eta \right] \nonumber \\&\quad -\left( \frac{\kappa \sigma _\theta }{\kappa -\alpha }\right) ^{2}\left( \mathrm{e}^{-\alpha t -\kappa s}+\mathrm{e}^{-\kappa t -\alpha s}\right) {\mathbb {E}}\left[ \int _{0}^{(s \wedge t)}\mathrm{e}^{(\kappa +\alpha ) \eta }\mathrm{d}\eta \right] \nonumber \\&={\mathbb {E}}[v_t]{\mathbb {E}}[v_s]+\frac{1}{2\alpha }\left( \frac{\kappa \sigma _\theta }{\kappa -\alpha }\right) ^{2}\mathrm{e}^{-\alpha (t+s)}(\mathrm{e}^{2\alpha (s \wedge t)}-1)\nonumber \\&\qquad +\frac{1}{2\kappa }\left( \frac{\kappa \sigma _\theta }{\kappa -\alpha }\right) ^{2}\mathrm{e}^{-\kappa (t+s)}(\mathrm{e}^{2\kappa (s \wedge t)}-1) \nonumber \\&\quad -\frac{1}{\kappa +\alpha }\left( \frac{\kappa \sigma _\theta }{\kappa -\alpha }\right) ^{2}\mathrm{e}^{-\kappa t -\alpha s)}(\mathrm{e}^{(\kappa +\alpha )(s \wedge t)}-1)\nonumber \\&\qquad -\frac{1}{\kappa +\alpha }\left( \frac{\kappa \sigma _\theta }{\kappa -\alpha }\right) ^{2}\mathrm{e}^{-\alpha t -\kappa s)}(\mathrm{e}^{(\kappa +\alpha )(s \wedge t)}-1) \nonumber \\&\quad +\frac{\sigma _v^2}{\kappa }\left( v_{0}+\frac{\alpha \beta }{(\kappa -\alpha )}-\frac{ \kappa \theta _{0}}{\kappa -\alpha }\right) \mathrm{e}^{-\kappa (t+s)}(\mathrm{e}^{\kappa (s \wedge t)}-1) \nonumber \\&\quad +\frac{\sigma _v^2 \kappa (\theta _0 - \beta )}{(\kappa -\alpha )(2\kappa -\alpha )}\mathrm{e}^{-\kappa (t+s)}(\mathrm{e}^{(2\kappa -\alpha )(s \wedge t)}-1) +\frac{\sigma _v^2 \beta }{2\kappa }\mathrm{e}^{-\kappa (t+s)}(\mathrm{e}^{2\kappa (s \wedge t)}-1). \end{aligned}$$

(42)

From (38) and (42), we obtain

$$\begin{aligned} \text {Var}[V]&= {\mathbb {E}}[V^2] - \left( E[V]\right) ^{2} \nonumber \\&=\frac{1}{2\alpha ^3 T^2}\left( \frac{\kappa \sigma _\theta }{\kappa -\alpha }\right) ^{2}\left( 4\mathrm{e}^{-\alpha T}-\mathrm{e}^{-2\alpha T}-3+2\alpha T\right) \nonumber \\&\quad +\frac{1}{2\kappa ^3 T^2}\left( \frac{\kappa \sigma _\theta }{\kappa -\alpha }\right) ^{2}\left( 4\mathrm{e}^{-\kappa T}-\mathrm{e}^{-2\kappa T}-3+2\kappa T\right) \nonumber \\&\quad -\frac{2}{T^2(\kappa +\alpha )}\left( \frac{\kappa \sigma _\theta }{\kappa -\alpha }\right) ^{2}\nonumber \\&\quad \left( \frac{T}{\kappa }+\frac{\mathrm{e}^{-\kappa T}}{\kappa ^2}-\frac{1}{\kappa ^2}+\frac{T}{\alpha }+\frac{\mathrm{e}^{-\alpha T}}{\alpha ^2}-\frac{1}{\alpha ^2}-\frac{(1-\mathrm{e}^{-\kappa T})(1-\mathrm{e}^{-\alpha T})}{\kappa \alpha }\right) \nonumber \\&\quad +\frac{\sigma _{v}^{2}}{\kappa ^{3} T^{2}}\left( v_{0}+\frac{\alpha \beta }{(\kappa -\alpha )}-\frac{ \kappa \theta _{0}}{\kappa -\alpha }\right) \left( 1-\mathrm{e}^{-2\kappa T}-2\kappa T\mathrm{e}^{-\kappa T}\right) \nonumber \\&\quad +\frac{2\sigma _v^2 \kappa (\theta _{0}-\beta )}{T^2(\kappa -\alpha )^{2}(\kappa -2\alpha )}\left( \frac{1}{\alpha }(1-\mathrm{e}^{-\alpha T}) -\frac{1}{\kappa }(1-\mathrm{e}^{-\kappa T})\right) \nonumber \\&\quad +\frac{\sigma _v^2 \kappa (\theta _{0}-\beta )}{T^2\kappa ^{2}(\kappa -\alpha )(\kappa -2\alpha )} \left( 2\mathrm{e}^{-\kappa T}-\mathrm{e}^{-2\kappa T}-1\right) \nonumber \\&\quad +\frac{\sigma _v^2 \beta }{2\kappa ^3 T^2 }\left( 4\mathrm{e}^{-\kappa T}-\mathrm{e}^{-2\kappa T}-3+2\kappa T\right) . \end{aligned}$$

(43)

Therefore, one can get a closed-form approximation formula of the fair strike $K^c_{\text {vol}}$ under the rDMR model using (41) and (43).