Strategic Growth with Recursive Preferences: Decreasing Marginal Impatience

Abstract

This paper studies a two-agent strategic model of capital accumulation with heterogeneity in preferences and income shares. Preferences are represented by recursive utility functions that satisfy decreasing marginal impatience. The stationary equilibria of this dynamic game are analyzed under two alternative information structures: one in which agents precommit to future actions, and another one where they use Markovian strategies. In both cases, we develop sufficient conditions to show the existence of these equilibria and characterize their stability properties. Under certain regularity conditions, a precommitment equilibrium shows monotone convergence of aggregate variables, but Markovian equilibria may exhibit nonmonotonic paths, even in the long-run.

Appendices

Appendix

Some Fundamental Issues: Details and Proofs

1.1 Joint Concavity

In this section, we develop sufficient conditions for the joint concavity of each player’s utility function. We base our analysis on the following results from Horn and Johnson [31].

Definition 4

Let $M_n$ be the space of real-valued symmetric matrices with element $A=[a_{ij}]$. The matrix A is said to be diagonally dominant if

$$\begin{aligned} |a_{ii}| \ge \sum _{j \ne i}|a_{ij}| \quad \text {for all } i=1,\ldots ,n. \end{aligned}$$

It is said to be strictly diagonally dominant if

$$\begin{aligned} |a_{ii}| > \sum _{j \ne i}|a_{ij}| \quad \text {for all } i=1,\ldots ,n. \end{aligned}$$

Theorem 3

If $A=[a_{ij}] \in M_n$ is strictly diagonally dominant and if $a_{ii} < 0$ for all $i=1,2,\ldots ,n$, then A is negative definite.

1.1.1 Strict Diagonal Dominance and Strict Concavity

To simplify the exposition, the superscripts $i,j=1,2$ will be omitted. First, we consider a finite-horizon version of the intertemporal utility function (1), which is simply

$$\begin{aligned} w_0^T(\mathbf {c}_T)=\sum _{t=0}^T\left( \prod _{s=0}^{t-1} \alpha (c_s)\right) u(c_t), \end{aligned}$$

(62)

where $1 \le T < \infty$ and $\mathbf {c}_T:=(c_0,c_1,\ldots ,c_T)$ denotes a finite consumption sequence, and develop some conditions to determine whether $w_0^T$ is concave. Second, we analyze the limiting behavior of this utility function as T tends to infinity.¹⁵

Some preliminaries are needed for the analysis. Let $\mathbf {c}_{t,T}:=(c_t,c_{t+1},\ldots ,c_{T-1},c_{T})$, with $\mathbf {c}_{0,T}:= \mathbf {c}_T$, denote a consumption subsequence of $\mathbf {c}_T$ starting at some $0 \le t < T$. The continuation utility associated to $\mathbf {c}_{t,T}$ will be defined as

$$\begin{aligned} w_t^T(\mathbf {c}_{t,T}):= \sum _{s=t}^T\left( \prod _{\tau =t}^{s-1}\alpha (c_\tau )\right) u(c_s). \end{aligned}$$

(63)

We also adopt the convention that $w_T^T = u(c_T)$.

To simplify notation, let $u_t:=u(c_t)$ and $\alpha _t:=\alpha (c_t)$, for each $c_t \ge 0$. Hence, the objective function can be written more succinctly as

$$\begin{aligned} w_0^T(\mathbf {c}_{T})=\sum _{t=0}^T\beta _t u_t, \end{aligned}$$

(64)

where $\beta _t:= \prod _{s=0}^{t-1}\alpha _s$ is the discount factor at period $t=0,1,\ldots ,T$. Then, we compute the first and second partial derivatives of $w_0^T$, which are given by

$$\begin{aligned} \frac{\partial {w_0^T}}{\partial {c_t}}= {\left\{ \begin{array}{ll} \beta _t\left( u_t'+\alpha _t'\,w_{t+1}^T\right) &{} \text {if }\, t=0,1,\ldots ,T-1,\\ \beta _T u_T' &{} \text {if }\, t=T, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2{w_0^T}}{\partial {c_s}\partial {c_t}}= {\left\{ \begin{array}{ll} \beta _t\left( u_t''+\alpha _t''\,w_{t+1}^T\right) &{} \text {if }\, s=t=0,1,\ldots ,T-1,\\ \frac{\alpha _t'}{\alpha _t}\,\beta _s\left( u_s'+\alpha _s'\,w_{s+1}^T\right) &{} \text {if }\, s \ne t=0,1,\ldots ,T-1,\\ \beta _t\,u_t'' &{} \text {if }\, s=t=T,\\ \frac{\alpha _t'}{\alpha _t}\beta _s u_s' &{} \text {if }\, s \ne t=T. \end{array}\right. } \end{aligned}$$

We also introduce the following notation, which will be used throughout the paper:

$$\begin{aligned} \delta _t:=\frac{\alpha _t'}{\alpha _t}, \quad U_t^T:=u_t'+\alpha _t'\,w_{t+1}^T, \quad \text {and} \quad W_t^T:=u_t''+\alpha _t''\,w_{t+1}^T, \end{aligned}$$

for all $t=0,1,\ldots ,T$.

As mentioned earlier, showing that (62) is strictly concave at $\mathbf {c}_T$ is equivalent to proving that the Hessian matrix of $w_0^T$ has negative diagonal entries and is strictly diagonally dominant at $\mathbf {c}_T$. The Hessian matrix of $w_0^T$ at $\mathbf {c}_T$ is given by:

$$\begin{aligned} {\mathscr {H}}(w_0^T):= \begin{bmatrix} W_0^T&\delta _0\beta _1 U_1^T&\cdots&\delta _0\beta _{T-1} U_{T-1}^T&\delta _0\beta _T u_T'\\ \delta _0\beta _1 U_1^T&\beta _1 W_1^T&\cdots&\delta _1\beta _{T-1} U_{T-1}^T&\delta _1\beta _T u_T'\\ \vdots&\vdots&\vdots&\ddots&\vdots \\ \delta _0\beta _{T-1} U_{T-1}^T&\delta _1\beta _{T-1} U_{T-1}^T&\cdots&\beta _{T-1} W_{T-1}^T&\delta _{T-1}\beta _T u_T'\\ \delta _0\beta _T u_T'&\delta _1\beta _T u_T'&\cdots&\delta _{T-1}\beta _T u_T'&\beta _T u_T''\\ \end{bmatrix}. \end{aligned}$$

(65)

Note that all the diagonal entries in this matrix are strictly negative. Applying the result from Theorem 3, the following $(T+1)$ inequalities must hold for the strict diagonal dominance of ${\mathscr {H}}$:

$$\begin{aligned} \beta _t\left( \delta _t U_t^T-W_t^T\right)&> \beta _t D_t +\delta _t\left( \sum _{\tau =t}^{T-1}\beta _\tau U_\tau ^T + \beta _T u_T'\right) ,&t=0,1\ldots ,T-1, \end{aligned}$$

(66)

$$\begin{aligned} \beta _T|u_T''|&> \beta _T D_T u_T', \end{aligned}$$

(67)

where $D_t : = \sum _{s=0}^{t-1}\delta _s$, for all t.¹⁶

Certain conditions must be imposed for (66)–(67) to be well defined in the limit as $T \rightarrow \infty$. Since most of our results are developed for neighborhoods of interior stationary points, it is reasonable to restrict the analysis to convergent positive consumption sequences. Then, we assume that $\mathbf {c}_T$ converges to some feasible value, say $c >0$. Let $w_t$ be the infinite-horizon continuation value at t, given by $w_t:=\lim _{T \rightarrow \infty } w_t^T$. This limit is well defined if the consumption sequence is convergent. In turn, this allows us to define

$$\begin{aligned} U_t:=\displaystyle \lim _{T \rightarrow \infty } U_t^T \quad \text {and} \quad W_t:=\displaystyle \lim _{T \rightarrow \infty } W_t^T, \quad \text {for all }\ t. \end{aligned}$$

Further suppose that ${\mathscr {U}}_t: = \lim _{T \rightarrow \infty }\ \sum _{\tau =t}^T \beta _\tau U_\tau$ exists in ${\mathbb {R}}_+$, for all t. Note that these definitions are consistent with the notation introduced in Sect. 4 and used throughout the paper. We can conclude that the conditions for strict diagonal dominance for the Hessian matrix ${\mathscr {H}}$ in the infinite-horizon case are

$$\begin{aligned}&\beta _t(\delta _t U_t-W_t) \ge \beta _t D_t +\delta _t\,{\mathscr {U}}_t,&t=0,1,\ldots , \end{aligned}$$

(68)

$$\begin{aligned}&\lim _{t \rightarrow \infty } \beta _t\left( |u_t''|-D_t u_t'\right) \ge 0, \end{aligned}$$

(69)

that are obtained taking limits in (66)–(67).

1.1.2 An Example

We consider similar functional forms as in Stern [52] and Erol et al. [26], adapted to our framework. The discount function is assumed to have the exponential form

$$\begin{aligned} \alpha (c) = {\bar{\alpha }} \exp \left[ -(c+\rho )^{-\gamma }\right] , \end{aligned}$$

with $0< {\bar{\alpha }} < 1$, $1< \rho < +\infty$, and $0< \gamma < 1$, and the periodic utility function belongs to the standard CRRA class,¹⁷

$$\begin{aligned} u(c)={\left\{ \begin{array}{ll} \dfrac{c^{1-\sigma }-1}{1-\sigma }, &{} \text {if}\, 0< \sigma < +\infty ,\ \sigma \ne 1,\\ \log (c), &{} \text {if}\, \sigma =1. \end{array}\right. } \end{aligned}$$

Then, for some positive consumption sequence $\mathbf {c}=\{c_t\}_{t=0}^\infty$ that converges to some $c >0$, we have that

$$\begin{aligned} \beta _t&= {\bar{\alpha }}^t {\text {e}}^{-\sum _{s=0}^{t-1}(c_s+\rho )^{-\gamma }}, \quad \delta _t= \frac{\gamma }{(c_t+\rho )^{1+\gamma }},\\ D_t&= \sum _{s=0}^{t-1} \frac{\gamma }{(c_s+\rho )^{1+\gamma }}, \quad \quad U_t = c_t^{-\sigma }+\frac{{\bar{\alpha }}\,{\text {e}}^{-(c_t+\rho )^{-\gamma }}\gamma }{(c_t+\rho )^{1+\gamma }}\,w_{t+1},\\ W_t&=-\sigma \,c_t^{-\sigma -1}+\frac{{\bar{\alpha }}\,{\text {e}}^{-(c_t+\rho )^{-\gamma }}\gamma ^2}{(c_t+\rho )^{2(1+\gamma )}}\left[ 1-\left( \tfrac{1+\gamma }{\gamma }\right) (c_t+\rho )^\gamma \right] \,w_{t+1}, \end{aligned}$$

where

$$\begin{aligned} w_t = \sum _{s=t}^\infty \left[ {\bar{\alpha }}^s {\text {e}}^{-\sum _{\tau =t}^{s-1}(c_\tau +\rho )^{-\gamma }}\right] \frac{c_s^{1-\sigma }-1}{1-\sigma }. \end{aligned}$$

Observe that $\lim _{t \rightarrow \infty } \beta _t =0$ and $0< \delta _t < \gamma$, for all t. Moreover, if $w_{t+1} > 0$, then $W_t$ is negative, as $c_t+ \rho > (\gamma /(1+\gamma ))^{\frac{1}{\gamma }}$.

In order to determine the conditions for strict diagonal concavity given in (68), we need the following

$$\begin{aligned} \delta _t U_t - W_t =&\sigma \,c_t^{-\sigma -1}\left[ 1 + \frac{\gamma \,c_t}{\sigma (c_t+\rho )^{1+\gamma }}\right] +\frac{{\bar{\alpha }}\gamma (1+\gamma )\,{\text {e}}^{-(c_t+\rho )^{-\gamma }}}{(c_t+\rho )^{2(1+\gamma )}}\,w_{t+1},\\ \beta _t\,D_t&={\bar{\alpha }}^t {\text {e}}^{-\sum _{s=0}^{t-1}(c_s+\rho )^{-\gamma }}\sum _{s=0}^{t-1} \frac{\gamma }{(c_s+\rho )^{1+\gamma }},\\ \delta _t\,{\mathscr {U}}_t&=\frac{\gamma }{(c_t+\rho )^{1+\gamma }}\sum _{\tau =t}^\infty {\bar{\alpha }}^\tau {\text {e}}^{-\sum _{s=t}^{\tau -1}(c_s+\rho )^{-\gamma }}\left[ c_\tau ^{-\sigma }+\frac{{\bar{\alpha }}\,{\text {e}}^{-(c_\tau +\rho )^{-\gamma }}\gamma }{(c_\tau +\rho )^{1+\gamma }}\,w_{\tau +1}\right] . \end{aligned}$$

Finally, (69) holds provided that

$$\begin{aligned} \beta _t\left( |u''(c_t)|-D_t u'(c_t)\right)&= {\bar{\alpha }}^t {\text {e}}^{-\sum _{s=0}^{t-1}(c_s+\rho )^{-\gamma }}\left[ \sigma \,c_t^{-\sigma -1}-\sum _{s=0}^{t-1} \frac{\gamma }{(c_s+\rho )^{1+\gamma }}\,c_t^{-\sigma }\right] \end{aligned}$$

is nonnegative as $t \rightarrow \infty$.

1.2 Existence

Proof of Proposition 1

Existence follows from standard arguments. The remaining of the proof is divided into two steps. $\square$

Step 1. The following “auxiliary problem” is directly related to the definition of variational utility

The assumption that $\mathbf {c}^i \in \ell _\infty$ is justified by the fact that $c_t^i \in [0,\theta ^i f(k_m)]$, for all t, in the original saddle-point problem ($\text {SVP}^i$). The first inequality restriction above could be also considered as an equality restriction. But this formulation allows to keep certain symmetry between the inf and the sup problems, and rules out an uninteresting solution with $\mathbf {B}^i=(1,0,0,\ldots ,0,\ldots )$ for any $\mathbf {c}^i \in \ell _\infty$, which could arise if the reverse inequality holds.

Clearly, the problem (VP$^i$) fits into the framework of Dechert [21], who solves an optimization problem of the form $\inf _{\mathbf {x} \in \ell _\infty }\ \left\{ F(\mathbf {x}):\varPhi (\mathbf {x}) \le 0\right\}$, where $F:\ell _\infty \rightarrow {\mathbb {R}}$ and $\varPhi :\ell _\infty \rightarrow \ell _\infty$. Simply put $\mathbf {x}:=\mathbf {B}^i$, define $F(\mathbf {x}):=\sum _{t=0}^\infty G_t(\mathbf {x})$, where $G_t(\mathbf {x})=\beta _t^i u_i(c_t^i)$ for each t, and $\varPhi (\mathbf {x})$ as $\varPhi _t(\mathbf {x}):=(\varPhi _t^1(\mathbf {x}),\varPhi _t^2(\mathbf {x}))$, for each t, where $\varPhi _t^1(\mathbf {x}):=\alpha _i(c_t^i)\beta _t^i-\beta _{t+1}^i$ and $\varPhi _t^2(\mathbf {x}):=-\beta _{t+1}^i$.

To characterize a solution, it suffices to show that (VP$^i$) satisfies the hypothesis of Theorems 2 and 3 in Dechert [21]. This is guaranteed by the following set of conditions:

• (A1) each $G_t$, $\varPhi _t^1$, and $\varPhi _t^2$ is convex and continuous for all t;

• (A2) for all $\mathbf {x} \in \ell _\infty$, $\{G_t\} \in \ell _1$ and $\{\varPhi _t\} \in \ell _\infty$;

• (A3) there exists $\mathbf {x}^0 \in \ell _\infty$ such that $\sup _t \varPhi _t(\mathbf {x}^0) < 0$ (Slater condition).

Conditions (A1) and (A2) are straightforward. To verify (A3), note that under assumptions (U1)–(U4) on $\alpha _i$ and $u_i$, for any ${\mathbf {c}}^i \in \ell _\infty$, it follows that $\alpha _i(0) \le \alpha _i(c_t^i) \le {\overline{\alpha }}_i < 1$, for all t and for each $i=1,2$. Then the sequence $\mathbf {x}^0 = (1,1,\ldots ,1,\ldots )$ yields $\varPhi _t^1(\mathbf {x}^0) = -\left( 1-\alpha _i(c_t^i)\right) \le -(1-{\overline{\alpha }}^i) < 0$ and $\varPhi _t^2(\mathbf {x}^0) = -1 < 0$, for all t, hence $\sup _t\varPhi _t(\mathbf {x}^0) < 0$ holds. Therefore, there exist $\mathbf {B}^i \in \ell _\infty$ and sequences of Lagrange multipliers, $\mathbf {m}^i:=\{\mu _{t+1}\}_{t=0}^\infty$ in $\ell _1$ and $\mathbf {n}^i :=\{\nu _{t+1}\}_{t=0}^\infty$ in $\ell _1$, such that

$$\begin{aligned} \mu _{t+1}^i + \nu _{t+1}^i = u_i(c_{t+1}^i) + \alpha _i(c_{t+1}^i) \mu _{t+2}^i,&t=0,1,\ldots , \end{aligned}$$

(70)

and the complementary slackness conditions

$$\begin{aligned} \mu _{t+1}^i\left[ \alpha _i(c_t^i)\beta _t^i-\beta _{t+1}^i\right]&= 0,&t=0,1,\ldots , \end{aligned}$$

(71a)

$$\begin{aligned} \nu _{t+1}^i\left( -\beta _{t+1}^i\right)&=0,&t=0,1,\ldots . \end{aligned}$$

(71b)

are satisfied.

In Dechert’s formulation, transversality conditions are implicit from (70)–(71). But the transversality condition $\lim _{t \rightarrow \infty }\ \mu _{t+1}^i\beta _{t+1}^i = 0$ in (5) has a more meaningful economic interpretation and can be obtained in the usual way. Assuming an infinite horizon $T \ge 1$, optimality implies that $\mu _{T+1}^i=-\nu _{T+1}^i$. But since (71b) must also hold at infinity, simply take $T \rightarrow \infty$, and the desired result follows. Note that $\beta _{t+1}^i = 0$ can never be optimal for any finite $t \ge 0$, then from (71), $\nu _{t+1}^i =0$ and $\mu _{t+1}^i > 0$ along any optimal path. Given that $\beta _{t+1}^i = \alpha _i(c_t^i)\beta _t^i$, for all t, $\beta _{t+1}^i \rightarrow 0$ as $t \rightarrow \infty$, which implies that the transversality condition is satisfied. It also follows that $\mathbf {m}^i \in (\ell _1)_+ \backslash \{0\}$.

Now, evaluate (70) at $t=0$ and multiply by $\beta _1^i$ on both sides of the equality to obtain

$$\begin{aligned} \beta _1^i\mu _1^i&= \beta _1^i u_i(c_1^i) + \beta _1^i\alpha _i(c_1^i)\mu _2^i = \beta _1^i u_i(c_1^i) + \beta _2^i\mu _2^i. \end{aligned}$$

Continuing this iterative procedure, at the Tth step we have that

$$\begin{aligned} \beta _1^i\mu _1^i = \beta _1^i u_i(c_1^i) + \cdots + \beta _T^i u_i(c_T^i) + \beta _{T+1}^i \mu _{T+1}^i. \end{aligned}$$

As $T \rightarrow \infty$, the transversality condition $\lim _{T \rightarrow \infty } \mu _{T+1}^i\beta _{T+1}^i = 0$ implies that

$$\begin{aligned} \mu _0^i := u(c_0^i)+ \beta _1^i\mu _1^i = \sum _{t=0}^\infty \beta _t^i u_i(c_t^i), \end{aligned}$$

hence $\mu _0^i$ is the optimal value of ($\text {SVP}^i$) for player i. In other words, the dual problem

yields the same value $\mu _0^i$ as (VP$^i$), for any $\mathbf {c}^i \in \ell _\infty$.

Step 2. Next, using (dVP$^i$), the original problem ($\text {SVP}^i$) can be reformulated in terms of $(\mathbf {c}^i,\mathbf {k}^i)$ and the dual variable $\mathbf {m}^i$ as follows

The analysis is similar to Step 1, applying additional results from Le Van and Saglam [34], since the objective and the restrictions now satisfy Inada conditions and can take values in the extended real line. The main difference is that the solution must be interior, which explains the fact that each decision variable is restricted to $(\ell _\infty )_+$ and the multipliers $\lambda _t^i$ and $\mu _{t+1}^i$ are strictly positive. Obviously, conditions (A1)–(A3) need to be appropriately reformulated. To verify these conditions, the arguments of Examples 1 and 2 in Le Van and Saglam [34] (pages 399–407) can be easily adapted to the current setup, so the details are left to the reader.

As the nonnegativity constraints can be safely ignored, the Lagrangian associated to (dSVP$^i$) is

$$\begin{aligned} L^i&:= u_i(c_0^i) + \alpha _i(c_0^i)\mu _1^i + \sum _{t=0}^\infty \left\{ \lambda _t^i\left[ \theta ^i f(k_t^i+k_t^j)-c_t^i - k_{t+1}^i\right] \right. \\&\quad \left. +\, \varepsilon _{t+1}^i\left[ u_i(c_{t+1}^i) + \alpha _i(c_{t+1}^i)\mu _{t+2}-\mu _{t+1}^i\right] \right\} . \end{aligned}$$

Then, from Theorem 2 in Le Van and Saglam [34], there exists an optimal solution $(\mathbf {c}^i,\mathbf {k}^i,\mathbf {m}^i)$ in the space $(\ell _\infty )_+ \times (\ell _\infty )_+ \times (\ell _\infty )_+$ and sequences of Lagrange multipliers $\mathbf {l}^i:=\{\lambda _t^i\}_{t=0}^\infty$ and $\mathbf {e}^i:=\{\varepsilon _{t+1}^i\}_{t=0}^\infty$ in $(\ell _1)_+ \times (\ell _1)_+$ satisfying

$$\begin{aligned}&\lambda _0^i = u_i'(c_0^i) + \alpha _i'(c_0^i) \mu _1^i , \end{aligned}$$

(72a)

$$\begin{aligned}&\lambda _{t+1}^i = \varepsilon _{t+1}^i\left[ u_i'(c_{t+1}^i) + \alpha _i'(c_{t+1}^i) \mu _{t+2}^i\right] ,&t=0,1,\ldots , \end{aligned}$$

(72b)

$$\begin{aligned}&\lambda _t^i = \lambda _{t+1}^i\theta ^i f'(k_{t+1}^i+k_{t+1}^j),&t=0,1,\ldots , \end{aligned}$$

(72c)

$$\begin{aligned}&\varepsilon _1^i = \alpha _i(c_0^i), \end{aligned}$$

(72d)

$$\begin{aligned}&\varepsilon _{t+2}^i = \alpha _i(c_{t+1}^i)\varepsilon _{t+1}^i ,&t=0,1,\ldots , \end{aligned}$$

(72e)

and the complementary slackness conditions

$$\begin{aligned} \lambda _t^i\left[ \theta ^i f(k_t^i+k_t^j)-c_t^i-k_{t+1}^i\right]&= 0,&t=0,1,\ldots , \end{aligned}$$

(73a)

$$\begin{aligned} \varepsilon _{t+1}^i\left[ u_i(c_{t+1}^i) + \alpha _i(c_{t+1}^i)\mu _{t+2}-\mu _{t+1}^i\right]&= 0,&t=0,1,\ldots . \end{aligned}$$

(73b)

Given that the solution is interior, (72a)–(72c) imply that $\lambda _t >0$, for all t. Hence $\mathbf {l}^i \in (\ell _1)_+ \backslash \{0\}$. It is also clear from (72d) and (72e) that $\varepsilon _{t+1}^i > 0$, for all t. Thus the first two inequality restrictions in (dSVP$^i$) must hold with equality. By duality, notice that $\varepsilon _{t+1}^i$ can be replaced with $\beta _{t+1}^i$ in the above conditions. As shown before, a combination of (72) and (73) yields the transversality condition $\lim _{t \rightarrow \infty } \lambda _t k_{t+1}^i =0$ in (5). Finally, conditions (3) and (4) in the statement of the proposition can be obtained by making the appropriate substitutions. This completes the proof. $\square$

1.2.1 Linearized Dynamical System

The optimality conditions for agent i form a discrete dynamical system in the variables $(\beta _t^i,c_t^i,k_t^i,\mu _t^i)$, taking the path of $k_t^j$ as given,

$$\begin{aligned} u_i(c_{t+1}^i) + \alpha _i(c_{t+1}^i)\mu _{t+1}^i&= \mu _t^i\\ \beta _{t+1}^i[u_i'(c_{t+1}^i)+\alpha _i'(c_{t+1}^i)\mu _{t+1}^i] \theta ^i f'(k_{t+1}^i+k_{t+1}^j)&= \beta _t^i[u_i'(c_t^i)+\alpha _i'(c_t^i)\mu _t^i],\\ k_{t+1}^i&= \theta ^if(k_t^i+k_t^j)-c_t^i\\ \beta _{t+1}^i&=\alpha _i(c_t^i)\beta _i^i. \end{aligned}$$

A stationary point $(c^i,c^j,\beta ^i,\beta ^j,k^i,k^j,\mu ^i,\mu ^j)$ with $c^i,c^j,k^i,k^j > 0$ for the dynamical system formed by (3a)–(3c) and (4a)–(4b) can be characterized as follows

$$\begin{aligned} \mu ^i&= \frac{u_i(c^i)}{1-\alpha _i(c^i)},\\ 1&=\alpha _i(c^i)\theta ^if'(k^i+k^j)\\ c^i&=\theta ^if(k^i+k^j)-k^i,\\ \beta ^i&=0. \end{aligned}$$

In fact, the system can be reduced in one variable, since the dynamics of $\beta _t^i$ depend entirely on $c_t^i$. Taking a first-order approximation in a neighborhood of a stationary point and defining deviations from any variable with respect to its stationary value as ${\hat{x}}_t^i:=x_t^i-x^i$, we have that

$$\begin{aligned} \left( u_i'+\alpha _i'\mu ^i\right) {\hat{c}}_{t+1}^i +\alpha _i\,{\hat{\mu }}_{t+1}^i&= {\hat{\mu }}_t^i,\\ \left( u_i''+\alpha _i''\mu ^i\right) {\hat{c}}_{t+1}^i + \alpha _i'\,{\hat{\mu }}_{t+1}^i&+ \left( u_i'+\alpha _i'\mu ^i\right) (f''/f')({\hat{k}}_{t+1}^i+{\hat{k}}_{t+1}^j)\\&= \left[ -(\alpha _i'/\alpha _i)\left( u_i'+\alpha _i'\mu ^i\right) +\left( u_i''+\alpha _i''\mu ^i\right) \right] {\hat{c}}_t^i +\alpha _i'\,{\hat{\mu }}_t^i\\ \alpha _i\,{\hat{k}}_{t+1}^i&= -\alpha _i\,{\hat{c}}_t^i+{\hat{k}}_t^i + {\hat{k}}_t^j, \end{aligned}$$

for $j \ne i=1,2$, and for all t. Thus, the coefficient matrices in (9) are given by

$$\begin{aligned} M:= \begin{bmatrix} U^i&0&0&0&\alpha _i&0\\ 0&U^j&0&0&0&\alpha _j\\ W^i&0&U^i\zeta&U^i\zeta&\alpha _i'&0\\ 0&W^j&U^j\zeta&U^j\zeta&0&\alpha _j'\\ 0&0&\alpha _i&0&0&0\\ 0&0&0&\alpha _j&0&0\\ \end{bmatrix} \quad \text {and} \quad N:= \begin{bmatrix} 0&0&0&0&1&0 \\ 0&0&0&0&0&1 \\ -U^i\omega _i&0&0&0&\alpha _i'&0 \\ 0&-U^j\omega _j&0&0&0&\alpha _j'\\ -\alpha _i&0&1&1&0&0\\ 0&-\alpha _j&1&1&0&0\\ \end{bmatrix}, \end{aligned}$$

where all functions are evaluated at the stationary point and

$$\begin{aligned} U^i := u_i' + \alpha _i'\,\mu ^i,\quad W^i := u_i'' + \alpha _i''\,\mu ^i, \quad \zeta := \frac{f''}{f'},\quad \text {and} \quad \omega _i := \frac{\alpha _i'}{\alpha _i}-\frac{W^i}{U^i}. \end{aligned}$$

This notation is consistent with the remaining of the paper, so these results are directly comparable with those developed in the Sects. 4 and 5.

1.3 The Strategy Space

Proof of Lemma 1

For simplicity, assume that $\alpha _i(c) \ge \alpha _j(c)$ holds for all $c \in [0,k_m]$, since the argument does not hinge on this particular assumption. By (T2), we have that $\alpha _i(0)f'(0^+) > 1$ (it could be infinity). From (T1)–(T2), the maximum sustainable level satisfies $f'(k_m) < 1$. This, together with (U1) and the fact that $f(k_m)-k_m > 0$, implies $\alpha _i(k_m)f'(k_m) < 1$. Hence the existence of $k_a^i \in (0,k_m)$ follows from the continuity of $\alpha _i$ and $f'$. The proof for $k_a^j \in (0,k_m)$ is analogous. $\square$

It follows from the condition for a stationary equilibrium (12) that

$$\begin{aligned} 1=\alpha _i(c_a^i)f'(k_a^i)=\alpha _j(c_a^j)f'(k_a^j), \end{aligned}$$

where

$$\begin{aligned} 0< c_a^i = f(k_a^i)-k_a^i \quad \text {and} \quad 0 < c_a^j = f(k_a^j)-k_a^j. \end{aligned}$$

Assume that $k_a^i < k_a^j$. Given that $f'(k_a^i)> f'(k_a^j) >1$, the above condition implies $\alpha _i(c_a^i)<\alpha _j(c_a^j)$. For this inequality to hold, $c_a^i$ must be sufficiently lower than $c_a^j$. In particular, this implies that

$$\begin{aligned} 0< f(k_a^i)-k_a^i < f(k_a^j)-k_a^j, \end{aligned}$$

or, equivalently,

$$\begin{aligned} \frac{f(k_a^i)-f(k_a^j)}{k_a^i-k_a^j} < 1. \end{aligned}$$

By the mean value theorem, there is a $k_a^i< x < k_a^j$ such that $f'(x) < 1$. But this contradicts the concavity of f. Hence, $k_a^j \le k_a^i$.

Precommitment Equilibria: Details and Proofs

Proof of Proposition 2

Since (23a) and (23b) hold for any interior stationary point, we have

$$\begin{aligned} 1&= \alpha _i(\overline{c}^i)f'(\overline{k})= \alpha _i(c_a^i)f'(k_a^i), \end{aligned}$$

(74a)

$$\begin{aligned} 1&= \alpha _j(\overline{c}^j)f'(\overline{k})= \alpha _j(c_a^j)f'(k_a^j), \end{aligned}$$

(74b)

hence $\alpha _i(\overline{c}^i) < 1$ and $\alpha _j(\overline{c}^j) < 1$ by (U1). This in turn implies $f'(\overline{k}) > 1$, $f'(k_a^i) > 1$, and $f'(k_a^j) > 1$. Next, divide (74a) by (74b) to obtain

$$\begin{aligned} 1=\frac{\alpha _i(\overline{c}^i)}{\alpha _j(\overline{c}^j)}=\frac{\alpha _i(c_a^i)f'(k_a^i)}{\alpha _j(c_a^j)f'(k_a^j)}. \end{aligned}$$

Given that $\alpha _i(\cdot ) \ge \alpha _j(\cdot )$, for the first equality to hold it must be the case that $\overline{c}^i \le \overline{c}^j$, which proves (i). $\square$

For part (ii), note that from (74a)–(74b) and the resource constraint, it follows that

$$\begin{aligned} 1 = \alpha _i(f(\overline{k})-\overline{k}-\overline{c}^j)f'(\overline{k}) =\alpha _i\left( f(\overline{k})-\overline{k}-\alpha _j^{-1}\left( \tfrac{1}{f'(\overline{k})}\right) \right) f'(\overline{k}). \end{aligned}$$

From the second equality above, the nonnegativity condition $\overline{c}^i \ge 0$ is equivalent to

$$\begin{aligned} \alpha _j(f(\overline{k})-\overline{k})f'(\overline{k}) \ge 1 = \alpha _j(f(k_a^j)-k_a^j)f'(k_a^j). \end{aligned}$$

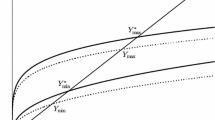
Hence, $\overline{k} \le k_a^j$. The remaining inequality $\overline{k} \le k_a^i$ follows from Lemma 1.

To show part (iii), rearrange (74a) and apply the result from part (ii) of this proposition to obtain

$$\begin{aligned} \frac{\alpha _i(\overline{c}^i)}{\alpha _i(c_a^i)}=\frac{f'(k_a^i)}{f'(\overline{k})} \le 1, \end{aligned}$$

hence the monotonicity of the discount factor implies $\overline{c}^i \le c_a^i$. The remaining inequality can be obtained applying a similar argument to (74b). This completes the proof. $\square$

Proof of Proposition 3

Given that the stationary equilibrium satisfies (P1), it follows that

$$\begin{aligned} \frac{\alpha _i'}{\alpha _i}(f'-1)+\frac{f''}{f'}< 0 \quad \text {and} \quad \frac{\alpha _j'}{\alpha _j}(f'-1)+\frac{f''}{f'} < 0 \end{aligned}$$

on $I^i \times I^j \times I^k$. Multiplying the first inequality above by $\alpha _i'/\alpha _i$ and the second inequality by $\alpha _j'/\alpha _j$, and adding up the result, we have

$$\begin{aligned} \left[ \left( \frac{\alpha _i'}{\alpha _i}\right) ^2+\left( \frac{\alpha _j'}{\alpha _j}\right) ^2\right] (f'-1)+\left( \frac{\alpha _i'}{\alpha _i}+\frac{\alpha _j'}{\alpha _j}\right) \frac{f''}{f'} < 0. \end{aligned}$$

Given that $\alpha _i'/\alpha _i,\,\alpha _j'/\alpha _j \ge 0$, Young’s inequality implies that

$$\begin{aligned} \frac{\alpha _i'}{\alpha _i}\frac{\alpha _j'}{\alpha _j}\le \frac{1}{2}\left( \frac{\alpha _i'}{\alpha _i}\right) ^2+\frac{1}{2}\left( \frac{\alpha _j'}{\alpha _j}\right) ^2 \le \left( \frac{\alpha _i'}{\alpha _i}\right) ^2+\left( \frac{\alpha _j'}{\alpha _j}\right) ^2. \end{aligned}$$

Hence, it follows that

$$\begin{aligned} \frac{\alpha _i'}{\alpha _i}\frac{\alpha _j'}{\alpha _j}(f'-1)+\left( \frac{\alpha _i'}{\alpha _i}+\frac{\alpha _j'}{\alpha _j}\right) \frac{f''}{f'} < 0, \end{aligned}$$

which is (31), the desired result.¹⁸$\square$

Proof of Theorem 1

Note that $\det (A) \ne 0$, so the matrix of coefficients A is locally invertible and, given that all elements of $D\varPhi (\overline{x})$ exist and are continuous in some neighborhood ${\mathscr {U}}$ of $\overline{x}$, the map $\varPhi$ is a local diffeomorphism.

It remains to prove that the eigenvalues of A satisfy (33). Note that its trace and determinant are

$$\begin{aligned} \mathrm {tr}(A)&=\frac{1}{\varDelta _0}\left[ 2\omega _i\omega _j -(\eta _i\omega _j-\delta _i\eta _j)-(\omega _i\eta _j-\eta _i\delta _j)\right] +f', \end{aligned}$$

(75)

$$\begin{aligned} \det (A)&=\frac{\omega _i\omega _j}{\varDelta _0}f'. \end{aligned}$$

(76)

By the Cayley–Hamilton theorem, the coefficients of the characteristic polynomial can be expressed in terms of traces of powers of A, one of them being the determinant of A.¹⁹ In particular, for $n=3$, the characteristic polynomial is given by

$$\begin{aligned} p(\lambda ):=\lambda ^3 - {{\mathrm{tr}}}(A)\lambda ^2 + \tfrac{1}{2}\left( {{\mathrm{tr}}}^2(A)-{{\mathrm{tr}}}(A^2)\right) \lambda - \det (A), \end{aligned}$$

and has the eigenvalues of A as roots. A graphical approach is useful for the characterization of $p(\lambda )$. Generally speaking, the graph of a third-degree polynomial, can be characterized by its roots, the intersection with the y-axis, a local maximum, a local minimum, and a point of inflection. $\square$

The remaining of the proof will be carried out in several steps which we formulate as independent lemmas.

Lemma 2

$p(-1)< p(0)< 0 < p(1)$.

Proof

Reordering terms in (75) yields

$$\begin{aligned} {{\mathrm{tr}}}(A)= \frac{2\omega _i\omega _j -\eta _i(\omega _j-\delta _j)-\eta _j(\omega _i-\delta _i)}{\varDelta _0} + f'. \end{aligned}$$

By (P1) and the fact that $\omega _i-\delta _i >0$ and $\omega _j-\delta _j > 0$, we have ${{\mathrm{tr}}}(A) > 0$. It is clear from (76) that $\det (A) > 0$. The linear coefficient of p is given by

$$\begin{aligned} \frac{{{\mathrm{tr}}}^2(A)-{{\mathrm{tr}}}(A^2)}{2}=\frac{\omega _i\omega _j-\eta _i\omega _j-\omega _i\eta _j}{\varDelta _0} + \frac{2\omega _i\omega _j}{\varDelta _0}f', \end{aligned}$$

which is positive with $\eta _i,\eta _j < 0$. These values completely describe the coefficients of the polynomial p. Hence, we will evaluate $p(\cdot )$ at certain reference points to help determine the stable and unstable local manifolds. Here we choose 0, 1, and $-1$ to obtain

$$\begin{aligned} p(0)&= -\frac{\omega _i\omega _j}{\varDelta _0},\\ p(1)&= \frac{\delta _i\delta _j\,(f'-1)-(\delta _i\eta _j+\eta _i\delta _j)}{\varDelta _0},\\ p(-1)&=-\left( \frac{4\omega _i\omega _j-\delta _i\delta _j}{\varDelta _0}\right) (f'+1)+\frac{\eta _i(2\omega _j-\delta _j)+(2\omega _i-\delta _i)\eta _j}{\varDelta _0}. \end{aligned}$$

Simple calculation shows that $p(-1)<p(0)$. It immediately follows that $p(-1)< p(0)< 0 < p(1)$ holds and the proof is complete. $\square$

The next result is useful to characterize the critical points of p.

Lemma 3

If $\eta _i < 0$ and $\eta _j < 0$, then $\frac{1}{3}{{\mathrm{tr}}}(A) > 1$.

Proof

We have already established that $f'({\bar{k}}) > 1$ for any given stationary point. Since the remaining entries of the main diagonal of A, are positive, it suffices to show that their sum is greater than two, or equivalently, that $F_1^i + F_1^j -2 > 0$. From (26), we have that

$$\begin{aligned} F_1^i +F_1^j - 2&= \frac{2\delta _i\delta _j-\eta _i(\omega _j-\delta _j)+(\omega _i-\delta _i)\eta _j}{\varDelta _0} > 0, \end{aligned}$$

and the desired result follows. $\square$

Lemma 4

Suppose that $\eta _i < 0$, $\eta _j < 0$ and ${{\mathrm{tr}}}(A^2)-\tfrac{1}{3}{{\mathrm{tr}}}^2(A)>0$. Then, $p(\lambda )$ has a local maximum at $r_1 > 0$, a local minimum at $r_2$, and a point of inflection at $r_3$ with $r_1< r_3 < r_2$ and $r_3 > 1$.

Proof

First differentiate p, and we are able to find two critical points which are the zeroes of $p'(\lambda )$ in ${\mathbb {R}}$, i.e., the solution of the quadratic equation

$$\begin{aligned} \lambda ^2-\tfrac{2}{3}{{\mathrm{tr}}}(A)\lambda +\tfrac{1}{6}\left( {{\mathrm{tr}}}^2(A)-{{\mathrm{tr}}}(A^2)\right) =0. \end{aligned}$$

Since ${{\mathrm{tr}}}(A^2)-\tfrac{1}{3}{{\mathrm{tr}}}^2(A)>0$, the critical points $r_1$ and $r_2$, given by

$$\begin{aligned} r_{1,2} = \tfrac{1}{3}{{\mathrm{tr}}}(A) \mp \tfrac{1}{2} \sqrt{\tfrac{2}{3}\left( {{\mathrm{tr}}}(A^2)-\tfrac{1}{3}{{\mathrm{tr}}}^2(A)\right) } \end{aligned}$$

(77)

are well defined.²⁰ In particular, taking into account the result of Lemma 3, it is easy to verify that $0< r_1 < r_2$. Differentiating $p'$ once more, we have that

$$\begin{aligned} p''(\lambda )=2\lambda -\tfrac{2}{3}{{\mathrm{tr}}}(A), \end{aligned}$$

thus $p''$ vanishes at $r_3 = \frac{1}{3}{{\mathrm{tr}}}(A)$ and $p''(\lambda )< (>)\ 0 \iff \lambda < (>)\ r_3$, respectively, so $r_3$ is a point of inflection. By simple inspection of (77), it is clear that $r_1< r_3 < r_2$, which immediately implies that $r_1$ is a local maximum and $r_2$ a local minimum of p in ${\mathbb {R}}$. Finally, applying Lemma 3 again, it follows that $r_3 > 1$. This completes the proof. $\square$

1.1 Analysis of the Stable Manifold

Let $\varPhi :X \rightarrow X$ be a map describing the nonlinear discrete dynamical system

$$\begin{aligned} x_{t+1} = \varPhi (x_t),&t=0,1,\ldots \end{aligned}$$

(78)

and let $\overline{x} \in X$ be a point such that $\overline{x} = \varPhi (\overline{x})$, i.e., a stationary point. By the stable manifold theorem, if $\varPhi$ is continuously differentiable in a neighborhood ${\mathscr {N}}$ of $\overline{x}$ and $A=D\varPhi (\overline{x})$ is the Jacobian matrix of $\varPhi$, then there exists a neighborhood ${\mathscr {U}} \subset {\mathscr {N}}$, and a continuously differentiable function $\phi : {\mathscr {U}} \rightarrow {\mathbb {R}}^2$, for which the matrix $D\phi (\overline{x})$ has full rank. Moreover, if $\{x_t\}$ is a solution to (78) with $x_0 \in {\mathscr {U}}$ and $\phi (x_0)=0$, then $\lim _{t \rightarrow \infty } x_t=\overline{x}$. The set of x values satisfying $\phi (x)=0$ is called the stable manifold of the nonlinear dynamical system.

By Jordan decomposition, the matrix A of the linearized system (78) around $\overline{x}$ can be written as $A=B^{-1} \varLambda B$, where B is nonsingular and $\varLambda$ is a diagonal matrix containing the eigenvalues of A. Hence, a solution can be expressed recursively in terms of these matrices

$$\begin{aligned} x_t = \overline{x} + B^{-1} \varLambda ^t B\,(x_0-\overline{x}). \end{aligned}$$

(79)

It is clear that $x_t \rightarrow \overline{x}$ if and only if $B(x_0-\overline{x})=w_0$, where $w_0^i=w_0^j=0$. Let ${\hat{x}}_t:=x_t-\overline{x}$ denote deviations from stationary values for all t. This condition is equivalent to

$$\begin{aligned} \begin{bmatrix} b_{11}&b_{12}&b_{13}\\ b_{21}&b_{22}&b_{23}\\ b_{31}&b_{32}&b_{33}\\ \end{bmatrix} \begin{bmatrix} {\hat{c}}_0^i\\ {\hat{c}}_0^j\\ {\hat{k}}_0\\ \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ w\\ \end{bmatrix}, \end{aligned}$$

(80)

where $b_{31}{\hat{c}}_0^i + b_{32}{\hat{c}}_0^j + b_{33}{\hat{k}}_0=w$ is a constant to be determined.

Then, (79) implies

$$\begin{aligned} \begin{bmatrix} {\hat{c}}_t^i \\ {\hat{c}}_t^j \\ {\hat{k}}_t \\ \end{bmatrix} =\frac{1}{\det (B)} \begin{bmatrix} M_{11}&M_{12}&M_{13}\\ M_{21}&M_{22}&M_{23}\\ M_{31}&M_{32}&M_{33}\\ \end{bmatrix} ^T \begin{bmatrix} (\overline{\lambda }_1)^t&0&0 \\ 0&(\overline{\lambda }_2)^t&0\\ 0&0&(\overline{\lambda }_3)^t\\ \end{bmatrix} \begin{bmatrix} b_{11}&b_{12}&b_{13}\\ b_{21}&b_{22}&b_{23}\\ b_{31}&b_{32}&b_{33}\\ \end{bmatrix} \begin{bmatrix} {\hat{c}}_0^i \\ {\hat{c}}_0^j \\ {\hat{k}}_0 \\ \end{bmatrix}, \end{aligned}$$

where $M_{ij}$ is the $3 \times 3$ matrix whose elements are the principal minors of B and $\det (B) \ne 0$. The stable root is assumed to be $\overline{\lambda }_3$, then solving the system above yields

$$\begin{aligned} {\hat{c}}_t^i =\frac{M_{31}}{\det (B)}\,w(\overline{\lambda }_3)^t, \quad {\hat{c}}_t^i =\frac{M_{32}}{\det (B)}\,w(\overline{\lambda }_3)^t, \quad \text {and} \quad {\hat{k}}_t =\frac{M_{33}}{\det (B)}\,w(\overline{\lambda }_3)^t, \end{aligned}$$

which represents a stable trajectory for all variables, since $0< \overline{\lambda }_3 < 1$. Now, (80) can be expressed as

$$\begin{aligned} \begin{bmatrix} b_{11}&b_{12}\\ b_{21}&b_{22}\\ \end{bmatrix} \begin{bmatrix} {\hat{c}}_0^i\\ {\hat{c}}_0^j\\ \end{bmatrix} =- \begin{bmatrix} b_{13}\\ b_{23}\\ \end{bmatrix} {\hat{k}}_0. \end{aligned}$$

Moreover, assuming $b_{11}b_{22}-b_{12}b_{21} \ne 0$, it follows that

$$\begin{aligned} \begin{bmatrix} {\hat{c}}_0^i\\ {\hat{c}}_0^j\\ \end{bmatrix} = -\frac{1}{b_{11}b_{22}-b_{12}b_{21}} \begin{bmatrix} b_{22}&-b_{12}\\ -b_{21}&b_{11}\\ \end{bmatrix} \begin{bmatrix} b_{13}\\ b_{23}\\ \end{bmatrix} {\hat{k}}_0, \end{aligned}$$

which yields ${\hat{c}}_0^i =(M_{31}/M_{33}){\hat{k}}_0$ and ${\hat{c}}_0^j =(M_{32}/M_{33}){\hat{k}}_0$. And solving for w again in (80), it follows that

$$\begin{aligned} w=\left( b_{31}\frac{M_{31}}{M_{33}}+b_{32}\frac{M_{32}}{M_{33}}+b_{33}\right) {\hat{k}}_0. \end{aligned}$$

In order to characterize the stable manifold, from the fact that $BA=\varLambda B$, we have

$$\begin{aligned} \begin{bmatrix} b_{11}&b_{12}&b_{13}\\ b_{21}&b_{22}&b_{23}\\ b_{31}&b_{32}&b_{33}\\ \end{bmatrix} \begin{bmatrix} \overline{F}_1^i&\overline{F}_2^i&\overline{F}_3^i\\ \overline{F}_2^j&\overline{F}_1^j&\overline{F}_3^j\\ -1&-1&\overline{f}'\\ \end{bmatrix} = \begin{bmatrix} \overline{\lambda }_1&0&0 \\ 0&\overline{\lambda }_2&0\\ 0&0&\overline{\lambda }_3\\ \end{bmatrix} \begin{bmatrix} b_{11}&b_{12}&b_{13}\\ b_{21}&b_{22}&b_{23}\\ b_{31}&b_{32}&b_{33}\\ \end{bmatrix}, \end{aligned}$$

which we can solve for arbitrary nonzero values of $b_{11}$, $b_{22}$, and $b_{33}$, therefore

$$\begin{aligned}&b_{12}=\left( \frac{\overline{F}_1^i-\overline{F}_2^i-\overline{\lambda }_1}{\overline{F}_1^j-\overline{F}_2^j-\overline{\lambda }_1}\right) b_{11},\quad b_{21}=\left( \frac{\overline{F}_1^j-\overline{F}_2^j-\overline{\lambda }_2}{\overline{F}_1^i-\overline{F}_2^i-\overline{\lambda }_2}\right) b_{22},\\&b_{13}=-\frac{1}{(\overline{f}'-\overline{\lambda }_1)}\left[ \overline{F}_3^j\left( \frac{\overline{F}_1^i-\overline{F}_2^i-\overline{\lambda }_1}{\overline{F}_1^j-\overline{F}_2^j-\overline{\lambda }_1}\right) +\overline{F}_3^i\right] b_{11},\\&b_{23}=-\frac{1}{(\overline{f}'-\overline{\lambda }_2)}\left[ \overline{F}_3^i\left( \frac{\overline{F}_1^j-\overline{F}_2^j-\overline{\lambda }_2}{\overline{F}_1^i-\overline{F}_2^i-\overline{\lambda }_2}\right) +\overline{F}_3^j\right] b_{22},\\&b_{31}=\left[ \frac{\overline{F}_1^j-\overline{F}_2^j-\overline{\lambda }_3}{(\overline{F}_1^i-\overline{\lambda }_3)(\overline{F}_1^j-\overline{\lambda }_3)-\overline{F}_2^i\overline{F}_2^j}\right] b_{33}, \quad \text {and}\\&b_{32}=-\frac{1}{\overline{F}_3^j}\left[ \frac{\overline{F}_3^i(\overline{F}_1^j-\overline{F}_2^j-\overline{\lambda }_3)}{(\overline{F}_1^i-\overline{\lambda }_3)(\overline{F}_1^j-\overline{\lambda }_3)-\overline{F}_2^i\overline{F}_2^j}+(\overline{f}'-\overline{\lambda }_3)\right] b_{33}. \end{aligned}$$

The stable manifold is the set of values $(c^i,c^j,k)\in {\mathscr {U}}$ such that $\phi (c^i,c^j,k)=0$ holds. By the implicit function theorem, there exist functions $\pi _i$ and $\pi _j$ such that

$$\begin{aligned} \phi ^i\left( \pi _i(k),\pi _j(k),k\right) =0,\quad \text {and} \quad \phi ^j\left( \pi _i(k),\pi _j(k),k\right) =0. \end{aligned}$$

Differentiating around $\overline{k}$, we obtain

$$\begin{aligned} \begin{bmatrix} \overline{\phi }_1^i&\overline{\phi }_2^i\\ \overline{\phi }_1^j&\overline{\phi }_2^j\\ \end{bmatrix} \begin{bmatrix} \pi _i'(\overline{k})\\ \pi _j'(\overline{k})\\ \end{bmatrix} = - \begin{bmatrix} \overline{\phi }_3^i\\ \overline{\phi }_3^j\\ \end{bmatrix}, \end{aligned}$$

(81)

where $\overline{\phi }_l^i$, $l=1,2,3$, denotes the partial derivative of $\phi ^i$ with respect to the lth argument, evaluated at the stationary point, and similarly for $\overline{\phi }_l^j$. In fact, the derivatives of the stable manifold at the stationary point are related to the coefficients of B as follows,

$$\begin{aligned} D\phi (\overline{x})= \begin{bmatrix} \overline{\phi }_1^i&\overline{\phi }_2^i&\overline{\phi }_3^i\\ \overline{\phi }_1^j&\overline{\phi }_2^j&\overline{\phi }_3^j\\ \end{bmatrix}= \begin{bmatrix} b_{11}&b_{12}&b_{13}\\ b_{21}&b_{22}&b_{23}\\ \end{bmatrix}. \end{aligned}$$

This allows to solve for the derivatives of the policy functions from (81), yielding

$$\begin{aligned} \overline{\pi }_i':=\pi _i'(\overline{k})=-\left( \frac{b_{13}b_{22} - b_{12}b_{23}}{b_{11}b_{22} - b_{12}b_{21}}\right) \quad \text {and} \quad \overline{\pi }_j':=\pi _j'(\overline{k})=-\left( \frac{b_{11}b_{23} - b_{13}b_{21}}{b_{11}b_{22} - b_{12}b_{21}}\right) . \end{aligned}$$

Equivalently,

$$\begin{aligned}&\overline{\pi }_i'=\frac{\left[ \overline{F}_3^i+\overline{E}^{ij}(\overline{\lambda }_1)\overline{F}_3^j\right] (\overline{f}'-\overline{\lambda }_2)-\overline{E}^{ij}(\overline{\lambda }_1)\left[ \overline{F}_3^i\overline{E}^{ji}(\overline{\lambda }_2)+\overline{F}_3^j\right] (\overline{f}'-\overline{\lambda }_1)}{(\overline{f}'-\overline{\lambda }_1)(\overline{f}'-\overline{\lambda }_2)\left[ 1-\overline{E}^{ij}(\overline{\lambda }_1)\overline{E}^{ji}(\overline{\lambda }_2)\right] },\\&\overline{\pi }_j'=\frac{\left[ \overline{F}_3^i\overline{E}^{ji}(\overline{\lambda }_2)+\overline{F}_3^j\right] (\overline{f}'-\overline{\lambda }_1)-\overline{E}^{ji}(\overline{\lambda }_2)\left[ \overline{F}_3^i+\overline{E}^{ij}(\overline{\lambda }_1)\overline{F}_3^j\right] (\overline{f}'-\overline{\lambda }_2)}{(\overline{f}'-\overline{\lambda }_1)(\overline{f}'-\overline{\lambda }_2)\left[ 1-\overline{E}^{ij}(\overline{\lambda }_1)\overline{E}^{ji}(\overline{\lambda }_2)\right] }, \end{aligned}$$

where

$$\begin{aligned} \overline{E}^{ij}(\overline{\lambda }_1):=\frac{\overline{F}_1^i-\overline{F}_2^i-\overline{\lambda }_1}{\overline{F}_1^j-\overline{F}_2^j-\overline{\lambda }_1} \quad \text {and} \quad \overline{E}^{ji}(\overline{\lambda }_2):=\frac{\overline{F}_1^j-\overline{F}_2^j-\overline{\lambda }_2}{\overline{F}_1^i-\overline{F}_2^i-\overline{\lambda }_2}. \end{aligned}$$

An appropriate set of conditions must be imposed on the model’s parameters for all previous values to be well defined, in particular $f' - \overline{\lambda }_1 \ne 0$, $f' - \overline{\lambda }_2 \ne 0$, $\overline{F}_1^j-\overline{F}_2^j-\overline{\lambda }_1 \ne 0$, $\overline{F}_1^i-\overline{F}_2^i-\overline{\lambda }_2 \ne 0$, and $(\overline{F}_1^j-\overline{F}_2^j-\overline{\lambda }_1)(\overline{F}_1^i-\overline{F}_2^i-\overline{\lambda }_2)-(\overline{F}_1^i-\overline{F}_2^i-\overline{\lambda }_1)(\overline{F}_1^j-\overline{F}_2^j-\overline{\lambda }_2) \ne 0$.

Markov Equilibria: Details and Proofs

Proof of Proposition 4

Let g be a continuous function satisfying (44). If g(k) has a stationary point $k^* > 0$, then

$$\begin{aligned} \varPsi \left[ k^*,g(k^*),g^2(k^*)\right] =\varPsi (k^*,k^*,k^*)=0. \end{aligned}$$

From (42) and (43), this implies $k^*=g(k^*)=f(k^*)-G^i(k^*,k^*)-G^j(k^*,k^*)$. Given that the strategies $G^i$, $G^j$ solve the first-order conditions (39), and taking into account that $U^i,U^j > 0$ for all $k \in (0,k_m]$, it follows that

$$\begin{aligned} \alpha _i\left( G^i(k^*,k^*)\right) [f'(k^*)-G_1^j(k^*,k^*)]&=1,\\ \alpha _j\left( G^j(k^*,k^*)\right) [f'(k^*)-G_1^i(k^*,k^*)]&=1, \end{aligned}$$

where $f'(k^*)-G_1^i(k^*,k^*)>0$ and $f'(k^*)-G_1^i(k^*,k^*)>0$ hold from optimality conditions. $\square$

1.1 Analysis of the Stable Manifold

The stable manifold theorem implies the existence of a neighborhood ${\mathscr {N}}$ of $(k^*,k^*)$ and a continuously differentiable function $\psi : {\mathscr {N}} \rightarrow {\mathbb {R}}$ such that for $k_0$ sufficiently close to $k^*$, there exists $k_1$ with $(k_1,k_0) \in {\mathscr {N}}$ and $\psi (k_1,k_0)=0$. This is true if the Jacobian matrix $[D\psi (k^*,k^*)]$ has full rank.

The linearized system $\varPsi$ can be represented in terms of the coefficients of the characteristic polynomial $P(\lambda )$ as $\varPsi _1^*(k_t-k^*) + \varPsi _2^*(k_{t+1}-k^*) + \varPsi _3^*(k_{t+2}-k^*)=0$, so that the behavior of $k_t$ near $k^*$ can be characterized by a $2 \times 2$ matrix

$$\begin{aligned} A:=\begin{bmatrix} -\frac{\varPsi _2^*}{\varPsi _3^*}&-\frac{\varPsi _1^*}{\varPsi _3^*}\\ \ 1&\ 0\\ \end{bmatrix}, \end{aligned}$$

which is nonsingular. By Jordan decomposition, A can be written as $A = B^{-1}\varLambda B$, where B is a nonsingular matrix, and $\varLambda$ a diagonal matrix with the eigenvalues $\lambda _1^*$ and $\lambda _2^*$ in the main diagonal. Using the fact that $BA=\varLambda B$, the stable manifold can be characterized from the following system

$$\begin{aligned} \begin{bmatrix} b_{11}&b_{12}\\ b_{21}&b_{22}\\ \end{bmatrix} \begin{bmatrix} -\frac{\varPsi _2^*}{\varPsi _3^*}&-\frac{\varPsi _1^*}{\varPsi _3^*}\\ \ 1&\ 0\\ \end{bmatrix}= \begin{bmatrix} \lambda _1^*&0\\ 0&\lambda _2^*\\ \end{bmatrix} \begin{bmatrix} b_{11}&b_{12}\\ b_{21}&b_{22}\\ \end{bmatrix}, \end{aligned}$$

and for any nonzero values of $b_{11}$ and $b_{22}$,

$$\begin{aligned} B=\begin{bmatrix} b_{11}&\left( \lambda _1^*+\frac{\varPsi _2^*}{\varPsi _3^*}\right) b_{11}\\ \left( \lambda _2^*+\frac{\varPsi _2^*}{\varPsi _3^*}\right) ^{-1}b_{22}&b_{22}\\ \end{bmatrix}. \end{aligned}$$

Note that the saving function must satisfy $\psi [g(k),k]=0$, hence its derivative is given by

$$\begin{aligned} g'(k^*)=-\psi ^{-1}_1(k^*,k^*)\,\psi _2(k^*,k^*). \end{aligned}$$

The derivatives of the stable manifold at the stationary point are

$$\begin{aligned} \psi _1(k^*,k^*)=\left( \lambda _2^*+\tfrac{\varPsi _2^*}{\varPsi _3^*}\right) ^{-1}b_{22}, \quad \text {and} \quad \psi _2(k^*,k^*)=b_{22}, \end{aligned}$$

which in turn implies

$$\begin{aligned} g'(k^*)=-\frac{\psi _2(k^*,k^*)}{\psi _1(k^*,k^*)}= \lambda _1^*. \end{aligned}$$

If the system is governed by $\lambda _2^*$ instead, then simply replace $\lambda _1^*$ with $\lambda _2^*$ in all previous calculations.

Proof of Theorem 2

Two technical lemmas complete the proof. In both cases, it is assumed that $\lambda$ and $I_\varepsilon$ are defined as in Sect. 5.3. $\square$

Lemma 5

Let $\{h_n\}_{n \in {\mathbb {N}}}$ be a sequence of functions in $D_{|\lambda |}(I_\varepsilon )$ which converges to h. Then, the sequence $h^2_n(k):=h_n(h_n(k))$ converges uniformly to $h^2(k):=h(h(k))$ for all $k \in I_\varepsilon$.

Proof

Since the family of functions in $D_{|\lambda |}(I_\varepsilon )$ is uniformly bounded and equicontinuous, by the Arzelà-Ascoli theorem, $h_n$ converges uniformly on $I_\varepsilon$. Given that h is continuous, hence uniformly continuous, for every $\upsilon > 0$, there is a $\delta > 0$ such that $k,k' \in I_\varepsilon$ with $|k-k'|< \delta$ implies $|h(k)-h(k')|< \upsilon$. On the other hand, there is a positive integer N such that $|h_n(k) - h(k)|<\delta$ for all $n>N$ and all $k \in I_\varepsilon$. The combination of both results immediately implies that for every $\upsilon > 0$, there is some N such that $|h_n(h_n(k))-h(h(k))| < \upsilon$ for all $n > N$ and all $k \in I_\varepsilon$. Hence $h^2_n(k)$ converges uniformly on $I_\varepsilon$ to $h^2(k)$. $\square$

Lemma 6

The operator $T:D_{|\lambda |}(I_\varepsilon ) \rightarrow D_{|\lambda |}(I_\varepsilon )$ is continuous in the sup norm.

Proof

Let $h_n$ be a sequence in $D_{|\lambda |}(I_\varepsilon )$ that converges to h and fix $\upsilon >0$. By a similar argument given in the main body of the proof, there exists a real number $m_2 \ne 0$ such that

$$\begin{aligned} \left| (Th_n)(k)-(Th)(k)\right|&=\left| H[k,h_n^2(k)]-H[k,h^2(k)]\right| \\&\le \left| m_2\right| \left| h_n^2(k)-h^2(k)\right| \\&\le |m_2||\lambda |\left| h_n(k)-h(k)\right| ,\\&= |m_2\lambda |\left| h_n(k)-h(k)\right| , \end{aligned}$$

for all n and for all $k \in I_\varepsilon$. Then, for some $0< \delta < \upsilon /(|m_2\lambda |)$, if $\Vert h_n-h\Vert < \delta$, we have

$$\begin{aligned} \left\| Th_n-Th \right\|&= \sup _{k \in I_\varepsilon }\left| H[k,h_n^2(k)]-H[k,h^2(k)]\right| ,\\&\le |m_2\lambda |\left| h_n(k)-h(k)\right| ,\\&\le |m_2\lambda |\Vert h_n-h\Vert \\&< |m_2\lambda |\delta ,\\&< \upsilon , \end{aligned}$$

which proves that T is continuous. $\square$