Abstract
In the last ten years, the resolution of the equation \(\bar{\partial}u=f\) with sharp estimates has been intensively studied for convex domains of finite type in \(\mathbb{C}^{n}\) by many authors. Generally, they used kernels constructed with holomorphic support function satisfying “good” global estimates. In this paper, we consider the case of lineally convex domains. Unfortunately, the method used to obtain global estimates for the support function cannot be carried out in that case. Then we use a kernel that does not directly give a solution of the \(\bar{\partial}\)-equation, but only a representation formula which allows us to end the resolution of the equation using Kohn’s L 2 theory.
As an application, we give the characterization of the zero sets of the functions of the Nevanlinna class for lineally convex domains of finite type.
Similar content being viewed by others
References
Alexandre, W.: Construction d’une fonction de support à la Diederich–Fornaess, vol. 54. IRMA, Lille, (2001). No. III
Alexandre, W.:
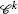 -Estimates for the \(\bar{\partial}_{b}\)-equation on convex domains of finite type. Mich. Math. J. 2, 357–382 (2005)
-Estimates for the \(\bar{\partial}_{b}\)-equation on convex domains of finite type. Mich. Math. J. 2, 357–382 (2005)
Alexandre, W.:
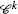 Estimates for \(\bar{\partial}\) on convex domain of finite type. Math. Z. 252, 473–496 (2006)
Estimates for \(\bar{\partial}\) on convex domain of finite type. Math. Z. 252, 473–496 (2006)
Berndtsson, B., Andersson, M.: Henkin–Ramirez formulas with weight factors. Ann. Inst. Fourier 32(2), 91–110 (1982)
Bonami, A., Charpentier, P.: Solutions de l’équation \(\bar{\partial}\) et zéros de la classe de Nevanlinna dans certains domains faiblement pseudo-convexes. Ann. Inst. Fourier XXXII(4), 53–89 (1982)
Bruna, J., Charpentier, Ph., Dupain, Y.: Zeros varieties for the Nevanlinna class in convex domains of finite type in \(\mathbb{C}^{n}\). Ann. Math. 147, 391–415 (1998)
Charpentier, P., Dupain, Y.: Pseudodistances et courants positifs dans les domaines de \(\mathbb{C}^{3}\). Ann. Sc. Norm. Super. Pisa, Cl. Sci. XXIV(2), 299–350 (1997)
Charpentier, P., Dupain, Y.: Extremal basis, geometrically separated domains and applications (2008)
Chang, D.C., Nagel, A., Stein, E.: Estimates for the \(\bar{\partial}\)-Neumann problem for pseudoconvex domains in \(\mathbb{C}^{2}\) of finite type. Acta Math. 169, 153–228 (1992)
Conrad, M.: Anisotrope optimale Pseudometriken für lineal konvex Gebeite von endlichem Typ (mit Anwendungen). Ph.D. thesis, Berg. Universität-GHS Wuppertal (2002)
Cumenge, A.: Sharp estimates for \(\bar{\partial}\) on convex domains of finite type. Ark. Mat. 39(1), 1–25 (2001)
Cumenge, A.: Zero sets of functions in the Nevanlinna or the Nevanlinna–Djrbachian classes. Pac. J. Math. 199(1), 79–92 (2001)
Diederich, K., Fornaess, J.E.: Lineally convex domains of finite type: holomorphic support functions. Manuscr. Math. 112, 403–431 (2003)
Diederich, K., Fischer, B.: Hölder estimates on lineally convex domains of finite type. Mich. Math. J. 54(2), 341–452 (2006)
Diederich, K., Fischer, B., Fornaess, J.E.: Hölder estimates on convex domains of finite type. Math. Z. 232, 43–61 (1999)
Diederich, K., Mazzilli, E.: Zero varieties for the Nevanlinna class on all convex domains of finite type. Nagoya Math. J. 163, 215–227 (2001)
Fischer, B.: Nonisotropic Hölder estimates on convex domains of finite type. Mich. Math. J. 52, 219–239 (2004)
Hefer, T.: Extremal bases and Hölder estimates for \(\bar{\partial}\) on convex domains of finite type. Mich. Math. J. 52, 573–602 (2004)
Henkin, G.M.: Solutions with bounds for the equations of H. Lewy and Poincaré–Lelong. Construction of functions of Nevanlinna class with given zeros in a strongly pseudoconvex domain. Dokl. Akad. Nauk SSSR 224(4), 771–774 (1975)
Kohn, J.J.: Global regularity for \(\bar{\partial}\) on weakly pseudo-convex manifolds. Trans. Am. Math. Soc. 181, 273–292 (1973)
McNeal, J.: Estimates on Bergman kernels of convex domains. Adv. Math. 109, 108–139 (1994)
Nikolov, N., Pflug, P., Thomas, P.J.: On different extremal bases for \(\mathbb{C}\)-convex domains (2009). arXiv:0912.4828v2
Skoda, H.: Valeurs au bord pour les solutions de l’opérateur \(\bar{\partial}\), et caractérisation des zéros des fonctions de la classe de Nevanlinna. Bull. Soc. Math. Fr. 104, 225–299 (1976)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Gennadi Henkin.
Rights and permissions
About this article
Cite this article
Charpentier, P., Dupain, Y. & Mounkaila, M. Estimates for Solutions of the \(\bar{\partial}\)-Equation and Application to the Characterization of the Zero Varieties of the Functions of the Nevanlinna Class for Lineally Convex Domains of Finite Type. J Geom Anal 24, 1860–1881 (2014). https://doi.org/10.1007/s12220-013-9398-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12220-013-9398-5



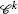 -Estimates for the
-Estimates for the  Estimates for
Estimates for