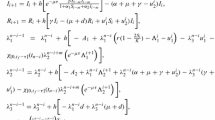Abstract
In this paper a Feynman-type path integral control approach is used for a recursive formulation of a health objective function subject to a fatigue dynamics, a forward-looking stochastic multi-risk susceptible–infective–recovered (SIR) model with risk-group’s Bayesian opinion dynamics toward vaccination against COVID-19. My main interest lies in solving a minimization of a policy-maker’s social cost which depends on some deterministic weight. I obtain an optimal lock-down intensity from a Wick-rotated Schrödinger-type equation which is analogous to a Hamiltonian–Jacobi–Bellman (HJB) equation. My formulation is based on path integral control and dynamic programming tools facilitates the analysis and permits the application of algorithm to obtain numerical solution for pandemic control model.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In current days we see “locking downs” of economies as a strategy to reduce the spread of COVID-19 which already has claimed more than 999,790 lives in the United States and more than 6 millions across the globe. Multiple countries have started this strategy to all the sectors of their economies except some essential service sectors such as healthcare and public safety. Different states in the United States locked down during different time periods based on their infection rates and extremely contagious transmission phase. Re-opening has been prompted by slowing down the infection rate and wanes public activities (Caulkins et al. 2021). One negative impact of a lengthy lock down of an economy may be a reluctance of people to come outside their homes for socioeconomic activities. A possible reason for this reluctance is that the people are too afraid to communicate in-person thinking about themselves getting infected by this virus. As a result, a store may face a reduction of customers and have to reduce the number of employees. If the store does not have enough inventory, it may have to eventually shut down. If a business is shut down, it can hard for it to reopen since it does not receive sufficient government financial support (Caulkins et al. 2021). This might be one reason why the Centers for Disease Control and Prevention (CDC) recommends a person infected with the omicron virus should isolate themselves for 5 days.
Condition for shut-down is determined when a healthcare cost function is minimized subject to a stochastic multi-risk susceptible–infectious–recovered (SIR) model (Kermack and McKendrick 1927). Almost all mathematical models of transmission of infectious disease models come from the SIR model. This is a main reason to use this model. There is much research regarding dynamic behavior of different epidemic models have been done (Beretta and Takeuchi 1995; Ma et al. 2004; Xiao and Ruan 2007; Rao 2014). The deterministic part of this stochastic SIR model consists of a saturated transmission rate which depends on the location of that person. If that person works in a urban area, then they might have more people interaction with more people than a person who lives in a rural area, which leads to a higher chance of getting infected. A diffusion aspect of the SIR model is needed when a person living in the rural area visits a city and interacts with others due to some arbitrary needs and gets in touch with others. On the other hand, poor air quality causes respiratory illness, affects adversely to cardiovascular health and deteriorates life expectancy (Delfino et al. 2005; Albrecht et al. 2021). In a similar manner a random environmental factor such as sudden change in the air quality due to volcanic eruptions, storms, wildfires and floods can affect the air quality drastically and lead to a more vulnerable atmosphere. Preexisting health conditions like obesity, diabetes, hypertension, weak immune system and higher age place a person toward higher risk of COVID-19 infection (Richardson et al. 2020; Albrecht et al. 2021).
Substantial recent research on the COVID-19 pandemic has adopted a control point of view, and lock-down measures as well as their medical, societal, and economic impacts are discussed in Anderson et al. (2020), Bayraktar et al. (2021), Charpentier et al. (2020), Ferguson et al. (2020), Hatchimonji et al. (2020), Hubert et al. (2022), Kantner and Koprucki (2020), Piguillem and Shi (2020), and Wilder-Smith et al. (2020). The previous papers assume the government act as a central planner, in the sense that it can impose on the population to control the epidemic in a way that is beneficial to the population as a whole (Hubert et al. 2022). However, though it is reasonable to assume that some people, by being afraid of getting sick, would reduce interactions with others, it would be a stretch to consider that all individuals will follow the government mandates regarding COVID-19 (Hubert et al. 2022). These individualistic points of view have been studied by Reluga (2010), Reluga (2013), as well as by Li et al. (2017) and Elie et al. (2020). In this way game theory has been introduced in the pandemic models. After the incidence of COVID-19 several risk factors and comorbidities such as obesity, preexisting health conditions like diabetes or hypertension, and advanced age have been found as the primal cause of spreading the pandemic (Albrecht et al. 2021; Richardson et al. 2020; Yang et al. 2020). An increase in environmental factors such as air pollution, temperature, and humidity has contributed to increasing the spread of COVID-19 in China (Jiang et al. 2020; Zhu et al. 2020). The effect of PM\(_{2.5}\) remains largely unexplored as the pandemic continues to spread (Albrecht et al. 2021). Events like raging wildfires in the western United States have increased the concentration of PM\(_{2.5}\) in the air (O’Dell et al. 2019). Albrecht et al. (2021) study whether this PM\(_{2.5}\) in the air has any impact of spreading COVID-19.
In this paper a Feynman-type path integral approach is used for a recursive formulation of a health objective function with a stochastic fatigue dynamics, forward-looking stochastic multi-risk SIR model and a Bayesian opinion network of a risk-group toward vaccination against COVID-19. The main interest of the paper is in solving a minimization problem \(\textbf{H}_{\theta }\) which depends on a deterministic weight \(\theta\) (Marcet and Marimon 2019). A Wick-rotated Schrödinger type equation (i.e., a Fokker–Plank diffusion equation) is obtained which is an analogous to a HJB equation (Yeung and Petrosjan 2006) and a saddle-point functional equation (Marcet and Marimon 2019). My formulation is based on path integral control and dynamic programming tools facilitates the analysis and permits the application of algorithm to obtain numerical solution for this stochastic pandemic control model. Furthermore, \(\textbf{H}_{\theta },\) with given initial conditions, is labeled as a continuation problem as its solution coincides with the solution from period s onward (Marcet and Marimon 2019). A terminal condition of the policy maker’s objective function makes it as a Lagrangian problem (Intriligator 2002).
Feynman path integral is a quantization method which uses the quantum Lagrangian function, while
Schrödinger’s quantization uses the Hamiltonian function (Fujiwara 2017). As this path integral approach provides a different view point from Schrödinger’s quantization, it is very useful tool not only in quantum physics but also in engineering, biophysics, economics and finance (Kappen 2005; Anderson et al. 2011; Yang et al. 2014a; Fujiwara 2017). These two methods are believed to be equivalent but, this equivalence has not fully proved mathematically as the mathematical difficulties lie in the fact that the Feynman path integral is not an integral by means of a countably additive measure (Johnson and Lapidus 2000; Fujiwara 2017). As the complexity and memory requirements of grid-based partial differential equation (PDE) solvers increase exponentially as the dimension of the system increases, this method becomes impractical in the case with high dimensions (Yang et al. 2014a). As an alternative one can use a Monte Carlo scheme and this is the main idea of path integral control (Kappen 2005; Theodorou et al. 2010; Theodorou 2011; Morzfeld 2015). This path integral control solves a class a stochastic control problems with a Monte Carlo method for a HJB equation and this approach avoids the need of a global grid of the domain of HJB equation (Yang et al. 2014a). If the objective function is quadratic and the differential equations are linear, then solution is given in terms of a number of Riccati equations which can be solved efficiently (Kappen 2007a; Pramanik and Polansky 2020a; Pramanik 2021a; Pramanik and Polansky 2021a). Although incorporate randomness with its HJB equation is straight forward but difficulties come due to dimensionality when a numerical solution is calculated for both of deterministic or stochastic HJB (Kappen 2007a). General stochastic control problem is intractable to solve computationally as it requires an exponential amount of memory and computational time because, the state space needs to be discretized and hence, becomes exponentially large in the number of dimensions (Theodorou et al. 2010; Theodorou 2011; Yang et al. 2014a). Therefore, in order to calculate the expected values it is necessary to visit all states which leads to the summations of exponentially large sums (Kappen 2007a; Yang et al. 2014a; Pramanik 2021a).
Acemoglu et al. (2020) suggest more restrictive policies about social interaction with people with advanced age reduce the COVID-19 infection for the rest of the population. In Acemoglu et al. (2020) the population is divided into three age groups: young (22–44), middle-aged (45–65), and advanced-aged (\(65+\)) where the only differences in interactions between these groups come from different lock-down policies. Then, they applied a deterministic multi-risk SIR model in each group and suggested that using a uniform lock-down policy for the policymakers targeting stricter lock-down policy to more advanced aged population, the fatality rate due to COVID-19 would be just above \(1\%\) (where uniform policy leads to a \(1.8\%\) fatality rate). Targeted policy reduces the economic damage from 24.3 to \(12.8\%\) of yearly gross domestic product (GDP) (Acemoglu et al. 2020). In addition, targeted policies such as changing in norms and laws segregating the young population from the older are imposed, fatalities and economic damages because of COVID-19 can be substantially low (Acemoglu et al. 2020). At the stages of the pandemic, most of the (non-pharmaceutical) interventions are classified into two groups such as testing and identification of infected individuals, and social distancing measures to reduce the transmission probabilities (Freiberger et al. 2022). Moreover, these groups of measures target certain subgroups of a networked population. To study such issues, Freiberger et al. (2022) propose an extension of the SIR model with additional compartments for quarantine and different courses of the disease across several network nodes. Freiberger et al. (2022) develop an optimal allocation and implement a numerical example of three symmetric regions that are prone to an asymmetric progression of the pandemic. Richard et al. (2021) observe that individuals with different ages spread the infection differently in a pandemic setting. Furthermore, the spread of infection also depends on the number of days they have been infected for. In the absence of pharmaceutical interventions, non-pharmaceutical interventions such as physical or social distancing are important factors to mitigate the pandemic (Richard et al. 2021). Richard et al. (2021) develop a methodology to determine the optimal age-stratified control strategy to implement as a function of the time. Their model is based on a double continuous structure in terms of host age and time since infection. By implementing an optimal control theory to this model, Richard et al. (2021) identify a minimized solution of deaths and costs associated with the implementation of the control strategy itself. Bonnans and Gianatti (2020) propose a pandemic model where the population is partitioned according to constant ages during the pandemic. They consider the infection age of the infected population to allow a better simulation of the infection propagation dependent on infection age. Furthermore, Bonnans and Gianatti (2020) investigate about how to estimate the coefficients from data available in the future and introduce a confinement variable as control.
The solutions to the optimal “locking down” problem are very complicated in the sense that if an economy imposes a stricter policy for a long time, it would be able to reduce the infection rate to a low level. If a short lock-down is applied then, the policy makers are softening the infection rate of COVID-19 from touching down the peak (Caulkins et al. 2021; Pramanik 2022a, b). Another assumption is that information regarding spreading of COVID-19 transmission is incomplete and imperfect. As a result, one might have multiple non-unique Skiba points or multiple solutions. Rigorous studies about Skiba points have been done in Skiba (1978); Grass (2012) and Sethi (2019). Aspri et al. (2021) take into account a SEIRD model with population divided into susceptibles, exposed but asymptotic, infected, recovered and deceased, and they obtain multiple lock-downs as well as Skiba points. Caulkins et al. (2020) suggest if the number of infected people required an intensive care exceeds the death rate of these patients increases relative to similar people who are able to receive appropriate care. A significant research on Skiba points can be found in Aspri et al. (2021), Caulkins et al. (2020, 2022), and Rowthorn and Maciejowski (2020). Rowthorn and Maciejowski (2020) consider a simple cost-benefit analysis based on an optimal control theory and incorporating the SIR model of disease propagation. They compute an optimal path for government intervention under a variety of conditions such as a cap on the permitted level of infection to avoid overload of the health system, and the introduction of a test and trace system. Although there is a growing literature on COVID-19 and its socioeconomic impacts related to extended lock-down time, length of lock-down and the appropriate time to lock down have not been extensively studied (Caulkins et al. 2021). Furthermore, I am using a new Feynman-type path integral approach which has an advantage over traditional Hamiltonian–Jacobi–Bellman (HJB) approach as the complexity and memory requirements of grid-based partial differential equation increases exponentially with the dimension of the system (Yang et al. 2014b; Pramanik 2020, 2021a).
One can transform a class of nonlinear HJB equations into linear equations by performing a logarithmic transformation. This transformation stems back to the early days of quantum mechanics which was first used by Schrödinger to relate HJB equation to the Schrödinger equation (Kappen 2007b). Because of this linear feature, backward integration of HJB equation over time can be replaced by computing expectation values under a forward diffusion process which requires a stochastic integration over trajectories that can be described by a path integral (Kappen 2007b; Pramanik and Polansky 2019; Pramanik 2021b). Furthermore, in more generalized case like Merton–Garman–Hamiltonian system, getting a solution through Pontryagin’s maximum principle is impossible and Feynman path integral method gives a solution (Baaquie 1997; Pramanik and Polansky 2020b, 2021b; Pramanik 2021a). Previous works using Feynman path integral method has been done in motor control theory by Kappen (2005), Theodorou et al. (2010) and Theodorou (2011). Applications of Feynman path integral in finance have been discussed rigorously in Baaquie (2007). A key assumption to get HJB is that the feasible set of action is constrained by a set of state and control variables only which does not satisfy many economic problems with forward-looking constraints, where the future actions are also in the feasible set of actions (Marcet and Marimon 2019). In the presence of a Forward-looking constraints, optimal plan does not satisfy Pontryagin’s maximum principle (Yeung and Petrosjan 2006) and the standard form of the solution ceases to exist because, the choice of an action carries an implicit promise about a future action (Marcet and Marimon 2019). The absence of a standard recursive (Ljungqvist and Sargent 2012) formulation complicates the dynamic control problem with high dimensions and fails to give a numerical solution of the system (Yang et al. 2014b; Marcet and Marimon 2019).
Another important context regarding COVID-19 infection is the rate of spread of COVID-19 in a community. The question of immunity and susceptibility is critical to the statistical analysis of infectious disease like COVID-19. Under the assumption that everybody in a community is susceptible to this pandemic one may be led to think that it is mildly infectious (Becker 2017). On the other hand, if everyone who had previously acquired immunity, is able to escape infection during this pandemic, one should conclude that it is highly infectious. Furthermore, the immunity status of individuals assessed by the tests on blood, saliva or excreta tests, is another determinant about the intensity of the spread of this pandemic (Becker 2017). Therefore, I am using network graph analysis to determine the spread of the infection. Based on the grouping, I classify the social network directed graph and determine the adjacency matrix without existence of a loop. Furthermore, an undirected network graph leads to a symmetric adjacency matrix (Pramanik 2016; Hua et al. 2019; Polansky and Pramanik 2021). The diagonal terms of this matrix are zero, and the off-diagonal terms have different values based on their weight in relation to the other persons in a community. For example, I give higher value to parents, spouses and siblings of a person compared to a person in distant relationship because if our person of interest gets infected by COVID-19, their parents, spouses and siblings are the ones who would be in risk to get infected by the pandemic.
Public opinion on taking the vaccine is an important factor in determining the spread of COVID-19. When the policymakers in the United States have decided to mandate vaccination in all the public sector employees, many people have gone for a protest and significant number of government employees take leave from their duties which has affected negatively toward those sectors such as New York Fire and Chicago Police Departments. Reasons for these negative opinions of people and employees include the belief that a government mandate for vaccination is against the civil right, and religious beliefs, respectively. As social networks are the results of individual opinions, consensus from social networks regarding COVID-19 vaccine mandates plays an important role in understanding the spread of infection. Although there is research on social networks (Jackson 2010; Goyal 2012; Sheng 2020), there is limited work on the role of personal opinions in vaccine mandates in influencing the spread of the disease. Sheng (2020) formalizes network as simultaneous-move game, where social links based on decisions are based on utility externalities from indirect friends and proposes a computationally feasible partial identification approach for large social networks. The statistical analysis of network formation goes dates back to the seminal work by Erdös and Rényi (1959) where a random graph is based on independent links with a fixed probability (Sheng 2020). Beyond Erdös–Rényi model, many methods have been designed to simulate graphs with characteristics like degree distributions, small world, and Markov type properties (Polansky and Pramanik 2021; Pramanik 2021c).
First part of Sect. 2 discusses about different types of COVID-19 spread and defines lock-down intensity. Section 2.1 describes different stochastic dynamics models and their properties, Sect. 2.2 discusses about Bayesian opinion dynamics of a risk-group toward vaccination against COVID-19, and Sect. 2.3 discusses the objective function of a policy maker. Theorem 1 in Sect. 3 is the main result of the paper. A closed form solution of lock-down intensity is calculated at the end of Sect. 3. Section 4 discusses a numerical study of the theoretical model, and finally, Sect. 5 contains concluding remarks and directions for future research.
Formulation of a pandemic model
In this section, I provide the construction of a stochastic SIR model, fatigue dynamics, infection rate dynamics, opinion dynamics against COVID-19 vaccination with a dynamic social cost as the objective function. Furthermore, I discuss how the stochastic programming method can be used to formulate a recursive formulation of a large class of pandemic control models with forward-looking stochastic dynamics.
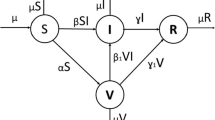
Acemoglu et al. (2020) consider three age groups young (22–44 years), middle-aged (45–65 years) and advanced-aged (65+ years). One can construct K total number age-groups based on a group’s vulnerability to COVID-19. I assume equal group sizes for simplicity. For finite and continuous time \(s\in [0,t]\) define a group vulnerable to COVID-19 is k such that, \(k=1,2,\ldots ,K\) with \(N_k\) be the initial population of an economy. Furthermore, I determine K large enough to ensure every agent in an age-group has homogenous behavior. At time s, the age-group (I will use the term risk-group instead of age-group because each group is vulnerable to COVID-19 at certain extent) k is subdivided into those susceptible (\(S_k\)), those infected (\(I_k\)), those recovered (\(R_k\)) and those deceased (\(D_k\)),
Individuals in risk-group k move from susceptible to infected, then either recover or pass away as well as groups also interact among themselves.
In Fig. 1 one can see how the state of an individual moves in a risk group. Furthermore, the virus spreads exponentially in a risk group as well as across the groups. Therefore, the COVID-19 transmission follows a dynamic Barabasi–Albert model where each new node is connected with existing nodes with a probability proportional to the number of links that the existing nodes already have (Barabási and Albert 1999).
In Fig. 2, I construct two realizations of random COVID-19 spread where the probability of each node depends on a person’s immunity level.
As lockdown and social distancing reduce interaction among people, I will treat “lockdown” as a policy. Let for risk-group k, \(L_k^b(s)\) is the total number of people willing to work before the pandemic and \(L_k^a(s,c)\) is the total number of people willing to work during pandemic which is a function of lockdown fatigue (due to COVID-19 deaths in kth risk-group) is denoted by c(s). Suppose, \(d_1,d_2,\in (0,1)^2\) are the factors representing the proportions of \(L_k^b(s)\) and \(L_k^a(s,c),\) respectively, who are actually working. Define a new variable \(e_k(s)=\frac{d_2L_k^a(s,c)}{d_1L_k^b(s)}\) as actual number of people working during pandemic as a proportion of those who are supposed to work without the presence of COVID-19. At the very early stages as people have little knowledge about COVID therefore, \(e_k(s)>1\). Furthermore, due to discoveries of vaccines and the incidence of the disease for more than a year, people’s opinion against vaccination might lead indifference in behavior toward going to work or not. Therefore, \(e_k(s)\downarrow 1\). In this case, policy makers come to place to restrict employment such that \(e_k(s)\in (0,1)\). Thus, under policy-maker’s intervention \(e_k(s)=\frac{d_0d_2L_k^a(s,c)}{d_1L_k^b(s)}\) where, \(d_0\in [0,1]\) is the parameter which is predetermined by the policymakers to restrict employment during pandemic. On the other hand, if the policy makers think an emergence of a new variant of COVID-19 is random they fix \(d_0=1\) and let the economy move on its way. For finite, continuous time \(s\in [0,t]\) the ratio \(e_k(0)=1\) and \(e_k(t)\in [0,1]\) is based on the condition of pandemic. Hence, \(\frac{\partial e_k}{\partial s}=u_k(s)\) represents the intensity of allowed employment and I use it as the stochastic control variable.
Stochastic SIR model
Following Caulkins et al. (2021) I assume a state variable \(z_k(s)\) capturing a “lockdown fatigue” through a stochastic accumulation dynamics determined by COVID-19 related unemployment rate for risk-group k is \([1-e_k(s)]\). The stochastic fatigue dynamics is given by
where \(\kappa _0\) indicates the rate of fatigue accumulation, \(\kappa _1\) is the rate of exponential decay,
denotes the probability that a link of the new node connects to Barabasi–Albert node \(k_i\) depends on the degree \(\eta _{k_i}\) at time s (Barabási and Albert 1999), \(\sigma _0^k\) is the diffusion coefficient, \(z_k^*\) is equilibrium value of \(z_k\) and \(B_0^k\) is a 1-dimensional Brownian motion. Under the absence of diffusion component and under extreme lockdown (i.e., \(e_k(s)=0\)) this state variable takes its maximum value \(Z_{\max }=\kappa _0/\left[ \kappa _1p(\eta _{k_i},s)\right]\).
Assumption 1
For \(t>0\), let \(\hat{\mu }(s,e_k,p,z_k):[0,t]\times [0,1]^2\times \mathbb{R} \rightarrow \mathbb{R}\) and \({\sigma _0^k(z_k)}: \mathbb{R} \rightarrow \mathbb{R}\) be some measurable function and, for some positive constant \(K_1\), \(z_k\in \mathbb{R}\) we have linear growth as
such that, there exists another positive, finite, constant \(K_2\) and for a different lockdown fatigue state variable \(\tilde{z}_k\) such that the Lipschitz condition,
\(\tilde{z}_k\in \mathbb{R}\) is satisfied and
Remark 1
The Lipschitz condition Assumption 1 guarantees that the stochastic fatigue dynamics represented by Eq. (1) has a unique solution by Picard–Lindelöf theorem. For the other stochastic differential equations in this paper I also assume similar assumptions hold such that they also have a unique solution. The beauty of this simplistic assumption is its powerful intuitive meaning: given a “lockdown fatigue” of risk-group k defined as \(z_k(s)\), the government implements all the abatement measures which make medical sense, comes up with a unique “lockdown intensity”.
Assumption 2
Assume \((\Omega ,\mathcal{F},\mathbb{P})\) is the stochastic basis where the filtration \(\{\mathcal{F}_s\}_{0\le s\le t}\) supports a 1-dimensional Brownian motion \(B_0^k(s)=\{B_0^k(s)\}_{0\le s\le t}\). \(\mathbb{F}^0\) is the collection of all \(\mathbb{R}\)-values progressively measurable process on \([0,t]\times \mathbb{R}\) and the subspaces are
and,
where \(\Omega\) is the Borel \(\sigma\)-algebra and \(\mathbb{P}\) is the probability measure (Carmona 2016). Furthermore, the 1-dimensional Brownian motion corresponding to lockdown fatigue for risk-group k is defined as
Remark 2
The first part of Assumption 2 defines two subspaces \(\mathbb{F}^2\) and \(\mathbb{S}^2\). The first subspace \(\mathbb{F}^2\) says that all expected values of the squared integrals of \(z_k(s)\) are finite, and if there is another random variable \(Y_k(s)\) then the supremum of absolute squared values are also finite. Since \(Y_k(s)\) is arbitrary I assume it is the upper bound of \(z_k(s)\). Along with the probability space \((\Omega ,\mathcal{F},\mathbb{P})\) this guarantees the integral form of Eq. (1) is a strict contraction in the Hilbert space. \(B_0^k\) in Assumption 2 defines a subspace where absolute value of \(z_k(s)\) is finite with probability measure \(\mathbb{P}\) almost surely. Combining the above two assumptions make sure that Eq. (1) not only have a finite a finite unique solution but also the solution exists in the Hilbert space.
Lemma 1
Suppose the initial lockdown fatigue of kth risk group \(z_k(0)\in \textbf{L}^2\) is independent of Brownian motion \(B_0^k(s)\) and the drift and the diffusion coefficients \(\hat{\mu }(s,e_k,p,z_k)\) and \(\sigma _0^k(z_k),\) respectively, follow Assumptions 1 and 2. Then, the lockdown fatigue dynamics in Eq. (1) is in space of the real valued process with filtration \(\{\mathcal{F}_s\}_{0\le s\le t}\) and this space is denoted by \(\mathbb{F}^2\). Furthermore, for some constant \(c_0>0\), continuous time \(s\in [0,t]\) and Lipschitz constants \(\hat{\mu }\) and \(\sigma _0^k\), the solution satisfies,
Remark 1
Assumptions 1 and 2 along with Lemma 1 imply that the “lockdown fatigue” dynamics has a strong unique solution in the Hilbert space and the solution has an upper bound expressed by Eq. (2).
Proof
See in “Appendix”.\(\square\)
The foundation of pandemic model of our paper is stochastic susceptibility–infection–recovery (SIR) structure. Following Acemoglu et al. (2020), new infections are proportional to the number are proportional to the number of susceptible (S) and infected people (I) of the initial population or \(\beta SI\). Furthermore, I assume that this infection rate \(\beta\) is subject to a random shocks (Lesniewski 2020), therefore,
where \(\theta >1\) to make the function \(\beta ^k(e_k,z_k)\) a convex function of \(e_k\) (i.e., \(\partial \beta ^k/\partial e_k>0\) and \(\partial ^2 \beta ^k/\partial e_k^2>0\)), \(\beta _1^k,\beta _2^k>0\) such that \(\partial \beta /\partial z_k>0\), \(\beta _1\) is the minimum level of infection risk produced if only the essential activities are open, \(\gamma \in (0,1)\) is the parameter which determines the degree of effectiveness of fatigue to spread infection, M is fine particulate matter (PM\(_{2.5}>12\,\upmu\)g/m\(^3\)) which is an air pollutant and have significant contribution to degrade a person’s health, \(\sigma _1^k(e_k(s),z_k(s))\) is a known diffusion coefficient infection dynamics and \(\textrm{d}B_1^k(s)\) is one dimensional standard Brownian motion of \(\beta (e_k,z_k)\). Therefore, in lack of the presence of lockdowns and isolations, the new infection rate of group k is
where \(\beta ^{kl}\) are parameters which control infection rate between two infection groups k and l and, \(\alpha \in [1,2]\) allows to control the returns of the scale matching (Acemoglu et al. 2020). For steady state values \(S_k^*\), \(I_k^*\) and \(R_k^*\) (Rao 2014), the risk-group k has the SIR state dynamics as
where \(\eta\) is birth rate, \(1/\left[ 1+rI(s)\right]\) is a measure of inhibition effect from behavioral change of a susceptible individual in group k, \(\tau\) is the natural death rate, \(\zeta\) is the rate at which recovered person loses immunity and returns to the susceptible class and \(\mu\) is the natural recovery rate of the infected individuals in risk-group k. \(\sigma _2^k\), \(\sigma _3^k\) and \(\sigma _4^k\) are assumed to be real constants and are defined as the intensity of stochastic environment and, \(B_2^k(s)\), \(B_3^k(s)\) and \(B_4^k(s)\) are standard one-dimensional Brownian motions (Rao 2014). It is important to note that in the dynamic systems (4) is a very general case of SIR model.
For a complete probability space \((\Omega ,\mathcal{F},\mathbb{P})\) with filtration starting from \(\{\mathcal{F}_s\}_{0\le s\le t}\), satisfying Assumptions 1 and 2. Let
where the norm \(|\textbf{Z}_k(s)|=\sqrt{z_k^2(s)+S_k^2(s)+I_k^2(s)+R_k^2(s)}\). Suppose, \(C^{2,1}(\mathbb{R}^4\times (0,\infty ),\mathbb{R}_+)\) be a family of all nonnegative functions \(\mathfrak{W}(s,\textbf{Z}_k)\) defined on \(\mathbb{R}^4\times (0,\infty )\) so that they are continuously twicely differentiable in \(\textbf{Z}_k\) and once in s. Consider a differential operator \(\textbf{D}\) associated with 4-dimensional stochastic differential equation for risk-group k
such that
where
and,
Now let \(\textbf{D}\) acts on function \(\mathfrak{W}\in C^{2,1}(\mathbb{R}^4\times (0,\infty );\mathbb{R}_+)\), such that
where T represents a transposition of a matrix.
Proposition 1
For any given set of initial values of risk-group k, \(\{z_k(0),S_k(0),I_k(0),R_k(0)\}\in \mathbb{R}^4\) with Assumptions 1 and 2 there exists a unique solution \(\{z_k(s),S_k(s),I_k(s),R_k(s)\}\) on \(s\in [0,t]\) and will remain in \(\mathbb{R}^4\) under incomplete and perfect information, where \(B^k=B_0^k=B_2^k=B_3^k=B_4^k\).
Proof
See in “Appendix”.\(\square\)
For theoretical purpose I rewrite theses equations as
Furthermore, it is assumed to be the System (6) follows Assumptions 1 and 2.
Opinion dynamics of a risk-group k toward vaccination against COVID-19
This section will discuss about the spread of kth risk-group’s opinion toward vaccination against COVID-19 in the society. In the previous section I assume each risk-group is constructed such a way that each agent in that group has homogeneous opinions. Heterogeneous opinions need to be addressed by a multi-layer social-network which would be an interesting topic for future research and currently is beyond the scope of this paper. As there are \(N_k\) agents in each of the K risk-groups therefore, total population is \(KN_k=N<\infty\). I assume that all risk-groups are connected to each other via an exogenous, directed network represented by graph \(\mathcal{G}\subseteq N\times N\) which also represents how one risk-group spreads its beliefs about vaccination against COVID-19 to other risk-groups. For example, If risk-group k gives its opinion to risk-group l, then I write \(k\rightarrow l\) or \((k,l)\in \mathcal{G}\). Furthermore, if risk-group l gets different opinion about COVID-19 vaccination from risk-group k more often then, k and l are group-neighbors \(\mathcal{N}_k(\mathcal{G})\) (Board and Meyer-ter Vehn 2021). As COVID-19 is known less than 2 years to us, people have incomplete information about this pandemic and this leads to an incomplete information about the social network under COVID-19. This information is captured by finite signals \(\chi _k\in X_k\) and a joint prior distributions over networks and signal profiles \(\varrho (\mathcal{G},\chi _k)\) (Board and Meyer-ter Vehn 2021). Now a random network \(G=(N,X,\varrho )\). Consider following four cases:
-
Deterministic social network \(\mathcal{G}\). Following Board and Meyer-ter Vehn (2021) signal spaces about the opinion of COVID-19 are assumed to be degenerate, \(|X_k|=1\), and the prior \(\varrho\) assigns probability 1 to \(\mathcal{G}\). Although complete information eases the situation, this is rare in current COVID-19 situation. As this pandemic is new, even policy makers do not have complete information. For example, at the middle of 2021 policymakers (such as Centers for Disease Control and Prevention (CDC)) announced that fully vaccinated people are completely safe against this pandemic. Now because of Omicron variant above 350,000 people are infected daily by January 2022. As a result, people lose trust on policy-makers and make their opinions based on their beliefs and faiths. This makes the learning dynamics about COVID-19 extremely complicated. This motivates to study random opinion network about pandemic with incomplete information.
-
Directed opinion network with finite types \(\gamma \in \Gamma\) where, for an individual risk-group k, first I independently draw a finite type \(\gamma \in \Gamma\) assuming any distribution with full support. After choosing kth risk-group’s opinion types \(\gamma\) against COVID-19 vaccination that risk-group randomly stubs each type \(\gamma '\). Then, during communication, type \(\gamma '\) randomly stubs to type \(\gamma '\) individual risk-groups. Now the individual risk-group knows total number of outlinks of each type in the sense that, what are their group-neighbor’s stand toward COVID-19 vaccination. The outlink at time s is denoted as a vector \(d=(s,d_{\gamma '})_{\gamma '}\in \mathbb{N}^{\gamma '}\) which is also realization of more generalized random vector \(\mathcal{D}_\gamma =(s,\mathcal{D}_{\gamma ,\gamma '})_{\gamma '}\) with expectation at time s is \(\mathbb{E}_s[\mathcal{D}_{\gamma ,\gamma '}]\) where \(\mathcal{D}=(s,\mathcal{D}_{\gamma ,\gamma '})_{\gamma ,\gamma '}\) is a time dependent or dynamic degree distribution.
-
Indirected opinion spread network with binary links and triangles. Following Board and Meyer-ter Vehn (2021) kth individual risk-group’s spreading their opinions about vaccination against COVID-19 might have \(\hat{d}\) binary stubs and \(\tilde{d}\) pairs of triangles.
From Fig. 3 it is clear that \(\hat{d}\) and \(\tilde{d}\) are the subset of the above graph. For example, if we consider individual risk-group 1, then from the first panel it has \(\hat{d}=3\) and in the second panel the same risk-group has two triangular stubs. We further assume, every individual risk-group knows their total number of binary and triangular stabs. In the world of COVID opinion spreading, if one individual risk-group shares their opinions to another risk-group very close to it then, the network connection might be triangular. On the other hand if individual risk-group k spreads its opinion to some stranger (i.e., another risk-group far from risk-group k’s opinions), it would be one time binary information transition.
-
Microscopic interaction among risk-groups. A kinetic model for opinion spread toward vaccination against COVID-19 (Cordier et al. 2005; Toscani et al. 2006). Let \(\omega _k\) denotes opinion of individual risk-group k and it varies continuously between \(-1\) and 1. Here \(-1\) represents an individual risk-group k’s extremely negative opinion for getting vaccinated against COVID-19, whereas 1 stands for completely opposite extreme opinion for COVID-19 vaccination. Following Toscani et al. (2006) I assume that directed and indirected interactions cannot destroy the bounds, which corresponds to imply that extreme opinions cannot be crossed.
At the beginning of the interaction risk-group k seeks to learn about the severity of COVID-19 with its own belief \(v_k\in \{L,H,\omega _k\}=\{0,1,[-1,1]\}\), where L stands for low severity of the disease and H stands for high severity. At \(s=0\) and for a fixed belief against getting vaccinated, all the risk-groups share a common prior Pr\((v_k=H|\omega _k)=p_0\in (0,1)\), independent of network \(\mathcal{G}\) and signals \(X_k\). As the pandemic spreads, individual risk-group k develops the need of information about the disease and start interacting at time \(s_k\sim U[0,1]\) (the uniform distribution where \(s_k\) is time-quantile during the presence of the pandemic). Based on the handling of the pandemic of the group-neighbors risk-group k updates its probabilities of beliefs about pandemic to Pr\((\omega _k^*)=p_k^*\), such that Pr\((\omega _k^*=-1)=0\) and \(\text{Pr}(\omega _k^*=1)=1\). In order to get information, risk-group k incurs some cost \(c_k\sim F[\underline{c},\bar{c}]\), where F is the distribution function with bounded density function f. risk-group k only gets exposure to the pandemic iff \(v_k=\{L,\omega _k\}\). If individual risk-group k does care about the severity of the disease, it interacts with other risk-groups frequently and transmits COVID-19. Interaction times \(s_k\) and the cost of disease information \(c_k\) are private information, independent within individual risk-groups in \(S_k, I_k\) and \(R_k\).
If individual risk-group k finds \(v_k=\{L,\omega _k\}\) and does not mind to interact with other risk-groups, its utility becomes 1. If risk-group k finds \(v_k=\{H,\omega _k\}\) then, it is reluctant to interact with other risk-groups. In this case there are two possibilities, if unknowingly risk-group k gets infected by the virus, its utility becomes 0 and furthermore, if individual risk-group k gets infected knowingly, its utility goes down to \(-U\). Finally, if risk-group k sees its group-neighbor gets infected by the virus but asymptotic, its posterior is \(p_k=1\) and does not mind to interact. If risk-group k gets infected by COVID-19 unknowingly, the posterior becomes \(p_k\le p_0\). Assume \(U\ge p_0/(1-p_0)\), which leads to an adoption to the pandemic is a dominated strategy. Furthermore, if \((p_k-c_k)\ge 0\), then individual risk-group k does not mind to interact with other risk-groups which might lead to get transmitted with the disease. On the other hand, if \((p_k-c_k)< 0\), then individual risk-group k finds \(v_k-\{H,\omega _k\}\) and tries to isolate from other risk-groups.
Example 1
Without loss of generality assume two independent risk-groups k and l who are interacted by a directed graph such that \(k\rightarrow l\). Before interaction, risk-group k and l have believes about COVID-19 vaccination as \(\omega _k\) and \(\omega _l\), respectively, where \((\omega _k,\omega _l)\in [-1,1]^2=\mathcal{I}^2\). Denote \(\text{Pr}_s(L|\omega _k)\) as the probability of individual risk-group k’s willingness to contact with other risk-groups at time s when it expects the severity of pandemic is less or L. Risk-group k starts its communication at uniform time \(s\in [0,t]\). As it is not rational for risk-group k to interact with other risk-groups when \(v_k\) is H, it is sufficient to keep track of the interaction probability conditional on \(v_k=L\). Furthermore, as risk-group k does not mind to interact as long as \(c_k\le p_0\) then \(\partial [\text{Pr}_s(L|\omega _k)]/\partial k=\text{Pr}(k\ \text{ is indifferent to interact}\ |\omega _k)=F(p_0)\), which is independent of time. Furthermore, the interaction of opinions among risk-groups k and l follow the stochastic dynamic systems represented by
where \(\varkappa \in (0,1/2)\) is the compromise propensity, the function \(\mathcal{Q}(.)\in [0,1]\) with \(\partial \mathcal{Q}/\partial \omega _k\le 0\) represents the local relevance of compromise (Toscani et al. 2006). It is important to know that, if \(e_k(s)\downarrow 0\) then there is a huge unemployment in the economy which means the incidence of pandemic is very severe. Under this case a difference in opinion \((\omega _k-\omega _l)\) does not affect the dynamic system and every risk-group needs to follow the policymakers’ protocols. On the other hand, if \(e_k(s)\downarrow 1\) then, opinion difference takes a major role to explain the above stochastic opinion dynamical systems. Finally \(\sigma _8^k(s)\) and \(\sigma _9^i(s)\) are the opinion diffusion coefficients with \(B_5^k(s)\) and \(B_6^l(s)\) as their corresponding Brownian motions.
As risk-group k interacted first, as a second mover individual risk-group l learns about the effect of pandemic from risk-group k. Furthermore, if risk-group l notices that, risk-group k does not mind interacting with other risk-groups, then k thinks the disease is not fatal and is not reluctant to interact with others and, vice versa. Therefore, individual risk-group l’s posterior probability that COVID-19 is not severe is
Individual risk-group l does not mind to interact with other risk-groups if \(c_l\le p\left[ \text{Pr}_s(L|\omega _k(s))\right]\). As \(\text{Pr}_s(L|\omega _k(s))\) changes based on the infection rate of the community, individual risk-group l’s optimistic approach to do social contact continues but the pessimistic approach kicks in only if \(\text{Pr}_s(L|\omega _k(s))\) is starting to decrease. Therefore, individual risk-group l’s tolerance rate is
By denoting \(\text{Pr}_s(L|\omega _k(s))=W_k(s)\) and considering the stochastic opinion dynamics I define a stochastic differential equation
Without loss of generality Eq. (7) becomes,
all the symbols have their usual meanings.
Let \(G=(N,X,\varrho )\) be a random network with signal profile \(\varrho (\mathcal{G},\chi _k)\). Like in the example above I assume individual risk-group l does not mind interacting socially with probability \(\text{Pr}_s(L|\omega _l)=W_l(s)\). As risk-group l does not have any prior knowledge about COVID-19 transmission network, its decision strictly depends on the actions of other risk-groups’ willingness to do so in the community \(\mathcal{G}\) with signals \(\varrho\). Let \(W_{l,\mathcal{G},\varrho ,\chi _l,\omega _l}(s)\) be a social interaction function for risk-group l subject to \((\mathcal{G},\chi _l,\omega _l)\) after expectation over other risk-groups’ time of social interaction is \(s_k\) with cost \(c_k\). After taking expectation on \((\mathcal{G},\chi _{-l},\omega _{-l})\), consider
be risk-group l’s interim social interaction function such that its signal is \(\chi _l\) and its own opinions \(\omega _l\). Risk-groups under Bayesian social network are willing to do social interaction if their group-neighbors are not reluctant to interact with others. Suppose, at least one of individual risk-group l’s neighbor has the interim social interaction function
such that \(c_l\le p_l\). To get a proper expression of \(W_{l,\mathcal{G},\chi _{-l},\omega _{-l}}(s)\) assume individual risk-group l first observes whether their group-neighbors are engaged in social interactions. If they interact then risk-group l gets the information that the pandemic is not severe and makes \(p_l=1\). On the other hand, if risk-group l finds out their neighbors are keeping social distancing then risk-group l will try to get more information if their opinions against the COVID-19 vaccination are very strong such that \(c_l\le \bar{c}_{l,\chi _l,\omega _l}:=p_l\), where \(\bar{c}_{l,\chi _l,\omega _l}\) is some arbitrary cut-off cost depending on \(\omega _l\). If individual risk-group l finds out that the transmission of the pandemic is very high, it will put \(p_l=0\). Therefore,
Lemma 2
For individual risk-groups k and l, the pair of social interaction functions \(\left( W_{k,\chi _{-k},\omega _{-k}}(s),W_{l,\chi _{-l},\omega _{-l}}(s)\right)\) on space \(F=(s,G,N,X,\varrho ,\mathcal{I})\) with conditional probabilities \(\text{Pr}_s(H|\omega _k)=1\) and \(\text{Pr}_s(H|\omega _l)=1\) in a same community. Then under non-intersecting graph \(\mathcal{G}\), different opinions and for a function \(h\in F\) we have total social interaction variation as
where the infimum is taken over all finite resolutions of F into pairs of non-intersecting subgraphs \(\mathcal{G}_i\) with \(I>1\).
Proof
See in “Appendix”. Lemma 2 implies that if social interaction function has bigger network (i.e., \(\mathcal{G}\)), then
will be small and vice versa. Therefore, if individual risk-group l observes higher proportion of its neighbors are doing social interactions, they will do so. Furthermore, norm of social interaction is always less than unity. Therefore, the most extreme opinions against COVID-19 vaccination do not exist in this model.\(\square\)
Suppose, \(\mathfrak{q}=\{\mathfrak{q}_k\}_{k\in K}\) represents the states of individual risk-group k, where \(\mathfrak{q}_k\in \{\bar{q},\hat{q},\tilde{q}\}\). If \(\bar{q}=\emptyset\) then risk-group k does not enter the COVID-19 network. If \(\mathfrak{q}_k=\hat{q}\) then risk-group k has entered the network but reluctant to do social interactions and finally, if \(\mathfrak{q}_k=\tilde{q}\), then risk-group k is in the network and is not maintaining social distance. Under the last case, Pr\(_s(L|\omega _k)\approx 1\). Let \(\Omega _E=\{0,1\}^E\) be the relevant finite sample space, containing configurations that allocate zeros and ones to the edge of \(\mathcal{G}\), where \(E\,=\) edge of finite pandemic network \(\mathcal{G}\) (Grimmett 1995). Consider \(\delta \in \Omega _E\) the following condition holds,
The random cluster measure on COVID-19 social network G with signal \(\varrho\) and state profile \(\mathfrak{q}\) is a probability measure at time \(s\in [0,t]\)
where \(\jmath (\delta )\) is the total number of open components of \(\delta\), \(\mathbb{E}\) is the space of all edges of the graph \(\mathcal{G}\) and, \(\Upsilon _{G,\varrho ,\mathfrak{q}}\) is a normalizing factor (or, partition function ) such that,
A partial ordering under \(\Omega _E\) given by \(\delta \le \delta '\) iff \(\delta (E)\le \delta ', \ \forall E\in \mathbb{E}\). A function \(\mho :\Omega _E\rightarrow \mathbb{E}\) is called increasing if \(\mho (\delta )\le \mho (\delta '),\ \forall \ \delta \le \delta '\). \(\mathcal{A}\) is an increasing event if its simple function \(\mathbbm { 1}_{\mathcal{A}}\) is increasing. Furthermore, if \(\iota\) be a probability measure and \(W_{k,\chi _{-k}\omega _{-k}}(s)\) be a random response function then, \(\iota \left[ W_{k,\chi _{-k}\omega _{-k}}(s)\right]\) is the conditional expectation of \(W_{k,\chi _{-k}\omega _{-k}}(s)\) under \(\iota\) (Grimmett 1995). In pandemic social network if \(\mho\) and \(W_{k,\chi _{-k}\omega _{-k}}(s)\) are increasing on the sample space \(\Omega _E\), then
Above inequality is called as Fortuin–Kasteleyn–Ginibre (FKG) inequality (Grimmett 1995) of pandemic social network. Let \(\mathbb{Z}^\gamma\) be a \(\gamma\)-dimensional hyperbolic Lattice such that risk-groups (i.e., vertices) \(y_1\) and \(y_2\) both are in it. For \(E\subseteq \mathbb{E}\), \(\mathcal{F}_E^k\) is the \(\sigma\)-field such that \(\mathcal{F}=\mathcal{F}_E^k\) (Grimmett 1995). \(\Lambda \subseteq \mathbb{Z}^\gamma\) is a box such that,
where \([y_1^\gamma ,y_2^\gamma ]\) is defined as \([y_1^\gamma ,y_2^\gamma ]\cap \mathbb{Z}\). The reason behind choosing a finite box \(\Lambda\) inside \(\mathbb{Z}^\gamma\) is under the presence of COVID-19 risk-groups are not able to move across regions. Furthermore, moving around the globe is much harder because different countries have different restriction measures, which leads risk-groups to stay at home. As after certain point of time the COVID-19 infections go down, risk-groups would do social interactions locally. On the other hand, if a COVID-19 restriction stays too long, risk-groups would reluctant to stay at home. In this paper I am ruling out this scenario. The box \(\Lambda\) generates a sub-social network of lattice \(\mathbb{L}\) with risk-group k with \(S_k,I_k\) and \(R_k\) combined as set \(\Lambda\) with the set of network connections \(\mathbb{E}_\Lambda\). Define the \(\sigma\)-field at time s outside the network of \(\Lambda\) as \(\mathcal{F}_\Lambda =\mathcal{F}_{\mathbb{E}{\setminus }\mathbb{E}_\Lambda }\) and \(\mathcal{F}=\cap _\Lambda \mathcal{F}_\Lambda\) as outside \(\sigma\)-field.
Definition 1
A probability distribution \(\phi\) on \(G=(N,X,\varrho )\) with filtration \(\mathcal{F}\) is called a random opinion cluster toward COVID-19 for three states \(\mathfrak{q}\) and signal profiles \(\varrho\) if
We denote this set as \(\mathbb{R}_{\varrho ,\mathfrak{q}}\).
Definition 2
A probability distribution \(\phi\) on \(G=(N,X,\varrho )\) with filtration \(\mathcal{F}\) is called a limit random opinion cluster toward COVID-19 for three states \(\mathfrak{q}\) and signal profiles \(\varrho\) if \(\exists \ \xi \in \Omega\) and an increasing sequence of opinion boxes \(\{\Lambda _n\}_{n\ge 1}\) such that
where \(\Lambda _n\rightarrow \mathbb{Z}^\gamma\) as \(n\rightarrow \infty\) (Grimmett 1995).
Furthermore, if the structure of network in a box \(\Lambda\) is same (i.e., \(\phi _{\Lambda ,\varrho ,\mathfrak{q}}^k=\phi _{\Lambda ,\varrho ,\mathfrak{q}}^l\) ), then for risk-groups k and l in the society are in \(\mathbb{R}_{\varrho ,\mathfrak{q}}\) and following Grimmett (1995) \(|\mathbb{R}_{\varrho ,\mathfrak{q}}|=1\).
Proposition 2
Let for any random network G with the signal profile \(\varrho\) and for \(\mathfrak{q}=\mathfrak{q}_3=\{\bar{q},\hat{q},\tilde{q}\}\) and social interactions of risk-group k as \(W_{k,\chi _{-k},\omega _{k}}\) exists and definitions 1 and 2 holds. Then there exists a unique random opinion distribution.
Proof
See in “Appendix”. Proposition 2 guarantees that if risk-group k has imperfect and complete information then under \(\mathfrak{q}_3\) the random network has a unique solution.\(\square\)
Objective function
So far I have discussed about the stochastic dynamic systems of fatigue (\(z_k\)), infection rate (\(\beta ^k\)), multi-risk SIR (\(S_k,I_k\) and \(R_k\)) and opinion of risk-group k (\(\omega _k\)) with its probability conditioned on less severity as \(W_k\). This section will discuss about the objective of the policy makers subject to the stochastic dynamics discussed above.
Let \(\mathcal{H}_k(s)\) be the total number individuals of risk-group k who need emergency care at time s. Hence, \(\mathcal{H}_k(s)=\check{h}I_k(s)\), where \(\check{h}\in (0,1)\) is some given proportionality constant available at time s (Acemoglu et al. 2020). Therefore, total number of people in K risk-groups who need emergency care is \(\mathcal{H}(s)=\sum _{k=1}^K\mathcal{H}_k(s)\). Following Acemoglu et al. (2020) I assume that probability of death such that the person was under emergency care as \(\varpi _k(s)=\varphi _k[\mathcal{H}(s)]\), for some given function \(\varphi _k\). In this analysis a cost of death or value of life is included as \(\breve{\chi }_k\) (Acemoglu et al. 2020). By value of life I mean value of increasing the survival probabilities marginally due to COVID-19. In other words, one can think about the impact of death on a family in risk-group k in terms of monetary loss and emotional losses of that person’s family as well as risk-group k. A policy maker considers this cost as non-pecuniary cost of death and is denoted by \(\breve{\chi }_k\check{h}\varpi _k(s)I_k(s)\) as \(\check{h}\varpi _k(s)I_k(s)\) is defined as the flow of death.
I assume that the detection of a person infected by COVID-19 is imperfect as well as their isolation status. Without loss of generality assume \(\tau _k\) be the constant probability that an infected person in risk-group k does not need an emergency care and based on that person’s \(F(p_0)\)-value risk-group k would decide whether it will isolate that person or not. If \(F(p_0)\downarrow 1\) then individual in risk-group k will not be isolated with probability \(\tau _kF(p_0)\) or simply \(\tau _k\). On the other hand, if \(F(p_0)\downarrow 0\), individual in risk-group k will be isolated with probability \(\tau _kF(p_0)\). Let \(\hat{\tau }_k\) be the probability where an individual in risk-group k is detected and need an emergency care for recovery. Hence, \(F(p_0)\) is not as powerful as the case for those who do not need ICU care. Therefore, I restrict the upper limit of \(F(p_0)\) as \(\hat{F}_p<1/2\). This part is some extension of Acemoglu et al. (2020) where individual opinion of risk-group k was not considered. Therefore, the probability that a person is infected by COVID-19, detected and isolated in risk-group k is
In the presence of Omicron, a completely vaccinated and boosted person in risk-group k would have some probability \(\tilde{\tau }_k\) to get infected by COVID-19 again. Therefore, I assume that the probability of a recovered person not to get infected by COVID-19 for risk-group k is \((1-\tilde{\tau }_k)\). Due to imperfect testing assume a fraction \(\breve{\tau }_k\) of recovered person in risk-group k with probability \((1-\tilde{\tau }_k)\) are allowed to join the workforce freely. Remaining part of the recovered population is either not identified (Acemoglu et al. 2020) or because of the traumatic experience their \(F(p_0)\) is very low and reluctant to join in the labor force. Therefore, the employment for somebody in kth risk-group at time s is given by
A policymaker has to control \(\{e_k(s)\}_{k\in K}\) for all \(s\in [0,t]\) where the dynamical system follows Eqs. (1), (4) and (7). Planner’s objective function is to minimize the expected present value of the social cost conditioned on the filtration \(\mathbb{F}^0\) as
where \(\theta _k>0\) is some known penalization constant, \(\rho \in (0,1)\) is time independent discount rate and \(\mathbb{E}_0\) is the conditional expectation at time 0 on the initial state variables \(z_k(0),S_k(0),I_k(0),R_k(0)\) and \(W_k(0)\) with filtration \(\mathbb{F}^0\).
Assumption 3
Following set of assumptions regarding the objective function is considered:
-
\(\{\mathcal{F}_s\}\) takes the values from a set \(\mathfrak{Z}\subset \mathbb{R}^{5K}\). \(\{\mathcal{F}_s\}_{s=0}^t\) is an exogenous Markovian stochastic processes defined on the probability space \((\mathfrak{Z}_\infty ,\mathbb{F}^0,\mathbb{P})\).
-
For all \(\{e_k(s),z_k(s),S_k(s),I_k(s),R_k(s),W_k(s)\}\), there exists an optimal lock intensity \(\{\overline{e}_k(s)\}_{s=0}^t\), with initial conditions \(z_k(0),S_k(0),I_k(0),R_k(0)\) and \(W_k(0)\), which satisfy the stochastic dynamics represented by Eqs. (1), (4) and (7) for all continuous time \(s\in [0,t]\).
-
The function \(\exp \{-\rho s\}\sum _{k=1}^K\theta _kz_k(s)\left[ N_k-\mathcal{E}_k(s)\right] +\breve{\chi }_k\check{h}\varpi _k(s)I_k(s)\) is uniformly bounded, continuous on both the state and control spaces and, for a given \(\{e_k(s),z_k(s),S_k(s),I_k(s),R_k(s),W_k(s)\}\), they are \(\mathbb{F}^0\)-measurable.
-
The function \(\exp \{-\rho s\}\sum _{k=1}^K\theta _kz_k(s)\left[ N_k-\mathcal{E}_k(s)\right] +\breve{\chi }_k\check{h}\varpi _k(s)I_k(s)\) is strictly convex with respect to the state and the control variables.
-
For all \(\{e_k(s),z_k(s),S_k(s),I_k(s),R_k(s),W_k(s)\}\), there exists a k-interior lock intensity \(\{\widetilde{e}_k(s)\}_{s=0}^t\), with initial conditions \(z_k(0),S_k(0),I_k(0),R_k(0)\) and \(W_k(0)\) satisfy Eqs. (1), (4) and (7), such that
$$\begin{aligned} & \mathbb{E}_0\left\{ \biggr [\exp \{-\rho s\}\sum _{k=1}^K\theta _kz_k(s)\left[ N_k-\mathcal{E}_k(s)\right] \right. \\ & \quad \left. +\breve{\chi }_k\check{h}\varpi _k(s)I_k(s)\biggr ]\biggr |\mathbb{F}^0\right\} >0, \end{aligned}$$and, for \(k\ne l\)
$$\begin{aligned} & \mathbb{E}_0\left\{ \biggr [\exp \{-\rho s\}\sum _{k=1}^K\theta _k\tilde{z}_k(s)\left[ N_k-{\widetilde{\mathcal{E}_k}}(s)\right] \right. \\ & q\left. +\breve{\chi }_k\check{h}\varpi _k(s)\tilde{I}_k(s)\biggr ]\biggr |\mathbb{F}^0\right\} \ge 0. \end{aligned}$$ -
In addition to the above argument, there exists an \(\varepsilon >0\) such that for all \(\{e_k(s),z_k(s),S_k(s),I_k(s),R_k(s),W_k(s)\}\),
$$\begin{aligned} & \mathbb{E}_0\left\{ \biggr [\exp \{-\rho s\}\sum _{k=1}^K\theta _k\tilde{z}_k(s)\left[ N_k-{\widetilde{\mathcal{E}_k}}(s)\right] \right. \\ & \quad \left. +\breve{\chi }_k\check{h}\varpi _k(s)\tilde{I}_k(s)\biggr ]\biggr |\mathbb{F}^0\right\} \ge \varepsilon . \end{aligned}$$
Definition 3
For individual risk-group k optimal state variables \(z_k^*(s),S_k^*(s),I_k^*(s),R_k^*(s)\) and, \(W_k^*(s)\) and their continuous optimal lock intensity \(e_k^*(s)\) constitute a stochastic dynamic equilibrium such that for all \(s\in [0,t]\) the conditional expectation of the objective function is
with the dynamics explained in Eqs. (1), (4) and (7), where \(\mathbb{F}_*^0\) is the optimal filtration starting at time 0 such that, \(\mathbb{F}_*^0\subset \mathbb{F}^0\).
Definition 4
Suppose, \(z_k,S_k,I_k,R_k\) and \(W_k\) are in a non-homogeneous Fellerian semigroup on continuous time interval [0, t] in \(\mathbb{R}^{6K}\). The infinitesimal generator \(\mathfrak{H}\) of \(\{z_k,S_k,I_k,R_k,W_k\}\) is defined by,
for \(\{z_k,S_k,I_k,R_k,W_k\}\in \mathbb{R}^{5K}\) where \(\textbf{H}_\theta ^k:\mathbb{R}^{6K}\rightarrow \mathbb{R}\) is a \(C_0^2(\mathbb{R}^{6K})\) function, \(\{z_k,S_k,I_k,R_k,W_k\}\) has a compact support, and at \(\{\bar{z}_k,\bar{S}_k,\bar{I}_k,\bar{R}_k,\bar{W}_k\}\) the limit exists where \(\mathbb{E}_s\) represents individual risk-group k’s conditional expectation on states \(\{z_k,S_k,I_k,R_k,W_k\}\) at continuous time s. Furthermore, if the above Fellerian semigroup is homogeneous over time, then \(\mathfrak{H} \textbf{H}_\theta ^k\) is exactly equal to the Laplace operator.
As \(\textbf{H}_\theta ^k\) is a \(\mathbb{F}^0\)-measurable function depending on s, there is a possibility that this function might have very large values and may be unstable. In order to stabilize the state variables \(z_k,S_k,I_k,R_k,W_k\) I take the natural logarithmic transformation and define a characteristic like operator as in Definition 5.
Definition 5
For a Fellerian semigroup \(\{z_k,S_k,I_k,R_k,W_k\}\) and for a small time interval \([s,s+\varepsilon ]\) with \(\varepsilon \downarrow 0\), define a characteristic-like operator where the process starts at s is defined as
for \(\{z_k,S_k,I_k,R_k,W_k\}\in \mathbb{R}^{5K}\), where \(\textbf{H}_\theta ^k:\mathbb{R}^{5K}\rightarrow \mathbb{R}\) is a \(C_0^2(\mathbb{R}^{5K})\) function, \(\mathbb{E}_s\) represents the conditional expectation of state variables \(\{z_k,S_k,I_k,R_k,W_k\}\) at time s, for \(\varepsilon >0\) and a fixed \(\textbf{H}_\theta ^k\) the sets of all open balls of the form \(B_\varepsilon \left( \textbf{H}_\theta ^k\right)\) contained in \(\mathcal{B}\) (set of all open balls) and as \(\varepsilon \downarrow 0\) then \(\log \mathbb{E}_s(\varepsilon ^2)\rightarrow \infty\).
Policy maker’s objective is to minimize the objective function expressed in Eq. (11) subject to the dynamic system represented by Eqs. (1), (6) and (8). Following Pramanik (2020) the quantum Lagrangian of risk-group k can be expressed as
where \(\lambda _i>0\) for all \(i=\{1,2,3,4\}\) are time independent quantum Lagrangian multipliers and \(\Delta\)’s represent small change of state variables in time interval \((s,s+\varepsilon )\) for all \(\varepsilon >0\) and \(\varepsilon \searrow 0\). As \(\lambda\)’s do not depend on time, they are considered as penalization constants. At time s risk-group k can predict based on all information available regarding state variables at that time, throughout interval \([s,s+\varepsilon ]\) it has the same conditional expectation which ultimately gets rid of the integration.
Main results
In this section I am going to determine an optimal lock intensity for risk-group k. By using Feynman-type path integral approach I find a Euclidean action function, define a transition wave function and finally, I derive a Fokker–Plank-type (i.e., Wick-rotated Schrödinger-type) equation of the system.
Proposition 3
Suppose, the domain of the quantum Lagrangian \(\mathcal{L}_k\) is non-empty, convex and compact denoted as \(\widetilde{\Xi }\) such that \(\widetilde{\Xi }\subset \mathbb{R}^{6K}\times G\). As \(\mathcal{L}_k: \widetilde{\Xi }\rightarrow \widetilde{\Xi }\) is continuous, then for any given positive constants \(\rho ,\theta _k,\breve{\xi }_k,\breve{h}\) and \(\varpi _k\), there exists a vector of state and control variables \(\bar{Z}_k^*=[e_k^*,z_k^*,S_k^*,I_k^*,R_k^*,W_k^*]^T\) in continuous time \(s\in [0,t]\) such that \(\mathcal{L}_k\) has a fixed-point in Brouwer sense, where T denotes the transposition of a matrix.
Proof
See in the “Appendix”.
Proposition 3 guarantees that the pandemic control problem at least one fixed point, which leads to the next Theorem 1. Theorem 1 is the main result of this paper. It uses a Euclidean path integral approach based on a Feynman-type action function to get an optimal “lock-down” intensity.\(\square\)
Theorem 1
Suppose, for all \(k\in \{1,2,\ldots ,K\}\) a social planner’s objective is to minimize \(\textbf{H}_\theta ^k\) subject to the stochastic dynamic system explained in Eqs. (1), (4) and (7) such that Assumptions (1)- (3) and Propositions 1-3 hold. For a \(C^2\)-function \(\tilde{f}_k(s,e_k,z_k,S_k,I_k,R_k,W_k)\) and for all \(s\in [0,t]\) there exists a function \(g_k(z_k,S_k,I_k,R_k,W_k)\in C^2([0,t]\times \mathbb{R}^{5K})\) such that \(\widetilde{Y}_k=g_k[z_k,S_k,I_k,R_k,W_k]\), with an Itô process \(\widetilde{Y}_k\), and for a non-singular matrix
optimal “lock-down” intensity \(e_k^*\) is the solution of the equation
where \(\Psi _s^{k\tau }\) is some transition wave function in \(\{\mathbb{R}^{5K}\times G\}\).
Sketch of the idea of the proof: The detailed proof is given in “Appendix”. Here I would like to go through the main idea of the proof. I have used a Feynman-type path integral control approach to determine the optimal lock-down intensity. First, based on the quantum Lagrangian function expressed in Eq. (12), I define the Euclidean action function for risk-group k for continuous time interval [0, t]. Then, I define a Euclidean action function for time interval \([s,s+\varepsilon ]\subset [0,t]\) such that \(\varepsilon =t/n\), where n is the total number of equal-lengthed time subintervals (i.e., \([s,s+\varepsilon ]\)) of the interval [0, t]. Furthermore, a transition wave function for time interval \([s,s+\varepsilon ]\), \(\Psi _{s,s+\varepsilon }^k(.)\) is defined on the Euclidean action function based on a Feynman path integral. Since, Brownian motion is continuous but not differentiable with respect to time, I have replaced the systems of functional forms of the stochastic differential equations in (12) by an Itô process \(g_k(.)\). Here g is a function which is at least twice differentiable with respect to time s, and the state variables \(z_k,S_k,I_k,R_k\) and \(W_k\) so that Itô lemma can be implemented on it. In this path integral control approach, appropriately choosing a g function is the central idea. The government determines the g function based on the historical performances of COVID-19 in an economy. As I assume the information of the pandemic environment is imperfect and incomplete, this method gives a different set optimal lock-down intensities than HJB approach which are not unique globally. In other words, the individuals do not have complete information on the dynamics of the state variables, and the function g is a signal about the pandemic environment determined by the government. Since, in this paper I am interested in the forward-looking solution, at the beginning of each time interval \([s,s+\varepsilon ]\), the government have information at just time s, and make expectations on the future. As a result, the conditional expectation \(\mathbb{E}_s\) becomes the objective function plus the g function at time s. Then implementing Itô lemma on g, first order Taylor series expansion on transition wave function, and shifted Gaussian integrals on all possible actions yield a Wick-rotated Schrödinger type equation. This Schrödinger type equation holds the information of the whole system of the pandemic environment. Finally, the solution for \(e_k(s)\) of the first order condition of the Wick-rotated Schrödinger type equation with respect to the control variable determines the optimal lock-down intensity.
Theorem 1 gives the solution of an optimal “lock-down” intensity for a generalized stochastic pandemic system. Consider a function
such that
with \(\partial g_k/\partial s=z_k+S_k+I_k+R_k+W_k\), \(\partial g_k/\partial X_i=s-1/X_i\), \(\partial ^2 g_k/\partial X_i^2=-1/X_i^2\) and \(\partial ^2 g_k/\partial X_i\partial X_j=0\), for all \(i\ne j\) where \(X_i\) is ith state variable for all \(i=1,\ldots ,5\) and \(\ln\) stands for natural logarithm. In other words, \(X_1=z_k, X_2=S_k,X_3=I_k, X_4=R_k\) and \(X_5=W_k\). Therefore,
where
In order to satisfy Eq. (13) Either \(\frac{\partial \tilde{f}_k}{\partial e_k}=0\) or \(\Psi _s^{k\tau }=0\). As \(\Psi _s^{k\tau }\) is a wave function, it cannot be zero. Therefore, \(\frac{\partial \tilde{f}_k}{\partial e_k}=0\). After setting the diffusion coefficient of Eq. (3) to zero the optimal lock-down intensity is,
where
and,
The expression \(e^*\) represents an optimal lock-down intensity. If all of the state variables attain their optimal values then, \(e^*\) achieves a global lock-down intensity.
Now I am going to discuss about the impacts of different variables on global lock-down intensity. Let at time s there exist K risk groups and \(e^*\) be an optimal global lock-down intensity such that if its value is high, the employment of the economy is high, the infection rate is low and vice versa. Consider the propensity constant \(\check{h}\in (0,1)\), constant probability that an infected person of risk-group k does not need an emergency care \(\tau _k\in [0,1]\), \(\text{Pr}(\text{k is indifferent to interact}|\omega _k)=F(p_0)<\hat{F}<1/2\), time-independent discount rate \(\rho \in (0,1)\), known penalizing constant \(\theta _k>0\), rate of fatigue accumulation \(k_0\in (0,1)\), constant natural death rate \(\tau\), opinion of individual risk group k as \(\omega _k\in [-1,1]\), local relevance of compromise \(\mathcal{Q}\in [0,1]\), compromise propensity \(\varkappa \in (0,1/2)\), birth rate as \(\eta\), parameter defines the degree of effectiveness of fatigue to spread infection \(\gamma \in (0,1)\), fine particular matter \(M=21\,\upmu\text{g/m}^3\), and the parameter which makes \(\beta ^k(e_k,z_k)\) convex as \(\theta >1\). Following is the discussion of impact of different factors other than constants on optimal lock-down intensity.
Case I: If the fraction of recovered persons allowed to join the work force for the second time is very high (i.e., \(\check{\tau }_k\downarrow 1\)), then after keeping other variables fixed,
As a result \(\widetilde{\mathcal{B}}\) falls which leads to a fall in optimal lock-down intensity \(e^*\). The main reason is that, due to the higher value of \(\check{\tau }_k\) the effect of \(\tilde{\tau }_k\) is not captured. Hence, there exists a misinformation that all the people are recovered from the pandemic but actually people with probability \(\tilde{\tau }_k\) are infected by COVID-19 after vaccinated and boosted. Now the COVID-19 infected population are in the labor force, which leads to more infection and more isolations. Therefore, \(e^*\) increases. On the other hand, if the fraction of recovered person is very low (i.e., \(\check{\tau }_k\downarrow 0\)), then full effect of \(\tilde{\tau }_k\) is observed and,
This means because of the misinformation the government sees nobody recovers from the pandemic. Therefore, \(\tilde{\mathcal{A}}_k\) will fall and,
This leads to a fall in \(e^*\). Intuitively, a very low \(\check{\tau }_k\) signals the government that, less number of recovered people are rejoining the workforce. Therefore, a high fraction of people either not confident to do social interaction on work place or get infected by the pandemic again. Government predicts that the recovery rate is low and imposes a stricter lock-down policy, and optimal lock-down intensity falls. If \(\tilde{\tau }_k\) is very high, then people think that going back to the work force might not a good idea, resulting \(\check{\tau }_k\) attains a very low value. The recovery rate \(R_k\) falls and infection rate \(I_k\) increases. This would lead to a rapid increase in \(\widetilde{\mathcal{C}}\). Eventually, optimal lock-down intensity falls.
Case II: Let at time 0, \(\omega _k<\omega _l\). Assume \(\text{Pr}_0(L|\omega _k(0))=W_k(0)\) is very low (i.e., \(W_k(0)\rightarrow 0\)). This implies the conditional probability of low infection such that risk group k has made an opinion is very low. Furthermore, for risk-groups k and l, suppose at time s, the opinions about the pandemic is same or \(\omega _k=\omega _l\). Therefore,
If both the risk groups k and l have the same negative opinions (i.e., \(\omega _k=\omega _l=-1\)), then \(\widetilde{\mathcal{B}}\) decreases which eventually leads to a fall in \(e^*\). Intuitively, if both the risk groups have same negative opinions, then individuals do not feel to come out and go to the work force fearing that the infection rate is very high. This would further reduce the probability \(W_k(s)\), \(\widetilde{\mathcal{B}}\), and eventually \(e^*\). On the other hand, if both the risk groups have positive but same opinion (i.e., \(\omega _k=\omega _l=1\)), then \(\text{Pr}_0(L|\omega _k(0))=W_k(0)\) is very high (\(W_k(0)\rightarrow 1\)) at the beginning and continues to take a high probabilistic value. Under the initial assumption of \(\omega _k<\omega _l\) leads to
Under positive opinion of \(\omega _k=\omega _l=1\) clearly increases \(\widetilde{\mathcal{B}}\), which leads to an increase in optimal lock-down intensity. Intuitively, positive opinions toward the virus makes people less afraid of COVID-19, and more individuals would appear at the work place. Now suppose, the two risk groups have extreme opinions in the sense that \(\omega _k=-1\) and \(\omega _l=1\). Irrespective of \(W_k(s)\), value of \(\widetilde{\mathcal{B}}\) falls, which eventually leads to a fall in \(e^*\). Intuitively, if the risk groups k and l have two extreme opinions toward the pandemic, then either of the groups has misinformation about the infection of the disease. Since by assumption, people are risk averse, misinformation from either side creates a risky work environment. As a result, less people are willing to go out and do the interaction. This phenomenon would pull down the optimal lock-down intensity.
Case III: The probability that a link of a new node connects to Barabasi–Albert node \(k_i\) defined as
If J takes a very large value then \(p(\eta _{k_i},s)\rightarrow 1\) with the fatigue dynamics \(z_k(s)\) has an upper bound \(\kappa _0/[\kappa _1p(\eta _{k_i},s)]\). A higher value of \(p(\eta _{k_i},s)\) leads to a reduction in \(\kappa _0(z_k)^\gamma /[\kappa _1p(\eta _{k_i},s)]\), which leads to an increase of \(\widetilde{\mathcal{C}}\), and a fall in optimal \(e^*\). Intuitively, a high value of J leads to a huge Barabasi–Albert network with higher probability that a link of a new node connects to another Barabasi–Albert network with exponentially increasing number of nodes. As the network is very large, any information can spread very fast including misinformation. In this network the infection of the pandemic spreads faster. As a result people are reluctant to go out to work even after a positive information about the disease spread. Since, people are risk-averse, they would wait at home longer and observe the severity of the disease before doing any social interaction.
Case IV: Finally, I will discuss about the effect of state variables in this system on the optimal lock-down intensity. First, an increase in susceptibility of risk group k leads to an increase in \(\tilde{\mathcal{A}}\), which leads to an increment in \(\widetilde{\mathcal{B}}\). The denominator part of \(e^*\) can be written as
Hence, an increase in \(S_k\) leads to a reduction in \(\widetilde{\mathcal{C}}\). Combining the movements \(\widetilde{\mathcal{B}}\) and \(\widetilde{\mathcal{C}}\) I conclude that optimal lock-down intensity would increase. Intuitively, if an economy has a huge portion of susceptible population compared to infected \(I_k\), people are willing to do social interactions as they predict the spread of the infection of COVID-19 is less. Second, an increment of rate of infection \(I_k\) leads to an increase in \(\tilde{\mathcal{A}}\). \(\widetilde{\mathcal{C}}\) has \(I_k\) on numerator and the denominator. Since \(r\in (0,1)\), the increment of \(I_k\) at the numerator is faster than its counterpart at the denominator. Therefore, \(\widetilde{\mathcal{C}}\) would increase along an increase of \(I_k\). Moreover, as \(\left[ 1-\check{h}\hat{\tau }_k\hat{F}_p-(1-\check{h})\tau _k F(p_0)\right] \in (0,1)\), the increment of \(\widetilde{\mathcal{B}}\) is less than the increment of \(\widetilde{\mathcal{C}}\) due to an increase in the infection rate, resulting a fall in \(e^*\). Intuitively, a higher infection rate in risk group k under Barabasi–Albert pandemic spread network leads to hinder in social interaction, resulting a significant decrease in optimal lock-down intensity. Third, an increase in recovery rate \(R_k\) increases \(\tilde{\mathcal{A}}\) and \(\widetilde{\mathcal{B}}\). Since, there is no \(R_k\) component in \(\widetilde{\mathcal{C}}\), an increment in \(R_k\) would increase \(e^*\). Intuitively, a higher recovery rate boosts the positive opinion against the spread of the infection, resulting an increase in optimal lock-intensity. Fourth, an increase in fatigue \(z_k\) has two different effects on \(\widetilde{\mathcal{B}}\) and \(\widetilde{\mathcal{C}}\). In \(\widetilde{\mathcal{B}}\), increasing \(\exp (-\rho s)\sum _{k=1}^K\theta _k\tilde{\mathcal{A}}z_k\) part dominates the decreasing part \(\kappa _0/z_k\). Hence, \(\widetilde{\mathcal{B}}\) is increasing. On the other hand, \(1-\kappa _0(z_k)^\gamma /[\kappa _1p(\eta _{k_i},s)]\) reduces as \(z_k\) increases leads to a fall in \(\widetilde{\mathcal{C}}\). Combining the effects I conclude that an increase in \(z_k\) leads to an increase in \(e^*\). Intuitively, because of the death of the loved ones one person feel fatigued. Although the person does not want to join the workforce, circumstances led them to join. Because, the loved one who passed away might be a bread earner of the family. These scenarios increase the optimal lock-down intensity. Finally, an increase in \(\text{Pr}_s(L|\omega _k(s))=W_k(s)\in [0,1]\) leads to a fall in \((s-1/W_k)\) and an increase in \(\sigma _8^k/(W_k)^2\). Since, I have assumed \(\omega _k<\omega _l\), an increment in \(W_k\) leads to a fall in
and an increase in \((1/2)\sigma _8^k(\omega _k-\omega _l)(W_k)^{-2}\). The relative effect depends on whichever of the above two terms are bigger. If
then \(\widetilde{\mathcal{B}}\) and \(e^*\) would fall and vice versa.
Numerical study
Values from Table 1 are used to perform a numerical study. Some of these values and initial state variables are obtained from Caulkins et al. (2021), Albrecht et al. (2021), and Rao (2014). Figure 4 represents 10 realizations of the fatigue dynamics represented in Eq. (1) with \(\sigma _0=0.2\). To plot these realizations I have assumed \(p(\eta _{k_i},s)=0.7\) and \(e_k(s)=0.6\). A higher value of \(p(\eta _{k_i},s)\) means a higher probability that a link of the new node connects to a Barabasi–Albert node \(k_i\), resulting a higher rate of spread of infection of the pandemic. On the other hand, assuming a higher \(e_k(s)\) reflects a higher lock-down intensity. At the beginning of the incidence of COVID-19 people have no idea about the severity of the disease. Therefore, even at the presence of high infection rate, they think it is a regular flue and go to the work force and get infected. Since, at the beginning no vaccines were available, many people lost their lives resulting to lead a depression to their family members. This leads to an increase in trend in fatigue dynamics over the time. Figure 5 represents a static relationship between fatigue and lock-down intensity which is strictly negative in nature. If there is a fall in lock-down intensity, less people are in the work-force and many lives are lost due to COVID-19. Hence, their family members are depressed due to the lives have been lost resulting and increment in fatigue rate.
Figure 6 represents one realization of 100 iterations of the infection dynamics in Eq. (3). Here I assume \(\gamma =0.02\), adjusted \(M=0.21\), and \(\sigma _1=0.025\). At initial infection rate of risk-group k, \(\beta _k(0)=0.4\), \(\beta _k\) falls drastically and then increased to a somewhat stable infection rate around 0.7. Intuitively, as at the beginning of the incidence of COVID-19 due to the imposition of strict social-distancing infection-rate falls to 0.3. This boosts the positive opinion of the people about the pandemic, and they are eager to come to their work places and do social interactions. As a result, the rate of infection rises and become stable around 0.7. Figure 7 shows twenty of these type of realizations of \(\beta _k(s)\) over time.
Figure 8 represents the stochastic SIR model in this environment. Instead of following Caulkins et al. (2021) to use 0.999 as \(S_k\), 0.001 as \(I_k\) and 0.001 as \(R_k\) I have used 0.5, 0.35 and 0.15 as S, I and R values for risk group k. The main reason is that, if I use the values given in Caulkins et al. (2021), the dynamic comparison of these three state variables become impossible. Moreover, I also keep the infection rate at 0.6 to do this simulation study. Since, the proportion of susceptible persons in risk group k is much higher compared to the proportion of infected and recovered people, I have assigned higher diffusion coefficient for \(s_k\) dynamics (i.e., \(\sigma _2=0.6\)). In Fig. 8 all of \(S_k\), \(I_k\) and \(R_k\) are decreasing where the rate of decrease of susceptibility is the lowest. In the model the rate of infection \(I_k\) is steadily declining. This implies, as a result of strict social distancing lower infection rate is achieved over time. On the other hand, at the initial stage the recovery rate of risk group k is increasing then, a steady fall is observed. Intuitively, because of the social distancing previously infected person recovered and join the work force. Since the infection rate of the pandemic is still high, newly recovered persons get infected again. Second time it is much harder for them to get recovered resulting a steady fall in the recovery rate over the time. Figure 9 shows 10 realizations of opinion dynamics under the assumption that the risk group l has perfectly positive attitude (i.e., \(\omega _l=1\)) toward COVID-19. The diffusion coefficient of the opinion dynamics is assumed to be 0.1 because of high volatile nature of the spread of information.
Almost all the realizations of the opinion dynamics in Fig. 9 are steadily falling to 0.3. This means over time, the probability that an individual believes that the impact of the disease is low such that \(\omega _k\) is known is 0.3. Therefore, people from risk group k think the impact of COVID-19 is severe even though the people from risk group l think that the infection of the pandemic is low.
Figure 10 shows the movement of optimal lock-down intensity over time. Initially it started at a very high level of 0.7 and steadily increased to 1. Then it has experience a huge decline to 0.25 at time 0.1. After an experience of little increase, the optimal lock-down intensity has declined again. Since after time point 0.13 the optimal lock-down intensity has declined, the dynamic social cost has been increase during the same as seen in Fig. 11. As from Fig. 11 it can be concluded that the social cost on an average steadily increasing throughout the time interval in discussion.
Discussion
This paper discuss about a stochastic optimization problem where a policy maker’s objective is to minimize a dynamic social cost \(\textbf{H}_\theta\) subject to a lock-down fatigue dynamics, COVID-19 infection \(\beta ^k\), a multi-risk SIR model and opinion dynamics of risk-group k where lock-down intensity is used as my control variable. Under certain conditions I was able to find out a closed form solution of lock-down intensity \(e^*\). First I have subdivided the entire population into K number of age-groups such that every person in a group has homogeneous opinion toward vaccination against COVID-19. As each of these group are vulnerable to the pandemic, I renamed the age-group as risk-group which is consistent with the literature (Acemoglu et al. 2020). As heterogenous opinion of individuals in a risk-group k concerns with multi-layer network, it would be a future research in this context.
A Feynman-type path integral approach has been used to determine a Fokker–Plank type of equation which reflects the entire pandemic scenario. Feynman path integral is a quantization method which uses the quantum Lagrangian function, while Schrödinger’s quantization uses the Hamiltonian function (Fujiwara 2017). As this path integral approach provides a different view point from Schrödinger’s quantization, it is very useful tool not only in quantum physics but also in engineering, biophysics, economics and finance (Kappen 2005; Anderson et al. 2011; Yang et al. 2014a; Fujiwara 2017). These two methods are believed to be equivalent, but this equivalence has not fully proved mathematically as the mathematical difficulties lie in the fact that the Feynman path integral is not an integral by means of a countably additive measure (Johnson and Lapidus 2000; Fujiwara 2017). As the complexity and memory requirements of grid-based partial differential equation (PDE) solvers increase exponentially as the dimension of the system increases, this method becomes impractical in the case with high dimensions (Yang et al. 2014a). As an alternative one can use a Monte Carlo scheme and this is the main idea of path integral control (Kappen 2005; Theodorou et al. 2010; Theodorou 2011; Morzfeld 2015). This path integral control solves a class a stochastic control problems with a Monte Carlo method for a HJB equation and this approach avoids the need of a global grid of the domain of HJB equation (Yang et al. 2014a). In future research I want to use this approach under \(\sqrt{8/3}\) Liouville-like quantum gravity surface (Pramanik 2021a).
References
Acemoglu D, Chernozhukov V, Werning I, Whinston MD et al (2020) A multi-risk SIR model with optimally targeted lockdown 2020. National Bureau of Economic Research, Cambridge, MA
Albrecht L, Czarnecki P, Sakelaris B (2021) Investigating the relationship between air quality and COVID-19 transmission. arXiv preprint arXiv:2103.13494
Anderson RN, Boulanger A, Powell WB, Scott W (2011) Adaptive stochastic control for the smart grid. Proc IEEE 99:1098–1115
Anderson RM, Heesterbeek H, Klinkenberg D, Hollingsworth TD (2020) How will country-based mitigation measures influence the course of the COVID-19 epidemic? The Lancet 395:931–934
Aspri A, Beretta E, Gandolfi A, Wasmer E (2021) Mortality containment vs. economics opening: optimal policies in a SEIARD model. J Math Econ 93:102490
Baaquie BE (1997) A path integral approach to option pricing with stochastic volatility: some exact results. J Phys I 7:1733–1753
Baaquie BE (2007) Quantum finance: path integrals and Hamiltonians for options and interest rates. Cambridge University Press, Cambridge
Barabási A-L, Albert R (1999) Emergence of scaling in random networks. Science 286:509–512
Bayraktar E, Cohen A, Nellis A (2021) A macroeconomic SIR model for COVID-19. Mathematics 9:1901
Becker NG (2017) Analysis of infectious disease data. Chapman and Hall/CRC, Boca Raton
Beretta E, Takeuchi Y (1995) Global stability of an SIR epidemic model with time delays. J Math Biol 33:250–260
Board S, Meyer-ter Vehn M (2021) Learning dynamics in social networks. Econometrica 89:2601–2635
Bonnans JF, Gianatti J (2020) Optimal control techniques based on infection age for the study of the COVID-19 epidemic. Math Model Nat Phenom 15:48
Carmona R (2016) Lectures on BSDEs, stochastic control, and stochastic differential games with financial applications. SIAM, Philadelphia
Caulkins J, Grass D, Feichtinger G, Hartl R, Kort PM, Prskawetz A, Seidl A, Wrzaczek S (2020) How long should the COVID-19 lockdown continue? PLoS ONE 15:e0243413
Caulkins JP, Grass D, Feichtinger G, Hartl RF, Kort PM, Prskawetz A, Seidl A, Wrzaczek S (2021) The optimal lockdown intensity for COVID-19. J Math Econ 93:102489
Caulkins JP, Grass D, Feichtinger G, Hartl RF, Kort PM, Prskawetz A, Seidl A, Wrzaczek S (2022) COVID-19 and optimal lockdown strategies: the effect of new and more virulent strains. Pandemics: insurance and social protection. Springer, Cham, pp 163–190
Charpentier A, Elie R, Laurière M, Tran VC (2020) COVID-19 pandemic control: balancing detection policy and lockdown intervention under ICU sustainability. Math Model Nat Phenom 15:57
Cordier S, Pareschi L, Toscani G (2005) On a kinetic model for a simple market economy. J Stat Phys 120:253–277
Delfino RJ, Sioutas C, Malik S (2005) Potential role of ultrafine particles in associations between airborne particle mass and cardiovascular health. Environ Health Perspect 113:934–946
Elie R, Hubert E, Turinici G (2020) Contact rate epidemic control of COVID-19: an equilibrium view. Math Model Nat Phenom 15:35
Erdös P, Rényi A (1959) On random graphs. Publ Math 6:290–297
Ferguson N, Laydon D, Nedjati-Gilani G, Imai N, Ainslie K, Baguelin M, Bhatia S, Boonyasiri A, Cucunubá Z, Cuomo-Dannenburg G et al (2020) Report 9: impact of non-pharmaceutical interventions (NPIs) to reduce COVID19 mortality and healthcare demand. Imp Coll Lond 10:491–497
Freiberger M, Grass D, Kuhn M, Seidl A, Wrzaczek S (2022) Chasing up and locking down the virus: optimal pandemic interventions within a network. J Public Econ Theory 24:1182–1217
Fujiwara D (2017) Rigorous time slicing approach to Feynman path integrals. Springer, Berlin
González-Dıaz J, Garcıa-Jurado I, Fiestras-Janeiro MG (2010) An introductory course on mathematical game theory. Graduate studies in mathematics, vol 115. American Mathematical Society, Providence
Goyal S (2012) Connections: an introduction to the economics of networks. Princeton University Press, Princeton
Grass D (2012) Numerical computation of the optimal vector field: exemplified by a fishery model. J Econ Dyn Control 36:1626–1658
Grimmett G (1995) The stochastic random-cluster process and the uniqueness of random-cluster measures. Ann Probab 23:1461–1510
Hatchimonji JS, Swendiman RA, Seamon MJ, Nance ML (2020) Trauma does not quarantine: violence during the COVID-19 pandemic. Ann Surg 272:e53
Hua L, Polansky A, Pramanik P (2019) Assessing bivariate tail non-exchangeable dependence. Stat Probab Lett 155:108556
Hubert E, Mastrolia T, Possamaï D, Warin X (2022) Incentives, lockdown, and testing: from Thucydides’ analysis to the COVID-19 pandemic. J Math Biol 84:1–48
Intriligator MD (2002) Mathematical optimization and economic theory. SIAM, Philadelphia
Jackson MO (2010) Social and economic networks. Princeton University Press, Princeton
Jiang Y, Wu X-J, Guan Y-J (2020) Effect of ambient air pollutants and meteorological variables on COVID-19 incidence. Infect Control Hosp Epidemiol 41:1011–1015
Johnson GW, Lapidus ML (2000) The Feynman integral and Feynman’s operational calculus. Clarendon Press, Oxford
Kantner M, Koprucki T (2020) Beyond just “flattening the curve’’: optimal control of epidemics with purely non-pharmaceutical interventions. J Math Ind 10:1–23
Kappen HJ (2005) Path integrals and symmetry breaking for optimal control theory. J Stat Mech: Theory Exp 2005:P11011
Kappen HJ (2007a) An introduction to stochastic control theory, path integrals and reinforcement learning. In: AIP conference proceedings, vol 887, pp 149–181. American Institute of Physics
Kappen HJ (2007b) An introduction to stochastic control theory, path integrals and reinforcement learning. In: AIP conference proceedings, vol 887, pp 149–181. American Institute of Physics
Kermack WO, McKendrick AG (1927) A contribution to the mathematical theory of epidemics. Proc R Soc Lond Ser A Contain Pap Math Phys Character 115:700–721
Lesniewski A (2020) Epidemic control via stochastic optimal control. arXiv preprint arXiv:2004.06680
Li J, Lindberg DV, Smith RA, Reluga TC (2017) Provisioning of public health can be designed to anticipate public policy responses. Bull Math Biol 79:163–190
Ljungqvist L, Sargent TJ (2012) Recursive macroeconomic theory. MIT Press, Cambridge
Ma W, Song M, Takeuchi Y (2004) Global stability of an SIR epidemicmodel with time delay. Appl Math Lett 17:1141–1145
Marcet A, Marimon R (2019) Recursive contracts. Econometrica 87:1589–1631
Moral P (2004) Feynman–Kac formulae, genealogical and interacting particle systems with applications. Springer, Berlin
Morzfeld M (2015) Implicit sampling for path integral control, Monte Carlo localization, and SLAM. J Dyn Syst Meas Control 137:051016
O’Dell K, Ford B, Fischer EV, Pierce JR (2019) Contribution of wildland-fire smoke to US PM2.5 and its influence on recent trends. Environ Sci Technol 53:1797–1804
Øksendal B (2003) Stochastic differential equations. In: Øksendal B (ed) Stochastic differential equations. Springer, Berlin, pp 65–84
Piguillem F, Shi L (2020) The optimal COVID-19 quarantine and testing policies. Einaudi Institute for Economics and Finance (EIEF), Rome
Polansky AM, Pramanik P (2021) A motif building process for simulating random networks. Comput Stat Data Anal 162:107263
Pramanik P (2016) Tail non-exchangeability. Northern Illinois University, DeKalb
Pramanik P (2020) Optimization of market stochastic dynamics. SN Oper Res Forum 1:1–17
Pramanik P (2021a) Effects of water currents on fish migration through a Feynman-type path integral approach under \(\sqrt{8/3}\) Liouville-like quantum gravity surfaces. Theory Biosci 140:205–223
Pramanik P (2021b) Optimization of dynamic objective functions using path integrals. Ph.D. thesis, Northern Illinois University
Pramanik P (2021c) Consensus as a Nash equilibrium of a stochastic differential game. arXiv preprint arXiv:2107.05183
Pramanik P (2021d) Optimization of dynamic objective functions using path integrals. Ph.D. thesis, Northern Illinois University
Pramanik P (2022a) On lock-down control of a pandemic model. arXiv preprint arXiv:2206.04248
Pramanik P (2022b) Stochastic control of a SIR model with non-linear incidence rate through Euclidean path integral. arXiv preprint arXiv:2209.13733
Pramanik P, Polansky AM (2019) Semicooperation under curved strategy spacetime. arXiv preprint arXiv:1912.12146
Pramanik P, Polansky AM (2020a) Motivation to run in one-day cricket. arXiv preprint arXiv:2001.11099
Pramanik P, Polansky AM (2020b) Optimization of a dynamic profit function using Euclidean path integral. arXiv preprint arXiv:2002.09394
Pramanik P, Polansky AM (2021a) Scoring a goal optimally in a soccer game under Liouville-like quantum gravity action. arXiv preprint arXiv:2108.00845
Pramanik P, Polansky AM (2021b) Optimal estimation of Brownian penalized regression coefficients. arXiv preprint arXiv:2107.02291
Rao F (2014) Dynamics analysis of a stochastic SIR epidemic model. In: Abstract and applied analysis 2014. Hindawi
Reluga TC (2010) Game theory of social distancing in response to an epidemic. PLoS Comput Biol 6:e1000793
Reluga TC (2013) Equilibria of an epidemic game with piecewise linear social distancing cost. Bull Math Biol 75:1961–1984
Richard Q, Alizon S, Choisy M, Sofonea MT, Djidjou-Demasse R (2021) Age-structured non-pharmaceutical interventions for optimal control of COVID-19 epidemic. PLoS Comput Biol 17:e1008776
Richardson S, Hirsch JS, Narasimhan M, Crawford JM, McGinn T, Davidson KW, Barnaby DP, Becker LB, Chelico JD, Cohen SL et al (2020) Presenting characteristics, comorbidities, and outcomes among 5700 patients hospitalized with COVID-19 in the New York City area. JAMA 323:2052–2059
Rowthorn R, Maciejowski J (2020) A cost-benefit analysis of the COVID-19 disease. Oxf Rev Econ Policy 36:S38–S55
Sethi SP (2019) Optimal control theory: applications to management science and economics, 3rd edn. Springer, Cham
Sheng S (2020) A structural econometric analysis of network formation games through subnetworks. Econometrica 88:1829–1858
Simon B (1979) Functional integration and quantum physics, vol 86. Academic Press, London
Skiba AK (1978) Optimal growth with a convex–concave production function. Econom: J Econom Soc 46:527–539
Theodorou EA (2011) Iterative path integral stochastic optimal control: theory and applications to motor control. University of Southern California, Los Angeles
Theodorou E, Buchli J, Schaal S (2010) Reinforcement learning of motor skills in high dimensions: a path integral approach. In: 2010 IEEE international conference on robotics and automation (ICRA), pp 2397–2403. IEEE
Toscani G et al (2006) Kinetic models of opinion formation. Commun Math Sci 4:481–496
Wilder-Smith A, Chiew CJ, Lee VJ (2020) Can we contain the COVID-19 outbreak with the same measures as for SARS? Lancet Infect Dis 20:e102–e107
Xiao D, Ruan S (2007) Global analysis of an epidemic model with nonmonotone incidence rate. Math Biosci 208:419–429
Yang I, Morzfeld M, Tomlin CJ, Chorin AJ (2014) Path integral formulation of stochastic optimal control with generalized costs. IFAC Proc Vol 47:6994–7000
Yang I, Morzfeld M, Tomlin CJ, Chorin AJ (2014) Path integral formulation of stochastic optimal control with generalized costs. IFAC Proc Vol 47:6994–7000
Yang J, Zheng Y, Gou X, Pu K, Chen Z, Guo Q, Ji R, Wang H, Wang Y, Zhou Y (2020) Prevalence of comorbidities and its effects in patients infected with SARS-CoV-2: a systematic review and meta-analysis. Int J Infect Dis 94:91–95
Yeung DW, Petrosjan LA (2006) Cooperative stochastic differential games. Springer Science & Business Media, Berlin
Zhu Y, Xie J, Huang F, Cao L (2020) Association between short-term exposure to air pollution and COVID-19 infection: evidence from China. Sci Total Environ 727:138704
Acknowledgements
The author is grateful to the Editor, Jürgen Jost, Co-Editor, Peter F. Stadler, and the reviewer for their constructive comments and suggestions which led to the improvement of an earlier version of this paper.
Funding
No funding was used to write this paper.
Author information
Authors and Affiliations
Contributions
The author declares that he has solely contributed the whole paper.
Corresponding author
Ethics declarations
Conflict of interest
The author declares that he has no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Lemma 1
For each optimal solution \(z_k^*\in \mathbb{F}^2\) of Eq. (1), define a squared integrable progressively measurable process \(X(z_k^*)\) by
I will show that \(X(z_k^*)\in \mathbb{F}^2\). Furthermore, as \(z_k^*\) is a solution of Eq. (1) iff \(X(z_k^*)=z_k^*\), I will show that X is the strict contraction of the Hilbert space \(\mathbb{F}^2\). Using the fact that
yields
Assumption 2 implies \(t\mathbb{E}|z_k(0)|^2<\infty\). It will be shown that the second and third terms of the right hand side of the inequality (15) are also finite. Assumption 1 implies,
Doob’s maximal inequality and Lipschitz assumption (i.e., Assumption 1) imply,
As X maps \(\mathbb{F}^2\) into itself, I show that it is strict contraction. To do so I change Hilbert norm \(\mathbb{F}^2\) to an equivalent norm. Following Carmona (2016) for \(a>0\) define a norm on \(\mathbb{F}^2\) by
If \(z_k(s)\) and \(y_k(s)\) are generic elements of \(\mathbb{F}^2\) where \(z_k(0)=y_k(0)\), then
by Lipschitz’s properties of drift and diffusion coefficients. Hence,
Furthermore, if \(c_0t\) is very large, X becomes a strict contraction. Finally, for \(s\in [0,t]\)
where the constant \(c_0\) depends on t, \(||\hat{\mu }||^2\) and \(||\sigma _0^k||^2\). Gronwall’s inequality implies,
\(\square\)
Proof of Proposition 1
As stochastic differential Eq. (1) and the SIR represented by the system (4) follow Assumption 1, there is a unique local solution on continuous time interval \([0,\hat{s})\), where \(\hat{s}\) is defined as the explosion point (Rao 2014). Therefore, Itô formula makes sure that there is a positive unique local solution for the system represented by Eqs. (1) and (4). In order to show global uniqueness one needs to show this local unique solution is indeed a global solution; in other words, \(\hat{s}=\infty\) almost surely.
Suppose, \(m_0>0\) is sufficiently large for the initial values of the state variables \(z_k(0)\), \(S_k(0)\), \(I_k(0)\) and \(R_k(0)\) in the interval \([1/m_0,m_0]\). For all \(m\ge m_0\) a sequence of stopping time is defined as
where it is assumed that the infimum of the empty set is infinity. As the explosion time is non-decreasing in m therefore, \(\hat{s}_\infty =\lim _{m\downarrow \infty }\hat{s}_m\) and \(\hat{s}_{\infty } \le \hat{s}_m\) a.s. I will show \(\hat{s}_\infty =\infty\) a.s. Suppose that the condition \(\hat{s}_\infty =\infty\) a.s. does not hold. Then \(\exists\) a \(t>0\) and \(\varepsilon >0\) such that \(\text{Pr}[\hat{s}_\infty \le t]>\varepsilon\). Hence, there is an integer \(m_1\ge m_0\) such that, \(\text{Pr}[\hat{s}_m\le t]\ge \varepsilon ,\ \forall m\ge m_1\).
Like before, define a nonnegative \(C^3\)-function \(\mathfrak{W}:\mathbb{R}^{4K}\rightarrow \mathbb{R}\) by
Itô’s formula implies
where I assume \(B^k=B_0^k=B_2^k=B_3^k=B_4^k\) or the system has same Brownian motion. Therefore,
where \(\mathfrak{M}\) is a positive constant. Integration of both sides of the Inequality (16) from 0 to \(\hat{s}_m\wedge t\) yield
where \(\hat{s}_m\wedge t=\min \{\hat{s}_m, t\}\). After taking expectations on both sides lead to
Define \(\aleph _m=\{\hat{s}_m\le t\},\ \forall m\ge m_1\). Previous discussion implies, for any \(\varepsilon >0\) there exists an integer \(m_1\ge m_0\) such that, \(\text{Pr}[\hat{s}_m\le t]\ge \varepsilon\) therefore, \(\text{Pr}(\aleph _m)\ge \varepsilon\). For each \(\wp \in \aleph _m\), \(\exists\) an i such that \(\hbar _i(\hat{s}_m,\wp )=m\ \text{or}\ 1/m\) for \(i=1,\ldots ,4\). Therefore, \(\mathfrak{W}\left[ z_k(\hat{s}_m,\wp ),S_k(\hat{s}_m,\wp ),I_k(\hat{s}_m,\wp ),R_k(\hat{s}_m,\wp )\right]\) has the lower bound \(\min \{m-1-\ln m, 1/m-1-\ln (1/m)\}\). This yields,
where \(\mathbbm {1}_{\aleph _m(\wp )}\) is a simple function on \(\aleph _m\). Letting \(m\downarrow \infty\) leads to \(\infty =\mathfrak{M} t+\mathfrak{W}[z_k(0),S_k(0),I_k(0),R_k(0)]<\infty\), which is a contradiction. \(\square\)
Proof of Lemma 2
As stochastic opinion dynamics is on F, this surface is oscillatory in nature. Total social interaction variation between two probabilistic interactions \(W_{k,\chi _{-k},\omega _{-k}}(s,h)\) and \(W_{l,\chi _{-l},\omega _{-l}}(s,h)\) can be defined in terms of a Hahn–Jordon orthogonal decomposition
such that
Therefore, for \(h\in F\),
Therefore,
Supremum over \(h\in F\) yields,
The reverse inequality can be checked trivially by introducing a simple function \(\mathbbm {1}_{\mathcal{G}}\), with \(\mathcal{G}\in \mathcal{E}\), belong to F. Therefore, we are able to show that
Now, by construction, there exists two disjoint subsets \(F_+\) and \(F_-\) such that, \(W^+(F_-)=0=W^-(F_+)\) (Moral 2004). For any graph \(\mathcal{G}\in \mathcal{E}\), \(W^+(\mathcal{G})=W(\mathcal{G} \cap F_+)\ge 0\) and, \(W^-(\mathcal{G})=-W(\mathcal{G} \cap F_+)\ge 0.\) Hence,
and,
Consider \(\hat{h}\) be another probability measure for any \(\mathcal{G}\in \mathcal{E}\) by,
By construction,
and,
As
by Eq. (18) one obtains
The reverse inequality is proved as follows. Suppose, \(\tilde{h}\) be a nonnegative measure such that for any graph \(\mathcal{G}\in \mathcal{E}\) we have
Assuming \(\mathcal{G}=F_+\) and \(\mathcal{G}=F_-\) give us
Therefore,
which implies
Taking the infimum over all the distributions \(\tilde{h} \le W_{k,\chi _{-k}\omega _{-k}}(s)\) and \(W_{l,\chi _{-l},\omega _{-l}}(s)\), we get
To prove the final part of the lemma note that,
and
Hence,
As \(F_+\) and \(F_-\) are mutually exclusive, therefore,
where the infimum is taken over all resolutions of F into pairs of non-intersecting subgraphs \(\mathcal{G}_i\), \(1\le i\le I\), \(I\ge 1\). Reverse inequality can be shown by using the definition of \(\hat{h}\). By Eq. (18) for any finite subgraph \(\mathcal{G}_i\in \mathcal{E}\), we have
Therefore,
By taking the infimum over all subgraphs yields
since
This completes the proof. \(\square\)
Proof of Proposition 2
Consider \(\mho :\Omega _E\rightarrow \mathbb{E}\) is an increasing function which represents the influence of risk-group k in the network which is a convex function of the odds of themselves to get the signals from the neighbors about their social interactions and is defined by \(\hat{\pi }=\log [\varrho /(1-\varrho )]\). Assume for \(\mathfrak{q}_3\), the signal profile \(\varrho\) of risk-group k is in \(\mathbb{D}\subseteq (0,1)\). Now suppose, \(\mathcal{J}\) is the total number of interactions of risk-group k with open edges with the set of edges with boxes \(\Lambda\) as \(\mathbb{E}_\Lambda\). Then by Theorem 4.2 of Grimmett (1995) and by Picard–Lindelof theorem there exists a unique random opinion in G (Board and Meyer-ter Vehn 2021). \(\square\)
Proof of Proposition 3
I have divided the proof into two cases.
\(\mathbf {Case\ I}\): There are total K-risk-groups with an individual risk-group k such that \(k=1,2,\ldots ,K\). I assume that \(m\subset \mathbb{N}\), a set \(\beth\) with condition \(|\beth |=m+1\), and affinely independent state variables and lock-down intensity \(\{Z_k(s)\}_{k\in \beth }\subset \mathbb{R}^{6K}\times G\) such that \(\widetilde{\Xi }\) coincides with the simplex convex set of \(\{ Z_k(s)\}_{k\in \beth }\). For each \(Z(s)\subset \Xi\), there is a unique way in which the vector Z(s) can be written as a convex combination of the extreme valued state variables and lock-down intensity, namely, \(Z(s)=\sum _{k\in \beth }\alpha _k(s,Z)Z_k(s)\) such that \(\sum _{k\in \beth }\alpha _k(s,Z)=1\) and \(\alpha _k(s,Z)\ge 0,\ \forall k\in \beth\) and \(s\in [0,t]\). For each risk-group k, define a set
By the continuity of the quantum Lagrangian of kth risk-group \(\{\mathcal{L}_k\}_{k\in \beth }\), \(\widetilde{\Xi }_k\) is closed. Now we claim that, for every \(\tilde{\beth } \subset \beth\), the convex set consists of \(\{Z_k\}_{k\in \tilde{\beth }}\) is proper subset of \(\bigcup _{k\in \tilde{\beth }}\widetilde{\Xi }_k\). Suppose \(\tilde{\beth }\subset \beth\) and Z(s) is also in the non-empty, convex set consists of the state variables and the lock-down intensity \(\{Z_k(s)\}_{k\in \tilde{\beth }}\). Therefore, there exists \(k\in \tilde{\beth }\) such that \(\alpha _k(s,Z)\ge \alpha _k\left[ \mathcal{L}_k(s,Z)\right]\) which implies \(Z(s)\in \tilde{\Xi }\subset \bigcup _{l\in \tilde{\beth }}\tilde{\Xi }_l\). By Knaster–Kuratowski–Mazurkiewicz Theorem, there is \(\bar{Z}_k^*\in \bigcap _{k\in \beth }\tilde{\Xi }_k\), in other words, the condition \(\alpha _k\left[ \mathcal{L}_k(s,\bar{Z}_k^*)\right] \le \alpha _k(s,\bar{Z}_k^*)\) for all \(k\in \beth\) and for each \(s\in [0,t]\) (González-Dıaz et al. 2010). Hence, \(\mathcal{L}_k(s,\bar{Z}_k^*)=\bar{Z}_k^*\) or \(\mathcal{L}_k\) has a fixed-point.
\(\mathbf {Case\ II}\): Again consider \(\widetilde{\Xi }\subset \mathbb{R}^{6K}\times G\) is a non-empty, convex and compact set. Then for \(m\subset \mathbb{N}\), a set \(\beth\) with condition \(|\beth |=m+1\), and affinely independent state variables and lock-down intensity \(\{Z_k(s)\}_{k\in \beth }\subset \mathbb{R}^{6K}\times G\) such that \(\widetilde{\Xi }\) is a proper subset of the convex set based on \(\{Z_k(s)\}_{k\in \beth }\) for all \(s\in [0,t]\). Among all the simplices, suppose \(\hat{\aleph }\) is the set with smallest m. Let \(\tilde{Z}(s)\) be a dynamic point in the m-dimensional interior of \(\hat{\aleph }\). Define \({\hat{\mathcal{L}}}_k\), an extension of \(\mathcal{L}_k\) to the whole simplex \(\hat{\aleph }\), as follows. For every \(Z(s)\in \hat{\aleph }\), let
and,
Therefore, \(\bar{\zeta }\) is continuous which implies \({\hat{\mathcal{L}}}_k(s,Z)\) is continuous. Since the codomain of \({\hat{\mathcal{L}}}_k(s,Z)\) is in \(\tilde{\Xi }\), every fixed-point of \({\hat{\mathcal{L}}}_k(s,Z)\) is also a fixed-point of \(\mathcal{L}_k\). Now by \(\mathbf {Case\ I}\), \({\hat{\mathcal{L}}}_k(s,Z)\) has a fixed-point and therefore, \(\mathcal{L}_k\) also does. \(\square\)
Proof of Theorem 1
From the quantum Lagrangian function expressed in Eq. (12), the Euclidean action function for risk-group k in [0, t] is given by
where \(\lambda _i>0\) for all \(i=\{1,2,3,4\}\) are time independent quantum Lagrangian multiplier. As at the beginning of the small time interval \([s,s+\varepsilon ]\), agent k does not have any future information, they make expectations based on their all state variables \(\{z_k,S_k,I_k,R_k,W_k\}\). For a penalization constant \(L_\varepsilon >0\) and for time interval \([s,s+\varepsilon ]\) such that \(\varepsilon \downarrow 0\) define a transition function from s to \(s+\varepsilon\) as
where \(\Psi _s^k(z_k,S_k,I_k,R_k,W_k)\) is the value of the transition function at time s with the initial condition
and the action function of risk-group k is,
where \(g_k(z_k,S_k,I_k,R_k,W_k)\in C^2([0,t]\times \mathbb{R}^{5K})\) such that Assumptions 1- 3 hold and \(\widetilde{Y}_k(\nu )=g_k[z_k,S_k,I_k,R_k,W_k]\), where \(\widetilde{Y}_k\) is an Itô process (Øksendal 2003) and,
where \(\Delta z_k=z_k(s+\varepsilon )-z_k(s)\), \(\Delta S_k=S_k(s+\varepsilon )-S_k(s)\), \(\Delta I_k=I_k(s+\varepsilon )-I_k(s)\), \(\Delta R_k=R_k(s+\varepsilon )-R_k(s)\) and \(\Delta W_k=W_k(s+\varepsilon )-W_k(s)\). In Eq. (19) \(L_\varepsilon\) is a positive penalization constant such that the value of \(\Psi _{s,s+\varepsilon }^k(.)\) becomes 1. One can think this transition function \(\Psi _{s,s+\varepsilon }^k(.)\) as some transition probability function on Euclidean space. I divide the time interval [0, t] into n small equal length time intervals \([s,s+\varepsilon ]\) such that \(\tau =s+\varepsilon\). After using Fubini’s theorem, the Euclidean action function for time interval \([s,\tau ]\) becomes,
After using the fact that \([\Delta z_k(s)]^2=[\Delta S_k(s)]^2=[\Delta I_k(s)]^2=[\Delta R_k(s)]^2=[\Delta W_k(s)]^2=\varepsilon\), and \(\mathbb{E}_s[\Delta B_0^k]=\mathbb{E}_s[\Delta B_2^k]=\mathbb{E}_s[\Delta B_3^k]=\mathbb{E}_s[\Delta B_4^k]=\mathbb{E}_s[\Delta B_7^k]\) for all \(\varepsilon \downarrow 0\), (with initial conditions \(z_k(0),S_k(0),I_k(0),R_k(0),W_k(0)\)) Itô’s formula and Baaquie (1997) imply,
where \(g_k=g_k(z_k,S_k,I_k,R_k,W_k)\).
Result in Eq. (19) implies,
For \(\varepsilon \downarrow 0\) define a new transition probability \(\Psi _s^{k\tau }\) centered around time \(\tau\). A Taylor series expansion (up to second order) of the left hand side of Eq. (20) yields,
as \(\varepsilon \downarrow 0\). For fixed s and \(\tau\) let \(z_k(s)=z_k(\tau )+\varsigma _1\), \(S_k(s)=S_k(\tau ) +\varsigma _2\), \(I_k(s)=I_k(\tau )+\varsigma _3\), \(R_k(s)=R_k(\tau )+\varsigma _4\) and \(W_k(s)=W_k(\tau )+\varsigma _5\). For some finite positive numbers \(c_i\) with \(i=1,\ldots ,5\) assume \(|\varsigma _1|\le \frac{c_1\varepsilon }{z_k(s)}\), \(|\varsigma _2|\le \frac{c_2\varepsilon }{S_k(s)}\), \(|\varsigma _3|\le \frac{c_3\varepsilon }{I_k(s)}\), \(|\varsigma _4|\le \frac{c_4\varepsilon }{R_k(s)}\) and, \(|\varsigma _5|\le \frac{c_5\varepsilon }{W_k(s)}\). Therefore, we get upper bounds of each state variable in this pandemic control model as \(z_k(s)\le c_1\varepsilon / (\varsigma _1)^2\), \(S_k(s)\le c_2\varepsilon / (\varsigma _2)^2\), \(I_k(s)\le c_3\varepsilon / (\varsigma _3)^2\), \(R_k(s)\le c_4\varepsilon / (\varsigma _4)^2\) and \(W_k(s)\le c_5\varepsilon / (\varsigma _5)^2\). Furthermore, by Fröhlich’s reconstruction Theorem (Simon 1979; Pramanik 2020, 2021d) and Assumptions 1–3 imply
as \(\varepsilon \downarrow 0\). For risk-group \(k\in \{1,2,\ldots ,K\}\) define a function
Therefore, after using the function \(\tilde{f}(s,e_k,z_k,S_k,I_k,R_k,W_k)\) Eq. (21) yields,
Consider \(\tilde{f}_k(s,e_k,\varsigma _1,\varsigma _2,\varsigma _3,\varsigma _4,\varsigma _5)\) is a \(C^2\)-function, then doing the Taylor series expansion up to second order yields
where
and,
as \(\varepsilon \downarrow 0\) and \(\Delta e_k(s)\downarrow 0\). Define \(\breve{m}_1=\varsigma _1-z_k\), \(\breve{m}_2=\varsigma _2-S_k\), \(\breve{m}_3=\varsigma _3-I_k\), \(\breve{m}_4=\varsigma _4-R_k\) and, \(\breve{m}_5=\varsigma _5-W_k\) such that \(\textrm{d}\breve{m}_i=\textrm{d}\varsigma _i\) for all \(i=\{1,\ldots ,5\}\). Therefore, after denoting \(\tilde{f}_k(s,e_k(s),\varsigma _1(\tau ),\varsigma _2(\tau ),\varsigma _3(\tau ),\varsigma _4(\tau ),\varsigma _5(\tau ))=\tilde{f}_k\) above expression becomes
Let
and
and
where the symmetric matrix \(\varvec{\Theta }_k\) is assumed to be positive semi-definite. The integrand in Eq. (22) becomes a shifted Gaussian integral,
where \(\textbf{J}_k^T\) is the transposition of \(\textbf{J}_k\), \({\breve{\textbf{m}_k}}^T\) is the transposition of \({\breve{\textbf{m}_k}}\) and \(\left( \varvec{\Theta }_k\right) ^{-1}\) is the inverse of \(\varvec{\Theta }_k\). Hence,
such that the inverse matrix \(\left( \varvec{\Theta }_k\right) ^{-1}>0\) exists. Similarly,
The system of equations expressed in (23) through (24) implies that the Wick-rotated Schrödinger type equation or the Fokker–Plank type equation is,
as \(\varepsilon \downarrow 0\). Assuming \(L_\varepsilon =\pi /\sqrt{\varepsilon | \varvec{\Theta }_k|}>0\) yields,
as \(\varepsilon \downarrow 0\). As \(z_k\le \varepsilon /c_1\varsigma _1^2\), assume \(|\varvec{\Theta }_k^{-1}|\le 2c_1\varepsilon (1-\varsigma _1^{-1})\) such that \(|(2\varvec{\Theta }_k)^{-1}+z_k|\le c_1\varepsilon\). In the similar fashion we assume \(|(2\varvec{\Theta }_k)^{-1}+S_k|\le c_2\varepsilon\), \(|(2\varvec{\Theta }_k)^{-1}+I_k|\le c_3\varepsilon\), \(|(2\varvec{\Theta }_k)^{-1}+R_k|\le c_4\varepsilon\) and \(|(2\varvec{\Theta }_k)^{-1}+W_k|\le c_5\varepsilon\). Therefore, \(|\varvec{\Theta }_k^{-1}|\le 2\varepsilon \min \left\{ c_1(1-\varsigma _1^{-1}),c_2(1-\varsigma _2^{-1}),c_3(1-\varsigma _3^{-1}),c_4(1-\varsigma _4^{-1}),c_5(1-\varsigma _5^{-1})\right\}\) such that \(|(2\varvec{\Theta }_k)^{-1}+z_k|\downarrow 0\), \(|(2\varvec{\Theta }_k)^{-1}+S_k|\downarrow 0\), \(|(2\varvec{\Theta }_k)^{-1}+I_k|\downarrow 0\), \(|(2\varvec{\Theta }_k)^{-1}+R_k|\downarrow 0\) and \(|(2\varvec{\Theta }_k)^{-1}+W_k|\downarrow 0\). Hence,
Therefore the Fokker–Plank type equation of this pandemic system is,
Finally, the solution of
is an optimal “lock down” intensity of risk-group k. Moreover, as \(\varsigma _1=z_k(s)-z_k(\tau )\), \(\varsigma _2=S_k(s)-S_k(\tau )\), \(\varsigma _3=I_k(s)-I_k(\tau )\), \(\varsigma _4=R_k(s)-R_k(\tau )\) and \(\varsigma _5=W_k(s)-W_k(\tau )\) for all \(\varepsilon \downarrow 0\), in Eq. (25), \(\varsigma _i\) for all \(i=\{1,\ldots ,5\}\) can be replaced by our original state variables. As the transition function \(\Psi _s^{k\tau }(z_k,S_k,I_k,R_k,W_k)\) is a solution of Eq. (25), the result follows. \(\square\)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Pramanik, P. Path integral control of a stochastic multi-risk SIR pandemic model. Theory Biosci. 142, 107–142 (2023). https://doi.org/10.1007/s12064-023-00388-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12064-023-00388-y
Keywords
- Pandemic control
- Multi-risk SIR model
- Bayesian opinion network
- Feynman-type path integrals
- Stochastic differential equations