Introduction

Recently, the WHO (World Health Organization) has urged the world to monitor the outbreak of avian influenza and possible mutation of influenza viruses (World Health Organization 2011). The 1918 pandemic was one of the deadliest public health menaces of recorded human history, claiming over 20 million lives (Stuart-Harris 1979). Although subsequent pandemics in 1957 (Asian Flu) and 1968 (Hong Kong Flu) resulted in milder outbreaks (Kilbourne 2006), the recent emergence of the highly pathogenic avian H5N1 influenza A viruses in wild bird populations in several regions of the world, together with recurrent flu cases of H5N1 viruses in humans (arising primarily from direct contact with poultry), have triggered a major scare for a pending pandemic influenza. The current projections of the potential impact of a prospective pandemic are alarming. The highly pathogenic H5N1 influenza A viruses are now endemic in avian populations in Southeast Asia, and human cases continue to rise. H5N1 represents a serious pandemic threat owing to the risk of a mutation generating a virus with increased transmissibility. In humans, avian influenza virus causes similar symptoms as other types of influenza. These include fever, cough, sore throat, muscle aches, conjunctivitis and, in extreme cases, severe breathing problems and pneumonia that may be fatal (Centers for Disease Control and Prevention 2010; World Health Organization 2011, 2012).

Avian influenza, being an emerging infectious disease in humans, is now receiving significant attention from the mathematical community. Faced with the H5N1 pandemic threat, strategies designed to contain an emerging pandemic should be considered a public health priority. Studies have documented the most significant risk factors for human H5N1 infection to be direct contact with sick or dead poultry or wild birds, or visiting a live poultry market (Centers for Disease Control and Prevention 2007). Since its emergence, a number of mathematical modeling studies, using stochastic as well as deterministic formulations, have been carried out to quantify the burden of a potential flu pandemic and assess various interventions (Alexander et al. 2004, 2008; Chowell et al. 2005; Doyle et al. 2006; Lipsitch et al. 2007; Longini et al. 2004). Nuño et al. (2006) analyzed a model to examine the role of hospital and community control measures, antiviral drugs and vaccination in combating a potential flu pandemic in a population, while a study by Gumel (2009) considered the dynamics of a two-strain influenza model and concluded that the influenza-related burden in humans increased as the mutation rate increased. Although many of these studies tend to emphasize the use of pharmaceutical interventions, it is generally believed that such interventions (antivirals and vaccines) would not be readily and widely available at the onset of the pandemic (Gumel 2009).

Nowadays, the spread of H5N1 virus is known to be under control, but the infection could re-emerge anytime in the future. H5N1 may mutate into a strain capable of efficient person to person transmission (Centers for Disease Control and Prevention 2007). However, none of the mathematical models of avian influenza have considered saturated incidence, which describes the effect of susceptible humans coming into contact with infected birds and or infected humans when effects such as crowding of infectives or protection measures taken by susceptibles are taken into account (Kaddar 2010). Moreover, there will be a potential threat of an uncontrollable outbreak, especially in developing countries where drugs and adequate health facilities for quarantine and isolation are not generally available. Hence it is instructive to carry out modeling studies that focus on the combination of pharmaceutical and non-pharmaceutical interventions with saturated incidence.

Several types of epidemic models have been studied, most of which have investigated the transmission rate of susceptible individuals who have been exposed to infected individuals (Gao et al. 2006; Kaddar 2009; Ruan and Wang 2003). Various incidence functions have been employed in epidemic models, of which the most popular are bilinear and saturated incidences. The bilinear (or mass-action) incidence rate is formulated by β SI where β is a positive constant, and S and I are the number of susceptible and infected individuals, respectively (Zhang et al. 2008; Zhou and Liu 2003). Bilinear incidence is based on the law of mass action, which requires a well-mixed population so that each infected individual has equal probability of infecting each susceptible individual. It has been employed for communicable diseases such as cholera, chickenpox and influenza (Du and Xu 2010). If a population is crowded or saturated with infectives, then saturated incidence is a better option (Gao et al. 2006; Yang et al. 2007). The saturated incidence rate takes the form \(\frac{\beta SI}{1+\alpha_1 S}\) or \(\frac{\beta SI}{1+\alpha_2 I}, \) where α 1, α 2 are positive constants. The saturated incidence rates \(\frac{\beta SI}{1+\alpha_1 S}\) and \(\frac{\beta SI}{1+\alpha_2 I}\) describe the behavioral change of the disease and saturation effect of the infective and susceptible individuals, respectively, when their numbers increase (Capasso and Serio 1978; Liu and Yang 2012; May and Anderson 1978; Wei and Chen 2008). That is, when S or I is large, \(\frac{\beta SI}{1+\alpha_1 S}\) or \(\frac{\beta SI}{1+\alpha_2 I}\) will respectively converge to a saturation point.

In this paper, we consider the half-saturated incidence rate \(\frac{\beta SI}{H+I}. \) The parameter β > 0 is the transmission rate and H is the half-saturation constant, i.e., the density of infected individuals in the population that yields 50 % possibility of contracting avian influenza. The main goal of this study is to formulate a deterministic mathematical model to interpret the spread of avian influenza from birds to humans using saturated incidence. We assess the potential impact of avian influenza in both the bird and the human populations because two types of outbreak of avian influenza may occur (Gumel 2009; Iwami et al. 2007). Therefore, the specific objectives are: to formulate and analyze a mathematical model of avian influenza that includes both the bird and human populations; to determine the threshold parameter that measures initial disease transmission; and to investigate the effect of saturated incidence on the transmission dynamics of the disease.

The model

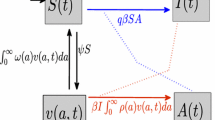
The population of birds and humans are represented by N b(t) and N h(t), respectively, at time t. The bird population is divided into two sub-populations: susceptible (S b) and infected (I b) birds. The number of susceptibles for the bird population is increased by new recruitment (birth), but reduced through natural death and infection (moving to class I b). On the other hand, the infected bird population is increased by the infection of susceptible birds whereas reduction is caused by natural mortality and death due to avian influenza. The total bird population at time t is formulated by N b = S b + I b. The human population is sub-divided into those who are susceptible (S h), infected with avian strain (I a), infected with mutant strain (I m), and recovered from avian and mutant strains (R h). The total population of humans at time t is given by N h = S h + I a + I m + R h. The number of susceptibles for the human population is increased by recruitment, but diminished by infection (moving to class I a or I m) and natural death. The number of infected humans with the avian strain is increased by the infection of susceptible humans and reduced through mutation (moving to class I m), recovery from the disease (moving to class R h), natural death and disease death. The growth of the population of infected humans with mutant strain is caused by the infection of susceptible humans and mutation of infected humans with the avian strain, but reduced by recovery from the disease (moving to class R h), natural death and disease death.

A schematic flowchart of this model is depicted in Fig. 1. The descriptions of the variables and associated parameters are given in Table 1.

Fig. 1
figure 1

Flowchart of the model

Full size image
Table 1 Description of the variables and associated parameters
Full size table

Model equations

Considering the above formulations and the flow diagram, we have the following system of nonlinear ordinary differential equations:

$$ \begin{aligned} S'_{\rm b}(t)&=\Uplambda_{\rm b}-\mu_{\rm b}S_{\rm b}-\frac{\beta_{\rm b} S_{\rm b} I_{\rm b}}{H_{\rm b}+I_{\rm b}}\\ I'_{\rm b}(t)&=\frac{\beta_{\rm b} S_{\rm b} I_{\rm b}}{H_{\rm b}+I_{\rm b}}-(\mu_{\rm b}+\delta_{\rm b})I_{\rm b}\\ S'_{\rm h}(t)&=\Uplambda_{\rm h}-\mu_{\rm h} S_{\rm h} -\frac{\beta_{\rm a} S_{\rm h} I_{\rm a}}{H_{\rm a}+I_{\rm a}}-\frac{\beta_{\rm m} S_{\rm h} I_{\rm m}}{H_{\rm m}+I_{\rm m}}-\frac{\beta_{\rm bh}S_{\rm h}I_{\rm b}}{H_{\rm bh}+I_{\rm b}}\\ I'_{\rm a}(t)&=\frac{\beta_{\rm bh}S_{\rm h}I_{\rm b}}{H_{\rm bh}+I_{\rm b}}+\frac{\beta_{\rm a} S_{\rm h} I_{\rm a}}{H_{\rm a}+I_{\rm a}}-(\mu_{\rm h}+d+\epsilon+\gamma_{\rm a})I_{\rm a}\\ I'_{\rm m}(t)&=\frac{\beta_{\rm m} S_{\rm h} I_{\rm m}}{H_{\rm m}+I_{\rm m}}+\epsilon I_{\rm a}-(\mu_{\rm h}+\alpha+\gamma_{\rm m})I_{\rm m}\\ R'_{\rm h}(t)&=\gamma_{\rm a} I_a+\gamma_{\rm m} I_{\rm m}-\mu_{\rm h} R_{\rm h}. \end{aligned} $$
(2.1)

The feasibility of the solution in model (2.1) is given in Appendix 1. In addition, the stability analysis of the avian-only and avian–human models are given in Appendices 2 and 3, respectively.

The effect of half-saturated incidence on the transmission dynamics of the disease

To investigate the effect of half-saturated incidence on the transmission dynamics of avian influenza, we would like to make a comparison of the total number of infected individuals using our model (2.1) and the following bilinear incidence model:

$$ \begin{aligned} S'_{\rm b}(t)&=\Uplambda_{\rm b}-\mu_{\rm b}S_{\rm b}-\beta_{\rm B} S_{\rm b} I_{\rm b} \\ I'_{\rm b}(t)&=\beta_{\rm B} S_{\rm b} I_{\rm b}-(\mu_{\rm b}+\delta_{\rm b})I_{\rm b} \\ S'_{\rm h}(t)&=\Uplambda_{\rm h}-\mu_{\rm h}S_{\rm h}-\beta_{\rm A} S_{\rm h} I_{\rm a}-\beta_{\rm M} S_{\rm h} I_{\rm m}-\beta_{\rm BH}S_{\rm h}I_{\rm b}\\ I'_{\rm a}(t)&=\beta_{\rm BH}S_{\rm h}I_{\rm b}+\beta_{\rm A} S_{\rm h} I_{\rm a}-(\mu_{\rm h}+d+\epsilon+\gamma_{\rm a})I_{\rm a}\\ I'_{\rm m}(t)&=\beta_{\rm M} S_{\rm h} I_{\rm m}+\epsilon I_{\rm a}-(\mu_{\rm h}+\alpha+\gamma_{\rm m})I_{\rm m} \\ R'_{\rm h}(t)&=\gamma_{\rm a}I_{\rm a}+\gamma_{\rm m} I_{\rm m}-\mu_{\rm h} R_{\rm h}, \end{aligned} $$
(3.1)

where β B, β A, β M and β BH are, respectively, the rates at which avian influenza is contracted by birds, human-to-human avian influenza is contracted, human-to-human mutant influenza is contracted and avian influenza is contracted from infected birds. All other parameters are defined in Table 1.

The unit measurements for all four infection rates (β B, β A, β M and β BH) are [number of individuals]−1 × [days]−1. The transmission parameters of model (3.1) are fixed at \(\beta_{\rm B}=\beta_{\rm A}=\frac{0.4}{200,000}\) per individual per day, β M = 0.3 β A per individual per day (Gumel 2009) and \(\beta_{\rm BH}=\frac{0.2}{100}\) per individual per day (Iwami et al. 2007), whereas the remaining parameter sample values in models (2.1) and (3.1) are as in Table 2. For both models (2.1) and (3.1), we assume the initial populations satisfy S b(0) = 2.06 × 109 and S h(0) = 109. In addition, the basic reproduction number of model (3.1) is defined as follows:

$$ \begin{aligned} R_{\rm AH}=\max\left \{\frac{\beta_{\rm B}\Uplambda_{\rm b}}{\mu_{\rm b}(\mu_{\rm b}+\delta_{\rm b})},\frac{\beta_{\rm A}\Uplambda_{\rm h}}{\mu_{\rm h}(\mu_{\rm h}+d+\epsilon+\gamma_{\rm a})}, \frac{\beta_{\rm M}\Uplambda_{\rm h}}{\mu_{\rm h}(\mu_{\rm h}+\alpha+\gamma_{\rm m})}\right\}. \end{aligned} $$
(3.2)
Table 2 Model parameters
Full size table

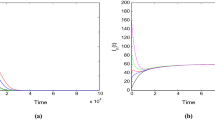
Figure 2 illustrates the effects of avian influenza transmission dynamics using bilinear incidence (model 3.1) and half-saturated incidence (model 2.1) It is worth mentioning that the total number of infected humans of the bilinear incidence model is known to decrease exponentially, and both models achieve the outcome of disease eradication. Model (3.1) produces an enormous number of infected humans compared to model (2.1); numerical simulations of model (3.1) produced around 65 % more than the maximum number of infected humans simulated by model (2.1). To achieve the state of disease eradication, half-saturated incidence typically requires more time than bilinear incidence.

Fig. 2
figure 2

Comparison between the effects of avian influenza transmission dynamics in models (2.1) and (3.1)

Full size image

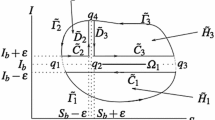
Figure 3 describes the effects of the rate of transmission in models (2.1) and (3.1) with respect to each term of R ah in (5.3) and R AH in (3.2). If the natural logarithms of all terms in R ah and R AH are equal to or less than zero, then the disease will die off, whereas if one of these terms is greater than zero, then the disease will persist. Figure 3 shows that β m and β M play an essential role in controlling R ah and R AH, respectively. This is because these two parameters are the coefficients of the nonlinear terms in both bilinear and half-saturated incidences. A small change in β m or β M will produce a disproportionate change in the outcome. By decreasing β m and β M in both models (2.1) and (3.1), the disease will be eradicated. Hence we conclude that \(\lim_{\beta_{\rm m} \to 0}R_{\rm ah}=0\) and \(\lim_{\beta_{\rm M} \to 0}R_{\rm AH}=0. \)

Fig. 3
figure 3

The effect of the transmission parameters on R ah and R AH

Full size image

Sensitivity analysis of R ah

We performed a sensitivity analysis of R ah (given by Eq. 5.3) using Latin Hypercube Sampling with 2,000 simulations per run. The ranges of the parameters are shown in Table 2 while the results are shown in Figs. 4 and 5. From Fig. 4, it can be observed that there are 7 parameters out of 16 to be considered: \(\Uplambda_{\rm h}, H_{\rm m}, \beta_{\rm m}, H_{\rm a}, \alpha, d\) and β a. These parameters are chosen as they have the greatest effect on the outcome. Figure 5 illustrates the sensitivity analysis of R ah, which is highly dependent on the particular seven parameters. From these figures, the simulations suggest that control of avian influenza is most likely to be achieved by lowering the values of \(\Uplambda_{\rm h}\) and β m. On the other hand, increasing H a, H m, α or d, or decreasing β a is unlikely to eradicate the disease.

Fig. 4
figure 4

Sensitivity of R ah to all parameters. Parameters with positive partial rank correlation coefficients will increase R ah when they are increased, while parameters with negative partial rank correlation coefficients will decrease R ah when they are increased

Full size image
Fig. 5
figure 5

Sensitivity analysis of R ah to the seven parameters which have the most significant effects on the outcome

Full size image

Figure 6 illustrates the effect of half-saturation constants (H b, H a and H m) with respect to each term of R ah in (5.3). If all three terms (i.e., ln R b, ln R h1 and ln R h2) are equal to or less than zero, then the disease will die off. Conversely, if one of these terms is greater than zero, then the disease will persist. Figure 6 shows that, within our given ranges, ln R h2 always has the largest value compared to ln R b and ln R h1 for every half-saturation constant. Hence, H m plays an important role in controlling the parameter R ah. For instance, increasing H m will lead us to disease eradication; that is, whenever H m → ∞, both R h2 → 0 and R ah → 0.

Fig. 6
figure 6

The effect of parameters H b, H a and H m on each term of R ah. All other parameters are at their sample values in Table 2

Full size image

Control strategies

To control the transmission of avian influenza, some control strategies such as pharmaceutical or/and non-pharmaceutical protections have to be considered (Bowman et al. 2005; Yang et al. 2009). For non-pharmaceutical protection, we implement personal protection and isolation, whereas we adopt vaccination for pharmaceutical protection.

Personal protection

There are several potential modes of avian influenza transmission such as the consumption of raw or undercooked infected poultry products, contact with oral/nasal mucous membrane or conjunctiva (for example, through swimming or bathing in a contaminated pond/pool), inhalation of contaminated dust or fine water droplets and human-to-human transmission (Food and Agriculture Organization of the United Nations 2008). Although the exact mode of human-to-human transmission remains unclear, there is reason to believe that unprotected contact with an infected person, respiratory secretions, body fluids or waste poses a higher risk for transmission, especially for health-care workers (HCWs) who are first responders (Food and Agriculture Organization of the United Nations 2008; World Health Organization 2006).

To reduce the mortality and infection rate of avian influenza, the general public—especially HCWs, and workers and employers who are involved in poultry agriculture or have frequent contact with wild birds—is advised to follow strict guidelines for personal protection. For example, one should take precautions for hygiene, using gloves, masks and other protective gear (Centers for Disease Control and Prevention 2012; Government of Ontario 2006; World Health Organization 2006).

As personal protection plays an essential role in preventing an outbreak, we investigated the impact of personal protection on controlling the spread of this disease in humans. We rescaled the transmission coefficients, (β a, β m, β bh), to (1 − cq) (β a, β m, β bh), where 0 ≤ c ≤ 1 is the fraction of population that has adopted personal protection and 0 < q ≤ 1 is the efficiency of personal protection. For c = 1, all the people in a particular community employ personal protection, whereas c = 0 means there is no one practicing personal protection. Further, the value q = 1 shows that the efficiency of personal protection is 100 %. Hence, the values of c and q are reciprocal to the rate of avian influenza transmission (Bowman et al. 2005).

The number of infected humans with respect to the avian (I a(t)) and mutant strains (I m(t)) are depicted in Figs. 7 and 8, respectively, with q  ∈ [0.1, 0.5, 0.9]. Figures 7a and 8a show results for the case of 30 % of the population employing personal protection, whereas Figs. 7b and 8b show results for the case of 80 % of the population employing personal protection. From Figs. 7 and 8, it can be observed that the values of c and q are reciprocal to the maximal points of I a and I m. Moreover, more people employing personal protection will reduce the values of I a and I m drastically compared to the efficiency of personal protection. Hence, we can conclude that although the efficiency of personal protection plays a role in reducing the rate of avian influenza infection, public awareness is the most effective method for controlling the spread of the disease. See Tchuenche et al. (2011) for more discussion.

Fig. 7
figure 7

The effects of personal protection on the avian strain

Full size image
Fig. 8
figure 8

The effects of personal protection on the mutant strain

Full size image

Isolation

Before an H5N1 vaccine is ready to be administered to the community to reduce the rate of avian influenza infection, isolation is one of the best choices of control strategy to reduce the transmission rate (World Health Organization 2007). Although the strategy of isolation might not lead to disease eradication, it can reduce the chance of a person making contact with an infected human (Gumel 2009). Hence we consider our model for the population of birds (\( S_{\rm b}' (t)\) and \( I_{\rm b}' (t) \)) and humans with isolation as follows:

$$ \begin{aligned} I'_{\rm a}(t)&=\frac{\beta_{\rm bh}S_{\rm h}I_{\rm b}}{H_{\rm bh}+I_{\rm b}}+\frac{\beta_{\rm a} S_{\rm h} I_{\rm a}}{H_{\rm a}+I_{\rm a}}-(\mu_{\rm h}+d+\epsilon+\psi_{\rm a})I_{\rm a} \\ I'_{\rm m}(t)&=\frac{\beta_{\rm m} S_{\rm h} I_{\rm m}}{H_{\rm m}+I_{\rm m}}+\epsilon I_{\rm a}-(\mu_{\rm h}+\alpha+\psi_{\rm m})I_{\rm m} \\ T'_{\rm a}(t)&=\psi_{\rm a}I_{\rm a}-(\mu_{\rm h}+d+\gamma_{\rm a})T_{\rm a} \\ T'_{\rm m}(t)&=\psi_{\rm m}I_{\rm m}-(\mu_{\rm h}+\alpha+\gamma_{\rm m})T_{\rm m} \\ R'_{\rm h}(t)&=\gamma_{\rm a}T_{\rm a}+\gamma_{\rm m}T_{\rm m}-\mu_{\rm h} R_{\rm h}. \end{aligned} $$
(5.1)

The quantities T a(t) and T m(t) represent the populations of isolated humans with avian strain at a rate of ψ a and mutant strain at a rate of ψ m at time t, respectively. The basic reproduction number of (5.1) can be expressed as

$$ R_{\rm T}=\max\left \{\frac{\beta_{\rm a}\Uplambda_{\rm h}}{H_{\rm a}\mu_{\rm h}(\mu_{\rm h}+d+\epsilon+\psi_{\rm a})}, \frac{\beta_{\rm m}\Uplambda_{\rm h}}{H_{\rm m}\mu_{\rm h}(\mu_{\rm h}+\alpha+\psi_{\rm m})}\right\}. $$

Several numerical simulations have been performed to validate the effect of the parameters ψ a and ψ m; see Figs. 9 and 10. Assuming that the parameters ψ a and ψ m are equal, we observe from Fig. 9 that the isolation of infected humans will lead to the reduction of the total number of infected humans (i.e., I a(t) + I m(t) + T a(t) + T m(t)). Thus, the values of ψ a and ψ m are reciprocal to the number of infected individuals. However, increasing the rate of isolation will not lead to eradication of the disease.

Fig. 9
figure 9

The effect of isolating infected humans when isolation rates are equal

Full size image

Furthermore, we studied the impact of only isolating infected humans with one strain (i.e., either the avian or mutant strain). Figure 10 shows that increasing the rate of isolation of infected humans with the avian strain gives a better performance in controlling the spread of the disease compared to isolation of those with the mutant strain. From Figs. 9 and 10, we can conclude that the transmission of the disease can be controlled much more efficiently by isolating infected humans with avian and mutant strains. This works better than the countermeasure of isolating infected humans with only one strain; however, it does not lead to disease eradication.

Fig. 10
figure 10

The impact of isolating humans infected with only one strain

Full size image

Vaccination

Controlling and diminishing the spread of avian influenza is a challenging task, as the disease is very infectious and able to mutate into highly pathogenic strains (Marangon et al. 2008). Consequently, vaccination of poultry or humans as a tool to manage, prevent or eradicate the disease has been recommended by the United Nations (Food and Agriculture Organization of the United Nations 2004). Here, we consider our model for the population of birds (S′b(t) and I′b(t)) and vaccination of humans as follows:

$$ \begin{aligned} S'_{\rm h}(t)&=(1-p)\Uplambda_{\rm h}-\mu_{\rm h}S_{\rm h}-\frac{\beta_{\rm a} S_{\rm h} I_{\rm a}}{H_{\rm a}+I_{\rm a}}-\frac{\beta_{\rm m} S_{\rm h} I_{\rm m}}{H_{\rm m}+I_{\rm m}}-\frac{\beta_{\rm bh}S_{\rm h}I_{\rm b}}{H_{\rm bh}+I_{\rm b}}\\ V'_{\rm h}(t)&=p\Uplambda_{\rm h}-(1-\phi) \frac{\beta_{\rm m}V_{\rm h}I_{\rm m}}{H_{\rm m}+I_{\rm m}}-\mu_{\rm h} V_{\rm h}\\ I'_{\rm m}(t)&=\frac{\beta_{\rm m} I_{\rm m}}{H_{\rm m}+I_{\rm m}}[S_{\rm h}+(1-\phi) V_{\rm h}]+\epsilon I_{\rm a}-(\mu_{\rm h}+\alpha+\gamma_{\rm m})I_{\rm m}. \end{aligned} $$
(5.2)

In this model, V h(t) represents the population of vaccinated humans, whereas p and ϕ denote the prevalence rate of the vaccination program and the efficacy of the vaccine, respectively. Further, we assume that vaccinated humans are fully protected from the avian strain, but partially protected from the mutant strain with a loss of protection effectiveness of the vaccination (Iwami et al. 2009). The basic reproduction number for this model (5.2) is as follows:

$$ R_{\rm V}=\max\left \{\frac{\beta_{\rm b} \Uplambda_{\rm b}}{H_{\rm b} \mu_{\rm b}(\mu_{\rm b}+\delta_{\rm b})}, \frac{\beta_{\rm a} \Uplambda_{\rm h}}{H_{\rm a}\mu_{\rm h}(\mu_{\rm h}+d+\epsilon+\gamma_{\rm a})}, \frac{\beta_{\rm m}\Uplambda_{\rm h}[1+p(1-\phi)]}{H_{\rm m}\mu_{\rm h}(\mu_{\rm h}+\alpha+\gamma_{\rm m})}\right\}. $$

We performed several numerical simulations to examine the effect of ϕ and to compare various control strategies (personal protection, isolation and vaccination). From Fig. 11, we find that the higher the efficacy of vaccine, the fewer the number of infected humans. After 90 days, there is very little reduction in the number of infections, even if 90 % of the population is vaccinated. After 150 days, the number of infections is low if both the efficacy of the vaccine and the vaccination coverage are high. However, if the vaccine only has moderate efficacy (less than 70 %), then very little is gained by vaccinating a large proportion of the population.

Fig. 11
figure 11

The impact of ϕ on the total number of infected humans at day 90 (top figure) and day 150 (bottom figure)

Full size image

In addition, Fig. 12 shows that, if there is an absence of control strategies, then we will need more time to combat the disease compared to those populations which have undergone vaccination. Note that by “combatting” the disease, we mean applying control strategies once infection has begun. Moreover, we cannot guarantee that the disease will not attack the population again in the future if there are no control strategies employed. From the same figure again, we can see that the number of infected humans begins to increase after day 450.

Fig. 12
figure 12

The effect of vaccination compared to no control methods

Full size image

On the other hand, Fig. 13 shows that, by employing non-pharmaceutical interventions (personal protection and isolation) and all of the proposed control methods, less time will be needed to eradicate the disease compared to only employing a pharmaceutical (vaccination) control strategy. In conclusion, the non-pharmaceutical control strategy is more effective than vaccination in battling the disease.

Fig. 13
figure 13

Comparison between the suggested control strategies

Full size image

Discussion

In this paper, we have conducted a study focusing on the effect of half-saturated incidence on the transmission dynamics of avian influenza. When half-saturated incidence is included (model 2.1), the effect is a significantly lower peak of the total number of infected humans compared to the case when half-saturated incidence is not included (model 3.1). However, when half-saturation is included, the disease takes longer to die off. Furthermore, the results of the sensitivity analysis of R ah suggest that increasing the half-saturation constants, especially H m, will lead to disease eradication. Particularly in this case, we obtain R ah < 1.

To control the outbreak, we proposed both non-pharmaceutical (personal protection and isolation) and pharmaceutical (vaccination) control strategies. From the outcomes that we have obtained, the total number of infected humans is reciprocal to the following: the fraction of the population that has adopted personal protection, the efficiency of personal protection, the rate of isolation of humans with the avian strain, the rate of isolation of humans with the mutant strain and the efficacy of the vaccine. Hence, by increasing these parameter values, we can control the spread of the disease more effectively and less time is required to battle the outbreak. Although vaccination gives better control of avian influenza transmission than any control strategies not employing vaccination, it takes longer to eradicate the disease compared to employing only non-pharmaceutical or all proposed control methods. However, adopting either pharmaceutical, non-pharmaceutical or all of the proposed control strategies will lead to disease eradication.

The recent H1N1 pandemic provided important lessons for future pandemics. Personal protection and isolation were judged to be successful in Singapore, when well implemented (Hospital Influenza Working Group 2009), but less so in other Asian countries (Chan et al. 2010). Conversely, even once a vaccine became available, distribution was problematic due to hoarding and underutilization (Fisher et al. 2011). This suggests that the recommendations we make here nevertheless need careful implementation once a pandemic occurs.

This model has several limitations, which should be noted. We have used constant human recruitments and bird inflow. We have also assumed that birds will not be infected with avian influenza from humans and infected birds will remain infected (i.e., infected birds will not move to, for example, a recovered or susceptible class). For the human population, we assumed that immunity was permanent.

If the half-saturation constant, H * = {H a, H m, H b, H bh} tends to infinity, then \(\beta_* S_* \frac{I_*}{H_*+I_*}\) tends to zero, where we denote β * = {β a, β m, β b, β bh}, S * = {S b, S h} and I * = {I b, I a, I m}. That is, the infection does not occur. Thus, the number of susceptibles, S *, will increase while the number of infected, I *, will decrease. Moreover, if H * approaches zero, then we will obtain the peak of infection. It is worth mentioning that the half-saturation constant for humans with the avian strain contracted from infected birds in this model is irrelevant. This is because there are no infected birds to infect humans if the half-saturation constant for birds with the avian strain approaches infinity. Hence, in this case, humans will not contract avian influenza from infected birds.

For future work, we propose a model which incorporates the saturation incidence rate, \(\frac{\beta SI}{1+\alpha_1 S}, \) where α 1 is a positive constant. In this case, we wish to study the role of the parameter α 1 in controlling the epidemic.

In summary, modeling avian influenza with half-saturated incidence gives insights into disease management that cannot be gleaned from mass-action (bilinear) modeling. By increasing the half-saturation constant for the mutant strain (through isolation techniques such as quarantine), in addition to other protection measures such as vaccination and personal protection, we can make the disease-free equilibrium globally stable and hence theoretically eradicate the disease. A comparison of the two models suggests that eradication is slower in the case of half-saturation. It follows that mass-action models may be overestimating the speed with which we might bring the disease under control.