1 Introduction

Multi-variant products enabling customers to individually specify their products by selecting product options can be produced at competitive prices on mixed-model assembly lines [1, 2]. Serving international markets with multi-variant products, companies may operate mixed-model assembly lines on various locations composing a production network [3,4,5]. Thus, production planning first has to assign orders to production locations and periods such as months in the medium-term before they are further assigned to mixed-model assembly lines and respective cycles in the short-term, i.e. they are sequenced on the lines [3, 5, 6].

The short-term assignment to lines and cycles is referred to as local order scheduling or local order assignment as it may take place at the locations of the production network individually [3]. Both the assignment to lines and to cycles of those lines can be conducted simultaneously because the assignment to lines is required for the assignment to cycles and the assignment to lines and to cycles may both be necessary at the same time for further planning of material requirements and workforce [3, 5]. Although the simultaneous assignment to lines and sequencing is a complex task, this is of major interest in case workers are flexibly assigned to stations across the lines of a production location and thus are not dedicated to a specific station at a specific line. This is particularly the case for the workers of the final assembly lines of the Airbus single-aisle A320 Family at Hamburg in Germany, Toulouse in France, Tianjin in China, and Mobile in the USA running with a cycle time of up to two and a half working days. Therefore, this paper introduces an optimization model for local order scheduling for mixed-model assembly lines consisting of the assignment to lines and to cycles.

The paper is structured as follows: in Sect. 2 literature regarding sequencing on mixed-model assembly lines is examined. This is followed by the introduction of an optimization model for local order scheduling integrating the assignment to lines in Sect. 3. In Sect. 4, the results of applying the model to the Airbus A320 Family are presented. A conclusion is given in Sect. 5.

2 Literature

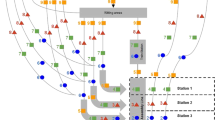
For a structured, two-dimensional representation of the multitude of internal as well as cross-company planning tasks that need to be considered in supply chain planning, the supply chain planning matrix depicted in Fig. 1 is usually taken into account [7]. Within the matrix the planning tasks are, on the one hand, assigned to hierarchical, vertical planning levels according to their time horizons [7]. On the other hand, the planning tasks are also classified according to the horizontal supply chain planning levels “procurement”, “production”, “distribution”, and “sales” [7].

Fig. 1
figure 1

Supply chain planning matrix (see [7,8,9])

Full size image

Local order scheduling, which is addressed in this paper in terms of assignment to lines and sequencing, refers to the short-term, operative level of production planning and scheduling being focused on the production at a specific location. For an available set of product variants or orders to be produced on mixed-model assembly lines, a production sequence for a certain planning horizon (day, shift) needs to be determined [2]. Sequencing generally concentrates on two basic objectives: the minimization of work overload and the levelling of material demand in terms of usage of parts [10]. On the one hand, mixed-model sequencing seeks to explicitly minimize sequence-dependent work overload by means of detailed scheduling considering the workload of each product variant at each station and car sequencing only implicitly minimizes sequence-dependent work overload by controlling the succession of product options causing a high workload [2]. On the other hand, level scheduling aims at levelling material demands by distributing them evenly over time, facilitating just-in-time supply [2]. As the complexity for levelling all the different parts of a certain product variant, being referred to as part-oriented level scheduling, might be considerably high [2], product options can be levelled instead [11] as they determine material requirements. This can be referred to as option-oriented level scheduling.

The optimization model presented in this paper combines mixed-model sequencing for the detailed consideration of workload to follow the objective of production, which is to minimize work overload, as well as level scheduling to also consider the objective of procurement, which is the levelling of material demand, within production planning and scheduling. Therefore, literature addressing mixed-model sequencing and level scheduling is subsequently explained in more detail. However, none of the approaches considers sequencing on multiple lines with workers flexibly being assigned to stations across lines as they all deal with the sequencing of one single line.

In order to compare sequencing approaches, the classification schemes for mixed-model sequencing and level scheduling proposed by Boysen et al. [2] are applied. The scheme for mixed-model sequencing categorizes respective approaches by means of parameters related to (1) characteristics of stations, (2) characteristics of the line, and (3) objectives [2]. One important design feature frequently addressed for mixed-model sequencing in the literature is the consideration of open stations (see e.g. [12,13,14,15]). This means that, in contrast to closed stations, one worker does not necessarily have to fulfill his task within the fixed station boundaries, but may rather exceed the station boundaries to a certain extent [16].

Another important feature is the consideration of concurrent work [2]. It refers to the fact that workers may start their tasks although the work of previous stations has not been finished [2]. Here, a necessary prerequisite is the allowance of open station boundaries [2]. Unlike the consideration of open stations, concurrent work has rarely been taken into account. Macaskill [17], for example, integrates concurrent work in his mathematical model for a flow-line, being investigated by means of simulation experiments for a small, self-contained assembly of vehicle front seats [17]. Moreover, Felbecker [18] considers concurrent work in his multi-product line sequencing approach [18].

Regarding the interval of launching product variants on the line, fixed rate and variable rate launching can be distinguished [2]. While most approaches suggest fixed rate launching, operating the line more flexibly and dynamically by means of variable rate launching is addressed by a few authors only (see e.g. [2, 12, 19, 20]).

With respect to the objectives it can be distinguished whether total work overload [21], idle time [18], line length [12], throughput time [12], duration of line stoppages [22], maximum displacement of workers from their reference point [23], or a combination of these criteria shall be minimized [2]. Only some of the authors (see e.g. [14, 16, 24]) consider multiple criteria and therefore monetarize the criteria to simultaneously minimize the respective costs.

Boysen et al. [2] categorize level scheduling approaches using parameters related to the categories “objectives” and “operational characteristics” [2]. The criteria which are especially important for the approach presented in this paper are the weighting function, the number of workstations, and the indicator defining whether input, output, or workload shall be levelled. Approaches that focus on these three criteria are presented by Xiaobo and Zhou [25], Xiaobo et al. [26], and Duplaga and Bragg [27]. Moreover, Sumichrast and Russell [28] as well as Cakir and Inman [29] level parts supply and use a weighting function for absolute deviations [28, 29].

The most relevant approaches in literature combining mixed-model sequencing and level scheduling are briefly outlined in the following. Celano et al. [30] developed a multi-objective genetic algorithm aiming at sequencing a mixed-model assembly line, focusing on the minimization of the duration of line stoppages as well as on a levelled material usage [30]. The genetic algorithm was tested by means of several numerical examples and good results could be obtained [30]. Since the numerical examples are merely fictitious, however, no reliable statement about the applicability in real-world use cases can be made [30]. Ponnambalam et al. [31] investigate the performance of genetic algorithms for sequencing while focusing on levelling part-usage, minimizing total work overload to be handled by utility workers as well as setup costs [31]. Kotani et al. [32] propose a new formulation of the sequencing problem for the Toyota production system aiming at the minimization of the line stoppage time as well as at ensuring a constant part usage rate [32]. While approaches such as those proposed by Bard et al. [10], Scholl [33] as well as Yano and Rachamadugu [34] use a weighted sum of these two objectives, Kotani et al. [32] consider the constant rate of part usage as a constraint in the optimization model [32]. With respect to the solution methodology, they suggest a two-phase approximation algorithm [32].

Summarizing the state of the art, it can be observed that there is a large variety of different sequencing approaches. Most of these approaches, however, do not consider multiple, monetarized criteria in the objective function that could enable a realistic weighting of the criteria in industrial applications. To the best knowledge of the authors, there is no approach that particularly combines mixed-model sequencing and level scheduling by monetarizing both criteria.

3 Optimization model for local order scheduling

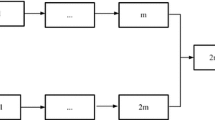
In this section, an optimization model for local order scheduling, assigning orders to lines and to cycles, is introduced. An assignment to a cycle of a line means that the assembly of an order is started with the beginning of that cycle at the first station. In the upcoming cycles, the order passes through the following stations of the line. All cycles of a line that contribute to the production of one order at the several stations is referred to as one slot. This is illustrated in Fig. 2. The orders of one period are the orders that are delivered within that period. Because the assembly of orders may not be finished in the same period as it is starting, all sub-periods from the beginning of the first cycle of the first slot of the period up to the completion of the first cycle of the last slot of the period are considered for the local order scheduling of one period. Hence, orders of the previous period are taken into account because they also cause workload and require material in some of the considered sub-periods. Variable rate launching is accounted for by respecting flexible but fixed cycle lengths and cycle starts according to Fig. 2.

Fig. 2
figure 2

Orders of one period (at the top) and orders of the previous period (at the bottom)

Full size image

In the objective function of the optimization model multiple criteria are monetarized and minimized using \(x\) as a set of binary decision variables \({x_{iu{v_u}}} \in \left\{ {0,~1} \right\}\) which describe the assignments of orders \(i \in \left\{ {1, \ldots ,I} \right\}\) to lines \(u \in \left\{ {1, \ldots ,U} \right\}~\) and cycles \({v_u} \in \left\{ {1, \ldots ,{V_u}} \right\}\) of the lines:

$$\hbox{min} \ f\left( x \right)={C^{OR}}\left( x \right)+{C^{OS}}\left( x \right)+{C^{WLD}}\left( x \right)+{C^{LS}}\left( x \right)$$
(1)

Herewith, order-related costs, order spacing costs, workload deviation costs, and level scheduling costs are considered for local order scheduling. The main objectives are the same as for the medium-term assignment of orders to production locations and periods [35], but they are respected on a more detailed level for the short-term scheduling of the orders at one location for one period. Moreover, in the objective function only aspects that can be influenced by the assignment of orders to lines and cycles are considered. Thus, e.g., costs for the employment of workers according to the planned capacities are not included. All notations used are given in Table 1.

Table 1 Notations
Full size table

Order-related costs cover inventory costs and penalty costs regarding late deliveries:

$${C^{OR}}\left( x \right)=\mathop \sum \limits_{{i \in \{ 1, \ldots ,I\} }} \mathop \sum \limits_{{u \in \{ 1, \ldots ,U\} }} \mathop \sum \limits_{{{v_u} \in \{ 1, \ldots ,{V_u}\} }} (C_{{iu{v_u}}}^{{inventory}}+C_{{iu{v_u}}}^{{penalty}}) \times {x_{iu{v_u}}}$$
(2)

Inventory costs occur if orders are completed before their earliest delivery time. So they cause costs for tied capital based on the required material depending on the basic product models and the additional product options of the orders as well as an interest rate. Moreover, costs for warehousing depending on the size of the product model have to be taken into account. Thus, inventory costs are:

$$\begin{gathered} C_{{iu{v_u}}}^{{inventory}}={\text{max}}\{ (r~ \times C_{i}^{{material}}+C_{i}^{{warehousing}}) \times (E{D_i} - P{D_{u{v_u}}}),~0\} \hfill \\ \forall i \in \{ 1, \ldots ,I\} ,~\forall u\ominus \{ 1, \ldots ,U\} ,~\forall {v_u} \in \{ 1, \ldots ,{V_u}\} \hfill \\ \end{gathered}$$
(3)

Penalty costs arise if orders are completed later than the latest delivery time:

$$\begin{gathered} C_{{iu{v_u}}}^{{penalty}}={\text{max}}\{ ~C_{i}^{{penalty}} \times (P{D_{u{v_u}}} - L{D_i}),0\} \hfill \\ \forall i \in \{ 1, \ldots ,I\} ,~\forall u \in \{ 1, \ldots ,U\} ,~\forall {v_u} \in \{ 1, \ldots ,{V_u}\} \hfill \\ \end{gathered}$$
(4)

Order spacing costs accrue in the case of violations against order spacing rules. Order spacing rules are customer-specific and reflect that a certain amount of time may be required between two consecutive deliveries for the same customer. Consequently, if two orders for the same customer violate the respective spacing rule according to their assignments to lines and cycles, one of the orders needs to be stored in order to respect the rule causing inventory costs and possibly also penalty costs for late delivery that apply additionally to the inventory costs and penalty costs introduced above.

The workload deviation costs take the workload deviations \({\Delta _t}\left( x \right)\), which are deviations of the workload demand of each sub-period depending on the assignment, as well as the basic product models and the additional product options of the orders, and the capacity of each sub-period \({K_t}\) at the considered location in the considered period into account:

$${\Delta _t}\left( x \right)={w_t}\left( x \right) - {K_t}$$
(5)
$${C^{WLD}}\left( x \right)=\mathop \sum \limits_{{t \in \{ 1, \ldots ,T\} }} C_{t}^{{WLD}}\left( {{\Delta _t}\left( x \right)} \right)$$
(6)

Therewith, mixed-model sequencing is applied by minimizing the costs related to work overload. Therefore, a piecewise linear cost function which depicts the costs for handling work overload is defined:

$$\begin{gathered} C_{t}^{{WLD}}\left( {{\Delta _t}\left( x \right)} \right)=\left\{ {\begin{array}{*{20}{c}} {0,~~{\Delta _t}\left( x \right) \leq {\beta _t}} \\ {{P^{regular}} \times ({\Delta _t}\left( x \right) - {\beta _t}),~~{\beta _t}<{\Delta _t}\left( x \right) \leq K_{t}^{{max}}} \\ {{P^{regular}} \times (K_{t}^{{max}} - {\beta _t})+{P^{irregular}} \times ({\Delta _t}\left( x \right) - K_{t}^{{max}}),~~{\Delta _t}\left( x \right)>K_{t}^{{max}}} \end{array}} \right. \hfill \\ \forall t \in \left\{ {1, \ldots ,T} \right\} \hfill \\ \end{gathered}$$
(7)

If the workload deviation \({\Delta _t}\left( x \right)\) is below \({\beta _t}\) or negative, there will be no additional costs because the workers can handle the workload with no or a little overtime. If the workload deviation \({\Delta _t}\left( x \right)\) exceeds the limit \({\beta _t}\), the workers have to do more overtime which may lead to additional costs with a cost rate for overtime of \({P^{regular}}\). If the limit \(K_{t}^{{max}}\) is exceeded, the work overload cannot be handled by the workers within the respective sub-period anymore. This causes costs with a higher cost rate \({P^{irregular}}\). In the case of open stations having the flexibility to shift work from one station to the subsequent one, respective costs are considered. Line stoppages that would mean a delay of the planned beginning of the cycles are thus not necessary since the work does not have to be completed in the stations as it would be the case for closed stations. However, due to a shift of workload to subsequent stations, additional working time on weekends might be required and delays might be caused so that respective costs can be anticipated for such irregular, undesired actions to handle high work overload. The more concurrent work to prevent such undesired actions might be possible, the lower such costs can be anticipated. The piecewise linear cost function illustrated in Fig. 3 enables to explicitly consider the costs that potentially apply depending on the work overload. By monetarizing the work overload, it is considered in the objective function among the other objectives without requiring a further weighting of them. In such a way, mixed-model sequencing and level scheduling, which will be introduced in the following, are combined in the optimization model for local order scheduling.

Fig. 3
figure 3

Piecewise linear workload deviation cost function

Full size image

The level scheduling costs consider costs regarding the level scheduling of basic product models and additional product options, which both implicate parts to be procured and assembled:

$${C^{LS}}\left( x \right)=C_{m}^{{LS}}\left( x \right)+C_{o}^{{LS}}\left( x \right)$$
(8)

As suggested by Boysen et al. [2], the even distribution of material over time induced by the sequence of the orders should be contemplated in the context of discrete time intervals of the just-in-time deliveries. This is considered by modelling levelling periods which reflect such time intervals within a production period. As each part to be levelled is assembled at a designated station of a line and should be available at the station when the respective cycle begins, a model or option belongs to a certain levelling period if the cycle for assembly of the respective part is started within that levelling period. Thus, for each levelling period a proportionate share of the amount of a model or option is calculated based on the total amount of the respective model or option within the period. Therefore, the share of the respective amount of cycles beginning within the levelling period with respect to the respective amount of cycles beginning in the overall period is taken into account. The formula for calculating the deviation from the proportionate distribution is given in the following for basic product models:

$$\begin{gathered} \Delta _{{m\tau }}^{{LS}}\left( x \right) \hfill \\ =\left( {\mathop \sum \limits_{{i \in \{ 1, \ldots ,~I|{m_i}=m\} }} \mathop \sum \limits_{{u \in \left\{ {1, \ldots ,~U} \right\}}} \mathop \sum \limits_{{{v_u} \in \{ 1, \ldots ,{V_u}|{\tau _{{v_u}}}=\tau \} }} {x_{iu{v_u}}}} \right) \hfill \\ - \left( {\frac{{\mathop \sum \nolimits_{{u \in \{ 1, \ldots ,U|u \in {U_m}\} }} K_{{u\tau }}^{{cycle}}}}{{\mathop \sum \nolimits_{{\tau \in \left\{ {1, \ldots ,{{{\rm T}}}} \right\}}} \mathop \sum \nolimits_{{u \in \{ 1, \ldots ,U|u \in {U_m}\} }} K_{{u\tau }}^{{cycle}}}} \times \mathop \sum \limits_{{i \in \{ 1, \ldots ,~I|{m_i}=m\} }} \mathop \sum \limits_{{u \in \left\{ {1, \ldots ,~U} \right\}}} \mathop \sum \limits_{{{v_u} \in \left\{ {1, \ldots ,{V_u}} \right\}}} {x_{iu{v_u}}}} \right) \hfill \\ \end{gathered}$$
(9)

In the given formula for deviations of basic product models it is assumed that the respective parts are required at the first station meaning that orders from the previous period have passed the first station and thus do not need to be considered. For options which require parts at a station after the first station, the respective cycles and also the orders from the previous period are considered. In case that several options are supplied by the same supplier, the options may be aggregated meaning that the amount of these options is included in total.

Costs for level scheduling of basic product models and of additional product options are calculated by applying piecewise linear costs functions in the same way as for workload deviations but reflecting costs for handling positive deviations from the proportionate distributions.

Constraints of the model ensure that each order is assigned to exactly one cycle and that each cycle beginning at the first station cannot handle more than one order. Furthermore, orders can only be assigned to cycles of lines on which the corresponding product models and options can be produced.

4 Results of the industrial application

The model presented above is validated in the industrial application of the final assembly of the Airbus A320 Family in Hamburg with the basic product models A319, A320, and A321. At the time of local order scheduling, it is defined which orders are produced for which month, i.e. period, of delivery and at which location as well as which product models and which options are chosen by the customers of the orders. For the application of the optimization model, customer orders to be delivered in June 2015 are considered to be assigned to the three mixed-model assembly lines being installed in Hamburg at that time as well as to their cycles. Each line in Hamburg can produce all product models and consists of five stations. After the lines, there are non-takted stations including paint stations. In the assembly lines, each aircraft remains at each of the stations for the exact cycle time (up to two and a half working days) before it is moved to the next station whereas in the non-takted area the time equals the processing time which can differ from aircraft to aircraft, especially at the paint station.

Earliest and latest delivery days as well as customer-specific spacing rules are considered. Options with a major impact on workload are taken into account to calculate the workload of an order based on its product model and its options. Moreover, paint days are considered as options regarding the paint stations being the bottleneck of the non-takted stations. Hence, level scheduling is applied to the aggregate number of paint days in order to proportionally distribute the paint workload among levelling periods for supporting the minimization of the throughput time as well as the number and duration of delays. Furthermore, an option indicating whether an order is a head of version (HoV), which is the first aircraft of a newly designed aircraft configuration, is included. Special engineering teams with limited capacity are required for a HoV so that a level scheduling of this option is desirable. Level scheduling is also applied to the product models A319 and A321 in order to proportionally distribute the respective fuselages inducing different workload at the internal plant supplying them. The product model A320 is implicitly proportionally distributed by considering the other two product models explicitly.

The model is solved with IBM ILOG CPLEX 12.7 with a time limit of 15 min and an optimality tolerance of 0.0001%. In the following, the model results are compared to the real planning of Airbus. Orders of the previous delivery month, which is May 2015, are considered as previous orders.

The overall costs of the objective function according to the cost terms considered for local order scheduling as introduced in Sect. 3 are illustrated in Fig. 4, comparing the real planning and the model solution. The considered overall costs of the model solution are 97% lower than for the real planning. Only order-related costs and workload deviation costs cannot be fully avoided by the model application. For the real planning and the model solution, no level scheduling costs for HoV occur and order-related costs only consist of penalty costs for late deliveries.

Fig. 4
figure 4

Overall cost structure of real planning and model solution

Full size image

In order to give a more detailed insight into the workload deviation costs, the daily workload deviations are illustrated in Fig. 5. Therefore, all days from the day of the start of assembly of the first order to be delivered in June 2015 to the day when the last order of the month is completed on the first station are considered as described in terms of the sub-periods in Sect. 3. It is demonstrated that the flexibility limit for flexibility at no charge is exceeded for both solutions, but the workload deviations are lower for the model solution and the flexibility limit for flexibility causing costs is exceeded on 6 days for the real planning. This explains the higher workload deviation costs of the real planning.

Fig. 5
figure 5

Workload deviations

Full size image

The results of level scheduling of paint, HoV, A319, and A321 are presented in detail in the following. For all of them weeks are chosen as levelling periods regarding the same days as considered for the workload deviations. The number of paint days deviating from the proportionate distribution are illustrated in Fig. 6 for each week. Higher costs would apply above the second boundary than above the first boundary, because the regular paint stations in Hamburg would not be able to handle the paint workload anymore and external paint would be necessary. The second boundary is neither exceeded for the real planning nor for the model solution, but for the real planning the first boundary is exceeded in week 4. This results in respective level scheduling costs for paint anticipating the impact caused by the paint overload.

Fig. 6
figure 6

Deviations from the proportionate distribution of number of paint days for each week

Full size image

For HoV, the costs for exceeding the second boundary are set extremely high so that it will not be exceeded by the model solution. Figure 7 shows that neither of the two boundaries is exceeded by the real planning or the model solution so that no level scheduling costs for HoV apply in both cases. This is not surprising as only one HoV has to be assigned for the considered delivery month.

Fig. 7
figure 7

Deviations from the proportionate distribution of number of HoV for each week

Full size image

For level scheduling of A319 and A321, only one boundary is applied. Figure 8 illustrates that the deviations of the number of A319 are exactly the same for the real planning and the model solution, both avoiding respective level scheduling costs. The deviations of the number of A321 exceed the boundary in week 4 for the real planning as illustrated in Fig. 9, whereas the boundary is not exceeded for the model solution. Thus, level scheduling costs for A321 apply for the real planning but are avoided by the model solution.

Fig. 8
figure 8

Deviations from the proportionate distribution of number of A319 for each week

Full size image
Fig. 9
figure 9

Deviations from the proportionate distribution of number of A321 for each week

Full size image

5 Conclusion

In this paper, an optimization model for local order scheduling assigning orders to mixed-model assembly lines and its cycles is presented. The approach considers multiple criteria in the objective function by monetarizing them. Mixed-model sequencing and level scheduling are combined as criteria for production and procurement and are integrated in the model by applying piecewise linear cost functions.

The optimization model is validated in the industrial application of the final assembly of Airbus A320 Family in Hamburg. As workers can flexibly fulfill tasks across stations of several lines, the simultaneous consideration of the assembly lines is of major importance. The model results demonstrate the costs savings in terms of order-related costs, order spacing costs, workload deviation costs, and level scheduling costs of the model solution compared to the real planning of Airbus.

Future research could further investigate the criticality and impact of a shift of individual tasks from one station to the subsequent one due to work overload according to local order scheduling, but also due to disturbances arising in the running production. Regarding the latter, there is potential to identify optimal reactions to disturbances making use of the available flexibility of production, suppliers, and supply logistics.