Abstract
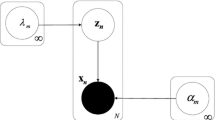
In this article, we propose a novel Bayesian nonparametric clustering algorithm based on a Dirichlet process mixture of Dirichlet distributions which have been shown to be very flexible for modeling proportional data. The idea is to let the number of mixture components increases as new data to cluster arrive in such a manner that the model selection problem (i.e. determination of the number of clusters) can be answered without recourse to classic selection criteria. Thus, the proposed model can be considered as an infinite Dirichlet mixture model. An expectation propagation inference framework is developed to learn this model by obtaining a full posterior distribution on its parameters. Within this learning framework, the model complexity and all the involved parameters are evaluated simultaneously. To show the practical relevance and efficiency of our model, we perform a detailed analysis using extensive simulations based on both synthetic and real data. In particular, real data are generated from three challenging applications namely images categorization, anomaly intrusion detection and videos summarization.










Similar content being viewed by others
Notes
Proportional data are the data that contain two constraints: non-negativity and unit-sum.
All figures with colors can be found in the electronic version of the paper.
Source code of PCA-SIFT: http://www.cs.cmu.edu/~yke/pcasift.
A connection is a sequence of TCP packets starting and ending at some well defined times, between which data flows to and from a source IP address to a target IP address under some well defined protocol.
References
Bishop CM (1999) Variational principal components. In: Proceedings of international conference on artificial neural networks (ICANN), vol. 1, pp 509–514
Blackwell D, MacQueen J (1973) Ferguson distributions via pólya urn schemes. Ann Stat 1(2):353–355
Blei DM, Jordan MI (2005) Variational inference for Dirichlet process mixtures. Bayesian Anal 1:121–144
Bosch A, Zisserman A, Munoz X (2006) Scene classification via pLSA. In: Proceedings of 9th European conference on computer vision (ECCV), pp 517–530
Bouguila N (2007) Spatial color image databases summarization. In: Proceedings of the IEEE international conference on acoustics, speech, and signal processing (ICASSP), Honolulu, pp I-953–I-956
Bouguila N (2012) Infinite Liouville mixture models with application to text and texture categorization. Pattern Recognit Lett 33(2):103–110
Bouguila N, Ziou D (2005a) Mml-based approach for finite dirichlet mixture estimation and selection. In: Perner P, Imiya A (eds) MLDM. Lecture Notes in Computer Science, vol 3587. Springer, Berlin, pp 42–51
Bouguila N, Ziou D (2005b) On fitting finite dirichlet mixture using ecm and mml. In: Singh S, Singh M, Apté C, Perner P (eds) ICAPR (1). Lecture Notes in Computer Science, vol 3686. Springer, Berlin, pp 172–182
Bouguila N, Ziou D (2005c) Using unsupervised learning of a finite Dirichlet mixture model to improve pattern recognition applications. Pattern Recognit Lett 26(12):1916–1925
Bouguila N, Ziou D (2006a) Online clustering via finite mixtures of dirichlet and minimum message length. Eng Appl Artif Intell 19(4):371–379
Bouguila N, Ziou D (2006b) Unsupervised selection of a finite Dirichlet mixture model: an mml-based approach. IEEE Trans Knowl Data Eng 18(8):993–1009
Bouguila N, Ziou D (2008) A Dirichlet process mixture of Dirichlet distributions for classification and prediction. In: Proceedings of the IEEE workshop on machine learning for signal processing (MLSP), pp 297–302
Bouguila N, Ziou D (2010) A Dirichlet process mixture of generalized Dirichlet distributions for proportional data modeling. IEEE Trans Neural Netw 21(1):107–122
Bouguila N, Wang JH, Hamza AB (2010) Software modules categorization through likelihood and Bayesian analysis of finite Dirichlet mixtures. J Appl Stat 37(2):235–252
Chang S, Dasgupta N, Carin L (2005) A Bayesian approach to unsupervised feature selection and density estimation using expectation propagation. In: Proceedings of the IEEE computer society conference on computer vision and pattern recognition (CVPR), pp 1043–1050
Csurka G, Dance CR, Fan L, Willamowski J, Bray C (2004) Visual categorization with bags of keypoints. In: Workshop on statistical learning in computer vision, 8th European conference on computer vision (ECCV), pp 1–22
Draper BA, Hanson AR, Riseman EM (1996) Knowledge-directed vision: control, learning, and integration. Proc IEEE 84:1625–1637
Drummond T, Caelli T (2000) Learning task-specific object recognition and scene understanding. Comput Vis Image Underst 80:315–348
Elkan C (2003) Using the triangle inequality to accelerate k-means. In: Proceedings of the international conference on machine learning (ICML), pp 147–153
Fan W, Bouguila N, Ziou D (2012) Variational learning for finite dirichlet mixture models and applications. IEEE Trans Neural Netw Learn Syst 23(5):762–774
Ferguson TS (1983) Bayesian density estimation by mixtures of normal distributions. Recent Adv Stat 24:287–302
Fraley C, Raftery AE (2003) Enhanced model-based clustering, density estimation, and discriminant analysis software: MCLUST. J Classif 20(2):263–286
Gibson D, Campbell N, Thomas B (2002) Visual abstraction of wildlife footage using Gaussian mixture models and the minimum description length criterion. In: Proceedings of international conference on pattern recognition (ICPR), vol. 2, pp 814–817
Gong Y, Liu X (2000) Video summarization using singular value decomposition. In: Proceedings of IEEE conference on computer vision and pattern recognition (CVPR), vol. 2, pp 174–180
Hansen KM, Tukey JW (1992) Tuning a major part of a clustering algorithm. Int Stat Rev 60(1):21–43
Hofmann T (2001) Unsupervised learning by probabilistic latent semantic analysis. Mach Learn 42(1/2):177–196
Hu W, Hu W, Maybank S (2008) Adaboost-based algorithm for network intrusion detection. IEEE Trans Syst Man Cybern Part B Cybern 38(2):577–583
Ishwaran H, James LF (2001) Gibbs sampling methods for stick-breaking priors. J Am Stat Assoc 96: 161–173
Ke Y, Sukthankar R (2004) PCA-SIFT: a more distinctive representation for local image descriptors. In: Proceedings of the IEEE computer society conference on computer vision and pattern recognition (CVPR), pp 506–513
Khan L, Awad M, Thuraisingham B (2007) A new intrusion detection system using support vector machines and hierarchical clustering. VLDB J 16:507–521
Korwar RM, Hollander M (1973) Contributions to the theory of Dirichlet processes. Ann Probab 1:705–711
Lin TI, Lee JC, Ho HJ (2006) On fast supervised learning for normal mixture models with missing information. Pattern Recognit Lett 39:1177–1187
Lippmann R, Haines JW, Fried DJ, Korba J, Das K (2000) Analysis and results of the 1999 DARPA off-line intrusion detection evaluation. In: Proceedings of the third international workshop on recent advances in intrusion detection. Springer, Berlin, pp 162–182
Liu T, Zhang HJ, Qi F (2003) A novel video key-frame-extraction algorithm based on perceived motion energy model. IEEE Trans Circuits Syst Video Technol 13(10):1006–1013
Liu Y, Chen K, Liao X, Zhang W (2004) A genetic clustering method for intrusion detection. Pattern Recognit 37(5):927–942
Ma Z, Leijon A (2010) Expectation propagation for estimating the parameters of the beta distribution. In: Proceedings of the IEEE international conference on acoustics, speech, and signal processing (ICASSP), pp 2082–2085
Maybeck PS (1982) Stochastic models, estimation and control. Academic Press, London
McHugh J, Christie A, Allen J (2000) Defending yourself: the role of intrusion detection systems. IEEE Softw 17(5):42–51
McLachlan G, Peel D (2000) Finite mixture models. Wiley, New York
Mikolajczyk K, Schmid C (2005) A performance evaluation of local descriptors. IEEE Trans Pattern Anal Mach Intell 27(10):1615–1630
Minka T (2001) Expectation propagation for approximate Bayesian inference. In: Proceedings of the conference on uncertainty in artificial intelligence (UAI), pp 362–369
Minka T, Ghahramani Z (2003) Expectation propagation for infinite mixtures. In: NIPS’03 workshop on nonparametric Bayesian methods and infinite models
Minka T, Lafferty J (2002) Expectation-propagation for the generative aspect model. In: Proceedings of the conference on uncertainty in artificial intelligence (UAI), pp 352–359
Neal RM (2000) Markov chain sampling methods for Dirichlet process mixture models. J Comput Graph Stat 9(2):249–265
Ngo CW, Ma YF, Zhang HJ (2003) Automatic video summarization by graph modeling. In: Proceedings of IEEE international conference on computer vision (ICCV), vol. 1, pp 104–109
Nilsback ME, Zisserman A (2006) A visual vocabulary for flower classification. In: Proceedings of the IEEE computer society conference on computer vision and pattern recognition (CVPR), vol 2, pp 1447–1454
Northcutt S, Novak J (2002) Network intrusion detection: an analyst’s handbook. New Riders Publishing
Pollard D (1982) A central limit theorem for k-means clustering. Ann Probab 10(4):919–926
Rasiwasia N, Vasconcelos N (2008) Scene classification with low-dimensional semantic spaces and weak supervision. In: Proceedings of IEEE conference on computer vision and pattern recognition (CVPR), pp 1–8
Rasmussen CE (2000) The infinite Gaussian mixture model. In: Proceedings of advances in neural information processing systems (NIPS). MIT Press, Cambridge, pp 554–560
Robert C, Casella G (1999) Monte Carlo statistical methods. Springer, Berlin
Sahouria E, Zakhor A (1999) Content analysis of video using principal components. IEEE Trans Circuits Syst Video Technol 9(8):1290–1298
Sethuraman J (1994) A constructive definition of Dirichlet priors. Stat Sin 4:639–650
Shen X, Ye J (2002) Adaptive model selection. J Am Stat Assoc 97(457):210–221
Singh S, Haddon J, Markou M (2001) Nearest-neighbour classifiers in natural scene analysis. Pattern Recognit 34:1601–1612
Teh YW, Jordan MI, Beal MJ, Blei DM (2004) Hierarchical Dirichlet processes. J Am Stat Assoc 101: 705–711
Truong BT, Venkatesh S (2007) Video abstraction: a systematic review and classification. ACM Trans Multimed Comput Commun Appl 3(1)
Wong MA, Lane T (1983) A kth nearest neighbour clustering procedure. J R Stat Soc Ser B (Methodological) 45(3):362–368
Ye N, Li X, Chen Q, Erman SM, Xu M (2001) Probabilistic techniques for intrusion detection based on computer audit data. IEEE Trans Syst Man Cybern Part A 31(4):266–274
Author information
Authors and Affiliations
Corresponding author
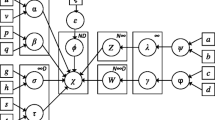
The calculation of \(Z_i\) in Eq. (17)
The calculation of \(Z_i\) in Eq. (17)
The normalized constant \(Z_i\) in Eq. (17) can be calculated as
where \(\bar{\lambda }_j\) is the expected value of \(\lambda _j\). Since the integration involved in Eq. (27) is analytically intractable, we tackle this problem by adopting the Laplace approximation to approximate the integrand with a Gaussian distribution as suggested in Ma and Leijon (2010).
First, we define \(h({\varvec{\alpha }}_j)\) as the integrand in Eq. (27):
Then, the normalized distribution for this integrand which is indeed a product of a Dirichlet distribution and a Gaussian distribution is given by
Our goal for the Laplace method the goal is to find a Gaussian approximation which is centered on the mode of the distribution \(\mathcal{H }({\varvec{\alpha }}_j)\). We may obtain the mode \({\varvec{\alpha }}_j^*\) numerically by setting the first derivative of \(\ln h({\varvec{\alpha }}_j)\) to 0, where \(\ln h({\varvec{\alpha }}_j)\) can be calculated by
Subsequently, we can calculate the first and second derivatives with respect to \({\varvec{\alpha }}_j\) as
and
where \(\varPsi (\cdot )\) is the digamma function. Then, we can approximate \(h({\varvec{\alpha }}_j)\) using the obtained mode as
where the precision matrix \(\widehat{A}_{j}\) is given by
Therefore, the integration of \(h({\varvec{\alpha }}_j)\) can be approximated by using Eq. (33) as
Finally, we can rewrite Eq. (27) as following:
Rights and permissions
About this article
Cite this article
Fan, W., Bouguila, N. Infinite Dirichlet mixture models learning via expectation propagation. Adv Data Anal Classif 7, 465–489 (2013). https://doi.org/10.1007/s11634-013-0152-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11634-013-0152-4
Keywords
- Clustering
- Expectation propagation
- Mixture model
- Dirichlet process
- Images categorization
- Anomaly intrusion detection
- Videos summarization