1 Introduction

Recently, energy harvesting (EH) technologies extend the lifetime of node by collecting ambient energy (solar, vibration, RF, etc.) from environment [1]. The system with EH nodes has been considered to provide extremely cost-effective and fully passive solutions in Internet of Things (IoT) [2], especially in places where conventional power source are not accessible. Though the operation, efficiency and maturity of energy harvesting systems vary with each other, it is indispensability to support long-term node availability in most of real scenarios. Within the operating time, the power supply of EH node should be no less than the power consumption [3]. However, the harvested energy is usually not continuous and sometimes limited due to the intermittent nature of energy sources. Nodes powered by harvested energy need energy storage and power management algorithm to provide uninterrupted power supply [4].

The efficiency of EH technologies is important to enhance node availability, while optimal power control plays a critical role in improving overall performance, especially in EH based wireless communication system [5]. Computing and communication are the main sources of power consumption during node operation. In most cases, the amount of power consumption on communication is bigger than other tasks, such like sensing and computing. Furthermore, it varies large along with the dynamic and unpredictable wireless channel. As a result, the power control problem of a EH based transmitter, which harvests energy from ambient environment and transmits information to remote wireless receivers with harvested energy is a big challenge [6]. The unknown wireless channel and intermittent nature of ambient environmental energy lead to the challenges of ensuring node continuity and maximizing communication throughput [7,8,9].

In practical scenarios, the characteristics of energy arrival rate and the coefficients of wireless channel are hard to be predicted. The learning theoretic approaches improve the power control strategies by identifying the model of energy arrival rate and channel distribution [10, 11]. However, the computing complexity increases sharply with the states number of energy arrival rate and wireless channel, that is unacceptable for low cost transmitter. Online convex optimization (OCO) [12] is a low complexity way to allocate power effectively by projecting power vector into feasible set, which is determined by constraints. However, the energy of battery may be exhausted if the average of harvested energy is below the maximum of feasible set. Then the OCO with stochastic constraints [13] is deeply analyzed, and a new algorithm of guaranteeing node continuity is proposed which required a costly big-capacity battery [14].

In order to remove the constraint of battery capacity, this paper proposes an improved gradient descent algorithm based on OCO for power control problem. The algorithm adjusts the size of feasible set with the State of charge (SOC) (range is [0, 1]). When the SOC is close to 1, the feasible set is almost full size, which indicates maximum power is allocated. Otherwise, the feasible set is a fractional subset of full size set, extra energy would be stored for future when the harvested energy is bigger than maximum of current fractional subset. By rigorous theoretical analysis, the conditions of energy availability guaranty and the lower bounder of average long term throughput are explicitly given. Furthermore, the throughput and battery state are analyzed, the simulations demonstrate the excellent results.

The benefits of proposed algorithm are as follows:

  • Firstly, comparing with learning theoretic approaches [11], the proposed algorithm has low complexity and only relies last historical information.

  • Secondly, the node continuity or energy available guaranty is fulfilled without a complex setting of battery capacity, which is indispensable in algorithm [14].

  • Thirdly, the proposed algorithm is scalable, that is easily to be deployed into the scenarios with one transmitter to many receivers.

The paper is organized as follows. In the second section, related work is discussed. In the third section, system model is given and the problem is formulated. The new algorithm is proposed in the fourth section. In the fifth section, the performances are analyzed including average long-term throughput and energy-availability guaranty. In the sixth section, simulations are shown and discussed to verify the advantageous properties. Finally, conclusion is given.

2 Related Work

The power control or the energy allocation problem in EH based wireless system has been widely researched. Existing research can be divided into two groups based on whether the information (about the energy arrival and channel state) assumed to be available at the transmitter or not.

In offline optimization group [15], EH transmitter has almost ideal knowledge of future energy arrival amount or perfect prediction of channel state. Solar-based EH systems work well under such assumption, where the amount of harvested energy is almost predictable. In [16], the authors model the energy arrival rate and channel distribution as Markov Process with known transition probability, optimize the power control by dynamic programming. The transmitter allocates more energy for transmission when the wireless channel is predicted to be good, less energy in bad channel. When the wireless channel or energy arrival rate is known partially, the power control strategies are implemented based on prediction of unknown part, such like the work on unknown channel distribution, on unknown energy arrival rate. In [17], the authors focus on the situation of hybrid energy storage, and battery imperfections situation is discussed in [18]. In [19], the authors consider a multi-hop EH communication system and cover all possible harvesting profiles including continuous and discrete cases. Overall the solution of offline strategies show the upper bound of optimized throughput.

In online optimization group [8, 10], EH transmitter is assumed to know the statistics of underling EH arrival process or to have causal information about their realizations. In this case, the EH arrival process is model as approximated model, and online methods make decision on energy allocation based on predefined models. The model could be Markov decision process (MDP) or regression model based on statistic data [20]. In practical situation, the future channel state is unknown, and the learning theoretic approach is suitable for unpredictable case [21]. In this case, the transmitter learns the optimal energy allocation policies by performing actions and observing their rewards. Learning-based algorithms manage to gain rewards by minimizing the gap between online rewards and offline optimal throughput. In [11], the authors assumed energy arrival and channel state as individual MDPs, and did not know the transition ratios. After a period of learning, the expected average throughput showed convergence in lower bounder. Recently deep reinforcement learning algorithm is implemented in a point-to-point EH wireless communication system where prior information about distribution on energy arrival process and channel coefficient both are not available [22].

For most EH-based wireless systems, the computational capability of node is limited. As a result, the computational complexity of power control algorithm must be considered. In most existing algorithms, the computational loads of value iteration or policy iteration algorithms increases sharply with the number of quantized states and/or actions [15]. The online convex optimization opens up a brand new way of optimizing energy allocation and long-term throughput. The Online descend gradient (ODG) algorithm, a traditional OCO algorithm, achieved acceptable regret on average long-term throughput in energy unlimited case [12]. However, the energy continuity is ignored. In limited energy capacity case, the authors in [13, 14] proposed an updated ODG version. By subtracting a vector, proposed algorithm help restrict total allocated energy. Related analysis showed the performance lower bounder based on assumption of huge battery capacity.

3 System Model

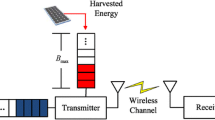
In this paper, a point-to-point EH communication system is considered. The general configuration is similar as [14]. There are n sub-channels between the transmitter and receiver. In the beginning of time slot t, the EH transmitter allocates energy with vector \(p[t] = [p_1[t], p_2[t],\ldots , p_i[t],\ldots ,p_n[t]]\), where \(p_i[t]\) is the energy allocated for sub-channel i in time slot t. Maximal transmission power of each time slot (\(P^{max}\)) is defined. The Feasible set (\({\mathbb {P}}\)) of energy allocation is defined as (1).

$$\begin{aligned} {\mathbb {P}}=\left\{ p\in {\mathbb {R}}^n:\sum _{i=1}^{n}p_i\le P^{max}\right\} . \end{aligned}$$
(1)

where \(p_i\ge 0, \forall i\in \{1,2,\ldots ,n\}\).

Battery capacity (\(E^{max}\)) is defined, and the harvested energy in time slot t is e[t], which is known only at the end of time slot t. Assume available energy in the beginning of time slot t is E[t]. The dynamics of E[t] is described in the following Eq. (2).

$$\begin{aligned} E[t+1]=E[t]+e[t]-P[t]. \end{aligned}$$
(2)

where \(P[t]=\sum _{i=1}^{n}p_i[t]\) and \(E^{max}\ge E[t+1]\ge 0\).

The states of all sub-channels in time slot t are displayed as a vector \(s[t]=[s_1[t], s_2[t],\ldots ,s_n[t]]\), which contains n sub-channels. The corresponding channel capacity of sub-channel i is \(log(1+p_i[t]s_i[t])\) when assigning \(p_i[t]\) energy into channel state \(s_i[t]\).

Fig. 1
figure 1

Basic system model

Full size image

The system model is shown in Fig. 1, where EH transmitter chooses \(p[t+1]\) at the beginning of time slot \(t+1\). We define the reward \(U_t(p[t];s[t])]\) as the sum throughput of all n sub-channels in (3).

$$\begin{aligned} U_t(p[t];s[t])=\sum _{i=1}^{n}\log (1+p_i[t]s_i[t]). \end{aligned}$$
(3)

Throughput with power p at channel s \((U_{t}(p;s))\) is defined, ant it is a non-negative, non-decreasing, and concave utility function. The \(U_t(p;s)\) is obtained at the end of time slot t by calculating (3), while power decision p[t] is decided at the beginning of time slot, where channel state and energy arrival of previous time slot is known, as shown in Fig. 1. So the objective of power control is to find a policy \(\pi\), a sequence of \(p[t], t=1,2,\ldots T\), so that the transmitter can send out as more information as possible by all sub-channels in T time slots. The mathematical description is as follow:

$$\begin{aligned} \max J_{\pi }=\frac{1}{T}\sum _{t=1}^{T}U_t(p;s), \end{aligned}$$
(4)

s.t (1) and (2).

4 Proposed Algorithm

In traditional OCO, the allocated power of next time slot \(P[t+1]\) is the projection in fixed feasible set of power vector, which is obtained by ODG method. The feasible set is restricted by \(E^{max}\). As a convex function, the allocated power \(P[t+1]\) would be equal to \(E^{max}\) without any restriction, for which a sketch in two-dimensional space is shown in Fig. 2a. In energy limited case, the energy availability conditions shown in (5) must be satisfied, that is energy allocation should be no more than available energy.

$$\begin{aligned} E[t+1]\ge P[t+1], \quad \forall t\in {0,1,2,\ldots T}. \end{aligned}$$
(5)

In [14], the authors subtract an additional vector from the power vector, so that the new power vector is moved into the inner of feasible set, and a sketch is shown in Fig. 2b. The modification ensures (5) with the buff provided by a big capacity battery. Inspired by fractional allocation policy in [15], this paper adjusts the feasible set size to ensure (5). The new algorithm obtains SOC (range is [0, 1]) at the beginning of time slot \(t+1\), and restricts feasible set of power control via SOC. The power control strategy is handled under the new feasible set. A sketch for the idea of proposed algorithm is shown in Fig. 2c.

Fig. 2
figure 2

Power control with OCO algorithms

Full size image

The description of the algorithm is shown as follows.

Algorithm:

Setup of the initial time \(t=1\):

\(p[1]=[0,0,\ldots 0]^T\) are the initial power of the channels, \(E[1]=E_{ini}\) is the initial energy.

Procedures:

At the end of each time slot \(t\in \{1,2,\ldots T\}\), do the follows:

Step 1: obtain current SOC \(q[t+1]\)

$$q[t + 1] = E[t + 1]/E^{{max}}$$
(6)

Step 2: Restrict the maximum of transmission power.

$$\begin{aligned} P_{q}^{{max}} = q[t + 1]P^{{max}} \hfill \\ {\mathbb{P}}_{q} = \left\{ {p \in \mathbb{R}^{n} :\sum\limits_{{i = 1}}^{n} {p_{i} } \le P_{q}^{{max}} ,} \right\} \hfill \\ \end{aligned}$$
(7)

where \(p_i\ge 0, \forall i\in {1,2,\ldots ,n}\)

Step 3: power control

$$\begin{aligned} p[t+1]=Proj_{{\mathbb {P}}_q}\{p[t]+q[t+1]\nabla _pU_t(p;s)\} \end{aligned}$$
(8)

where \(Proj_{{\mathbb {P}}_q}\{\cdot \}\) represents the projection onto feasible set \({\mathbb {P}}_q\) and \(\nabla _pU_t(p;s)\) represents a gradient of function \(\nabla _pU_t(p;s)\) at point \(p=p[t]\).

As shown in Fig. 1 and the algorithm description, the SOC value (\(0\le q[t+1]\le 1\)) is available when deciding energy allocation \(p[t+1]\), because SOC relies on \(E[t+1]\) only. In the step 2, the feasible set of power control is restricted by SOC, which is dynamic along with harvested energy and allocated energy. In step 3, projection is done in the restricted feasible set.

5 Algorithm Analysis

When deploying OCO into energy allocation problem in EH based wireless system, the energy availability guarantee should be fulfilled as (5). Then the regret of actions should be analysed in order to provide the lower bounder of performance. In the following part, the power control policy of proposed algorithm is analysed in above two aspects.

5.1 Energy Availability Guaranty

In order to implement the power control decision in proposed algorithm, the SOC in time slot \(t+1\) must satisfy following energy availability constraint (5).

Theorem 1

(Energy guaranty) If \(P^{max}\le E^{max}\) , then the energy availability is guaranteed.

Proof

Based on the definition of \(Proj\{\cdot \}\) and algorithm design, we obtain

$$\begin{aligned}P[t+1]\le \frac{E[t+1]}{E^{max}}P^{max}=\frac{P^{max}}{E^{max}}E[t+1]\end{aligned}$$

If \(P^{max}\le E^{max}\), then

$$\begin{aligned}P[t+1]\le \frac{P^{max}}{E^{max}}E[t+1]\le E[t+1].\end{aligned}$$

\(\square\)

5.2 Lower Bound for Long-Term Average Expected Throughput

Upper bound on the diameter of \({\mathbb {P}} (D)\) is defined, that is, \(\forall x, y\in {\mathbb {P}}, \Vert x-y\Vert \le D\). Upper bound of the gradient of \(U_{t}(p; s) (G)\) is defined, that is, \(\Vert \nabla _p U_t(p;s)\Vert \le G, \forall p\in {\mathbb {P}}, t\in \{1,2,\ldots T\}\). Then we give the main result of this paper.

Theorem 2

(Main Result) If the long term average throughput is defined as (4), then under proposed algorithm, when \(T\rightarrow \infty\), the lower bounder of average long term throughput can be given by

$$\begin{aligned} \lim _{T\rightarrow \infty }\frac{1}{T}\sum _{t=1}^{T}U_t(p;s)\ge & \, \lim _{T\rightarrow \infty }\frac{1}{T}\sum _{t=1}^{T}U_t(p^*;s)\nonumber \\& \,(GD+\frac{G^2}{2}), \end{aligned}$$
(9)

where \(p^*=\arg \max _{p\in {\mathbb {P}}}\sum _{t=1}^{T}U_t(p;s)\) in energy unlimited situation.

Before proving the Theorem 2, we need to introduce the following three lemmas first.

Lemma 1

Let \(p_z=Proj_{{\mathbb {P}}}\{p\}\), and \(p_y=Proj_{{\mathbb {P}}_q}\{p\}\), where \(q\in [0,1]\), Then for any \(p\in R^n\), \(\Vert p_z-p_y\Vert \le (1-q)D\).

Proof

  1. 1.

    If \(p\notin {\mathbb {P}}\), then \(\Vert p_z-p_y\Vert \le (1-q)D\).

  2. 2.

    If \(p\in {\mathbb {P}}\), but \(p\notin {\mathbb {P}}_q\), then \(\Vert p_z-p_y\Vert \le (1-q)D\).

  3. 3.

    If \(p\in {\mathbb {P}}_q\), then \(\Vert p_z-p_y\Vert =0\).

\(\square\)

Lemma 2

Based on proposed algorithm description, \(q[t+1]\) follows the below inequality constraint.

$$\begin{aligned} q[t+1]\ge \left( 1-\frac{P^{max}}{E^{max}}\right) q[t]. \end{aligned}$$

Proof

Based on projection definition, we obtain

$$\begin{aligned} P[t]=\sum _{i=1}^{n}p_i[t]\le P^{max}q[t]=P^{max}\frac{E[t]}{E^{max}}. \end{aligned}$$

Recall

$$\begin{aligned} E[t+1] = E[t]+e[t]-P[t]. \end{aligned}$$

Then

$$\begin{aligned} E[t+1]\ge & \, E[t]+e[t]-P^{max}\frac{E[t]}{E^{max}} \\ ~\ge & \, \left( 1-\frac{P^{max}}{E^{max}}E[t]\right) \end{aligned}$$

Therefore,

$$\begin{aligned} q[t+1]\ge \left( 1-\frac{P^{max}}{E^{max}}\right) q[t]. \end{aligned}$$

\(\square\)

Lemma 3

[12] Let \(c_1,c_2,\ldots c_T: {\mathbb {P}} \rightarrow {\mathbb {R}}\) be an arbitrary sequence of convex differentiable functions. Let \(p_1, \ldots , p_T\in {\mathbb {P}}\) be defined by \(p_1=0\) and \(p_{t+1} =Proj_{{\mathbb {P}}}\{p_t+\eta \nabla c_t(p_t)\}\), then for \(G=\max \Vert \nabla c_t(p_t)\Vert\),

$$\begin{aligned} \max _{p\in {\mathbb {P}}}\sum _{t=1}^{T}c_t(p)-\sum _{t=1}^{T}c_t(p_t)\le \frac{D^2}{\eta }+T\eta \frac{G^2}{2}. \end{aligned}$$

Below we give the proof of our main result.

Proof of Theorem 2

Let energy vector p[t] is the output of the proposed algorithm, based on Lemma 1, we can get

$$\begin{aligned} \Vert p_z-p\Vert \le (1-q)D. \end{aligned}$$

Then for all \(p, p_z\in {\mathbb {P}}_q\) and at time slot t, we have

$$\begin{aligned} |U_t(p_z;s)-U_t(p;s)|\le & \, G\Vert p_z-p\Vert \nonumber \\ ~\le & \, GD(1-q[t]). \end{aligned}$$
(10)

Sum (10) from \(t=1\) to \(t=T\), and consider Lemma 2, we obtain

$$\begin{aligned} \sum _{t=1}^{T}U_t(p;s)\ge & \, \sum _{t=1}^{T}U_t(p_z;s)-GDT+ GD\sum _{t=1}^{T}q[t] \\= & \, \sum _{t=1}^{T}U_t(p_z;s)-GDT\\&+GDq[1]\sum _{1}^{T}\left( 1-\frac{P^{max}}{E^{max}}\right) ^{T-t}\\\ge & \, \sum _{t=1}^{T}U_t(p_z;s)-GDT+ GD\frac{E[1]}{P^{max}} \end{aligned}$$

The \(p_z\) and p are the output of Zinkevich’s policy [12] and proposed policy, respectively. Considering Lemma 3, we get

$$\begin{aligned} \sum _{t=1}^{T}U_t(p^*;s)-\sum _{t=1}^{T}U_t(p_z;s)\le \frac{D^2}{2q[t+1]}+\frac{G^2}{2}\sum _{t=1}^{T}q[t]. \end{aligned}$$
(11)

Combine (11) and (12), then we get

$$\begin{aligned} \sum _{t=1}^{T}U_t(p;s)\ge & \, \sum _{t=1}^{T}U_t(p^*;s)+GD\frac{E[1]}{P^{max}}-\frac{D^2}{2q[t+1]}\\&-GDT-\frac{G^2}{2}\sum _{t=0}^{T}q[t]\\\ge & \, \sum _{t=1}^{T}U_t(p^*;s)+GD\frac{E[1]}{P^{max}}-\frac{D^2}{2q[t+1]}\\&-(GD+\frac{G^2}{2})T \end{aligned}$$

From Theorem 1, one gets \(E[t]\ge P[t]\). Then \(\frac{1}{q[t+1]}\) is bounded. Finally,

$$\begin{aligned} \lim _{T\rightarrow \infty }\frac{1}{T}U_t(p;s)\ge \lim _{T\rightarrow \infty }\frac{1}{T}U_t(p^*;s)-(GD+\frac{G^2}{2}) \end{aligned}$$

\(\square\)

6 Simulations

In this section, the properties of proposed power control algorithm on EH based wireless system are analyzed. In EH transmitter, there are two sub-channels, which are two independent Rayleigh fading channels. The maximum transmitting power is set to 10. The energy harvesting rate follows uniform distribution within [0, \(E^{max}\)]. Firstly, the energy availability guarantee of proposed algorithm is demonstrated. Then the comparison on average long-term throughput between proposed algorithm and algorithm in [14] are shown under different setups. The simulation settings are listed in Table 1.

Table 1 Simulation parameters
Full size table

Energy Availability Guarantee Figure 3 shows the trajectories of \(E[t]-P[t]\) with different \(E^{max}\) under the condition of \(E^{max}\ge P^{max}\). When \(E^{max}=50\), the remaining power is fluctuating between 10 and 30 as shown in red line. When \(E^{max}=10\), the remaining power is fluctuating between 0 and 10 as shown in blue line. It can be seen that \(E[t]-P[t]\ge 0\) always holds as time goes on, then it is clearly that the energy availability is guaranteed as long as the inequality \(E^{max}\ge P^{max}\) is satisfied.

The minimal required battery capacity is \(P^{max}\), which is 10 in simulation. However, the minimal required battery capacity [14] exceeds 100, which is much bigger than 10. A small required battery capacity is easy to reduce the overall node cost.

Fig. 3
figure 3

Energy availability

Full size image

Average Long-Term Throughput Analysis Figure 4 shows the average long term throughput trajectories of the proposed algorithm with different E(e[t]), where the E[e(t)] is the mean value of e(t). We can get that the performance relies on the energy harvest rate, that is, when average value of e(t) increases, the average throughput also increases. The sum throughput of all sub-channels is a convex function of allocated power.

Fig. 4
figure 4

Average long-term throughput with different energy harvest rate e[t]

Full size image

In the following part, the comparisons of average long-term throughput and battery state are demonstrated in Figs. 5 and 6, respectively. The average harvest rate e[t] equals to 4 is an example of low energy harvesting rate, while 2 is an example of extremely low energy harvesting rate. In both figures, red color solid and dotted lines are the results of our proposed algorithm, the blues are the results of the compared algorithm in [14]. Regardless of the average harvest rate e[t], we see that both algorithms achieve throughput convergence along with the time slot. In Fig. 5, the solid lines indicate that proposed algorithm outperforms counterpart, the dotted lines share similar performance. Overall, proposed algorithm utilizes harvested energy better.

In order to deeply analyze the throughput performance, the battery state is shown. In Fig. 6, the SOC follows a flat oscillation in proposed algorithm, while in other algorithm, the battery level fluctuates in a wider range. The proposed algorithm uses the SOC as a negative input so as to reduce the dynamic of SOC. In compared algorithm, the allocated powers rely on the subtracted vector, which is mostly affected by the channel distribution. As a result, the blue solid and dotted lines show similar fluctuation level when the channel distribution is same. The SOC dynamic of our proposed algorithm is more conducive to extend battery lifetime comparing with the other algorithm, as deep charge-discharge cycle may reduce the battery lifetime. Furthermore, the average SOC of proposed algorithm is below another algorithm’s, that is the main reason of achieving higher throughput.

Fig. 5
figure 5

Average long-term throughput comparison

Full size image
Fig. 6
figure 6

Battery state comparison

Full size image

7 Conclusions

In this paper, a power control problem in EH based wireless communication system aiming to maximize throughput is discussed in this paper. In our setup, the wireless transmitter does not know any future information about channel state and energy arrival rate. The setup is reasonable in actual situation. This paper proposes a simple online algorithm which fulfils energy availability guarantee, and achieves outstanding performance in average long-term throughput. The required battery capacity is small, which is suitable for low-cost wireless sensor node. The battery states are smooth in simulations, which is good for battery lifetime. Furthermore, the analysis model is scalable and is also suitable for one transmitter sends out information to many receivers respectively.