1 Framework and goals

Most robust multivariate methods either explicitly or implicitly assume that the available data, say \(\{\varvec{x}_1,\ldots ,\varvec{x}_n\}\), have been generated by a p-variate random vector \(\varvec{X}\) whose distribution function \(F_{\varvec{X}}\) is an element within the following family

$$\begin{aligned} {\mathcal {C}} = \{F_{\varvec{X}}: F_{\varvec{X}} = (1-\varepsilon )F_0 + \varepsilon F_1, \varepsilon \in [0,1) \}. \end{aligned}$$
(1)

In this model \(F_0\) is the distribution function of the “good” part of the data, i.e. \(F_0\) represents the postulated null model, \(F_1\) is the contaminant distribution, which is usually left unspecified except at most for the assumption of some regularity conditions, and \(\varepsilon \) is the contamination rate. Unless \(F_0\) in (1) is free of parameters, as it happens in the contamination models for digits of Cerioli et al. (2019) and Barabesi et al. (2022), consistent estimation of the parameters in \(F_0\) from \(\{\varvec{x}_1,\ldots ,\varvec{x}_n\}\) is crucial for correct identification of the outliers from \(F_1\) and for more elaborated statistical tasks under model (1), such as dimension reduction, classification and clustering (see, e.g., Hubert et al. 2008; Farcomeni and Greco 2015).

Estimation requires the adoption of robust high-breakdown techniques, in order to avoid the well-known effects of masking and swamping. However, the operational implementation of such high-breakdown techniques typically relies on the additional assumption that “good” data come from a multivariate normal distribution. In the one-population case this is stated as

Assumption 1

In model (1), \(F_0\) is the distribution function of a p-variate normal random vector with mean vector \(\mu \) and dispersion matrix \(\varSigma \).

A further common requirement (see Rousseeuw and Leroy 1987, p. 14) is the following

Assumption 2

Model (1) holds with \(\varepsilon < 1/2\).

In this work we focus on trimmed estimators of \(\mu \) and \(\varSigma \) taking the form

$$\begin{aligned} \widetilde{\mu }_{\alpha _n} = \frac{1}{w_{\alpha _n}}\sum _{i=1}^n w_{i,\alpha _n}\varvec{x}_i \end{aligned}$$
(2)

and

$$\begin{aligned} \widetilde{\varSigma }_{\alpha _n} = \frac{\eta _{\alpha ,p}}{w_{\alpha _n}} \sum _{i=1}^n w_{i,\alpha _n} (\varvec{x}_i - \widetilde{\mu }_{\alpha _n})(\varvec{x}_i - \widetilde{\mu }_{\alpha _n})^{\tiny {\textsf {T}}}, \end{aligned}$$
(3)

where \(\alpha _n\) is a pre-specified tuning constant chosen in [0, 0.5) and possibly depending on the sample size n, while \(w_{i,\alpha _n} \in \{0,1\}\) and \(w_{\alpha _n} = \sum _{i=1}^n w_{i,\alpha _n}\), with \(\alpha =\underset{n}{\lim }\; \alpha _n\). The constant \(\eta _{\alpha ,p}\) is a dimension-dependent scaling factor ensuring consistency of \(\widetilde{\varSigma }_{\alpha _n}\) when \(\varepsilon =0\) and \(n\rightarrow \infty \). If Assumption 1 holds and robust estimation looks for a subset of “central” observations according to a suitable criterion, such as minimization of the volume of the estimated scatter, this consistency factor is (Croux and Haesbroeck 1999)

$$\begin{aligned} \eta _{\alpha ,p} = \frac{1-\alpha }{F_{\chi ^2_{p+2}}(\chi ^2_{p,1-\alpha })}, \end{aligned}$$
(4)

where \(F_{\chi ^2_p}\) is the distribution function of a \(\chi ^2_p\) random variable, while

$$\begin{aligned} \chi ^2_{p,1-\alpha } = F_{\chi ^2_p}^{-1}(1-\alpha ) \end{aligned}$$
(5)

is its \((1-\alpha )\)th quantile. In small and moderate samples, the consistency factor can be supplemented with a bias-correction factor computed by simulation under Assumption 1 (Pison et al. 2002).

The weights \(w_{i,\alpha _n}\) in (2) and (3) are often defined in such a way that \(w_{\alpha _n} = \lfloor (1-\alpha _n)n\rfloor \), where \(\lfloor \;\rfloor \) denotes the floor function. The number \(\alpha _n\) thus gives the trimming level, which is the proportion of sample observations discarded by the robust procedure. The squared robust Mahalanobis-type distances

$$\begin{aligned} \widetilde{d}_{i,\alpha _n}^2 = (\varvec{x}_i - \widetilde{\mu }_{\alpha _n})^{\tiny {\textsf {T}}}\widetilde{\varSigma }_{\alpha _n}^{-1}(\varvec{x}_i - \widetilde{\mu }_{\alpha _n}), \qquad i=1,\ldots ,n, \end{aligned}$$
(6)

are then used for outlier identification and, more generally, for robustly ordering multivariate data (Cerioli 2010). Finite-sample corrections for the tail quantiles of these distances are obtained by Cerioli et al. (2009), again under Assumption 1.

We do not here address the issue (and the potential advantages) of performing a data-dependent choice of \(\alpha _n\), for which we refer to Cerioli et al. (2018, 2019), Clarke and Grose (2023) and to the references therein. We instead settle in the worst-case scenario of highest contamination and fix

$$\begin{aligned} \alpha _n = {\left\{ \begin{array}{ll} \left( \lfloor (n-p+1)/2 \rfloor - 1\right) /n \qquad \text {if} \; (n-p+1) \; \text {is even} \\ \lfloor (n-p+1)/2 \rfloor /n \qquad \qquad \;\;\, \text {if} \; (n-p+1) \; \text {is odd}, \end{array}\right. } \end{aligned}$$

which corresponds to the maximal value of the (replacement) breakdown point

$$\begin{aligned} \kappa _n = \frac{\lfloor (n-p+1)/2 \rfloor }{n} \end{aligned}$$
(7)

of \(\widetilde{\mu }_{\alpha _n}\) and \(\widetilde{\varSigma }_{\alpha _n}\) for sample size n. In this case,

$$\begin{aligned} \alpha = \underset{n}{\lim }\; \alpha _n = \frac{1}{2}. \end{aligned}$$

With a slight abuse of notation, in the consistency arguments that follow we then replace the finite-sample trimming level \(\alpha _n\) from (7) with its limiting value \(\alpha =1/2\).

The first goal of this work, addressed in Sect. 2, is to derive a simple and easily computable expression for the consistency factor to be used in formula (3) when Assumption 1 is replaced by the more general

Assumption 3

In model (1), \(F_0\) is the distribution function of a p-variate Student-t random vector with mean vector \(\mu \), dispersion matrix \(\varSigma \) and \(\nu \) degrees of freedom, where \(\nu \ge 3\) is integer.

The motivation for our work comes from the need to move towards a more general notion of robustness, where the stringent normality constraint for the “good” part of the data is relaxed. Our general approach could then be combined with the popular notion that the Student-t distribution accommodates mild forms of outlyingness (see, e.g., Peel and McLachlan 2000). In that case, the use of high-breakdown estimators in place of the classical ones will further robustify the results by preventing the effect of the most extreme observations, that might follow a different and possibly non-elliptical data generating process. Furtermore, we remark that examination of the behavior of robust estimators under more realistic elliptical models for uncontaminated data is becoming increasingly popular in several research domains: see Pokojovy and Jobe (2022) and Lopuhaä et al. (2022) for recent examples.

A potential problem with Assumption 3 is that the degrees of freedom parameter \(\nu \) is usually unknown in applications and must be estimated from \(\{\varvec{x}_1,\ldots ,\varvec{x}_n\}\), together with \(\mu \) and \(\Sigma \). The second purpose of our work is then to develop an estimation procedure for \(\nu \) based on the robust distances (6). We accomplish this task in Sect. 3, where we follow a Monte Carlo approach. In Sects. 4 and 5 we provide extensive empirical evidence about the performance of our method, both through simulation and the analysis of two real data sets.

Although Assumption 3 allows for heavier tails than Assumption 1, it retains an elliptical structure for \(F_0\). The development of formal robust methods when \(F_0\) is the distribution function of a skew random vector is an important task (see Schreurs et al. 2021, for a recent contribution) that however lies outside the scope of the present work, requiring the development of extended notions of trimming. Similarly, in this work we do not question the validity of Assumption 2, from which the requirement \(\alpha _n \in [0,0.5)\) follows, but we refer to Cerioli et al. (2019) for a study of the effects and potential advantages of its relaxation.

2 Consistency correction

Although our approach is general and could be applied to any trimmed estimator of type (3), for concreteness we refer to the popular Minimum Covariance Determinant estimator (MCD) of Rousseeuw and Leroy (1987, p. 262–265). For trimming level \(\alpha _n\), the MCD subset of \(\{\varvec{x}_1,\ldots ,\varvec{x}_n\}\) is defined as the subset of \(w_{\alpha _n}\) observations in the sample whose covariance matrix has the smallest determinant. Let \(S_{\alpha _n} = \{i_1,\ldots ,i_{w_{\alpha _n}}\}\) denote the set of the indexes of the observations belonging to this subset. The MCD estimators of \(\mu \) and \(\varSigma \) are then obtained through (2) and (3), with weights

$$\begin{aligned} w_{i,\alpha _n} = {\left\{ \begin{array}{ll} 1 \qquad \text {if} \; i \in S_{\alpha _n} \\ 0 \qquad \text {otherwise}. \end{array}\right. } \end{aligned}$$

The MCD estimator is consistent under very general conditions on \(F_0\) (Cator and Lopuhaä 2010, 2012) and attains the breakdown bound (7) with the value of \(\alpha _n\) selected in Sect. 1. Paindaveine and Van Bever (2014) also obtain a Bahadur representation result for (3) that leads to MCD-based inference procedures for shape under elliptical models.

The consistency factor is derived through the functional representation of the MCD estimator, as given by Croux and Haesbroeck (1999) and Cator and Lopuhaä (2010). In particular, let \(\varvec{X}\) be an absolutely-continuous random vector defined on \({\mathbb {R}}^p\). We assume that the probability density function of \(\varvec{X}\) is

$$\begin{aligned} f_{\varvec{X}}(\varvec{x}) = \vert \varSigma \vert ^{-1/2}\phi ((\varvec{x}-\mu )^{\tiny {\textsf {T}}}\varSigma ^{-1}(\varvec{x}-\mu )), \end{aligned}$$
(8)

where \(\phi : {\mathbb {R}}^+ \rightarrow {\mathbb {R}}^+\) is a non-negative and differentiable function (named generator) with strictly negative derivative. In the case of the multivariate Student-t distribution, the probability density function reduces to

$$\begin{aligned}{} & {} f_{\varvec{X}}(\varvec{x})=\frac{\Gamma ((\nu +p)/2)}{\Gamma (\nu /2)(\nu -2)^{p/2}\pi ^{p/2}} \nonumber \\{} & {} \quad \times \vert \varSigma \vert ^{-1/2}\left( 1+\frac{1}{\nu -2}\,(\varvec{x}-\mu ) ^T\varSigma ^{-1}(\varvec{x}-\,\mu )\right) ^{-(\nu +p)/2},\nonumber \\ \end{aligned}$$
(9)

for \(\nu >2\). We remark that the previous probability density function is suitably parametrized with respect the usual expression (see, e.g., Fang et al. 1990, p. 85) in order to let \(\varSigma \) be the dispersion matrix of the random vector \(\varvec{X}\).

The existence of a consistency factor under elliptical models was proved by Butler et al. (1993), while Croux and Haesbroeck (1999) originally suggested computation through the use of symbolic programming. Numerical integration could also be feasible at the multivariate Student-t distribution. Nevertheless, we argue that the availability of a simpler formula only requiring one or few calls to standard numerical routines, as we obtain in Proposition 1, may be useful for several purposes. First, this formula can be easily implemented in virtually all programming languages, thus widening the audience for potential applications of high-breakdown estimators beyond the usual normality assumption. Second, it is also better suited to be plugged into more sophisticated procedures that make repeated use of robust estimators and distances, such as robust methods based on monitoring, where a possibly long sequence of trimming levels is exploited (see, e.g., Hubert et al. 2012; Cerioli et al. 2018). Also the algorithm developed in Sect. 3 for estimating the usually unknown value of \(\nu \) from data falls within the latter class of methods and its implementation benefits from our simplified expression. Finally, numerical methods are no longer required in the bivariate case, where our result simplifies to the analytic formula derived in Corollary 1.

We emphasize that the consistency factor becomes a function of \(\nu \) under Assumption 3. Therefore, it is now denoted as \(\eta _{\alpha ,p}(\nu )\).

Proposition 1

If Assumption 3 holds, then the consistency factor in (3) is

$$\begin{aligned} \eta _{\alpha ,p}(\nu )= & {} \Bigg \{\frac{\nu -2}{(1-\alpha ) p} \int _0^{1-\alpha } \frac{1}{1-I_u^{-1}(p/2,\nu /2)}du \nonumber \\{} & {} \quad - \frac{\nu -2}{p}\Bigg \}^{-1}, \end{aligned}$$
(10)

where \(I_x(a,b)\) is the regularized Beta function of parameters a and b.

Proof

Let \(T = (\varvec{X}-\mu )^{\tiny {\textsf {T}}}\varSigma ^{-1}(\varvec{X}-\mu )\). Under (8), the probability density function of T is

$$\begin{aligned} f_T(t)=\frac{\pi ^{p/2}}{\Gamma (p/2)}\,t^{p/2-1}\phi (t)\varvec{1}_{{\mathbb {R}}^{+}}(t), \end{aligned}$$

where \(\Gamma \) is the Gamma function and \(\varvec{1}_A\) is the indicator function of set A. Let \(F_T\) be the distribution function of T. From Cator and Lopuhaä (2010, Formula (4.3)), we obtain that

$$\begin{aligned} \eta _{\alpha ,p}(\nu ) = \left\{ \frac{\pi ^{p/2}}{2(1-\alpha )\Gamma (p/2+1)}\,\int _0^{F_T^{-1}(1-\alpha )}t^{p/2}\phi (t)dt\right\} ^{-1}, \end{aligned}$$

which can be written as

$$\begin{aligned}{} & {} \eta _{\alpha ,p}(\nu ) = \left\{ \frac{1}{(1-\alpha ) p}\,\int _0^{F_T^{-1}(1-\alpha )}tf_T(t)dt\right\} ^{-1}\nonumber \\{} & {} \quad = \left\{ \frac{1}{(1-\alpha ) p}\,\int _0^{1-\alpha } F_T^{-1}(u)du\right\} ^{-1}. \end{aligned}$$
(11)

By assuming the Student-t generator, from (9) we have

$$\begin{aligned} \phi (t)=\frac{\Gamma ((\nu +p)/2)}{\Gamma (\nu /2)(\nu -2)^{p/2}\pi ^{p/2}}\left( 1+\frac{1}{\nu -2}\,t\right) ^{-(\nu +p)/2}. \end{aligned}$$

It then holds

$$\begin{aligned}{} & {} \quad f_T(t)=\frac{\Gamma ((\nu +p)/2)}{\Gamma (\nu /2)\Gamma (p/2)(\nu -2)^{p/2}}\,t^{p/2-1}\\{} & {} \quad \left( 1+\frac{1}{\nu -2}\,t\right) ^{-(\nu +p)/2}\varvec{1}_{{\mathbb {R}}^{+}}(t). \end{aligned}$$

The transformation

$$\begin{aligned} Y=\frac{T}{\nu -2+T} \end{aligned}$$

gives rise to a standard Beta distribution with shape parameters (p/2) and \((\nu /2)\). If \(F_Y\) denotes the distribution function of Y, it then holds \(F_Y(x)=I_x(p/2,\nu /2)\), where \(I_x(a,b)\) is the regularized Beta function of parameters a and b. Hence,

$$\begin{aligned} F_T(t)=F_Y\left( \frac{t}{\nu -2+t}\right) , \end{aligned}$$
(12)

from which

$$\begin{aligned} F_T^{-1}(u)= & {} \frac{(\nu -2) F_Y^{-1}(u)}{1-F_Y^{-1}(u)} = (\nu -2)\,\left( \frac{1}{1-F_Y^{-1}(u)}-1\right) \\= & {} (\nu -2)\,\left( \frac{1}{1-I_u^{-1}(p/2,\nu /2)}-1\right) \end{aligned}$$

for \(u\in [0,1]\). The result thus follows from (11). \(\square \)

Table 1 reports the values of \(1/\eta _{\alpha ,p}(\nu )\), which is the appropriate scaling factor for the squared robust distances in (6), obtained from Proposition 1 for some selected values of p and \(\nu \), when \(\alpha =0.5\). Following (10), each value of \(\eta _{\alpha ,p}(\nu )\) in the table is easily computed through standard numerical routines, available in many programming languages. We refer to the Supplementary Material for more details on the routines of our choice and on a number of popular alternatives.

It is worth remarking that the result in Proposition 1 holds more generally than under Assumption 3, as it only requires \(\nu >2\) when \(F_0\) is the distribution function of a p-variate Student-t random vector with \(\nu \) degrees of freedom. In Assumption 3, the additional condition that \(\nu \) must be an integer is instead appropriate for the Monte Carlo estimation method developed in Sect. 3. We nevertheless argue that this condition does not entail substantial restrictions on the method applicability. Furthermore, it holds that

$$\begin{aligned} \underset{\nu \rightarrow \infty }{\lim }\; \eta _{\alpha ,p}(\nu ) = \eta _{\alpha ,p}, \end{aligned}$$

as it should be.

Table 1 Values of \(1/\eta _{\alpha ,p}(\nu )\) from Proposition 1 for selected values of p and \(\nu \), when \(\alpha =0.5\)
Full size table

A remarkably simple analytic expression for \(\eta _{\alpha ,p}(\nu )\) can be further derived in the special case where \(p=2\).

Corollary 1

If Assumption 3 holds and \(p=2\), then

$$\begin{aligned} \eta _{\alpha ,2}(\nu ) = \left\{ \frac{\nu }{2(1-\alpha )}\,\left( 1-\alpha ^{1-2/\nu }\right) -\frac{\nu -2}{2}\right\} ^{-1}. \end{aligned}$$
(13)

Proof

If Assumption 3 holds with \(p=2\),

$$\begin{aligned} f_T(t)=\frac{\nu }{2(\nu -2)}\,\left( 1+\frac{1}{\nu -2}\,t\right) ^{-\nu /2-1}\varvec{1}_{{\mathbb {R}}^{+}}(t). \end{aligned}$$

Therefore,

$$\begin{aligned} F_T(t)=\left( 1-\left( 1+\frac{1}{\nu -2}\,t\right) ^{-\nu /2}\right) \varvec{1}_{{\mathbb {R}}^{+}}(t) \end{aligned}$$

and

$$\begin{aligned} F_T^{-1}(u)=(\nu -2)((1-u)^{-2/\nu }-1) \end{aligned}$$

for \(u \in [0,1]\), from which the result follows. \(\square \)

Furthermore, from (13) we obtain that

$$\begin{aligned} \lim _{\nu \rightarrow \infty }\eta _{\alpha ,2}(\nu ) = \left\{ 1+\frac{\alpha }{1-\alpha }\log \alpha \right\} ^{-1}, \end{aligned}$$

in agreement with result (4) corresponding to the multivariate normal case. As an example, Fig. 1 considers the case \(\nu =5\) and depicts the value of \(1/\eta _{\alpha ,2}(5)\) for \(\alpha \in [0,0.5)\).

Fig. 1
figure 1

Plot of \(1/\eta _{\alpha ,2}(5)\) for \(\alpha \in [0,0.5)\)

Full size image

We conclude this section by evaluating the effect of model misspecification. For this purpose, we assume to wrongly work under Assumption 1 with \(\varSigma =I_p\), where \(I_p\) is the p-dimensional identity matrix, while instead Assumption 3 holds true with \(\nu \) degrees of freedom. In this case, the standard MCD estimate \(\widetilde{\varSigma }_{\alpha _n}\) includes \(\eta _{\alpha ,p}\) from (4) as its consistency factor and targets \(I_p\). However, it follows from (9) that the true dispersion matrix of the data generating process is \(\frac{\nu }{\nu -2}I_p\), which is estimated by

$$\begin{aligned} \widetilde{\varSigma }_{\alpha _n}(\nu )=\frac{\eta _{\alpha ,p}(\nu )}{\eta _{\alpha ,p}} \widetilde{\varSigma }_{\alpha _n}. \end{aligned}$$

Matrix \(\widetilde{\varSigma }_{\alpha _n}(\nu )\) is the MCD estimate that includes \(\eta _{\alpha ,p}(\nu )\) from Proposition 1 as its consistency factor for (asymptotic) trimming level \(\alpha \) and \(\nu \) degrees of freedom. To appreciate the advantage of (10) over (4) under Assumption 3, we need to make the targeted dispersion matrices comparable. We thus define the squared Frobenius matrix norms

$$\begin{aligned} \widetilde{\varDelta }_{\alpha _n,p}(\nu ) = \Vert I_p - \frac{\nu -2}{\nu }\widetilde{\varSigma }_{\alpha _n}(\nu )\Vert ^2 \end{aligned}$$

and

$$\begin{aligned} \widetilde{\varDelta }_{\alpha _n,p} = \Vert I_p - \widetilde{\varSigma }_{\alpha _n}\Vert ^2. \end{aligned}$$

In \(\widetilde{\varSigma }_{\alpha _n}\) we now also incorporate the bias-correction factor of Pison et al. (2002), which is instead unknown for \(\widetilde{\varSigma }_{\alpha _n}(\nu )\), in order to make the scenario less favorable for Assumption 3. Table 2 reports the comparison of the discrepancy measures \(100 {\textrm{E}}[\widetilde{\varDelta }_{\alpha _n,p}(\nu )]/p\) and \(100{\textrm{E}}[\widetilde{\varDelta }_{\alpha _n,p}]/p\), for \(\alpha =0.5\) and different values of n, p and \(\nu \), computed on 1000 samples generated under Assumption 3. As expected, the value of \({\textrm{E}}[\widetilde{\varDelta }_{\alpha _n,p}(\nu )]\) decreases steadily as n grows, while the effect of choosing the inappropriate model, and thus the inappropriate scaling, is paramount especially when \(\nu \) or n (or both) are low.

Table 2 Discrepancy measure \(100{\textrm{E}}[\widetilde{\varDelta }_{\alpha _n,p}(\nu )]/p\) computed on 1000 samples generated under Assumption 3
Full size table

3 Robust estimation of the degrees of freedom

3.1 Rationale

The consistency factor \(\eta _{\alpha ,p}(\nu )\) obtained in Proposition 1 depends on the value of \(\nu \), which is usually unknown. When the non-robust maximum likelihood estimators of \(\mu \) and \(\varSigma \) are adopted, several alternative estimators of \(\nu \) exist and one which is particularly suited to the present context is based on an extension of the EM algorithm. However, numerical instabilities and other issues are sometimes reported with this estimator (Hasannasab et al. 2021; Pascal et al. 2021). We argue that such issues may be possibly related with the unsuspected presence of outliers or other forms of contamination in the data, according to model (1), as well as with the occurrence of singularities and non interesting local maximizers of the likelihood function, as it happens with EM-type algorithms (García-Escudero et al. 2015). It is an open issue whether the same approach can be robustified by the use of (2) and (3), or by the inclusion of a trimming step in the appropriate version of the EM algorithm. In this work we then suggest an indirect procedure for robustly estimating the value of \(\nu \) in Assumption 3.

Our basic idea is to select the value of \(\nu \) that provides the best fit to the squared robust distances obtained from the trimmed estimators of location and scatter. For simplicity, and for stressing the portability of our method, in what follows we take \(\{\widetilde{d}_{1,\alpha _n}^2, \ldots , \widetilde{d}_{n,\alpha _n}^2\}\) in (6) to denote the squared robust distances incorporating the normal-distribution consistency correction \(1/\eta _{\alpha ,p}\), which is the standard output of the robust estimation procedure in most available software packages. We instead write

$$\begin{aligned} \widetilde{d}_{i,\alpha _n,\nu }^2 = \frac{\eta _{\alpha ,p}}{\eta _{\alpha ,p}(\nu )} \widetilde{d}_{i,\alpha _n}^2, \qquad i=1,\ldots ,n, \end{aligned}$$
(14)

for the squared robust distances that should be used under Assumption 3, when the appropriate consistency factor \(\eta _{\alpha ,p}(\nu )\) from Proposition 1 replaces \(\eta _{\alpha ,p}\) in (3). By recalling the proof of Proposition 1, \(F_T\) becomes the limiting distribution of the random variables (14) when \(\mu \) and \(\varSigma \) are estimated consistently. In principle, we could then choose \(\nu \) by minimizing a discrepancy measure between the empirical distribution of the squared robust (t-adjusted) distances \(\{\widetilde{d}_{1,\alpha _n,\nu }^2, \ldots , \widetilde{d}_{n,\alpha _n,\nu }^2\}\) and \(F_T\). This would be a somewhat simple and cheap task, since Equation (12) shows that \(F_T\) depends on the regularized Beta function of parameters p/2 and \(\nu /2\) under Assumption 3.

However, reliance on the asymptotic distribution of the squared robust distances (14) for the estimation of \(\nu \) could open the door to two orders of potential difficulties. The first one is that several different algorithms typically attempt to compute the same trimmed estimator, thus providing alternative approximations to the same (intractable) objective function. For instance, the popular R package robustbase (Todorov and Filzmoser 2009) allows three possible options for the MCD estimator, namely the default Fast-MCD algorithm of Rousseeuw and Van Driessen (1999) with random selection of a pre-specified number of initial subsamples of minimum cardinality, the same algorithm with enumeration of all the possible initial subsamples or of a large number of them, and the deterministic MCD algorithm proposed by Hubert et al. (2012). Furthermore, other algorithmic proposals exist for the same task that might be preferable in different frameworks (Chakraborty and Chaudhuri 2008; De Ketelaere et al. 2020; Boudt et al. 2020; Kalina and Tichavsky 2022), and also the default Fast-MCD algorithm comes with a number of arguments (Fauconnier and Haesbroeck 2009; Mächler 2022) that should be possibly tuned to the specific problem at hand. The second shortcoming is that the finite-sample bias of (3) is often non-negligible, even if the appropriate consistency correction is adopted. Pison et al. (2002) evaluate this bias for the Fast-MCD algorithm under Assumption 1, while to the best of our knowledge similar results are not yet available under Assumption 3. Again, including the available (but wrong) finite sample correction in (3) or excluding it (at the expense of a greater bias) could lead to different solutions, without any clear indication about which one should be preferred.

To overcome the difficulties mentioned above, we exploit a Monte Carlo approach in which we estimate the distribution function of the squared robust distances. Monte Carlo estimation of the same distribution function is also the backbone of the correction method developed by Cerioli et al. (2009) when the observations actually follow Assumption 1. For simplicity we base our computations on the standard output (6) of most of the available packages for robust estimation of \(\mu \) and \(\varSigma \), possibly after inclusion of the bias-correction factor of Pison et al. (2002). However, we emphasize that the same results could be obtained with any other scaling of these robust distances, such as (14), provided that the scaling is easily computable as in Proposition 1, or even with the uncorrected squared distances \(\{\eta _{\alpha ,p}\widetilde{d}_{1,\alpha _n}^2, \ldots , \eta _{\alpha ,p}\widetilde{d}_{n,\alpha _n}^2\}\). Indeed, an important bonus of our Monte Carlo approach is that it leads to cancel out the bias induced by the specific distance choice, as well as other possible algorithmic effects.

3.2 Monte Carlo simulation of the robust distances

In our Monte Carlo approach, we first obtain an estimate of the distribution function of the squared robust distances (6) under Assumption 3 for each (integer) value of the degrees of freedom below a fixed threshold, say \(\nu _{\textrm{max}}\). This threshold should be chosen according to problem-specific or practical considerations. For computational simplicity, in what follows we set \(\nu _{\textrm{max}}=20\), which seems to be close enough to the limiting normal case for many practical purposes. Of course, larger values of \(\nu _{\textrm{max}}\) may be selected when appropriate, at the expense of an increased computing burden.

Let \(\widetilde{d}_{(i),\alpha _n}^2\) be the ith order statistic of the squared robust distances (6) in the available sample \(\{\varvec{x}_1,\ldots ,\varvec{x}_n\}\). Not all the observations in the sample provide information about the parameters of \(F_0\) in model (1) when \(\varepsilon >0\). Indeed, the expected number of sample observations generated by \(F_0\) under such a model is

$$\begin{aligned} m_n = \lfloor n (1-\varepsilon ) \rfloor . \end{aligned}$$
(15)

Only \(\{\widetilde{d}_{(1),\alpha _n}^2, \ldots , \widetilde{d}_{(m_n),\alpha _n}^2\}\) should thus be used to infer the true value of \(\nu \) under Assumption 3, provided that \(F_0\) and \(F_1\) are sufficiently well separated. In that case \(\{\widetilde{d}_{(m_n+1),\alpha _n}^2, \ldots , \widetilde{d}_{(n),\alpha _n}^2\}\) would likely come from \(F_1\) and contribute to bias the estimator of \(\nu \).

The first ingredient of our approach is a set of Monte Carlo estimates of the expectation of the \(i\hbox {th}\) ordered squared robust distance \(\widetilde{d}_{(i),\beta _n}^2\), for \(i \in \{1,\ldots ,m_n\}\), under \(F_0\). Each squared robust distance is computed from a sample of \(m_n\) observations with trimming level

$$\begin{aligned} \beta _n = \frac{\alpha _n-\varepsilon }{1-\varepsilon }. \end{aligned}$$
(16)

We remark that the choice of the original trimming level \(\alpha _n\) would be inappropriate in our simulation scheme. If \(\varepsilon >0\) in (15), then \(m_n < n\) and only the first \(m_n\) sample order statistics \(\{\widetilde{d}_{(1),\alpha _n}^2, \ldots , \widetilde{d}_{(m_n),\alpha _n}^2\}\) are used to infer the value of \(\nu \). These robust distances will exhibit the variability of random quantities from a sample of \(m_n\) “good” observations, to which trimming level \(\beta _n\) (not \(\alpha _n\)) is applied. In fact, the choice of trimming (16) ensures that the cardinality of the MCD subset is preserved when the original sample \(\{\varvec{x}_1,\ldots ,\varvec{x}_n\}\), to which trimming level \(\alpha _n\) is applied, is replaced by a sample of reduced size \(m_n\), since for the latter the MCD estimator is computed on \(w_{\beta _n} = \lfloor (1-\beta _n)m_n\rfloor \approx \lfloor (1-\alpha _n)n\rfloor \) observations. We also note that other robust procedures based on iteration, such as those of García-Escudero and Gordaliza (2005) and Riani et al. (2009), show the importance of rescaling the initial trimming level when a preliminary indication of the number of “good” observations is available, in order to take the appropriate sampling variability into account. Such an update is also at the heart of the computation of the consistency factor for the reweighted MCD estimator of scatter under Assumption 1 (see, e.g., Croux and Haesbroeck 2000, p. 604).

The required set of estimates is obtained under the hypothesis that Assumption 3 holds with \(\nu \in \{3,\ldots ,\nu _{\textrm{max}}\}\). Therefore, each element in this set of Monte Carlo estimates is denoted by \(\bar{d}_{(i),\beta _n,\nu }^*\), for \(i=1,\ldots ,m_n\) and \(\nu =3,\ldots ,\nu _{\textrm{max}}\), to emphasize dependence on the degrees of freedom under \(F_0\). Specifically, \(\bar{d}_{(i),\beta _n,\nu }^*\) is computed from B replicates of the data-generating process of artificial samples of size \(m_n\), say \(\{\varvec{x}^{*}_{1,\nu ,b},\ldots ,\varvec{x}^{*}_{m_n,\nu ,b}\}\) for \(b=1,\ldots ,B\), where the p-dimensional random vectors \(\varvec{x}^{*}_{1,\nu ,b},\ldots ,\varvec{x}^{*}_{m_n,\nu ,b}\) are simulated according to Assumption 3 and yield the estimators (again dependence on the degrees of freedom under \(F_0\) is emphasized in subscripts)

$$\begin{aligned} \widetilde{\mu }^*_{\beta _n,\nu ,b} = \frac{1}{w_{\beta _n}}\sum _{i=1}^{m_n} w_{i,\beta _n}\varvec{x}^*_{i,\nu ,b} \end{aligned}$$
(17)

and

$$\begin{aligned}{} & {} \widetilde{\varSigma }^*_{\beta _n,\nu ,b} = \frac{\eta _{\beta ,p}}{w_{\beta _n}} \sum _{i=1}^{m_n} w_{i,\beta _n} (\varvec{x}^*_{i,\nu ,b} - \widetilde{\mu }^*_{\beta _n,\nu ,b})\nonumber \\{} & {} \quad (\varvec{x}^*_{i,\nu ,b} - \widetilde{\mu }^*_{\beta _n,\nu ,b})^{\tiny {\textsf {T}}}, \end{aligned}$$
(18)

with \(\beta = \underset{n}{\lim }\; \beta _n\) and \(w_{\beta _n}=\sum \limits _{i=1}^{m_n} w_{i,\beta _n}\). Correspondingly, for \(i=1,\ldots ,m_n\), we compute

$$\begin{aligned}{} & {} (\widetilde{d}^*_{i,\beta _n,\nu ,b})^2 = (\varvec{x}^*_{i,\nu ,b}- \widetilde{\mu }^*_{\beta _n,\nu ,b})^{\tiny {\textsf {T}}}(\widetilde{\varSigma }^* _{\beta _n,\nu ,b})^{-1}\nonumber \\{} & {} \quad (\varvec{x}^*_{i,\nu ,b} - \widetilde{\mu }^*_{\beta _n,\nu ,b}). \end{aligned}$$
(19)

Then, for \(i=1,\ldots ,m_n\), \((\widetilde{d}^*_{(i),\beta _n,\nu ,b})^2\) denotes the ith order statistics of the squared robust distances (19) in artificial sample \(\{\varvec{x}^{*}_{1,\nu ,b},\ldots ,\varvec{x}^{*}_{m_n,\nu ,b}\}\) and

$$\begin{aligned} \bar{d}_{(i),\beta _n,\nu }^* = \frac{1}{B} \sum _{b=1}^B (\widetilde{d}^*_{(i),\beta _n,\nu ,b})^2. \end{aligned}$$
(20)

The pseudocode of our Monte Carlo estimation procedure is provided as Algorithm 1.

Algorithm 1
figure a

Monte Carlo algorithm for estimating the expectation of \(\widetilde{d}_{(i),\beta _n}^2\) under \(F_0\)

Full size image

Remark 1

Comparison of (3) and (18) with the same trimming level shows that the actual value of the consistency factor does not affect the estimation criteria to be described below, provided that the same scaling – or even no scaling – is used for computing both \(\widetilde{d}_{(i),\alpha _n}^2\) and the Monte Carlo estimate \(\bar{d}_{(i),\alpha _n,\nu }^*\). As anticipated in Sect. 3.1, this feature provides our approach with a kind of “algorithmic robustness”, which may also apply to the other algorithmic choices and tuning parameters to be selected for the computation of (2) and (3).

Remark 2

In order to infer the value of \(\nu \) in \(F_0\), the first \(m_n\) ordered squared robust distances \(\widetilde{d}_{(1),\alpha _n}^2,\ldots ,\widetilde{d}_{(m_n),\alpha _n}^2\) in the available sample \(\{\varvec{x}_1,\ldots ,\varvec{x}_n\}\) are compared with the corresponding Monte Carlo estimates computed from simulated samples of size \(m_n\) for varying degrees of freedom. However, in (20) trimming level \(\beta _n\) is adopted instead of \(\alpha _n\). The estimate \(\bar{d}_{(i),\beta _n,\nu }^*\) must then be rescaled when \(\varepsilon >0\) in order to take into account the different effect of trimming on \(\widetilde{d}_{(i),\alpha _n}^2\) and \({\widetilde{d}}_{(i),\beta _n,\nu }^2\). For \(i=1,\ldots ,m_n\) and \(\nu \in \{3,\ldots ,\nu _{\textrm{max}}\}\), we compute the scaled order statistics

$$\begin{aligned} \delta _{(i),\alpha _n,\nu }^* = \frac{\eta _{\beta ,p}}{\eta _{\alpha ,p}}\; \bar{d}_{(i),\beta _n,\nu }^*, \end{aligned}$$
(21)

where the required consistency factors are obtained from (4) with \(\alpha = \underset{n}{\lim }\; \alpha _n\) and \(\beta = \underset{n}{\lim }\; \beta _n\).

Remark 3

It is clear that the Monte Carlo estimate \(\bar{d}_{(i),\beta _n,\nu }^*\) is not appropriate for further statistical analysis under Assumption 3, because it incorporates the normal consistency factor (4) instead of the appropriate factor from Proposition 1. Therefore, when the computations are based on the standard output of most of the available packages as above, at the end of our procedure \(\bar{d}_{(i),\beta _n,\nu }^*\) must be rescaled by factor

$$\begin{aligned} \frac{\eta _{\beta ,p}}{\eta _{\beta ,p}(\check{\nu })}, \end{aligned}$$

where \(\check{\nu }\) denotes the selected estimate of \(\nu \), according to the criteria described in Sect. 3.3, to be inserted in (10). The same holds for the empirical squared robust distances \(\widetilde{d}_{i,\alpha _n}^2\), that must be rescaled as in (14).

3.3 Minimum-distance estimates of \(\nu \)

Let \(\widetilde{F}^*_{m_n,\nu }\) be the Monte Carlo estimate of the distribution function of the \(m_n\) scaled squared robust distances (21) when Assumption 3 holds with \(\nu \in \{3,\ldots ,\nu _{\textrm{max}}\}\). Correspondingly, let \(\widetilde{F}_{m_n,\nu }\) denote the empirical distribution function of the first \(m_n\) squared robust distances (6), which are supposed to be generated by \(F_0\) when (1) holds with contamination rate \(\varepsilon \). A very natural estimator of \(\nu \) is the Wasserstein distance between \(\widetilde{F}_{m_n}\) and \(\widetilde{F}^*_{m_n,\nu }\), which is computed as

$$\begin{aligned} \widetilde{\nu }_W = \arg \min \limits _{\nu } \sum _{i=1}^{m_n} \vert \widetilde{d}_{(i),\alpha _n}^2 - \delta _{(i),\alpha _n,\nu }^*\vert . \end{aligned}$$
(22)

Another choice is the Kolmogorov-Smirnov statistic

$$\begin{aligned} \widetilde{\nu }_K = \arg \min \limits _{\nu } \underset{x \in [0,1]}{\sup }\vert \widetilde{F}_{m_n}(x)- \widetilde{F}^*_{m_n,\nu }\vert . \end{aligned}$$
(23)

Both \(\widetilde{\nu }_W\) and \(\widetilde{\nu }_K\) enjoy the properties of the corresponding metrics.

To provide a reference we also compute the squared norm between vectors of order statistics

$$\begin{aligned} \widetilde{\nu }_{L_2} = \arg \min \limits _{\nu } \sum _{i=1}^{m_n} \left( \widetilde{d}_{(i),\alpha _n}^2 - \delta _{(i),\alpha _n,\nu }^*\right) ^2. \end{aligned}$$
(24)

Furthermore, we compare \(\widetilde{\nu }_W\) and \(\widetilde{\nu }_K\) with their non-robust counterparts

$$\begin{aligned} \widehat{\nu }_W = \arg \min \limits _{\nu } \sum _{i=1}^{n} \vert \hat{d}_{(i)}^2 - \bar{d}_{(i),\nu }^*\vert \end{aligned}$$
(25)

and

$$\begin{aligned} \widehat{\nu }_K = \arg \min \limits _{\nu } \underset{x \in [0,1]}{\sup }\vert \widehat{F}_{n}(x) - \widehat{F}^*_{n,\nu }\vert , \end{aligned}$$
(26)

where \(\hat{d}_{(1)}^2,\ldots ,\hat{d}_{(n)}^2\) are the order statistics of the squared Mahalanobis distances

$$\begin{aligned} \hat{d}_i^2 = (\varvec{x}_i - \widehat{\mu })^{\tiny {\textsf {T}}}\widehat{\varSigma }^{-1}(\varvec{x}_i - \widehat{\mu }), \qquad i=1,\ldots ,n, \end{aligned}$$
(27)

computed from the full-sample estimators \(\widehat{\mu }\) and \(\widehat{\varSigma }\), which are obtained from (2) and (3) with \(\alpha _n=0\), \(w_{i,0}=1\) for \(i=1,\ldots ,n\), and \(\eta _{0,p}=1\). Correspondingly, \(\{\bar{d}_{(1),\nu }^*, \ldots , \bar{d}_{(n),\nu }^*\}\) are the Monte Carlo estimates of the same ordered squared distances when Assumption 3 holds with \(\nu \in \{3,\ldots ,\nu _{\textrm{max}}\}\), while \(\widehat{F}_{n}\) and \(\widehat{F}^*_{n,\nu }\) are the empirical distribution functions of \(\{\hat{d}_1^2,\ldots ,\hat{d}_n^2\}\) and \(\{\bar{d}_{(1),\nu }^*, \ldots , \bar{d}_{(n),\nu }^*\}\), respectively.

Table 3 Monte Carlo estimates of \({\textrm{E}}[\widetilde{\nu }_W]\), \({\textrm{E}}[\widetilde{\nu }_K]\) and \({\textrm{E}}[\widetilde{\nu }_{L_2}]\) based on 1000 replicates of model (1) with \(\varepsilon =0\) and \(F_0\) following Assumption 3
Full size table
Table 4 Monte Carlo estimates of \({\textrm{E}}[\widehat{\nu }_W]\) and \({\textrm{E}}[\widehat{\nu }_K]\) based on 1000 replicates of model (1) with \(\varepsilon =0\) and \(F_0\) following Assumption 3
Full size table

4 Simulation experiments

We study the empirical properties of \(\widetilde{\nu }_W\) and \(\widetilde{\nu }_K\) (and occasionally also those of alternative estimators of \(\nu \)) under different scenarios involving \(\nu \in \{3,6,9\}\) and \(p\in \{2,5\}\). In our simulations we usually take \(n\in \{500,1000,2000\}\), as in Table 2, since we are interested in consistency correction of trimmed estimators and in the corresponding behavior of robust distances in relatively large samples. As mentioned in Sect. 3.1, the possibility of computing further adjustments for finite-sample bias in the vein of Pison et al. (2002) is left for further research. In all the simulations that follow we compute the trimmed estimators (2) and (3) through the Fast-MCD algorithm of Rousseeuw and Van Driessen (1999). We also adopt the default configuration of this algorithm derived from the R package robustbase.

Unless otherwise stated, we perform 1000 simulations to estimate the expected value and the standard deviation of each estimator in each configuration. Furthermore, we use \(B=10000\) Monte Carlo replicates in the computation of (20). The specific choice \(\nu _{\textrm{max}}=20\) has only a marginal effect on the estimated properties of \(\widetilde{\nu }_W\) and \(\widetilde{\nu }_K\), since we obtain \(\widetilde{\nu }_W=\widetilde{\nu }_K=\nu _{\textrm{max}}\) in a limited proportion of simulations concerning the cases with the largest values of \(\nu \). This proportion is otherwise negligible in the other instances.

4.1 Scenario I: All observations from the multivariate Student-t distribution

We assume that model (1) holds with \(\varepsilon =0\), so that Assumption 3 is verified for all the observations. We take \(\mu =(0,\ldots ,0)^{\tiny {\textsf {T}}}\) and assume that the random variables \((X_1,\ldots ,X_p)\) are independent.

The motivation for this scenario is twofold. On the one hand, it can anticipate the effect of introducing robust estimation in application domains, such as finance (Gupta et al. 2013), where Student-t models are often advocated, when some mild form of contamination is suspected. In this respect, our approach can measure whether the loss of efficiency due to trimming is appreciable or not. It can also provide a way to possibly robustify the EM algorithms that are used to estimate \(\nu \). On the other hand, this scenario corresponds to the new “null model” under Assumption 3. It thus allows us to investigate the fit between the empirical distribution of the squared robust distances (6) and their theoretical asymptotic distribution, which can be derived under Assumption 3 (see the proof of Proposition 1).

Table 3 reports the Monte Carlo estimates of \({\textrm{E}}[\widetilde{\nu }_W]\), \({\textrm{E}}[\widetilde{\nu }_K]\) and \({\textrm{E}}[\widetilde{\nu }_{L_2}]\), together with the corresponding standard errors. The results appear to be generally good, with a slight (but systematic) improvement in bias over both n and p, while the standard errors are obviously smaller when n increases. Although no estimator is uniformly best over the different configurations, the performance of \(\widetilde{\nu }_W\) is generally preferable to that of \(\widetilde{\nu }_K\) and \(\widetilde{\nu }_{L_2}\), except perhaps when \(\nu =3\), since the Kolmogorov-Smirnov statistic \(\widetilde{\nu }_K\) suffers from a larger variability when \(\nu \) grows. It is apparent that estimation of \(\nu \) becomes more difficult when its true value is large, as the distribution tails tend to become similar across different values of \(\nu \). However, it is seen that the ability to recover the true value of \(\nu \) improves for all the estimators under consideration if n increases, even when \(\nu =9\).

To benchmark the null performance of estimators based on robust distances, we repeat part of the analysis by using the classical Mahalanobis distances (27) and by computing the corresponding estimators \(\widehat{\nu }_W\) and \(\widehat{\nu }_K\). Since no contamination is present in this scenario, classical methods are expected to outperform their robust counterparts. Table 4 confirms the expectation. However, it also shows that the finite-sample bias and the loss of efficiency implied by trimming in the estimation of \(\nu \) are usually minor, even if the chosen robust estimators achieve the maximal breakdown point \(\kappa _n\).

We conclude our analysis of this scenario by examining the effect of estimation of \(\nu \) on the discrepancy measures \(100{\textrm{E}}[\widetilde{\varDelta }_{\alpha _n,p}(\nu )]/p\) and \(100{\textrm{E}}[\widetilde{\varDelta }_{\alpha _n,p}]/p\). Table 5 displays these measures computed on the same replicates of model (1) in the most problematic instance where \(p=2\), when \(\nu \) is estimated either by \(\widetilde{\nu }_W\) or by \(\widetilde{\nu }_K\). Comparison with Table 2 clearly shows that the relative amount of bias induced by our Monte Carlo approach to estimation of \(\nu \) is minor and negligible with respect to that determined by the use of the incorrect consistency factor (4).

Fig. 2
figure 2

Index plot of the ordered squared distances for one representative sample generated under Scenario II with \(n=1000\), \(p=5\) and \(\nu =6\). Left: classical Mahalanobis distances (27). Right: robust distances (6) from the MCD estimator

Full size image
Table 5 Discrepancy measure \(100{\textrm{E}}[\widetilde{\varDelta }_{\alpha _n,p}(\nu )]/p\) computed on 1000 samples generated under Assumption 3 with \(p=2\) and \(\nu \) estimated by \(\widetilde{\nu }_W\) or by \(\widetilde{\nu }_K\)
Full size table

4.2 Scenario II: Heavy contamination

In our second scenario we assume that model (1) holds with \(\varepsilon =0.3\), in order to describe a situation where evidence of the need to adopt high-breakdown techniques is cogent. In particular, we define \(F_0\) as in Scenario I, with \(\mu =(0,\ldots ,0)^{\tiny {\textsf {T}}}\) and p independent variables, while \(F_1\) is the distribution function of a multivariate Student-t distribution with mean vector \(\mu =(\lambda _1,\ldots ,\lambda _p)^{\tiny {\textsf {T}}}\), \(\nu _1\) degrees of freedom and p independent variables. In the mean vector of the contaminant distribution we choose \(\lambda _1 = \ldots = \lambda _p = \lambda \) and \(\lambda =20\), to obtain enough separation between \(F_0\) and \(F_1\). We also choose \(\nu _1=3\) to provide an example of strong contamination by \(F_1\).

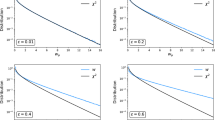
We start our analysis with the performance of the non-robust estimator \(\widehat{\nu }_W\), as a specimen of the behavior of methods based on the classical Mahalanobis distances (27). The effect of masking is paramount, since we obtain \(\widehat{\nu }_W = \nu _{\textrm{max}}\) in all the configurations that we consider. Also note that we fix \(\nu _{\textrm{max}}=20\), so that allowing a larger parameter space will make all the estimates of \(\nu \) even closer to the limiting normal case. Therefore, we can argue that Assumption 3 breaks down to Assumption 1 if the non-robust estimators \(\widehat{\mu }\) and \(\widehat{\varSigma }\) are adopted in this heavily contaminated scenario. Further evidence of masking is provided by the left-hand panel of Fig. 2, which displays the index plot of the ordered squared Mahalanobis distances (27) for one representative sample of this scenario with \(n=1000\), \(p=5\) and \(\nu =6\). Not surprisingly, the real data structure is hidden when location and scatter are estimated through \(\widehat{\mu }\) and \(\widehat{\varSigma }\).

The actual amount of contamination can instead be easily deduced by inspection of the right-hand panel of Fig. 2, which shows the index plot of the ordered squared robust distances (6) for the same data of the left panel. Even without the help of a formal outlier detection rule, that would require an appropriate scaling as in (14), we can set \(\varepsilon =0.3\) in (15) and correspondingly compute \(\beta _n\), as well as the scaled order statistics \(\{\delta _{(1),\alpha _n,\nu }^*,\ldots ,\delta _{(m_n),\alpha _n,\nu }^*\}\). Table 6 focuses on the estimators of \(\nu \) under consideration and reports the Monte Carlo estimates of \({\textrm{E}}[\widetilde{\nu }_W]\), \({\textrm{E}}[\widetilde{\nu }_K]\) and \({\textrm{E}}[\widetilde{\nu }_{L_2}]\), together with standard errors. In this scenario we add the configuration \(n=4000\) and \(p=2\) (based on 500 replicates), which can help to understand the performance of estimators in larger samples under such a nasty contamination scheme. The overall performance of our estimators closely resembles that observed under Scenario I, with \(\widetilde{\nu }_K\) again exhibiting larger variability when \(\nu \) increases and \(\widetilde{\nu }_{L_2}\) being generally outperformed.

Table 6 Monte Carlo estimates of \({\textrm{E}}[\widetilde{\nu }_W]\), \({\textrm{E}}[\widetilde{\nu }_K]\) and \({\textrm{E}}[\widetilde{\nu }_{L_2}]\) based on 1000 replicates of model (1) (500 replicates when \(n=4000\)) with \(\varepsilon =0.3\) and \(F_0\) following Assumption 3
Full size table

The advantage of selecting the appropriate model under this heavy contamination scenario is depicted in Table 7, again for the most problematic case \(p=2\). Since only \(m_n\) observations are now generated under Assumption 3, the actual trimming level (16) of the MCD subset must be taken into account in the computation of the appropriate consistency factor, which is \(\eta _{\beta ,p}(\nu )\), where \(\beta =\underset{n}{\lim }\; \beta _n\). We then write \(\widetilde{\varDelta }_{\beta _n,p}(\nu )\) and \(\widetilde{\varDelta }_{\beta _n,p}\) for the corresponding squared norms. We observe a relative increase in the multivariate bias under Assumption 3, as expected, but this increase is still negligible if compared to that computed under mistaken confidence on Assumption 1.

Table 7 Discrepancy measure \(100{\textrm{E}}[\widetilde{\varDelta }_{\beta _n,p}(\nu )]/p\) computed on 1000 samples generated under Assumption 3 with \(p=2\) and \(\nu \) estimated by \(\widetilde{\nu }_W\) or by \(\widetilde{\nu }_K\).
Full size table

4.3 Scenario III: misspecification of the contamination rate

We conclude our simulation experiment with an assessment of the stability of the proposed estimators of \(\nu \) when the contamination rate \(\varepsilon \) is misspecified. We have seen that \(\widetilde{\nu }_W\) and \(\widetilde{\nu }_K\) exhibit good empirical properties when \(\varepsilon \) is known, when it is zero, or when it can be inferred reliably from the data, as in the right-hand panel of Fig. 2. We are now interested in evaluating the empirical behavior of our estimators under mild violations of the last scenario. For this purpose, we assume that the data generating process still follows the heavy-contamination specifications of Scenario II, with \(\varepsilon =0.3\), but that \(\varepsilon ^\dag \ne \varepsilon \) is mistakenly assumed in formula (15) and in the subsequent computations.

We cannot expect any sensible estimator of \(\nu \), even if based on robust principles, to perform equally well under wild differences between \(\varepsilon \) and \(\varepsilon ^\dag \). The main reason is that the choice of a wrong value of the contamination rate in (15) induces bias in the ordered squared robust distances \(\{\bar{d}_{(1),\beta _n,\nu }^*,\ldots ,\bar{d}_{(m_n),\beta _n,\nu }^*\}\), which is mirrored by a wrong scaling factor in (21). Nevertheless, we would like to observe that good properties are somewhat preserved when \(\varepsilon ^\dag \) is close to \(\varepsilon \). Table 8 thus provides the estimates of \(E[\widetilde{\nu }_W]\) and \(E[\widetilde{\nu }_K]\) under the frame of Scenario II for \(n=1000\) and \(p=2\), when \(\vert \varepsilon ^\dag - \varepsilon \vert \le 0.03\). For simplicity, we now base our estimates on 500 replicates of model (1) and take \(B=5000\) in the computation of (20). Comparison with Table 6 shows that both \(\widetilde{\nu }_W\) and \(\widetilde{\nu }_K\) are sensitive to the choice of the contamination rate. If \(\varepsilon ^\dag > \varepsilon \) the tails of the distribution of the squared robust distances are not properly taken into account, so that a consequence similar to masking is observed. On the contrary, the effect of the contaminated distribution tails on the estimators, and especially on \(E[\widetilde{\nu }_W]\), is magnified when \(\varepsilon ^\dag < \varepsilon \), leading to favor low values of the degrees of freedom under the selected choice of \(F_1\).

Table 8 Monte Carlo estimates of \({\textrm{E}}[\widetilde{\nu }_W]\) and \({\textrm{E}}[\widetilde{\nu }_K]\) based on 500 replicates of model (1) with the specifications of Scenario II and \(B=5000\), in the case \(n=1000\) and \(p=2\)
Full size table
Table 9 As Table 8, but now for estimators \(\widetilde{\nu }_{W_{0.5}}\) and \(\widetilde{\nu }_{K_{0.5}}\)
Full size table

Our suggestion in order to reduce the bias due to misspecification of \(\varepsilon \) is to discard the largest squared robust distances in (22) and (23). We thus compute the \(\varphi \)-trimmed estimators of \(\nu \):

$$\begin{aligned} \widetilde{\nu }_{W_{\varphi }} = \arg \min \limits _{\nu } \sum _{i=1}^{\lfloor m_n(1-\varphi ) \rfloor } \vert \widetilde{d}_{(i),\alpha _n}^2 - \delta _{(i),\alpha _n,\nu }^*\vert , \end{aligned}$$
(28)

and

$$\begin{aligned} \widetilde{\nu }_{K_{\varphi }} = \arg \min \limits _{\nu } \underset{x \in [0,1-\varphi ]}{\sup }\vert \widetilde{F}_{m_n}(x) - \widetilde{F}^*_{m_n,\nu }\vert , \end{aligned}$$
(29)

with \(\varphi \in [0,0.5]\). Typical choices may include \(\varphi =0.5\), which only considers the first half of the squared robust distances, or \(\varphi =0.25\), if there are indications that the contamination rate is substantially lower that 50% (Hubert et al. 2008).

Table 9 exhibits the performance of the trimmed estimators with \(\varphi =0.5\) in the same setting of Table 8. It is seen that the empirical properties of both \(\widetilde{\nu }_{W_{0.5}}\) and \(\widetilde{\nu }_{K_{0.5}}\) are now much closer to those displayed in Sect. 4.2, when the true value of \(\varepsilon \) is inserted in (15) and in the subsequent computations. Although for simplicity we do not report detailed results here, we also find that the increase in bias and the reduction in efficiency implied by the adoption of \(\widetilde{\nu }_{W_{\varphi }}\) and \(\widetilde{\nu }_{K_{\varphi }}\), instead of \(\widetilde{\nu }_W\) and \(\widetilde{\nu }_K\), are usually minor in Scenario II. These trimmed estimators can thus be recommended whenever there is some uncertainty about the value of the contamination rate. We do not here address the possibility of adopting different strategies when some a priori information is available on the sign of \(\varepsilon - \varepsilon ^\dag \), as suggested by Table 9, and the consequences of non-ignorable overlap between \(F_0\) and \(F_1\) in model (1).

Another promising strategy that we leave for further research is to analyze the sequence of minimum values attained by the sums in (22), or attained by the supreme values in (23), when considering a grid of tentative contamination rates \(\varepsilon ^\dag \) belonging to interval [0, 0.5). We currently use these sums (or suprema, respectively) to infer the value of \(\nu \) for a fixed and supposedly known \(\varepsilon \), but we argue that they could also provide useful information for the purpose of determining the contamination rate \(\varepsilon \) when it is unknown. Preliminary experiments seem indeed to confirm that the tentative contamination rate \(\varepsilon ^\dag \) where the smallest value of the selected divergence measure is observed can often be a sensible choice for the unknown value of \(\varepsilon \). In this respect, we note that we take advantage of the behavior already observed in Table 8: a choice of \(\varepsilon ^\dag < \varepsilon \) results in including Mahalanobis distances corresponding to contaminated observations which depart from the simulated ones, while a value of \(\varepsilon ^\dag \) larger than needed leads to omit a fraction of wrongly discarded observations in the tails of \(F_0\), thus yielding incorrect calibration. Of course, our envisaged data-dependent determination of \(\varepsilon \) should also entail estimation of \(\nu \) through the associated divergence \(\widetilde{\nu }_W\) or \(\widetilde{\nu }_K\). Although we do not pursue this path here, we believe that further investigation of these preliminary ideas could provide an extension of the proposal for determining the contamination rate given by García-Escudero and Gordaliza (2005) under Assumption 1.

5 Data analysis

5.1 Image denoising

The use of Student-t models is becoming increasingly popular in the field of image processing (see Hasannasab et al. 2021 and the references therein). A benchmark data set for this task, also considered by Pokojovy and Jobe (2022), is available from the UCI Machine Learning Repository at https://archive.ics.uci.edu/ml/datasets/Image+Segmentation.

In these data, 2310 instances were drawn randomly from a database of seven outdoor images. The images were then hand-segmented to create a classification for every pixel. Each instance is formed by a \(3\times 3\) pixel region and each image is formed by 330 instances.

Our methodology relies on the one-population Assumption 3 and we are not interested in the more complex task of image segmentation. We thus analyze the image labeled as GRASS, which is the supposedly most homogeneous one in the whole data set. We focus on the three available variables directly related to the classical RGB color decomposition. These variables provide the average of the Red, Green and Blue values, respectively, over each pixel region. For the GRASS image thus \(n=330\) and \(p=3\). Although closer inspection of the data shows that a three-variate Student-t model may hold only as a crude approximation for the RGB variables of the GRASS image, we take this image denoising application as a practical example of the situation where the contamination rate can be easily inferred by inspection of the robust distances, as described under Scenario II. A further question of interest concerns the supposed homogeneity of the analyzed image. We do not instead address the possible issue of spatial correlation among adjacent pixels or instances.

We start our empirical investigation by looking at the estimated value of \(\nu \) based on the Monte Carlo distribution of the squared robust distances \(\widetilde{d}_{1,\alpha _n}^2,\ldots ,\widetilde{d}_{330,\alpha _n}^2\), i.e. by assuming \(\varepsilon =0\) in (15). Application of (22) and (23) yields \(\widetilde{\nu }_W = \widetilde{\nu }_K = 5\), corresponding to \(\eta _{0.5,3}(5) = 1/0.260 = 3.85\). On the contrary, the non-robust distances (27) would lead to the larger estimates \(\widehat{\nu }_W=9\) and \(\widehat{\nu }_K=8\). This discrepancy and comparison with the findings of Sect. 4.2 suggest that some mild form of noise or contamination may indeed be present in the original GRASS image.

We then replace 30 instances of the GRASS image with a random sample of instances from the SKY image of the same data set. Such a contamination produces an index plot of the ordered squared distances (displayed in the Supplementary Material) which is similar to that given in the right-hand panel of Fig. 2 and which allows us to define \(m_n=300\) in (15). With this choice of \(m_n\), the Monte Carlo procedure for estimating the expectation of \(\widetilde{d}_{(i),\beta _n}^2\) under \(F_0\), described in Algorithm 1, again yields \(\widetilde{\nu }_W = \widetilde{\nu }_K = 5\). Our approach thus proves to be robust to the contaminated pixels. In the Supplementary Material we report the estimated model parameters before and after contamination of the GRASS image, as well as a link to the specific data under investigation and to the output of Algorithm 1.

Fig. 3
figure 3

Squared robust distances for the contaminated series of index returns. Left: index plot of the ordered squared distances. Right: time series view of the squared distances

Full size image

We conclude our analysis of the contaminated GRASS image with some results about outlier identification through the squared robust distances \(\widetilde{d}_{1,\alpha _n}^2,\ldots ,\widetilde{d}_{330,\alpha _n}^2\). Although we have already argued in Sect. 4.3 that the development of an automated formal procedure for jointly estimating \(\nu \) and \(\varepsilon \), and thus for detecting outliers under Assumption 3, is outside the scope of the present work, the index plot displayed in the left-hand panel of Fig. 1 of the Supplementary Material can be fruitfully complemented with distributional arguments. By comparing the observed distances with the estimated quantiles of their exact distribution for clean samples of size \(m_n=300\), we see that 34 instances are labeled as outliers at the 5% significance level if Assumption 3 holds with \(\nu =5\). Among the outliers we obviously find all the contaminating instances from SKY but also a few observations from the original image, thus supporting the idea that some possible weak and isolated form of contamination might affect the supposedly homogeneous GRASS image. On the other hand, a plethora of potential false discoveries would arise under the light tails of Assumption 1. In that case as many as 64 squared robust distances would exceed the corresponding asymptotic cut off \(\chi ^2_{3,0.95}\), while just a few distances less are below the scaled-F threshold of Hardin and Rocke (2005), which is more accurate than the asymptotic cut off in moderately-sized normal samples.

5.2 Stock index returns

Gupta et al. (2013, Chapter 10) argue that elliptically contoured distributions are often suitable to describe stock returns and provide both theoretical and empirical evidence of this behavior. In particular they consider daily data from Morgan Stanley Capital International for the equity markets returns of three developed countries (Germany, UK and USA), to which they fit Student-t models with fixed degrees of freedom. Estimation of the degrees of freedom in a multivariate Student-t model for daily returns is considered by Dominicy et al. (2013), while Ley and Neven (2015) propose an efficient and possibly robust test for \(\nu \) in the same context. Li (2017) also supports the adoption of Student-t models for daily index returns.

To show the performance of our approach in a low-dimensional financial scenario, where we only look at the relationship between markets and exclude any sophisticated form of serial dependence in each series, we analyze bivariate data on the daily stock index returns of the Canadian and UK equity markets available from Li (2018). Specifically, we take the observations corresponding to the working days of years 1991 and 1992, so that in our data set \(n=520\) and \(p=2\). We then simulate the shock of a financial crisis by replacing the last 60 observations of the data set with the daily stock index returns observed in the same countries from 15/09/2008 onwards, the date when Lehman Brothers filed for bankruptcy. As for the previous application, the Supplementary Material provides a link to the data and gives further numerical results that complement those reported below.

Our approach gives \(\widetilde{\nu }_W=6\) and \(\widetilde{\nu }_K=5\) for the two-years bivariate series of uncontaminated index returns, assuming \(\varepsilon =0\), with a slight discordance that might perhaps be attributed to a mild difference in the kurtosis of the two marginal return series after trimming. Nevertheless, these results are in good agreement with those obtained through the non-robust distances (27), that lead to \(\widehat{\nu }_W=\widehat{\nu }_K=6\). Following the findings of Sect. 4.1, we thus conclude that a bivariate Student-t model with 6 degrees of freedom may provide a sensible representation of the joint distribution of such returns, as indeed expected in the presence of a relatively homogeneous data-generating process for the stock index returns.

The situation is instead very different when we replace the last 60 bivariate observations with pairs of index returns exhibiting the very high volatility typical of periods of great financial instability and turbulence, such as the last months of 2008. The estimated entries of \(\varSigma \) are grossly inflated by this contamination and the need for robust methods becomes paramount. However, the index plot of the ordered squared robust distances (6), displayed in left-hand panel of Fig. 3, now does not allow straightforward identification of the contamination rate. Neither is this information available by looking at the time series of the squared robust distances (right-hand panel of Fig. 3), which shows a clear change in regime around Day 460, but also many small distances after that date. To infer the bivariate structure of the data, we then rescale the squared robust distances as in (14). These rescaled distances are available through the Supplementary Material for \(\nu =3,\ldots ,20\).

In the absence of an automated procedure for jointly estimating \(\nu \) and \(\varepsilon \), we take advantage of the preliminary estimate \(\check{\nu }=6\) and of the informal ideas briefly sketched in Sect. 4.3 for the purpose of reaching a tentative estimate of the contamination rate. We then see that the 45 largest squared robust distances \(\widetilde{d}_{i,\alpha _n,6}^2\) are above the asymptotic 0.99 quantile of T, which is 14.57, and correspondingly compute the contamination rate as \(\varepsilon =45/520\). We finally plug in the value in (15). With this choice of \(\varepsilon \), we consistently obtain \(\widetilde{\nu }_W=6\) and \(\widetilde{\nu }_K=5\), as before, while the non-robust estimates of \(\nu \) become completely unreliable for the contaminated series (ranging from \(\widehat{\nu }_K=3\), to \(\widehat{\nu }_W=9\) and \(\widehat{\nu }_{L_2}=\nu _{\textrm{max}}\)). The trimmed discrepancy measures (28) and (29) with \(\varphi =0.25\), a sensible amount of trimming given the chosen value of \(\varepsilon \), yield the estimate \(\widetilde{\nu }_{W_{0.25}} = \widetilde{\nu }_{W_{0.25}} = 5\), for which we obtain \(\eta _{0.5,2}(5)=4.97\) under Assumption 3. Although stringent sensitivity checks would be difficult without knowing the true value of either \(\nu \) and \(\varepsilon \), we note that similar results mainly pointing to \(\widetilde{\nu }=5\) are obtained by adopting slightly different choices of \(\varepsilon \), such as \(\varepsilon =50/520\) from the asymptotic 0.975 quantile of T on 5 degrees of freedom. Furthermore, a value of 5 or 6 degrees of freedom is still a plausible tentative estimate of \(\nu \) when our approach is applied with \(\varepsilon =0\) to the shorter series made by the first 460 bivariate observations of returns, as it would be the case if we only had available the right-hand panel of Fig. 3.

Finally, we apply the outlier identification approach already depicted in Sect. 5.1 to the squared robust distances \(\widetilde{d}_{1,\alpha _n}^2,\ldots ,\widetilde{d}_{520,\alpha _n}^2\) from this data set. If we compare the observed distances with the estimated quantiles of their exact distribution for clean samples of size \(m_n=475\), we see that 49 observations are labeled as outliers at the 5% significance level if Assumption 3 holds with \(\nu =5\). In this example not all the contaminant returns are anomalous with respect to the baseline model, and indeed a few of them do not stand out in our robust analysis, but only 6 genuine pairs of returns are wrongly declared to be outliers under the bivariate Student-t model with \(\nu =5\) (if we believe it being the true data-generating process). Not surprisingly, the rate of false detections is instead much higher under the bivariate normal model, with 41 uncontaminated pairs spotted by the asymptotic cut off \(\chi ^2_{2,0.95}\) and two less by the scaled-F threshold of Hardin and Rocke (2005). On the other hand, the gain in power implied by the simplistic assumption of light tails is very limited (only 6 contaminated returns in the asymptotic framework) and does not compensate the large swamping effect that occurs before the volatility break.

6 Concluding remarks

Motivated by the large prevalence of a normality assumption for the “good” part of the data in the operational usage of (multivariate) high-breakdown estimators based on trimming, in this work we have addressed two issues. The first one concerns the derivation of a ready-to-use formula for the factor that makes the trimmed estimator of scatter consistent under a multivariate Student-t model with \(\nu >2\) degrees of freedom, with the aim of extending the feasibility of a robust approach to heavy-tail scenarios. Although the proof of the existence of such a factor is available since long time (Butler et al. 1993; Croux and Haesbroeck 1999), our formula is very simple and only involves standard numerical routines, which are available in virtually all programming languages. It can thus be easily plugged into more sophisticated procedures that make repeated use of robust estimators and distances, such as methods that monitor the effects of different choices in the level of trimming (Riani et al. 2009; Hubert et al. 2012; Cerioli et al. 2018, 2019; Clarke and Grose 2023), large-scale outlier detection tools for anti-fraud applications (Perrotta et al. 2020) and robust versions of the EM algorithm for classification purposes (Cappozzo et al. 2020b, a). Also the extension of our formula to regression problems becomes straightforward. In that framework, an important and difficult problem that crucially relies on the consistency factor is how to obtain a consistent estimator of the proportion of “good” observations (Berenguer-Rico et al. 2023).

We argue that the adoption of elliptical models in real-world applications involving high-breakdown estimators has been discouraged by the requirement of estimating the tail parameter of the model, which is usually unknown. Therefore, in the second part of our work, we have developed a Monte Carlo procedure for obtaining an integer estimate of the degrees of freedom parameter of the assumed multivariate Student-t model. Our procedure takes advantage of a suitably rescaled version of the squared robust Mahalanobis-type distances computed from high-breakdown estimators. Estimation of \(\nu \) from the quantiles of t-based Mahalanobis distances has been advocated, but not pursued, by Ley and Neven, (2015, p. 123). We can thus see our approach also as a robust development along that suggested path.

Admittedly, there remain a number of open issues that deserve further research. The first apparent shortcoming of our method concerns the assumption of an integer value of \(\nu \) in the postulated multivariate Student-t distribution. Although we do not believe it to be a substantial limitation in most practical situations, this assumption could be potentially relaxed by considering the match between the empirical and the asymptotic distribution of the squared robust distances, even if at the likely expense of a larger finite-sample bias, as explained in Sect. 3.1. The most relevant methodological open problem is, in our opinion, the derivation of the theoretical properties of the suggested estimators of \(\nu \), about which we have provided substantial empirical evidence both through simulation and data analysis. These properties, that still appear to be out of reach, would provide a solid methodological ground for the development of more efficient iterative procedures based on reweighting and of formal outlier detection rules, such as those of García-Escudero and Gordaliza (2005) and Cerioli (2010), under Student-t models, thus improving over the heuristic approach adopted in our data analysis examples of Sect. 5. We also acknowledge the intrinsic limitation of popular multivariate trimming methods, like the MCD estimator adopted in this work, to elliptical low-dimensional models. Boudt et al. (2020, p. 125) note that the usual approximations to the distribution of the squared robust distances do not work in a high-dimensional framework when they are computed from a regularized version of the MCD. The extension of the results of this paper to non-elliptical and high-dimensional data generating processes is thus another important task for future research.

Finally, we have briefly argued in Sect. 4.3 that simultaneous determination of both \(\nu \) and \(\varepsilon \) in an automated fashion is an important open problem that deserves further theoretical and empirical attention. Our conjecture looks in the direction of exploring a grid of tentative contamination rates, but further substantial work is needed. We also believe that such an automated procedure could be a promising framework for establishing the hoped-for formal outlier detection rules mentioned above.