A relation among tangle, 3-tangle, and von Neumann entropy of entanglement for three qubits

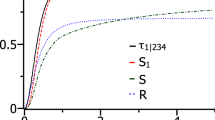
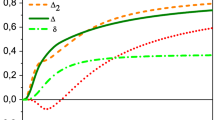
Abstract

In this paper, we derive a general formula of the tangle for pure states of three qubits and present three explicit local unitary (LU) polynomial invariants. Our result goes beyond the classical work of tangle, 3-tangle, and von Neumann entropy of entanglement for Acín et al.’ Schmidt decomposition (ASD) of three qubits by connecting the tangle, 3-tangle, and von Neumann entropy for ASD with Acín et al.’s LU invariants. In particular, our result reveals a general relation among tangle, 3-tangle, and von Neumann entropy, together with a relation among their averages. The relations can help us find the entangled states satisfying distinct requirements for tangle, 3-tangle, and von Neumann entropy. Moreover, we obtain all the states of three qubits of which tangles, concurrence, 3-tangle, and von Neumann entropy do not vanish and these states are endurable when one of three qubits is traced out. We indicate that for the three-qubit W state, its average von Neumann entropy is maximal only within the W SLOCC class, and that under ASD the three-qubit GHZ state is the unique state of which the reduced density operator obtained by tracing any two qubits has the maximal von Neumann entropy.

Appendices

Appendix A. Calculation of tangles

(A) Calculating $\tau _{AB}$

From the definition of $\tau _{AB}$ in Eq. (2), we obtain the characteristic polynomial (CP) of $\rho _{AB}\overline{\rho _{AB}}$ as follows,

$$\begin{aligned} (X^{2}-\Delta X+\Theta ^{2})X^{2}, \end{aligned}$$

(A2)

where

$$\begin{aligned} \Theta= & {} |(c_{0}c_{7}-c_{2}c_{5})^{2}+(c_{1}c_{6}-c_{3}c_{4})^{2} \nonumber \\{} & {} -2(c_{0}c_{7}+c_{2}c_{5})(c_{1}c_{6}+c_{3}c_{4}) \nonumber \\{} & {} +4c_{0}c_{3}c_{5}c_{6}+4c_{1}c_{2}c_{4}c_{7}|, \end{aligned}$$

(A3)

$$\begin{aligned} \Delta= & {} 2\left( \left| c_{0}\right| ^{2}+\left| c_{1}\right| ^{2}\right) \left( \left| c_{6}\right| ^{2}+\left| c_{7}\right| ^{2}\right) \nonumber \\{} & {} +2\left( \left| c_{2}\right| ^{2}+\left| c_{3}\right| ^{2}\right) \left( \left| c_{4}\right| ^{2}+\left| c_{5}\right| ^{2}\right) \nonumber \\{} & {} +2\left| c_{0}c_{6}^{*}+c_{1}c_{7}^{*}\right| ^{2}+2\left| c_{2}c_{4}^{*}+c_{3}c_{5}^{*}\right| ^{2} \nonumber \\{} & {} -4*re(\left( c_{0}c_{2}^{*}+c_{1}c_{3}^{*}\right) \left( c_{6}c_{4}^{*}+c_{7}c_{5}^{*}\right) ) \nonumber \\{} & {} -4*re(\left( c_{0}c_{4}^{*}+c_{1}c_{5}^{*}\right) \left( c_{6}c_{2}^{*}+c_{7}c_{3}^{*}\right) ), \end{aligned}$$

(A4)

and re(c) indicates the real part of a complex number c. Moreover, one can find

$$\begin{aligned} 4\Theta =\tau _{ABC}\text {.} \end{aligned}$$

(A5)

Hence, the eigenvalues of $\rho _{AB}\overline{\rho _{AB}}$ are 0, 0,  and $\frac{\Delta \pm \sqrt{\Delta ^{2}-4\Theta ^{2}}}{2}$. It is known that $\rho _{AB}\overline{\rho _{AB}}$ has only real and nonnegative eigenvalues [13]. Then, by the definition of $\tau _{AB}$ in Eq. (2), we obtain

$$\begin{aligned} \tau _{AB}= & {} \left( \sqrt{\frac{\Delta +\sqrt{\Delta ^{2}-4\Theta ^{2}}}{2}} -\sqrt{\frac{\Delta -\sqrt{\Delta ^{2}-4\Theta ^{2}}}{2}}\right) ^{2} \nonumber \\= & {} \Delta -2\Theta \nonumber \\= & {} \Delta -\frac{\tau _{ABC}}{2}. \end{aligned}$$

(A6)

(B) Calculating $\tau _{AC}$

Similarly, we can obtain the CP of $\rho _{AC}\overline{\rho _{AC}}$ as follows,

$$\begin{aligned} X^{2}(X^{2}-\Phi X+\Upsilon ^{2}), \end{aligned}$$

(A7)

where

$$\begin{aligned} \Upsilon =\Theta , \end{aligned}$$

(A8)

$$\begin{aligned} \Phi= & {} 2\left( \left| c_{0}\right| ^{2}+\left| c_{2}\right| ^{2}\right) \left( \left| c_{5}\right| ^{2}+\left| c_{7}\right| ^{2}\right) \nonumber \\{} & {} +2\left( \left| c_{1}\right| ^{2}+\left| c_{3}\right| ^{2}\right) \left( \left| c_{4}\right| ^{2}+\left| c_{6}\right| ^{2}\right) \nonumber \\{} & {} +2\left| c_{0}c_{5}^{*}+c_{2}c_{7}^{*}\right| ^{2}+2\left| c_{1}c_{4}^{*}+c_{3}c_{6}^{*}\right| ^{2} \nonumber \\{} & {} -4*re(\left( c_{0}c_{1}^{*}+c_{2}c_{3}^{*}\right) \left( c_{5}c_{4}^{*}+c_{7}c_{6}^{*}\right) ) \nonumber \\{} & {} -4*re(\left( c_{0}c_{4}^{*}+c_{2}c_{6}^{*}\right) \left( c_{5}c_{1}^{*}+c_{7}c_{3}^{*}\right) ). \nonumber \\{} & {} \end{aligned}$$

(A9)

Then, we obtain

$$\begin{aligned} \tau _{AC}=\Phi -2\Upsilon =\Phi -\frac{\tau _{ABC}}{2}. \end{aligned}$$

(A10)

(C) Calculating $\tau _{BC}$

Similarly, the characteristic polynomial of $\rho _{BC}\overline{\rho _{BC}}$ is given by

$$\begin{aligned} X^{2}(X^{2}-\Psi X+\digamma ^{2}), \end{aligned}$$

(A11)

where

$$\begin{aligned} \digamma =\Theta , \end{aligned}$$

(A12)

$$\begin{aligned} \Psi= & {} 2\left( \left| c_{0}\right| ^{2}+\left| c_{4}\right| ^{2}\right) \left( \left| c_{3}\right| ^{2}+\left| c_{7}\right| ^{2}\right) \nonumber \\{} & {} +2\left( \left| c_{1}\right| ^{2}+\left| c_{5}\right| ^{2}\right) \left( \left| c_{2}\right| ^{2}+\left| c_{6}\right| ^{2}\right) \nonumber \\{} & {} +2\left| c_{0}c_{3}^{*}+c_{4}c_{7}^{*}\right| ^{2}+2\left| c_{1}c_{2}^{*}+c_{5}c_{6}^{*}\right| ^{2} \nonumber \\{} & {} -4*re(\left( c_{0}c_{1}^{*}+c_{4}c_{5}^{*}\right) \left( c_{3}c_{2}^{*}+c_{7}c_{6}^{*}\right) ) \nonumber \\{} & {} -4*re(\left( c_{0}c_{2}^{*}+c_{4}c_{6}^{*}\right) \left( c_{3}c_{1}^{*}+c_{7}c_{5}^{*}\right) ). \end{aligned}$$

(A13)

Then, we obtain

$$\begin{aligned} \tau _{BC}=\Psi -2\digamma =\Psi -\frac{\tau _{ABC}}{2}. \end{aligned}$$

(A14)

(D) By solving CKW equations [13]

$$\begin{aligned} \tau _{AB}+\tau _{AC}+\tau _{ABC}= & {} \tau _{A(BC)}, \end{aligned}$$

(A15)

$$\begin{aligned} \tau _{AB}+\tau _{BC}+\tau _{ABC}= & {} \tau _{B(AC)}, \end{aligned}$$

(A16)

$$\begin{aligned} \tau _{AC}+\tau _{BC}+\tau _{ABC}= & {} \tau _{C(AB)}, \end{aligned}$$

(A17)

where $\tau _{A(BC)}=4\det \rho _{A}$, $\tau _{B(AC)}=4\det \rho _{B}$, and $\tau _{C(AB)}=4\det \rho _{C}$, we obtain

$$\begin{aligned} \tau _{AB} =&\frac{\tau _{A(BC)}+\tau _{B(AC)}-\tau _{C(AB)}-\tau _{ABC}}{2},\end{aligned}$$

(A18)

$$\begin{aligned} \tau _{AC} =&\frac{\tau _{A(BC)}-\tau _{B(AC)}+\tau _{C(AB)}-\tau _{ABC}}{2},\end{aligned}$$

(A19)

$$\begin{aligned} \tau _{BC} =&\frac{-\tau _{A(BC)}+\tau _{B(AC)}+\tau _{C(AB)}-\tau _{ABC}}{2} . \end{aligned}$$

(A20)

When the 3-tangle $\tau _{ABC}$ is zero, we obtain the following,

$$\begin{aligned} \Delta= & {} \frac{\tau _{A(BC)}+\tau _{B(AC)}-\tau _{C(AB)}}{2}, \end{aligned}$$

(A21)

$$\begin{aligned} \Phi= & {} \frac{\tau _{A(BC)}-\tau _{B(AC)}+\tau _{C(AB)}}{2}, \end{aligned}$$

(A22)

$$\begin{aligned} \Psi= & {} \frac{-\tau _{A(BC)}+\tau _{B(AC)}+\tau _{C(AB)}}{2}. \end{aligned}$$

(B1)

Obviously, $\Delta$, $\Phi$, $\Psi$ are simple polynomial of degree 4 although it is hard to compute $\det \rho _{A}$, $\det \rho _{B}$, and $\det \rho _{C}$.

Appendix B The GHZ state is unique state of three qubits which has maximally von Neumann entropy

Claim: If a state of three qubits possesses the maximal von Neumann entropy, $S(\rho _{\mu })=\ln 2$, where $\mu \in \{A,B,C\}$, then the state must be GHZ.

Proof: Clearly, $S(\rho _{\mu })$ increases strictly monotonically as $\alpha _{\mu }$ increases. Therefore, $S(\rho _{\mu })=\ln 2$ iff $\alpha _{\mu }=1/4$. Thus, we have the following equations

$$\begin{aligned} \alpha _{A}= & {} J_{2}+J_{3}+J_{4}=1/4, \\ \alpha _{B}= & {} J_{1}+J_{3}+J_{4}=1/4, \\ \alpha _{C}= & {} J_{1}+J_{2}+J_{4}=1/4, \end{aligned}$$

(B2)

and we obtain

$$\begin{aligned} J_{1}=J_{2}=J_{3}. \end{aligned}$$

(B3)

Using Tables 1 and 2, equation (B1) leads to

$$\begin{aligned} \lambda _{0}^{4}-\lambda _{0}^{2}(1-\lambda _{1}^{2})+1/4=0. \end{aligned}$$

(B4)

From (B5), we have a solution

$$\begin{aligned} \lambda _{1}= & {} 0, \end{aligned}$$

(B5)

$$\begin{aligned} \lambda _{0}= & {} 1/\sqrt{2}, \end{aligned}$$

(B6)

$$\begin{aligned} \lambda _{2}^{2}+\lambda _{3}^{2}+\lambda _{4}^{2}= & {} 1/2. \end{aligned}$$

(B7)

Using $J_{2}=J_{3}$ in Eq. (B4), we have

$$\begin{aligned} \lambda _{2}=\lambda _{3}. \end{aligned}$$

(B8)

From that $J_{1}=J_{2}$ in Eq. (B4), we obtain

$$\begin{aligned} \lambda _{2}\lambda _{3}=\lambda _{0}\lambda _{2}. \end{aligned}$$

(B9)

There are two scenarios for $\lambda _{2}$: $\lambda _{2}\ne 0$ and $\lambda _{2}=0$. The first scenario is impossible since if $\lambda _{2}\ne 0$, then from Eqs. (B7, B9, B10), we obtain

$$\begin{aligned} \lambda _{0}=\lambda _{2}=\lambda _{3}=1/\sqrt{2}. \end{aligned}$$

(B10)

From Eq. (B8), we know clearly that Eq. (B11) cannot hold. Therefore, $\lambda _{2}$ must be zero.

With $\lambda _2=0$, from Eqs. (B8, B9) we obtain

$$\begin{aligned} \lambda _{2}= & {} \lambda _{3}=0, \end{aligned}$$

(B11)

$$\begin{aligned} \lambda _{4}= & {} 1/\sqrt{2}. \end{aligned}$$

(B12)

The state satisfying Eqs. (B6, B7, B12, B13 ) is just GHZ.

Appendix C The extrema for W SLOCC class

We next find an extrema of m with the constraint of $\sum _{i=0}^{3}\lambda _{i}^{2}=1$ for the W SLOCC class. For states of W SLOCC class, $\alpha _{A}=\lambda _{0}^{2}(\lambda _{2}^{2}+\lambda _{3}^{2})$, $\alpha _{B}=\lambda _{3}^{2}(\lambda _{0}^{2}+\lambda _{2}^{2})$, and $\alpha _{C}=\lambda _{2}^{2}(\lambda _{0}^{2}+\lambda _{3}^{2})$

We define

$$\begin{aligned} F=\frac{1}{3}(S(\rho _{A})+S(\rho _{B})+S(\rho _{C}))+\ell (\sum _{i=0}^{3}\lambda _{i}^{2}-1), \end{aligned}$$

(B13)

where $\ell$ is the Lagrange multiplier. In light of the constrained extreme theorem, we need to solve the equations $\frac{\partial F}{\partial \lambda _{i}}=0$, for $i=0,1,2,3$, and $\frac{\partial F}{\partial \ell }=0$ to find the extrema. From $\frac{\partial F}{\partial \lambda _{1}}=2\ell \lambda _{1}=0$, we obtain $\lambda _{1}=0$. Then, F is reduced to

$$\begin{aligned} F=\frac{1}{3}(S(\rho _{A})+S(\rho _{B})+S(\rho _{C}))+\ell (\lambda _{0}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}-1). \end{aligned}$$

(C1)

From $\frac{\partial F}{\partial \ell }=0$, we obtain

$$\begin{aligned} \lambda _{0}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}=1. \end{aligned}$$

(C2)

From Eq. (C2), we obtain

$$\begin{aligned} \frac{\partial F}{\partial \lambda _{0}}=\frac{1}{3}\left[ \frac{\partial S(\rho _{A})}{\partial \lambda _{0}}+\frac{\partial S(\rho _{B})}{\partial \lambda _{0}}+\frac{\partial S(\rho _{C})}{\partial \lambda _{0}} \right] +2\ell \lambda _{0}, \end{aligned}$$

(C3)

where

$$\begin{aligned} \frac{\partial S(\rho _{\mu })}{\partial \lambda _{0}}=\frac{dS(\rho _{\mu }) }{d\alpha _{\mu }}\frac{\partial \alpha _{\mu }}{\partial \lambda _{0}}, \mu \in \{A,B,C\}. \end{aligned}$$

(C4)

The derivative of $S(\rho _{A})$ is

$$\begin{aligned} \frac{dS(\rho _{A})}{d\alpha _{A}}=-\left[ \frac{d\eta _{A}^{(1)}}{d\alpha _{A}}(1+\ln \eta _{A}^{(1)})+\frac{d\eta _{A}^{(2)}}{d\alpha _{A}}(1+\ln \eta _{A}^{(2)})\right] , \end{aligned}$$

(C5)

where

$$\begin{aligned} \frac{d\eta _{A}^{(1)}}{d\alpha _{A}}=-\frac{1}{\sqrt{1-4\alpha _{A}}},\frac{ d\eta _{A}^{(2)}}{d\alpha _{A}}=\frac{1}{\sqrt{1-4\alpha _{A}}}. \end{aligned}$$

(C6)

Thus,

$$\begin{aligned} \frac{dS(\rho _{A})}{d\alpha _{A}}= & {} -\left[ -\frac{1+\ln \eta _{A}^{(1)}}{ \sqrt{1-4\alpha _{A}}}+\frac{1+\ln \eta _{A}^{(2)}}{\sqrt{1-4\alpha _{A}}} \right] \nonumber \end{aligned}$$

(C7)

$$\begin{aligned}= & {} -\frac{1}{\sqrt{1-4\alpha _{A}}}\ln \frac{\eta _{A}^{(2)}}{\eta _{A}^{(1)} }. \end{aligned}$$

(C8)

Similarly, we obtain

$$\begin{aligned} \frac{dS(\rho _{B})}{d\alpha _{B}}= & {} -\frac{1}{\sqrt{1-4\alpha _{B}}}\ln \frac{\eta _{B}^{(2)}}{\eta _{B}^{(1)}}, \end{aligned}$$

(C9)

$$\begin{aligned} \frac{dS(\rho _{C})}{d\alpha _{C}}= & {} -\frac{1}{\sqrt{1-4\alpha _{C}}}\ln \frac{\eta _{C}^{(2)}}{\eta _{C}^{(1)}}. \end{aligned}$$

(C10)

From Eqs. (C5, C8, C9, C10), we obtain

$$\begin{aligned} \frac{\partial S(\rho _{A})}{\partial \lambda _{0}}= & {} -\frac{2\lambda _{0}(\lambda _{2}^{2}+\lambda _{3}^{2})}{\sqrt{1-4\alpha _{A}}}\ln \frac{ \eta _{A}^{(2)}}{\eta _{A}^{(1)}}, \end{aligned}$$

(C11)

$$\begin{aligned} \frac{\partial S(\rho _{B})}{\partial \lambda _{0}}= & {} -\frac{2\lambda _{0}\lambda _{3}^{2}}{\sqrt{1-4\alpha _{B}}}\ln \frac{\eta _{B}^{(2)}}{\eta _{B}^{(1)}}, \end{aligned}$$

(C12)

$$\begin{aligned} \frac{\partial S(\rho _{C})}{\partial \lambda _{0}}= & {} -\frac{2\lambda _{0}\lambda _{2}^{2}}{\sqrt{1-4\alpha _{C}}}\ln \frac{\eta _{C}^{(2)}}{\eta _{C}^{(1)}}. \end{aligned}$$

(C13)

From Eqs. (C4, C11, C12, C13) and $\frac{ \partial F}{\partial \lambda _{0}}=0$, we obtain

$$\begin{aligned} \ell= & {} \frac{1}{3}\left( \frac{\lambda _{2}^{2}+\lambda _{3}^{2}}{\sqrt{ 1-4\alpha _{A}}}\ln \frac{\eta _{A}^{(2)}}{\eta _{A}^{(1)}} \right. \nonumber \\{} & {} +\frac{\lambda _{3}^{2}}{\sqrt{1-4\alpha _{B}}}\ln \frac{\eta _{B}^{(2)}}{ \eta _{B}^{(1)}} \nonumber \\{} & {} \left. +\frac{\lambda _{2}^{2}}{\sqrt{1-4\alpha _{C}}}\ln \frac{\eta _{C}^{(2)}}{\eta _{C}^{(1)}} \right) . \end{aligned}$$

(C14)

Similarly, we consider

$$\begin{aligned} \frac{\partial F}{\partial \lambda _{2}}=\frac{1}{3}\left( \frac{\partial S(\rho _{A})}{\partial \lambda _{2}}+\frac{\partial S(\rho _{B})}{\partial \lambda _{2}}+\frac{\partial S(\rho _{C})}{\partial \lambda _{2}}\right) +2\ell \lambda _{2}. \end{aligned}$$

(C15)

Clearly,

$$\begin{aligned} \frac{\partial S(\rho _{\mu })}{\partial \lambda _{2}}=\frac{dS(\rho _{\mu }) }{d\alpha _{\mu }}\frac{\partial \alpha _{\mu }}{\partial \lambda _{2}},\mu \in \{A,B,C\}. \end{aligned}$$

(C16)

From Eqs. (C8, C9, C10, C15, C16) and $\frac{\partial F}{\partial \lambda _{2}}=0$, we obtain

$$\begin{aligned} \ell= & {} \frac{1}{3}\left( \frac{\lambda _{0}^{2}}{\sqrt{1-4\alpha _{A}}}\ln \frac{\eta _{A}^{(2)}}{\eta _{A}^{(1)}} \right. \nonumber \\{} & {} +\frac{\lambda _{3}^{2}}{\sqrt{1-4\alpha _{B}}}\ln \frac{\eta _{B}^{(2)}}{ \eta _{B}^{(1)}} \nonumber \\{} & {} \left. +\frac{\lambda _{0}^{2}+\lambda _{3}^{2}}{\sqrt{1-4\alpha _{C}}} \ln \frac{\eta _{C}^{(2)}}{\eta _{C}^{(1)}} \right) . \end{aligned}$$

(C17)

Similarly, from $\frac{\partial F}{\partial \lambda _{3}}=0$ we obtain

$$\begin{aligned} \ell= & {} \frac{1}{3}\left( \frac{\lambda _{0}^{2}}{\sqrt{1-4\alpha _{A}}}\ln \frac{\eta _{A}^{(2)}}{\eta _{A}^{(1)}} \right. \nonumber \\{} & {} +\frac{\lambda _{0}^{2}+\lambda _{2}^{2}}{\sqrt{1-4\alpha _{B}}}\ln \frac{ \eta _{B}^{(2)}}{\eta _{B}^{(1)}} \nonumber \\{} & {} \left. +\frac{\lambda _{2}^{2}}{\sqrt{1-4\alpha _{C}}}\ln \frac{\eta _{C}^{(2)}}{\eta _{C}^{(1)}}\right) . \end{aligned}$$

(C18)

From Eqs. (C3, C14, C17), we obtain

$$\begin{aligned} \frac{1-2\lambda _{0}^{2}}{\sqrt{1-4\alpha _{A}}}\ln \frac{\eta _{A}^{(2)}}{ \eta _{A}^{(1)}}=\frac{1-2\lambda _{2}^{2}}{\sqrt{1-4\alpha _{C}}}\ln \frac{ \eta _{C}^{(2)}}{\eta _{C}^{(1)}}. \end{aligned}$$

(C19)

From Eqs. (C3, C14, C18), we obtain

$$\begin{aligned} \frac{1-2\lambda _{0}^{2}}{\sqrt{1-4\alpha _{A}}}\ln \frac{\eta _{A}^{(2)}}{ \eta _{A}^{(1)}}=\frac{1-2\lambda _{3}^{2}}{\sqrt{1-4\alpha _{B}}}\ln \frac{ \eta _{B}^{(2)}}{\eta _{B}^{(1)}}. \end{aligned}$$

(C20)

From Eqs. (C3, C17, C18), we obtain

$$\begin{aligned} \frac{1-2\lambda _{3}^{2}}{\sqrt{1-4\alpha _{B}}}\ln \frac{\eta _{B}^{(2)}}{ \eta _{B}^{(1)}}=\frac{1-2\lambda _{2}^{2}}{\sqrt{1-4\alpha _{C}}}\ln \frac{ \eta _{C}^{(2)}}{\eta _{C}^{(1)}}. \end{aligned}$$

(C21)

When $\lambda _{0}=\lambda _{2}=\lambda _{3}$, Eqs. (C19, C20, C21) hold. Via Eq. (C3), one can see that $\lambda _{0}=\lambda _{2}=\lambda _{3}=1/\sqrt{3}$ is an extrema of m with the constraint $\sum _{i=0}^{3}\lambda _{i}^{2}=1$.

Appendix D. CKW inequalities for GHZ SLOCC class

Note that for the GHZ SLOCC class, $\lambda _{0}\lambda _{4}\ne 0$. There is also an additional constraint $\sum _{i=0}^{4}\lambda _{i}^{2}=1$.

(A) When $\lambda _{1}=\lambda _{3}=0$ and $\lambda _{2}\ne 0$, we have

$$\begin{aligned} A=\frac{4}{3}(\lambda _{0}^{2}\lambda _{2}^{2}). \end{aligned}$$

Clearly,

$$\begin{aligned} A=\frac{4}{3}(\lambda _{0}^{2}\lambda _{2}^{2})\le \frac{4}{3}\left( \frac{ \lambda _{0}^{2}+\lambda _{2}^{2}}{2}\right) ^{2}=\frac{1}{3}\left( 1-\lambda _{4}^{2}\right) ^{2}<\frac{1}{3} \end{aligned}$$

Similarly, we can obtain $A<\frac{1}{3}$ for the case with $\lambda _{1}=\lambda _{2}=0,\lambda _{3}\ne 0$ and the case with $\lambda _{2}=\lambda _{3}=0,\lambda _{1}\ne 0$.

(B) When $\lambda _{1}\lambda _{3}\ne 0$ and $\lambda _{2}=0$, A is reduced to

$$\begin{aligned} A=\frac{4}{3}(\lambda _{0}^{2}\lambda _{3}^{2}+\lambda _{1}^{2}\lambda _{4}^{2}). \end{aligned}$$

In light of constrained extreme theorem, we consider the following function

$$\begin{aligned} U=\frac{4}{3}(\lambda _{0}^{2}\lambda _{3}^{2}+\lambda _{1}^{2}\lambda _{4}^{2})+q(\lambda _{0}^{2}+\lambda _{1}^{2}+\lambda _{3}^{2}+\lambda _{4}^{2}-1). \end{aligned}$$

From $\frac{\partial U}{\partial \lambda _{i}}=0$, obtain only one extreme $\lambda _{0}=\lambda _{1}=\lambda _{3}=\lambda _{4}=\frac{1}{2}$, i.e., $\frac{1}{2}(|000\rangle +|100\rangle +|110\rangle +|111\rangle )$, at which $\max A=\frac{1}{6}$.

(C) When $\lambda _{1}\lambda _{2}\ne 0$ and $\lambda _{3}=0$, A is reduced to

$$\begin{aligned} A=\frac{4}{3}(\lambda _{0}^{2}\lambda _{2}^{2}+\lambda _{1}^{2}\lambda _{4}^{2}). \end{aligned}$$

The discussion is similar to (B), and there is only one extreme $\lambda _{0}=\lambda _{1}=\lambda _{2}=\lambda _{4}=\frac{1}{2}$, i.e., $\frac{1}{2} (|000\rangle +|100\rangle +|101\rangle +|111\rangle )$, $\max A=\frac{1}{6}$.

(D) When $\lambda _{1}=0$ and $\lambda _{2}\lambda _{3}\ne 0$, then

$$\begin{aligned} A=\frac{4}{3}(\lambda _{0}^{2}\lambda _{3}^{2}+\lambda _{0}^{2}\lambda _{2}^{2}+\lambda _{2}^{2}\lambda _{3}^{2}). \end{aligned}$$

The constraint is

$$\begin{aligned} \lambda _{0}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}+\lambda _{4}^{2}=1, \end{aligned}$$

where $\lambda _{4}$ is considered as a parameter. In light of constrained extreme theorem, for a fixed $\lambda _{4}$, when $\lambda _{0}=\lambda _{2}=\lambda _{3}$, i.e., $\lambda _{0}|000\rangle +\lambda _{0}|101\rangle +\lambda _{0}|110\rangle +\lambda _{4}|111\rangle$, then $\ A$ has the maximum $A=4\lambda _{0}^{4}=\frac{4}{9}(1-\lambda _{4}^{2})^{2}<\frac{4}{9}$ .

(E) When $\lambda _{1}\lambda _{2}\lambda _{3}\ne 0$, let

$$\begin{aligned} f=\frac{4}{3}(\lambda _{0}^{2}\lambda _{3}^{2}+\lambda _{0}^{2}\lambda _{2}^{2}+(\lambda _{1}\lambda _{4}+\lambda _{2}\lambda _{3})^{2}). \end{aligned}$$

Clearly, $A\le f$. We next calculate the maximum value of f. The constraint reads $\lambda _{0}^{2}+\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}+\lambda _{4}^{2}=1.$ In light of the constrained extreme theorem, we consider the function

$$\begin{aligned} F=f+g(\lambda _{0}^{2}+\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}+\lambda _{4}^{2}-1). \end{aligned}$$

From $\frac{\partial F}{\partial \lambda _{i}}=0$, $i=0,1,2,3,4,$ we obtain $\lambda _{1}=\lambda _{2}=\lambda _{3}=\lambda _{4}$ and $\lambda _{0}=0$. Thus, f has the maximum value $\frac{1}{3}$. However, we require that $\lambda _{0}$ do not vanish. From $\sum _{i=0}^{4}\lambda _{i}^{2}=1$, we get $\lambda _{0}^{2}+4\lambda _{4}^{2}=1$. Thus, when $\lambda _{1}=\lambda _{2}=\lambda _{3}=\lambda _{4}$, $A=\frac{4}{3}((2\lambda _{4}^{2}))(1-2\lambda _{4}^{2})<1/3.$ Clearly, $\lim _{\lambda _{0}\rightarrow 0}A=\frac{1}{3}$. For example, when $\lambda _{0}^{2}=\frac{1 }{100}$, then $A=\frac{3333}{10\,000}\approx \frac{1}{3}$.