1 Introduction

A time series is an essential data structure consisting of a sequence of numerical values appear in chronological order. Recently, time series analysis has become crucial for predicting dynamic phenomena in various applications, including climate change [1,2,3,4,5], financial markets [6,7,8,9], energy management [10, 11], manufacturing, and transportation planning [12,13,14]. Time-series forecasting is categorized into univariate and multivariate forecasting based on the number of target variables to be forecasted [15]. Time-series forecasting (TSF) is a vital area within data mining, revolving around the prediction of future trends through the analysis of past values observations [16,17,18]. It plays a vital role in several practical scenarios. For instance, improved combustion environments can be designed by predicting coal-fired power generation, and better planning of power supply and demand can be achieved by predicting wind power generation in the following weeks to ensure stable power system operation [19].

In recent years, researchers have used deep neural networks (DNNs) applied in various fields and have extraordinary impact in solving many problems [20]. Currently, there are three main types of deep learning-based time-series forecasting models: recurrent neural network (RNN)-based [21, 22], TCN-based [23, 24], and transformer-based [25]. The RNN-based method faces challenges such as gradient vanishing, gradient explosion, and limited parallelism. The primary working capability of the transformer-based model originates from the multi-head attention. However, this mechanism is permutable and reversible, leading to loss of time-series information. Additionally, the self-attention mechanism within transformers computes pairwise similarities for all elements, resulting in quadratic growth in both temporal and spatial complexities as the time series length increases. For the TCN-based method, although the TSF method based on these general models achieved good results, it failed to adequately account for the unique characteristics of the time-series data in the modelling process. By contrast, the TCN-based method requires deeper layers to achieve a larger local receptive field. With this, the network can be traced back to the farther past such that the receptive field of each layer exponentially increases, however, this also causes the network to become deeper, which may increase the computational cost and training time.

Given the above problems, we proposed a Fourier enhancement network based on wavelet decomposition to capture sequence features for forecasting and modelling. Specifically, we designed a new module for extracting time-series information: feature extraction based on Fourier enhancement. The Fourier enhancement module can better extract the correlation between sequences, such as periodicity or seasonality, because the original sequence information can be converted to frequency-domain information after Fourier transform, and it can also enhance the frequency domain through this module, reducing the influence of noise and improving the performance of extracting sequence features.

However, it is insufficient to rely solely on FEMEX to extract information from original sequences. There is significantly different information in the sequence than in the original data. Inspired by this, we proposed trend decomposition and wavelet transform to process data entering FEMEX. When the data enter the wavelet transform, they obtain detailed and approximation functions at different scales, allowing the extraction of time–frequency localized features in the sequence, thus improving the prediction performance.

The following are our main contributions in this paper:

  1. (1)

    We proposed W-FENet. This applies trend extraction and wavelet transform to decompose the original sequence into multiple subseries at different scales and model the temporal correlations in the subsequences with the aim of adaptive learning and capturing temporal patterns in a long-term temporal forecasting environment.

  2. (2)

    By studying sample convolution in time-series forecasting, we designed a new feature extraction structure: Fourier enhancement based on feature extraction (FEMEX). This module captures sequence features well, and can improve the prediction efficiency.

  3. (3)

    The experimental results on three benchmark datasets covering energy, economy, and weather indicate that our model outperforms previous forecasting models. Specifically, our model achieved a relative improvement of MSE with 11.1% and MAE with 6.36%.

The rest of this paper is organized as follows: Sect. 2 reviews the related work. In Sect. 3, the describes our model. Section 4 presents experimental results. In the end, Sect. 5 summarizes the study and provides possible trends for subsequent research.

2 Relate Work

This section briefly reviews related work on time series forecasting, temporal temperature enhancement approaches, and wavelet transforms in time series.

2.1 Time Series Forecasting

In the early stages of time-series forecasting, traditional mathematical models like vector autoregressive (VAR) [26] and autoregressive integrated moving average (ARIMA) [27] were commonly used. The introduction of a support vector machine (SVR) [28] brought a conventional machine learning approach to predict future values. The Gaussian distribution [29] models the future distribution instead of assuming a specific functional form for predictions. Nevertheless, these classical models face limitations when dealing with high-dimensional data, as they are primarily suitable for univariate predictions and cannot handle complicated data distributions.

With the increase in the amount of available data and deep learning techniques have advanced, neural networks have demonstrated superior performance compared to traditional models in time-series forecasting. RNNs [30] and TCNs [31] are two common deep models used to model sequence data. RNNs exhibit an excellent ability to capture time dependence and have become popular [32]. Two variants of RNN (i.e. long short-term memory (LSTM) [33] and gated recursive unit (GRU) [34]) have notably enhanced the best performance in time-series forecasting. Nevertheless, there are still notable challenges when it comes to acquiring and effectively utilizing long-sequence features. This challenge can be understood in two ways. First, directly training the RNN on long time series still experiences the problem of vanishing gradients and explosions. Second, cells must remember both short- and long-term information, leading to a trade-off between capturing these two types of information.

On the other hand, relying on its attention mechanism for continuous innovation in text processing and time series analysis with better effectiveness and efficiency, transformer architectures have been extensively adopted in TSF tasks. Zhou et al. [35] designed a selective sparse attention mechanism aimed at reducing the model’s time complexity the from \({\rm O}\left( {L2} \right)\) to \({\rm O}\left( {LLogL} \right)\) to achieve higher efficiency. Inspired by the former model, Autoformer [51] adopts a more effective sequence fragment-level correlation and designs a new time-series forecasting model with a new decomposition architecture and an autocorrelation mechanism. Liu et al. [36] proposed a tree-structured pyramid attention to reduce complexity and enhance the capture of time dependence.

With further research on time-series forecasting algorithms, the focus is biased toward designing new architectures to address the challenge of error accumulation in long time series forecasting [37, 38]. Oreshkin et al. introduced the N-Beats model [39], which is built by stacking multiple layers of fully connected stacks and introduces a bi-residual structure. Liu et al. designed the SCINet model [40], which improves the sample convolution and interaction to effectively model time-series models with complicated temporal dynamics. In addition, there is also ensemble learning to solve extreme cases, such as model collapse caused by mitigating structural mismatches that can easily occur in a single model. Du et al. designed a dynamic ensemble model based on Bayesian optimization [41], which is tuned and trained by the Bayesian Optimization Algorithm (BOA), and finally, the ensemble outputs using the optimal combination of configurations. Gao et al. proposed an online deep learning model based on the ensemble deep random vector functional link (edRVFL) [42], which decomposes, learns, and aggregates through three components: the online decomposition, the online training, and the online dynamic ensemble.

2.2 Temporal Feature Enhancement Approaches

Recently, the feature enhancement has become an important issue in various fields. They are widely used in language, text, and other applications. With limited data availability, data augmentation has become an effective strategy for solving time-series problems [56]. In response to the above problems, research has focused on four schemes: (1) Time-domain to frequency-domain conversion, (2) Unbalanced class enhancement, (3) Gaussian processing methods, and (4) A deeper neural network enhancement model method [57]. In this study, we focused on frequency-domain enhancement. The Fourier transform is a classical mathematical tool widely used in signal processing and spectrum analysis. Due to the good development of deep learning in recent years, researchers have begun to investigate the combination of the Fourier transform and deep learning. For example, Sutskever et al. [43] proposed a sequence-to-sequence (Seq2Seq) model, wherein they utilized a Fourier transform to process the time–frequency characteristics of the input sequence. Li et al. [44] introduced the Fourier transform into a neural network model to solve parametric partial differential equations.

2.3 Wavelet Transform in Time Series

Wavelet transform is a waveform oscillation technique used to localize the characteristics of a signal. Unlike the Fourier Transform, it can accurately capture not only the frequency information of a signal, but also the location of the signal in time. Wavelet transform consists of two main types: (1) Continuous wavelet transform (CWT), which transforms the signal in a continuous time range., and (2) Discrete wavelet transform (DWT), which performs the transform on a finite number of discrete data points. Our study focuses on DWT, which uses orthogonal basis representation to represent signals. Therefore, DWT is an efficient signal analysis method. Due to the ability of wavelet transform to enhance the frequency domain features and improve the signal-to-noise ratio of the sequence, researchers have combined the wavelet transform with different deep learning models to improve the performance of the models. For example, Sasal et al. [45] proposed a univariate time-series forecasting framework based on wavelet transform. Guo et al. [46] employed wavelet decomposed approximation functions fed into the model restore missing details in tasks. Multi-level wavelet [47] transforms amplify the receptive field for image restoration without losing information. Williams et al. [48] used a wavelet transform to change the original sequence into multiple-level detail functions and approximation functions, and discarded the bottom detail function (cD1) to decrease the feature dimension in the task. The Haar wavelet neural network was combined with multi-level processing in reference [49] for image texture analysis and image text generation. In reference [50], ResNet was modified by integrating the initial layer with a wavelet scattering network, achieving considerable performance in image recognition with fewer parameters. Gao et al. [51] achieved fast learning, extrapolation process, and elimination noise by echo state network and empirical wavelet transform (EWT).

3 W-FENet

We defined a multivariate point prediction problem in discrete time. A sample of multivariate sequence with length \(L\): \(\left\{ {x_{1} ,..., \, x_{L} } \right\}\), \(x_{i} \in R^{d}\), and \(d\) denotes the number of features. The data at timestamp \(t\) is \(x_{t}\), and a fixed-length \(\tau\) is set as the length of the prediction window to predict \(\tau\) future values. The predicted values of \(\hat{X}\) is expressed as follows:

$$ \hat{X}_{t + \tau } = f\left( {x_{t - N + 1,} x_{t - N + 2} ,...,x_{t} } \right), $$
(1)

where \(N\) is the length of the lookback window, and \( x_{t - N + 1:t} \, = \left\{ { \, x_{t - N + 1} , \ldots , \, x_{t} } \right\}\) is the lookback window at time point \(t\). For brevity, we used \(X\) and \(\hat{X}\) to denote the historical and predicted data.

3.1 Architecture Analysis

We introduce our W-FENet model, a network architecture for time-series forecasting and modelling that includes trend decomposition and wavelet extraction, FEMEX, U-net improvement [55], and double residual connection. The overall framework of our model is shown in Fig. 1. Our model adopted a codec structure. In encoder, our model via a linear layer to mine features and the Fourier enhancement module to enhance the frequency domain information, better capture the frequency domain features, and extract more accurate and informative frequency domain features from the enhanced data.

Fig. 1
figure 1

Overall framework of the W-FENet model

Full size image

Subsequently, we extracted the correlation between broader time-series data using a downsampling operation. Finally, we used a fully connected network as a decoder prediction. Using the decoder, we remap the features extracted by the encoder to the original data space to reconstruct the prediction results.

In addition, we are aware that information loss may be caused during the feature downsampling process. Therefore, to compensate for this information loss, we divided the original data into two subsequences and compensated for them using interactive learning.

3.2 Trend Decomposition and Wavelet Extraction

We performed a series of processing steps to extract and utilize temporal information and to adapt to learning and capturing temporal patterns in long-series time prediction. First, we decompose the raw data using a moving average technique to derive the data with a trend \(X_{T}\), where the step size of the moving average is \(k\). However, this type of processing leads to the loss of time-series information. Therefore, we further residualise the trend data to obtain the residual data \(X_{R}\). The trend data \(X_{T}\) and residual data \(X_{R}\) obtained are shown in Fig. 2. The processes are expressed as follows:

$$ X_{T} = AvgPool\left( {Padding\left( X \right)} \right)_{k} $$
(2)
$$ X_{R} = X - X_{T} $$
(3)
Fig. 2
figure 2

Trend and residual data

Full size image

In the residual data, there is still much information that can help with the prediction of the model. To capture this information, we applied the discrete wavelet decomposition technique (DWT) to decompose the residual data into multiple approximation functions \(\left( {cA} \right)\) and detailed functions \(\left( {cD} \right)\). Approximation functions provide information regarding the overall trend of the residual data, whereas detailed functions can capture subtle temporal variations. We processed the wavelet-decomposed functions using FEMEX to further analyze and utilize the timing information in these approximate and detailed functions. This feature extraction process helps extract more representative and valuable features that reveal deeper timing patterns. Finally, we merged the processed approximation and detail functions using wavelet reconstruction to restore them to the standard form of the original data. The decomposition and reconstruction processes are as follows:

$$ cA_{n} = downsample\left( {conv\left( {X_{R} ,lowpass\_filter} \right)} \right) $$
(4)
$$ cD_{n} = downsample\left( {conv\left( {X_{R} ,highpass\_filter} \right)} \right) $$
(5)
$$ x\left[ n \right] = \sum\limits_{k = - \infty }^{\infty } {\left( {y_{high} \left[ k \right] \cdot g\left[ {2k - n} \right]) + (y_{low} \left[ k \right] \cdot h\left[ {2k - n} \right]} \right)} $$
(6)

Equation 1.4 shows the process of discrete wavelet decomposition and the calculation of the detail and approximate functions. Equation 1.5 describes the wavelet reconstruction process. \(g\left[ {} \right]\) and \(h\left[ {} \right]\) are high-pass and low-pass filters, respectively. The relationship between them is expressed as follows:

$$ g\left[ {I - 1 - n} \right] = \left( { - 1} \right)^{n} \cdot h\left( n \right) $$
(7)

As shown in Fig. 3, the subsequence set \(X_{original} = \left\{ {cD_{1} ,cD_{2} ,...,cD_{i} ,cA_{4} } \right\}\) is called the i-level DWT result of \(X_{original}\). This multi-level structure allows us to observe the original time series on different scales. Specifically, the detail functions preserve finer details, while the approximation functions capture slowly changing trends.

Fig. 3
figure 3

Multi-level wavelet decomposition diagram, where \(cA_{i}\) represents the approximate function and \(cD_{i}\) represents the detail function

Full size image

This method combines the moving average, residual processing, discrete wavelet decomposition, and time-series information feature extraction, aiming to capture and utilize the features in the original series data to the greatest extent possible to improve the understanding and prediction ability of long-term time patterns.

3.3 Feature Extraction Module Based on Fourier Enhancement (FEMEX)

A multilayer feed-forward neural network cascade neuron is set up to extract the time correlation and consider more comprehensive sequence information in the time series. To offset the potential information loss that may be caused by downsampling, we adopted the trend data \(X_{T}\) obtained by trend decomposition and multiple detail functions and approximation functions obtained by wavelet extraction as inputs, which are separated into two subsequences (i.e. \(X_{odd}\) and \(X_{even}\)). Information loss is compensated for by the interactive learning of the two sequences.

$$ X_{odd}^{s} = X_{odd} \odot \exp \left( {\varphi \left( {X_{even} } \right)} \right) $$
(8)
$$ X_{even}^{s} = X_{even} \odot \exp \left( {\phi \left( {X_{odd} } \right)} \right) $$
(9)

\({\text{X}}_{even}^{s}\), \({\text{X}}_{odd}^{s}\) is the hidden state of the projection after training by two feedforward neural networks, where \(\odot\) is the product of elements, and \(\varphi\) and \(\phi\) are the training structures we used the feedforward neural network to build, where the training parameters are different, \(\varphi = \phi = \tanh \left( {F\left( {dropout\left( {L{\text{Re}} lu\left( {F\left( {} \right)} \right)} \right)} \right)} \right)\).

The frequency-domain features of the data can be highlighted by converting the time-domain information into frequency-domain information using a Fourier enhancement module. Making these features more visible and recognizable can help the model better capture periodicities, trends, and patterns in the data.

$$ X_{odd}{\prime} = X_{odd}^{s} + P\left( {X_{even}^{s} } \right) $$
(10)
$$ X_{even}{\prime} = X_{even}^{s} + U\left( {X_{odd}^{s} } \right) $$
(11)

As shown in Eqs. (10) and (11), \({\text{X}}_{even}{\prime}\), \({\text{X}}_{odd}{\prime}\) is the final output of the interactive learning module, where \(P\) and \(U\) are functions of the same structure with different Fourier enhancement parameters based on Fourier transforms, \(P = U = \tanh \left( {FE\left( {dropout\left( {L{\text{Re}} lu\left( {FE\left( {} \right)} \right)} \right)} \right)} \right)\), \(FE\) are Fourier enhancement functions. The FEMEX structure is shown in Fig. 4.

Fig. 4
figure 4

Schematic structure of FEMEX, integrate denotes the integration of the parity subsequence into the sequence interval before decomposition

Full size image

3.4 U-net Improvement

In this part, we improve the U-shaped structure to analyze time-series data and efficiently capture sequence features. A residual connection was added at the end to enable a U-shaped structure to extract information better than the trend data.

Using a U-shaped structure for downsampling can extensively expand the receptive field and extract the correlation between time series data to efficiently capture features between series. Our model mines the potential features in the data and provides richer information for subsequent analysis and prediction. The architecture has N layers. First, the features of a more extensive range of time series data are extracted by downsampling compression information, and each layer of input is derived from the output of the previous layer. Second, in the upsampling stage, the downsampling compression information of the same layer is first combined, and then the upsampling embedding is performed. Subsequently, the remaining residual data after trend decomposition is connected to the last layer of the encoder through the residuals to make the sequence more predictable. The specific process is shown in Fig. 5. Finally, the coded part \(X_{en}\) is obtained after going through this structure, and the \(X_{en}\) of the coding output is input into the full connection layer to decode and predict \(X_{de}\). The process is represented as follows:

$$ X_{de} = Fc\left( {X_{en} } \right) $$
(12)
Fig.5
figure 5

Illustration of the U-net Improvement structure. Effectively use the U-net structure to extract information from different receptive fields. To ensure that there will not be too much information loss, we use the residual connection to connect the down-sampled data and the up-sampled data at the same layer

Full size image

3.5 Double Residual Connection

The classic deep learning residual network architecture passes the results from the upper stack to the following stack, and the upper stack output residuals are added to the output of the lower stack. These deepening network models can improve trainability. However, in this study, simple deepening and residual connections lead to overfitting, and some features that cannot be trained are not well mined. A hierarchical double-residual topology was used. The proposed architecture has two residual branches: one running on the reverse prediction of each layer and the other running on the prediction branch of each layer. This hierarchical double-residual topology can better uncover latent data features, enhancing both model performance and trainability. The following equations describe this operation:

$$ f^{i} = W_{for}^{i - 1} x^{i - 1} + \theta_{for} $$
(13)
$$ b^{i} = W_{back}^{i - 1} x^{i - 1} + \theta_{back} $$
(14)
$$ x_{b}^{l} = x^{l} - \hat{b}^{l} $$
(15)
$$ \hat{y} = \sum\limits_{l} {\hat{f}^{l} } + \sum\limits_{l} {\hat{x}_{b}^{l} } $$
(16)

where \(f\) and \(b\) are obtained by forward and reverse predictions, respectively. The forward prediction of \(f\) is stacked, and the reverse prediction \(b\) is subtracted from the current stack input, which is also stacked onto the predicted value.

The blocks are organized into stacks using the double residual stacking principle to obtain higher prediction accuracy, but it also leads to increased time complexity. we perform intermediate supervision on all stack outputs using basic fact values to learn intermediate time features. The predicted value of the \(m\) th stack, \(x^{l}\) of length \(\tau\), is connected to part of the input \(X_{t - N + 1:t}\) and fed as input to the \(\left( {m + 1} \right)\) stacks, where \(l = 1,...,m - 1\). M is the total number of stacks in the stack structure. The process is expressed as follows:

$$ x^{{_{l + 1} }} = cat\left( {x^{{_{l} }} ,x^{{_{l - 1} }} } \right) $$
(17)

where \(x^{l}\) is the output value obtained from the output of the first layer after reverse prediction, followed by the reverse residual. \(x^{l - 1}\) is the input of the first layer.

The model considers both forward and reverse predictions to capture data patterns. The backcast part can help the model understand the data and provide more information for prediction, making the prediction of the downstream block easier. This structure also promotes smooth gradient backpropagation.

4 Experiment

This section presents a comparison of our model with state-of-the-art time-series forecasting models. We conducted experiments using three popular benchmark datasets (i.e. ETT (Electricity Transformer Temperature), Exchange, and Weather) to evaluate our model. We compared it with recent time-series forecasting models (i.e. SCI-Net, Preformer, Autoformer, and Informer) as baseline models. Additionally, we performed ablation experiments on important modules of the model to assess the effectiveness of these modules in our W-FENet model.

4.1 Dataset

We completed experiments using three public benchmark datasets to illustrate the broad applicability of our approach, as summarised in Table 1. For each dataset, the task was to predict the T-step of the future trajectory within a given step context window.

Table 1 Details of datasets
Full size table

ETT: As described by Wu et al. (2021), ETT contains power-related data collected from two power stations in China within two years. We used multiple sampling times to obtain different datasets (i.e. ETTh1, ETTm1, ETTm2) to discover the performance of the model for different granularity data.

Exchange: Exchange [52] collected 17 years of daily exchange rates for eight countries, starting in 1990.

Weather: This dataset consisted of climate data recorded by the Max Planck Institute in 2020. It was recorded every ten minutes and included 21 climatic features, such as temperature and pressure.

4.2 Implementation Details

For all adjustable hyperparameters on all datasets, we needed to have performed a grid search for these hyperparameters. The final hyperparameters determined after grid search are shown in Table 2. We used the learning rate decaying the ADAM optimizer to optimize our model and set an early stopping strategy in model training. All experiments are implemented with PyTorch.

Table 2 Setting of hyperparameters
Full size table

4.3 Baseline

Multivariate time prediction. We selected several advanced models for comparison with the proposed model. The methods are compared and evaluated as follows:

  1. (1)

    SCINet: This model is based on a dilated casual convolution. It is a recursive downsampling convolution-interaction architecture. It uses multiple convolution filters in each layer to extract different and effective sequence features from the downsampled subsequences or information.

  2. (2)

    Preformer [53]: It is a transformer-based model that designs multi-scale segment-correlation (MSSC). It improves efficiency of time-series forecasting, extracts more effective features from the sequence, and avoids segment length selection.

  3. (3)

    Autoformer [54]: It is a new decomposition architecture model with an autocorrelation mechanism based on transformer.

  4. (4)

    Informer [35]: This model was a transformer-based model. It proposes a sparse attention mechanism improving the quadratic time complexity and high memory consumption of the attention mechanism.

4.4 Evaluation Settings

In order to make the experimental comparisons fairer, this study uses the mean absolute error (MAE) and mean square error (MSE) as rubrics to assess the accuracy and performance of our method. MAE is the mean value of the absolute difference between the true and predicted values, and MSE is the mean value of the square sum of the errors between the true and predicted values. The two error evaluation values are expressed in Eqs. (18) and (19).

$$ MSE = \frac{1}{H}\sum\limits_{\tau = t}^{t + H} {\left( {y_{\tau } - \hat{y}_{\tau } } \right)^{2} } $$
(18)
$$ MAE = \frac{1}{H}\sum\limits_{\tau = t}^{t + H} {\left| {y_{\tau } - \hat{y}_{\tau } } \right|^{2} } $$
(19)

where \(H\) is the predicted length, \(y_{\tau }\) and \(\hat{y}_{\tau }\) are the predicted and true values, respectively.

4.5 Main Results

To better compare our model with baselines, we conducted a comprehensive multivariate prediction comparison experiment on various datasets under various settings. We followed the same evaluation protocol to compare the prediction performances. The input length was 96 for all datasets, and the prediction length was changed based on the selection frequency. The prediction lengths were selected as {48, 96, 168, 228, 192, 336, 720}. In these tables, we have bolded the results with the best results, and only the ones after that are underlined.

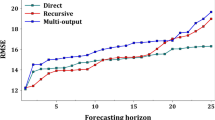
According to Table 3, our model is superior to the other models in most cases. For instance, under the input length of 96 and output length of 48 setting, our model obtains 6.37% (0.361→0.338) relative MSE improvement for ETTh1, 6.62% (0.136→0.127) for Weather and 36.71% (0.079→0.050) for Exchange compared with those of the previous advanced models. In addition, our model also performs relatively well in the long-term prediction, reflecting the relatively stable performance of our model. Compared with the baselines, our model adaptively extracts the trend pattern and uses wavelet decomposition to mine deeper information, thus improving prediction performance. In Fig. 6, we can observe the prediction comparison between our model and the baselines more intuitively. The prediction accuracy comparison diagram at the baseline is shown in Fig. 7. However, in a few cases, its performance was slightly worse than that of the other models. Preformer achieves better long-term prediction performance on the hourly ETT data set and every 15-min ETT data machine and two factors are identified here: (1) The attention mechanism focuses on the weights of the global elements, which play a crucial role in long-term sequence prediction. (2) It uses the multi-scale correlation self-attention mechanism of MSSC and the multi-scale segmentation correlation of PreMSSC with prediction paradigm. The query described in the preceding section can be employed for predicting unknown segments.

Table 3 Multivariate time series forecasting results on ETT, Weather, and Exchange
Full size table
Fig. 6
figure 6

W-FENet compares the prediction results of ETTh1 a, ETTm1 b, ETTm2 c, and Weather d data sets with the baselines

Full size image
Fig. 7
figure 7

W-FENet compares the predictive outcome metrics (MSE) of the ETTh1 a, ETTm1 b, Exchange c, and Weather d datasets to the baseline, the lower MSE means better performance. The Lookback window length is 96, and the prediction lengths include {48, 96, 192, 288, 336, 720}

Full size image

As shown in Fig. 6, we plotted the multivariate prediction results of the model on different benchmark datasets in comparison. The blue dotted line represents the true values, the orange solid line is the prediction result of the W-FENet model, and the prediction results of the rest of the benchmark models are marked with different makers and colors. Our model can accurately predict cycles, trends, and even some small fluctuations. Although in some dataset predictions, i.e. in Fig. 6d, there is a difference in the peak position of the prediction and the true value, our method predicts the trendiness more closely compared to the other benchmark models.

4.6 Ablation Study

We conducted comparative experiments on several variants of the model on all the datasets to evaluate the impact of each gradual used in our model.

4.6.1 Performance of FEMEX

To explore whether FEMEX can improve the prediction performance of the model, we performed ablation experiments on FEMEX on ETTh1, ETTm1, Weather, and Exchange, as listed in Table 4. FEMEX in the table refers to the W-FENet model with a Fourier-enhanced feature extraction module. To make a fair comparison, we replaced FEMEX with a time convolution TCN and set the hyperparameters, such as batch and learning rates, to be consistent. Based on Table 4, compared to the other feature extraction modules, using FEMEX for feature extraction achieves a good prediction performance.

Table 4 Ablation of FEMEX modules
Full size table

4.6.2 Influence of Trend Decomposition and Wavelet Extraction

Trend decomposition and wavelet decomposition are effective for capturing more features. Wavelet decomposition decomposes the raw series into detail and approximation functions, whereas trend data in the series are obtained using trend decomposition, which is particularly important for the performance of our model. To demonstrate the effectiveness of this module, we remove the trend decomposition and wavelet extraction module from the model to obtain a model without trend decomposition and wavelet decomposition. The results predicted by feeding raw data into the model without this module are listed in Table 5.

Table 5 Ablation of other modules
Full size table

4.6.3 Impact of Other Modules

We performed ablation experiments on these modules using different datasets to explore whether the other modules in our model were efficient for prediction, as shown in Table 5. No double residuals indicate that our model removed these double residuals. The absence of a U-net indicates that our model did not undergo U-net processing. The results of the ablation study showed that the model with these modules predicted better than that without them in almost all cases, proving that the U-net improvement and double residual connection are helpful for prediction tasks. Figure 8 shows the prediction accuracies of the ablation experiments for each module.

Fig. 8
figure 8

Different modules' ablation performance (MSE, MAE) is tested on three large datasets of ETT, Weather, and Exchange. The lookback window is selected as 96, and the prediction step is 48. We use our model prediction results to compare with ablation experiments

Full size image

4.7 Discussion

In this part, we analyze the impact of two important hyper-parameters on W-FENet (i.e. the number of stack layers and the number of wavelet decomposition stages). To analyze the stack layers, we deepened the stack layers to obtain more sequence information. The results are shown in Fig. 9 that we can better extract the features between sequences as the stack gets deeper. However, if the stack is too deep, the complexity of the model will be too high, and overfitting may occur. Considering prediction performance and computational efficiency, we selected three layers with stack of three. For the series of wavelet decompositions, we analyzed the effect of different wavelet decomposition layers on prediction performance. We attempted multiple decomposition layers and compared them from the shallow to deep layers. The results showed that with an increase in the number of decomposition layers, the representation ability and complexity of the model also increased. A deeper decomposition level can better capture detailed information in a time series. However, it may also introduce more redundant information, as shown in Fig. 3. Considering prediction performance and computational efficiency, we selected a moderate number of wavelet decomposition layers. In our experiment, the model with three decomposition layers exhibited good performance in extracting trends and detailed information.

Fig. 9
figure 9

The parameters are adjusted using a grid search. Each grid represents a unique parameter combination. Each colored cell in the grid is plotted in different green colors. The color scale reflects the difference between MAE and MSE, where darker shades of green signify lower MSE and MAE values, indicating superior prediction performance

Full size image

Secondly, we will use the same size of the lookback window as previous state-of-the-art models for two reasons: firstly, as shown in Table 6, too small a lookback window leads to a decrease in the model's ability to capture features of the long-series a lookback window that is too large will show a reduction in prediction accuracy and increase the time complexity. Secondly, choosing the same size of the lookback window as the previous state-of-the-art models can better illustrate the fairness of our experiments.

Table 6 Forecasting results as the lookback window size grows
Full size table

In addition, we considered whether the decomposition method could be replaced using other more advanced methods to validate the excellent performance of our modeling framework, such as EWT. Therefore, we tried to change the DWT to EWT at the base of our model, and Table 7 lists the experimental comparison of our model with the model that changes the DWT to EWT in W-FENet on the benchmark dataset ETTh1. As seen from Table 7, using EWT as a decomposition method improves the prediction performance in some cases.

Table 7 Multivariate time series forecasting results on ETTh1
Full size table

Finally, the above experiments indicate that our method achieves a better prediction performance and smaller errors than the other four methods in most cases for different real-world datasets. In most cases, our model shows better performance. However, in a more long-term prediction, our model performance presents a decreasing trend. Therefore, we must consider how to improve the long-term predictive ability of our model. According to the results, we find that the long-term prediction ability of the Preformer works better than that of the other models because of the segmented self-attention mechanism adopted in the Preformer. This suggests that we need to further explore global features, which can help enhance the long-term predictive power of our models. We can also consider more efficient approaches to obtaining global features in the future.

5 Conclusions

This study presented a new time-series forecasting model, wavelet-based Fourier-enhanced network model decomposition (W-FENet), for time-series modelling and prediction. In the W-FENet, we introduced a new feature extraction module called the Fourier-enhanced feature extraction module (FEMEX). This module uses a Fourier transform to transform time–frequency information to highlight the frequency-domain features of the data and make these features more prominent and identifiable. Compared with previous studies, it can fully capture the local details, overall trends, nonlinear relationships, and frequency domain characteristics of sequence information and improve the performance of time series modelling and prediction. The effectiveness of our model was demonstrated by its ability to exhibit state-of-the-art predictive performance under various experimental settings on different benchmark datasets.

In the future, we plan to propose more effective methods to obtain global features to improve the prediction performance of our model in long-series forecasting. In addition, we consider that ensemble learning may help mitigate extreme cases such as model collapse due to structural mismatch. Therefore, we plan to use ensemble learning methods in future studies to compensate for the shortcomings of a single model and improve the prediction performance of the model.