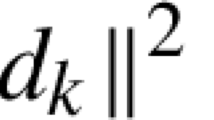Abstract
This work is on constrained large-scale non-convex optimization where the constraint set implies a manifold structure. Solving such problems is important in a multitude of fundamental machine learning tasks. Recent advances on Riemannian optimization have enabled the convenient recovery of solutions by adapting unconstrained optimization algorithms over manifolds. However, it remains challenging to scale up and meanwhile maintain stable convergence rates and handle saddle points. We propose a new second-order Riemannian optimization algorithm, aiming at improving convergence rate and reducing computational cost. It enhances the Riemannian trust-region algorithm that explores curvature information to escape saddle points through a mixture of subsampling and cubic regularization techniques. We conduct rigorous analysis to study the convergence behavior of the proposed algorithm. We also perform extensive experiments to evaluate it based on two general machine learning tasks using multiple datasets. The proposed algorithm exhibits improved computational speed, e.g., a speed improvement from \(12\% \:\text {to} \:227\%\), and improved convergence behavior, e.g., an iteration number reduction from \(\mathcal{O}\left(\max\left(\epsilon_g^{-2}\epsilon_H^{-1},\epsilon_H^{-3}\right)\right) \,\text {to}\: \mathcal{O}\left(\max\left(\epsilon_g^{-2},\epsilon_H^{-3}\right)\right)\), compared to a large set of state-of-the-art Riemannian optimization algorithms.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In modern machine learning, many learning tasks are formulated as non-convex optimization problems. This is because, as compared to linear or convex formulations, they can often capture more accurately the underlying structures within the data, and model more precisely the learning performance (or losses). There is an important class of non-convex problems of which the constraint sets possess manifold structures, e.g., to optimize over a set of orthogonal matrices. A manifold in mathematics refers to a topological space that locally behaves as an Euclidean space near each point. Over a D-dimensional manifold \({\mathcal {M}}\) in a d-dimensional ambient space (\(D< d\)), each local patch around each data point (a subset of \({\mathcal {M}}\)) is homeomorphic to a local open subset of the Euclidean space \({\mathbb {R}}^D\). This special structure enables a straightforward adoption of any unconstrained optimization algorithm for solving a constrained problem over a manifold, simply by applying a systematic way to modify the gradient and Hessian calculation. The modified calculations are called the Riemannian gradients and the Riemannian Hessians, which will be rigorously defined later. Such an accessible method for developing optimized solutions has benefited many applications and encouraged the implementation of various optimization libraries.
A representative learning task that gives rise to non-convex problems over manifolds is low-rank matrix completion, widely applied in signal denoising, recommendation systems and image recovery (Liu et al., 2019). It is formulated as optimization problems constrained on fixed-rank matrices that belong to a Grassmann manifold. Another example task is principal component analysis (PCA) popularly used in statistical data analysis and dimensionality reduction (Shahid et al., 2015). It seeks an optimal orthogonal projection matrix from a Stiefel manifold. A more general problem setup than PCA is the subspace learning (Mishra et al., 2019), where a low-dimensional space is an instance of a Grassmann manifold. When training a neural network, in order to reduce overfitting, the orthogonal constraint that provides a Stiefel manifold structure is sometimes imposed over the network weights (Anandkumar & Ge, 2016). Additionally, in hand gesture recognition (Nguyen et al., 2019), optimizing over a symmetric definite positive (SDP) manifold has been shown effective.
Recent developments in optimization on Riemannian manifolds (Absil et al., 2009) have offered a convenient and unified solution framework for solving the aforementioned class of non-convex problems. The Riemannian optimization techniques translate the constrained problems into unconstrained ones on the manifold whilst preserving the geometric structure of the solution. For example, one Riemannian way to implement a PCA is to preserve the SDP geometric structure of the solutions without explicit constraints (Horev et al., 2017). A simplified description of how Riemannian optimization works is that it first applies a straightforward way to modify the calculation of the first-order and second-order gradient information, then it adopts an unconstrained optimization algorithm that uses the modified gradient information. There are systematic ways to compute these modifications by analyzing the geometric structure of the manifold. Various libraries have implemented these methods and are available to practitioners, e.g., Manopt (Boumal et al., 2014) and Pymanopt (Townsend et al., 2016).
Among such techniques, Riemannian gradient descent (RGD) is the simplest. To handle large-scale computation with a finite-sum structure, Riemannian stochastic gradient descent (RSGD) (Bonnabel, 2013) has been proposed to estimate the gradient from a single sample (or a sample batch) in each iteration of the optimization. Here, an iteration refers to the process by which an incumbent solution is updated with gradient and (or) higher-order derivative information; for example, Eq. (3) in the upcoming text defines an RSGD iteration. Convergence rates of RGD and RSGD are compared in Zhang and Sra (2016) together with a global complexity analysis. The work concludes that RGD can converge linearly while RSGD converges sub-linearly, but RSGD becomes computationally cheaper when there is a significant increase in the size of samples to process, also it can potentially prevent overfitting. By using RSGD to optimize over the Stiefel manifold, Pölitz et al. (2016) attempts to improve interpretability of domain adaptation and has demonstrated its benefits for text classification.
A major drawback of RSGD is the variance issue, where the variance of the update direction can slow down the convergence and result in poor solutions. Typical techniques for variance reduction include the Riemannian stochastic variance reduced gradient (RSVRG) (Zhang et al., 2016) and the Riemannian stochastic recursive gradient (RSRG) (Kasai et al., 2018). RSVRG reduces the gradient variance by using a momentum term, which takes into account the gradient information obtained from both RGD and RSGD. RSRG follows a different strategy and considers only the information in the last and current iterations. This has the benefit of avoiding large cumulative errors, which can be caused by transporting the gradient vector along a distant path when aligning two vectors at the same tangent plane. It has been shown by Kasai et al. (2018) that RSRG performs better than RSVRG particularly for large-scale problems.
The RSGD variants can suffer from oscillation across the slopes of a ravine (Kumar Roy et al., 2018). This also happens when performing stochastic gradient descent in Euclidean spaces. To address this, various adaptive algorithms have been proposed. The core idea is to control the learning process with adaptive learning rates in addition to the gradient momentum. Riemannian techniques of this kind include R-RMSProp (Kumar Roy et al., 2018), R-AMSGrad (Cho & Lee, 2017), R-AdamNC (Becigneul & Ganea, 2019), RPG (Huang & Wei, 2021) and RAGDsDR (Alimisis et al., 2021).
Although improvements have been made for first-order optimization, they might still be insufficient for handling saddle points in non-convex problems (Mokhtari et al., 2018). They can only guarantee convergence to stationary points and do not have control over getting trapped at saddle points due to the lack of higher-order information. As an alternative, second-order algorithms are normally good at escaping saddle points by exploiting curvature information (Kohler & Lucchi, 2017; Tripuraneni et al., 2018). Representative examples of this are the trust-region (TR) methods. Their capacity for handling saddle points and improved convergence over many first-order methods has been demonstrated in Weiwei et al. (2013) for various non-convex problems. The TR technique has been extended to a Riemannian setting for the first time by Absil et al. (2007), referred to as the Riemannian TR (RTR) technique.
It is well known that what prevents the wide use of the second-order Riemannian techniques in large-scale problems is the high cost of computing the exact Hessian matrices. Inexact techniques are therefore proposed to iteratively search for solutions without explicit Hessian computations. They can also handle non-positive-definite Hessian matrices and improve operational robustness. Two representative inexact examples are the conjugate gradient and the Lanczos methods (Zhu, 2017; Xu et al., 2016). However, their reduced complexity is still proportional to the sample size, and they can still be computationally costly when working with large-scale problems. To address this issue, the subsampling technique has been proposed, and its core idea is to approximate the gradient and Hessian using a batch of samples. It has been proved by Shen et al. (2019) that the TR method with subsampled gradient and Hessian can achieve a convergence rate of order \({\mathcal {O}}\left( \frac{1}{k^{2/3}}\right)\) with k denoting the iteration number. A sample-efficient stochastic TR approach is proposed by Shen et al. (2019) which finds an \((\epsilon , \sqrt{\epsilon })\)-approximate local minimum within a number of \({\mathcal {O}}(\sqrt{n}/\epsilon ^{1.5})\) stochastic Hessian oracle queries where n denotes the sample number. The subsampling technique has been applied to improve the second-order Riemannian optimization for the first time by Kasai and Mishra (2018). Their proposed inexact RTR algorithm employs subsampling over the Riemannian manifold and achieves faster convergence than the standard RTR method. Nonetheless, subsampling can be sensitive to the configured batch size. Overly small batch sizes can lead to poor convergence.
In the latest development of second-order unconstrained optimization, it has been shown that the adaptive cubic regularization technique (Cartis et al., 2011) can improve the standard and subsampled TR algorithms and the Newton-type methods, resulting in, for instance, improved convergence and effectiveness at escaping strict saddle points (Kohler & Lucchi, 2017; Xu et al., 2020). To improve performance, the variance reduction techniques have been combined into cubic regularization and extended to cases with inexact solutions. Example works of this include (Zhou & Gu, 2020; Zhou et al., 2019) which were the first to rigorously demonstrate the advantage of variance reduction for second-order optimization algorithms. Recently, the potential of cubic regularization for solving non-convex problems over constraint sets with Riemannian manifold structures has been shown by Zhang and Zhang (2018), Agarwal et al. (2021).
We aim at improving the RTR optimization by taking advantage of both the adaptive cubic regularization and subsampling techniques. Our problem of interest is to find a local minimum of a non-convex finite-sum minimization problem constrained on a set endowed with a Riemannian manifold structure. Letting \(f_i:{\mathcal {M}}\rightarrow {\mathbb {R}}\) be a real-valued function defined on a Riemannian manifold \({\mathcal {M}}\), we consider a twice differentiable finite-sum objective function:
In the machine learning context, n denotes the sample number, and \(f_i({\textbf{x}})\) is a smooth real-valued and twice differentiable cost (or loss) function computed for the i-th sample. The n samples are assumed to be uniformly sampled, and thus \({\mathbb {E}}\left[ f_i({\textbf{x}})\right] = \lim _{n \rightarrow \infty } \frac{1}{n}\sum _{i=1}^{n}f_i({\textbf{x}})\).
We propose a cubic Riemannian Newton-like (RN) method to solve more effectively the problem in Eq. (1). Specifically, we enable two key improvements in the Riemannian space, including (1) to approximate the Riemannian gradient and Hessian using the subsampling technique and (2) to improve the subproblem formulation by replacing the trust-region constraint with a cubic regularization term. The resulting algorithm is named Inexact Sub-RN-CR.Footnote 1. After introducing cubic regularization, it becomes more challenging to solve the subproblem, for which we demonstrate two effective solvers based on the Lanczos and conjugate gradient methods. We provide convergence analysis for the proposed Inexact Sub-RN-CR algorithm and present the main results in Theorems 3 and 4. Additionally, we provide analysis for the subproblem solvers, regarding their solution quality, e.g., whether and how they meet a set of desired conditions as presented in Assumptions 1–3, and their convergence property. The key results are presented in Lemma 1, Theorem 2, Lemmas 2 and 3. Overall, our results are satisfactory. The proposed algorithm finds an \(\left( \epsilon _g,\epsilon _H\right)\)-optimal solution (defined in Sect. 3.1) in fewer iterations than the state-of-the-art RTR (Kasai & Mishra, 2018). Specifically, the required number of iterations is reduced from \({\mathcal {O}}\left( \max \left( \epsilon _g^{-2}\epsilon _H^{-1},\epsilon _H^{-3}\right) \right)\) to \({\mathcal {O}}\left( \max \left( \epsilon _g^{-2},\epsilon _H^{-3}\right) \right)\). When being tested by extensive experiments on PCA and matrix completion tasks with different datasets and applications in image analysis, our algorithm shows much better performance than most state-of-the-art and popular Riemannian optimization algorithms, in terms of both the solution quality and computing time.
2 Notations and preliminaries
We start by familiarizing the readers with the notations and concepts that will be used in the paper, and recommend (Absil et al., 2009) for a more detailed explanation of the relevant concepts. The manifold \({\mathcal {M}}\) is equipped with a smooth inner product \(\langle \cdot ,\cdot \rangle _{{\textbf{x}}}\) associated with the tangent space \(T_{{\textbf{x}}}{\mathcal {M}}\) at any \({\textbf{x}}\in {\mathcal {M}}\), and this inner product is referred to as the Riemannian metric. The norm of a tangent vector \({\varvec{\eta }}\in T_{{\textbf{x}}}{\mathcal {M}}\) is denoted by \(\left\| {\varvec{\eta }} \right\| _{{\textbf{x}}}\), which is computed by \(\left\| {\varvec{\eta }} \right\| _{{\textbf{x}}} =\sqrt{\langle {\varvec{\eta }},{\varvec{\eta }} \rangle _{{\textbf{x}}}}\). When we use the notation \(\left\| {\varvec{\eta }} \right\| _{{\textbf{x}}}\), \({\varvec{\eta }}\) by default belongs to the tangent space \(T_{{\textbf{x}}}{\mathcal {M}}\). We use \({\textbf{0}}_{{\textbf{x}}}\in T_{{\textbf{x}}} {\mathcal {M}}\) to denote the zero vector of the tangent space at \({\textbf{x}}\). The retraction mapping denoted by \(R_{{\textbf{x}}}\left( {\varvec{\eta }}\right) :T_{{\textbf{x}}}{\mathcal {M}}\rightarrow {\mathcal {M}}\) is used to move \({\textbf{x}}\in {\mathcal {M}}\) in the direction \({\varvec{\eta }}\in T_{{\textbf{x}}}{\mathcal {M}}\) while remaining on \({\mathcal {M}}\), and it is an equivalent version of \({\textbf{x}} +{\varvec{\eta }}\) in an Euclidean space. The pullback of f at \({\textbf{x}}\) is defined by \({\hat{f}}({{\varvec{\eta }}}) = f(R_{{\textbf{x}}}({{\varvec{\eta }}}))\), and \({\hat{f}}({\textbf{0}}_{{\textbf{x}}}) = f({\textbf{x}})\). The vector transport operator \({\mathcal {T}}_{{\textbf{x}}}^{{\textbf{y}}}({\textbf{v}}): T_{\textbf{x}}{\mathcal {M}} \rightarrow T_{\textbf{x}}{\mathcal {M}}\) moves a tangent vector \({\textbf{v}} \in T_{{\textbf{x}}}{\mathcal {M}}\) from a point \({\textbf{x}}\in {\mathcal {M}}\) to another \({\textbf{y}}\in {\mathcal {M}}\). We also use a shorthand notation \({\mathcal {T}}_{{\varvec{\eta }}}({{\textbf{v}}})\) to describe \({\mathcal {T}}_{{\textbf{x}}}^{{\textbf{y}}}({\textbf{v}})\) for a moving direction \({{\varvec{\eta }}} \in T_{{\textbf{x}}}{\mathcal {M}}\) from \({\textbf{x}}\) to \({\textbf{y}}\) satisfying \(R_{{\textbf{x}}}\left( {\varvec{\eta }}\right) = {\textbf{y}}\). The parallel transport operator \({\mathcal {P}}_{{\varvec{\eta }},\gamma } ({\textbf{v}})\) is a special instance of the vector transport. It moves \({\textbf{v}}\in T_{{\textbf{x}}}{\mathcal {M}}\) in the direction of \({\varvec{\eta }}\in T_{{\textbf{x}}}{\mathcal {M}}\) along a geodesic \(\gamma :[0,1]\rightarrow {\mathcal {M}}\), where \(\gamma (0)={\textbf{x}}\), \(\gamma (1)={\textbf{y}}\) and \(\gamma ^{\prime }(0) = {\varvec{\eta }}\), and during the movement, it has to satisfy the parallel condition on the geodesic curve. We simplify the notation \({\mathcal {P}}_{{\varvec{\eta }},\gamma } ({\textbf{v}})\) to \({\mathcal {P}}_{{\varvec{\eta }}} ({\textbf{v}})\). Figure 1 illustrates a manifold and the operations over it. Additionally, we use \(\Vert \cdot \Vert\) to denote the \(l_2\)-norm operation in a Euclidean space.
The Riemannian gradient of a real-valued differentiable function f at \({\textbf{x}}\in {\mathcal {M}}\), denoted by \(\textrm{grad}f({\textbf{x}})\), is defined as the unique element of \({\mathcal {T}}_{\textbf{x}}{\mathcal {M}}\) satisfying \(\langle \textrm{grad}f({\textbf{x}}),{{\varvec{\xi }}} \rangle _{\textbf{x}}={\mathcal {D}}f({\textbf{x}})[{{\varvec{\xi }}}],\ \forall {{\varvec{\xi }}}\in T_{\textbf{x}}{\mathcal {M}}\). Here, \({\mathcal {D}}f({\textbf{x}})[{{\varvec{\xi }}}]\) generalizes the notion of the directional derivative to a manifold, defined as the derivative of \(f(\gamma (t))\) at \(t=0\) where \(\gamma (t)\) is a curve on \({\mathcal {M}}\) such that \(\gamma (0)={\textbf{x}}\) and \({\dot{\gamma }}(0)={{\varvec{\xi }}}\). When operating in an Euclidean space, we use the same notation \({\mathcal {D}}f({\textbf{x}})[{{\varvec{\xi }}}]\) to denote the classical directional derivative. The Riemannian Hessian of a real-valued differentiable function f at \({\textbf{x}}\in {\mathcal {M}}\), denoted by \({{\textrm{Hess}}} f({\textbf{x}})[{{\varvec{\xi }}}]: T_{\textbf{x}}{\mathcal {M}} \rightarrow T_{\textbf{x}}{\mathcal {M}}\), is a linear mapping defined based on the Riemannian connection, as \({{\textrm{Hess}}} f({\textbf{x}})[{{\varvec{\xi }}}] ={\tilde{\nabla }}_{{{\varvec{\xi }}}} {{\textrm{grad}}} f({\textbf{x}})\). The Riemannian connection \({\tilde{\nabla }}_{{{\varvec{\xi }}}}{\varvec{\eta }}: T_{\textbf{x}}{\mathcal {M}}\times T_{\textbf{x}}{\mathcal {M}} \rightarrow T_{\textbf{x}}{\mathcal {M}}\), generalizes the notion of the directional derivative of a vector field. For a function f defined over an embedded manifold, its Riemannian gradient can be computed by projecting the Euclidean gradient \(\nabla f({\textbf{x}})\) onto the tangent space, as \(\textrm{grad}f({\textbf{x}})=P_{T_{\textbf{x}}{\mathcal {M}}}\left[ \nabla f({\textbf{x}})\right]\) where \(P_{T_{\textbf{x}}{\mathcal {M}}}[\cdot ]\) is the orthogonal projection onto \(T_{\textbf{x}}{\mathcal {M}}\). Similarly, its Riemannian Hessian can be computed by projecting the classical directional derivative of \({{\textrm{grad}}}f({\textbf{x}})\), defined by \(\nabla ^2 f({\textbf{x}})[{{\varvec{\xi }}}] = {\mathcal {D}} \textrm{grad}f({\textbf{x}}) [{{\varvec{\xi }}}]\), onto the tangent space, resulting in \(\textrm{Hess}f({\textbf{x}})[{{\varvec{\xi }}}]=P_{T_{\textbf{x}}{\mathcal {M}}}\left[ \nabla ^2 f({\textbf{x}})[{{\varvec{\xi }}}]\right]\). When the function f is defined over a quotient manifold, the Riemannian gradient and Hessian can be computed by projecting \(\nabla f({\textbf{x}})\) and \(\nabla ^2 f({\textbf{x}})[{{\varvec{\xi }}}]\) onto the horizontal space of the manifold.
Taking the PCA problem as an example (see Eqs (60) and (61) for its formulation), the general objective in Eq. (1) can be instantiated by \(\min _{{\textbf{U}}\in {{\textrm{Gr}}}\left( r,d\right) }\) \(\frac{1}{n}\sum _{i=1}^n\left\| {\textbf{z}}_i-\textbf{UU}^T{\textbf{z}}_i\right\| ^2\), where \({\mathcal {M}}={{\textrm{Gr}}}\left( r,d\right)\) is a Grassmann manifold. The function of interest is \(f_i({\textbf{U}}) = \left\| {\textbf{z}}_i-\textbf{UU}^T{\textbf{z}}_i\right\| ^2\). The Grassmann manifold \({{\textrm{Gr}}}\left( r,d\right)\) contains the set of r-dimensional linear subspaces of the d-dimensional vector space. Each subspace corresponds to a point on the manifold that is an equivalence class of \(d\times r\) orthogonal matrices, expressed as \({\textbf{x}} = \left[ {\textbf{U}}\right] :=\left\{ \textbf{UO}:{\textbf{U}}^T{\textbf{U}}={\textbf{I}},{\textbf{O}}\in {{\textrm{O}}}\left( r\right) \right\}\) where \({{\textrm{O}}}\left( r\right)\) denotes the orthogonal group in \({\mathbb {R}}^{r\times r}\). A tangent vector \({{\varvec{\eta }}} \in T_{{\textbf{x}}} {{\textrm{Gr}}}(r,d)\) of the Grassmann manifold has the form \({{\varvec{\eta }}}={\textbf{U}}^\bot {\textbf{B}}\) (Edelman et al., 1998), where \({\textbf{B}}\in {\mathbb {R}}^{(d-r)\times r}\), and \({\textbf{U}}^\bot \in {\mathbb {R}}^{d\times (d-r)}\) is the orthogonal complement of \({\textbf{U}}\) such that \(\left[ {\textbf{U}},{\textbf{U}}^{\bot }\right]\) is orthogonal. A commonly used Riemannian metric for the Grassmann manifold is the canonical inner product \(\langle {\varvec{\eta }},{\varvec{{{\varvec{\xi }}}}}\rangle _{{\textbf{x}}}=\textrm{tr}({\varvec{\eta }}^T{\varvec{{{\varvec{\xi }}}}})\) given \({\varvec{\eta }},{\varvec{{{\varvec{\xi }}}}}\in T_{{\textbf{x}}}{{\textrm{Gr}}}(r,d)\), resulting in \(\left\| {{\varvec{\eta }}}\right\| _{{\textbf{x}}}=\Vert {{\varvec{\eta }}}\Vert\) (Section 2.3.2 of Edelman et al. (1998)). As we can see, the Riemannian metric and the norm here are equivalent to the Euclidean inner product and norm. The same result can be derived from another commonly used metric of the Grassmann manifold, i.e., \(\langle {{\varvec{\eta }}}, {{\varvec{\xi }}}\rangle _{{\textbf{x}}}=\textrm{tr}\left( {{\varvec{\eta }}}^T\left( {\textbf{I}}-\frac{1}{2}{\textbf{U}}{\textbf{U}}^{T}\right) {{\varvec{\xi }}}\right)\) for \({{\varvec{\eta }}},{{\varvec{\xi }}}\in T_{{\textbf{x}}}{{\textrm{Gr}}}(r,d)\) (Section 2.5 of Edelman et al. (1998)). Expressing two given tangent vectors as \({{\varvec{\eta }}}={\textbf{U}}^{\bot }{\textbf{B}}_{\eta }\) and \({{\varvec{\xi }}} ={\textbf{U}}^{\bot }{\textbf{B}}_{\xi }\) with \({\textbf{B}}_{\eta }, {\textbf{B}}_{\xi }\in {\mathbb {R}}^{(d-r)\times r}\), we have
Here we provide a few examples of the key operations explained earlier on the Grassmann manifold, taken from Boumal et al. (2014). Given a data point \([{\textbf{U}}]\), a moving direction \({{\varvec{\eta }}}\) and the step size t, one way to construct the retraction mapping is through performing singular value decomposition (SVD) on \({\textbf{U}}+t{{\varvec{\eta }}}\), i.e., \({\textbf{U}}+t{{\varvec{\eta }}}=\bar{{\textbf{U}}}{\textbf{S}}\bar{{\textbf{V}}}^T\), and the new data point after moving is \(\left[ \bar{{\textbf{U}}}\bar{{\textbf{V}}}^T\right]\). A transport operation can be implemented by projecting a given tangent vector using the orthogonal projector \({\textbf{I}} - {\textbf{U}}{\textbf{U}}^T\). Both Riemannian gradient and Hessian can be computed by projecting the Euclidean gradient and Hessian of \(f({\textbf{U}})\) using the same projector \({\textbf{I}} - {\textbf{U}}{\textbf{U}}^T\).
2.1 First-order algorithms
To optimize the problem in Eq. (1), the first-order Riemannian optimization algorithm RSGD updates the solution at each k-th iteration by using an \(f_i\) instance, as
where \(\beta _k\) is the step size. Assume that the algorithm runs for multiple epochs referred to as the outer iterations. Each epoch contains multiple inner iterations, each of which corresponds to a randomly selected \(f_i\) for calculating the update. Letting \({\textbf{x}}_k^t\) be the solution at the t-th inner iteration of the k-th outer iteration and \(\tilde{{\textbf{x}}}_k\) be the solution at the last inner iteration of the k-th outer iteration, RSVRG employs a variance reduced extension (Zhang et al., 2016) of the update defined in Eq. (3), given as
where
Here, the full gradient information \({{\textrm{grad}}}f\left( \tilde{{\textbf{x}}}_{k-1}\right)\) is used to reduce the variance in the stochastic gradient \({\textbf{v}}_k^t\). As a later development, RSRG (Kasai et al., 2018) suggests a recursive formulation to improve the variance-reduced gradient \({\textbf{v}}_k^t\). Starting from \({\textbf{v}}_k^0={{\textrm{grad}}} f\left( \tilde{{\textbf{x}}}_{k-1}\right)\), it updates by
This formulation is designed to avoid the accumulated error caused by a distant vector transport.
2.2 Inexact RTR
For second-order Riemannian optimization, the Inexact RTR (Kasai & Mishra, 2018) improves the standard RTR (Absil et al., 2007) through subsampling. It optimizes an approximation of the objective function formulated using the second-order Taylor expansion within a trust region \(\varDelta _k\) around \({\textbf{x}}_k\) at iteration k. A moving direction \({\varvec{\eta }}_k\) within the trust region is found by solving the subproblem at iteration k:
where \({\textbf{G}}_k\) and \({\textbf{H}}_k[{\varvec{\eta }}]\) are the approximated Riemannian gradient and Hessian calculated by using the subsampling technique. The approximation is based on the current solution \({\textbf{x}}_k\) and the moving direction \({{\varvec{\eta }}}\), calculated as
where \({\mathcal {S}}_g\), \({\mathcal {S}}_H\subset \left\{ 1,\ldots ,n\right\}\) are the sets of the subsampled indices used for estimating the Riemannian gradient and Hessian. The updated solution \({\textbf{x}}_{k+1}=R_{{\textbf{x}}_k}({\varvec{\eta }}_k)\) will be accepted and \(\varDelta _k\) will be increased, if the decrease of the true objective function f is sufficiently large as compared to that of the approximate objective used in Eq. (7). Otherwise, \(\varDelta _k\) will be decreased because of the poor agreement between the approximate and true objectives.
3 Proposed method
3.1 Inexact sub-RN-CR algorithm
We propose to improve the subsampling-based construction of the RTR subproblem in Eq. (7) by cubic regularization. This gives rise to the minimization
where
Here, \(0<\epsilon _g <1\) is a user-specified parameter that plays a role in convergence analysis, which we will explain later. The core objective component \(h_{{\textbf{x}}_k}({\varvec{\eta }})\) is formulated by extending the adaptive cubic regularization technique (Cartis et al., 2011), given as
with
and
where the subscript k is used to highlight the pullback of f at \({\textbf{x}}_k\) as \({\hat{f}}_k(\cdot )\). Overall, there are four hyper-parameters to be set by the user, including the gradient norm threshold \(0<\epsilon _{\sigma } <1\), the dynamic control parameter \(\gamma >1\) to adjust the cubic regularization weight, the model validity threshold \(0<\tau <1\), and the initial trust parameter \(\sigma _0\). We will discuss the setup of the algorithm in more detail.

We expect the norm of the approximate gradient to approach \(\epsilon _g\) with \(0<\epsilon _g <1\). Following a similar treatment in Kasai and Mishra (2018), when the gradient norm is smaller than \(\epsilon _g\), the gradient-based term is ignored. This is important to the convergence analysis shown in the next section.
The trust region radius \(\varDelta _k\) is no longer explicitly defined, but replaced by the cubic regularization term \(\frac{\sigma _k}{3}\Vert {\varvec{\eta }}\Vert _{{\textbf{x}}_k}^3\), where \(\sigma _k\) is related to a Lagrange multiplier on a cubic trust-region constraint. Naturally, the smaller \(\sigma _k\) is, the larger a moving step is allowed. Benefits of cubic regularization have been shown in Griewank (1981), Kohler and Lucchi (2017). It can not only accelerate the local convergence especially when the Hessian is singular, but also help escape better strict saddle points than the TR methods, providing stronger convergence properties.
The cubic term \(\frac{\sigma _k}{3}\Vert {\varvec{\eta }}\Vert _{{\textbf{x}}_k}^3\) is equipped with a dynamic penalization control through the adaptive trust quantity \(\sigma _k\ge 0\). The value of \(\sigma _k\) is determined by examining how successful each iteration k is. An iteration k is considered successful if \(\rho _k\ge \tau\), and unsuccessful otherwise, where the value of \(\rho _k\) quantifies the agreement between the changes of the approximate objective \({\hat{m}}_k({{\varvec{\eta }}})\) and the true objective \(f({\textbf{x}})\). The larger \(\rho _k\) is, the more effective the approximate model is. Given \(\gamma >1\), in an unsuccessful iteration, \(\sigma _k\) is increased to \(\gamma \sigma _k\) hoping to obtain a more accurate approximation in the next iteration. On the opposite, \(\sigma _k\) is decreased to \(\frac{\sigma _k}{\gamma }\), relaxing the approximation in a successful iteration, but it is still restricted within the lower bound \(\epsilon _\sigma\). This bound \(\epsilon _\sigma\) helps avoid solution candidates with overly large norms \(\Vert {\varvec{\eta }}_k\Vert _{{\textbf{x}}_k}\) that can cause an unstable optimization. Below we formally define what an (un)successful iteration is, which will be used in our later analysis.
Definition 1
(Successful and Unsuccessful Iterations) An iteration k in Algorithm 1 is considered successful if the agreement \(\rho _k\ge \tau\), and unsuccessful if \(\rho _k< \tau\). In addition, based on Step (12) of Algorithm 1, a successful iteration has \(\sigma _{k+1}\le \sigma _k\), while an unsuccessful one has \(\sigma _{k+1}>\sigma _k\).
3.2 Optimality examination
The stopping condition of the algorithm follows the definition of \(\left( \epsilon _g,\epsilon _H\right)\)-optimality (Nocedal & Wright, 2006), stated as below.
Definition 2
(\((\epsilon _g,\epsilon _H)\)-optimality) Given \(0<\epsilon _g,\epsilon _H<1\), a solution \({\textbf{x}}\) satisfies \(\left( \epsilon _g,\epsilon _H\right)\)-optimality if
for all \({\varvec{\eta }}\in T_{{\textbf{x}}}{\mathcal {M}}\), where \({\textbf{I}}\) is an identity matrix.
This is a relaxation and a manifold extension of the standard second-order optimality conditions \(\left\| {{\textrm{grad}}}f({\textbf{x}})\right\| _{{\textbf{x}}}=0\) and \(\text {Hess}f({\textbf{x}})\succeq 0\) in Euclidean spaces (Mokhtari et al., 2018). The algorithm stops (1) when the gradient norm is sufficiently small and (2) when the Hessian is sufficiently close to being positive semidefinite.
To examine the Hessian, we follow a similar approach as in Han et al. (2021) by assessing the solution of the following minimization problem:
which resembles the smallest eigenvalue of the Riemannian Hessian. As a result, the algorithm stops when \(\left\| {{\textrm{grad}}}f({\textbf{x}})\right\| _{{\textbf{x}}}\le \epsilon _g\) (referred to as the gradient condition) and when \(\lambda _{min}({\textbf{H}}_k) \ge -\epsilon _H\) (referred to as the Hessian condition), where \(\epsilon _g, \epsilon _H \in (0,1)\) are the user-set stopping parameters. Note, we use the same \(\epsilon _g\) for thresholding as in Eq. (11). Pseudo code of the complete Inexact Sub-RN-CR is provided in Algorithm 1.
3.3 Subproblem solvers
The step (9) of Algorithm 1 requires to solve the subproblem in Eq. (10). We rewrite its objective function \({\hat{m}}_k({{\varvec{\eta }}})\) as below for the convenience of explanation:
where \(\delta =1\) if \(\Vert {\textbf{G}}_k\Vert _{{\textbf{x}}_k}\ge \epsilon _g\), otherwise \(\delta =0\). We demonstrate two solvers commonly used in practice.
3.3.1 The Lanczos method
The Lanczos method (Gould et al., 1999) has been widely used to solve the cubic regularization problem in Euclidean spaces (Xu et al., 2020; Kohler & Lucchi, 2017; Cartis et al., 2011; Jia et al., 2021) and been recently adapted to Riemannian spaces (Agarwal et al., 2021). Let D denote the manifold dimension. Its core operation is to construct a Krylov subspace \({\mathcal {K}}_D\), of which the basis \(\{{\textbf{q}}_i\}_{i=1}^D\) spans the tangent space \({{\varvec{\eta }}}\in T_{{\textbf{x}}_k}{\mathcal {M}}\). After expressing the solution as an element in \({\mathcal {K}}_D\), i.e., \({{\varvec{\eta }}}:=\sum _{i=1}^D y_i{\textbf{q}}_i\), the minimization problem in Eq. (17) can be converted to one in Euclidean spaces \({\mathbb {R}}^D\), as
where \({\textbf{T}}_D \in {\mathbb {R}}^{D\times D}\) is a symmetric tridiagonal matrix determined by the basic construction process, e.g., Algorithm 1 of Jia et al. (2021). We provide a detailed derivation of Eq. (18) in Appendix A. The global solution of this converted problem, i.e., \({\textbf{y}}^*=\left[ y_1^{*},y_2^{*},\ldots ,y_D^{*}\right]\), can be found by many existing techniques, see Press et al. (2007). We employ the Newton root finding method adopted by Section 6 of Cartis et al. (2011), which was originally proposed by Agarwal et al. (2021). It reduces the problem to a univariate root finding problem. After this, the global solution of the subproblem is computed by \({{\varvec{\eta }}}_{k}^* =\sum _{i=1}^D y_i^*{\textbf{q}}_i\).

In practice, when the manifold dimension D is large, it is more practical to find a good solution rather than the global solution. By working with a lower-dimensional Krylov subspace \({\mathcal {K}}_l\) with \(l<D\), one can derive Eq. (18) in \({\mathbb {R}}^l\), and its solution \({\textbf{y}}^{*l}\) results in a subproblem solution \({{\varvec{\eta }}}_{k}^{*l} = \sum _{i=1}^l y_i^{*l}{\textbf{q}}_i\). Both the global solution \({{\varvec{\eta }}}_{k}^*\) and the approximate solution \({{\varvec{\eta }}}_{k}^{*l}\) are always guaranteed to be at least as good as the solution obtained by performing a line search along the gradient direction, i.e.,
because \(\alpha {\textbf{G}}_k\) is a common basis vector shared by all the constructed Krylov subspaces \(\{{\mathcal {K}}_l\}_{i=1}^D\). We provide pseudo code for the Lanczos subproblem solver in Algorithm 2.
To benefit practitioners and improve understanding of the Lanczos solver, we analyse the gap between a practical solution \({{\varvec{\eta }}}_{k}^{*l}\) and the global minimizer \({{\varvec{\eta }}}_{k}^*\). Firstly, we define \(\lambda _{max}({\textbf{H}}_k)\) in a similar manner to \(\lambda _{min}({\textbf{H}}_k)\) as in Eq. (16). It resembles the largest eigenvalue of the Riemannian Hessian, as
We denote a degree-l polynomial evaluated at \({\textbf{H}}_k[{{\varvec{\eta }}}]\) by \(p_{l}\left( {\textbf{H}}_k\right) [{{\varvec{\eta }}}]\), such that
for some coefficients \(c_0, \; c_1, \;\ldots , \; c_l \in {\mathbb {R}}\). The quantity \({\textbf{H}}_k^l[{{\varvec{\eta }}}]\) is recursively defined by \({\textbf{H}}_k\left[ {\textbf{H}}_k^{l-1}\left[ {{\varvec{\eta }}}\right] \right]\) for \(l=2,3,\ldots\) We define below an induced norm, as
where the identity mapping operator works as \({{\textrm{Id}}}[{\varvec{\eta }}] = {{\varvec{\eta }}}\). Now we are ready to present our result in the following lemma.
Lemma 1
(Lanczos Solution Gap) Let \({{\varvec{\eta }}}_{k}^*\) be the global minimizer of the subproblem \({\hat{m}}_k\) in Eq. (10). Denote the subproblem without cubic regularization in Eq. (7) by \({\bar{m}}_k\) and let \(\bar{{{\varvec{\eta }}}}_k^*\) be its global minimizer. For each \(l>0\) , the solution \({{\varvec{\eta }}}_{k}^{*l}\) returned by Algorithm 2 satisfies
where \(\tilde{{\textbf{H}}}_k[{{\varvec{\eta }}}]:=({\textbf{H}}_k + \sigma _k\left\| {{\varvec{\eta }}}_{k}^*\right\| _{{\textbf{x}}_k}{{\textrm{Id}}})[{{\varvec{\eta }}}]\) for a moving direction \({{\varvec{\eta }}}\) , and \(\phi _l\left( \tilde{{\textbf{H}}}_k\right)\) is an upper bound of the induced norm \(\left\| p_{l+1}\left( \tilde{{\textbf{H}}}_k\right) -{{\textrm{Id}}}\right\| _{{\textbf{x}}_k}\).
We provide its proof in Appendix B. In Euclidean spaces, Carmon and Duchi (2018) has shown that \(\phi _l({\textbf{H}}_k)=2e^{\frac{-2(l+1)}{\sqrt{ \lambda _{max}({\textbf{H}}_k)\lambda _{min}^{-1}({\textbf{H}}_k)} }}\). With the help of Lemma 1, this could serve as a reference to gain an understanding of the solution quality for the Lanczos method in Riemannian spaces.
3.3.2 The conjugate gradient method
We experiment with an alternative subproblem solver by adapting the non-linear conjugate gradient technique in Riemannian spaces. It starts from the initialization of \({{\varvec{\eta }}}_{k}^0={\textbf{0}}_{{\textbf{x}}_k}\) and the first conjugate direction \({\textbf{p}}_1 = -{\textbf{G}}_k\) (negative gradient direction). At each inner iteration i (as opposed to the outer iteration k in the main algorithm), it solves the minimization problem with one input variable:
The global solution of this one-input minimization problem can be computed by zeroing the derivative of \({\hat{m}}_k\) with respect to \(\alpha\), resulting in a polynomial equation of \(\alpha\), which can then be solved by eigen-decomposition (Edelman & Murakami, 1995). Its root that possesses the minimal value of \({\hat{m}}_k\) is retrieved. The algorithm updates the next conjugate direction \({\textbf{p}}_{i+1}\) using the returned \(\alpha _i^*\) and \({\textbf{p}}_i\). Pseudo code for the conjugate gradient subproblem solver is provided in Algorithm 3.

Convergence of a conjugate gradient method largely depends on how its conjugate direction is updated. This is controlled by the setting of \(\beta _i\) for calculating \({\textbf{p}}_{i +1}= -{\textbf{r}}_{i}+\beta _i{\mathcal {P}}_{\alpha _i^*{\textbf{p}}_i}{\textbf{p}}_{i}\) in Step (17) of Algorithm 3. Working in Riemannian spaces under the subsampling setting, it has been proven by Sakai and Iiduka (2021) that, when the Fletcher–Reeves formula (Fletcher & Reeves, 1964) is used, i.e.,
where
a conjugate gradient method can converge to a stationary point with \(\lim _{i\rightarrow \infty }\) \(\left\| {{\textrm{grad}}} f\left( {\textbf{x}}_k^i\right) \right\| _{{\textbf{x}}_k^i}=0\). Working in Euclidean spaces, Wei et al. (2006) has shown that the Polak–Ribiere–Polyak formula, i.e.,
performs better than the Fletcher–Reeves formula. Building upon these, we propose to compute \(\beta _i\) by a modified Polak–Ribiere–Polyak formula in Riemannian spaces in Step (16) of Algorithm 3, given as
We prove that the resulting algorithm converges to a stationary point, and present the convergence result in Theorem 1, with its proof deferred to Appendix C.
Theorem 1
(Convergence of the Conjugate Gradient Solver) Assume that the step size \(\alpha _i^*\) in Algorithm 3 satisfies the strong Wolfe conditions (Hosseini et al., 2018), i.e., given a smooth function \(f:{\mathcal {M}}\rightarrow {\mathbb {R}}\) , it has
with \(0<c_1<c_2<1\). When Step (16) of Algorithm 3 computes \(\beta _i\) by Eq. (28), Algorithm 3 converges to a stationary point, i.e., \(\lim _{i\rightarrow \infty } \left\| {\textbf{G}}_k^i\right\| _{{\textbf{x}}_k^i}=0\).
In practice, Algorithm 3 terminates when there is no obvious change in the solution, which is examined in Step (4) by checking whether the step size is sufficiently small, i.e., whether \(\alpha _i \le 10^{-10}\) (Section 9 in (Agarwal et al., 2021)). To improve the convergence rate, the algorithm also terminates when \({\textbf{r}}_{i}\) in Step (13) is sufficiently small, i.e., following a classical criterion (Absil et al., 2007), to check whether
for some \(\theta ,\kappa >0\).
3.3.3 Properties of the subproblem solutions
In Algorithm 2, the basis \(\{{\textbf{q}}_i\}_{i=1}^D\) is constructed successively starting from \(q_1 = {\textbf{G}}_k\), while the converted problem in Eq. (18) is solved for each \({\mathcal {K}}_l\) starting from \(l=1\). This process allows up to D inner iterations. The solution \({{\varvec{\eta }}}_{k}^{*}\) obtained in the last inner iteration where \(l=D\) is the global minimizer over \({\mathbb {R}}^D\). Differently, Algorithm 3 converges to a stationary point as proved in Theorem 1. In practice, a maximum inner iteration number m is set in advance. Algorithm 3 stops when it reaches the maximum iteration number or converges to a status where the change in either the solution or the conjugate direction is very small.
The convergence property of the main algorithm presented in Algorithm 1 relies on the quality of the subproblem solution. Before discussing it, we first familiarize the reader with the classical TR concepts of Cauchy steps and eigensteps but defined for the Inexact RTR problem introduced in Sect. 2.2. According to Section 3.3 of Boumal et al. (2019), when \({\hat{m}}_k\) is the RTR subproblem, the closed-form Cauchy step \(\hat{{{\varvec{\eta }}}}_k^C\) is an improving direction defined by
It points towards the gradient direction with an optimal step size computed by the \(\min (\cdot ,\cdot )\) operation, and follows the form of the general Cauchy step defined by
According to Section 2.2 of Kasai and Mishra (2018), for some \(\nu \in (0,1]\), the eigenstep \({\varvec{\eta }}_k^E\) satisfies
It is an approximation of the negative curvature direction by an eigenvector associated with the smallest negative eigenvalue.
The following three assumptions on the subproblem solution are needed by the convergence analysis later. We define the induced norm for the Hessian as below:
Assumption 1
(Sufficient Descent Step) Given the Cauchy step \({{\varvec{\eta }}} _k^C\) and the eigenstep \({{\varvec{\eta }}} _k^E\) for \(\nu \in (0,1]\), assume the subproblem solution \({{\varvec{\eta }}}_{k}^{*}\) satisfies the Cauchy condition
and the eigenstep condition
where
The two last inequalities in Eqs. (36) and (37) concerning the Cauchy step and eigenstep are derived in Lemma 6 and Lemma 7 of Xu et al. (2020). Assumption 1 generalizes Condition 3 in Xu et al. (2020) to the Riemannian case. It assumes that the subproblem solution \({{\varvec{\eta }}}_{k}^{*}\) is better than the Cauchy step and eigenstep, decreasing more the value of the subproblem objective function. The following two assumptions enable a stronger convergence result for Algorithm 1, which will be used in the proof of Theorem 4.
Assumption 2
(Sub-model Gradient Norm Cartis et al., 2011; Kohler & Lucchi, 2017) Assume the subproblem solution \({{\varvec{\eta }}}_{k}^{*}\) satisfies
where \(\kappa _\theta \in (0,1/6]\).
Assumption 3
(Approximate Global Minimizer (Cartis et al., 2011; Yao et al., 2021)) Assume the subproblem solution \({{\varvec{\eta }}}_{k}^{*}\) satisfies
Driven by these assumptions, we characterize the subproblem solutions and present the results in the following lemmas. Their proofs are deferred to Appendix D.
Lemma 2
(Lanczos Solution) The subproblem solution obtained by Algorithm 2 when being executed D (the dimension of \({\mathcal {M}}\)) iterations satisfies Assumptions 1, 2, 3. When being executed \(l<D\) times, the solution satisfies the Cauchy condition in Assumption 1, also Assumptions 2and 3.
Lemma 3
(Conjugate Gradient Solution) The subproblem solution obtained by Algorithm 3 satisfies the Cauchy condition in Assumption 1. Assuming \({\hat{m}}_k({{\varvec{\eta }}})\approx f(R_{{\textbf{x}}_k}({{\varvec{\eta }}}))\) , it also satisfies
and approximately the first condition of Assumption 3, as
In practice, Algorithm 2 based on lower-dimensional Krylov subspaces with \(l<D\) returns a less optimal solution, while Algorithm 3 returns at most a local minimum. They are not guaranteed to satisfy the eigenstep condition in Assumption 1. But the early-returned solutions from Algorithm 2 still satisfy Assumptions 2 and 3. However, solutions from Algorithm 3 do not satisfy these two Assumptions exactly, but they could get close in an approximate manner. For instance, according to Lemma 3, \(\left\| \nabla _{{{\varvec{\eta }}}}{\hat{m}}_k\left( {{\varvec{\eta }}}_{k}^{*} \right) \right\| _{{\textbf{x}}_k}\approx 0\), and we know that \(0 \le \kappa _\theta \min \left( 1, \left\| {{\varvec{\eta }}}_k^* \right\| _{{\textbf{x}}_k} \right) \Vert {\textbf{G}}_k\Vert _{{\textbf{x}}_k}\); thus, there is a fair chance for Eq. (41) in Assumption 2 to be met by the solution from Algorithm 3. Also, given that \({{\varvec{\eta }}}_k^*\) is a descent direction, it has \(\langle {\textbf{G}}_k, {{\varvec{\eta }}}_k^*\rangle _{{\textbf{x}}_k}\le 0\). Combining this with Eq. (45) in Lemma 3, there is a fair chance for Eq. (42) in Assumption 2 to be met. We present experimental results in Sect. 5.5, showing empirically to what extent the different solutions satisfy or are close to the eigenstep condition in Assumption 1, Assumptions 2 and 3.
3.4 Practical early stopping
In practice, it is often more efficient to stop the optimization earlier before meeting the optimality conditions and obtain a reasonably good solution much faster. We employ a practical and simple early stopping mechanism to accommodate this need. Algorithm 1 is allowed to terminate earlier when: (1) the norm of the approximate gradient continually fails to decrease for K times, and (2) when the percentage of the function decrement is lower than a given threshold, i.e.,
for a consecutive number of K times, with K and \(\tau _f>0\) being user-defined.
For the subproblem, both Algorithms 2 and 3 are allowed to terminate when the current solution \({{\varvec{\eta }}}_k\), i.e., \({{\varvec{\eta }}}_k = {{\varvec{\eta }}}_{k}^{*l}\) for Algorithm 2 and \({{\varvec{\eta }}}_k = {{\varvec{\eta }}}_{k}^{i}\) for Algorithm 3, satisfies
This implements an examination of Assumption 2. Regarding Assumption 1, both Algorithms 2 and 3 optimize along the direction of the Cauchy step in their first iteration and thus satisfy the Cauchy condition. Therefore there is no need to examine it. As for the eigenstep condition, it is costly to compute and compare with the eigenstep in each inner iteration, so we do not use it as a stopping criterion in practice. Regarding Assumption 3, according to Lemma 2, it is always satisfied by the solution from Algorithm 2. Therefore, there is no need to examine it in Algorithm 2. As for Algorithm 3, the examination by Eq. (47) also plays a role in checking Assumption 3. For the first condition in Assumption 3, Eq. (42) is equivalent to \(\langle \nabla _{{{\varvec{\eta }}}}{\hat{m}}_k\left( {{\varvec{\eta }}}_{k}^{*} \right) ,{{\varvec{\eta }}}_{k}^{*}\rangle _{{\textbf{x}}_k}=0\) (this results from Eq. (106) in Appendix D.2). In practice, when Eq. (47) is satisfied with a small value of \(\left\| \nabla _{{{\varvec{\eta }}}}{\hat{m}}_k\left( {{\varvec{\eta }}}_k^* \right) \right\| _{{\textbf{x}}_k}\), it has \(\left\langle \nabla _{{{\varvec{\eta }}}}{\hat{m}}_k\left( {{\varvec{\eta }}}_{k}^* \right) ,{{\varvec{\eta }}}_{k}^*\right\rangle _{{\textbf{x}}_k}\approx 0\), indicating that the first condition of Assumption 3 is met approximately. Also, since \(\langle {\textbf{G}}_k,{{\varvec{\eta }}}_k^*\rangle _{{\textbf{x}}_k}\le 0\) due to the descent direction \({{\varvec{\eta }}}_k^*\), the second condition of Assumption 3 has a fairly high chance to be met.
4 Convergence analysis
4.1 Preliminaries
We start from listing those assumptions and conditions from existing literature that are adopted to support our analysis. Given a function f, the Hessian of its pullback \(\nabla ^2{{\hat{f}}}\left( {\textbf{x}}\right) [\mathbf {{{\varvec{\eta }}}}]\) and its Riemannian Hessian \({{\textrm{Hess}}} f\left( {\textbf{x}}\right) [{\varvec{\eta }}]\) are identical when a second-order retraction is used (Boumal et al., 2019), and this serves as an assumption to ease the analysis.
Assumption 4
(Second-order Retraction (Boumal, 2020)) The retraction mapping is assumed to be a second-order retraction. That is, for all \({\textbf{x}}\in {\mathcal {M}}\) and all \({{\varvec{\eta }}}\in T_{\textbf{x}}{\mathcal {M}}\), the curve \(\gamma (t):=R_{\textbf{x}}(t{{\varvec{\eta }}})\) has zero acceleration at \(t=0\), i.e., \(\gamma ''(0)=\frac{{\mathcal {D}}^2}{dt^2}R_{\textbf{x}}(t{{\varvec{\eta }}})\big |_{t=0}=0\).
The following two assumptions originate from the assumptions required by the convergence analysis of the standard RTR algorithm (Boumal et al., 2019; Ferreira & Svaiter, 2002), and are adopted here to support the inexact analysis.
Assumption 5
(Restricted Lipschitz Hessian) There exists \(L_H>0\) such that for all \({\textbf{x}}_k\) generated by Algorithm 1 and all \({\varvec{\eta }}_k\in T_{{\textbf{x}}_k}{\mathcal {M}}\), \({\hat{f}}_k\) satisfies
and
where \({\mathcal {P}}^{-1}\) denotes the inverse process of the parallel transport operator.
Assumption 6
(Norm Bound on Hessian) For all \({\textbf{x}}_k\), there exists \(K_H\ge 0\) so that the inexact Hessian \({\textbf{H}}_k\) satisfies
The following key conditions on the inexact gradient and Hessian approximations are developed in Euclidean spaces by Roosta–Khorasani and Mahoney (2019) (Section 2.2) and Xu et al. (2020) (Section 1.3), respectively. We make use of these in Riemannian spaces.
Condition 1
(Approximation Error Bounds) For all \({\textbf{x}}_k\) and \({\varvec{\eta }}_k\in T_{{\textbf{x}}_k}{\mathcal {M}}\), suppose that there exist \(\delta _g,\delta _H>0\), such that the approximate gradient and Hessian satisfy
As will be shown in Theorem 2 later, these allow the used sampling size in the gradient and Hessian approximations to be fixed throughout the training process. As a result, it can serve as a guarantee of the algorithmic efficiency when dealing with large-scale problems.
4.2 Supporting theorem and assumption
In this section, we prove a preparation theorem and present new conditions required by our results. Below, we re-develop Theorem 4.1 in Kasai and Mishra (2018) using the matrix Bernstein inequality (Gross, 2011). It provides lower bounds on the required subsampling size for approximating the gradient and Hessian in order for Condition 1 to hold. The proof is provided in Appendix E.
Theorem 2
(Gradient and Hessian Sampling Size) Define the suprema of the Riemannian gradient and Hessian
Given \(0<\delta <1\) , Condition 1is satisfied with probability at least \(\left( 1-\delta \right)\) if
where \(|{\mathcal {S}}_g|\) and \(|{\mathcal {S}}_H|\) denote the sampling sizes, while d and r are the dimensions of \({\textbf{x}}\).
The two quantities \(\delta _g\) and \(\delta _H\) in Condition 1 are the upper bounds of the gradient and Hessian approximation errors, respectively. The following assumption bounds \(\delta _g\) and \(\delta _H\).
Assumption 7
(Restrictions on \(\delta _g\) and \(\delta _H\)) Given \(\nu \in (0,1]\), \(K_H\ge 0\), \(L_H>0\), \(0<\tau , \epsilon _g<1\), we assume that \(\delta _g\) and \(\delta _H\) satisfy
As seen in Eqs. (55) and (56), sampling sizes \(|{\mathcal {S}}_g|\) and \(|{\mathcal {S}}_H|\) are directly proportional to the probability \((1-\delta )\) but inversely proportional to the error tolerances \(\delta _g\) and \(\delta _H\), respectively. Hence, a higher \((1-\delta )\) and smaller \(\delta _g\) and \(\delta _H\) (affected by \(K_H\) and \(L_H\)) require larger \(|{\mathcal {S}}_g|\) and \(|{\mathcal {S}}_H|\) for estimating the inexact Riemannian gradient and Hessian.
4.3 Main results
Now we are ready to present our main convergence results in two main theorems for Algorithm 1. Different from Sun et al. (2019) which explores the escape rate from a saddle point to a local minimum, we study the convergence rate from a random point.
Theorem 3
(Convergence Complexity of Algorithm 1) Consider \(0<\epsilon _g,\epsilon _H<1\) and \(\delta _g,\delta _H>0\). Suppose that Assumptions 4, 5, 6and 7hold and the solution of the subproblem in Eq. (10) satisfies Assumption 1. Then, if the inexact gradient \({\textbf{G}}_k\) and Hessian \({\textbf{H}}_k\) satisfy Condition 1, Algorithm 1 returns an \(\left( \epsilon _g,\epsilon _H\right)\)-optimal solution in \({\mathcal {O}}\left( \max \left( \epsilon _g^{-2},\epsilon _H^{-3}\right) \right)\) iterations.
The proof along with the supporting lemmas is provided in Appendices F.1 and F.2. When the Hessian at the solution is close to positive semi-definite which indicates a small \(\epsilon _H\), the Inexact Sub-RN-CR finds an \(\left( \epsilon _g,\epsilon _H\right)\)-optimal solution in fewer iterations than the Inexact RTR, i.e., \({\mathcal {O}}\left( \max \left( \epsilon _g^{-2},\epsilon _H^{-3}\right) \right)\) iterations for the Inexact Sub-RN-CR as compared to \({\mathcal {O}}\left( \max \left( \epsilon _g^{-2}\epsilon _H^{-1},\epsilon _H^{-3}\right) \right)\) for the Inexact RTR (Kasai & Mishra, 2018). Such a result is satisfactory. Combining Theorems 2 and 3, it leads to the following corollary.
Corollary 1
Consider \(0<\epsilon _g,\epsilon _H<1\) and \(\delta _g,\delta _H>0\). Suppose that Assumptions 4, 5, 6and 7hold and the solution of the subproblem in Eq. (10) satisfies Assumption 1. For any \(0<\delta <1\), suppose Eqs. (55) and (56) are satisfied at each iteration. Then, Algorithm 1 returns an \(\left( \epsilon _g,\epsilon _H\right)\)-optimal solution in \({\mathcal {O}}\left( \max \left( \epsilon _g^{-2},\epsilon _H^{-3}\right) \right)\) iterations with a probability at least \(p=(1-\delta )^{{\mathcal {O}}\left( \max \left( \epsilon _g^{-2},\epsilon _H^{-3}\right) \right) }\).
The proof is provided in Appendix F.3. We use an example to illustrate the effect of \(\delta\) on the approximate gradient sample size \(|{\mathcal {S}}_g|\). Suppose \(\epsilon ^{-2}_g > \epsilon ^{-3}_H\), then \(p=(1-\delta )^{{\mathcal {O}}\left( \epsilon _g^{-2}\right) }\). In addition, when \(\delta = {\mathcal {O}}\left( \epsilon ^2_g/10\right)\), \(p\approx 0.9\). Replacing \(\delta\) with \({\mathcal {O}}\left( \epsilon ^2_g/10\right)\) in Eqs. (55) and (56), it can be obtained that the lower bound of \(|{\mathcal {S}}_g|\) is proportional to \(\ln \left( 10\epsilon ^{-2}_g\right)\).
Combining Assumption 3 and the stopping condition in Eq. (47) for the inexact solver, a stronger convergence result can be obtained for Algorithm 1, which is presented in the following theorem and corollary.
Theorem 4
(Optimal Convergence Complexity of Algorithm 1) Consider \(0<\epsilon _g,\epsilon _H<1\) and \(\delta _g,\delta _H>0\). Suppose that Assumptions 4, 5, 6and 7hold and the solution of the subproblem satisfies Assumptions 1, 2and 3. Then, if the inexact gradient \({\textbf{G}}_k\) and Hessian \({\textbf{H}}_k\) satisfy Condition 1and \(\delta _g\le \delta _H\le \kappa _\theta \epsilon _g\) , Algorithm 1 returns an \(\left( \epsilon _g,\epsilon _H\right)\)-optimal solution in \({\mathcal {O}}\left( \max \left( \epsilon _g^{-\frac{3}{2}},\epsilon _H^{-3}\right) \right)\) iterations.
Corollary 2
Consider \(0<\epsilon _g,\epsilon _H<1\) and \(\delta _g,\delta _H>0\). Suppose that Assumptions 4, 5, 6and 7hold, and the solution of the subproblem satisfies Assumptions 1, 2and 3. For any \(0<\delta <1\), suppose Eqs. (55) and (56) are satisfied at each iteration.
Then, Algorithm 1 returns an \(\left( \epsilon _g,\epsilon _H\right)\)-optimal solution in \({\mathcal {O}}\left( \max \left( \epsilon _g^{-\frac{3}{2}},\epsilon _H^{-3}\right) \right)\) iterations with a probability at least \(p=(1-\delta )^{{\mathcal {O}}\left( \max \left( \epsilon _g^{-\frac{3}{2}},\epsilon _H^{-3}\right) \right) }\).
The proof of Theorem 4 along with its supporting lemmas is provided in Appendices G.1 and G.2. The proof of Corollary 2 follows Corollary 1 and is provided in Appendix G.3.
4.4 Computational complexity analysis
We analyse the number of main operations required by the proposed algorithm. Taking the PCA task as an example, it optimizes over the Grassmann manifold \({{\textrm{Gr}}}\left( r,d\right)\). Denote by m the number of inexact iterations and D the manifold dimension, i.e., \(D=d\times (d-r)\) for the Grassmann manifold. Starting from the gradient and Hessian computation, the full case requires \({\mathcal {O}}(ndr)\) operations for both in the PCA task. By using the subsampling technique, these can be reduced to \({\mathcal {O}}(|{\mathcal {S}}_g|dr)\) and \({\mathcal {O}}(|{\mathcal {S}}_H|dr)\) by gradient and Hessian approximation. Following an existing setup for cost computation, i.e., Inexact RTR method (Kasai & Mishra, 2018), the full function cost evaluation takes n operations, while the approximate cost evaluation after subsampling becomes \({\mathcal {O}}(|{\mathcal {S}}_n|dr)\), where \({\mathcal {S}}_n\) is the subsampled set of data points used to compute the function cost. These show that, for large-scale practices with \(n\gg \max \left( |{\mathcal {S}}_g|, |{\mathcal {S}}_H|,|{\mathcal {S}}_n| \right)\), the computational cost reduction gained from the subsampling technique is significant.
For the subproblem solver by Algorithm 2 or 3, the dominant computation within each iteration is the Hessian computation, which as mentioned above requires \({\mathcal {O}}(|{\mathcal {S}}_H|dr)\) operations after using the subsampling technique. Taking this into account to analyze Algorithm 1, its overall computational complexity becomes \({\mathcal {O}}\left( \max \left( \epsilon _g^{-2}, \epsilon _H^{-3} \right) \right) \times \left[ {\mathcal {O}}(n + |{\mathcal {S}}_g|dr )+ {\mathcal {O}}\left( m| {\mathcal {S}}_H|d^2(d-r)r\right) \right]\) based on Theorem 3, where \({\mathcal {O}}(n + |{\mathcal {S}}_g|dr)\) corresponds to the operations for computing the full function cost and the approximate gradient in an outer iteration. This overall complexity can be simplified to \({\mathcal {O}}\left( \max \left( \epsilon _g^{-2}, \epsilon _H^{-3}\right) \right) \times {\mathcal {O}}(n + |{\mathcal {S}}_g|dr + m|{\mathcal {S}}_H|d^2(d-r)r)\), where \({\mathcal {O}}(m|{\mathcal {S}}_H|d^2(d-r)r)\) is the cost of the subproblem solver by either Algorithm 2 or Algorithm 3. Algorithm 2 is guaranteed to return the optimal subproblem solution within at most \(m=D=d\times (d-r)\) inner iterations, of which the complexity is at most \({\mathcal {O}}(|{\mathcal {S}}_H|d^2(d-r)^2r^2)\). Such a polynomial complexity is at least as good as the ST-tCG solver used in the Inexact RTR algorithm. For Algorithm 3, although m is not guaranteed to be bounded and polynomial, we have empirically observed that m is generally smaller than D in practice, presenting a similar complexity to Algorithm 2.
5 Experiments and result analysis
We compare the proposed Inexact Sub-RN-CR algorithm with state-of-the-art and popular Riemannian optimization algorithms. These include the Riemannian stochastic gradient descent (RSGD) (Bonnabel, 2013), Riemannian steepest descent (RSD) (Absil et al., 2009), Riemannian conjugate gradient (RCG) (Absil et al., 2009), Riemannian limited memory BFGS algorithm (RLBFGS) (Yuan et al., 2016), Riemannian stochastic variance-reduced gradient (RSVRG) (Zhang et al., 2016), Riemannian stochastic recursive gradient (RSRG) (Kasai et al., 2018), RTR (Absil et al., 2007), Inexact RTR (Kasai & Mishra, 2018) and RTRMC (Boumal & Absil, 2011). Existing implementations of these algorithms are available in either Manopt (Boumal et al., 2014) or Pymanopt (Townsend et al., 2016) library. They are often used for algorithm comparison in existing literature, e.g., by Inexact RTR (Kasai & Mishra, 2018). Particularly, RSGD, RSD, RCG, RLBFGS, RTR and RTRMC algorithms have been encapsulated into Manopt, and RSD, RCG and RTR also into Pymanopt. RSVRG, RSRG and Inexact RTR are implemented by Kasai and Mishra (2018) based on Manopt. We use existing implementations to reproduce their methods. Our Inexact Sub-RN-CR implementation builds on Manopt.
For the competing methods, we follow the same parameter settings from the existing implementations, including the batch size (i.e. sampling size), step size (i.e. learning rate) and the inner iteration number to ensure the same results as the reported ones. For our method, we first keep the common algorithm parameters the same as the competing methods, including \(\gamma\), \(\tau\), \(\epsilon _g\) and \(\epsilon _H\). Then, we use a grid search to find appropriate values of \(\theta\) and \(\kappa _\theta\) for both Algorithms 2 and 3. Specifically, the searching grid for \(\theta\) is (0.02, 0.05, 0.1, 0.2, 0.5, 1), and the searching grid for \(\kappa _\theta\) is (0.005, 0.01, 0.02, 0.04, 0.08, 0.16). For the parameter \(\kappa\) in Algorithm 3, we keep it the same as the other conjugate gradient solvers. The early stopping approach as described in Sect. 3.4 is applied to all the compared algorithms.
Regarding the batch setting, which is also the sample size setting for approximating the gradient and Hessian, we adopt the same value as used in existing subsampling implementations to keep consistency. Also, the same settings are used for both the PCA and matrix completion tasks. Specifically, the batch size \(\left| {\mathcal {S}}_g\right| = n/100\) is used for RSGD, RSVRG and RSRG where \({\mathcal {S}}_H\) is not considered as these are first-order methods. For both the Inexact RTR and the proposed Inexact Sub-RN-CR, \(\left| {\mathcal {S}}_H\right| =n/100\) and \(\left| {\mathcal {S}}_g \right| = n\) is used. This is to follow the existing setting in Kasai and Mishra (2018) for benchmark purposes, which exploits the approximate Hessian but the full gradient. In addition to these, we experiment with another batch setting of \(\left\{ \left| {\mathcal {S}}_H\right| =n/100,\left| {\mathcal {S}}_g\right| =n/10\right\}\) for both the Inexact RTR and Inexact Sub-RN-CR. This is flagged by (G) in the algorithm name, meaning that the algorithm uses the approximate gradient in addition to the approximate Hessian. Its purpose is to evaluate the effect of \({\mathcal {S}}_g\) in the optimization.
Evaluation is conducted based on two machine learning tasks of PCA and low-rank matrix completion using both synthetic and real-world datasets with \(n\gg d\gg 1\). Both tasks can be formulated as non-convex optimization problems on the Grassmann manifold Gr\(\left( r,d\right)\). The algorithm performance is evaluated by oracle calls and the run time. The former counts the number of function, gradient, and Hessian-vector product computations. For instance, Algorithm 1 requires \(n+|{\mathcal {S}}_g|+m|{\mathcal {S}}_H|\) oracle calls each iteration, where m is the number of iterations of the subproblem solver. Regarding the user-defined parameters in Algorithm 1, we use \(\epsilon _\sigma =10^{-18}\). Empirical observations suggest that the magnitude of the data entries affects the optimization in its early stage, and hence these factors are taken into account in the setting of \(\sigma _0\). Let \({\textbf{S}}=[s_{ij}]\) denote the input data matrix containing L rows and H columns. We compute \(\sigma _0\) by considering the data dimension, also the averaged data magnitude normalized by its standard deviation, given as
where \(\mu _S = \frac{1}{LH}\sum _{i\in [L], j\in [H]}s_{i,j}\) and dim(M) is the manifold dimension.
Regarding the early stopping setting in Eq. (46), \(K=5\) is used for both tasks, and we use \(\tau _f = 10^{-12}\) for MNIST and \(\tau _f = 10^{-10}\) for the remaining datasets in the PCA task. In the matrix completion task, we set \(\tau _f = 10^{-10}\) for the synthetic datasets and \(\tau _f = 10^{-3}\) for the real-world datasets. For the early stopping settings in Eq. (47) and in Step (13) of Algorithm 3, we adopt \(\kappa _\theta =0.08\) and \(\theta =0.1\). Between the two subproblem solvers, we observe that Algorithm 2 by the Lanczos method and Algorithm 3 by the conjugate gradient perform similarly. Therefore, we report the main results using Algorithm 2, and provide supplementary results for Algorithm 3 in a separate Sect. 5.4.
5.1 PCA experiments
PCA can be interpreted as a minimization of the sum of squared residual errors between the projected and the original data points, formulated as
where \({\textbf{z}}_i \in {\mathbb {R}}^{d}\). The objective function can be re-expressed as one on the Grassmann manifold via
One synthetic dataset P1 and two real-world datasets including MNIST (LeCun et al., 1998) and Covertype (Blackard & Dean, 1999) are used in the evaluation. The P1 dataset is firstly generated by randomly sampling each element of a matrix \({\textbf{A}}\in {\mathbb {R}}^{n\times d}\) from a normal distribution \({\mathcal {N}}(0,1)\). This is then followed by a multiplication with a diagonal matrix \({\textbf{S}}\in {\mathbb {R}}^{d\times d}\) with each diagonal element randomly sampled from an exponential distribution \(Exp (2)\), which increases the difference between the feature variances. After that, a mean-subtraction preprocessing is applied to \({\textbf{A}}{\textbf{S}}\) to obtain the final P1 dataset. The \(\left( n,d,r\right)\) values are: \(\left( 5\times 10^5,10^3,5\right)\) for P1, \(\left( 6\times 10^4,784,10\right)\) for MNIST, and \(\left( 581012,54,10\right)\) for Covertype. Algorithm accuracy is assessed by optimality gap, defined as the absolute difference \(|f-f^*|\), where \(f=-\frac{1}{n}\sum _{i=1}^n{\textbf{z}}_i^T\hat{{\textbf{U}}}\hat{{\textbf{U}}}^T{\textbf{z}}_i\) with \(\hat{{\textbf{U}}}\) as the optimal solution returned by Algorithm 1. The optimal function value \(f^*=-\frac{1}{n}\sum _{i=1}^n{\textbf{z}}_i^T\tilde{{\textbf{U}}}\tilde{{\textbf{U}}}^T{\textbf{z}}_i\) is computed by using the eigen-decomposition solution \(\tilde{{\textbf{U}}}\), which is a classical way to obtain PCA result without going through the optimization program.
Figure 2 compares the optimality gap changes over iterations for all the competing algorithms. Additionally, Fig. 3 summarizes their accuracy and convergence performance in optimality gap and run time. Figure 4a reports the performance without using early stopping for the P1 dataset. It can be seen that the Inexact Sub-RN-CR reaches the minima with the smallest iteration number for both the synthetic and real-world datasets. In particular, the larger the scale of a problem is, the more obvious the advantage of our Inexact Sub-RN-CR is, evidenced by the performance difference.
However, both the Inexact RTR and Inexact Sub-RN-CR achieve their best PCA performance when using a full gradient calculation accompanied by a subsampled Hessian. The subsampled gradient does not seem to result in a satisfactory solution as shown in Fig. 2 with \(\left| {\mathcal {S}}_g\right| =n/10\). Additionally, we report more results for the Inexact RTR and the proposed Inexact Sub-RN-CR in Fig. 4b on the P1 dataset with different gradient batch sizes, including \(\left| {\mathcal {S}}_g\right| \in \left\{ n/1.5,n/2,n/5,n/10\right\}\). They all perform less well than \(\left| {\mathcal {S}}_g\right| =n\). More accurate gradient information is required to produce a high-precision solution in these tested cases. A hypothesis on the cause of this phenomenon might be that the variance of the approximate gradients across samples is larger than that of the approximate Hessians. Hence, a sufficiently large sample size is needed for a stable approximation of the gradient information. Errors in approximate gradients may cause the algorithm to converge to a sub-optimal point with a higher cost, thus performing less well. Another hypothesis might be that the quadratic term \({\textbf{U}}{\textbf{U}}^T\) in Eq. (61) would square the approximation error from the approximate gradient, which could significantly increase the PCA reconstruction error.
By fixing the gradient batch size \(\left| {\mathcal {S}}_g\right| =n\) for both the Inexact RTR and Inexact Sub-RN-CR, we compare in Fig. 4c, d their sensitivity to the used batch size for Hessian approximation. We experiment with \(\left| {\mathcal {S}}_H\right| \in \{n/10,n/10^2\), \(n/10^3,n/10^4\}\). It can be seen that the Inexact Sub-RN-CR outperforms the Inexact RTR in almost all cases except for \(\left| {\mathcal {S}}_H\right| =n/10^4\) for the MNIST dataset. The Inexact Sub-RN-CR possesses a rate of increase in oracle calls significantly smaller for large sample sizes. This implies that the Inexact Sub-RN-CR is more robust than the Inexact RTR to batch-size change for inexact Hessian approximation.
5.2 Low-rank matrix completion experiments
Low-rank matrix completion aims at completing a partial matrix \({\textbf{Z}}\) with only a small number of entries observed, under the assumption that the matrix has a low rank. One way to formulate the problem is shown as below
where \(\varOmega\) denotes the index set of the observed matrix entries. The operator \({\mathcal {P}}_\varOmega : {\mathbb {R}}^{d\times n}\rightarrow {\mathbb {R}}^{d\times n}\) is defined as \({\mathcal {P}}_\varOmega \left( {\textbf{Z}}\right) _{ij}={\textbf{Z}}_{ij}\) if \(\left( i,j \right) \in \varOmega\), while \({\mathcal {P}}_\varOmega \left( {\textbf{Z}}\right) _{ij}=0\) otherwise. We generate it by uniformly sampling a set of \(|\varOmega |=4r(n+d-r)\) elements from the dn entries. Let \({\textbf{a}}_i\) be the i-th column of \({\textbf{A}}\), \({\textbf{z}}_i\) be the i-th column of \({\textbf{Z}}\), and \({\varOmega }_i\) be the subset of \({\varOmega }\) that contains sampled indices for the i-th column of \({\textbf{Z}}\). Then, \({\textbf{a}}_i\) has a closed-form solution \({\textbf{a}}_i=({\textbf{U}}_{{\varOmega }_i})^{\dagger }{\textbf{z}}_{\varOmega _i}\) (Kasai & Mishra, 2018), where \({\textbf{U}}_{{\varOmega }_i}\) contains the selected rows of \({\textbf{U}}\), and \({\textbf{z}}_{\varOmega _i}\) the selected elements of \({\textbf{z}}_i\) according to the indices in \(\varOmega _i\), and \(\dagger\) denotes the pseudo inverse operation. To evaluate a solution \({\textbf{U}}\), we generate another index set \({\tilde{\varOmega }}\), which is used as the test set and satisfies \({\tilde{\varOmega }}\cap \varOmega = \emptyset\), following the same way as generating \(\varOmega\). We compute the mean squared error (MSE) by
In evaluation, three synthetic datasets and a real-world dataset Jester (Goldberg et al., 2001) are used where the training and test sets are already predefined by Goldberg et al. (2001). The synthetic datasets are generated by following a generative model similar to Ngo and Saad (2012) based on SVD. Specifically, to develop a synthetic dataset, we generate two matrices \({\textbf{A}}\in {\mathbb {R}}^{d\times r}\) and \({\textbf{B}}\in {\mathbb {R}}^{n\times r}\) with their elements independently sampled from the normal distribution \({\mathcal {N}}(0,1)\). Then, we generate two orthogonal matrices \({\textbf{Q}}_A\) and \({\textbf{Q}}_B\) by applying the QR decomposition (Trefethen & Bau, 1997) respectively to \({\textbf{A}}\) and \({\textbf{B}}\). After that, we construct a diagonal matrix \({\textbf{S}}\in {\mathbb {R}}^{r\times r}\) of which the diagonal elements are computed by \(s_{i,i}=10^{3+\frac{(i-r)\log _{10}(c)}{r-1}}\) for \(i=1,\ldots ,r\), and the final data matrix is computed by \({\textbf{Z}}={\textbf{Q}}_A{\textbf{S}}{\textbf{Q}}_B^T\). The reason to construct \({\textbf{S}}\) in this specific way is to have an easy control over the condition number of the data matrix, denoted by \(\kappa ({\textbf{Z}})\), which is the ratio between the maximum and minimum singular values of \({\textbf{Z}}\). Because \(\kappa ({\textbf{Z}}) = \frac{\sigma _{max}({\textbf{Z}})}{\sigma _{min}({\textbf{Z}})}=\frac{10^3}{10^{3-\log _{10}(c)} }=c\), we can adjust the condition number by tuning the parameter c. Following this generative model, each synthetic dataset is generated by randomly sampling two orthogonal matrices and constructing one diagonal matrix subject to the constraint of condition numbers, i.e., \(c=\kappa ({\textbf{Z}})=5\) for M1 and \(c=\kappa ({\textbf{Z}})=20\) for M2 and M3. The \(\left( n,d,r\right)\) values of the used datasets are: \(\left( 10^5,10^2,5\right)\) for M1, \(\left( 10^5,10^2,5\right)\) for M2, \(\left( 3\times 10^4,10^2,5\right)\) for M3, and \(\left( 24983,10^2,5\right)\) for Jester.
Figure 5 compares the MSE changes over iterations, while Figs. 6 and 7 summarize both the MSE performance and the run time in the same plot for different algorithms and datasets. In Fig. 6, the Inexact Sub-RN-CR outperforms the others in most cases, and it can even be nearly twice as fast as the state-of-the-art methods for cases with a larger condition number (see dataset M2 and M3). This shows that the proposed algorithm is efficient at handling ill-conditioned problems. In Fig. 7, the Inexact Sub-RN-CR achieves a sufficiently small MSE with the shortest run time, faster than the Inexact RTR and RTRMC. Unlike in the PCA task, the subsampled gradient approximation actually helps to improve the convergence. A hypothesis for explaining this phenomenon could be that, as compared to the quadratic term \({\textbf{U}}{\textbf{U}}^T\) in the PCA objective function, the linear term \({\textbf{U}}\) in the matrix completion objective function accumulates fewer errors from the inexact gradient, making the optimization more stable.
Additionally, Fig. 8a compares the Inexact RTR and the Inexact Sub-RN-CR with varying batch sizes for gradient estimation and with fixed \(|{\mathcal {S}}_H| =n\). The M1–M3 results show that our algorithm exhibits stronger robustness to \(|{\mathcal {S}}_g|\), as it converges to the minima with only 50\(\%\) additional oracle calls when reducing \(|{\mathcal {S}}_g|\) from n/10 to \(n/10^2\), whereas Inexact RTR requires twice as many calls. For the Jester dataset, in all settings of gradient sample sizes, our method achieves lower MSE than the Inexact RTR, especially when \(|{\mathcal {S}}_g|=n/10^4\). Figure 8b compares sensitivities in Hessian sample sizes \(|{\mathcal {S}}_H|\) with fixed \(|{\mathcal {S}}_g| =n\). Inexact Sub-RN-CR performs better for the synthetic dataset M3 with \(\left| {\mathcal {S}}_H\right| \in \{n/10,n/10^2\}\), showing roughly twice faster convergence. For the Jester dataset, Inexact Sub-RN-CR performs better with \(\left| {\mathcal {S}}_H\right| \in \{n/10,n/10^2,n/10^3\}\) except for the case of \(\left| {\mathcal {S}}_H\right| =n/10^4\), which is possibly because the construction of the Krylov subspace requires a more accurately approximated Hessian.
To summarize, we have observed from both the PCA and matrix completion tasks that the effectiveness of the subsampled gradient in the proposed approach can be sensitive to the choice of the practical problems, while the subsampled Hessian steadily contributes to a faster convergence rate.
5.3 Imaging applications
In this section, we demonstrate some practical applications of PCA and matrix completion, which are solved by using the proposed optimization algorithm Inexact Sub-RN-CR, for analyzing medical images and scene images.
5.3.1 Functional connectivity in fMRI by PCA
Functional magnetic-resonance imaging (fMRI) can be used to measure brain activities and PCA is often used to find functional connectivities between brain regions based on the fMRI scans (Zhong et al., 2009). This method is based on the assumption that the activation is independent of other signal variations such as brain motion and physiological signals (Zhong et al., 2009). Usually, the fMRI images are represented as a 4D data block subject to observational noise, including 3 spatial dimensions and 1 time dimension. Following a common preprocessing routine (Sidhu et al., 2012; Kohoutová et al., 2020), we denote an fMRI data block by \({\textbf{D}}\in {\mathbb {R}}^{u\times v\times w\times T}\) and a mask by \({\textbf{M}}\in \{0,1\}^{u\times v\times w}\) that contains d nonzero elements marked by 1. By applying the mask to the data block, we obtain a feature matrix \({\textbf{f}}\in {\mathbb {R}}^{d\times T}\), where each column stores the features of the brain at a given time stamp. One can increase the sample size by collecting k fMRI data blocks corresponding to k human subjects, after which the feature matrix is expanded to a larger matrix \({\textbf{F}}\in {\mathbb {R}}^{d\times kT}\).
In this experiment, an fMRI dataset referred to as ds000030 provided by the OpenfMRI database (Poldrack & Gorgolewski, 2017) is used, where \(u=v=64\), \(w=34\), and \(T=184\). We select \(k=13\) human subjects and use the provided brain mask with \(d=228483\). The dimension of the final data matrix is \((n,d)=(2392,228483)\), where \(n=kT\). We set the rank as \(r=5\) which is sufficient to capture over \(93\%\) of the variance in the data. After the PCA processing, each computed principal component can be rendered back to the brain reconstruction by using the open-source library Nilearn (Abraham et al., 2014). Figure 9 displays the optimization performance, where the Inexact Sub-RN-CR converges faster in terms of both run time and oracle calls. For our method and the Inexact RTR, adopting the subsampled gradient leads to a suboptimal solution in less time than using the full gradient. We speculate that imprecise gradients cause an oscillation of the optimization near local optima. Figure 10 compares the results obtained by our optimization algorithm with those computed by eigen-decomposition. The highlighted regions denote the main activated regions with positive connectivity (yellow) and negative connectivity (blue). The components learned by the two approaches are similar, with some cases learned by our approach tending to be more connected (see Fig. 10a and c).
5.3.2 Image recovery by matrix completion
In this application, we demonstrate image recovery with matrix completion using a \((W,H,C)=2519\times 1679\times 3\) scene image selected from the BIG dataset (Cheng et al., 2020). As seen in Fig. 12a, this image contains rich texture information. The values of (n, d, r) for conducting the matrix completion task are (1679, 2519, 20) where we use a relatively large rank to allow more accurate recovery. The sampling ratio for observing the pixels is set as \({{\textrm{SR}}}=\frac{\left| \varOmega \right| }{W\times H\times C} =0.6\). Figure 11 compares the performance of different algorithms, where the Inexact Sub-RN-CR takes the shortest time to obtain a satisfactory solution. The subsampled gradient promotes the optimization speed of the Inexact Sub-RN-CR without sacrificing much the MSE error. Figure 12 illustrates the recovered image using three representative algorithms, providing similar visual results.
5.4 Results of conjugate gradient subproblem solver
We experiment with Algorithm 3 for solving the subproblem. In Step (3) of Algorithm 3, the eigen-decomposition method (Edelman & Murakami, 1995) used to solve the minimization problem has a complexity \({\mathcal {O}}(C^3)\) where \(C=4\) is the fixed degree of the polynomial. Figures 13, 14, 15 and 16 display the results for both the PCA and matrix completion tasks. Overall, Algorithm 3 can obtain the optimal results with the fastest convergence speed, as compared to the opponent approaches. We have observed that, in general, Algorithm 3 provides similar results to Algorithm 2, but they differ in run time. For instance, Algorithm 2 runs \(18\%\) faster for the PCA task with the MNIST dataset and \(20\%\) faster for the matrix completion task with the M1 dataset, as compared to Algorithm 3. But Algorithm 3 runs \(17\%\) faster than Algorithm 2 for the matrix completion task with the M2 dataset. A hypothesis could be that Algorithm 2 performs well on well-conditioned data (e.g. MNIST and M1) because of its strength of finding the global solution, while for ill-conditioned data (e.g. M2), it may not show significant advantages over Algorithm 3. Moreover, from the computational aspect, the Step (3) in Algorithm 3 is of \({\mathcal {O}}(C^3)\) complexity, which tends to be faster than solving Eq. (18) as required by Algorithm 2. Overall this makes Algorithm 3 probably a better choice than Algorithm 2 for processing ill-conditioned data.
5.5 Examination of convergence analysis assumptions
As explained in Sects. 3.3.3 and 3.4, the eigenstep condition in Assumptions 1, 2 and 3, although are required by convergence analysis, are not always satisfied by a subproblem solver in practice. In this experiment, we attempt to estimate the probability P that an assumption is satisfied in the process of optimization, by counting the number of outer iterations of Algorithm 1 where an assumption holds. We repeat this entire process five times (\(T=5\)) to attain a stable result. Let \(N_i\) be the number of outer iterations where the assumption is satisfied, and \(M_i\) the total number of outer iterations, in the i-th repetition (\(i=1,\;2,\;\ldots ,5\)). We compute the probability by \(P=\frac{\sum _{i\in [T]}N_i}{\sum _{i\in [T]}M_i}\). Experiments are conducted for the PCA task using the P1 dataset.
In order to examine Assumption 2, which is the stopping criterion in Eq. (47), we temporarily deactivate the other stopping criteria. We observe that Algorithm 2 can always produce a solution that satisfies Assumption 2. However, Algorithm 3 has only \(P\approx 50\%\) chance to produce a solution satisfying Assumption 2. The reason is probably that when computing \({\textbf{r}}_i\) in Step (11) of Algorithm 3, the first-order approximation of \(\nabla f(R_{{\textbf{x}}_k}({{\varvec{\eta }}}_k^*))\) is used rather than the exact \(\nabla f(R_{{\textbf{x}}_k}({{\varvec{\eta }}}_k^*))\) for the sake of computational efficiency. This can result in an approximation error.
Regarding the eigenstep condition in Assumption 1, it can always be met by Algorithm 2 with \(P\approx 100\%\). This indicates that even a few inner iterations are sufficient for it to find a solution pointing in the direction of negative curvature. However, Algorithm 3 has a \(P\approx 70\%\) chance to meet the eigenstep condition. This might be caused by insufficient inner iterations according to Theorem 1. Moreover, the solution obtained by Algorithm 3 is only guaranteed to be stationary according to Theorem 1, rather than pointing in the direction of the negative curvature. This could be a second cause for Algorithm 3 not to meet the eigenstep condition in Eq. (34).
While about Assumption 3, according to Lemma 2, Algorithm 2 always satisfies it. This is verified by our results with \(P=100\%\). Algorithm 3 has a \(P\approx 80\%\) chance to meet Assumption 3 empirically. This empirical result matches the theoretical result indicated by Lemma 3 where solutions from Algorithm 3 tend to approximately satisfy Assumption 3.
6 Conclusion
We have proposed the Inexact Sub-RN-CR algorithm to offer an effective and fast optimization for an important class of non-convex problems whose constraint sets possess manifold structures. The algorithm improves the current state of the art in second-order Riemannian optimization by using cubic regularization and subsampled Hessian and gradient approximations. We have also provided rigorous theoretical results on its convergence, and empirically evaluated and compared it with state-of-the-art Riemannian optimization techniques for two general machine learning tasks and multiple datasets. Both theoretical and experimental results demonstrate that the Inexact Sub-RN-CR offers improved convergence and computational costs. For instance, the achieved iteration number reduction is from \(\mathcal{O}\left(\max\left(\epsilon_g^{-2}\epsilon_H^{-1},\epsilon_H^{-3}\right)\right) \text {to} \:\mathcal{O}\left(\max\left(\epsilon_g^{-2},\epsilon_H^{-3}\right)\right)\) as compared to Kasai and Mishra (2018). When calculating the ratio of the computing time between our method (unit 1) and the best-performing state of the art, we have obtained 18 ratio values ranging from \(1{:}1.12 \:\text {to}\: 1 {:} 3.27\), corresponding to the 9 different datasets that we have used and the two versions of the proposed method (with Lanczos and CG subproblem solvers). Converting the time ratio \(1{:} t\) to a speed improvement by \(\frac{\left(1-1/t\right)}{1/t} = t-1\), the proposed method has resulted in a speed improvement between \(12\%\) and \(227\%\) with an average improvement of \(62\%\) and a median improvement of \(48\%\). Although the proposed method is promising in solving large-sample problems, there remains an open and interesting question of whether the proposed algorithm can be effective in training a constrained deep neural network. This is more demanding in its required computational complexity and convergence characteristics than many other machine learning problems, and it is more challenging to perform the Hessian approximation. Our future work will pursue this direction.
Data Availability
All the used data is publicly available benchmark data.
Notes
The abbreviation Sub-RN-CR comes from Sub-sampled Riemannian Newton-like Cubic Regularization. We follow the tradition of referring to a TR method enhanced by cubic regularization as a Newton-like method (Cartis et al., 2011) The implementation of the Inexact Sub-RN-CR is provided in https://github.com/xqdi/isrncr.
References
Abraham, A., Pedregosa, F., Eickenberg, M., Gervais, P., Mueller, A., Kossaifi, J., Gramfort, A., Thirion, B., & Varoquaux, G. (2014). Machine learning for neuroimaging with scikit-learn. Frontiers in Neuroinformatics, 8, 14.
Absil, P. A., Baker, C. G., & Gallivan, K. A. (2007). Trust-region methods on Riemannian manifolds. Foundations of Computational Mathematics, 7(3), 303–330.
Absil, P. A., Mahony, R., & Sepulchre, R. (2009). Optimization algorithms on matrix manifolds. Princeton University Press.
Agarwal, N., Boumal, N., Bullins, B., & Cartis, C. (2021). Adaptive regularization with cubics on manifolds. Mathematical Programming, 188(1), 85–134.
Alimisis, F., Orvieto, A., Bécigneul, G., & Lucchi, A. (2021). Momentum improves optimization on riemannian manifolds. In International conference on artificial intelligence and statistics (pp. 1351–1359). PMLR.
Anandkumar, A., & Ge, R. (2016). Efficient approaches for escaping higher order saddle points in non-convex optimization. In Conference on learning theory (pp. 81–102).
Becigneul, G., & Ganea, O. E. (2019). Riemannian adaptive optimization methods. In International conference on learning representations.
Blackard, J. A., & Dean, D. J. (1999). Comparative accuracies of artificial neural networks and discriminant analysis in predicting forest cover types from cartographic variables. Computers and Electronics in Agriculture, 24(3), 131–151.
Bonnabel, S. (2013). Stochastic gradient descent on Riemannian manifolds. IEEE Transactions on Automatic Control, 58(9), 2217–2229.
Boumal, N. (2020). An introduction to optimization on smooth manifolds.
Boumal, N., & Absil, P. A. (2011). Rtrmc: A Riemannian trust-region method for low-rank matrix completion. In Advances in neural information processing systems (pp. 406–414).
Boumal, N., Absil, P. A., & Cartis, C. (2019). Global rates of convergence for nonconvex optimization on manifolds. IMA Journal of Numerical Analysis, 39(1), 1–33.
Boumal, N., Mishra, B., Absil, P. A., & Sepulchre, R. (2014). Manopt, a matlab toolbox for optimization on manifolds. The Journal of Machine Learning Research, 15(1), 1455–1459.
Carmon, Y., & Duchi, J. C. (2018). Analysis of krylov subspace solutions of regularized non-convex quadratic problems. Advances in Neural Information Processing Systems, 31
Cartis, C., Gould, N. I., & Toint, P. L. (2011). Adaptive cubic regularisation methods for unconstrained optimization. Part i: Motivation, convergence and numerical results. Mathematical Programming, 127(2), 245–295.
Cheng, H. K., Chung, J., Tai, Y. W., Tang, C. K. (2020). Cascadepsp: Toward class-agnostic and very high-resolution segmentation via global and local refinement. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (pp. 8890–8899).
Cho, M. & Lee, J. (2017). Riemannian approach to batch normalization. In Advances in neural information processing systems (pp. 5225–5235).
Conn, A. R., Gould, N. I., & Toint, P. L. (2000). Trust region methods. SIAM.
Edelman, A., Arias, T. A., & Smith, S. T. (1998). The geometry of algorithms with orthogonality constraints. SIAM Journal on Matrix Analysis and Applications, 20(2), 303–353.
Edelman, A., & Murakami, H. (1995). Polynomial roots from companion matrix eigenvalues. Mathematics of Computation, 64(210), 763–776.
Ferreira, O. P., & Svaiter, B. F. (2002). Kantorovich’s theorem on newton’s method in Riemannian manifolds. Journal of Complexity, 18(1), 304–329.
Fletcher, R., & Reeves, C. M. (1964). Function minimization by conjugate gradients. The Computer Journal, 7(2), 149–154.
Goldberg, K., Roeder, T., Gupta, D., & Perkins, C. (2001). Eigentaste: A constant time collaborative filtering algorithm. Information Retrieval, 4(2), 133–151.
Gould, N., Lucidi, S., Roma, M., & Toint, P. L. (1999). Solving the trust-region subproblem using the Lanczos method. Siam Journal on Optimization, 9(2), 504–525.
Griewank, A. (1981). The modification of Newton’s method for unconstrained optimization by bounding cubic terms. Tech. rep., Technical report NA/12.
Gross, D. (2011). Recovering low-rank matrices from few coefficients in any basis. IEEE Transactions on Information Theory, 57(3), 1548–1566.
Han, A., Mishra, B., Jawanpuria, P. K., & Gao, J. (2021). On Riemannian optimization over positive definite matrices with the bures-wasserstein geometry. Advances in Neural Information Processing Systems, 34.
Horev, I., Yger, F., & Sugiyama, M. (2017). Geometry-aware principal component analysis for symmetric positive definite matrices (pp. 493–522). Springer.
Hosseini, S., Huang, W., & Yousefpour, R. (2018). Line search algorithms for locally lipschitz functions on Riemannian manifolds. SIAM Journal on Optimization, 28(1), 596–619.
Huang, W., & Wei, K. (2021). Riemannian proximal gradient methods. Mathematical Programming, 1–43.
Jia, X., Liang, X., Shen, C. & Zhang, L. H. (2021). Solving the cubic regularization model by a nested restarting Lanczos method.
Kasai, H. & Mishra, B. (2018). Inexact trust-region algorithms on Riemannian manifolds. In Advances in neural information processing systems (pp. 4249–4260).
Kasai, H., Sato, H. & Mishra, B. (2018). Riemannian stochastic recursive gradient algorithm. In International conference on machine learning (pp. 2516–2524).
Kohler, J. M. & Lucchi, A. (2017) Sub-sampled cubic regularization for non-convex optimization. In Proceedings of the 34th international conference on machine learning (Vol. 70, pp. 1895–1904). JMLR. org
Kohoutová, L., Heo, J., Cha, S., Lee, S., Moon, T., Wager, T. D., & Woo, C. W. (2020). Toward a unified framework for interpreting machine-learning models in neuroimaging. Nature Protocols, 15(4), 1399–1435.
Kumar Roy, S., Mhammedi, Z. & Harandi, M. (2018). Geometry aware constrained optimization techniques for deep learning. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 4460–4469).
LeCun, Y., Bottou, L., Bengio, Y., & Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278–2324.
Liu, X., He, J., Duddy, S. & O’Sullivan, L. (2019). Convolution-consistent collective matrix completion. In International conference on information and knowledge management (pp. 2209–2212).
Mishra, B., Kasai, H., Jawanpuria, P., & Saroop, A. (2019). A Riemannian gossip approach to subspace learning on Grassmann manifold. Machine Learning, 108(10), 1783–1803.
Mokhtari, A., Ozdaglar, A. & Jadbabaie, A. (2018). Escaping saddle points in constrained optimization. In Advances in neural information processing systems (pp. 3629–3639).
Ngo, T., & Saad, Y. (2012). Scaled gradients on grassmann manifolds for matrix completion. Advances in Neural Information Processing Systems, 25.
Nguyen, X. S., Brun, L., Lézoray, O. & Bougleux, S. (2019). A neural network based on spd manifold learning for skeleton-based hand gesture recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 12036–12045).
Nocedal, J., & Wright, S. (2006). Numerical optimization. Springer.
Poldrack, R. A., & Gorgolewski, K. J. (2017). Openfmri: Open sharing of task fmri data. Neuroimage, 144, 259–261.
Pölitz, C., Duivesteijn, W., & Morik, K. (2016). Interpretable domain adaptation via optimization over the stiefel manifold. Machine Learning, 104(2), 315–336.
Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. (2007). Chapter 9: Root finding and nonlinear sets of equations. Book: Numerical Recipes: the art of scientific computing (Vol. 10). Cambridge University Press.
Qi, C. (2011). Numerical optimization methods on Riemannian manifolds.
Roosta-Khorasani, F., & Mahoney, M. W. (2019). Sub-sampled newton methods. Mathematical Programming, 174(1), 293–326.
Sakai, H., & Iiduka, H. (2021). Sufficient descent Riemannian conjugate gradient methods. Journal of Optimization Theory and Applications, 190(1), 130–150.
Sato, H., & Iwai, T. (2015). A new, globally convergent Riemannian conjugate gradient method. Optimization, 64(4), 1011–1031.
Shahid, N., Kalofolias, V., Bresson, X., Bronstein, M. & Vandergheynst, P. (2015). Robust principal component analysis on graphs. In Proceedings of the IEEE international conference on computer vision (pp. 2812–2820).
Shen, Z., Zhou, P., Fang, C. & Ribeiro, A. (2019). A stochastic trust region method for non-convex minimization. arXiv:1903.01540
Sidhu, G. S., Asgarian, N., Greiner, R., & Brown, M. R. (2012). Kernel principal component analysis for dimensionality reduction in fmri-based diagnosis of adhd. Frontiers in Systems Neuroscience, 6, 74.
Sun, Y., Flammarion, N. & Fazel, M. (2019). Escaping from saddle points on Riemannian manifolds. arXiv:1906.07355
Townsend, J., Koep, N., & Weichwald, S. (2016). Pymanopt: A python toolbox for optimization on manifolds using automatic differentiation. The Journal of Machine Learning Research, 17(1), 4755–4759.
Trefethen, L. N., & Bau, D., III. (1997). Numerical linear algebra (Vol. 50). Siam.
Tripuraneni, N., Stern, M., Jin, C., Regier, J., & Jordan, M. I. (2018). Stochastic cubic regularization for fast nonconvex optimization. Advances in Neural Information Processing Systems, 31.
Tropp, J. A. (2015). An introduction to matrix concentration inequalities. arXiv:1501.01571
Wei, Z., Yao, S., & Liu, L. (2006). The convergence properties of some new conjugate gradient methods. Applied Mathematics and computation, 183(2), 1341–1350.
Weiwei, Y., Yueting, Y., Chenhui, Z., & Mingyuan, C. (2013). A newton-like trust region method for large-scale unconstrained nonconvex minimization. In Abstract and applied analysis (Vol. 2013). Hindawi.
Xu, P., Roosta, F., & Mahoney, M. W. (2020). Newton-type methods for non-convex optimization under inexact hessian information. Mathematical Programming, 184(1), 35–70.
Xu, Z., Zhao, P., Cao, J. & Li, X. (2016). Matrix eigen-decomposition via doubly stochastic Riemannian optimization. In International conference on machine learning (pp. 1660–1669).
Yao, Z., Xu, P., Roosta, F., & Mahoney, M. W. (2021). Inexact nonconvex newton-type methods. Informs Journal on Optimization, 3(2), 154–182.
Yuan, X., Huang, W., Absil, P. A., & Gallivan, K. A. (2016). A Riemannian limited-memory bfgs algorithm for computing the matrix geometric mean. Procedia Computer Science, 80, 2147–2157.
Zhang, H. & Sra, S. (2016). First-order methods for geodesically convex optimization. In Conference on learning theory (pp. 1617–1638).
Zhang, H., Reddi, S. J. & Sra, S. (2016). Riemannian svrg: Fast stochastic optimization on riemannian manifolds. In Advances in neural information processing systems (pp. 4592–4600).
Zhang, J. & Zhang, S. (2018). A cubic regularized newton’s method over Riemannian manifolds. arXiv:1805.05565
Zhong, Y., Wang, H., Lu, G., Zhang, Z., Jiao, Q., & Liu, Y. (2009). Detecting functional connectivity in fmri using pca and regression analysis. Brain Topography, 22(2), 134–144.
Zhou, D. & Gu, Q. (2020). Stochastic recursive variance-reduced cubic regularization methods. In International conference on artificial intelligence and statistics (pp. 3980–3990). PMLR.
Zhou, D., Xu, P., & Gu, Q. (2019). Stochastic variance-reduced cubic regularization methods. Journal of Machine Learning Research, 20(134), 1–47.
Zhu, X. (2017). A Riemannian conjugate gradient method for optimization on the stiefel manifold. Computational Optimization and Applications, 67(1), 73–110.
Funding
The work is funded by The University of Manchester - China Scholarship Council joint scholarship.
Author information
Authors and Affiliations
Contributions
Both authors contributed equally to the work.
Corresponding author
Ethics declarations
Conflict of interest
None.
Ethics approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Both authors consent.
Code availability
The code will be made publicly available after the work is accepted, and will be sent to reviewers upon request (see footnote 1).
Additional information
Editor: Lam M. Nguyen.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Derivation of Lanczos method
Instead of solving the subproblem in the tangent space \({{\varvec{\eta }}}\in T_{{\textbf{x}}_k}{\mathcal {M}}\) of the manifold dimension D, the Lanczos method solves it within a Krylov subspace \({\mathcal {K}}_l\), where l can range from 1 to D. This subspace is defined by the span of the following elements:
where, for \(l \ge 2\), \({\textbf{H}}_k^l[{\textbf{G}}_k]\) is recursively defined by \({\textbf{H}}_k\left[ {\textbf{H}}^{l-1}_k\left[ {\textbf{G}}_k\right] \right]\). Its orthonormal basis \({\textbf{Q}}_l=\{{\textbf{q}}_1,\ldots ,{\textbf{q}}_l\}\), where \({\textbf{Q}}_l^T{\textbf{Q}}_l={\textbf{I}}\), is successively constructed to satisfy
for \(i,j\in [n]\), where \(\left( {\textbf{T}}_l\right) _{i,j}\) denotes the ij-th element of the matrix \({\textbf{T}}_l\). Each element \({{\varvec{\eta }}}\in {\mathcal {K}}_l\) in the Krylov subspace can be expressed as \({{\varvec{\eta }}} =\sum _{i=1}^l y_i {\textbf{q}}_i\). Store these \(\{y_i\}_{i=1}^l\) in the vector \({\textbf{y}}\in {\mathbb {R}}^l\), the subproblem objective function \(\mathop {\min }_{{{\varvec{\eta }}}\in {\mathcal {K}}_l} {\hat{m}}({{\varvec{\eta }}})\) is minimized in the Krylov subspace instead. By substituting \({{\varvec{\eta }}}:=\sum _{i=1}^l y_i {\textbf{q}}_i\) into \({\hat{m}}({{\varvec{\eta }}})\), the objective function becomes
The properties \({\textbf{q}}_i\perp {\textbf{q}}_j\) for \(i\ne j\) and \({\textbf{G}}_k\perp {\textbf{q}}_i\) for \(i\ne 1\) are used in the derivation. Therefore, to solve \(\min _{{{\varvec{\eta }}}\in T_{{\textbf{x}}_k} {\mathcal {M}}}\ {\hat{m}}({{\varvec{\eta }}})\) is equivalent to
Appendix B: Proof of Lemma 1
Proof
Let \(\lambda _* = \sigma _k\left\| {{\varvec{\eta }}}_{k}^*\right\|\). The Krylov subspaces are invariant to shifts by scalar matrices, therefore \({\mathcal {K}}_l({\textbf{H}}_k, {\textbf{G}}_k)= {\mathcal {K}}_l({\textbf{H}}_k + \lambda _*{{\textrm{Id}}}, {\textbf{G}}_k) = {\mathcal {K}}_l(\tilde{{\textbf{H}}}_k, {\textbf{G}}_k)\) (Carmon & Duchi, 2018), where the definition of \({\mathcal {K}}_l({\textbf{H}}_k, {\textbf{G}}_k)\) follows Eq. (64). Let \({{\varvec{\xi }}}_l\in {\mathcal {K}}_l\) be the solution found in the Krylov subspace \({\mathcal {K}}_l({\textbf{H}}_k, {\textbf{G}}_k)\), which is thus an element of \({\mathcal {K}}_l(\tilde{{\textbf{H}}}_k, {\textbf{G}}_k)\) expressed by
for some values of \(c_0,\;c_1, \;\ldots ,\; c_l \in {\mathbb {R}}\). According to Section 6.2 of Absil et al. (2009), a global minimizer \(\bar{{{\varvec{\eta }}}}_k^*\) of the RTR subproblem without cubic regularization in Eq. (7) is expected to satisfy the Riemannian quasi-Newton equation:
where \(\lambda _*\ge \max (-\lambda _{min}({\textbf{H}}_k), 0)\) and \(\lambda _*\left( \varDelta _k-\left\| \bar{{{\varvec{\eta }}}}_k^*\right\| _{{\textbf{x}}_k}\right) =0\) according to Corollary 7.2.2 of Conn et al. (2000). Using the approximate gradient and Hessian, the inexact minimizer is expected to satisfy
Introduce \({{\varvec{\zeta }}}_l=(1-\alpha ){{\varvec{\xi }}}_l\) where \(\alpha =\frac{\left\| {{\varvec{\xi }}}_l\right\| _{{\textbf{x}}_k}-\left\| \bar{{{\varvec{\eta }}}}_k^*\right\| _{{\textbf{x}}_k}}{\max \left( \left\| {{\varvec{\xi }}}_l\right\| _{{\textbf{x}}_k},\left\| \bar{{{\varvec{\eta }}}}_k^*\right\| _{{\textbf{x}}_k}\right) }\). When \(\left\| {{\varvec{\xi }}}_l\right\| _{{\textbf{x}}_k}<\left\| \bar{{{\varvec{\eta }}}}_k^*\right\| _{{\textbf{x}}_k}\), we start from the fact that \(\left( \left\| \bar{{{\varvec{\eta }}}}_k^*\right\| _{{\textbf{x}}_k}-\left\| {{\varvec{\xi }}}_l\right\| _{{\textbf{x}}_k}\right) ^2\ge 0\), which results in the following:
When \(\left\| {{\varvec{\xi }}}_l\right\| _{{\textbf{x}}_k}\ge \left\| \bar{{{\varvec{\eta }}}}_k^*\right\| _{{\textbf{x}}_k}\), it has
This concludes that for any \({{\varvec{\xi }}}_l\), it has \(\left\| {{\varvec{\zeta }}}_l\right\| _{{\textbf{x}}_k}\le \left\| \bar{{{\varvec{\eta }}}}_k^*\right\| _{{\textbf{x}}_k}\).
We introduce the notation \({\tilde{m}}_k\) to denote the subproblem in Eq. (7) using the inexact Hessian \(\tilde{{\textbf{H}}}_k\). Let \(\psi _{k}^*= \left( p_{l+1}\left( \tilde{{\textbf{H}}}_k\right) -{{\textrm{Id}}}\right) [\bar{{{\varvec{\eta }}}}_k^*]\) and \(\iota \left( \tilde{{\textbf{H}}}_k\right) =\frac{\lambda _{max}(\tilde{{\textbf{H}}}_k)}{\lambda _{min}(\tilde{{\textbf{H}}}_k)}\). Since \(\phi _l\left( \tilde{{\textbf{H}}}_k\right)\) is the upper bound of \(\left\| p_{l+1}\left( \tilde{{\textbf{H}}}_k\right) -{{\textrm{Id}}}\right\| _{{\textbf{x}}_k}\), it has \(\left\| \psi _{k}^*\right\| _{{\textbf{x}}_k} \le \phi _l\left( \tilde{{\textbf{H}}}_k\right) \left\| \bar{{{\varvec{\eta }}}}_k^*\right\| _{{\textbf{x}}_k}\). Then, we have
To derive Eq. (74), \({\textbf{G}}_k=-\tilde{{\textbf{H}}}_k[\bar{{{\varvec{\eta }}}}_k^*]\) from Eq. (71) is used. To derive Eq. (75), we use the definition in Eq. (35), where for a non-zero \({{\varvec{\xi }}}\in T_{{\textbf{x}}_k}{\mathcal {M}}\), it has
Equation (75) also uses (1) the fact of \(\alpha \ge -1\) which comes from the fact of \(\alpha\) being in the form of \(\frac{a-b}{\max (a,b)}\), and thus \(1-\alpha \le 2\), (2) the definition of the smallest and largest eigenvalues in Eqs. (16) and (20), which gives \(\frac{\langle {{\varvec{\eta }}},\tilde{{\textbf{H}}[{{\varvec{\eta }}}]}\rangle _{{\textbf{x}}_k}}{\langle {{\varvec{\xi }}},\tilde{{\textbf{H}}[{{\varvec{\xi }}}]}\rangle _{{\textbf{x}}_k}}\le \frac{\lambda _{max}(\tilde{{\textbf{H}}}_k)}{\lambda _{min}(\tilde{{\textbf{H}}}_k)}\) for and any unit tangent vectors \({{\varvec{\eta }}}\) and \({{\varvec{\xi }}}\), and (3) the fact that
To derive Eq. (77), we use
Next, as \({{\varvec{\eta }}}_k^{*l}\) is the optimal solution in the subspace \({\mathcal {K}}_l({\textbf{H}}_k, {\textbf{G}}_k)\), we have \({\bar{m}}_k\left( {{\varvec{\eta }}}_k^{*l}\right) \le {\bar{m}}_k\left( {{\varvec{\zeta }}}^l\right)\), and hence
We then show that the Lanczos method exhibits at least the same convergence property as above for the subsampled Riemannian cubic-regularization subproblem. Let \({{{\varvec{\eta }}}}_k^*\) be the global minimizer for the subproblem \({\hat{m}}_k\) in Eq. (10). \({{{\varvec{\eta }}}}_k^*\) is equivalent to \(\bar{{{\varvec{\eta }}}}_k^*\) in the RTR subproblem with \(\varDelta _k=\left\| {{{\varvec{\eta }}}}_k^*\right\| _{{\textbf{x}}_k}\) and \(\lambda _*=\sigma _k\left\| {{{\varvec{\eta }}}}_k^*\right\| _{{\textbf{x}}_k}\) (Carmon & Duchi, 2018). Then, letting \({{\varvec{\eta }}}_k^{*l}\) be the minimizer of \({\hat{m}}_k\) over \({\mathcal {K}}_l({\textbf{H}}_k, {\textbf{G}}_k)\) satisfying \(\left\| {{{\varvec{\eta }}}}_k^{*l}\right\| _{{\textbf{x}}_k}\le \left\| {{{\varvec{\eta }}}}_k^*\right\| _{{\textbf{x}}_k}=\varDelta _k\), we have
Combining this with Eq. (81), it has
This completes the proof. \(\square\)
Appendix C: Proof of Theorem 1
Proof
We first prove the relationship between \({\textbf{G}}_k^i\) and \({\textbf{r}}_i\). According to Algorithm 3, \({\textbf{r}}_0={\textbf{G}}_k^0={\textbf{G}}_k\). Then for \(i>0\), we have
where \(\approx\) comes from the first-order Taylor extension and Eq. (85) follows the Step (11) in Algorithm 3.
The exact line search in the Step. (3) of Algorithm 3 approximates
Zeroing the derivative of Eq. (86) with respect to \(\alpha\) gives
where \(\approx\) results from the use of subsampled gradient \({\textbf{G}}_k^i\) to approximate the full gradient \(\nabla f({\textbf{x}}_k^i)\). We then show that each \({\textbf{p}}_i\) is a sufficient descent direction, i.e., \(\left\langle {\textbf{G}}_k^{i},{\textbf{p}}_{i+1}\right\rangle _{{\textbf{x}}_k^{i}}\le -C\left\| {\textbf{G}}_k^i\right\| _{{\textbf{x}}_k^i}^2\) for some constant \(C>0\) (Sakai & Iiduka, 2021). When \(i=0\), \({\textbf{p}}_1 = {\textbf{G}}_k^0\), and thus \(\left\langle {\textbf{G}}_k^{0},{\textbf{p}}_{1}\right\rangle _{{\textbf{x}}_k^{0}}=-\left\| {\textbf{G}}_k^0\right\| _{{\textbf{x}}_k^0}^2\). When \(i>0\), from Step (17) in Algorithm 3 and Eq. (85), we have \({\textbf{p}}_{i+1} \approx -{\textbf{G}}_k^i + \beta _i{\textbf{p}}_i\). Applying the inner product to both sides by \({\textbf{G}}_k^{i}\), we have
with a selected \(C>0\). Here, Eq. (89) builds on Eq. (87). Given the sufficient descent direction \({\textbf{p}}_i\) and the strong Wolfe conditions satisfied by \(\alpha _i^*\), Theorem 2.4.1 in Qi (2011) shows that the Zoutendijk Condition holds (Sato & Iwai, 2015), i.e.,
Next, we show that \(\beta _i\) is upper bounded. Using Eq. (85), we have
where \(c_3>1\) is some constant.
Now, we prove \(\lim _{i\rightarrow \infty } \left\| {\textbf{G}}_k^i\right\| _{{\textbf{x}}_k^i}=0\) by contradiction. Assume that \(\lim _{i\rightarrow \infty } \left\| {\textbf{G}}_k^i\right\| _{{\textbf{x}}_k^i}>0\), that is, for all i, there exists \(\gamma >0\) such that \(\left\| {\textbf{G}}_k^i\right\| _{{\textbf{x}}_k^i}>\gamma >0\). Squaring Step (17) of Algorithm 3 and applying Eqs. (30), (85), (89) and (91), we have
where \({\hat{C}}=1+2c_2C>1\). Applying this repetitively, we have
where Eqs. (93) uses (91) and \({\textbf{p}}_1={\textbf{G}}_k^0\), and the last inequality uses \(\left\| {\textbf{G}}_k^i\right\| _{{\textbf{x}}_k^i}>\gamma\). Subsequently, this gives
Combing Eqs. (89) and (94), we have
This contradicts Eq. (90) and completes the proof. \(\square\)
Appendix D: Subproblem solvers
1.1 D.1 Proof of Lemma 2
1.1.1 D.1.1 The case of \(l=D\)
Proof
Assumption 1: Regarding the Cauchy condition in Eq. (36), it is satisfied simply because of Eqs. (19) and (33). Regarding the eigenstep condition, the proof is also fairly simple. The solution \({{\varvec{\eta }}}_k^*\) from Algorithm 2 with \(l=D\) is the global minimizer over \({\mathbb {R}}^{D}\). As the subspace spanned by Cauchy steps and eigensteps belongs to \({\mathbb {R}}^D\), i.e., \({{\textrm{Span}}}\left\{ {{\varvec{\eta }}}_k^C, {{\varvec{\eta }}}_k^E\right\} \in {\mathbb {R}}^D\), we have
Hence, the solution from Algorithm 2 satisfies the eigenstep condition in Eq. (37) from Assumption 1.
Assumption 2: As stated in Section 3.3 of Cartis et al. (2011), any minimizer, including the global minimizer \({{\varvec{\eta }}}_{k}^{*}\) from Algorithm 2, is a stationary point of \({\hat{m}}_k\), and naturally has the property \(\nabla _{{{\varvec{\eta }}}}{\hat{m}}_k( {{\varvec{\eta }}}_{k}^{*})={\textbf{0}}_{{\textbf{x}}_k}\). Hence, it has \(\left\| \nabla _{{{\varvec{\eta }}}}{\hat{m}}_k( {{\varvec{\eta }}}_{k}^{*})\right\| _{{\textbf{x}}_k}=0\le \kappa _\theta \min \left( 1, \left\| {{\varvec{\eta }}}_k^* \right\| _{{\textbf{x}}_k} \right) \Vert {\textbf{G}}_k\Vert _{{\textbf{x}}_k}\). Assumption 2 is then satisfied.
Assumption 3: Given the above-mentioned property of the global minimizer \({{\varvec{\eta }}}_k^*\) of \({\hat{m}}_k\) from Algorithm 2, i.e., \(\nabla _{{{\varvec{\eta }}}}{\hat{m}}_k( {{\varvec{\eta }}}_{k}^{*})={\textbf{0}}_{{\textbf{x}}_k}\), and using the definition of \(\nabla _{{{\varvec{\eta }}}}{\hat{m}}_k( {{\varvec{\eta }}}_{k}^{*})\), it has
Applying the inner product operation with \({{\varvec{\eta }}}_k^*\) to both sides of Eq. (97), it has
and this corresponds to Eq. (42). As \({{\varvec{\eta }}}_k^*\) is a descent direction, we have \(\langle {\textbf{G}}_k, {{\varvec{\eta }}}_k^*\rangle _{{\textbf{x}}_k}\le 0\). Combining this with Eq. (98), it has
and this is Eq. (43). This completes the proof. \(\square\)
1.1.2 D.1.2 The case of \(l<D\)
Proof
Cauchy condition in Assumption 1: Implied by Eq. (19), any intermediate solution \({{\varvec{\eta }}}_k^{*l}\) satisfies the Cauchy condition.
Assumption 2: As stated in Section 3.3 of Cartis et al. (2011), any minimizer \({{\varvec{\eta }}}^*\) of \({\hat{m}}_k\) admits the property \(\nabla _{{{\varvec{\eta }}}}{\hat{m}}_k( {{\varvec{\eta }}}^{*})={\textbf{0}}_{{\textbf{x}}_k}\). Since each \({{\varvec{\eta }}}_k^{*l}\) is the minimizer of \({\hat{m}}_k\) over \({\mathcal {K}}_l\), it has \(\nabla _{{{\varvec{\eta }}}}{\hat{m}}_k( {{\varvec{\eta }}}_k^{*l})={\textbf{0}}_{{\textbf{x}}_k}\). Then, it has \(\left\| \nabla _{{{\varvec{\eta }}}}{\hat{m}}_k( {{\varvec{\eta }}}_{k}^{*l})\right\| _{{\textbf{x}}_k}=0\le \kappa _\theta \min \left( 1, \left\| {{\varvec{\eta }}}_k^{*l} \right\| _{{\textbf{x}}_k} \right) \Vert {\textbf{G}}_k\Vert _{{\textbf{x}}_k}\). Assumption 2 is then satisfied.
Assumption 3: According to Lemma 3.2 of Cartis et al. (2011), a global minimizer of \({\hat{m}}_k\) over a subspace of \({\mathbb {R}}^D\) satisfies Assumption 3. As the solution \({{\varvec{\eta }}}_k^{*l}\) in each iteration of Algorithm 2 is a global solution over the subspace \({\mathcal {K}}_l\), each \({{\varvec{\eta }}}_k^{*l}\) satisfies Assumption 3. \(\square\)
1.2 D.2 Proof of Lemma 3
Proof
For Cauchy Condition of Assumption 1: In the first iteration of Algorithm 3, the step size is optimized along the steepest gradient direction, as in the classical steepest-descent method of Cauchy, i.e.,
At each iteration i of Algorithm 3, the line search process in Eq. (24) aims at finding a step size that can achieve a cost decrease, otherwise the step size will be zero, meaning that no strict decrease can be achieved and the algorithm will stop at Step (4). Because of this, we have
Given \({{\varvec{\eta }}}_{k}^{i}={{\varvec{\eta }}}_{k}^{i-1}+\alpha _i^*{\textbf{p}}_i\) in Algorithm 3, we have
Then, considering all \(i=1,2,...\), we have
This shows Algorithm 3 always returns a solution better than or equal to the Cauchy step.
For \(\left\| \nabla _{{{\varvec{\eta }}}} {\hat{m}}_k({{\varvec{\eta }}})\right\| _{{\textbf{x}}_k}\approx 0\): The approximation concept (\(\approx\)) of interest here builds on the fact that \({\hat{m}}_k({{\varvec{\eta }}})\) is used as the approximation of the real objective function \(f(R_{{\textbf{x}}_k}({{\varvec{\eta }}}))\). By assuming \({\hat{m}}_k({{\varvec{\eta }}})\approx f(R_{{\textbf{x}}_k}({{\varvec{\eta }}}))\), it leads to
Let \({\textbf{G}}_{k+1}\) be the subsampled gradient evaluated at \(R_{{\textbf{x}}_k}({{\varvec{\eta }}}_k^*)\). Based on Theorem 1, it has \({\textbf{G}}_{k+1}= \lim _{i\rightarrow \infty }{\textbf{G}}_k^i\) where \({\textbf{G}}_k^i\) is the resulting subsampled gradient after i inner iterations. Since \({\textbf{G}}_{k+1}\) is the approximate gradient of the full gradient \(\nabla f(R_{{\textbf{x}}_k}({{\varvec{\eta }}}_k^*))\), it has \(\nabla f(R_{{\textbf{x}}_k}({{\varvec{\eta }}}_k^*))={\mathbb {E}}[{\textbf{G}}_{k+1}]={\mathbb {E}}[\lim _{i\rightarrow \infty }{\textbf{G}}_k^i]\). Hence, it has
which indicates the equality holds as \(\left\| \nabla _{{{\varvec{\eta }}}} f\left( R_{{\textbf{x}}_k}({{\varvec{\eta }}}_k^*)\right) \right\| _{{\textbf{x}}_k} = 0\). Combining this with Eq. (104), it completes the proof.
For Condition 1of Assumption 3: Using the definition of \(\nabla _{{{\varvec{\eta }}}}{\hat{m}}_k( {{\varvec{\eta }}}_{k}^{*})\) as in Eq. (97), it has
Also, since \(\left\| \nabla _{{{\varvec{\eta }}}}{\hat{m}}_k( {{\varvec{\eta }}}_{k}^{*})\right\| _{{\textbf{x}}_k}\approx 0\), we have
Combining Eqs. (106) and (107), this results in Eq. (45), which completes the proof. \(\square\)
Appendix E: Proof of theorem 2
1.1 E.1 Matrix Bernstein inequality
We build the proof on the matrix Bernstein inequality. We restate this inequality in the following lemma.
Lemma 4
(Matrix Bernstein Inequality (Gross, 2011; Tropp, 2015)) Let \({\textbf{A}}_1,\ldots ,{\textbf{A}}_n\) be independent, centered random matrices with the common dimension \(d_1\times d_2\). Assume that each one is uniformly bounded:
Given the matrix sum \({\textbf{Z}}=\sum _{i=1}^n{\textbf{A}}_i\) , we define its variance \(\nu ({\textbf{Z}})\) by
Then
This lemma supports us to prove Theorem 2 as below.
1.2 E.2 Main Proof
Proof
Following the subsampling process, a total of \(|{\mathcal {S}}_g|\) matrices are uniformly sampled from the set of n Riemannan gradients \(\left\{ {{\textrm{grad}}}f_i({\textbf{x}}) \subseteq {\mathbb {R}}^{d\times r}\right\} _{i=1}^n\). We denote each sampled element as \({\textbf{G}}^{(i)}_{{\textbf{x}}}\), and it has
Define the random matrix
Our focus is the type of problem as in Eq. (1), therefore it has
Define a random variable
Its variance satisfies
Take \({\textbf{G}}^{(i)}_{{\textbf{x}}}={{\textrm{grad}}}f_1({\textbf{x}})\) as an example and applying the definition of \(K_{g_{max}}\) in Eq. (53), we have
where the first inequality uses \((a+b)^2\le 2a^2+2b^2\). Combining Eqs. (115) and (116), it has
Now we are ready to apply Lemma 4. Given \({\mathbb {E}}\left[ \frac{1}{|{\mathcal {S}}_g|}{\textbf{X}}_i\right] =\frac{1}{|{\mathcal {S}}_g|}{\mathbb {E}}[{\textbf{X}}_i]={\textbf{0}}\) and according to the superma definition \(\left\| \frac{1}{|{\mathcal {S}}_g|}{\textbf{X}}_i\right\| _{\textbf{x}}=\frac{1}{|{\mathcal {S}}_g|}\Vert {\textbf{X}}_i\Vert _{\textbf{x}}\le \frac{K_{g_{max}}}{|{\mathcal {S}}_g|}\), the following is obtained from the matrix Bernstein inequality:
of which the last equality implies
In simple words, with a probability at least \(1-\delta\), we have \(\Vert {\textbf{X}}\Vert _{\textbf{x}} < \epsilon\).
Letting
this results in the sample size bound as in Eq. (55)
Therefore, we have \(\Vert {\textbf{X}}\Vert _{\textbf{x}} \le \delta _g\). Expanding \({\textbf{X}}\), we have the following satisfied with a probability at least \(1-\delta\):
which is Eq. (51) of Condition 1.
The proof of the other sample size bound follows the same strategy. A total of \(|{\mathcal {S}}_H|\) matrices are uniformly sampled from the set of n Riemannan Hessians \(\left\{ \nabla ^2{\hat{f}}_i({\textbf{0}}_x)[{{\varvec{\eta }}}] \subseteq {\mathbb {R}}^{d\times r} \right\} _{i=1}^n\). We denote each sampled element as \({\textbf{H}}^{(i)}_{{\textbf{x}}}[{{\varvec{\eta }}}]\), and it has
Define the random matrix
For the problem defined in Eq. (1) with a second-order retraction, it has
Define a random variable
Its variance satisfies
Take \({\textbf{H}}^{(i)}_{\textbf{x}}[{{\varvec{\eta }}}]=\nabla ^2{\hat{f}}_1 ({\textbf{0}}_x)[{{\varvec{\eta }}}]\) as an example and applying the definition of \(K_{H_{max}}\) in Eq. (54), we have
where the first inequality uses \((a+b)^2\le 2a^2+2b^2\), and \({{\varvec{\eta }}}\) is the current moving direction being optimized in Eq. (10). Combining Eq. (130) and Eq. ((131), we have
We then apply Lemma 4. Given \({\mathbb {E}}\left[ \frac{1}{|{\mathcal {S}}_H|}{\textbf{Y}}_i\right] =\frac{1}{|{\mathcal {S}}_H|}{\mathbb {E}}[{\textbf{Y}}_i]={\textbf{0}}\) and according to the superma definition \(\left\| \frac{1}{|{\mathcal {S}}_H|}{\textbf{Y}}_i\right\| _{\textbf{x}}=\frac{1}{|{\mathcal {S}}_H|}\Vert {\textbf{Y}}_i\Vert _{\textbf{x}}\le \frac{K_{H_{max}}\left\| {{\varvec{\eta }}}\right\| _{{\textbf{x}}}}{|{\mathcal {S}}_H|}\), the following is obtained from the matrix Bernstein inequality:
of which the last equality indicates
In simple words, with probability at least \(1-\delta\), we have \(\Vert {\textbf{Y}}\Vert _{\textbf{x}} < \epsilon\). By letting
which results in the sample size bound in Eq. (56)
And we have \(\Vert {\textbf{Y}}\Vert _{\textbf{x}} \le \delta _H\left\| {{\varvec{\eta }}}\right\| _{{\textbf{x}}}\). Expanding \({\textbf{Y}}\), we have the following satisfied with a probability at least \(1-\delta\):
which is Eq. (52) of Condition 1. \(\square\)
Appendix F: Theorem 3 and Corollary 1
1.1 F.1 Supporting Lemmas for Theorem 3
Lemma 5
Suppose Condition 1and Assumptions 1, 2hold, then for the case of \(\Vert {\textbf{G}}_k\Vert \ge \epsilon _g\) , we have
Proof
We start from the left-hand side of Eq. (141), and this leads to
where the first inequality uses the Cauchy–Schwarz inequality and the second one uses Eqs. (48), (51) and (52). It can be seen that the term \(\left\langle {\textbf{G}}_k,{\varvec{\eta }}_k\right\rangle _{{\varvec{x}}_k}\) can not be neglected because of the condition \(\Vert {\textbf{G}}_k\Vert \ge \epsilon _g\) based on Eq. (11). This then results in the term \(\delta _g\Vert {\varvec{\eta }}_k\Vert _{{\varvec{x}}_k}\) in Eq. (142). \(\square\)
Lemma 6
Suppose Condition 1and Assumptions 1, 2hold, then for the case of \(\Vert {\textbf{G}}_k\Vert <\epsilon _g\) and \(\lambda _{min}({\textbf{H}}_k)<-\epsilon _H\) , we have
Proof
For each \({\varvec{\eta }}_k\), at least one of the two inequalities is true:
Without loss of the generality, we assume \(\langle {\varvec{\eta }}_k,\text {grad}f({\varvec{x}}_k)\rangle _{{\varvec{x}}_k}\le 0\) which is also an assumption adopted by Yao et al. (2021), and it has
The condition \(\Vert {\textbf{G}}_k\Vert <\epsilon _g\) and \(\lambda _{min}({\textbf{H}}_k)<-\epsilon _H\) in this case means that the term \(\left\langle {\textbf{G}}_k,{\varvec{\eta }}_k\right\rangle _{{\varvec{x}}_k}\) can be neglected based on Eq. (11) but the optimization process is not yet finished. The effect is that \(\delta _g\Vert {\varvec{\eta }}_k\Vert _{{\varvec{x}}_k}\) no more exists in Eq. (146) unlike Eq. (142). \(\square\)
Lemma 7
Suppose Condition 1and Assumptions 1, 2, 3, 4, 5hold, then when \(\Vert {\textbf{G}}_k\Vert \ge \epsilon _g\) and \(\sigma _k\ge L_H\) , we have
Proof
According to Lemma 6 of Xu et al. (2020), it has
Then we consider two cases for \(\left\| {\varvec{\eta }}_k^C\right\| _{{\varvec{x}}_k}\).
(i) If \(\Vert {\varvec{\eta }}_k\Vert _{{\varvec{x}}_k}\le \left\| {\varvec{\eta }}_k^C\right\| _{{\varvec{x}}_k}\), since \(\sigma _k\ge L_H\), it follows that
(ii) If \(\Vert {\varvec{\eta }}_k\Vert _{{\varvec{x}}_k}\ge \left\| {\varvec{\eta }}_k^C\right\| _{{\varvec{x}}_k}\), since \(\sigma _k\ge L_H\), we have
The third inequality follows from Eq. (148). The fourth inequality holds since the function \(h(x)=\frac{\left( \sqrt{\alpha ^2+x}-\alpha \right) ^2}{x}\) is an increasing function of x for \(\alpha \ge 0\). The penultimate inequality also holds given Eqs. (57), (58) and \(\frac{1-\tau }{12} \le \frac{1}{12}\) since \(\tau \in (0,1]\). \(\square\)
Lemma 8
Suppose Condition 1and Assumptions 1, 2, 4, 5hold, then when \(\Vert {\textbf{G}}_k\Vert \le \epsilon _g\) and \(\lambda _{min}({\textbf{H}}_k)\le -\epsilon _H\) , if \(\sigma _k\ge L_H\) , we have
Proof
From Lemma 7 in Xu et al. (2020), we have
Then we consider two cases for \(\left\| {\varvec{\eta }}_k^E\right\| _{{\varvec{x}}_k}\).
(i) If \(\Vert {\varvec{\eta }}_k\Vert _{{\varvec{x}}_k}\le \left\| {\varvec{\eta }}_k^E\right\| _{{\varvec{x}}_k}\), since \(\sigma _k\ge L_H\), it follows that
(ii) If \(\Vert {\varvec{\eta }}_k\Vert _{{\varvec{x}}_k}\ge \left\| {\varvec{\eta }}_k^E\right\| _{{\varvec{x}}_k}\), since \(\sigma _k\ge L_H\), we have
The third inequality follows from Eqs. (58) and (152), and the fourth one holds since \(|\lambda _{min}({\textbf{H}}_k)|\ge \epsilon _H\) and \(\tau <1\). \(\square\)
Lemma 9
Suppose Assumptions 1, 2, 3, 4, 5hold, then when \(\Vert {\textbf{G}}_k\Vert _{{\varvec{x}}_k}\ge \epsilon _g\) , if \(\sigma _k\ge L_H\) , the iteration k is successful, i.e., \(\rho _k\ge \tau\) and \(\sigma _{k+1}\le \sigma _k\).
Proof
We have that
where the first inequality follows from Eqs. (36), Eq. (141), the second inequality from Eqs. (147), (36), (39), and the third follows from Eq. (148). The last two inequalities hold given Eqs. (57), (58) and the fact that the function \(h(x)=\frac{x}{\left( \sqrt{\alpha ^2+x}-\alpha \right) ^2}\) is decreasing with \(\alpha >0\). Consequently, we have \(\rho _k\ge \tau\) and that the iteration is successful. Based on Step (12) of Algorithm 1, we have \(\sigma _{k+1}=\max (\sigma _k/\gamma ,\epsilon _\sigma )\le \sigma _k\). \(\square\)
Lemma 10
Suppose Condition 1 and Assumption 1,2, 4, 5hold, then when \(\Vert {\textbf{G}}_k\Vert _{{\varvec{x}}_k}< \epsilon _g\) and \(\lambda _{min}({\textbf{H}}_k)\le -\epsilon _H\) , if \(\sigma _k\ge L_H\) , the iteration k is successful, i.e., \(\rho _k\ge \tau\) and \(\sigma _{k+1}\le \sigma _k\).
Proof
We have that
where the first and second inequalities follow from Eqs. (143), (37), (151), (40). The last inequality uses Eq. (58). Consequently, we have \(\rho _k\ge \tau\) which indicates the iteration is successful. Based on Step (12) of Algorithm 1, we have \(\sigma _{k+1}=\max (\sigma _k/\gamma ,\epsilon _\sigma )\le \sigma _k\). \(\square\)
Lemma 11
Suppose Condition 1 and Assumptions 1, 2, 3, 4, 5hold, then for all k , we have
Proof
We prove this lemma by contradiction by considering the two following cases.
(i) If \(\sigma _0 \le 2\gamma L_H\), we assume there exists an iteration \(k\ge 0\) that is the first unsuccessful iteration such that \(\sigma _{k+1}=\gamma \sigma _k>2\gamma L_H\). This implies \(\sigma _k> L_H\) and \(\sigma _{k+1}>\sigma _k\). Since the algorithm fails to terminate at iteration k, we have \(\Vert {\varvec{G_k}}\Vert _{{\varvec{x}}_k}\ge \epsilon _g\) or \(\lambda _{min}({\textbf{H}}_k)<-\epsilon _H\). Then, according to Lemmas 9 and 10, iteration k is successful and thus \(\sigma _{k+1}=\max (\sigma _k/\gamma , \epsilon _\sigma )\le \sigma _k\). This contradicts the earlier statement of \(\sigma _{k+1}>\sigma _k\). We thus have \(\sigma _k \le 2\gamma L_H\) for all k.
(ii) If \(\sigma _0>2\gamma L_H\), similarly, we assume there exists an iteration \(k\ge 0\) that is the first unsuccessful iteration such that \(\sigma _{k+1}=\gamma \sigma _k>\sigma _0\). This implies \(\sigma _k> L_H\) and \(\sigma _{k+1}>\sigma _k\). Since the algorithm fails to terminate at iteration k, we have \(\Vert {\varvec{G_k}}\Vert _{{\varvec{x}}_k}\ge \epsilon _g\) or \(\lambda _{min}({\textbf{H}}_k)<-\epsilon _H\). According to Lemmas 9 and 10, iteration k is successful and thus \(\sigma _{k+1}=\max (\sigma _k/\gamma , \epsilon _\sigma )\le \sigma _k\), which is a contradiction. Thus, we have \(\sigma _k \le \sigma _0\) for all k. \(\square\)
1.2 F.2 Main Proof of Theorem 3
Proof
Letting \(\sigma _b=\max \left( \sigma _0, 2\gamma L_H \right)\), when \(\Vert {\textbf{G}}_k\Vert \ge \epsilon _g\), from Eq. (36) and Lemma 11 we have
When \(\Vert {\textbf{G}}_k\Vert <\epsilon _g\) and \(\lambda _{min}({\textbf{H}}_k)\le -\epsilon _H\), from Eq. (37) and Lemma 11, we have
Let \({\mathcal {S}}_{succ}\) be the set of successful iterations before Algorithm 1 terminates and \({\hat{f}}_{min}\) be the function minimum. Since \({\hat{f}}_k({\varvec{\eta }}_k)\) is monotonically decreasing, we have
where \(\kappa =\min \left( \frac{\nu ^3}{6\sigma _b^2},\frac{1}{2\sqrt{3}} \min \left( \frac{1}{K_H},\frac{1}{\sqrt{\sigma _b}}\right) \right)\). Let \({\mathcal {S}}_{fail}\) be the set of unsuccessful iterations and T be the total iterations of the algorithm. Then we have \(\sigma _T=\sigma _0\gamma ^{|{\mathcal {S}}_{fail}|-|{\mathcal {S}}_{succ}|}\).
Combining it with \(\sigma _T\le \sigma _b\) from Lemma 11, we have
Finally, combining Eqs. (160), (161), we have
This completes the proof. \(\square\)
1.3 F.3 Main Proof of Corollary 1
Proof
Under the given assumptions, when Theorem 3 holds, Algorithm 1 returns an \(\left( \epsilon _g,\epsilon _H\right)\)-optimal solution in \(T={\mathcal {O}}\left( \max \left( \epsilon _g^{-2},\epsilon _H^{-3}\right) \right)\) iterations. Also, according to Theorem 2, at an iteration, Condition 1 is satisfied with a probability \((1-\delta )\), where the probability \((1-\delta )\) at the current iteration can be independently achieved by selecting proper subsampling sizes for the approximate gradient and Hessian. Let E be the event that Algorithm 1 returns an \(\left( \epsilon _g,\epsilon _H\right)\)-optimal solution and \(E_i\) be the event that Condition 1 is satisfied at iteration i. According on Theorem 3, when event E happens, it requires Condition 1 to be satisfied for all the iterations, thus we have
This completes the proof. \(\square\)
Appendix G: Theorem 4 and Corollary 2
1.1 G.1 Supporting Lemmas for Theorem 4
The proof of Theorem 4 builds on an existing lemma, which we restate as follows.
Lemma 12
(Sufficient Function Decrease (Lemma 3.3 in Cartis et al. 2011)) Suppose the solution \({\varvec{\eta }}_k\) satisfies Assumption 3, then we have
The proof also needs another lemma that we develop as below.
Lemma 13
(Sufficiently Long Steps) Suppose Condition 1and Assumptions 1, 2, 3, 4, 5hold. If \(\delta _g\le \delta _H\le \kappa _\theta \epsilon _g\) , Algorithm 3 returns a solution \({\varvec{\eta }}_k\) such that
when \(\Vert {\textbf{G}}_{k+1}\Vert _{{\varvec{x}}_{k+1}}\ge \epsilon _g\) for \(k>0\) and when the inner stopping criterion of Eq. (47) is used. Here \(\kappa _s=\min \left( 1/\sqrt{(L_H+2\sigma _b+\frac{\epsilon _g}{3}+\frac{L_l}{3})},1/\sqrt{\frac{5L_H}{3}+\frac{10\sigma _b}{3}+\frac{11L_l}{9}}\right)\) with \(L_l > 0\) and \(\sigma _b = \max \left( \sigma _0,2\gamma L_H\right)\).
Proof
By differentiating the approximate model, we have
where the first inequality follows from the triangle inequality and the second inequality from Eqs. (49), (51) and (52). Additionally, from Lemma 3.8 in Kasai et al. (2018), we have
where \(L_l>0\) is a constant. Then, we have
with the first inequality following from the triangle inequality and the second from Eqs. (51), (52) and (167). Then, by combining Eqs. (47), (166) and (168), with \(\theta _k:=\kappa _\theta \min (1,\left\| {{\varvec{\eta }}}_k^i\right\| _{{\textbf{x}}_k})\) we obtain
This results in
Subsequently, it has
In the above derivation, we use the property of the parallel transport that preserves the length of the transported vector. The last inequality in Eq. (170) is based on Eqs. (51) and the triangle inequality.
Now, we consider the following two cases. (i) If \(\Vert {\varvec{\eta }}_{k}\Vert _{{\varvec{x}}_k}\ge 1\), from Eq. (47) we have \(\theta _k=\kappa _\theta\), and therefore
This then gives
where the last inequality holds because \(\delta _g\le \delta _H\le \kappa _{\theta }\epsilon _g\) and \(\kappa _{\theta }<\frac{1}{6}\). (ii) If \(\Vert {\varvec{\eta }}_{k}\Vert _{{\varvec{x}}_k}< 1\), then \(\theta _k=\kappa _\theta \Vert {\varvec{\eta }}_{k}\Vert _{{\varvec{x}}_k}<\kappa _\theta\). Given Eq. (168) and \(\delta _g\le \delta _H\le \kappa _{\theta }\epsilon _g\), it has
Then, we have
which results in
This completes the proof. \(\square\)
1.2 G.2 Main Proof of Theorem 4
Let \(\sigma _b = \max \left( \sigma _0,2\gamma L_H\right)\), \(\sigma _{min}=\min \left( \sigma _k\right)\) for \(k\ge 0\) and \({\mathcal {S}}_{succ}^1\) be the set of successful iterations such that \(\Vert {\textbf{G}}_{k+1}\Vert _{{\varvec{x}}_{k+1}}\ge \epsilon _g\) for \(k\in {\mathcal {S}}_{succ}^1\). As \({\hat{f}}_k({\varvec{\eta }}_k)\) is monotonically decreasing, we have
where \(\kappa _1=\frac{1}{6} \min \left( \frac{\nu ^3}{\sigma _b^2},\epsilon _\sigma \kappa _s^3\right)\). The fourth inequality follows from Eqs. (37) and (164), while the fifth from Eq. (165).
Let \({\mathcal {S}}_{succ}^2\) be the set of successful iterations such that \(\Vert {\textbf{G}}_{k+1}\Vert _{{\varvec{x}}_{k+1}}<\epsilon _g\) and \(\lambda _{min}({\textbf{H}}_{k+1})<-\epsilon _H\) for \(k\in {\mathcal {S}}_{succ}^2\). Then there is an iteration \(t\in {\mathcal {S}}_{succ}^2\) in which \(\Vert {\textbf{G}}_{t}\Vert _{{\varvec{x}}_{t}}\ge \epsilon _g\) and \(\Vert {\textbf{G}}_{t+1}\Vert _{{\varvec{x}}_{t+1}}<\epsilon _g\). Thus, we have
and this results in
where \(\kappa _2=\frac{\nu ^3}{6\sigma _b^2}\). The second and third inequalities follow from Eqs. (157) and (37), respectively. Then, the bound for the total number of successful iterations is
where the extra iteration corresponds to the final successful iteration of Algorithm 1 with \(\lambda _{min}({\textbf{H}}_{k+1})\ge -\epsilon _H\). Then, similar to Eq. (162), we have the improved iteration bound for Algorithm 1 given as
where \(C=\frac{{\hat{f}}_0({\varvec{0}}_{{\varvec{x}}_0})-{\hat{f}}_{min}}{\tau \kappa _1} + \frac{{\hat{f}}_t({\varvec{\eta }}_t)-{\hat{f}}_{min}}{\tau \kappa _2}\). This completes the proof. \(\square\)
1.3 G.3 Main Proof of Corollary 2
Although this follows exactly the same way as to prove Corollary 1, we repeat it here for the convenience of readers.
Proof
Under the given assumptions, when Theorem 4 holds, Algorithm 1 returns an \(\left( \epsilon _g,\epsilon _H\right)\)-optimal solution in \(T={\mathcal {O}}\left( \max \left( \epsilon _g^{-\frac{3}{2}},\epsilon _H^{-3}\right) \right)\) iterations. Also, according to Theorem 2, at an iteration, Condition 1 is satisfied with a probability \((1-\delta )\), where the probability \((1-\delta )\) at the current iteration can be independently achieved by selecting proper subsampling sizes for the approximate gradient and Hessian. Let E be the event that Algorithm 1 returns an \(\left( \epsilon _g,\epsilon _H\right)\)-optimal solution and \(E_i\) be the event that Condition 1 is satisfied at iteration i. According on Theorem 4, when event E happens, it requires Condition 1 to be satisfied for all the iterations, thus we have
This completes the proof. \(\square\)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Deng, Y., Mu, T. Faster Riemannian Newton-type optimization by subsampling and cubic regularization. Mach Learn 112, 3527–3589 (2023). https://doi.org/10.1007/s10994-023-06321-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10994-023-06321-0