Abstract
We develop new adaptive algorithms for temporal integration of nonlinear evolution equations on tensor manifolds. These algorithms, which we call step-truncation methods, are based on performing one time step with a conventional time-stepping scheme, followed by a truncation operation onto a tensor manifold. By selecting the rank of the tensor manifold adaptively to satisfy stability and accuracy requirements, we prove convergence of a wide range of step-truncation methods, including explicit one-step and multi-step methods. These methods are very easy to implement as they rely only on arithmetic operations between tensors, which can be performed by efficient and scalable parallel algorithms. Adaptive step-truncation methods can be used to compute numerical solutions of high-dimensional PDEs, which, have become central to many new areas of application such optimal mass transport, random dynamical systems, and mean field optimal control. Numerical applications are presented and discussed for a Fokker-Planck equation with spatially dependent drift on a flat torus of dimension two and four.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Consider the initial value problem
where \(f: \Omega \times [0,T] \rightarrow \mathbb {R}\) is a d-dimensional (time-dependent) scalar field defined on the domain \(\Omega \subseteq \mathbb {R}^d\) (\(d\ge 2\)), and \(\mathcal N\) is a nonlinear operator which may depend on the variables \({{\varvec{x}}}=(x_1,\ldots ,x_d)\) and may incorporate boundary conditions. By discretizing (1) in \(\Omega \), e.g., by finite differences, finite elements, or pseudo-spectral methods, we obtain the system of ordinary differential equations
Here, \({{\varvec{f}}}:[0,T]\rightarrow {\mathbb R}^{n_1\times n_2 \times \cdots \times n_d}\) is a multi-dimensional array of real numbers (the solution tensor), and \({\varvec{N}}\) is a tensor-valued nonlinear map (the discrete form of \(\mathcal {N}\) corresponding to the chosen spatial discretization). The number of degrees of freedom associated with the solution \({{\varvec{f}}}(t)\) to the Cauchy problem (2) is \(N_{\text {dof}}=n_1 \cdot n_2 \cdots n_d\) at each time \(t\ge 0\), which can be extremely large even for small d. For instance, the solution to the Boltzmann-BGK equation on a 6-dimensional flat torus [4] with 128 points in each variable \(x_i\) (\(i=1,\ldots ,6)\) yields \(N_{\text {dof}}=128^6=4398046511104\) degrees of freedom at each time t.
In order to reduce the number of degrees of freedom in the solution tensor \({{\varvec{f}}}(t)\), we seek a representation of the solution on a low-rank tensor format [7, 13, 22] for all \(t \ge 0\). To complement the low-rank structure of \({{\varvec{f}}}(t)\), we also represent the operator \({\varvec{N}}\) in a compatible low-rank format, allowing for an efficient computation of \({{\varvec{N}}}({{\varvec{f}}}(t))\) at each time t in (2). One method for the temporal integration of (2) on a smooth tensor manifold with constant rank [18, 34] is dynamic tensor approximation [11, 12, 21, 28]. This method keeps the solution \({{\varvec{f}}}(t)\) on the tensor manifold for all \(t \ge 0\) by integrating the projection of (2) onto the tangent space of the manifold foward in time. While such an approach has proven effective, it also has inherent computational drawbacks. Most notably, the system of evolution equations arising from the projection of (2) onto the tangent space of the tensor manifold contains inverse auto-correlation matrices which may become ill-conditioned as time integration proceeds. This problem was addressed in [26, 27] by using operator splitting time integration methods (see also [5]).
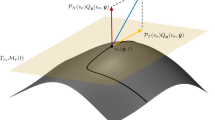
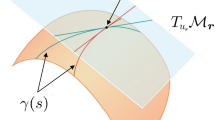
A graphical representation of a step-truncation method to integrate equation (2) on a Hierarchical Tucker tensor manifold \(\mathcal{H}_{{\varvec{r}}}\) with multilinear rank \({\varvec{r}}\). The \({{\varvec{u}}}_k\) denote time snapshots of the numerical approximation to (2) obtained using a conventional time-stepping scheme, the \({{\varvec{g}}}_k\) are time snapshots of the exact solution \({{\varvec{f}}}(k\varDelta t)\) projected onto \(\mathcal{H}_{{\varvec{r}}}\), and the \({{\varvec{f}}}_k\) are time snapshots of the step-truncation solution on \(\mathcal{H}_{{\varvec{r}}}\)
A different class of algorithms to integrate the Cauchy problem (2) on a low-rank tensor manifold was recently proposed in [19, 32, 35]. These algorithms are based on integrating the solution \({{\varvec{f}}}(t)\) off the tensor manifold for a short time using any conventional time-stepping scheme, and then mapping it back onto the manifold using a tensor truncation operation. We will refer to these methods as step-truncation methods. To describe these methods further, let us discretize the ODE (2) in time with a conventional one-step scheme on an evenly-spaced temporal grid
where \({{\varvec{u}}}_{k}\) denotes an approximation of \({{\varvec{f}}}(k\varDelta t)\) for \(k=0,1,\ldots \), and \(\varvec{\varPhi }\) is an increment function. To obtain a step-truncation scheme, we simply apply a nonlinear projection (truncation operator), denoted by \(\mathfrak {T}_{{\varvec{r}}}(\cdot )\), onto a tensor manifold with multilinear rank \({\varvec{r}}\) [3, 4, 14, 15, 23] to the scheme (3). This yields
where \({{\varvec{f}}}_{k}\) here denotes an approximation of \(\mathfrak {T}_{{\varvec{r}}}({{\varvec{f}}}(k\varDelta t))\) for \(k=0,1,\ldots \). The need for tensor rank-reduction when iterating (3) can be easily understood by noting that tensor operations such as the application of an operator to a tensor and the addition between two tensors naturally increase tensor rank [23]. Hence, iterating (3) with no rank reduction can yield a fast increase in tensor rank, which, in turn, can tax computational resources significantly. Step-truncation algorithms of the form (4) were subject to a thorough error analysis in [19], where convergence results were obtained in the context of fixed-rank tensor integrators, i.e., integrators in which the tensor rank \({\varvec{r}}\) in (4) is kept constant at each time step (Fig. 1).
In this paper, we develop adaptive step-truncation algorithms in which the tensor rank \({\varvec{r}}\) is selected at each time step based on desired accuracy and stability constraints. These methods are very simple to implement as they rely only on arithmetic operations between tensors, which can be performed by efficient and scalable parallel algorithms [2, 9, 15].
The paper is organized as follows. In Sect. 2, we review low-rank integration techniques for time-dependent tensors, including dynamic approximation and step-truncation methods. In Sect. 3, we develop a new criterion for tensor rank adaptivity based on local error estimates. In Sect. 4, we prove convergence of a wide range rank-adaptive step-truncation algorithms, including one-step methods of order 1 and 2, and multi-step methods of arbitrary order. In Sect. 5 we establish a connection between rank-adaptive step-truncation methods and rank-adaptive dynamical tensor approximation. In Sect. 6 we present and discuss numerical applications of the proposed algorithms. In particular, we study a prototype problem with rapidly varying rank and a Fokker-Planck equation with spatially dependent drift on a flat torus of dimension two and four.
2 Low-Rank Integration of Time-Dependent Tensors
Denote by \(\mathcal{H}_{{\varvec{r}}}\subseteq \mathbb {R}^{n_1\times n_2\times \cdots \times n_d}\) the manifold of hierarchical Tucker tensors with multilinear rank \({{\varvec{r}}}= \{r_{\alpha }\}\) corresponding to a prescribed dimension tree \(\alpha \in \mathcal{T}_d\) [34].
Remark 1
Every tensor \({{\varvec{f}}}\in \mathbb {R}^{n_1\times n_2\times \cdots \times n_d}\) has an exact hierarchical Tucker (HT) decomposition [14]. Thus, if \({\varvec{f}}\) is not the zero tensor, then \({\varvec{f}}\) belongs to a manifold \(\mathcal{H}_{{\varvec{r}}}\) for some \({\varvec{r}}\).
We begin by introducing three maps which are fundamental to the analysis of low-rank tensor integration. First, we define the nonlinear map
Here, \(\overline{\mathcal{H}}_{{\varvec{r}}}\) denotes the closure of the tensor manifold \(\mathcal{H}_{{\varvec{r}}}\) and contains all tensors of multilinear rank smaller than or equal to \({\varvec{r}}\) [34]. The map (5) provides the optimal rank-\({\varvec{r}}\) approximation of a tensor \({{\varvec{f}}} \in \mathbb {R}^{n_1\times n_2\times \cdots \times n_d}\). The second map, known as high-order singular value decomposition (HOSVD) [15], is defined as a composition of linear maps obtained from a sequence of singular value decompositions of appropriate matricizations of the tensor \({\varvec{f}}\) . Such map can be written explicitely as
where \(\mathcal{T}_d^1\dots \mathcal{T}_d^p\) are the layers of the dimension tree \(\mathcal{T}_d\). The map (6) provides a quasi-optimal rank-\({\varvec{r}}\) approximation of the tensor \({{\varvec{f}}} \in \mathbb {R}^{n_1\times n_2\times \cdots \times n_d}\), and is related to the optimal rank-\({\varvec{r}}\) truncation by the inequalities [14]
When combined with linear multistep integration schemes, the sub-optimal approximation (6) has proven to yield stable step-truncation methods [32]. The third map we define is an orthogonal projection onto the tangent space \(T_{{\varvec{f}}}\mathcal{H}_{{\varvec{r}}}\) of \(\mathcal{H}_{{\varvec{r}}}\) at the point \({\varvec{f}}\). This projection is defined by the minimization problem
which is a linear function of \({{\varvec{v}}}\) (\({\varvec{v}}\) is the solution to a linearly constrained least squares problem).
With these three maps defined, hereafter we describe two methods for integrating (2) on the manifold \(\mathcal{H}_{{\varvec{r}}}\). Before doing so, let us discretize the temporal domain of interest [0, T] into \(N+1\) evenly-spacedFootnote 1 time instants,
and let
be a convergent one-step schemeFootnote 2
approximating the solution to the initial value problem (2). In (10), \({{\varvec{u}}}_k\) denotes the numerical solution to (2) at time instant \(t_k\).
2.1 Best Tangent Space Projection (B-TSP) Method
The first method we present maps the initial condition \({{\varvec{f}}}_0\) onto the manifold \(\mathcal{H}_{{\varvec{r}}}\) using either (5) or (6) and then utilizes the orthogonal projection (8) to project \({{\varvec{N}}}({{\varvec{f}}}(t))\) onto the tangent space \(T_{{\varvec{f}}}\mathcal{H}_{{\varvec{r}}}\) at each time. We write this method as (see [28])
where \({\mathfrak T}_{{\varvec{r}}}\) is either the mapping in (5) or (6). Discretizing (11) with a one-step method (10) yields the fully discrete scheme
While the scheme (12) has proven effective, explicitly computing the orthogonal projection \(\mathcal{P}_{{{\varvec{w}}}}{{\varvec{N}}}({{\varvec{w}}})\) comes with computational drawbacks. Most notably, inverse auto-correlation matrices of tensor modes appear in the projection [28] (see also [20, 21, 26]). If the tensor solution is comprised of small singular values, then the auto-correlation matrices are ill-conditioned. It has been shown in [26] that this phenomenon is due to the curvature of the tensor manifold \(\mathcal{H}_{{\varvec{r}}}\) being inversely proportional to the smallest singular value present in the tensor solution. Thus, special care is required when choosing an integration scheme for (11). Operator splitting methods [26, 27] and unconventional integration schemes [5] have been introduced to integrate (11) when the tensor solution is comprised of small singular values. It has also been shown in [19] that by using an extrinsic representation, the artificial stiffness due to the tensor manifold curvarture can be avoided. Since this method comes from a minimization principle over the tensor manifold tangent space, we refer to it as the best tangent space projection (B-TSP) method.
2.2 Step-Truncation Methods (B-ST, SVD-ST)
The second method we present allows the solution to leave the tensor manifold \({\mathcal{H}}_{{\varvec{r}}}\), and then maps it back onto the manifold at each time step. Applying either (5) or (6) to the right hand side of (10) results in a step-truncation method
which is a low-rank tensor approximation to (2). We will refer to (13) as the fixed-rank best step-truncation (B-ST) method and to (14) as the fixed-rank SVD step-truncation (SVD-ST) method. This definition emphasizes that the multivatiate tensor rank \({{\varvec{r}}}\) does not change with time. The schemes (13) and (14) were studied extensively in [19]. One of the main findings is that a low-rank approximability condition is required in order to obtain error estimates for the low-rank tensor approximation to (2). The low-rank approximability condition can be written as
for all \({ \bar{{\varvec{f}}}}\in \mathcal{H}_{{\varvec{r}}}\) in a suitable neighbourhood of the exact solution. Under this assumption, it can be shown that a one-step integration scheme with arbitrary order increment function \(\varvec{\varPhi }\) applied to (13) or (14) results in an approximation to (2) with error dominated by E. As an alternative to the fixed-rank schemes (13)–(14) combined with the low-rank approximability assumption (15), we propose the following rank-adaptive step-truncation schemes
The selection of a new rank \({{\varvec{r}}}_k\) at each time step allows us to obtain convergence results for step-truncation schemes without assuming (15). We will refer to the schemes (16) and (17) as rank-adaptive B-ST and rank-adaptive SVD-ST, respectively.
3 Consistency of Step-Truncation Methods
In this section, we prove a number of consistency results for step-truncation methods. In particular, we show that the fixed-rank step-truncation method (13) is consistent with the B-TSP method (12), and the rank-adaptive step-truncation methods (16)–(17) are consistent with the fully discrete system (10) (provided the truncation ranks are chosen to satisfy a suitable criterion). Our analysis begins with stating a few known results for the truncation operator \({\mathfrak T}_{{\varvec{r}}}^{\text {best}}\). Consider the formal power series expansion of \({\mathfrak T}_{{\varvec{r}}}^{\text {best}}\) around \({\varvec{f}}\in \mathcal{H}_{{\varvec{r}}}\)
where \(\partial \mathfrak T_{{\varvec{r}}}^{\text {best}}({{\varvec{f}}})/ \partial {\varvec{f}}\) denotes the Jacobian of \({\mathfrak T}_{{\varvec{r}}}^{\text {best}}\) at \({{\varvec{f}}}\), \({{\varvec{v}}}\in \mathbb {R}^{n_1\times n_2\times \cdots \times n_d}\), and \(\varepsilon \in \mathbb {R}\) is small. Since \({{\varvec{f}}}\in \mathcal{H}_{{\varvec{r}}}\), we have that \({\mathfrak T}_{{\varvec{r}}}^{\text {best}}({{\varvec{f}}}) = {{\varvec{f}}}\), which allows us to write (18) as
In the following Lemma we show that the Jacobian \(\partial \mathfrak T_{{\varvec{r}}}^{\text {best}}({{\varvec{f}}})/\partial {\varvec{f}}\) coincides with the orthogonal projection (8) onto the tangent space \(T_{{\varvec{f}}}\mathcal{H}_{{\varvec{r}}}\).
Lemma 1
(Smoothness of the best truncation operator) The map \({\mathfrak T}_{{\varvec{r}}}^{\text {best}}(\cdot )\) is continuously differentiable on \(\mathcal{H}_{{\varvec{r}}}\). Moreover,
where \(\mathcal{P}_{{{\varvec{f}}}}\) is the orthogonal projection (8) onto the tangent space of \(\mathcal{H}_{{\varvec{r}}}\) at \({{\varvec{f}}}\).
This result has been proven in [24] and [1] for finite-dimensional manifolds. A slightly different proof which holds for finite-dimensional manifolds without boundary is given in [29]. In Appendix 1 we provide an alternative proof which is based primarily on linear algebra rather than differential geometry. With Remark 1 in mind, we can apply Lemma 1 to every tensor except the zero tensor. We now use Lemma 1 to prove consistency between the fixed-rank B-ST method (13) and the B-TSP method (12).
Proposition 1
(Consistency of B-ST and B-TSP) Let \({\varvec{\varPhi }}({{\varvec{N}}}, {{\varvec{f}}}, \varDelta t)\) denote an order-p increment function defining a one-step temporal integration scheme as in (10) and let \({{\varvec{f}}}_{k}\in \mathcal{H}_{{\varvec{r}}}\). We have that
i.e., B-ST is at least order 1 consistent with B-TSP in \(\varDelta t\).
This proposition follows immediately from using the perturbation series (19) together with Lemma 1. Next, we provide a condition for rank selection in the rank-adaptive methods (16)–(17) which guarantees a consistent approximation to equation (2).
Proposition 2
(Rank selection for B-ST consistency) Let \({\varvec{\varPhi }}({{\varvec{N}}}, {{\varvec{f}}}_k, \varDelta t)\) be an order-p increment function. The step-truncation method
approximates (2) with order-p local truncation error if and only if there exists an \(M>0\) (independent of k) such that the rank \({{\varvec{r}}}_{k}\) at time index k satisfies the inequality
Proof
Denote by \({{\varvec{f}}}(t_{k+1})\) the exact solution to \({{d}{{\varvec{f}}}}/{{ d} t} ={{\varvec{N}}}({{\varvec{f}}})\) with initial condition \({{\varvec{f}}}_k\) at time \(t_k\). For the forward implication, suppose there exists a constant \(C_1\) such that \(\left| \left| {{\varvec{f}}}(t_{k+1}) - {{\varvec{f}}}_{k+1} \right| \right| _2\le C_1 \varDelta t^{p+1}\). Then,
where \(C_2\) is a constant. To prove the converse, we estimate the local truncation error as
where \(C_2\) is a constant. \(\square \)
Recalling Remark 1, for any given tensor \({{\varvec{a}}}_k \in \mathbb {R}^{n_1 \times \cdots \times n_d}\) there exists a rank \({{\varvec{r}}}_k\) which makes the left hand side of the inequality (21) equal to zero. Thus, there always exists a rank \({{\varvec{r}}}_k\) which satisfies (21). Using consistency of the rank-adaptive B-ST scheme (16) proven in Proposition 2, we can easily obtain consistency results for step-truncation methods based on quasi-optimal truncation operators such as \({\mathfrak T}_{{\varvec{r}}}^{\text {SVD}}\). To do so, we first show that the local truncation error of SVD-ST scheme (14) is dominated by the local truncation error of the B-ST scheme (13).
Lemma 2
(Error bound on the SVD step-truncation scheme) Let \({{\varvec{f}}}(t_{k+1})\) denote the exact solution to \({{\text{ d }}{{\varvec{f}}}}/{{\text{ d }} t} ={{\varvec{N}}}({{\varvec{f}}})\) with initial condition \({{\varvec{f}}}_k\) at time \(t_k\), and let \({\varvec{\varPhi }}({{\varvec{N}}}, {{\varvec{f}}}, \varDelta t)\) be an order-p increment function. The local truncation error of the SVD-ST integrator (14) satisfies
Proof
First, we apply triangle inequality
Since the increment function \({\varvec{\varPhi }}({{\varvec{N}}}, {{\varvec{f}}}(\tau ), \varDelta t)\) is of order p, we can replace the first term at the right hand side of (22) by \(K\varDelta t^{p+1}\), i.e.,
where K is a constant. Next, we use the inequality (7) to obtain
Another application of triangle inequality yields
Finally, collecting like terms yields the desired result. \(\square \)
By combining Proposition 2 and Lemma 2, it is straightforward to prove the following consistency result for the rank-adaptive SVD-ST integrator (16).
Corollary 1
(Rank selection for SVD-ST consistency) Let \({\varvec{\varPhi }}({{\varvec{N}}}, {{\varvec{f}}}_k, \varDelta t)\) be an order-p increment function. The step-truncation method
approximates (2) with order-p local truncation error if and only if there exists an \(M>0\) such that the rank \({{\varvec{r}}}_{k}\) at time index k satisfies the inequality
Note that by inequality (7), the statement in (23) is equivalent to
for another constant \(M' > 0\), which depends on d. Consistency results analogous to Corollary 1 for step-truncation integrators based on any quasi-optimal truncation can be obtained in a similar way.
3.1 Error Constants
In this section we provide a lower bound for the constant M appearing in Corollary 1. To simplify the presentation we develop the bounds for the matrix case (\(d=2\)) and note that similar results for \(d>2\) can be obtained by using the hierarchical approximability theorem discussed in [14].
With reference to Corollary 1, let \(\{\sigma _i\}\) be the set of singular values of \({{\varvec{a}}}_k\) and let \({{\varvec{a}}}_k - {\mathfrak T}_{r_k}({{\varvec{a}}}_k)={{\varvec{E}}}_k \in {\mathbb {R}}^{n_1\times n_2}\) be the error matrix due to tensor truncation. Then the local consistency condition (23) can be written as
Equation (25) can be used to obtain the following lower bound for the coefficient M
The lower bound can be explicitly computed if we have available the decay rate of the singular values \(\{ \sigma _i \}\). For instance, if the singular values decay exponentially fast (as in the case of singular values considered in [31]), i.e., \(\sigma ^2_i \le Cq^i\) for some \(C>0\) and \(q\in (0,1)\), Then by the geometric series formula we have that
which yields \(Cq \ge (1-q)\Vert {{\varvec{a}}}_k\Vert _2^2\). In this case we may bound the local error as
Inserting this bound into (26) and recalling that \(Cq \ge (1-q)\left\| {{\varvec{a}}}_k\right\| _2^2\) and \(\left\| {{\varvec{a}}}_k\right\| _2 \ge \left\| {{\varvec{E}}}_k\right\| _2\) we obtain
Equation (27) establishes a relationship between the local error coefficient M, the solution rank \(r_k\) at time step k, the time step \(\varDelta t\), and the 2-norm of the solution \({{\varvec{a}}}_k\) at time step k.
A similar relation can be derived for singular values \(\{\sigma _i\}\) decaying algebraically, i.e., \(\sigma _i^2 \le Ci^{-1-2s}\), where \(s\in \mathbb {N}\). It was shown in [16] that this decay rate occurs when discretizing an s-times differentiable bivariate function. Moreover, it was also shown that
where K is a constant related to the measure of the domain of the aforementioned s-times differentiable bivariate function. Therefore, if we choose the rank \(r_k\) to satisfy the inequality
then we have that condition (23) is also satisfied. An expression for K may be found in Theorem 3.3 of [16].
4 Convergence of Rank-Adaptive Step-Truncation Schemes
We have shown that the proposed methods are consistent, now we prove convergence. To do so, let us assume that the increment function \({\varvec{\varPhi }}({{\varvec{N}}}, {{\varvec{f}}}, \varDelta t)\) satisfies the following stability condition: There exist constants \(C,D,E \ge 0\) and a positive integer \(m \le p\) so that as \(\varDelta t\rightarrow 0\), the inequality
holds for all \(\hat{{\varvec{f}}},\tilde{{\varvec{f}}} \in \mathbb {R}^{n_1 \times \cdots \times n_d}\). This assumption is crucial in our development of global error analysis for rank-adaptive step-truncation methods.
Theorem 1
(Global error for rank-adaptive schemes) Let \({{\varvec{f}}}(t)\) be the exact solution to (2), assume \({\varvec{N}}\) is Lipschitz continuous with constant L, and let \({\varvec{\varPhi }}({{\varvec{N}}}, {{\varvec{f}}}, \varDelta t)\) be an order-p increment function satisfying the stability criterion (28). If
is an order-p consistent step-truncation method, where \({\mathfrak {T}}_{{{\varvec{r}}}_k} = {\mathfrak {T}}_{{{\varvec{r}}}_k}^{\text {best}}\) or \({\mathfrak {T}}_{{{\varvec{r}}}_k} = {\mathfrak {T}}_{{{\varvec{r}}}_k}^{\text {SVD}}\) (see Proposition 2 or Corollary 1), then the global error satisfies
where \(z = \min (p,m)\). The constant Q depends on the local error and stability coefficients of the increment function \({\varvec{\varPhi }}\), and the truncation constant M in (21) (or \(M'\) in (24)).
Proof
We induct on the number of time steps (i.e., N in (9)), assuming that \(\varDelta t\) is small enough for the local error estimations to hold true. The base case is given by one step error (\(N=1\)) which is local truncation error. Thus, from our consistency assumption we immediately obtain
which proves the base case. Now, assume that the error after \(N-1\) steps satisfies
where \(z = \min (p,m)\). Letting \({{\varvec{a}}}_k = {{\varvec{f}}}_k + \varDelta t{\varvec{\varPhi }}({{\varvec{N}}}, {{\varvec{f}}}_{k}, \varDelta t)\) denote one step prior to truncation, we expand the final step error in terms of penultimate step
where \(K_{N-1}\) is a local error constant for the untruncated scheme (10). Expanding \({{\varvec{a}}}_{N-1}\) and using the triangle inequality we find
Using our assumption that the increment function is stable, (28) yields
Finally, recalling that \(z=\min (p,m)\), we obtain
concluding the proof. \(\square \)
Since the constants M, C, D, and E are fixed in time, the local error coefficients \(K_{j}\), which depend only on the untruncated scheme (10), determine if the error blows up as the temporal grid is refined. Hereafter we provide several examples of globally convergent rank-adaptive step-truncation methods. In each example, \(\mathfrak {T}_{{{\varvec{r}}}}\) denotes any optimal or quasi-optimal truncation operator, e.g., the best rank-\({\varvec{r}}\) truncation operator (5) or the SVD truncation operator (6).
4.1 Rank-Adaptive Euler Scheme
Our first example is a first-order method for solving (2) based on Euler forward. From Theorem 1, we know that the scheme
is order one in \(\varDelta t\), provided the vector field \({\varvec{N}}\) is Lipschitz and the truncation rank \({{\varvec{r}}}_{k}\) satisfies
for all \(k = 1,2,\ldots \). Applying the nonlinear vector field \({\varvec{N}}\) to the solution tensor \({\varvec{f}}\) can result in a tensor with large rank. Therefore, it may be desirable to apply a tensor truncation operator to \({{\varvec{N}}}({{\varvec{f}}})\) at each time step. To implement this, we build the additional truncation operator into the increment function
to obtain the new scheme
We now determine conditions for \({{\varvec{s}}}_k\) and \({{\varvec{r}}}_k\) which make the scheme (33) first-order. To address consistency, suppose \({{\varvec{f}}}(t_{k+1})\) is the analytic solution to (2) with initial condition \({{\varvec{f}}}_k\) at time \(t_k\). Then, bound the local truncation error as
From this bound, we see that by selecting \({{\varvec{s}}}_k\) and \({{\varvec{r}}}_k\) so that
for all \(k = 1,2,\ldots \), yields an order one local truncation error for (33). To address stability, we show that the increment function (32) satisfies (28) with \(m = 1\), assuming \({\varvec{N}}\) is Lipschitz. Indeed,
where L is the Lipschitz constant of \({\varvec{N}}\). Now applying Theorem 1 proves that the rank-adaptive Euler method (33) has \(O(\varDelta t)\) global error.
4.2 Rank-Adaptive Explicit Midpoint Scheme
Consider the following rank-adaptive step-truncation method based on the explicit midpoint rule (see [17, II.1])
We have proven in Theorem 1 that (34) is order 2 in \(\varDelta t\), provided the vector field \({\varvec{N}}\) is Lipschitz and the truncation rank \({{\varvec{\alpha }}}_{k}\) satisfies
for all \(k = 1,2,\ldots \). Here,
denotes the solution tensor at time \(t_{k+1}\) prior to truncation. For the same reasons we discussed in Sect. 4.1, it may be desirable to insert truncation operators inside the increment function. For our rank-adaptive explicit midpoint method we consider the increment function
which results in the step-truncation scheme
Following a similar approach as in Sect. 4.1, we aim to find conditions on \({{\varvec{\alpha }}}_k\), \({{\varvec{\beta }}}_k\) and \({{\varvec{\gamma }}}_k\) so that the local truncation error of the scheme (36) is order 2. For ease of notation, let us denote the truncation errors by \(\varepsilon _{{{\varvec{\kappa }}}} = \left\| {{\varvec{g}}} - {\mathfrak {T}}_{{{\varvec{\kappa }}}} ({{\varvec{g}}})\right\| _2\), where \({{\varvec{\kappa }}}={{\varvec{\alpha }}}_k\), \({{\varvec{\beta }}}_k\), or \({{\varvec{\gamma }}}_k\). The local truncation error of the scheme (36) can be estimated as
where L is the Lipschitz constant of \({\varvec{N}}\). From this bound, we see that if the truncation ranks \({{\varvec{\alpha }}}_k, {{\varvec{\beta }}}_k\) and \({{\varvec{\gamma }}}_k\) are chosen such that
for some constants A, B, and G, then the local truncation error of the scheme (36) is order 2 in \(\varDelta t\). Also, if (37) is satisfied then the stability requirement (28) is also satisfied. Indeed,
holds for all tensors \(\hat{{\varvec{f}}}, \tilde{{\varvec{f}}} \in \mathbb {R}^{n_1 \times \cdots \times n_d}\). To arrive at the above relationship, we applied triangle inequality several times to pull out the \(\varepsilon _{{\varvec{\kappa }}}\) terms and then used Lipschitz continuity of \({\varvec{N}}\) multiple times. Thus, if the truncation ranks \({{\varvec{\alpha }}}_k, {{\varvec{\beta }}}_k\) and \({{\varvec{\gamma }}}_k\) are chosen to satisfy (37) and the vector field \({\varvec{N}}\) is Lipschitz, then Theorem 1 proves the method (36) has \(O(\varDelta t^2)\) global error.
4.3 Rank-Adaptive Adams-Bashforth Scheme
With some minor effort we can extend the rank-adaptive global error estimates to the well-known multi-step methods of Adams and Bashforth (see [17, III.1]). These methods are of the form
where s is the number of steps. A rank-adaptive step-truncation version of this method is
In order to obtain a global error estimate for (39), we follow the same steps as before. First we prove consistency, then we prove stability, and finally combine these results to obtain a global convergence result. For consistency, let \({{\varvec{f}}}_0={{\varvec{f}}}(t_0)\), \({{\varvec{f}}}_1={{\varvec{f}}}(t_1)\), \(\dots \), \({{\varvec{f}}}_{s-1}={{\varvec{f}}}(t_{s-1})\) be the exact solution to (2) given at the first s time steps. For ease of notation, we do not let the truncation rank depend on time step k as we are only analyzing one iteration of the multi-step scheme (39). Also, define the truncation errors \(\varepsilon _{{\varvec{\kappa }}} = \left\| {{\varvec{g}}} - {\mathfrak {T}}_{{\varvec{\kappa }}}({{\varvec{g}}})\right\| _2\), where \({{\varvec{\kappa }}}={{\varvec{\alpha }}}\), \({{\varvec{\beta }}}\), \({{{\varvec{\gamma }}}(j)}\), \(j=0,\dots ,s-1\). The local error admits the bound
The last term is the local error for an order-s Adams-Bashforth method (38). Therefore, the local error of the step-truncation method (39) is also of order s if the truncation ranks \({{\varvec{\alpha }}}\), \({{\varvec{\beta }}}\), and \({{{\varvec{\gamma }}}(j)}\) are chosen such that
To address stability, we first need to generalize the stability condition (28) to the increment function
for the multi-step method (38). A natural choice is
Clearly, for \(s=1\) the criterion (42) specializes to the stability criterion given in (28). We have the bound
where we used triangle inequality to set aside the \({\varepsilon }_{{\varvec{\kappa }}}\) terms and subsequently applied Lipschitz continuity multiple times. From the above inequality, it is seen that if (40) is satisfied, then the stability condition (42) is also satisfied with \(m = s\). With the consistency and stability results for the multistep step-truncation method (39) just obtained, it is straightforward to obtain the following global error estimate for (39).
Corollary 2
(Global error of rank-adaptive Adams-Bashforth scheme) Assume \({{\varvec{f}}}_0={{\varvec{f}}}(t_0)\), \({{\varvec{f}}}_1={{\varvec{f}}}(t_1)\), \(\dots \), \({{\varvec{f}}}_{s-1}={{\varvec{f}}}(t_{s-1})\) are given initial steps for a convergent order-s method of the form (38), and assume \({\varvec{N}}\) is Lipschitz with constant L. If the rank-adaptive step-trunctation method (39) is order-s consistent with (2), and the corresponding increment function \({\varvec{\varPhi }}\) defined in (41) satisfies the stability condition (42), then the global error satisfies
where Q depends only on the local error constants of the Adams-Bashforth scheme (38).
Proof
The proof is based on an inductive argument on the number of steps taken (N in equation (9)), similar to the proof of Theorem 1. First, notice that by assuming the method (39) is order-s consistent, we immediately obtain (38) for the base case \(N = s\). Now, suppose that
for all k, \(1\le k \le N-s\). It can be immediately verified that (29)–(30) were derived without reference to a one-step method, so we can follow a very similar string of inequalities to obtain
Applying the stability condition (42) yields
The above inequality together with the inductive hypothesis (43) implies
concluding the proof. \(\square \)
Similar to Theorem 1, only the constants \(K_j\) appearing in (44) depend on the time step (note that \(Q_i\) also depends on \(K_j\)). Moreover, the constants \(K_j\) depend only on the multi-step method (38), and not on truncation.
5 Consistency Between Rank-Adaptive B-TSP and Step-Truncation Schemes
In Sect. 3, Proposition 1, we have shown that the fixed-rank step-truncation method (13) is consistent with the fixed-rank B-TSP method (12). In this section we connect our rank-adaptive step-truncation schemes (16)–(17) with the rank-adaptive B-TSP method we recently proposed in [10]. In particular, we prove that the rank requirements for consistency in the rank-adaptive B-TSP method are equivalent to the rank requirements for a consistent step-truncation method as the temporal step size is sent to zero. The rank-adaptive criterion for B-TSP checks if the normal component \(\left\| ({{\varvec{I}}} - {\mathcal{P}_{{\varvec{f}}}}) {{\varvec{N}}}({{\varvec{f}}}) \right\| _2\) of \({{\varvec{N}}}({{\varvec{f}}})\) relative to the tangent space \(T_{{{\varvec{f}}}} \mathcal{H}_{ {\varvec{r}}}\) is smaller than a threshold \(\varepsilon _{\text {inc}}\), i.e., if
If (45) is violated, then a rank increase is triggered and integration continues. It was proven in [10] that rank-adaptive B-TSP methods are consistent if the threshold in (45) is chosen as \(\varepsilon _{\text {inc}} = K\varDelta t\) for any constant \(K>0\). We now show that this consistency condition for rank-adaptive B-TSP is equivalent to our rank selection requirements (21) and (24) in the limit \(\varDelta t\rightarrow 0\).
Proposition 3
(Geometric interpretation of rank addition) Let \({{\varvec{g}}}\in \mathcal{H}_{{\varvec{r}}}\) and \({{\varvec{v}}}\in {\mathbb R}^{n_1\times n_2\times \dots \times n_d}\). The following are equivalent as \(\varDelta t\rightarrow 0\):
Proof
The equivalence between (47) and (48) is an immediate consequence of (7). We now prove that (46) is equivalent to (47). For the forward implication, assume \(\left\| ({{\varvec{I}}} - {\mathcal{P}_{{\varvec{g}}}}) {{\varvec{v}}} \right\| _2\le K\varDelta t\). We have
where \(C\ge 0\) denotes a constant obtained by a Taylor expansion of \({\mathfrak {T}}_{{{\varvec{r}}}}^{\text {best}}\) (see (18)). Setting \(M \ge K+C\), proves the forward implication. Conversely, if we assume \( \left\| ({{\varvec{g}}} + \varDelta t{{\varvec{v}}}) - {\mathfrak {T}}_{{{\varvec{r}}}}^{\text {best}}({{\varvec{g}}} + \varDelta t {{\varvec{v}}})\right\| _2 \le M\varDelta t^{2}\), then
Setting \(K \ge M+C\), we prove (47) implies (46).
\(\square \)
The rank increase criterion (46) for B-TSP offers geometric intuition which is not apparent from the step-truncation rank criterions (47)–(48). That is, the solution rank should increase if the dynamics do not admit a sufficient approximation on the tensor manifold tangent space. Moreover, the accuracy required for approximating the dynamics depends directly on the time step size \(\varDelta t\) and the desired order of accuracy. We emphasize that by applying condition (46) to (12) it is possible to develop a rank-adaptive version of the step-truncation scheme recently proposed in [19]. Specifically, the solution rank \({\varvec{r}}\) at each time step can be chosen to satisfy a bound on the component of (12) normal to the tensor manifold \(\mathcal{H}_{{\varvec{r}}}\).
6 Numerical Applications
In this section we present and discuss numerical applications of the proposed rank-adaptive step-truncation methods. We have seen that these methods are defined by parameters summarized in Table 1.
To choose such parameters in each numerical example we proceed as follows: We first choose the time step \(\varDelta t\) so that the scheme without tensor truncation is stable. Theorem 1 then guarantees convergence of the rank-adaptive step-truncation scheme for any selection of the other parameters, e.g., \(M_1\) and \(M_2\) in the rank-adaptive Euler scheme listed in Table 1. For guidance on how to select the remaining parameters one may apply the results of Sect. 3.1, which are based on the knowledge of the singular values of the solution. An alternative heuristic criterion is to select the free parameters roughly inverse to the time step so that the local error parameters, e.g., \(\varepsilon _{{\varvec{r}}}\) and \(\varepsilon _{{\varvec{s}}}\) in Table 1, do not exceed a specified threshold \(\varepsilon ^*\), i.e., \(\varepsilon _{{\varvec{r}}}\le \varepsilon ^*\) and \(\varepsilon _{{\varvec{s}}}\le \varepsilon ^*\).
6.1 Rank Shock Problem
In this section we test ability of the proposed rank-adaptive schemes to track accuracy and rank for a problem where the rank of the vector field suddenly jumps to a higher value. To this end, consider the following matrix-valued ordinary differential equation
where \({{\varvec{A}}}\) is a symmetric negative definite matrix and \({{\varvec{v}}}(t)\) a forcing term that switches between a low rank and high rank matrix
In Eq. (49) \({{\varvec{A}}}{{\varvec{f}}} + {{\varvec{f}}}{{\varvec{A}}}^{\top }\) is a stabilizing term which is tangent to the fixed rank manifold at all time while \({{\varvec{v}}}(t)\) steers the solution off of the fixed rank manifold. For our numerical experiment we let \({\varvec{A}}\) take the form
which is a finite difference stencil with shifted eigenvalues. We set \(a=1\) and \(b=3\) to ensure the matrix \({\varvec{A}}\) is diagonally dominant with negative eigenvalues. This guarantees that the initial value problem (49) will be stable regardless of how large the \(N \times N\) matrix size is, for our demonstration we set \(N=100\). For the forcing term \({{\varvec{v}}}(t)\) we set
Rank shock problem. Numerical performance of rank-adaptive Euler method applied to the ODE (49)–(50). It is seen that the method accurately tracks the overall shape of the reference solution rank, which was computed to a singular value threshold of \(10^{-12}\). Moreover, the numerical error behaves as expected, decreasing as steady-state is approached
with ranks \(r_{\text {low}} = 6\) and \(r_{\text {high}}=25\). Here, \({{\varvec{\psi }}}_j[i] = \sin (2\pi ij/N)\), \({{\varvec{\phi }}}_j[i] = \cos (2\pi ij/N)\) and \(\sigma ^j=(3/4)^j\). Since the vector field is discontinuous in time, we apply the order 1 rank-adaptive Euler method with parameters summarized in Table 2.
For quantification of the numerical error, we use the root mean square error of matrices (Frobenious norm)
To obtain a reference solution \({f}_{\text {ref}}\) we simply integrate (49) using RK4. As seen in Fig. 2, the numerical solution successfully tracks the overall shape of the reference solution’s rank over time. The numerical error also behaves as expected, decreasing as a steady-state is approached.
Numerical solution to the Fokker-Planck equation (55) in dimension \(d=2\) with initial condition (57) obtained using three distinct methods: rank-adaptive explicit Euler (33), two-step rank-adaptive Adams-Bashforth (39), and a reliable reference solution obtained by solving the ODE (2) corresponding to (55). The numerical results are obtained on a \(50\times 50\) spatial grid. The parameters for the step-truncation integrators we used in this example are detailed in Table 3
6.2 Fokker-Planck Equation
In this section we apply the proposed rank-adaptive step-truncation algorithms to a Fokker-Planck equation with space-dependent drift and constant diffusion, and demonstrate their accuracy in predicting relaxation to statistical equilibrium. As is well-known, the Fokker-Planck equation describes the evolution of the probability density function (PDF) of the state vector solving the Itô stochastic differential equation (SDE)
Here, \({\varvec{X}}_t\) is the d-dimensional state vector, \({\varvec{\mu }}({\varvec{X}}_t)\) is the d-dimensional drift, \(\sigma \) is a constant drift coefficient and \({\varvec{W}}_t\) is an d-dimensional standard Wiener process. The Fokker-Planck equation that corresponds to (54) has the form
where \(f_0({\varvec{x}})\) is the PDF of the initial state \({\varvec{X}}_0\). In our numerical demonstrations, we set \(\sigma = 2\),
where the functions \(\gamma (x)\), \(\xi (x)\), and \(\phi (x)\) are \(2 \pi \)-periodic. Also, in (56) \(x_{i+d}=x_i\). We solve (55) on the flat torus \(\Omega =[0,2\pi ]^d\) with dimension \(d=2\) and \(d=4\).
Fokker-Planck equation (55) in dimension \(d=2\) with initial condition (57). \(L^2(\Omega )\) error of rank-adaptive Euler forward, rank-adaptive AB2, and rank-adaptive Lie-Trotter [10] (with normal vector threshold \(10^{-4}\)) solutions with respect to the reference solution. The numerical results are obtained on a \(50\times 50\) spatial grid
Fokker-Planck equation (55) in dimension \(d=2\) with initial condition (57). Rank versus time for rank-adaptive step-truncation Euler forward, AB2, rank-adaptive Lie-Trotter with normal vector threshold \(10^{-4}\) [10], and reference numerical solutions. The numerical results are obtained on a \(50\times 50\) spatial grid. The reference solution rank was computed with a singular value tolerance of \(\varepsilon _\mathrm{tol}^{-12}\)
Marginal probability density function (59) obtained by integrating numerically the Fokker-Planck equation (55) in dimension \(d=4\) with initial condition (58) using two methods: rank-adaptive Euler forward and rank-adaptive AB2. The reference solution computed with a variable time step size RK4 method with absolute tolerance of \(10^{-14}\) computed on a grid with \(20^4=160000\) evenly-spaced points
6.3 Two-Dimensional Fokker-Planck Equation
Set \(d=2\) in (55) and consider the initial condition
where \(m_0\) is a normalization factor. Discretize (57) on a two-dimensional grid of evenly-spaced points and then truncate the initial tensor (matrix) within machine accuracy into HT format. Also, set \(\gamma (x) = \sin (x)\), \(\xi (x) = \cos (x)\), and \(\phi (x)=\exp (\sin (x)) + 1\) for the drift functions in (55). In Fig. 3, we plot the numerical solution of the Fokker-Planck equation (55) in dimension \(d=2\) corresponding to the initial condition (57). We computed our solutions with four different methods:
-
1
Rank-adaptive explicit Euler (33);
-
2
Two-step rank-adaptive Adams-Bashforth (AB) method (39);
-
3
Rank-adaptive tensor method with Lie-Trotter operator splitting integrator [10];
-
4
RK4 method applied to the ODE (2) corresponding to a full tensor product discretization of (55). We denote this reference solution as \(f_{\text {ref}}\).
The parameters we used for the rank-adaptive step-truncation methods 1. and 2. are summarized in Table 3. The steady state was determined for this computation by halting execution when \(\left\| \partial f_{\text {ref}}/\partial t\right\| _{L^2(\Omega )}\) was below the numerical threshold \(10^{-13}\). This occurs at approximately \(t \approx 24\) for the initial condition (57). The numerical results in Fig. 3 shows that the step-truncation methods listed above match all visual behavior of the reference solution. Observing Figs. 4 and 5, we note that while the rank-adaptive AB2 methods nearly doubles the digits of accuracy (in the \(L^2(\Omega )\) norm), only a modest increase in rank is required to achieve this gain in accuracy. This is because the rank in each adaptive step-truncation scheme is determined by the increment function \(\varvec{\varPhi }\) (which defines the scheme), the nonlinear operator \({\varvec{N}}\), and the truncation error threshold (which depends on \(\varDelta t\)). More precisely, the closer \({\varvec{\varPhi }}({{\varvec{N}}},{{\varvec{f}}},\varDelta t)\) is to the tangent space of the manifold \(\mathcal{H}_{{\varvec{r}}}\) at \({{\varvec{f}}}_k\), the less the rank will increase in next time step. In our demonstration, this occurs as the solution \({{\varvec{f}}}_k\) approaches steady state, since, as the rate at which the probability density evolves in time slows down, the quantity \(\left\| {\varvec{\varPhi }}({{\varvec{N}}},{{\varvec{f}}},\varDelta t)\right\| _2\) tends to zero. Consequently, \(\left\| ({{\varvec{I}}} - {\mathcal{P}_{{\varvec{g}}}}) {\varvec{\varPhi }}({{\varvec{N}}},{{\varvec{f}}},\varDelta t)\right\| _2\) will also tend towards zero since \({{\varvec{I}}} - {\mathcal{P}_{{\varvec{g}}}}\) is a bounded linear operator. For fixed \(\varDelta t\), this means that the rank increase conditions (46)–(48) will have a smaller likelihood of being triggered. As we shrink \(\varDelta t\), the truncation error requirements for consistency (46)–(48) become more demanding, and thus a higher solution rank is expected. In Figs. 4 and 5 we also see that the rank-adaptive tensor method with Lie-Trotter integrator proposed in [10] performs better on this problem than rank-adaptive step-truncation methods, especially when the solution approaches the steady state. However, it should be noted that the rank-adaptive method with operator splitting and normal vector control is considerably more involved to implement than the step-truncation methods, which are essentially slight modifications of a standard single-step or multi-step method. In Fig. 6 we demonstrate numerically the global error bound we proved in Theorem 1. The error scaling constant Q turns out to be \(Q=2\) for rank-adaptive AB2, \(Q=5\) for rank-adaptive midpoint, and \(Q=0.6\) for rank-adaptive Euler forward.
\(L^2(\Omega )\) error of numerical solutions to the Fokker-Planck equation (55) in dimension \(d=4\) with initial condition (58). The parameters we used for all rank-adaptive step-truncation methods are summarized in Table 4. The rank-adaptive Lie-Trotter method uses a threshold of \(10^{-2}\) for the PDE component normal to the tensor manifold (see [10])
Rank versus time for the numerical solutions of Fokker-Planck equation (55) in dimension \(d=4\) with initial condition (58) (left column: \(0\le t\le 6.25\), right column: \(0\le t\le 0.1\)). We truncate the reference solution to \(\varepsilon _\mathrm{tol}\) in HT format. The rank-adaptive Lie-Trotter method uses a threshold of \(10^{-2}\) for the PDE component normal to the tensor manifold (see [10])
6.4 Four-Dimensional Fokker-Planck Equation
Next, we present numerical results for the Fokker-Planck equation (55) in dimension \(d=4\). In this case, the best truncation operator (5) is not explicitly known. Instead, we use the step-truncation method (17), with truncation operator \({\mathfrak T}_r^{\text {SVD}}\) defined in (6) (see [14, 23] for more details). We set the initial condition as
where \(m_0\) is a normalization constant. Clearly, (58) can be represented exactly in a hierarchical Tucker tensor format provided we use an overall maximal tree rank of \(r_{0}=2L\). For our numerical simulations we choose \(L=10\). We change the drift functions slightly from the two-dimensional example we discussed in the previous section. Specifically, here we set \(\gamma (x) = \sin (x)\), \(\xi (x)=\exp (\sin (x)) + 1\), and \(\phi (x) = \cos (x)\) and repeat all numerical tests presented in Sect. 6.3, i.e., we run three rank-adaptive step-truncation simulations with different increment functions: one based on Euler forward (33) and one based AB2 (39). The parameters we used for these methods are summarized in Table 4.
For spatial discretization, we use the Fourier pseudo-spectral method with \(20^4 = 160000\) points. We emphasize that a matrix representing the discretized Fokker- Planck operator at the right hand side of (55) would be very sparse and require approximately 205 gigabytes in double precision floating point format. The solution vector requires 1.28 megabytes of memory (160000 floating point numbers in double precision). The HTucker format reduces these memory costs considerably. The large threshold solution of Fig. 9 is only 25 kilobytes when stored to disk using the HTucker Matlab software package [23]. The spatial differential operator for the Fokker-Planck equation can also be represented in HTucker format, and costs only 21 kilobytes. The storage savings are massive, so long as the rank is kept low. In Fig. 7, we plot a few time snapshots of the marginal PDF
we obtained by integrating (55) in time with rank-adaptive Euler forward and rank-adaptive AB2. In Fig. 8 we plot the error of step truncation solutions to the Fokker-Plank equation relative to the reference solution. In Fig. 9 we plot the solution rank versus time for all rank-adaptive step-truncation integrators summarized in Table 4. The results largely reflect those of the two dimensional domain. However, a notable difference is the abrupt change in rank. This is because the density function in this case relaxes to steady state fairly quickly. Numerically, the steady state is determined by halting execution when \(\left\| \partial f_{\text {ref}}/\partial t\right\| _2\) is below the numerical threshold \(10^{-8}\). This happens at approximately \(t \approx 6.25\) for the initial condition (58). As the rate of change in the density function becomes very small, we see that the rank no longer changes. This happens near time \(t=0.1\) (see Fig. 9).
The proposed rank-adaptive step-truncation methods can provide solutions with varying accuracy depending the threshold, i.e., the parameters summarized in Table 4. To show this, in Fig. 9 we compare the rank dynamics in the adaptive AB2 simulations obtained with small or large thresholds. Note that the solution computed with a large error threshold is rather low rank (see Fig. 9). We also see that the rank can be kept near the rank of the initial condition, if desired (again see Fig. 9). Finally, in Fig. 10 we plot the error \(L^2(\Omega )\) error at \(T=0.1\) versus \(\varDelta t\) for two different rank-adaptive step-truncation methods, i.e., Euler and AB2. It is that the order of AB2 is slightly larger than 2. This can be explained by noting that the error due to rank truncation is essentially a sum of singular values. Such singular values can be smaller than the truncation thresholds \({\varepsilon }_{{\varvec{\kappa }}}\) (\({\varvec{\kappa }}={\varvec{r}}, {\varvec{s}}, {\varvec{\alpha }}\), ...), suggesting the theoretical bounds may not be tight.
Data Availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
Code Availability
The code generated during the current study is available from the corresponding author on reasonable request.
Notes
In order to streamline our presentation, we will develop our theory using evenly-spaced temporal grids. A similar theory can be developed for grids with variable time step size.
As is well known, the scheme (10) includes all explicit Runge-Kutta methods [17]. For example, the Heun method (explicit RK2) takes the form (10) with
$$\begin{aligned} {\varvec{\varPhi }}({{\varvec{N}}},{{\varvec{f}}}_k,\varDelta t) = \frac{1}{2}\left[ {{\varvec{N}}}({{\varvec{f}}}_k)+{{\varvec{N}}}\left( {{\varvec{f}}}_k+\varDelta t {{\varvec{N}}}({{\varvec{f}}}_k)\right) \right] . \end{aligned}$$Explicit linear multistep methods can be expressed in a similar form by replacing the argument \({{\varvec{f}}}_k\) with an array \(\{{{\varvec{f}}}_k,{{\varvec{f}}}_{k-1},\ldots \}\) (see Sect. 4.3).
References
Absil, P.A., Malick, J.: Projection-like retractions on matrix manifolds. SIAM J. Optim. 22(1), 135–158 (2012)
Austin, W., Ballard, G., Kolda, T.G.: Parallel tensor compression for large-scale scientific data. In: IPDPS’16: Proceedings of the 30th IEEE International Parallel and Distributed Processing Symposium, pp. 912–922 (2016). https://doi.org/10.1109/IPDPS.2016.67
Boelens, A.M.P., Venturi, D., Tartakovsky, D.M.: Parallel tensor methods for high-dimensional linear PDEs. J. Comput. Phys. 375, 519–539 (2018)
Boelens, A.M.P., Venturi, D., Tartakovsky, D.M.: Tensor methods for the Boltzmann-BGK equation. J. Comput. Phys. 421, 109744 (2020)
Ceruti, G., Lubich, C.: An unconventional robust integrator for dynamical low-rank approximation. BIT Numerical Mathematics pp. 1–22 (2021)
Cheng, M., Hou, T.Y., Zhang, Z.: A dynamically bi-orthogonal method for time-dependent stochastic partial differential equations I: derivation and algorithms. J. Comput. Phys. 242, 843–868 (2013)
Chertkov, A., Oseledets, I.: Solution of the Fokker-Planck equation by cross approximation method in the tensor train format. Front. Artif. Intell. 4 (2021)
Da Silva, C., Herrmann, F.J.: Optimization on the hierarchical Tucker manifold-applications to tensor completion. Linear Algebra Appl. 481, 131–173 (2015)
Daas, H.A., Ballard, G., Benner, P.: Parallel algorithms for tensor train arithmetic. SIAM J. Sci. Comput. 44(1), C25–C53 (2022)
Dektor, A., Rodgers, A., Venturi, D.: Rank-adaptive tensor methods for high-dimensional nonlinear PDEs. J. Sci. Comput. 88(36), 1–27 (2021)
Dektor, A., Venturi, D.: Dynamically orthogonal tensor methods for high-dimensional nonlinear PDEs. J. Comput. Phys. 404, 109125 (2020)
Dektor, A., Venturi, D.: Dynamic tensor approximation of high-dimensional nonlinear PDEs. J. Comput. Phys. 437, 110295 (2021)
Dolgov, S., Khoromskij, B., Oseledets, I.: Fast solution of parabolic problems in the tensor train/quantized tensor train format with initial application to the Fokker-Planck equation. SIAM J. Sci. Comput. 34(6), A3016–A3038 (2012)
Grasedyck, L.: Hierarchical singular value decomposition of tensors. SIAM J. Matrix Anal. Appl. 31(4), 2029–2054 (2010)
Grasedyck, L., Löbbert, C.: Distributed hierarchical SVD in the hierarchical Tucker format. Numer. Linear Algebra Appl. 25(6), e2174 (2018)
Griebel, M., Li, G.: On the decay rate of the singular values of bivariate functions. SIAM J. Numer. Anal. 56(2), 974–993 (2018)
Hairer, E., Wanner, G., Norsett, S.P.: Solving ordinary differential equations I: Nonstiff problems, Springer Series in Computational Mathematics,, vol. 8, second revised edition. edn. Springer Berlin Heidelberg, Berlin, Heidelberg (1993)
Holtz, S., Rohwedder, T., Schneider, R.: On manifolds of tensors of fixed TT-rank. Numer. Math. 120(4), 701–731 (2012)
Kieri, E., Vandereycken, B.: Projection methods for dynamical low-rank approximation of high-dimensional problems. Comput. Methods Appl. Math. 19(1), 73–92 (2019)
Koch, O., Lubich, C.: Dynamical low-rank approximation. SIAM J. Matrix Anal. Appl. 29(2), 434–454 (2007)
Koch, O., Lubich, C.: Dynamical tensor approximation. SIAM J. Matrix Anal. Appl. 31(5), 2360–2375 (2010)
Kolda, T., Bader, B.W.: Tensor decompositions and applications. SIREV 51, 455–500 (2009)
Kressner, D., Tobler, C.: Algorithm 941: htucker - a Matlab toolbox for tensors in hierarchical Tucker format. ACM Trans. Math. Softw. 40(3), 1–22 (2014)
Lewis, A.S., Malick, J.: Alternating projections on manifolds. Math. Op. Res. 33(1), 216–234 (2008)
Liu, J., Liu, X., Ma, X.: First-order perturbation analysis of singular vectors in singular value decomposition. IEEE Trans. Signal Process. 56(7), 3044–3049 (2008)
Lubich, C., Oseledets, I.V.: A projector-splitting integrator for dynamical low-rank approximation. BIT Numer. Math. 54(1), 171–188 (2014)
Lubich, C., Oseledets, I.V., Vandereycken, B.: Time integration of tensor trains. SIAM J. Numer. Anal. 53(2), 917–941 (2015)
Lubich, C., Rohwedder, T., Schneider, R., Vandereycken, B.: Dynamical approximation by hierarchical Tucker and tensor-train tensors. SIAM J. Matrix Anal. Appl. 34(2), 470–494 (2013)
Marz, T., Macdonald, C.B.: Calculus on surfaces with general closest point functions. SIAM J. Numer. Anal. 50(6), 3303–3328 (2012)
Musharbash, E., Nobile, F., Zhou, T.: Error analysis of the dynamically orthogonal approximation of time dependent random PDEs. SIAM J. Sci. Comput. 37(2), A776–A810 (2015)
Opmeer, M.R.: Decay of singular values of the gramians of infinite-dimensional systems. In: 2015 European Control Conference (ECC), pp. 1183–1188 (2015). https://doi.org/10.1109/ECC.2015.7330700
Rodgers, A., Venturi, D.: Stability analysis of hierarchical tensor methods for time-dependent PDEs. J. Comput. Phys. 409, 109341 (2020)
Stewart, G.W.: Perturbation theory for the singular value decomposition. Tech. rep. (1998)
Uschmajew, A., Vandereycken, B.: The geometry of algorithms using hierarchical tensors. Linear Algebra Appl. 439(1), 133–166 (2013)
Venturi, D.: The numerical approximation of nonlinear functionals and functional differential equations. Phys. Rep. 732, 1–102 (2018)
Funding
This research was supported by the U.S. Air Force Office of Scientific Research (AFOSR) grant FA9550-20-1-0174 and by the U.S. Army Research Office (ARO) grant W911NF-18-1-0309.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was supported by the U.S. Army Research Office grant W911NF1810309, and by the U.S. Air Force Office of Scientific Research grant FA9550-20-1-0174.
Appendices
A Proof of Lemma 1
In this section, we present a proof of Lemma 1 which is specific to \(\mathcal{H}_{{\varvec{r}}}\). First, we start by constructing an open set centered about a point with known rank.
Lemma 3
Let \({{\varvec{f}}}\in \mathcal{H}_{{\varvec{r}}}\) be a point on the hierarchical Tucker manifold of constant rank. Let \({{\varvec{v}}}\in T_{{\varvec{f}}}\mathcal{H}_{{\varvec{r}}}\) be an arbitrary vector in the tangent plane of \(\mathcal{H}_{{\varvec{r}}}\) at \({\varvec{f}}\). Then there exists \(\eta >0\) such that for all \(\varepsilon \) satisfying \(0\le \varepsilon \le \eta \), we have \({{\varvec{f}}}+ \varepsilon {{\varvec{v}}} = {{\varvec{g}}} \in \mathcal{H}_{{\varvec{r}}}\). As a consequence, if \(U_{{\varvec{f}}}\subseteq T_{{\varvec{f}}}\mathcal{H}_{{\varvec{r}}}\) is a closed and bounded set containing the origin, then there exists an open subset \(V_{{\varvec{f}}}\subseteq U_{{\varvec{f}}}\) such that \({{\varvec{f}}} + {{\varvec{h}}}\in \mathcal{H}_{{\varvec{r}}}\), for all \({{\varvec{h}}}\in V_{{\varvec{f}}}\) .
Proof
First, consider a simpler problem, in which we have two matrices \({{\varvec{A}}},{{\varvec{B}}}\in {\mathbb R}^{n\times m}\), where \({\varvec{A}}\) is full column rank. Consider the function
Clearly, \(p(\eta )\) is a polynomial and thus smooth in \(\eta \). Moreover, \(p(0)\ne 0\) since \({{\varvec{A}}}\) is full column rank. Since p is smooth, there exists some \(\eta > 0\) such that \(p(\varepsilon )\ne 0\) for all \(\varepsilon \in [0,\eta ]\). Since the full-rank hierarchical Tucker manifold is defined via the full column rank constraints on an array of matrices corresponding to matricizations of the tensor [34], we can apply the principle above to every full column rank matrix associated with the tree, using addition of a point and a tangent as referenced in Proposition 3 of [8]. We have now proved the part one of the lemma where \(\eta \) is taken to be the minimum over the tree nodes. As for existence of an open set, suppose \(U_{{\varvec{f}}}\) is open and bounded. Now we apply the above matrix case to the boundary \(\partial U_{{\varvec{f}}}\), giving us a star shaped set \(S_{{\varvec{f}}}\subseteq U_{{\varvec{f}}}\). Letting \(V_{{\varvec{f}}} = S_{{\varvec{f}}}\setminus \partial S_{{\varvec{f}}}\) be the interior, completes the proof of the lemma. \(\square \)
We use the open set constructed above to prove smoothness using the same techniques as [29].
Proof
(Lemma 1) Let \({{\varvec{f}}} \in \mathcal{H}_{{\varvec{r}}} \subseteq {\mathbb R}^{n_1\times n_2 \times \cdots \times n_d}\). By Lemma 3, there exists an open norm-ball \(B({{\varvec{f}}}, \kappa )\) located at \({{\varvec{f}}}\) with radius \(\kappa >0\) so that
Let \(\mathcal{U}_{{\varvec{f}}} = \mathcal{H}_{{\varvec{r}}} \cap B({{\varvec{f}}}, \kappa )\) be a set which is open in the topology of \(\mathcal{H}_{{\varvec{r}}}\). Also, let \(({{\varvec{q}}}_{{{\varvec{f}}}}, {{\varvec{q}}}_{{{\varvec{f}}}}^{-1}(\mathcal{U}_{{{\varvec{f}}}}))\) be a local parametrization at \({{\varvec{f}}}\). For the parametrizing coordinates, we take an open subset \({{\varvec{q}}}_{{{\varvec{f}}}}^{-1}(\mathcal{U}_{{{\varvec{f}}}})=V_{{{\varvec{f}}}}\subseteq T_{{{\varvec{f}}}}\mathcal{H}_{{\varvec{r}}}\) of the tangent space embedded in \({\mathbb R}^{n_1\times n_2 \times \cdots \times n_d}\). This means that the parametrization \({{\varvec{q}}}_{{{\varvec{f}}}}\) takes tangent vectors as inputs and maps them into tensors in \(\mathcal{H}_{{\varvec{r}}}\), i.e.
Moreover, we assume that the coordinates are arranged in column major ordering as a vector. This allows for the Jacobian \(\partial {{{\varvec{q}}}}_{{{\varvec{f}}}} /\partial {{\varvec{v}}}\) to be a basis for the tangent space \(T_{{{\varvec{f}}}}\mathcal{H}_{{\varvec{r}}}\). Note that \(\partial {{\varvec{q}}}_{{{\varvec{f}}}} /\partial {{\varvec{v}}}\) is a \((n_1 n_2 \cdots n_d)\times \text {dim}(T_{{{\varvec{f}}}}\mathcal{H}_{{\varvec{r}}})\) matrix with real coefficients. Now, let \({{\varvec{M}}}({{\varvec{f}}})\) be a matrix of column vectors spanning the space orthogonal to \(T_{{\varvec{f}}}\mathcal{H}_{{\varvec{r}}}\) in \({\mathbb R}^{n_1\times n_2 \times \cdots \times n_d}\). Since the two linear spaces are disjoint, we have a local coordinate map for the ball \(B({{\varvec{f}}}, \kappa )\), given by
where \({\varvec{v}}\) is tangent and \({\varvec{g}}\) is normal (both column vectors). By construction,
is smooth in both \({\varvec{v}}\) and \({\varvec{g}}\). Therefore, we can take the total derivative on the embedded space and apply the chain rule to obtain the Jacobian of \({\mathfrak T}_{{\varvec{r}}}^{\text {best}}({{\varvec{f}}})\). Doing so, we have
where the symbol \([\cdot |\cdot ]\) denotes column concatenation of matrices, \(n^\perp \) is the dimension of the normal space \((T_{{\varvec{f}}}\mathcal{H}_{{\varvec{r}}})^\perp \), \({{\varvec{M}}}_i\) is the i-th column of \({\varvec{M}}\), and \({g}_i\) is the i-th component of \({\varvec{g}}\). We can take \({{\varvec{g}}} = {{\varvec{0}}}\) since the above expression extends smoothly from the embedding space onto \(\mathcal{H}_{{\varvec{r}}}\). Hence, the Jacobian of \(\mathfrak {T}^{\text {best}}\) is the solution to the linear equation
Since the right factor of the left hand side has a pair of orthogonal blocks, we can write the inverse using the pseudo-inverse of the blocks, i.e.,
The right hand side is the block concatenation of the rows of each pseudo-inverse. Plugging the above expression into (66), we find
which is exactly the expression for the orthogonal projection onto the tangent space [28]. This completes the proof. \(\square \)
B Step-truncation methods for matrix-valued ODEs on matrix manifolds with fixed rank
To make Lemma 1 concrete, in this Appendix we write down \({\mathfrak T}_{{\varvec{r}}}^{\text {best}}\) and its Jacobian \(\mathcal{P}_{{{\varvec{f}}}}\) for problems where \({{\varvec{f}}}\in \mathbb {R}^{n_1 \times n_2}\) is a matrix. In this situation, the tree rank \({\varvec{r}}\) is just a single integer r. One can see from the accuracy inequalities for best truncation proven in [14] that the \({\mathfrak T}_{r}^{\text {best}}\) is obtained from truncating the smallest \(\text {min}(n_1,n_2) - r\) singular values and singular vectors. For simplicity, we will write down the best truncation scheme for (2) using the Euler forward method. This gives
Assuming that we are fixing rank to be the same as the initial condition for all k, we have that \({\mathfrak T}_{r}^{\text {best}}({{\varvec{f}}}_k) = {{\varvec{f}}}_k\). Now we can apply SVD perturbation theory [25, 33] to express the best truncation operator in terms of a power series expansion in \(\varDelta t\). Representing our decomposition as the a tuple of matrices \(({{\varvec{\Sigma }}}_k,{{\varvec{Q}}}_k,{{\varvec{V}}}_k)\), where \({{\varvec{f}}}_k={{\varvec{Q}}}_k {{\varvec{\Sigma }}}_k{{\varvec{V}}}_k^\top \) and \({{\varvec{f}}}_{k+1}={{\varvec{Q}}}_{k+1} {{\varvec{\Sigma }}}_{k+1}{{\varvec{V}}}_{k+1}^\top \) is the reduced singular value decomposition, we have that
Here, \(\odot \) denotes is the element-wise (Hadamard) product of matrices, and the matrix
is skew-symmetric and stores information about the differences of the singular values. The \(\text {diag}(\cdot )\) operation zeros out all elements off of the diagonal. The tangent space projection operator is the coefficient of the \(\varDelta t\) terms. From here, we can see that the evolution equation corresponding to (69) is
By setting \({{\varvec{U}}} = {{\varvec{Q}}}{{\varvec{\Sigma }}}\) It can be verified that the pair \(({{\varvec{U}}},{{\varvec{V}}})\) satisfy the dynamically bi-orthogonal equations of [6]. It should be noted that this is not the only parametrization of the fixed-rank solution \({{\varvec{f}}} = {{\varvec{Q}}}{{\varvec{\Sigma }}}{{\varvec{V}}}^\top \). Of particular interest is the closely related projection method given by the DDO approximation
Which is equivalent to the SVD equations above in the sense that
as long as the singular values are distinct and the equation holds at \(t=0\). A comparison of methods for fixed rank initial value problems is given in [30].
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rodgers, A., Dektor, A. & Venturi, D. Adaptive Integration of Nonlinear Evolution Equations on Tensor Manifolds. J Sci Comput 92, 39 (2022). https://doi.org/10.1007/s10915-022-01868-x
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-022-01868-x