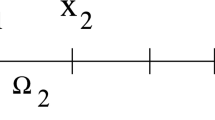Spectral Method and Spectral Element Method for Three Dimensional Linear Elliptic System: Analysis and Application

Abstract

In this paper, a least-squares spectral method and a non-conforming least-squares spectral element method for three dimensional linear elliptic system will be presented. Differentiability estimates and the main stability theorem for the proposed method are proven. Using the regularity estimate and the proposed stability estimates, we introduce a suitable preconditioner and show that the condition number of the preconditioned system is $O((\ln W)^2)$ (where W is degree of polynomials). Then we establish the error estimates of the proposed method. Specific numerical results based on linear elasticity problem, fourth order problem and sixth order problem are discussed to reflect the efficiency of the proposed method.

1 Introduction

In applied mathematics, engineering and scientific computing, there are many problems which attract much attention to compute the numerical solution of linear elliptic system. Linear elasticity problem, fourth order elliptic problem and sixth order elliptic problem etc. are some examples. In continuum mechanics, elasticity theory is widely used in continuum models. The main use of elasticity theory is that it describes the behaviour of the solid materials after deformation by external forces. In case of relatively small deformation, the theory of linear elasticity plays an important role. In linear elasticity, we get the stress–strain relation in form of the constitutive equation. One of the example of the elastic material is isotropic homogeneous where the constitutive equation is defined in any two terms of the six moduli (i.e. bulk modulus, Young’s modulus, Lamé’s first parameter, shear modulus, Poisson’s ratio and p-wave modulus). The other type of the elastic material is the isotropic inhomogeneous in which the inhomogeneity is imported from position-dependent Lamé’s parameters [28]. Some similar models can also get in the elasticity analysis of biomolecules [34,35,36].

In last few decades, spectral method is widely used to solve partial differential equations numerically. The main feature of spectral method is high accuracy. We refer to [3, 16, 29,30,31] for the analysis and various applications of spectral method/spectral element method.

Dutt et al. [8,9,10] introduced a nonconforming hp/spectral element for three dimensional elliptic problems with mixed Neumann and Dirichlet boundary conditions on non-smooth domains. This method is an exponentially accurate method for elliptic problems with mixed Neumann and Dirichlet boundary conditions on non-smooth domains. Dutt et al. [8,9,10] used a geometric mesh and the auxiliary map of the form $z=\ln \xi$ to remove the singularities at the corners and the edges. In the remaining part of the domain usual Cartesian coordinate system is used. Schötzau et al. [26, 27] presented hp-DGFEM for second-order elliptic problems in polyhedra and established exponential convergence for second-order elliptic problems in polyhedra.

Recently, Khan et al. [20] presented a spectral element method for scalar valued elliptic interface problem. In this paper, we introduce a least-squares spectral method and a fully non-conforming least-squares spectral element method (LSSEM) for three dimensional linear elliptic system. The proposed theory is valid for the coupled and the decoupled systems. Thus, we can use this theory to solve elasticity problem and higher order PDE such as fourth order and sixth order etc. In this paper, we derive the regularity result for 3-D linear elliptic systems which is main key ingredient to prove the stability theorem. We also discuss a priori error estimates for the proposed method. Specifically, the proposed formulation is based on minimizing the quadratic form which consists the sum of the squares of a weighted squared norm of the residuals in the partial differential equation, the sum of the residuals in the boundary conditions in fractional Sobolev norms and enforce the continuity along the inter-element boundary by adding a term which measures the sum of the squares of the jump in the function and its derivatives in fractional Sobolev norms. We refer to [6,7,8,9,10,11,12, 15, 17,18,19,20,21,22] for the analysis and application of LSSEM to solve various types of partial differential equation in 2-D and 3-D.

One of the popular least-square method is first order based formulation in which the higher order PDE is reduced into first order PDE system and it is solved by least-square principle. To solve the first order based least square formulation, we need to compute the stiffness matrix and the mass matrix. The proposed least-squares formulation is free from any kind of first order reformulation. For computing the solution, the normal equation is solved by preconditioned conjugate gradient method. The optimality of condition number for the preconditioned system is also shown. Integrals which are in the numerical scheme, are computed efficiently by Gauss-quadrature rule. One of the major advantage to use the proposed approach is that there is no need to compute the stiffness matrix and the mass matrix. For more details, we refer to Sect. 4. The proposed method is nonconforming in the sense that the discrete solution space of LSSEM is not subset of $\mathbf{H }^2(\varOmega )$ (The definition of $\mathbf{H }^2(\varOmega )$ is given in Sect. 2). This is the reason that we enforce the continuity along the inter-element boundary by adding a term which measures the sum of the square of the jump of the function and its derivatives in appropriate norms. The feature of the nonconformity in the proposed method is the main motivation to use parallelization. An error estimate in $H^1$ norm (if the solution is continuous across the interface) is proven. In case of analytic data, the proposed methods achieve exponential accuracy.

The rest of this paper is organized as follows. In Sect. 2, the required function spaces and the three dimensional elliptic system problem are presented. Section 3 is devoted to discuss the discretization of the domain and the stability estimate. In Sect. 4, we formulate the numerical scheme with the help of stability estimate. The preconditioning and parallelization issues are discussed in Sect. 5. Section 6 is devoted to derive error estimates. To validate the theory, specific numerical results are presented in Sect. 7.

2 Preliminaries and Problem Formulation

Let $\varOmega$ be an open bounded, simply-connected domain with boundary $\partial \varOmega =\varGamma$. Assume that the boundary $\varGamma$ is smooth ($C^2$ -regularity). We denote vectors in bold letters such as ${\varvec{x}}=(x_{1},x_{2},x_{3})$ and so on. By $\mathbf{H }^{m}(\varOmega )=({H}^{m}(\varOmega ))^3$ we denote the usual Sobolev space of integer order m furnished with the norm $||\cdot ||_{m, \varOmega }$ defined by,

$$\begin{aligned} ||\mathbf{u }({\varvec{x}})||_{m,\varOmega }^{2}=\sum _{j=1}^{3}\int _{\varOmega } \sum _{|{\varvec{\alpha }}|\le m}| \partial ^{{\varvec{\alpha }}} u_{j}|^{2}d{\varvec{x}}. \end{aligned}$$

where $\mathbf{u }=(u_1,u_2,u_3)^\top$, ${\varvec{\alpha }}=(\alpha _1,\alpha _2,\alpha _3), |{\varvec{\alpha }}|=\alpha _1+\alpha _2+\alpha _3,\; \partial ^{{\varvec{\alpha }}}(\cdot )=\partial ^{\alpha _1}_{x_1}\partial ^{\alpha _2}_{x_2}\partial ^{\alpha _3}_{x_3}(\cdot ) =(\cdot )_{x_{1}^{{\alpha }_{1}}x_{2}^{{\alpha }_{2}}x_{3}^{{\alpha }_{3}}}$ is the distributional (weak) derivative of u.

Let w be the two dimensional function defined on E, where E is either S (master square) or T (master triangle). Now we define fractional Sobolev space of order $\sigma$, where $0<\sigma <1$,

$$\begin{aligned} \Vert {w}\Vert _{\sigma ,E}^2 = \Vert {w}\Vert _{0,E}^2 + \int _E\int _E\frac{\left( {w}(x_1,x_2)-{w}(x^{\prime }_1, x^{\prime }_2)\right) ^2}{\left( (x_1-x^{\prime }_1)^2+(x_2-x^{\prime }_2)^2\right) ^{1+\sigma }} dx_1\,dx_2\,dx^{\prime }_1\,dx^{\prime }_2 \end{aligned}$$

However, if E is S then we prefer to use the equivalent norm [23],

$$\begin{aligned} \Vert {w}\Vert _{\sigma , \varGamma _l}^2&= \Vert {w}\Vert _{0,E}^2 + \int _{-1}^{1}\int _{-1}^{1}\int _{-1}^{1} \frac{({w}(x_1,x_2)-{w}(x^{\prime }_1, x_2))^2}{(x_1-x^{\prime }_1)^{1+2\sigma }}\,dx_1\,dx^{\prime }_1\,dx_2 \\&\quad +\,\int _{-1}^{1}\int _{-1}^{1}\int _{-1}^{1}\frac{({w}(x_1,x_2)-{w}(x_1, x^{\prime }_2))^2}{(x_2-x^{\prime }_2)^{1+2\sigma }}\,dx_2\,dx^{\prime }_2\,dx_1. \end{aligned}$$

Moreover,

$$\begin{aligned} \Vert {w}\Vert _{1+\sigma , \varGamma _{l}}^2 = \Vert {w}\Vert _{0,E}^2+\left\| \,\frac{\partial {w}}{\partial x_1} \,\right\| _{\sigma , E}^2+\left\| \,\frac{\partial {w}}{\partial x_2}\,\right\| _{\sigma , E}^2. \end{aligned}$$

2.1 Linear Elliptic System

Let $\mathbf{x }=(x_1,x_2,x_3), \mathbf{u }=(u_{1},u_{2},u_{3})^\top$, $\mathbf{F }=(F_1(\mathbf{x }),F_2(\mathbf{x }),F_3(\mathbf{x }))^\top$ and $\mathbf{g }=(g_1,g_2,g_3)^\top$ define as a point in a space, the solution vector, external force and boundary data. Consider the elliptic system problem

$$\begin{aligned} \mathbf {L} \mathbf{u }=-\nabla \cdot ({\mathcal {A}}\nabla \mathbf{u })+\mathbf{b }\cdot \nabla \mathbf{u }+c(\mathbf{x })\mathbf{u }&=\mathbf{F }\quad \text{ in }\;\varOmega , \end{aligned}$$

(2.1)

$$\begin{aligned} \mathbf{u }&=\mathbf{g }\quad \text{ on }\;\varGamma , \end{aligned}$$

(2.2)

where ${\mathcal {A}}=(\{a_{r,s}\}_{{r,s=1,2,3}})$ and $\mathbf{b }=(b_1,b_2,b_3)^\top$. The coefficients $a_{r,s}$, $b_{r}$, c satisfy the following assumptions:

• 1. The coefficients $\{a_{r,s}\}_{{r,s=1,2,3}}$, ${\{b_{r}\}_{r=1,2,3}}$, c are smooth.

• 2. The matrix ${\mathcal {A}}=(\{a_{r,s}\}_{{r,s=1,2,3}})$ is symmetric and postive definite.

• 3. $\mathbf{b }$ and c satisfy the following condition:

  $$\begin{aligned} -\frac{1}{2}\nabla \cdot \mathbf{b }(\mathbf{x })+c(\mathbf{x })\ge 0\quad \forall \mathbf{x }\in \varOmega . \end{aligned}$$

The problem (2.1)–(2.2) is well posed and its solution $\mathbf{u }$ satisfies the following regularity estimate.

Theorem 2.1

(Regularity Estimate) If $\mathbf{F }\in \mathbf{L }^{2}(\varOmega )$, and $\mathbf{g }\in \mathbf{H }^{\frac{3}{2}}(\varGamma )$, then the solution $\mathbf{u }\in \mathbf{H }^{2}(\varOmega )$ and

$$\begin{aligned} ||\mathbf{u }||_{2,\varOmega }\le C(||\mathbf{F }||_{0,\varOmega }+||\mathbf{g }||_{\frac{3}{2},\varGamma }), \end{aligned}$$

(2.3)

where C is a positive constant depending on the domain $\varOmega$ and the coefficients $\{a_{r,s}\}_{{r,s=1,2,3}}, \mathbf{b }$, c.

Proof

If $\mathbf{g }\in \mathbf{H }^{3/2}({\varGamma })$ then we can find $\bar{\mathbf{u }}\in \mathbf{H }^2(\varOmega )$ with $\bar{\mathbf{u }}=\mathbf{g }$ on $\varGamma$ and it satisfies

$$\begin{aligned} ||\bar{\mathbf{u }}||_{2,\varOmega }\le C_1 ||\mathbf{g }||_{3/2,\varGamma }, \end{aligned}$$

(2.4)

where $C_1$ is a positive constant. Using the trace theorem [23] gives

$$\begin{aligned} ||\mathbf{g }||_{3/2,\varGamma }\le C_2 ||\bar{\mathbf{u }}||_{2,\varOmega }, \end{aligned}$$

(2.5)

where $C_2$ is a positive constant. Let $\mathbf{w }=\mathbf{u }-\bar{\mathbf{u }}$, where $\mathbf{u }$ solves the problem (2.1)–(2.2). Then $\mathbf{w }$ satisfies the following problem

$$\begin{aligned} \mathbf{L }\mathbf{w }&=\mathbf{F }-\mathbf{L }\bar{\mathbf{u }}\quad \text{ in } \quad \varOmega \nonumber \\ \mathbf{w }&=0\quad \text{ on }\quad \varGamma . \end{aligned}$$

(2.6)

From [4, 5], we have

$$\begin{aligned} ||\mathbf{w }||_{2,\varOmega }&\le C_3(||\mathbf{F }-\mathbf{L }\bar{\mathbf{u }}||_{0,\varOmega }+||{\mathbf{w }}||_{1,\varOmega }), \end{aligned}$$

(2.7)

$$\begin{aligned}&\le C_3 ||\mathbf{F }||_{0,\varOmega }+C_4||\mathbf{g }||_{3/2,\varGamma }+C_3||\mathbf{w }||_{1,\varOmega }, \end{aligned}$$

(2.8)

where $C_3$ and $C_4$ are positive constants and $C_4=C_1 C_3$.

Next, we estimate $||\mathbf{w }||_{1,\varOmega }$. The weak formulation of the problem (2.6) reads: find $\mathbf{w }\in \mathbf{H }^{1}_{{0}}(\varOmega )$ such that

$$\begin{aligned} \int _{\varOmega }{\mathcal {A}} \nabla \mathbf{w }:\nabla \mathbf{v } d\mathbf{x }+\int _{\varOmega } ((\mathbf{b }\cdot \nabla \mathbf{w }) \cdot \mathbf{v }+c \mathbf{w }\cdot \mathbf{v }) d\mathbf{x }=\int _{\varOmega }{(\mathbf{F }-\mathbf{L }\bar{\mathbf{u }})}\cdot \mathbf{v }d\mathbf{x } \;\forall \mathbf{v }\in \mathbf{H }^1_0(\varOmega ), \end{aligned}$$

where ${\mathbb {A}}:{\mathbb {B}}=\sum _{i,j} {\tilde{a}}_{i,j}{\tilde{b}}_{i,j}$ with the matrices ${\mathbb {A}}=(\{{\tilde{a}}_{i,j}\}_{i,j=1,2,3})$ and ${\mathbb {B}}=(\{{\tilde{b}}_{i,j}\}_{i,j=1,2,3})$.

Using integration by parts gives

$$\begin{aligned} \int _{\varOmega }{\mathcal {A}} \nabla \mathbf{w }:{\nabla }\mathbf{v } d\mathbf{x }-\int _{\varOmega } (\mathbf{w }\mathbf{b }^\top :\nabla \mathbf{v }+(c-\nabla \cdot \mathbf{b }) \mathbf{w }\cdot \mathbf{v }) d\mathbf{x }&=\int _{\varOmega }(\mathbf{F }-\mathbf{L }\bar{\mathbf{u }})\cdot \mathbf{v }d\mathbf{x }\nonumber \\&\quad \forall \mathbf{v }\in \mathbf{H }^1_0(\varOmega ). \end{aligned}$$

(2.9)

Making specific choice $\mathbf{v }=\mathbf{w }$ and using the assumption of the coefficients and the Poincaré inequality, we have

$$\begin{aligned} ||\mathbf{w }||_{1,\varOmega }\le C_5(||\mathbf{F }||_{0,\varOmega }+||\mathbf{g }||_{3/2,\varGamma }), \end{aligned}$$

(2.10)

where $C_5$ is a positive constant. Combining (2.7) and (2.10) gives

$$\begin{aligned} ||\mathbf{w }||_{2,\varOmega }\le C_6 (||\mathbf{F }||_{0,\varOmega }+||\mathbf{g }||_{3/2,\varGamma }), \end{aligned}$$

(2.11)

for a positive constant $C_6>0$. Moreover, we have

$$\begin{aligned} ||\mathbf{u }||_{2,\varOmega }&\le C_7(||\mathbf{w }||_{2,\varOmega }+||\bar{\mathbf{u }}||_{2,\varOmega }),\nonumber \\&\le C(||\mathbf{F }||_{0,\varOmega }+||\mathbf{g }||_{3/2,\varGamma }), \end{aligned}$$

(2.12)

where $C_7$ and C are positive constants. $\square$

Remark 2.1

Throughout the paper positive constants depend either on the domain $\varOmega$ or the coefficients $\{a_{r,s}\}_{{r,s=1,2,3}}, \mathbf{b }$, c, or both.

3 Discretization and Stability Estimate

Assume that $\varOmega$ is a hexahedron in ${\mathbb {R}}^3$ with the boundary $\varGamma =\displaystyle {\cup }_{j=1}^{6}\varGamma _{j}$. Now, the domain $\varOmega$ is divided into a set of finite number of elements consisting of curvilinear hexahedrons, tetrahedrons and prisms (say) $\varOmega ^{1},\varOmega ^{2},\ldots ,\varOmega ^{L}$.

Define, Q as the bi-unit cube $Q=(-1,1)^3$. Now, we define the analytic map $M^{l}$ from Q to $\varOmega ^{l}$ [1, 8,9,10, 16]

$$\begin{aligned} x_1=X^{l}({\varvec{\lambda }}),\;\; \;x_2=Y^{l}({\varvec{\lambda }})\;\;\;\text{ and }\;\;\;x_3=Z^{l}({\varvec{\lambda }}),\; \end{aligned}$$

where, $l=1,\ldots ,L$ and ${\varvec{\lambda }}=(\lambda _1,\lambda _2,\lambda _3)$.

Let $\{{\tilde{u}}^{l}_{i}\}$ be the spectral element functions as the tensor product of polynomials of degree W in each variable $\lambda _{1},\lambda _{2}$ and $\lambda _{3}$ as follows

$$\begin{aligned} {\tilde{u}}_{i}^{l}({\varvec{\lambda }})=\sum _{r=0}^{W} \sum _{s=0}^{W}\sum _{t=0}^{W}\alpha ^{i}_{r,s,t} \lambda _{1}^{r}\lambda _{2}^{s} \lambda _{3}^{t}, \quad \forall i=1,2,3. \end{aligned}$$

Now, we define the spectral element functions $\{u^{l}_{1},u^{l}_{2},u^{l}_{3}\}_{l}$ on physical space $\varOmega ^{l}$

$$\begin{aligned} u^{l}_{1}({\varvec{x}})= {\tilde{u}}_{1}^{l}((M^{l})^{-1}),\;\; u^{l}_{2}({\varvec{x}})= {\tilde{u}}_{2}^{l}((M^{l})^{-1}),\;\;u^{l}_{3}({\varvec{x}})= {\tilde{u}}_{3}^{l}((M^{l})^{-1}). \end{aligned}$$

Let $\{{\mathcal {F}}_{u_{i}}\}$ be the spectral element representation of the function $u_{i}^l$ i.e.

$$\begin{aligned} \{{\mathcal {F}}_{u_{1}}\}=\left\{ \{{\tilde{u}}^{l}_{1}({\varvec{\lambda }})\}_{l}\right\} \,,\{{\mathcal {F}}_{u_{2}}\}=\left\{ \{{\tilde{u}}^{l}_{2}({\varvec{\lambda }})\}_{l}\right\} \,,\{{\mathcal {F}}_{u_{3}}\}=\left\{ \{{\tilde{u}}^{l}_{3}({\varvec{\lambda }})\}_{l}\right\} \,. \end{aligned}$$

Define $\{{\mathcal {F}}_{\mathbf{u }}\}$ as the the spectral element representation of whole system i.e.

$$\begin{aligned} \{{\mathcal {F}}_{\mathbf{u }}\}=\left\{ {\mathcal {F}}_{u_{1}},{\mathcal {F}}_{u_{2}},{\mathcal {F}}_{u_{3}}\right\} \,. \end{aligned}$$

The space of spectral element functions on Q is denoted by $S^{W}\{{\mathcal {F}}_{\mathbf{u }}\}$.

Remark 3.1

However, we discuss the theoretical results for the general polynomial. But we use the Legendre polynomial to solve the problem numerically. Thus, the spectral element functions $\{{\tilde{u}}^{l}_{i}\}$, defined on Q, are given as

$$\begin{aligned} {\tilde{u}}_{i}^{l}({\varvec{\lambda }})=\sum _{r=0}^{W} \sum _{s=0}^{W}\sum _{t=0}^{W}\alpha ^{i}_{r,s,t} L_r(\lambda _{1}) L_s(\lambda _{2}) L_t(\lambda _{3}), \quad \forall i=1,2,3, \end{aligned}$$

where $L_r(\cdot )$ represents the Legendre polynomial of degree r.

3.1 Stability Estimate

Define $\varOmega ^{l}$ as a typical element in $\varOmega$ with its faces $\{\varGamma _{j}^{l}\}_{1\le j\le 6}$. Then we have

$$\begin{aligned} \int _{\varOmega ^{l}} |\mathbf{L }\mathbf{u }|^{2} d{\varvec{x}}=\int _{Q}|{\mathcal {L}}\tilde{\mathbf{u }}^{l}|^{2} J^{l} d{\varvec{\lambda }}, \end{aligned}$$

where ${\mathcal {L}}$ is the differential operator $\mathbf{L }$ in ${\varvec{\lambda }}=(\lambda _1,\lambda _2,\lambda _3)$ coordinates and $J^{l}({\varvec{\lambda }})$ denotes the Jacobian of the mapping $M^{l}({\varvec{\lambda }})$ from Q to $\varOmega ^{l}$. Choosing ${\mathcal {L}}^{l}={\mathcal {L}} \sqrt{J^{l}}$, then

$$\begin{aligned} \int _{\varOmega ^{l}} |\mathbf{L }\mathbf{u }|^{2} d{\varvec{x}}=\int _{Q}|{\mathcal {L}}^{l}\tilde{\mathbf{u }}^{l}|^{2} d{\varvec{\lambda }}. \end{aligned}$$

Assume that $\varOmega ^m$ and $\varOmega ^n$ are two adjacent elements in the domain $\varOmega$ and $\varGamma _{j}^{m}$ be a face of $\varOmega ^m$ and $\varGamma _{k}^n$ be a face of $\varOmega ^n$ such that $\varGamma _{j}^m=\varGamma _{k}^n$ i.e. $\varGamma _{j}^m$ is a face common to both $\varOmega ^m$ and $\varOmega ^n$. Let $\left. {[u]}\right| _{\varGamma _{j}^{m}}$ denote the jump in u across the face $\varGamma _{j}^m$. We assume the face $\varGamma _{j}^m$ is the image of $\lambda _3=-1$ under the mapping $M^{m}$ which maps Q to $\varOmega ^{m}$ and also the image of $\lambda _{3}=1$ under the mapping $M^{n}$ which maps Q to $\varOmega ^{n}$. Then $\left. {[u]}\right| _{\varGamma _{j}^m}$ is a function of only $\lambda _1$ and $\lambda _2$. Moreover, $\varGamma _{j}^m$ is the image of the master square $S=(-1,1)^2$ under these mappings. However, the analysis remains valid if it is the image of T, the master triangle, too. By chain rule, it follows:

$$\begin{aligned} ({u}^{m}_i)_{x_k}=({\tilde{u}}_{i}^{m})_{\lambda _{1}} (\lambda _{1})_{x_k}+({\tilde{u}}_{i}^{m})_{\lambda _{2}} (\lambda _{2})_{x_k}+ ({\tilde{u}}_{i}^{m})_{\lambda _{3}} (\lambda _{3})_{x_k}, \end{aligned}$$

for $i,k=1,2,3$. Then we define the jump along the inter element boundaries as follows:

$$\begin{aligned} ||[\mathbf{u }]||_{0,{\varGamma _{j}^m}}^{2}&=||\tilde{\mathbf{u }}^{m}(\lambda _{1},\lambda _{2},-1) - \tilde{\mathbf{u }}^{n}(\lambda _{1},\lambda _{2},1)||_{0,{S}}^{2}\;\;\text{ and }\;\;\\ ||[(\mathbf{u })_{x_{k}}]||_{\frac{1}{2},{\varGamma _{j}^m}}^{2}&=||(\tilde{\mathbf{u }}^{m})_{x_{k}}(\lambda _{1},\lambda _{2},-1) - (\tilde{\mathbf{u }}^{n})_{x_{k}}(\lambda _{1},\lambda _{2},1)||_{\frac{1}{2},{S}}^{2}. \end{aligned}$$

Now along the boundary $\varGamma =\displaystyle {\cup }_{j=1}^{6}{\varGamma _{j}}$, let $\varGamma _{j}^{s}\subseteq \varGamma _{j}$ (for some j) be the image of $\lambda _{2}=1$ under the mapping $M^{m}$ which maps Q to $\varOmega ^{m}$. Then,

$$\begin{aligned} ||\mathbf{u }||_{0,\varGamma _{j}^{s}}^{2}+\left| \left| \frac{\partial \mathbf{u }}{\partial T}\right| \right| _{\frac{1}{2}, \varGamma _{j}^{s}}^{2}=||\tilde{\mathbf{u }}(\lambda _{1},1,\lambda _{3})||_{0,S}^{2} +\left| \left| \frac{\partial \tilde{\mathbf{u }}}{\partial T}(\lambda _{1},1,\lambda _{3})\right| \right| _{\frac{1}{2},S}^{2}, \end{aligned}$$

where $\frac{\partial \tilde{\mathbf{u }}}{\partial T}$ is tangential derivative of $\tilde{\mathbf{u }}$.

Now we define the quadratic form ${\mathcal {V}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\}) ={\mathcal {V}}^{W}(\{u_1^l,u_2^l,u_3^l\}_{l})$ of spectral element method by

$$\begin{aligned} {\mathcal {V}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})&={\mathcal {V}}^{W}_{residual}(\{{\mathcal {F}}_{\mathbf{u }}\})+{\mathcal {V}}^{W}_{jump}(\{{\mathcal {F}}_{\mathbf{u }}\})+{\mathcal {V}}^{W}_{boundary}(\{{\mathcal {F}}_{\mathbf{u }}\}) \end{aligned}$$

with

$$\begin{aligned} {\mathcal {V}}^{W}_{residual}(\{{\mathcal {F}}_{\mathbf{u }}\})&=\sum _{l=1}^{L}||({\mathcal {L}}^{l})\tilde{\mathbf{u }}^{l} ({\varvec{\lambda }})||^{2}_{0,Q},\\ {\mathcal {V}}^{W}_{jump}(\{{\mathcal {F}}_{\mathbf{u }}\})&=\sum _{\varGamma _{j}^l\subset \varOmega }\Bigg (||[\mathbf{u }]||^{2}_{0,\varGamma _{j}^l} +\sum _{\i =1}^{3}||[(\mathbf{u })_{x_i}]||^{2}_{1/2,\varGamma _{j}^l}\Bigg ),\\ {\mathcal {V}}^{W}_{boundary}(\{{\mathcal {F}}_{\mathbf{u }}\})&=\sum _{\varGamma _{j}^s\subseteq \varGamma }\Bigg (||\mathbf{u }||^{2}_{0,\varGamma _{j}^s}+\left| \left| \frac{\partial \mathbf{u }}{\partial T}\right| \right| ^{2}_{\frac{1}{2},\varGamma _{j}^s}\Bigg ). \end{aligned}$$

Remark 3.2

To define the quadratic form of spectral method, we just define the above quadratic form ${\mathcal {V}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})$ for $L=1$. Thus, ${\mathcal {V}}^{W}_{jump}(\{{\mathcal {F}}_{\mathbf{u }}\})$ disappears in the quadratic form ${\mathcal {V}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})$. Then the resulting quadratic form ${\mathcal {V}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})$ for spectral method is as follows:

$$\begin{aligned} {\mathcal {V}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})&= ||({\mathcal {L}})\tilde{\mathbf{u }} ({\varvec{\lambda }})||^{2}_{0,Q}+\sum _{j=1}^{6}\Bigg (||\mathbf{u }||^{2}_{0,{\varGamma _{j}}}+\left| \left| \frac{\partial \mathbf{u }}{\partial T}\right| \right| ^{2}_{\frac{1}{2},{\varGamma _{j}}}\Bigg ). \end{aligned}$$

(3.1)

Theorem 3.1

(Stability estimate) For W large enough there exists a constant $C>0$ such that

$$\begin{aligned} \sum _{l=1}^{L}||\tilde{\mathbf{u }}^{l}({\varvec{\lambda }})||^{2}_{2,Q}\le C(\ln W)^2 {\mathcal {V}}^{W} (\{{\mathcal {F}}_{\mathbf{u }}\}). \end{aligned}$$

(3.2)

Proof

From Lemma 3.1, there exists $\{\{\tilde{\mathbf{v }}^{l}({\varvec{\lambda }})\}_l\}$ such that $\mathbf{w }=\mathbf{u }+\mathbf{v }\in \mathbf{H }^{2}(\varOmega )$. Then, the well-known Minkowski inequality gives

$$\begin{aligned} \sum _{l=1}^{L}||\tilde{\mathbf{u }}^{l}({\varvec{\lambda }})||^{2}_{2,Q}&\le C\left( \sum _{l=1}^{L}||\tilde{\mathbf{u }}^{l}+\tilde{\mathbf{v }}^{l}||^{2}_{2,Q}+\sum _{l=1}^{L}||\tilde{\mathbf{v }}^{l}||^{2}_{2,Q}\right) . \end{aligned}$$

(3.3)

Applying the regularity result stated in Theorem 2.1 implies

$$\begin{aligned} \sum _{l=1}^{L}||\tilde{\mathbf{u }}^{l}({\varvec{\lambda }})||^{2}_{2,Q}&\le C\left( \sum _{l=1}^{L}||({\mathcal {L}}^{l})\tilde{\mathbf{u }}^{l}||^{2}_{2,Q}+||\mathbf{w }||_{\frac{3}{2},\varGamma }^{2} + \sum _{l=1}^{L}||\tilde{\mathbf{v }}^{l}||^{2}_{2,Q}\right) . \end{aligned}$$

(3.4)

Combining Lemmas 3.1 and 3.2 and (3.4) leads to the stated result (3.2). $\square$

3.2 Technical Estimates

Lemma 3.1

Let $\{{\mathcal {F}}_{\mathbf{u }}\}\in S^{W}$. Then there exists $\{{\mathcal {F}}_{\mathbf{v }}\}$ such that $\mathbf{v }^{l}\in \mathbf{H }^{2}(Q),l=1,2,\ldots ,L$ and $\mathbf{u }+\mathbf{v }\in \mathbf{H }^{2}(\varOmega )$. Moreover, the following estimate holds:

$$\begin{aligned} \sum _{l=1}^{L}||\tilde{\mathbf{v }}^{l}||^{2}_{\mathbf{2 },Q} \le C (\ln W)^2 {\mathcal {V}}^{W}_{jump}(\{{\mathcal {F}}_{\mathbf{u }}\}). \end{aligned}$$

(3.5)

Proof

Let $P_j, j=1,\ldots ,8$ denote nodes of cube Q. Then we do the first correction $\mathbf{r }^{l}({\varvec{\lambda }})=(r_{1}^l({\varvec{\lambda }}),r_{2}^l({\varvec{\lambda }}),r_{3}^l({\varvec{\lambda }}))^\top$ on the nodes of $Q=(M^{l})^{-1}(\varOmega ^{l})$. In addition, these node corrections satisfy the following condition:

$$\begin{aligned} (\mathbf{u }^{l}+\mathbf{r }^{l})(P_j)=&\bar{\mathbf{u }}(P_j)\;\;\text{ and }\;\;((\mathbf{u }^{l})_{x_k}+(\mathbf{r }^{l})_{x_k})(P_j)=\bar{\mathbf{u }}_{x_k}(P_j),\nonumber \\&\quad \forall j=1,\ldots ,8, \; k=1,2,3, \end{aligned}$$

(3.6)

where $\bar{\mathbf{u }}=({\bar{u}}_1,{\bar{u}}_2,{\bar{u}}_3)^\top$ is the averages of the values of $\mathbf{u }^{l}=({u}^{l}_1,{u}^{l}_2,{u}^{l}_3)^\top$ at $P_j$ over all elements which have $P_{j}$ as a node.

Assume that $\mathbf{r }^{l}({\varvec{\lambda }})=(r_{1}^l({\varvec{\lambda }}),r_{2}^l({\varvec{\lambda }}),r_{3}^l({\varvec{\lambda }}))^\top$ have the following values on nodes:

$$\begin{aligned} (r_{1}^l(P_j),r_{2}^l(P_j),r_{3}^l(P_j))^\top&=\mathbf{r }^{l}(P_j)=\mathbf{a }_j=(a_{j,1},a_{j,2},a_{j,3})^\top ,\\ ((r_{1}^l)_{x_1}(P_j),(r_{2}^l)_{x_1}(P_j),(r_{3}^l)_{x_1}(P_j))^\top&=(\mathbf{r }^{l})_{x_{1}}(P_j)=\mathbf{b }_j=(b_{j,1},b_{j,2},b_{j,3})^\top ,\\ ((r_{1}^l)_{x_2}(P_j),(r_{2}^l)_{x_2}(P_j),(r_{3}^l)_{x_2}(P_j))^\top&=(\mathbf{r }^{l})_{x_{2}}(P_j)=\mathbf{c }_j=(c_{j,1},c_{j,2},c_{j,3}),\\ ((r_{1}^l)_{x_3}(P_j),(r_{2}^l)_{x_3}(P_j),(r_{3}^l)_{x_3}(P_j))&=(\mathbf{r }^{l})_{x_{3}}(P_j)=\mathbf{d }_j=(d_{j,1},d_{j,2},d_{j,3})^\top , \end{aligned}$$

for $j=1,\ldots ,8$. We can compute $\mathbf{a }_j, \mathbf{b }_j, \mathbf{c }_j$ and $\mathbf{d }_j$ from (3.6). Then, it holds:

$$\begin{aligned} ||\mathbf{r }^{l}||_{{2},Q}^{2}=\sum _{k=1}^{3}||{r}^{l}_{k}||_{{2},Q}^{2}\le C\sum _{j=1}^{8}\sum _{k=1}^{3}\left( |a_{j,k}|^2+|b_{j,k}|^2+|c_{j,k}|^2+|d_{j,k}|^2\right) . \end{aligned}$$

(3.7)

Using (7.8) of [33] and the result in Appendix C of [14] gives

$$\begin{aligned} \sum _{l=1}^{L}||\mathbf {r} ^{l}||^{2}_{2,Q} =\sum _{l=1}^{L}\sum _{k=1}^{3}||{{r}}_{k}^{l}||^{2}_{2,Q}&\le C (\ln W)\, {\mathcal {V}}^W_{jump}(\{{\mathcal {F}}_{\mathbf{u }}\}). \end{aligned}$$

(3.8)

Now we define $({y}^{l}_{1}({\varvec{\lambda }}), {y}^{l}_{2}({\varvec{\lambda }}), {y}^{l}_{3}({\varvec{\lambda }}))^\top =\mathbf{y }^{l}({\varvec{\lambda }})=\mathbf{u }^{l}({\varvec{\lambda }})+\mathbf{r }^{l}({\varvec{\lambda }})=({u}_{1}^{l}({\varvec{\lambda }})+{r}^{l}_{1}({\varvec{\lambda }}),{u}_{2}^{l}({\varvec{\lambda }})+{r}^{l}_{2}({\varvec{\lambda }}),{u}_{3}^{l}({\varvec{\lambda }})+{r}^{l}_{3}({\varvec{\lambda }}))^\top$. Next, we do the second correction $\mathbf{s }^{l}({\varvec{\lambda }})=({s}^{l}_{1}({\varvec{\lambda }}),{s}^{l}_{2}({\varvec{\lambda }}),{s}^{l}_{3}({\varvec{\lambda }}))$ on the sides of $Q=(M^{l})^{-1}(\varOmega ^{l})$. Let $\mathbf{t }$ be a point of a side $I_j$ of $Q=(M^{l})^{-1}(\varOmega ^{l})$ then

$$\begin{aligned} (\mathbf{y }^{l}+\mathbf{s }^{l})(\mathbf{t })&=\bar{\mathbf{y }}(\mathbf{t }),\;\;\text{ and }\;\;((\mathbf{y }^{l})_{x_i}+(\mathbf{s }^{l})_{x_i})(\mathbf{t })=\bar{\mathbf{y }}_{x_i}(\mathbf{t }),\;\text{ for }\;i=1,2,3, \end{aligned}$$

(3.9)

where each component ${\bar{y}}_k (k=1,2,3)$ of $\bar{\mathbf{y }}(\mathbf{t })=({\bar{y}}_1(\mathbf{t }),{\bar{y}}_2(\mathbf{t }),{\bar{y}}_3(\mathbf{t }))^\top$ represents the averages of the values of ${y}^{l}_k (k=1,2,3)$ at $\mathbf{t }$ over all elements which have $I_{j}$ as a side. In addition, $s^{l}_{j}(\mathbf{t })=0 \;(j=1,2,3)$ if $\mathbf{t }$ is a node of Q. Furthermore, we have

$$\begin{aligned} ||\mathbf{s }^{l}||_{{2},Q}^{2}=\sum _{k=1}^{3}||{s}^{l}_{k}||_{{2},Q}^{2}\le C\sum _{j=1}^{12}\sum _{k=1}^{3}\left( ||s^{l}_{k}||^2_{0,I_j}+\sum _{i=1}^{3}||(s^{l}_{k})_{x_i}||^2_{0,I_j}\right) . \end{aligned}$$

(3.10)

Using Lemma 7.11 of [33] (or Lemma 5.3 of [24]) in (3.10) implies

$$\begin{aligned} \sum _{l=1}^{L}||\mathbf {s} ^{l}||^{2}_{\mathbf{2 },Q} =\sum _{l=1}^{L}\sum _{k=1}^{3}||{{s}}_{k}^{l}||^{2}_{2,Q}&\le C (\ln W)\,{\mathcal {V}}^W_{jump}(\{{\mathcal {F}}_{\mathbf{u }}\}). \end{aligned}$$

(3.11)

Next, we define $({z}^{l}_{1}({\varvec{\lambda }}), {z}^{l}_{2}({\varvec{\lambda }}), {z}^{l}_{3}({\varvec{\lambda }}))=\mathbf {z} ^{l}({\varvec{\lambda }})=\mathbf{u }^{l}({\varvec{\lambda }})+\mathbf{r }^{l}({\varvec{\lambda }})+\mathbf{s }^{l}({\varvec{\lambda }})=({u}_{1}^{l}({\varvec{\lambda }})+{r}^{l}_{1}({\varvec{\lambda }})+{s}_{1}^{l}({\varvec{\lambda }}),{u}_{2}^{l}({\varvec{\lambda }})+{r}^{l}_{2}({\varvec{\lambda }})+{s}_{2}^{l}({\varvec{\lambda }}),{u}_{3}^{l}({\varvec{\lambda }})+{r}^{l}_{3}({\varvec{\lambda }})+{s}_{3}^{l}({\varvec{\lambda }}))$. Then we do the third correction $\mathbf {f} ^{l}=({{f}}^{l}_{1},{{f}}^{l}_{2},{{f}}^{l}_{3})$ on the face of cube $Q=(M^{l})^{-1}(\varOmega ^{l})$ such that $f^{l}_{j}=0 \;(j=1,2,3)$ for all sides and nodes of $Q=(M^{l})^{-1}(\varOmega ^{l})$, and ${f}^{l}_{j}\in H^{2}(Q)$ for all l and j. Let

$$\begin{aligned} {{f}}^{l}_{j}|_{F_1}&={\mathcal {E}}_{1,j}=\frac{1}{2}({{z}}^{l}_{j}-{{z}}^{m}_{j})|_{F_1},\nonumber \\ ({f}^{l}_{j})_{x_1}|_{F_1}&={\mathcal {F}}_{1,j}=\frac{1}{2}({{z}}^{l}_{j}-{{z}}^{m}_{j})_{x_1}|_{F_1},\nonumber \\ ({f}^{l}_{i})_{x_2}|_{F_1}&={\mathcal {G}}_{1,j}=\frac{1}{2}({{z}}^{l}_{j}-{{z}}^{m}_{j})_{x_2}|_{F_1},\nonumber \\ ({f}^{l}_{j})_{x_3}|_{F_1}&={\mathcal {H}}_{1,j}=\frac{1}{2}({{z}}^{l}_{j}-{{z}}^{m}_{j})_{x_3}|_{F_1}, \end{aligned}$$

(3.12)

for $j=1,2,3$, where $F_1$ denotes the common face of $Q=(M^{l})^{-1}(\varOmega ^{l})$ and $Q=(M^{m})^{-1}(\varOmega ^{m})$. In same manner, we can define ${\mathcal {E}}_{k,j}, {\mathcal {F}}_{k,j}, {\mathcal {G}}_{k,j}$ and ${\mathcal {H}}_{k,j}$ for the remaining face $k=2,\ldots ,6$. If faces ${F}_{j}\subseteq \varGamma _j, j=1,\ldots ,6$, then ${\mathcal {E}}_{k,j}, {\mathcal {F}}_{k,j}, {\mathcal {G}}_{k,j}$ and ${\mathcal {H}}_{k,j}$ are defined to be identically zero. Now we estimate the following term

$$\begin{aligned} \int _{-1}^{1}\int _{0}^{1}&\frac{ |(\partial _{\lambda _2}{\mathcal {E}}_{1,j})(1-t,-1,\lambda _3)-{\mathcal {G}}_{2,j}(1,-1+t,\lambda _3)|^2}{t}d\lambda _3 dt\\&\le C\left\{ \int _{-1}^{1}\int _{0}^{1}\frac{ |(\partial _{\lambda _2}{\mathcal {E}}_{1,j})(-1+t,-1,\lambda _3)|^2}{t}d\lambda _3 dt\right. \\&\quad \left. + \int _{-1}^{1}\int _{0}^{1}\frac{ |{\mathcal {G}}_{2,j}(-1,-1-t,\lambda _3)|^2}{t}d\lambda _3 dt\right\} . \end{aligned}$$

Applying Theorem 4.79 and Theorem 4.82 of [25] gives

$$\begin{aligned} \int _{-1}^{1}\int _{0}^{1}&\frac{ |(\partial _{\lambda _2}{\mathcal {E}}_{1,j})(1-t,-1,\lambda _3)-{\mathcal {G}}_{2,j}(1,-1+t,\lambda _3)|^2}{t}d\lambda _3 dt\\&\le C (\ln W)^2(||\partial _{\lambda _2}{\mathcal {E}}_{1,j}||_{1/2,\varGamma _{j}^l}+||{\mathcal {G}}_{2,j}||_{1/2,\varGamma _{j}^l}). \end{aligned}$$

Similarly, we can prove estimates for all the terms given in Theorem 5.2 of [2]. Then, it holds:

$$\begin{aligned} \sum _{l=1}^{L}||\mathbf{z }^{l}||^{2}_{2,Q} =\sum _{l=1}^{L}\sum _{k=1}^3||z_{k}^{l}||^{2}_{2,Q}&\le C (\ln W)^2\,{\mathcal {V}}^W_{jump}(\{{\mathcal {F}}_{\mathbf{u }}\}). \end{aligned}$$

(3.13)

Finally, we define $({v}^{l}_{1}({\varvec{\lambda }}), {v}^{l}_{2}({\varvec{\lambda }}), {v}^{l}_{3}({\varvec{\lambda }}))^\top =\mathbf{v }^{l}_{i}({\varvec{\lambda }})=\mathbf{r }^{l}({\varvec{\lambda }})+\mathbf{s }^{l}({\varvec{\lambda }})+\mathbf{z }^{l}({\varvec{\lambda }})=({r}_{1}^{l}({\varvec{\lambda }})+{s}^{l}_{1}({\varvec{\lambda }})+{z}_{1}^{l}({\varvec{\lambda }}),{r}_{2}^{l}({\varvec{\lambda }})+{s}^{l}_{2}({\varvec{\lambda }})+{z}_{2}^{l}({\varvec{\lambda }}),{r}_{3}^{l}({\varvec{\lambda }})+{s}^{l}_{3}({\varvec{\lambda }})+{z}_{3}^{l}({\varvec{\lambda }}))^\top$. Then, combining (3.8), (3.11) and (3.13) leads to the stated result. $\square$

Lemma 3.2

Let $\mathbf{w }=\mathbf{u }+\mathbf{v }\in H^{2}(\varOmega )$. Here $\{{\mathcal {F}}_{\mathbf{u }}\}\in S^{W}$ and $\{{\mathcal {F}}_{\mathbf{v }}\}$ is as defined in Lemma 3.1. Then the estimate

$$\begin{aligned} ||\mathbf{w }||_{\frac{3}{2},\varGamma }^{2} \le C(\ln W)^2&\Big ({\mathcal {V}}^{W}_{jump}(\{{\mathcal {F}}_{\mathbf{u }}\}) +{\mathcal {V}}^{W}_{boundary}(\{{\mathcal {F}}_{\mathbf{u }}\})\Big ). \end{aligned}$$

(3.14)

holds. Here $||\mathbf{v }||_{3/2,\varGamma _{j}^s}^{2}=\inf _{\mathbf{q }|_{\varGamma _{j}^s}=\mathbf{v }}\{||\mathbf{q }||_{H^{2}(Q)}\}$ is as defined in [14].

Proof

Using Lemma 3.1, we can find $\{{\mathcal {F}}_{\mathbf{v }}\}$ such that $\mathbf{w }=\mathbf{u }+\mathbf{v }\in H^{2}(\varOmega )$. From Minkowski inequality, we obtain

$$\begin{aligned} ||\mathbf{w }||_{{\frac{3}{2}},\varGamma }^{2}&\le C\sum _{\varGamma _{j}^s\subseteq \varGamma }||\mathbf{u }+\mathbf{v }||_{{\frac{3}{2}},\varGamma _{j}^s}^{2}\le C\sum _{\varGamma _{j}^s\subseteq \varGamma }(||\mathbf{u }||_{{\frac{3}{2}},\varGamma _{j}^s}^2+||\mathbf{v }||_{{\frac{3}{2}},\varGamma _{j}^s}^2). \end{aligned}$$

(3.15)

Applying the trace theorem of Sobolev space implies

$$\begin{aligned} ||\mathbf{w }||_{\frac{3}{2},\varGamma }&\le C\Big ({\mathcal {V}}^W_{boundary}(\{{\mathcal {F}}_{\mathbf{u }}\}) +\sum _{l=1}^{L}||\tilde{\mathbf{v }}^{l}||^{2}_{\mathbf{2 },Q}\Big ). \end{aligned}$$

(3.16)

Using Lemma 3.1 in (3.16) gives the desired result. $\square$

4 Numerical Scheme

Let $\mathbf{F }=(F_{1},F_{2},F_{3})^\top$ and $\tilde{\mathbf{F }}=({\tilde{F}}_{1},{\tilde{F}}_{2},{\tilde{F}}_{3})^\top$. Assume that $J^{l}({\varvec{\lambda }})$ be the Jacobian of the mapping $M^{l}({\varvec{\lambda }})$ from Q to $\varOmega ^l$. Then

$$\begin{aligned} {{\tilde{F}}}_{k}({\varvec{\lambda }})=F_{k}(M^{l}({\varvec{\lambda }}))\;\; \text{ and }\;\;{{\tilde{F}}}^{l}_{k}({\varvec{\lambda }})={{\tilde{F}}}_{k}({\varvec{\lambda }})\sqrt{J^{l}({\varvec{\lambda }})}, \end{aligned}$$

for $k=1,2,3$.

In same manner, we define $\mathbf{u }=(u_{1},u_{2},u_{3})^\top$. Then the boundary condition $(u_1,u_2,u_3)^\top =\mathbf{u }=\mathbf{g }$ on $\varGamma$. Let $\varGamma _j\cap \partial \varOmega ^{m}$ denotes as the image of the mapping $M^{m}$ of Q onto $\varOmega ^{m}$ corresponding to the side $\lambda _{1}=1$ and

$$\begin{aligned} (h^{m}_{1}(\lambda _{2},\lambda _{3}),h^{m}_{2}(\lambda _{2},\lambda _{3}),h^{m}_{3}(\lambda _{2},\lambda _{3}))=\mathbf{h }^{m}(\lambda _{2},\lambda _{3})\; {:=}\, \mathbf{g }(M^{m}(1,\lambda _{2},\lambda _{3}) \end{aligned}$$

for $-1\le \lambda _{2},\lambda _{3}\le 1$, where $\mathbf{g }(M^{m}({\tilde{\lambda }}) )=({g}_1(M^{m}({\tilde{\lambda }}) ),{g}_2(M^{m}({\tilde{\lambda }} ),{g}_3(M^{m}({\tilde{\lambda }}) ))$ with ${\tilde{\lambda }}=(1,\lambda _2,\lambda _3)$.

Define the functional

$$\begin{aligned} {\mathcal {R}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})&={\mathcal {R}}^{W}_{residual}(\{{\mathcal {F}}_{\mathbf{u }}\})+{\mathcal {R}}^{W}_{jump}(\{{\mathcal {F}}_{\mathbf{u }}\})+{\mathcal {R}}^{W}_{boundary}(\{{\mathcal {F}}_{\mathbf{u }}\}) \end{aligned}$$

with

$$\begin{aligned} {\mathcal {R}}^{W}_{residual}(\{{\mathcal {F}}_{\mathbf{u }}\})&=\sum _{l=1}^{L}||({\mathcal {L}}^{l})\tilde{\mathbf{u }}^{l} ({\varvec{\lambda }})-{\tilde{\mathbf{F }}^{l}}({\varvec{\lambda }})||^{2}_{0,Q},\\ {\mathcal {R}}^{W}_{jump}(\{{\mathcal {F}}_{\mathbf{u }}\})&=\sum _{\varGamma _{j}^l\subset \varOmega }\Bigg (||[\mathbf{u }]||^{2}_{0,\varGamma _{j}^l} +\sum _{\iota =1}^{3}||[(\mathbf{u })_{x_\iota }]||^{2}_{1/2,\varGamma _{j}^l}\Bigg ),\\ {\mathcal {R}}^{W}_{boundary}(\{{\mathcal {F}}_{\mathbf{u }}\})&=\sum _{\varGamma _{j}^s\subseteq \varGamma }\Bigg (||\mathbf{u }-\mathbf{h }^{m}||^{2}_{0,\varGamma _{j}^s}+\left| \left| \left( \frac{\partial \mathbf{u }}{\partial T}\right) -\left( \frac{\partial \mathbf{h }^{m}}{\partial T}\right) \right| \right| ^{2}_{\frac{1}{2},\varGamma _{j}^s}\Bigg ). \end{aligned}$$

Remark 4.1

To define the numerical scheme for spectral method, we just define the above functional ${\mathcal {R}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})$ for $L=1$. Thus, ${\mathcal {R}}^{W}_{jump}(\{{\mathcal {F}}_{\mathbf{u }}\})$ disappears in the functional ${\mathcal {R}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})$. Then the resulting quadratic form ${\mathcal {R}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})$ for spectral method is as follows:

$$\begin{aligned} {\mathcal {R}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})&= ||({\mathcal {L}})\tilde{\mathbf{u }} ({\varvec{\lambda }})-{\tilde{\mathbf{F }}}({\varvec{\lambda }})||^{2}_{0,Q}+\sum _{j=1}^{6}\Bigg (||\mathbf{u }-\mathbf{h }||^{2}_{0,{\varGamma _{j}}}+\left| \left| \frac{\partial \mathbf{u }}{\partial T}-\left( \frac{\partial \mathbf{h }}{\partial T}\right) \right| \right| ^{2}_{\frac{1}{2},{\varGamma _{j}}}\Bigg ). \end{aligned}$$

(4.1)

Our numerical scheme may be written as follows:

We find${\mathcal {F}}_{\mathbf{z }}\in {{\mathcal {S}}}^{W}$which minimizes the functional${\mathcal {R}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})$over all${\mathcal {F}}_{\mathbf{u }}\in {{\mathcal {S}}}^{W}$, where${{\mathcal {S}}}^{W}$is the space of spectral element functions${\mathcal {F}}_{\mathbf{u }}$.

4.1 Symmetric Formulation

Our method is a least-squares method. Thus, we solve the normal equation using the preconditioned conjugate gradient method (PCGM). Assume that the normal equations be

$$\begin{aligned} A^TAU=A^TG. \end{aligned}$$

Define

$$\begin{aligned} U^{W}_{1;(W+1)^2k+(W+1)i+j+1}&={\tilde{u}}_{1}(\lambda _{1,i}^W,\lambda _{2,j}^W,\lambda _{3,k}^W),\;\;\text{ for }\;0\le i,j,k\le W,\\ U^{W}_{2;(W+1)^2k+(W+1)i+j+1}&={\tilde{u}}_{2}(\lambda _{1,i}^W,\lambda _{2,j}^W,\lambda _{3,k}^W),\;\;\text{ for }\;0\le i,j,k\le W,\\ U^{W}_{3;(W+1)^2k+(W+1)i+j+1}&={\tilde{u}}_{3}(\lambda _{1,i}^W,\lambda _{2,j}^W,\lambda _{3,k}^W),\;\;\text{ for }\;0\le i,j,k\le W, \end{aligned}$$

and

$$\begin{aligned} U^{2W}_{1;(W+1)^2k+(W+1)i+j+1}&={\tilde{u}}_{1}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W},\lambda _{3,k}^{2W}),\;\;\text{ for }\;0\le i,j,k\le 2W,\\ U^{2W}_{2;(W+1)^2k+(W+1)i+j+1}&={\tilde{u}}_{2}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W},\lambda _{3,k}^{2W}),\;\;\text{ for }\;0\le i,j,k\le 2W,\\ U^{2W}_{3;(W+1)^2k+(W+1)i+j+1}&={\tilde{u}}_{3}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W},\lambda _{3,k}^{2W}),\;\;\text{ for }\;0\le i,j,k\le 2W. \end{aligned}$$

Let $\mathbf{U }^W$ and $\mathbf{U }^{2W}$ be denoted as

$$\begin{aligned} \mathbf{U }^{W}=\begin{bmatrix} U^{W}_{1} \\ U^{W}_{2} \\ U^{W}_{3} \end{bmatrix}\quad \text{ and }\quad \mathbf{U }^{2W}=\begin{bmatrix} U^{2W}_{1} \\ U^{2W}_{2} \\ U^{2W}_{3} \end{bmatrix}. \end{aligned}$$

Note that we use Gauss–Lobatto–Legendre (GLL) quadrature formula to compute the integrals given in the minimization formulation. The details regarding computation of numerical scheme is discussed in “Appendix”. Finally, we obtain the following representation of the minimization formulation for each element:

$$\begin{aligned} (V_{\alpha }^{2W})^T O_{\alpha }^{2W}\quad \text{ for }\;\alpha =1,2,3, \end{aligned}$$

where $O_{\alpha }^{2W}$ is a $(2W+1)^3$ vector. Furthermore, there exist matrices $G^W_{\alpha }$, where $\alpha =1,2,3$, such that

$$\begin{aligned} V_{1}^{2W}=G^{W}_1V_{1}^{W}, V_{2}^{2W}=G^{W}_2V_{2}^{W}\; \text{ and }\;V_{3}^{2W}=G^{W}_3V_{3}^{W}. \end{aligned}$$

Then we obtain

$$\begin{aligned} (V_{\alpha }^{2W})^T O_{\alpha }^{2W}=(V_{\alpha }^{W})^T ((G^W_{\alpha })^T O_{\alpha }^{2W})\quad \text{ for }\;\alpha =1,2,3. \end{aligned}$$

Assume that $\gamma _{l}^{W}$ be the normalizing factors which are used to compute the discrete Legendre transform as

$$\begin{aligned} \gamma _{l}^{W}={\left\{ \begin{array}{ll}(l+\frac{1}{2})^{-1}, &{}\text{ if }\;l<W,\\ \frac{2}{W}, &{}\text{ if }\;l=W.\end{array}\right. } \end{aligned}$$

Define $\{O_{\alpha ;i,j,k}\}_{0\le i,j,k\le 2W}, \alpha =1,2,3$ as $O_{\alpha ;i,j,k}= O^{2W}_{\alpha ; k(2W+1)^2+j(2W+1)+i}$.

• 1. Define $O_{\alpha ;i,j,k}\leftarrow O_{\alpha ;i,j,k}/w^{2W}_i w^{2W}_j w^{2W}_k$.

• 2. Compute $\{\varTheta _{\alpha ;i,j,k}\}_{0\le i,j,k\le 2W}, \alpha =1,2,3$ the Legendre transform of $\{O_{\alpha ;i,j,k}\}_{ i,j,k}$. Then

  $$\begin{aligned} \varTheta _{\alpha ;i,j,k}\leftarrow \gamma _{i}^{2W}\gamma _{j}^{2W}\gamma _{k}^{2W}\varTheta _{\alpha ;i,j,k}. \end{aligned}$$

• 3. Compute $\theta _{\alpha ;i,j,k}\leftarrow \varTheta _{\alpha ;i,j,k}/\gamma _{i}^{W}\gamma _{j}^{W}\gamma _{k}^{W},\;0\le i,j,k\le W$.

• 4. Compute $\varLambda _{\alpha }$, the inverse Legendre transform of $\theta _{\alpha }$. Then

  $$\begin{aligned} \varLambda _{\alpha ;i,j,k}\leftarrow w^{W}_i w^{W}_j w^{W}_k\varLambda _{\alpha ;i,j,k} \end{aligned}$$

• 5. Define a vector $J_{\alpha }, \alpha =1,2,3$ which is of dimension $(W+1)^3$ as

  $$\begin{aligned} J_{\alpha ; k(W+1)^2+j(W+1)+i}=\varLambda _{\alpha ;i,j,k}. \end{aligned}$$

Hence, $J_\alpha =(G^W_{\alpha })^T O^{2W}_\alpha , \alpha =1,2,3$. This gives us $A^{T}(G-AU)$.

Remark 4.2

Note that the system corresponding ${\mathcal {R}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})$ is overdetermined because our approach is least-square. Let A, G and U be the $m\times n$ matrix with $m>n$, $m\times 1$ vector, and $n\times 1$ vector, respectively. Thus $A^T(G-AU)$ becomes $n\times 1$ vector and $(G-AU)$ becomes $m\times 1$ vector. It is clear from our algorithm that we don’t need to compute the stiffness matrix and the mass matrix to calculate the $A^T(G-AU)$. The memory of the storing $A^{T}(G-AU)$ is less compare to store $(G-AU)$. Hence, the proposed method is cheap and efficient to compute the residual in comparison of $h-p$ finite element method. For more details, we refer to [13, 32]. Specifically, the comparison between $h-p$ fem and LSSEM for $2-D$ elliptic problems is discussed in Section 5 in [32]. The similar comparison also holds for $3-D$ elliptic problems.

5 Preconditioning and Parallelization

First, we define the quadratic form ${\mathcal {U}}^{W} (\{{\mathcal {F}}_{\mathbf{u }}\})$ by

$$\begin{aligned} {\mathcal {U}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})=\sum _{l=1}^{L}||{\mathbf{u }}^{l}||^{2}_{\mathbf{2 },Q} =\sum _{l=1}^{L}\sum _{k=1}^{3}||{{u}}_{k}^{l}||^{2}_{{2},Q}. \end{aligned}$$

(5.1)

${\mathcal {U}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})$ is the preconditioner for ${\mathcal {V}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})$. Note that ${\mathcal {V}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})$ is equivalent to the functional ${\mathcal {R}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})$ with zero data. Next we estimate the condition number of preconditioner ${\mathcal {U}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})$. To obtain the lower bound, we use the trace theorem for Sobolev spaces. Then

$$\begin{aligned} {\mathcal {V}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})\le K \;{\mathcal {U}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\}), \end{aligned}$$

(5.2)

where, K is a constant. Using Theorem 3.1 gives

$$\begin{aligned} \frac{1}{C(\log W)^{2}}{\mathcal {U}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})\le \;{\mathcal {V}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\}). \end{aligned}$$

(5.3)

Combining (5.2) and (5.3) implies

$$\begin{aligned} \frac{1}{C}{\mathcal {V}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})\le {\mathcal {U}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})\le C(\log W)^{2}\;{\mathcal {V}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\}), \end{aligned}$$

(5.4)

where C is a positive constant. Thus, the condition number of the preconditioned system is $O({(\log W)^{2}})$. For each element, the preconditioner corresponds to the following quadratic form

$$\begin{aligned} {\mathcal {B}}({\mathbf{u }}) =||{\mathbf{u }}||^{2}_{\mathbf{2 },Q}=\sum _{k=1}^{3}||{{u}}_{k}||^{2}_{{2},Q}, \end{aligned}$$

(5.5)

where, $\mathbf{u }={\mathbf{u }}({\varvec{\lambda }})=({u}_1({\varvec{\lambda }}),{u}_2({\varvec{\lambda }}),{u}_3({\varvec{\lambda }}))^\top$. Here each component ${u}_k({\varvec{\lambda }})(k=1,2,3)$ is a polynomial of degree W in $\lambda _1,\lambda _2$ and $\lambda _3$ separately.

Using the idea of [10], we can define the new quadratic form ${\mathcal {C}}(u)$ and show that ${\mathcal {C}}(u)$ is spectrally equivalent to ${\mathcal {B}}(u)$. The new quadratic form ${\mathcal {C}}(u)$ can be diagonalized using the separation of variables. Hence, the action of the matrix corresponding to the quadratic form ${\mathcal {C}}(u)$ will be easy to compute. In algorithm, each element is mapped onto a single processor (core) for ease of parallelism. Thus, during the PCGM process, the interchange of informations based on the value of function and its derivatives at inter-element boundaries confine the communication between neighbouring processors. Note that there are two global scalers namely the approximate solution and the search direction which need to compute for update in each iterations. Thus, it is clear that the communication between inter-processor is quite small. We note that PCGM take $O(W\ln W)$ iteration to compute the numerical solution with exponential accuracy.

6 Error Estimates

Lemma 6.1

Let $({U}^{l}_{1}({\varvec{\lambda }}),{U}^{l}_{2}({\varvec{\lambda }}),{U}^{l}_{3}({\varvec{\lambda }}))^\top =\mathbf{U }^{l}({\varvec{\lambda }})=\mathbf{u }(M^{l}({\varvec{\lambda }}))=({u}_{1}(M^{l}({\varvec{\lambda }})), {u}_{2}(M^{l}({\varvec{\lambda }})),{u}_{3}(M^{l}({\varvec{\lambda }})))^\top$ for ${\varvec{\lambda }}\in Q, l=1,\ldots , L$. Then there exist functions $\varPhi ^{l}=(\phi _{1}^{l},\phi _{2}^{l},\phi _{3}^l)^\top$ such that each $\phi ^{l}_{k}({\varvec{\lambda }})$ is a polynomial of degree W in each variable separately. Then for W large enough, there exists constant $C_s$ such that the estimate

$$\begin{aligned} \sum _{l=1}^{L}||{\varPhi }^{l}({\varvec{\lambda }})-\mathbf{U }^{l}({\varvec{\lambda }})||^{2}_{2,Q} \le C_{s}\;W^{-2s+7}(\mathbf{I }). \end{aligned}$$

holds, where, $\mathbf{I }=\displaystyle {\sum _{l=1}^{L}}||\mathbf{U }^{l}({\varvec{\lambda }})||^{2}_{s,Q}$ and $s\ge 2$ is a positive real number which represent the regularity index of $\mathbf{u }$.

Proof

From the approximation result of [3], we can find a polynomial $\phi ^{l}_{k}({\varvec{\lambda }})$ of degree W in each variable separately such that

$$\begin{aligned} ||U^{l}_{k}({\varvec{\lambda }})- \phi ^{l}_{k}({\varvec{\lambda }})||^{2}_{n,Q} \le C_{s} W^{4n-2s-1}||U^{l}_{k}||^{2}_{s,Q}\quad \forall l=1,\ldots ,L,\;\forall k=1,2,3, \end{aligned}$$

with $W>s$, $C_{s}=C_{1}e^{2s}$, $s>0$ and $0< n\le s$. Thus, for $n=2$, it follows:

$$\begin{aligned} ||U^{l}_{k}({\varvec{\lambda }})-\phi ^{l}_{k}({\varvec{\lambda }})||^{2}_{2,Q} \le C_{s} W^{-2s+7}||U^{l}_{k}||^{2}_{s,Q}\quad \forall l=1,\ldots ,L,\;\;\forall k=1,2,3. \end{aligned}$$

(6.1)

Using (6.1), it holds:

$$\begin{aligned} ||\mathbf{U }^{l}({\varvec{\lambda }})-\varPhi ^{l}({\varvec{\lambda }})||^{2}_{2,Q}=\sum _{k=1}^{3}||U^{l}_{k}({\varvec{\lambda }})-\phi ^{l}_{k}({\varvec{\lambda }})||^{2}_{2,Q}&\le C_{s} W^{-2s+7}\sum _{k=1}^3||U^{l}_{k}||^{2}_{s,Q}\\&\le C_{s} W^{-2s+7}||\mathbf{U }^{l}||^{2}_{s,Q}. \end{aligned}$$

Summing over $l=1,\ldots ,L$ leads to the stated result. $\square$

Lemma 6.2

Let $({U}^{l}_{1}({\varvec{\lambda }}),{U}^{l}_{2}({\varvec{\lambda }}),{U}^{l}_{3}({\varvec{\lambda }}))^\top =\mathbf{U }^{l}({\varvec{\lambda }})=\mathbf{u }(M^{l}({\varvec{\lambda }}))=({u}_{1}(M^{l}({\varvec{\lambda }})), {u}_{2}(M^{l}({\varvec{\lambda }})),{u}_{3}(M^{l}({\varvec{\lambda }})))^\top$ for ${\varvec{\lambda }}\in Q, l=1,\ldots , L$. Then there exist functions $\varPhi ^{l}=(\phi _{1}^{l},\phi _{2}^{l},\phi _{3}^l)^\top$ such that each $\phi ^{l}_{k}({\varvec{\lambda }})$ is a polynomial of degree W in each variable separately. Then for W large enough, there exists constant $C_s$ such that the estimate

$$\begin{aligned} {\mathcal {R}}^{W}(\{{\mathcal {F}}_{\varPhi }\})\le C_{s}\;W^{-2s+7}(\mathbf{I }). \end{aligned}$$

holds, where, $\mathbf{I }=\displaystyle {\sum _{l=1}^{L}}||\mathbf{U }^{l}({\varvec{\lambda }})||^{2}_{s,Q}$ and $\{{\mathcal {F}}_{\varPhi }\}=\{\varPhi ^{l}\}$.

Proof

First we consider the set of functions $\{{\mathcal {F}}_{\varPhi }\}=\{\{\varPhi ^l ({\varvec{\lambda }})\}_{l}\}$. Recall the definition of ${\mathcal {R}}^{W}(\{{\mathcal {F}}_{\varPhi }\})$ is

$$\begin{aligned} {\mathcal {R}}^{W}(\{{\mathcal {F}}_{\varPhi }\})&= {\mathcal {R}}^W_{residual}(\{{\mathcal {F}}_{\varPhi }\}) + {\mathcal {R}}^W_{jump}(\{{\mathcal {F}}_{\varPhi }\}) + {\mathcal {R}}^W_{boundary}(\{{\mathcal {F}}_{\varPhi }\}) \end{aligned}$$

with

$$\begin{aligned} {\mathcal {R}}^W_{residual}(\{{\mathcal {F}}_{\varPhi }\})&:=\sum _{l=1}^{L} ||({\mathcal {L}}^{l})\varPhi ^{l}({\varvec{\lambda }})-\tilde{\mathbf{F }}^{l}({\varvec{\lambda }})||^{2}_{0,Q},\\ {\mathcal {R}}^W_{jump}(\{{\mathcal {F}}_{\varPhi }\})&:=\sum _{\varGamma _{j}^l\subset \varOmega } \left( ||[\varPhi ]||^{2}_{0,\varGamma _{j}^l} +\sum _{i=1}^{3}||[(\varPhi )_{x_i}]||^{2}_{\frac{1}{2},\varGamma _{j}^l}\right) , \nonumber \\ {\mathcal {R}}^W_{boundary}(\{{\mathcal {F}}_{\varPhi }\})&:=\sum _{\varGamma _{j}^s\subseteq \varGamma }\left( ||\varPhi -\mathbf{h }^{m}||^{2}_{0,\varGamma _{j}^s} +\left| \left| \left( \frac{\partial \varPhi }{\partial T}\right) -\left( \frac{\partial \mathbf{h }^{m}}{\partial T}\right) \right| \right| ^{2}_{\frac{1}{2},\varGamma _{j}^s}\right) . \end{aligned}$$

Using the idea of Theorem 6.1 from [20] and Theorem 5.1 from [21], we can conclude that

$$\begin{aligned} {\mathcal {R}}^W_{residual}(\{{\mathcal {F}}_{\varPhi }\})&\le C_s W^{-2s+7} (\mathbf{I }), \end{aligned}$$

(6.2)

$$\begin{aligned} {\mathcal {R}}^W_{jump}(\{{\mathcal {F}}_{\varPhi }\})&\le C_s W^{-2s+7} (\mathbf{I }), \end{aligned}$$

(6.3)

$$\begin{aligned} {\mathcal {R}}^W_{boundary}(\{{\mathcal {F}}_{\varPhi }\})&\le C_s W^{-2s+7} (\mathbf{I }), \end{aligned}$$

(6.4)

where, $\mathbf{I }=\displaystyle {\sum _{l=1}^{L}}||\mathbf{U }^{l}(\lambda _{1},\lambda _{2}, \lambda _{3})||^{2}_{s,Q}$.

Combining (6.2), (6.3) and (6.4) implies

$$\begin{aligned} {\mathcal {R}}^{W}(\{{\mathcal {F}}_{\varPhi }\})\le C_{s} W^{-2s+7} (\mathbf{I }). \end{aligned}$$

$\square$

Theorem 6.1

Let $({U}^{l}_{1}({\varvec{\lambda }}),{U}^{l}_{2}({\varvec{\lambda }}),{U}^{l}_{3}({\varvec{\lambda }}))=\mathbf{U }^{l}({\varvec{\lambda }})=\mathbf{u }(M^{l}({\varvec{\lambda }}))=({u}_{1}(M^{l}({\varvec{\lambda }})), {u}_{2}(M^{l}({\varvec{\lambda }})),{u}_{3}(M^{l}({\varvec{\lambda }})))$ for $({\varvec{\lambda }})\in Q, l=1,\ldots , L$ and let ${\mathcal {F}}_{\varTheta }\in S^W$ minimizes the functional ${\mathcal {R}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})$ over all ${\mathcal {F}}_{\mathbf{u }}\in S^W$. Then for W large enough there exists constant $C_s$ such that the estimate

$$\begin{aligned} \sum _{l=1}^{L}||{\varTheta }^{l}({\varvec{\lambda }})-U^{l}({\varvec{\lambda }})||^{2}_{2,Q} \le C_{s}\;W^{-2s+7}(\mathbf{I }). \end{aligned}$$

holds, where, $\mathbf{I }=\displaystyle {\sum _{l=1}^{L}}||\mathbf{U }^{l}(\lambda _{1},\lambda _{2}, \lambda _{3})||^{2}_{s,Q}.$

Proof

First, the error is divided into two parts as follows:

$$\begin{aligned} ||{\varTheta }^{l}_{k}({\varvec{\lambda }})-U_{k}^{l}({\varvec{\lambda }})||^{2}_{2,Q}\le C\Big (||{\varTheta }^{l}_{k}({\varvec{\lambda }})-\phi _{k}^{l}({\varvec{\lambda }})||^{2}_{2,Q}+||{\phi }^{l}_{k}({\varvec{\lambda }})-U_{k}^{l}({\varvec{\lambda }})||^{2}_{2,Q}\Big ) \end{aligned}$$

(6.5)

Next we estimate the first term of R.H.S. of (6.5). Let ${\mathcal {F}}_{\varTheta }$ minimizes ${\mathcal {R}}^{W}(\{{\mathcal {F}}_{\mathbf{v }}\})$ over all ${\mathcal {F}}_{\mathbf{v }}$, then

$$\begin{aligned} {\mathcal {R}}^{W}(\{{\mathcal {F}}_{\varPhi }\})={\mathcal {R}}^{W}(\{{\mathcal {F}}_{\varTheta }\}) +{{\mathcal {V}}}^{W}\left( \{{\mathcal {F}}_{\varPhi -\varTheta }\}\right) . \end{aligned}$$

Hence, it holds:

$$\begin{aligned} {{\mathcal {V}}}^{W}\left( \{{\mathcal {F}}_{\varPhi -\varTheta }\}\right) \le {\mathcal {R}}^{W} (\{{\mathcal {F}}_{\varPhi }\}). \end{aligned}$$

Applying the stability Theorem 3.1 and Lemma 6.2 implies

$$\begin{aligned} \sum _{l=1}^{L}||({\varTheta }^{l}({\varvec{\lambda }})-{\varPhi }^{l}({\varvec{\lambda }}))||^{2}_{2,Q}&\le C_{s}W^{-2s+7}(\mathbf{I }). \end{aligned}$$

(6.6)

Combining Lemma 6.1, (6.5) and (6.6) gives:

$$\begin{aligned} \sum _{l=1}^{L}||U^{l}({\varvec{\lambda }}) -{\varTheta }^{l}({\varvec{\lambda }})||^{2}_{2,Q}&\le C_{s} W^{-2s+7}(\mathbf{I }). \end{aligned}$$

(6.7)

$\square$

Remark 6.1

Note that If $\mathbf{U }^{l}$ is analytic, then there exist constants C and d such that

$$\begin{aligned} ||\mathbf{U }^{l}||^{2}_{s,Q}\le (Cd^s s!)^{2},\quad \forall l=1,\ldots ,L \end{aligned}$$

Applying Stirling’s formula as in [10] with a proper choice of s, we can find a $b>0$ such that

$$\begin{aligned} \sum _{l=1}^{L}||\mathbf{U }^{l}({\varvec{\lambda }})-{\varTheta }^{l} ({\varvec{\lambda }})||^{2}_{2,Q}\le C e^{-bW}. \end{aligned}$$

Remark 6.2

To compute the non-conforming spectral element solution, we solve the normal equations using PCGM. After computing the numerical solution, there is a possibility to get the conforming solution by a correction. Hence, we can show that the error between the conforming numerical solution and the exact solution in the $H^1$ norm is also exponentially small in W. We refer to [9] for more information about these corrections. Moreover, it also holds:

$$\begin{aligned} ||\mathbf{u }-\mathbf{z }||_{1,\varOmega }\le C e^{-bW}, \end{aligned}$$

where C and $b>0$ are constants and $\mathbf{z }$ is the corrected solution.

Now. we estimate the error in terms of number of degrees of freedom. Our algorithm is quite simple based on O(1) number of elements in $\varOmega$. In addition, each element has $O(W^{3})$ degrees of freedom for each component $\mathbf{u }^l=(u_{1}^{l},u_{2}^{l},u_{3}^{l})^\top$. In next lemma, we present the bound of error estimate in terms of degrees of freedom.

Theorem 6.2

Let $\{{\mathcal {F}}_{\varTheta }\}$ minimize ${\mathcal {R}}^{W}(\{{\mathcal {F}}_{\mathbf{u }}\})$ over all $\{{\mathcal {F}}_{\mathbf{u }}\}\in {{\mathcal {S}}}^{W}(\varOmega )$. Then there exist constants C and b (independent of L and W) such that

$$\begin{aligned} {\mathcal {U}}^{W}\left( \{{\mathcal {F}}_{(\varTheta -\mathbf{u })}\}\right) \le Ce^{-bW_{dof}^{1/3}}, \end{aligned}$$

(6.8)

where ${\mathcal {U}}^{W}\left( \{{\mathcal {F}}_{(\varTheta -\mathbf{u })}\}\right)$ is given in (5.1) and $W_{dof}=dim({{\mathcal {S}}}^{W}(\varOmega ))=\#$ degrees of freedom.

7 Numerical Results

Let $u_{ap}$ and $u_{ex}$ denote the spectral element solution and the exact solution, respectively. Next we define the relative error as follows:

$$\begin{aligned} ||E||_{rel} =\frac{||u_{ap}-u_{ex}||_{H^{1}}}{||u_{ex}||_{H^{1}}}. \end{aligned}$$

All numerical results given in this section are computed using a FORTRAN-90 code. We use a Intel(R) Xeon(R) CPU E7- 8870 @ 2.40GHz based machine for our computations. More details are as follows: Number of CPU (Physically)-8, Cores per CPU (Physically)-10 and Threads per CPU -20. Recall that each element is mapped onto a single processor (core) for ease of parallelism. We use Message Passing Interface (MPI) based library for inter processor communication.

Let $\epsilon$ be the tolerance to stop the PCGM. Then the stopping criterion based on the relative norm of the residual vector for the normal equations is less than $\epsilon$. Let $\kappa$ be the condition number of the preconditioner. To satisfy the stopping criterion, we need to perform $O\left( \frac{\sqrt{\kappa }}{2}|\log \left( \frac{2}{\epsilon }\right) |\right)$ iterations of the PCGM. Specifically, we need to perform $O(W(\ln W))$ iterations of the PCGM to compute the numerical solution with an accuracy of $O(e^{-bW})$. Note that each iteration takes $O(W^3)$ operation-time on a parallel computer with O(W) processors. Hence it is clear that the method needs $O(W^{4}(\ln W))$ operation-time to compute the solution to an accuracy of $O(e^{-bW})$. In all numerical results, we use the same discretization of the domain as shown in Fig. 1.

Remark 7.1

It is well known that singularities based on corners, edges and edge-corner arise in 3-D cubic domain. But, in our computations, we take our data in a way that the solution does not have any singularities.

Fig. 1

a Mesh 1, b Mesh 2

Example 1

Consider the problem

$$\begin{aligned} -\varDelta \mathbf{u }&=\mathbf{f } \quad \text{ in }\quad \varOmega =(-1,1)^3,\\ \mathbf{u }&= \mathbf{g } \quad \text{ on }\quad \varGamma , \end{aligned}$$

The exact solution $\mathbf{u }=(u_1,u_2,u_3)^\top$ is given by:

$$\begin{aligned} \mathbf{u } = {\left\{ \begin{array}{ll} u_1=\cos (\pi x) \sin (\pi y) \sin (\pi z) \\ u_2=\sin (\pi x) \cos (\pi y) \sin (\pi z)) \\ u_3=-2 \sin (\pi x) \sin (\pi y) \cos (\pi z) . \end{array}\right. } \end{aligned}$$

The computed results based on spectral method and spectral element method are presented in Tables 1 and 2. Tables 1 and 2 represent the relative error in $H^1-$norm with the number of iterations and CPU time against W. From Tables 1, 2 and Fig. 2, it is clear that the error decays exponentially with respect to W . In Table 3, the number of iterations and CPU time with preconditioner and with out preconditioner are provided with respect to W. It shows the effectiveness of the proposed preconditioner in terms of time and iteration count. In Fig. 3, the graph of iteration count grows with $O(W \ln W)$.

Table 1 Performance of spectral method for Example 1 on Mesh 1

Table 2 Performance of spectral element method for Example 1 on Mesh 2

Table 3 Performance of the method for Example 1 on Mesh 2

Fig. 2

a Error versus W (spectral method), b error versus W (Spectral element method) for Example 1

Fig. 3

Iteration count versus W (spectral element method)

Example 2

(Biharmonic problem with simply supported boundary condition) Consider the problem

$$\begin{aligned} \varDelta ^2 {u}&={f} \quad \text{ in }\quad \varOmega =(-1,1)^3,\\ u&= {g}_1 \quad \text{ on }\quad \varGamma , \\ \varDelta {u}&= {g}_2 \quad \text{ on }\quad \varGamma . \end{aligned}$$

Let $v=-\varDelta u$, then

$$\begin{aligned} -\varDelta {v}&={f} \quad \text{ in }\quad \varOmega ,\\ v+\varDelta {u}&=0 \quad \text{ in }\quad \varOmega ,\\ u&= {g}_1 \quad \text{ on }\quad \varGamma , \\ v&= {g}_2 \quad \text{ on }\quad \varGamma . \end{aligned}$$

The exact solution u is given by:

$$\begin{aligned} u=\cos (\pi x) \sin (\pi y) \sin (\pi z). \end{aligned}$$

Here, we first convert the fourth order problem to second order elliptic system. Then, we solve the problem. Tables 4 and 5 display the computed results based on spectral method and spectral element method. Specifically, Tables 4 and 5 represent the relative error in $H^1-$norm with the number of iterations and CPU time against W. Note that, in Tables 4, 5 and Fig. 4, the error decays exponentially with respect to W. It is easy to see that the convergence rates of u and $v=\varDelta u$ are similar. In Fig. 5, the graph of iteration count grows with $O(W \ln W)$.

Table 4 Performance of the method for Example 2 on Mesh 1

Table 5 Performance of the method for Example 2 on Mesh 2

Fig. 4

a Error versus W (spectral method), b error versus W (Spectral element method) for Example 2

Fig. 5

Iteration count versus W (spectral element method)

Example 3

(Linear elasticity problem with non-homogeneous boundary condition) Consider the following three dimensional steady state linear elasticity problem

$$\begin{aligned} \nabla \cdot {\mathbb {T}}&=-\mathbf{F }\quad \text{ in }\quad \varOmega =(0,1)^3,\\ \mathbf{u }&= {\mathbf{g }} \quad \text{ on }\quad \varGamma . \end{aligned}$$

where

$$\begin{aligned} {\mathbb {T}}=\lambda \mathbf{tr} (\sigma )I+2\mu \sigma . \end{aligned}$$

(7.1)

Here $(\lambda , \mu ), I$ and $\sigma$ are respectively the Lamé’s parameters, $3\times 3$ identity matrix and stress tensor. The stress tensor and the Lamé’s parameters can also be written as follows:

$$\begin{aligned} \sigma =\frac{1}{2} (\nabla \mathbf{u }+(\nabla \mathbf{u })^T), \quad \mu =\frac{E}{2(1+\nu )},\quad \lambda =\frac{E\nu }{(1+\nu )(1-2\nu )}, \end{aligned}$$

(7.2)

where E and $\nu$ are Young modulus and Poisson ratio, respectively (Table 6). The exact solution $\mathbf{u }=(u_1,u_2,u_3)^\top$ is given by:

$$\begin{aligned} \mathbf{u } = {\left\{ \begin{array}{ll} u_1=(x^2+1)(y^2+1)(z^2+1)\exp (x+y+z)\\ u_2=(x^2+1)(y^2+1)(z^2+1)\exp (x+y+z)\\ u_3=(x^2+1)(y^2+1)(z^2+1)\exp (x+y+z). \end{array}\right. } \end{aligned}$$

In this example, we fix $E=1$ and the values of $\nu$ are as follows:

Table 6 Values of $\nu$

Here, we are presenting the numerical results of linear elasticity equation with three different choices of Poisson ratio. Numerical results based on spectral method and spectral element method for all three cases are presented in Tables 7 and 8. From Tables 7, 8 and Fig. 6, it is clear that the error decays exponentially with respect to W. Moreover, the convergence rate of the error in all three choices are similar.

Table 7 Performance of the method for Example 3 on Mesh 1

Table 8 Performance of the method for Example 3 on Mesh 2

Fig. 6

a Error versus W (spectral method), b error versus W (spectral element method) for Example 3

Example 4

(Six order elliptic equation) Consider the problem

$$\begin{aligned} \varDelta ^3 {u}&={f} \quad \text{ in }\quad \varOmega =\left( 0,\frac{1}{2}\right) ^3,\\ u&= {g}_1 \quad \text{ on }\quad \varGamma , \\ \varDelta {u}&= {g}_2 \quad \text{ on }\quad \varGamma . \\ \varDelta ^2{u}&= {g}_3 \quad \text{ on }\quad \varGamma . \end{aligned}$$

Let $v=\varDelta ^2 u$, and $w=\varDelta u$ then

$$\begin{aligned} \varDelta {v}&={f} \quad \text{ in }\quad \varOmega ,\\ -v+\varDelta {w}&=0 \quad \text{ in }\quad \varOmega ,\\ -w+\varDelta {u}&=0 \quad \text{ in }\quad \varOmega ,\\ u&= {g}_1 \quad \text{ on }\quad \varGamma , \\ v&= {g}_2 \quad \text{ on }\quad \varGamma . \\ w&= {g}_3 \quad \text{ on }\quad \varGamma . \end{aligned}$$

The exact solution u is given by:

$$\begin{aligned} u=\sin (\pi x) \sin (\pi y) \sin ( \pi z). \end{aligned}$$

We first introduce two new variables $v=\varDelta ^2 u$ and $w=\varDelta u$, and convert six order problem into second order elliptic system. Numerical results based on spectral method and spectral element method are presented in Tables 9 and 10. From Tables 9, 10 and Fig. 7, it is clear that the error decays exponentially with respect to W. To convert the six order elliptic equation to second order elliptic system, we obtain the same convergence order for each components. Hence, higher order derivative $\varDelta ^2 u=v$ and $\varDelta u=w$ also obtain same convergence order as the convergence order of u.

Table 9 Performance of the method for Example 4 on Mesh 1

Table 10 Performance of the method for Example 4 on Mesh 2

Fig. 7

a Error versus W (spectral method), b error versus W (spectral element method) for Example 4

Example 5

Consider the problem

$$\begin{aligned} -\nabla \cdot ( {\mathcal {A}}\nabla \mathbf{u })&=\mathbf{f } \quad \text{ in }\quad \varOmega =(0,1)^3,\\ \mathbf{u }&= \mathbf{g } \quad \text{ on }\quad \varGamma , \end{aligned}$$

where ${\mathcal {A}}=\exp (x+y+z)I$ and I is the $3\times 3$ identity matrix. The exact solution $\mathbf{u }=(u_1,u_2,u_3)^\top$ is given by:

$$\begin{aligned} \mathbf{u } = {\left\{ \begin{array}{ll} u_1=(x+y+z)\exp (x+y+z)\\ u_2=(x+y+z)\exp (x+y+z)\\ u_3=(x+y+z)\exp (x+y+z). \end{array}\right. } \end{aligned}$$

In Table 11, we present the computed results based on spectral method and spectral element method. Specifically, Table 11 represents the relative error in $H^1-$norm. It is clear from Table 11 and Fig. 8 that the error decays exponentially with respect to W. Thus, it confirms that the proposed theory is also valid for the problem with variable coefficients.

Table 11 Performance of spectral method for Example 5 on Mesh 1 and Mesh 2

Fig. 8

a Error versus W (spectral method), b error versus W (spectral element method) for Example 5

Remark 7.2

In this remark, we present the numerical results for the problems discussed in Examples 3 and 5. Specifically, we solve the problems in the complex domain (unit sphere) $\varOmega =\{(x,y,z)\in {\mathbb {R}}^3:\sqrt{x^2+y^2+z^2} <1\}$. We divided our domain into 7 curvilinear hexahedrons, for more details see also [20, Example 7.3]. We present the convergence results for Example 3 in Fig. 9a and for Example 5 in Fig. 9b using spectral element method. Figure 9a, b reflect that the error decays exponentially in W.

Fig. 9

a Error versus W (spectral element method) Example 3 (Case 1), b error versus W (spectral element method) for Example 5 with the spherical domain

Table 12 Performance of spectral method for Example 6 on Mesh 1

Table 13 Performance of spectral method for Example 6 on Mesh 2

Fig. 10

a Error versus W (spectral method), b error versus W (spectral element method) for Example 6

Example 6

Consider the problem

$$\begin{aligned} -\varDelta \mathbf{u }&=\mathbf{f } \quad \text{ in }\quad \varOmega =(0,1)^3,\\ \mathbf{u }&= \mathbf{g } \quad \text{ on }\quad \varGamma . \end{aligned}$$

The exact solution $\mathbf{u }=(u_1,u_2,u_3)^\top$ is given by:

$$\begin{aligned} \mathbf{u } = {\left\{ \begin{array}{ll} u_1=(x^{\alpha }+y^{\alpha }+z^{\alpha })\\ u_2=(x^{\alpha }+y^{\alpha }+z^{\alpha })\\ u_3=(x^{\alpha }+y^{\alpha }+z^{\alpha }), \end{array}\right. } \end{aligned}$$

where $\alpha \ge 2$ is a positive real number.

In this example, we want to show the convergence rate of the proposed methods for the solutions that are not smooth enough. The exact solution $\mathbf{u }$ has two properties. First, It is smooth for the positive integer $\alpha$. Second, it is not analytic for the positive non-integer $\alpha$. We denote ${\tilde{\alpha }}$ by the greatest integer less than or equal to $\alpha$. If $\alpha$ is not integer, then $\partial ^{{\tilde{\alpha }}}_x$, $\partial ^{{\tilde{\alpha }}}_y$ and $\partial ^{{\tilde{\alpha }}}_z$ have singularities near to zero. In Tables 12 and 13, we can easily see that the error is equal to machine accuracy for the polynomial order $W\ge 3$ and $\alpha =3$. In case of $\alpha =3.5$, the error decays with the low convergence rate. We plot the convergence rate for the different choices of $\alpha$ in Fig. 10a, b. The convergence rate of the error increases from $\alpha =2.5$ to $\alpha =6.5$ in Fig 10a, b.

8 Conclusions and Future Work

In this article, a least-squares spectral method and a fully non-conforming least-squares spectral element method are studied for three dimensional elliptic system problems. In both cases (spectral method and spectral element method), it is shown that the error in the computed solution decays exponentially in polynomial degree W. Computational results for specific test problems confirm the estimates obtained for the error and computational complexity. Our algorithm is quite simple and easy to implement on parallel computers. We plan to develop numerical schemes for three dimensional elliptic system with corner singularity and edge singularity in future work.

Appendix

In this section, we briefly discuss the process to compute the integrals that are involved in numerical scheme. The process is similar to those for elliptic equations (for more details, see also [14, 32]). Thus, we give a brief overview to compute numerical scheme and refer to [13, 14, 32] for more details.

Recall that, we compute the integrals on the element domain $\varOmega _l$. In numerical scheme, we map to each element $\varOmega _l$ to the cube $Q=(-1,1)^3$. Thus, we present the computation for Q. First, we compute the following integral term

$$\begin{aligned} ||{\mathcal {L}}_{i}\tilde{\mathbf{u }}-F_{i}||_{0,Q}^2, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {L}}_{i}\tilde{\mathbf{u }}={\mathcal {L}}_{i,1}\tilde{{u}}_1+ {\mathcal {L}}_{i,2}\tilde{{u}}_2 +{\mathcal {L}}_{i,3}\tilde{{u}}_3 \end{aligned}$$

and

$$\begin{aligned} {\mathcal {L}}_{i,k}\tilde{{u}}_k&=A_{k,1}^{i}({\tilde{u}}_k)_{\lambda _1\lambda _1} +A_{k,2}^i({\tilde{u}}_k)_{\lambda _2\lambda _2}+A_{k,3}^i ({\tilde{u}}_k)_{\lambda _3\lambda _3}+A_{k,4}^i({\tilde{u}}_k)_{\lambda _1\lambda _2} +A_{k,5}^i({\tilde{u}}_k)_{\lambda _2\lambda _3}\\&\quad +\,A_{k,6}^i ({\tilde{u}}_k)_{\lambda _1\lambda _3}+A_{k,7}^i({\tilde{u}}_k)_{\lambda _1} +A_{k,8}^i({\tilde{u}}_k)_{\lambda _2}+A_{k,9}^{i}({\tilde{u}}_k)_{\lambda _3}+A_{k,10}^{i}({\tilde{u}}_k). \end{aligned}$$

Here $A_{k,j}^i$, $i,k=1,2,3, j=1,\ldots ,10$ are analytic coefficients.

The variation of the above integral is as follows:

$$\begin{aligned} \int _{Q}({\mathcal {L}}_{i}\tilde{\mathbf{v }})({\mathcal {L}}_{i}\tilde{\mathbf{u }}-F_{i})d{\varvec{\lambda }}=&\int _{Q}({\mathcal {L}}_{i,1}\tilde{{v}}_1+{\mathcal {L}}_{i,3}\tilde{{v}}_2+{\mathcal {L}}_{i,3}\tilde{{v}}_3)({\mathcal {L}}_{i}\tilde{\mathbf{u }}-F_{i})d{\varvec{\lambda }}\end{aligned}$$

First, we deal with the following integral

$$\begin{aligned} \int _{Q}({\mathcal {L}}_{i,k}\tilde{{v}}_k)({\mathcal {L}}_{i}\tilde{\mathbf{u }}-F_{i})d{\varvec{\lambda }}. \end{aligned}$$

Using integration by parts, it follows:

$$\begin{aligned} \int _{Q}({\mathcal {L}}_{i,k}\tilde{{v}}_k)({\mathcal {L}}_{i}\tilde{\mathbf{u }}-F_{i})d{\varvec{\lambda }}&= \int _{Q}\tilde{{v}}_k({\mathcal {L}}_{i,k})^{T} ({\mathcal {L}}_{i}\tilde{\mathbf{u }}-F_{i})d{\varvec{\lambda }}+{\mathscr {R}}_{term}, \end{aligned}$$

with

$$\begin{aligned} {\mathscr {R}}_{term}=&\int _S {\mathscr {I}}_1(1,\lambda _2,\lambda _3)d\lambda _2d\lambda _3-\int _S {\mathscr {I}}_2(1,\lambda _2,\lambda _3)d\lambda _2d\lambda _3\\&+\int _{-1}^{1}v_k(A_{k,4} \mathbf{Z }_i)(1,1,\lambda _3)d\lambda _3-\int _{-1}^{1}v_k(A_{k,4} \mathbf{Z }_i)(1,-1,\lambda _3)d\lambda _3\\&+\int _S {\mathscr {I}}_3(\lambda _1,1,\lambda _3)d\lambda _1d\lambda _3-\int _S {\mathscr {I}}_4(\lambda _1,-1,\lambda _3)d\lambda _1d\lambda _3\\&+\int _{-1}^{1}v_k(A_{k,5} \mathbf{Z }_i)(\lambda _1,1,1)d\lambda _1-\int _{-1}^{1}v_k(A_{k,5} \mathbf{Z }_i)(\lambda _1,1,-1)d\lambda _1\\&+\int _S {\mathscr {I}}_5(\lambda _1,\lambda _2,1)d\lambda _1d\lambda _2-\int _S {\mathscr {I}}_6(\lambda _1,\lambda _2,-1)d\lambda _1d\lambda _2\\&+\int _{-1}^{1}v_k(A_{k,6} \mathbf{Z }_i)(1,\lambda _2,1)d\lambda _2-\int _{-1}^{1}v_k(A_{k,6} \mathbf{Z }_i)(-1,\lambda _2,1)d\lambda _2, \end{aligned}$$

where

$$\begin{aligned} {\mathscr {I}}_1&=\Big ((A_{k,1}^i ({\tilde{v}}_k)_{\lambda _1}+A_{k,7}^i {\tilde{v}}_k)\mathbf {Z} _i-{\tilde{v}}_k((A^i_{k,1}\mathbf{Z }_i)_{\lambda _1}+(A^{i}_{k,4}{} \mathbf {Z} _i)_{\lambda _2}+(A^{i}_{k,6}{} \mathbf {Z} _i)_{\lambda _3})\Big ),\\ {\mathscr {I}}_2&=\Big ((A_{k,1}^i ({\tilde{v}}_k)_{\lambda _1}+A_{k,4}^i({\tilde{v}}_k)_{\lambda _2}+A_{k,7}^i {\tilde{v}}_k)\mathbf {Z} _i-{\tilde{v}}_k((A^i_{k,1}\mathbf{Z }_i)_{\lambda _1}+(A^{i}_{k,6}{} \mathbf {Z} _i)_{\lambda _3})\Big ),\\ {\mathscr {I}}_3&=\Big ((A_{k,2}^i ({\tilde{v}}_k)_{\lambda _2}+A_{k,8}^i {\tilde{v}}_k)\mathbf {Z} _i-{\tilde{v}}_k((A^i_{k,2}\mathbf{Z }_i)_{\lambda _2}+(A^{i}_{k,4}{} \mathbf {Z} _i)_{\lambda _1}+(A^{i}_{k,5}{} \mathbf {Z} _i)_{\lambda _3})\Big ),\\ {\mathscr {I}}_4&=\Big ((A_{k,2}^i ({\tilde{v}}_k)_{\lambda _2}+A_{k,5}^i({\tilde{v}}_k)_{\lambda _3}+A_{k,8}^i {\tilde{v}}_k)\mathbf {Z} _i-{\tilde{v}}_k((A^i_{k,2}\mathbf{Z }_i)_{\lambda _2}+(A^{i}_{k,4}{} \mathbf {Z} _i)_{\lambda _1})\Big ),\\ {\mathscr {I}}_5&=\Big ((A_{k,3}^i ({\tilde{v}}_k)_{\lambda _3}+A_{k,9}^i {\tilde{v}}_k)\mathbf {Z} _i-{\tilde{v}}_k((A^i_{k,3}\mathbf{Z }_i)_{\lambda _3}+(A^{i}_{k,5}{} \mathbf {Z} _i)_{\lambda _2}+(A^{i}_{k,6}{} \mathbf {Z} _i)_{\lambda _1})\Big ),\\ {\mathscr {I}}_6&=\Big ((A_{k,3}^i ({\tilde{v}}_k)_{\lambda _3}+A_{k,5}^i({\tilde{v}}_k)_{\lambda _1}+A_{k,9}^i {\tilde{v}}_k)\mathbf {Z} _i-{\tilde{v}}_k((A^i_{k,3}\mathbf{Z }_i)_{\lambda _3}+(A^{i}_{k,6}{} \mathbf {Z} _i)_{\lambda _2})\Big ), \end{aligned}$$

$\mathbf{Z }_i= ({\mathcal {L}}_{i}\tilde{\mathbf{u }}-F_{i})$, $Q=(-1,1)^3$ and $S=(-1,1)^2$. Now, we use the Gauss-Lobatto-Legendre (GLL) quadrature formula with $2W+1$ points to evaluate the integrals in above expression. Let $\lambda _{k,0}^{2W}, \lambda _{k,1}^{2W}, \ldots , \lambda _{k,2W}^{2W} (k=1,2,3)$ be the quadrature points in each direction and $w_{k,0}^{2W}, w_{k,1}^{2W}, \ldots , w_{k,2W}^{2W}$ represent the corresponding weights. Let $D^{2W}=d_{i,j}^{2W}$ represent the differentiation matrix. If ${\tilde{l}}$ is a polynomial of degree less than or equal to 2W, then

$$\begin{aligned} \frac{d{\tilde{l}}}{d\lambda _k}(\lambda _{k,i}^{2W})=\sum _{j=0}^{2W}d_{i,j}^{2W} {\tilde{l}}(\lambda _{k,i}^{2W}). \end{aligned}$$

Thus, we have

$$\begin{aligned}&\int _{Q}\tilde{{v}}_k({\mathcal {L}}_{i,k})^{T} ({\mathcal {L}}_{i}\tilde{\mathbf{u }}-F_{i})d{\varvec{\lambda }}\\&\quad \approx \sum _{i_1=0}^{2W}\sum _{j_1=0}^{2W}\sum _{k_1=0}^{2W} {\tilde{v}}_k(\lambda _{1,i_1}^{2W},\lambda _{2,j_1}^{2W},\lambda _{3,k_1}^{2W})\big (w_{1,i_1}^{2W}w_{2,j_1}^{2W}w_{3,k_1}^{2W}({\mathcal {L}}_{i,k})^{T} \mathbf{Z }_{i}(\lambda _{1,i_1}^{2W},\lambda _{2,j_1}^{2W},\lambda _{3,k_1}^{2W})\big ) \end{aligned}$$

and

$$\begin{aligned}&\int _S {\mathscr {I}}_1(1,\lambda _2,\lambda _3)d\lambda _2d\lambda _3\approx \\&\quad \sum _{i_1=0}^{2W}\sum _{j_1=0}^{2W}\sum _{k_1=0}^{2W} {\tilde{v}}_k(\lambda _{1,i_1}^{2W},\lambda _{2,j_1}^{2W},\lambda _{3,k_1}^{2W})\big (w_{2,j_1}^{2W}w_{3,k_1}^{2W}d^{2W}_{2W,i_1}(A_{k,1}^i \mathbf{Z }_{i})(1,\lambda _{2,j_1}^{2W},\lambda _{3,k_1}^{2W})\big )\\&\qquad +\sum _{j_1=0}^{2W}\sum _{k_1=0}^{2W} {\tilde{v}}_k(1,\lambda _{2,j_1}^{2W},\lambda _{3,k_1}^{2W})\big (w_{2,j_1}^{2W}w_{3,k_1}^{2W}(A_{k,7}^i\mathbf{Z }_{i}-(A_{k,1}^i\mathbf{Z }_i)_{\lambda _1}-(A_{k,5}^i\mathbf{Z }_i)_{\lambda _3}\\&\qquad -(A_{k,5}^i\mathbf{Z }_i)_{\lambda _2})(1,\lambda _{2,j_1}^{2W},\lambda _{3,k_1}^{2W})\big ). \end{aligned}$$

Similarly, we can write the expression for the remaining terms of ${\mathscr {R}}_{term}$. To arrange $\tilde{\mathbf{u }}=({\tilde{u}}_1,{\tilde{u}}_2,{\tilde{u}}_3)$ in lexicographic order, we define

$$\begin{aligned} U^{W}_{1;(W+1)^2k+(W+1)i+j+1}&={\tilde{u}}_{1}(\lambda _{1,i}^W,\lambda _{2,j}^W,\lambda _{3,k}^W),\;\;\text{ for }\;0\le i,j,k\le W,\\ U^{W}_{2;(W+1)^2k+(W+1)i+j+1}&={\tilde{u}}_{2}(\lambda _{1,i}^W,\lambda _{2,j}^W,\lambda _{3,k}^W),\;\;\text{ for }\;0\le i,j,k\le W,\\ U^{W}_{3;(W+1)^2k+(W+1)i+j+1}&={\tilde{u}}_{3}(\lambda _{1,i}^W,\lambda _{2,j}^W,\lambda _{3,k}^W),\;\;\text{ for }\;0\le i,j,k\le W, \end{aligned}$$

and

$$\begin{aligned} U^{2W}_{1;(W+1)^2k+(W+1)i+j+1}&={\tilde{u}}_{1}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W},\lambda _{3,k}^{2W}),\;\;\text{ for }\;0\le i,j,k\le 2W,\\ U^{2W}_{2;(W+1)^2k+(W+1)i+j+1}&={\tilde{u}}_{2}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W},\lambda _{3,k}^{2W}),\;\;\text{ for }\;0\le i,j,k\le 2W,\\ U^{2W}_{3;(W+1)^2k+(W+1)i+j+1}&={\tilde{u}}_{3}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W},\lambda _{3,k}^{2W}),\;\;\text{ for }\;0\le i,j,k\le 2W. \end{aligned}$$

In same manner, we define

$$\begin{aligned} \mathbf {Z} ^{2W}_{1;(W+1)^2k+(W+1)i+j+1}&={\mathcal {L}}_{1}\tilde{\mathbf{u }}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W},\lambda _{3,k}^{2W})-F_{1}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W},\lambda _{3,k}^{2W}),\\ \mathbf {Z} ^{2W}_{2;(W+1)^2k+(W+1)i+j+1}&={\mathcal {L}}_{2}\tilde{\mathbf{u }}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W},\lambda _{3,k}^{2W})-F_{2}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W},\lambda _{3,k}^{2W}),\\ \mathbf {Z} ^{2W}_{3;(W+1)^2k+(W+1)i+j+1}&={\mathcal {L}}_{3}\tilde{\mathbf{u }}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W},\lambda _{3,k}^{2W})-F_{3}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W},\lambda _{3,k}^{2W}). \end{aligned}$$

Thus, the final form is as follows:

$$\begin{aligned} \int _{Q}({\mathcal {L}}_{i,k}\tilde{{v}}_k)({\mathcal {L}}_{i}\tilde{\mathbf{u }}-F_{i})d{\varvec{\lambda }}&\approx (V^{2W}_k)^TR_i^k \mathbf{Z }^{2W}_i. \end{aligned}$$

Here each $R^k_i (i,k=1,2,3)$ is a matrix such that $R_{i}^k\mathbf{Z }_{i}^{2W}(i,k=1,2,3)$ is easily computed.

Similarly, we have

$$\begin{aligned} \int _{Q}({\mathcal {L}}_{i}\tilde{\mathbf{v }}_k)({\mathcal {L}}_{i}\tilde{\mathbf{u }}-F_{i})d{\varvec{\lambda }}&= \int _{Q}({\mathcal {L}}_{i,1}\tilde{{v}}_k)({\mathcal {L}}_{i}\tilde{\mathbf{u }}-F_{i})d{\varvec{\lambda }}+\int _{Q}({\mathcal {L}}_{i,2}\tilde{{v}}_k)({\mathcal {L}}_{i}\tilde{\mathbf{u }}-F_{i})d{\varvec{\lambda }}\\&\quad +\,\int _{Q}({\mathcal {L}}_{i,3}\tilde{{v}}_k)({\mathcal {L}}_{i}\tilde{\mathbf{u }}-F_{i})d{\varvec{\lambda }},\\&\approx (V^{2W}_1)^TR^1_i \mathbf{Z }^{2W}_i+(V^{2W}_2)^TR^2_i \mathbf{Z }^{2W}_i+(V^{2W}_3)^TR^3_i \mathbf{Z }^{2W}_i. \end{aligned}$$

Finally, we can conclude that

$$\begin{aligned} \sum _{i=1}^3\int _{Q}({\mathcal {L}}_{i}\tilde{\mathbf{v }})({\mathcal {L}}_{i}\tilde{\mathbf{u }}-F_{i})d{\varvec{\lambda }}&\approx (V_{1}^{2W})^TR^1_1\mathbf {Z} ^{2W}_{1}+(V_{1}^{2W})^TR^1_2\mathbf {Z} ^{2W}_{2} +(V_{1}^{2W})^TR^1_3\mathbf {Z} ^{2W}_{3} \\&\quad +\,(V_{2}^{2W})^TR^2_1\mathbf {Z} ^{2W}_{1} +(V_{2}^{2W})^TR^2_2\mathbf {Z} ^{2W}_{2} +(V_{2}^{2W})^TR^2_3\mathbf {Z} ^{2W}_{3}\\&\quad +\,(V_{3}^{2W})^TR^3_1\mathbf {Z} ^{2W}_{1} +(V_{3}^{2W})^TR^3_2\mathbf {Z} ^{2W}_{2}+(V_{3}^{2W})^TR^3_3\mathbf {Z} ^{2W}_{3}. \end{aligned}$$

Now we compute the boundary terms in norm $H^{1/2} (S)$. Let ${\tilde{l}}$ be the polynomial of degree 2W in $\lambda _1$ and $\lambda _2$ separately.

$$\begin{aligned} ||{\tilde{l}}||_{\frac{1}{2},S}^2=&||{\tilde{l}}||_{0,S}^2+\int _{Q}\frac{({\tilde{l}}(\lambda _1,\lambda _2))-{\tilde{l}}(\lambda _1^{'},\lambda _2))}{(\lambda _1-\lambda _1^{'})^2}d\lambda _1d\lambda _1^{'}d\lambda _2\\&+\int _{Q}\frac{({\tilde{l}}(\lambda _1,\lambda _2))-{\tilde{l}}(\lambda _1,\lambda _2^{'}))}{(\lambda _2-\lambda _2^{'})^2}d\lambda _2d\lambda _2^{'}d\lambda _1. \end{aligned}$$

Applying the Gauss Lobatto Legendre quadrature rule implies

$$\begin{aligned} ||{\tilde{l}}||_{\frac{1}{2},S}=&\sum _{i=0}^{2W}\sum _{j=0}^{2W} w_{i}^{2W}w_{j}^{2W}{\tilde{l}}^{2}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W})\\&+\sum _{j=0}^{2W}\sum _{i=0,i^{'}\ne i}^{2W}\sum _{i^{'}=0}^{2W}w_{i}^{2W}w_{j}^{2W}w_{i^{\prime }}^{2W}\frac{({\tilde{l}}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W}))-{\tilde{l}}(\lambda _{1,i^{'}}^{2W},\lambda _{2,j}^{2W}))}{(\lambda _{1,i}^{2W}-\lambda _{1,i^{\prime }}^{2W})^2}\\&+\sum _{i=0}^{2W}\sum _{j=0,j^{\prime }\ne j}^{2W}\sum _{j^{\prime }=0}^{2W}w_{i}^{2W}w_{j}^{2W}w_{j^{\prime }}^{2W}\frac{({\tilde{l}}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W}))-{\tilde{l}}(\lambda _{1,i}^{2W},\lambda _{2,j^{\prime }}^{2W}))}{(\lambda _{2,j}^{2W}-\lambda _{2,j^{\prime }}^{2W})^2}\\&+\sum _{i=0}^{2W}\sum _{j=0}^{2W} w_{i}^{2W}w_{j}^{2W}\Big (\frac{d}{d\lambda _1}{\tilde{l}}(\lambda _{1,i}^{2W},\lambda _{2,j^{\prime }}^{2W}))\Big )\\&+\sum _{i=0}^{2W}\sum _{j=0}^{2W} w_{i}^{2W}w_{j}^{2W}\Big (\frac{d}{d\lambda _2}{\tilde{l}}(\lambda _{1,i}^{2W},\lambda _{2,j^{\prime }}^{2W}))\Big ). \end{aligned}$$

Hence, there exists a symmetric positive definite matrix $H^{2W}$ such that

$$\begin{aligned} ||{\tilde{l}}||_{\frac{1}{2},S}=\sum _{i=0}^{2W}\sum _{j=0}^{2W}\sum _{i^{\prime }=0}^{2W}\sum _{j^{\prime }=0}^{2W}{\tilde{l}}(\lambda _{1,i}^{2W},\lambda _{2,j}^{2W})) H^{2W}_{i,j,i^{\prime },j^{\prime }}{\tilde{l}}(\lambda _{1,i^{\prime }}^{2W},\lambda _{2,j^{\prime }}^{2W})). \end{aligned}$$

Now, we compute the typical boundary term of the following form

$$\begin{aligned} ||({\mathcal {T}}_{k,1}({\tilde{u}}_k)_{\lambda _1}+ {\mathcal {T}}_{k,2}({\tilde{u}}_k)_{\lambda _2}+{\mathcal {T}}_{k,3}({\tilde{u}}_k)_{\lambda _3})(\lambda _1,\lambda _2,1)-q_k||_{\frac{1}{2},S}^2, \end{aligned}$$

(8.1)

where each ${\mathcal {T}}_{k,i} (i,k=1,2,3)$ is analytic coefficient and each $q_k (k=1,2,3)$ is given boundary data. The variation of the above term (8.1) is as follows:

$$\begin{aligned} \approx&\sum _{i,j=0}^{2W}\sum _{i^{\prime },j^{\prime }=0}^{2W} ({\mathcal {T}}_{k,1}({\tilde{v}}_k)_{\lambda _1}+ {\mathcal {T}}_{k,2}({\tilde{v}}_k)_{\lambda _2}+{\mathcal {T}}_{k,3}({\tilde{v}}_k)_{\lambda _3})(\lambda _{1,i_1}^{2W},\lambda _{2,j_1}^{2W},1)H^{2W}_{i,j,i^{\prime },j^{\prime }} \\&\times \left( ({\mathcal {T}}_{k,1}({\tilde{u}}_k)_{\lambda _1}+ {\mathcal {T}}_{k,2}({\tilde{u}}_k)_{\lambda _2}+{\mathcal {T}}_{k,3}({\tilde{u}}_k)_{\lambda _3})(\lambda _{1,i_1}^{2W},\lambda _{2,j_1}^{2W},1)-q_k(\lambda _{1,i_1}^{2W},\lambda _{2,j_1}^{2W})\right) \end{aligned}$$

Now we define

$$\begin{aligned}&\mathbf {X} ^{2W}_{k;i_1,j_1}=\sum _{i^{\prime },j^{\prime }=0}^{2W}H^{2W}_{i_1,j_1,i^{\prime },j^{\prime }} \Big ( ({\mathcal {T}}_{k,1}({\tilde{u}}_k)_{\lambda _1}+ {\mathcal {T}}_{k,2}({\tilde{u}}_k)_{\lambda _2}+{\mathcal {T}}_{k,3}({\tilde{u}}_k)_{\lambda _3})(\lambda _{1,i_1}^{2W},\lambda _{2,j_1}^{2W},1)\\&\quad -q_k(\lambda _{1,i_1}^{2W},\lambda _{2,j_1}^{2W})\Big ). \end{aligned}$$

Then we have

$$\begin{aligned}&\sum _{i,j=0}^{2W}\sum _{i^{\prime },j^{\prime }=0}^{2W} ({\mathcal {T}}_{k,1}({\tilde{v}}_k)_{\lambda _1}+ {\mathcal {T}}_{k,2}({\tilde{v}}_k)_{\lambda _2}+{\mathcal {T}}_{k,3}({\tilde{v}}_k)_{\lambda _3})(\lambda _{1,i_1}^{2W},\lambda _{2,j_1}^{2W},1) \mathbf {X} ^{2W}_{k;i_1,j_1}\\&\quad =\sum _{i_1=0}^{2W}\sum _{i_2=0}^{2W}\sum _{j_1=0}^{2W} {\tilde{v}}_k(\lambda _{1,i_1}^{2W},\lambda _{2,j_1}^{2W},1)d^{2W}_{i_1,i_2}\Big ({\mathcal {T}}_1(\lambda _{1,i_1}^{2W},\lambda _{2,j_1}^{2W},1)\mathbf {X} ^{2W}_{k;i_1,j_1}\Big )\\&\qquad +\sum _{i_1=0}^{2W}\sum _{j_1=0}^{2W}\sum _{j_2=0}^{2W} {\tilde{v}}_k(\lambda _{1,i_1}^{2W},\lambda _{2,j_1}^{2W},1)d^{2W}_{j_1,j_2}\Big ({\mathcal {T}}_2(\lambda _{1,i_1}^{2W},\lambda _{2,j_1}^{2W},1)\mathbf {X} ^{2W}_{k;i_1,j_1}\Big )\\&\qquad +\sum _{i_1=0}^{2W}\sum _{j_1=0}^{2W}\sum _{k_2=0}^{2W} {\tilde{v}}_k(\lambda _{1,i_1}^{2W},\lambda _{2,j_1}^{2W},\lambda _{3,k_2}^{2W})d^{2W}_{i_1,i_2}\Big ({\mathcal {T}}_3(\lambda _{1,i_1}^{2W},\lambda _{2,j_1}^{2W},1)\mathbf {X} ^{2W}_{k;i_1,j_1}\Big )\\&\quad =(V_k^{2W})^T {\mathcal {E}}_kX_{k}^{2W} \end{aligned}$$

where ${\mathcal {E}}_k, k=1,2,3$, are $(2W+1)^3\times (2W+1)^3$ matrices and ${\mathcal {E}}_k X_{k}^{2W}, k=1,2,3$ can be easily computed. In same manner, we can evaluate the variation of each term which is involved in the quadratic form ${\mathcal {R}}^{W}$. Combining all integrals for an element, we obtain

$$\begin{aligned}&\sum _{i=1}^{3} \int _{Q}({\mathcal {L}}_{i} \tilde{\mathbf{v }})^T({\mathcal {L}}_{i}\tilde{\mathbf{u }}-F_{i})d{\varvec{\lambda }}+ \text{ inter } \text{ element } \text{ jump } \text{ term } \text{ variation }\\&\qquad \text{ or/and } \text{ boundary } \text{ term } \text{ variation }\\&\quad =(V_{1}^{2W})^TR_1^1\mathbf {Z} ^{2W}_{1}+(V_{1}^{2W})^TR_2^1\mathbf {Z} ^{2W}_{2} +(V_{1}^{2W})^TR_3^1\mathbf {Z} ^{2W}_{3} \\&\qquad +(V_{2}^{2W})^TR_1^2\mathbf {Z} ^{2W}_{1} +(V_{2}^{2W})^TR_2^2\mathbf {Z} ^{2W}_{2} +(V_{2}^{2W})^TR_3^2\mathbf {Z} ^{2W}_{3}\\&\qquad +(V_{3}^{2W})^TR_1^3\mathbf {Z} ^{2W}_{1} +(V_{3}^{2W})^TR_2^3\mathbf {Z} ^{2W}_{2}+(V_{3}^{2W})^TR_3^3\mathbf {Z} ^{2W}_{3}+\cdots \\&\quad =(V_{1}^{2W})^{T} O_{1}^{2W}+(V_{2}^{2W})^{T} O_{2}^{2W}+(V_{3}^{2W})^{T} O_{3}^{2W}. \end{aligned}$$

Here $O_{1}^{2W}=R_1^1\mathbf {Z} ^{2W}_{1}+R_2^1\mathbf {Z} ^{2W}_{2}+R_3^1\mathbf {Z} ^{2W}_{3}+\cdots$ , $O_{2}^{2W}=R_1^2\mathbf {Z} ^{2W}_{1}+R_2^2\mathbf {Z} ^{2W}_{2}+R_3^2\mathbf {Z} ^{2W}_{3}+\cdots$ and $O_{3}^{2W}=R_1^3\mathbf {Z} ^{2W}_{1}+R_2^3\mathbf {Z} ^{2W}_{2}+R_3^3\mathbf {Z} ^{2W}_{3}+\cdots$ are $(2W+1)^3$ vectors which can be easily evaluated. Furthermore, there exist matrices $G^W_{\alpha },\alpha =1,2,3$, such that

$$\begin{aligned} V_{1}^{2W}=G^{W}_1V_{1}^{W}, V_{2}^{2W}=G^{W}_2V_{2}^{W}\; \text{ and }\;V_{3}^{2W}=G^{W}_3V_{3}^{W}. \end{aligned}$$

Then we have

$$\begin{aligned} (V_{\alpha }^{2W})^T O_{\alpha }^{2W}=(V_{\alpha }^{W})^T ((G^W_{\alpha })^T O_{\alpha }^{2W})\quad \text{ for }\;\alpha =1,2,3. \end{aligned}$$