To share or not to share: the optimal advertising effort with asymmetric advertising effectiveness

Abstract

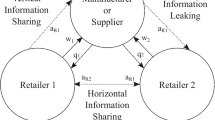
In this paper, we study a two-stage model in which a manufacturer expands to a new market through a local retailer and has private information on the advertising effectiveness. The manufacturer chooses the information sharing format with the retailer, either no information sharing or mandatory information sharing. Under no information sharing format, the manufacturer and the retailer play a signaling game. We derive both separating and pooling equilibria and conduct equilibrium refinements for the signaling game. Under mandatory information sharing format, the manufacturer simply informs the retailer the advertising effectiveness. We also establish the stylized model and derive the optimal advertising effort. By comparing the manufacturer’s ex ante profit under the two information sharing formats, we find that the manufacturer always prefers mandatory information sharing, under which both the advertising effort and profit can be higher. We also observe that unlike the common case that the channel members may have different preference over the information sharing formats, the manufacturer and the retailer can actually achieve alignment. While some previous studies suggest that the manufacturer and the retailer may have different preference over the information sharing formats, we find that they can actually achieve alignment with asymmetric information on advertising effectiveness.

Appendix

Proof of Proposition 1

Recall that the retailer’s best response retailing price to the manufacturer’s advertising effort $e$ is $p_{j} \left( {e;w} \right) = \frac{{a + \beta_{j} e + bw}}{2b}$, and given this price the manufacturer’s profit ${{\Pi }}_{ij}^{M} \left( {e;w} \right)$ is given by (1). We then derive the manufacturer’s optimal advertising effort by maximizing ${{\Pi }}_{ij}^{M} \left( {e;w} \right)$. Taking the first- and second-order derivatives over $e$ on Eq. (1), we have

$$ \frac{{d{{\Pi }}_{ij}^{M} \left( {e;w} \right)}}{de} = - 2ke + \left( {\beta_{i} - \frac{{\beta_{j} }}{2}} \right)w,\;{\text{and}}\;\frac{{d^{2} {{\Pi }}_{ij}^{M} \left( {e;w} \right)}}{{de^{2} }} = - 2k < 0. $$

Thus, for any given $w$, ${{\Pi }}_{ij}^{M} \left( {e;w} \right)$ is concave in $e$, and the optimal advertising effort can be obtained by solving $\frac{{d{{\Pi }}_{ij}^{M} \left( {e;w} \right)}}{de} = 0$. We have $e_{ij} \left( w \right) = \frac{{\left( {2\beta_{i} - \beta_{j} } \right)w}}{4k}$. Substituting it to $p_{j} \left( {e;w} \right)$, we have $p_{j} \left( w \right) = \frac{{4k\left( {a + bw} \right) + \left( {2\beta_{i} - \beta_{j} } \right)\beta_{j} w}}{8kb}$. The manufacturer and the retailer’s profits can then be obtained directly by using $e_{ij} \left( w \right)$ and $p_{j} \left( w \right)$. □

Proof of Proposition 2

Recall that we consider the following belief structure for the retailer: If $e \le \hat{e}^{sep}$, then the retailer believes that the advertising effectiveness is $\beta_{l}$; and if $e > \hat{e}^{sep}$, then the retailer believes that the advertising effectiveness is $\beta_{h}$. Under this belief structure, a perfect Bayesian separating equilibrium exists if and only $\hat{e}^{sep} \ge 0$ and the following constraints are satisfied

$$ \mathop {\hbox{max} }\limits_{{e \le \hat{e}^{sep} }} {{\Pi }}_{hl}^{M} \left( e \right) \le \mathop {\hbox{max} }\limits_{{e > \hat{e}^{sep} }} {{\Pi }}_{hh}^{M} \left( e \right), $$

(A1)

and

$$ \mathop {\hbox{max} }\limits_{{e > \hat{e}^{sep} }} {{\Pi }}_{lh}^{M} \left( e \right) \le \mathop {\hbox{max} }\limits_{{e \le \hat{e}^{sep} }} {{\Pi }}_{ll}^{M} \left( e \right). $$

(A2)

Condition (A1) requires that the $h$-type manufacturer cannot make a higher profit if it mimics the $l$-type one, and condition (A2) requires that the $l$-type manufacturer cannot make a higher profit if it mimics the $h$-type one. These two conditions guarantee that the manufacturer can achieve separating.

Consider condition (A1). For any belief structure with $\hat{e}^{sep} \ge e_{hh}$, we have

$$ \mathop {\hbox{max} }\limits_{{e \le \hat{e}^{sep} }} {{\Pi }}_{hl}^{M} \left( e \right) \ge {{\Pi }}_{hl}^{M} \left( {e_{hh} } \right) > {{\Pi }}_{hh}^{M} \left( {e_{hh} } \right) > \mathop {\hbox{max} }\limits_{{e > \hat{e}^{sep} }} {{\Pi }}_{hh}^{M} \left( e \right), $$

where the first inequality holds because $\hat{e}^{sep} \ge e_{hh}$ and $e_{hl} > e_{hh}$, the second inequality holds because ${{\Pi }}_{hl}^{M} \left( e \right) > {{\Pi }}_{hh}^{M} \left( e \right)$ for any $e$, and the last inequality holds because $\hat{e}^{sep} \ge e_{hh}$; see also Fig. 2 for illustration. In this case, condition (A1) can never be satisfied. Thus, we restrict our attention to the case $\hat{e}^{sep} < e_{hh}$, with which $\mathop {\hbox{max} }\limits_{{e > \hat{e}^{sep} }} {{\Pi }}_{hh}^{M} \left( e \right) = {{\Pi }}_{hh}^{M}$. Then, from (1) and (2), condition (A1) can be rewritten as

$$ \mathop {\hbox{max} }\limits_{{e \le \hat{e}^{sep} }} \left\{ { - ke^{2} + \left( {\beta_{h} - \frac{{\beta_{l} }}{2}} \right)we + \frac{{\left( {a - bw} \right)w}}{2}} \right\} \le \frac{{\left( {a - bw} \right)w}}{2} + \frac{{\beta_{h}^{2} w^{2} }}{16k}, $$

which implies that

$$ \hat{e}^{sep} \le \bar{e}^{sep} : = \frac{{w\left[ {2\beta_{h} - \beta_{l} - \sqrt {\left( {3\beta_{h} - \beta_{l} } \right)\left( {\beta_{h} - \beta_{l} } \right)} } \right]}}{4k}. $$

(A3)

See Fig. 2 for the illustration. This threshold corresponds to $x$-axis value of the intersection point that the horizontal line $y = {{\Pi }}_{hh}^{M} \left( {e_{hh} } \right)$ crossing the curve ${{\Pi }}_{hl}^{M} \left( e \right)$.

Regarding the $h$-type manufacturer’s profit, we can easily check that

$$ \mathop {argmax}\limits_{e} {{\Pi }}_{hh}^{M} \left( e \right) = \frac{{\beta_{h} w}}{4k} > \bar{e}^{sep} \ge \hat{e}^{sep} . $$

Clearly, it is optimal for the $h$-type manufacturer to set $e_{h}^{sep} = \frac{{\beta_{h} w}}{4k}$. Regarding the $l$-type manufacturer’s profit ${{\Pi }}_{ll}^{M} \left( e \right)$, Proposition 1 shows that ${{\Pi }}_{ll}^{M} \left( e \right)$ is concave in $e$ and $\arg \mathop {\hbox{max} }\limits_{e} {{\Pi }}_{ll}^{M} \left( e \right) = \frac{{\beta_{l} w}}{4k}$. Thus, the $l$-type manufacturer’s decision depends on the magnitude between $\frac{{\beta_{l} w}}{4k}$ and the threshold $\bar{e}^{sep} .$

• If $\bar{e}^{sep} \le \frac{{\beta_{l} w}}{4k}$, i.e., $1 < \theta \le 3$, then ${{\Pi }}_{ll}^{M} \left( e \right)$ increases for $e \le \hat{e}^{sep}$, and thus $\mathop {\hbox{max} }\limits_{{e \le \hat{e}^{sep} }} {{\Pi }}_{ll}^{M} \left( e \right) = {{\Pi }}_{ll}^{M} \left( {\hat{e}^{sep} } \right)$. In this case, condition (A2) is more likely to be satisfied with a larger $\hat{e}^{sep}$. Thus, we can set $\hat{e}^{sep} = \bar{e}^{sep}$, and let $e_{l}^{sep} = \hat{e}^{sep}$ to get the most profitable equilibrium outcome for the manufacturer.

• If $\bar{e}^{sep} > \frac{{\beta_{l} w}}{4k}$, i.e., $\theta > 3$, then ${{\Pi }}_{ll}^{M} \left( e \right)$ reaches its global maximum value for $e \le \hat{e}^{sep}$, i.e., $\mathop {\hbox{max} }\limits_{{e \le \hat{e}^{sep} }} {{\Pi }}_{ll}^{M} \left( e \right) = {{\Pi }}_{ll}^{M} \left( {\frac{{\beta_{l} w}}{4k}} \right)$. In this case, condition (A2) is clearly satisfied. See Fig. 2 for the illustration. Thus, it is most profitable for the manufacturer to set $\hat{e}^{sep} = \frac{{\beta_{l} w}}{4k}$, and then let $e_{l}^{sep} = \hat{e}^{sep}$.

To summarize, Proposition 2 is proved. □

Proof of Proposition 3

Recall that the retailer’s belief structure on pooling is as follows. If $e \le \hat{e}^{pool}$, then the retailer cannot update his prior belief; and if $e > \hat{e}^{pool}$, then the retailer believes that the advertising effectiveness is $\beta_{h}$. Under this belief structure, there exists a perfect Bayesian pooling equilibrium if and only if $\hat{e}^{pool} \ge 0$ and the following constraints are satisfied

$$ \mathop {\hbox{max} }\limits_{{e \le \hat{e}^{pool} }} {{\Pi }}_{hp}^{M} \left( e \right) = {{\Pi }}_{hp}^{M} \left( {\hat{e}^{pool} } \right), $$

(A4)

$$ \mathop {\hbox{max} }\limits_{{e \le \hat{e}^{pool} }} {{\Pi }}_{lp}^{M} \left( e \right) = {{\Pi }}_{lp}^{M} \left( {\hat{e}^{pool} } \right), $$

(A5)

$$ \mathop {\hbox{max} }\limits_{{e \le \hat{e}^{pool} }} {{\Pi }}_{hp}^{M} \left( e \right) \ge \mathop {\hbox{max} }\limits_{{e > \hat{e}^{pool} }} {{\Pi }}_{hh}^{M} \left( e \right), $$

(A6)

and

$$ \mathop {\hbox{max} }\limits_{{e \le \hat{e}^{pool} }} {{\Pi }}_{lp}^{M} \left( e \right) \ge \mathop {\hbox{max} }\limits_{{e > \hat{e}^{pool} }} {{\Pi }}_{lh}^{M} \left( e \right). $$

(A7)

Conditions (A4) and (A5) ensure that both the $h$-type manufacturer and the $l$-type manufacturer achieve the most profitable outcome at $\hat{e}^{pool}$. Condition (A6) guarantees that the $h$-type manufacturer wants to pool, because pooling is more profitable than separating; and condition (A7) makes sure that the $l$-type manufacturer also wants to pool, because pooling is more profitable than being regarded as the $h$-type one.

Before investigating the conditions (A4)–(A6), we first show the relation among the profit functions ${{\Pi }}_{ih}^{M} \left( e \right)$, ${{\Pi }}_{il}^{M} \left( e \right)$, and ${{\Pi }}_{ip}^{M} \left( e \right)$ for $i = h,l.$ From (1) and (5), it is easy to show that

$$ {{\Pi }}_{il}^{M} \left( e \right) \ge {{\Pi }}_{ip}^{M} \left( e \right) > {{\Pi }}_{ih}^{M} \left( e \right), $$

(A8)

and $e_{il} \left( w \right) > e_{ip} \left( w \right) > e_{ih} \left( w \right)$. See Fig. 6 for the illustration.

Fig. 6

The relation among the profit functions

Consider conditions (A4) and (A5). From (5), it is easy to see that when the $i$-type manufacturer chooses to pool, the profit ${{\Pi }}_{ip}^{M} \left( e \right)$ is concave in $e$, and the first best advertising effort is $e_{ip} = \frac{{\left( {2\beta_{i} - \mu } \right)^{ + } w}}{4k}$, where $i = h.l$. Then, to have the conditions (A4) and (A5) be satisfied, we must have

$$ \hat{e}^{pool} \le \hbox{min} \left\{ {e_{hp} ,e_{lp} } \right\} = e_{lp} = \frac{{\left( {2\beta_{l} - \mu } \right)^{ + } w}}{4k}. $$

(A9)

Next, we discuss the conditions (A6) and (A7).

Recall that ${{\Pi }}_{hh}^{M} \left( e \right)$ attains the maximum value at $\frac{{\beta_{h} w}}{4k}$. From (A9) and $\beta_{h} - \left( {2\beta_{l} - \mu } \right) = \left( {1 + \alpha } \right)\left( {\beta_{h} - \beta_{l} } \right) > 0$, we have $\frac{{\beta_{h} w}}{4k} > e_{lp} \ge \hat{e}^{pool}$. Thus, regarding the right-hand side of (A6), we have

$$ \mathop {\hbox{max} }\limits_{{e > \hat{e}^{pool} }} {{\Pi }}_{hh}^{M} \left( e \right) = {{\Pi }}_{hh}^{M} \left( {\frac{{\beta_{h} w}}{4k}} \right) = \frac{{\left( {a - bw} \right)w}}{2} + \frac{{\beta_{h}^{2} w^{2} }}{16k}. $$

Note also that ${{\Pi }}_{hp}^{M} \left( e \right)$ is concave in $e$. Thus, (A9) implies that ${{\Pi }}_{hp}^{M} \left( e \right)$ increases for $e \le \hat{e}^{pool}$. Thus,

$$ \mathop {\hbox{max} }\limits_{{e \le \hat{e}^{pool} }} {{\Pi }}_{hp}^{M} \left( e \right) = {{\Pi }}_{hp}^{M} \left( {\hat{e}^{pool} } \right) = - k\hat{e}^{{pool}^{2}} + \left( {\beta_{h} - \frac{\mu }{2}} \right)w\hat{e}^{pool} + \frac{{\left( {a - bw} \right)w}}{2}. $$

Therefore, from the above two equations,

$$ \begin{aligned} & \mathop {\hbox{max} }\limits_{{e \le \hat{e}^{pool} }} {{\Pi }}_{hp}^{M} \left( e \right) - \mathop {\hbox{max} }\limits_{{e > \hat{e}^{pool} }} {{\Pi }}_{hh}^{M} \left( e \right) \\ & \quad = - k\hat{e}^{{pool}^{2} }+ \left( {\beta_{h} - \frac{\mu }{2}} \right)w\hat{e}^{pool} + \frac{{\left( {a - bw} \right)w}}{2} - \left[ {\frac{{\left( {a - bw} \right)w}}{2} + \frac{{\beta_{h}^{2} w^{2} }}{16k}} \right] \\ & \quad = - k\hat{e}^{{pool}^{2}} + \left( {\beta_{h} - \frac{\mu }{2}} \right)w\hat{e}^{pool} - \frac{{\beta_{h}^{2} w^{2} }}{16k}. \\ \end{aligned} $$

To have condition (A6) satisfied, we let $\mathop {\hbox{max} }\limits_{{e \le \hat{e}^{pool} }} {{\Pi }}_{hp}^{M} \left( e \right) - \mathop {\hbox{max} }\limits_{{e > \hat{e}^{pool} }} {{\Pi }}_{hh}^{M} \left( e \right) \ge 0$ and obtain

$$ \frac{{w\left[ {\left( {2\beta_{h} - \mu } \right) - \sqrt {\left( {3\beta_{h} - \mu } \right)\left( {\beta_{h} - \mu } \right)} } \right]}}{4k} \le \hat{e}^{pool} \le \frac{{w\left[ {\left( {2\beta_{h} - \mu } \right) + \sqrt {\left( {3\beta_{h} - \mu } \right)\left( {\beta_{h} - \mu } \right)} } \right]}}{4k}. $$

(A10)

Regarding condition (A7), first note from (A9) that $\mathop {\hbox{max} }\limits_{{e \le \hat{e}^{pool} }} {{\Pi }}_{lp}^{M} \left( e \right) = {{\Pi }}_{lp}^{M} \left( {\hat{e}^{pool} } \right)$. From Proposition 1, ${{\Pi }}_{lh}^{M} \left( e \right)$ attains the maximum value at $e_{lh} = \frac{{\left( {2\beta_{l} - \beta_{h} } \right)^{ + } w}}{4k} \le \frac{{\left( {2\beta_{l} - \mu } \right)^{ + } w}}{4k} = e_{lp}$. Thus, the value of the left-hand side of (A7) depends on the magnitude between $e_{lh}$ and $\hat{e}^{pool}$ as detailed in the following two subcases.

• If $e_{lh} < \hat{e}^{pool}$, i.e., $\frac{{\left( {2\beta_{l} - \beta_{h} } \right)^{ + } w}}{4k} < \hat{e}^{pool}$, then $\mathop {\hbox{max} }\limits_{{e > \hat{e}^{pool} }} {{\Pi }}_{lh}^{M} \left( e \right) = {{\Pi }}_{lh}^{M} \left( {\hat{e}^{pool} } \right)$. In this case, condition (A7) turns to be ${{\Pi }}_{lp}^{M} \left( {\hat{e}^{pool} } \right) \ge {{\Pi }}_{lh}^{M} \left( {\hat{e}^{pool} } \right)$, which clearly holds from (A8); see Fig. 6 for the illustration. Therefore, in this subcase, condition (A7) holds if $\frac{{\left( {2\beta_{l} - \beta_{h} } \right)^{ + } w}}{4k} < \hat{e}^{pool} .$

• If $\hat{e}^{pool} \le e_{lh}$, i.e., $\hat{e}^{pool} \le \frac{{\left( {2\beta_{l} - \beta_{h} } \right)^{ + } w}}{4k}$, then $\mathop {\hbox{max} }\limits_{{e > \hat{e}^{pool} }} {{\Pi }}_{lh}^{M} \left( e \right) = {{\Pi }}_{lh}^{M} \left( {e_{lh} } \right)$. In this case, condition (A7) turns to be ${{\Pi }}_{lp}^{M} \left( {\hat{e}^{pool} } \right) \ge {{\Pi }}_{lh}^{M} \left( {e_{lh} } \right)$, i.e.,

$$ \begin{aligned} & {{\Pi }}_{lp}^{M} \left( {\hat{e}^{pool} } \right) - {{\Pi }}_{lh}^{M} \left( {e_{lh} } \right) \\ & \quad = \left[ { - k\hat{e}^{{pool}^{2}} + \left( {\beta_{l} - \frac{\mu }{2}} \right)w\hat{e}^{pool} + \frac{{\left( {a - bw} \right)w}}{2}} \right] - \left[ {\frac{{\left( {a - bw} \right)w}}{2} + \frac{{\left( {2\beta_{l} - \beta_{h} } \right)^{2} w^{2} }}{16k}} \right] \\ & \quad = - k\hat{e}^{{pool}^{2}} + \left( {\beta_{l} - \frac{\mu }{2}} \right)w\hat{e}^{pool} - \frac{{\left( {2\beta_{l} - \beta_{h} } \right)^{2} w^{2} }}{16k} \ge 0. \\ \end{aligned} $$

One can show that only if $\theta \le 1 + \frac{2}{1 + \alpha }$, the above inequality is valid for the $\hat{e}^{pool}$ such that

$$ \frac{{\left[ {\left( {2\beta_{l} - \mu } \right) - \sqrt {\left( {\beta_{h} - \mu } \right)\left( {4\beta_{l} - \beta_{h} - \mu } \right)} } \right]w}}{4k} \le \hat{e}^{pool} \le \frac{{\left[ {\left( {2\beta_{l} - \mu } \right) + \sqrt {\left( {\beta_{h} - \mu } \right)\left( {4\beta_{l} - \beta_{h} - \mu } \right)} } \right]w}}{4k}, $$

Recall that this subcase requires $\hat{e}^{pool} \le \frac{{\left( {2\beta_{l} - \beta_{h} } \right)^{ + } w}}{4k}$. It is easy to show that

$$ \frac{{\left[ {\left( {2\beta_{l} - \mu } \right) - \sqrt {\left( {\beta_{h} - \mu } \right)\left( {4\beta_{l} - \beta_{h} - \mu } \right)} } \right]w}}{4k} < \frac{{\left( {2\beta_{l} - \beta_{h} } \right)^{ + } w}}{4k} < \frac{{\left[ {\left( {2\beta_{l} - \mu } \right) + \sqrt {\left( {\beta_{h} - \mu } \right)\left( {4\beta_{l} - \beta_{h} - \mu } \right)} } \right]w}}{4k}. $$

Therefore, in this subcase, condition (A7) requires that

$$ \frac{{\left[ {\left( {2\beta_{l} - \mu } \right) - \sqrt {\left( {\beta_{h} - \mu } \right)\left( {4\beta_{l} - \beta_{h} - \mu } \right)} } \right]w}}{4k} \le \hat{e}^{pool} \le \frac{{\left( {2\beta_{l} - \beta_{h} } \right)^{ + } w}}{4k}. $$

Combining the above two subcases, if $\theta \le 1 + \frac{2}{1 + \alpha }$, then the validity of condition (A7) requires that

$$ \hat{e}^{pool} \ge \frac{{\left[ {\left( {2\beta_{l} - \mu } \right) - \sqrt {\left( {\beta_{h} - \mu } \right)\left( {4\beta_{l} - \beta_{h} - \mu } \right)} } \right]w}}{4k}, $$

(A11)

if $\theta > 1 + \frac{2}{1 + \alpha }$, then the validity of condition (A7) requires that

$$ \hat{e}^{pool} > \frac{{\left( {2\beta_{l} - \beta_{h} } \right)^{ + } w}}{4k}. $$

(A12)

To summarize, a pooling equilibrium, if exists, shall satisfy (A9), (A10), and either (A11) or (A12), depending on whether $\theta \le 1 + \frac{2}{1 + \alpha }$ or $\theta > 1 + \frac{2}{1 + \alpha }$. If $\theta \le 1 + \frac{2}{1 + \alpha }$, which implies that $\theta < 3$, then we can show that $\frac{{w\left[ {\left( {2\beta_{h} - \mu } \right) - \sqrt {\left( {3\beta_{h} - \mu } \right)\left( {\beta_{h} - \mu } \right)} } \right]}}{4k} > \frac{{\left[ {\left( {2\beta_{l} - \mu } \right) - \sqrt {\left( {\beta_{h} - \mu } \right)\left( {4\beta_{l} - \beta_{h} - \mu } \right)} } \right]w}}{4k}$. Thus, the solution set satisfying (A9), (A10), and (A11) is

$$ \frac{{w\left[ {\left( {2\beta_{h} - \mu } \right) - \sqrt {\left( {3\beta_{h} - \mu } \right)\left( {\beta_{h} - \mu } \right)} } \right]}}{4k} \le \hat{e}^{pool} \le \frac{{\left( {2\beta_{l} - \mu } \right)^{ + } w}}{4k}. $$

(A13)

If $\theta > 1 + \frac{2}{1 + \alpha }$, which implies that $\theta > 2$, then we can show that $\frac{{\left( {2\beta_{l} - \beta_{h} } \right)^{ + } w}}{4k} = 0 < \frac{{w\left[ {\left( {2\beta_{h} - \mu } \right) - \sqrt {\left( {3\beta_{h} - \mu } \right)\left( {\beta_{h} - \mu } \right)} } \right]}}{4k}$. Thus, the solution set satisfying (A9), (A10), and (A12) is

$$ \frac{{w\left[ {\left( {2\beta_{h} - \mu } \right) - \sqrt {\left( {3\beta_{h} - \mu } \right)\left( {\beta_{h} - \mu } \right)} } \right]}}{4k} \le \hat{e}^{pool} \le \frac{{\left( {2\beta_{l} - \mu } \right)^{ + } w}}{4k}. $$

(A14)

Note that the inequalities (A13) and (A14) are identical. Therefore, a pooling equilibrium exists if

$$ 2\beta_{l} - \mu \ge 0\quad {\text{and}}\quad \frac{{w\left[ {\left( {2\beta_{h} - \mu } \right) - \sqrt {\left( {3\beta_{h} - \mu } \right)\left( {\beta_{h} - \mu } \right)} } \right]}}{4k} \le \frac{{\left( {2\beta_{l} - \mu } \right)^{ + } w}}{4k}, $$

from which we obtain $\theta \le \frac{1 + \alpha }{\alpha }$ and $\theta \le \frac{{\alpha^{2} - 2\alpha - 3}}{{\alpha^{2} - 4\alpha - 1}}$, respectively. It is easy to check that that $\frac{{\alpha^{2} - 2\alpha - 3}}{{\alpha^{2} - 4\alpha - 1}} < \frac{1 + \alpha }{\alpha }$. Thus, a pooling equilibrium exists if $\theta \le \frac{{\alpha^{2} - 2\alpha - 3}}{{\alpha^{2} - 4\alpha - 1}}$, i.e., $\theta \le \bar{\theta }\left( \alpha \right).$

In this case, the manufacturer’s most profitable pooling equilibrium is to set $\hat{e}^{pool} = \frac{{\left( {2\beta_{l} - \mu } \right)^{ + } w}}{4k}$, and let $e^{pool} = \hat{e}^{pool}$. Proposition 3 is proved. □

Proof of Proposition 4

When $\theta \le \bar{\theta }\left( \alpha \right)$, where $\bar{\theta }\left( \alpha \right) = \frac{{3 + 2\alpha - \alpha^{2} }}{{1 + 4\alpha - \alpha^{2} }} \in \left[ {1,3} \right]$, there exist pooling and separating equilibria for the manufacturer. The LMSE selects the equilibrium that is more profitable for the $l$-type manufacturer. Thus, to prove Proposition 4, it suffices to show that the $l$-type manufacturer makes a higher profit when she chooses pooling rather than separating, if and only if $1 < \theta \le \bar{\theta }\left( \alpha \right)$.

Consider an $l$-type manufacturer. From Proposition 3, the pooling profit is

$$ {{\Pi }}_{lp}^{M} \left( {e^{pool} } \right) = \frac{{\left( {a - bw} \right)w}}{2} + \frac{{\left( {2\beta_{l} - \mu } \right)^{2} w^{2} }}{16k}; $$

and from Proposition 2, the separating profit (note the $l$-type manufacturer conducts costly separating when $\theta \le \bar{\theta }\left( \alpha \right)$ is

$$ {{\Pi }}_{ll}^{M} \left( {e_{l}^{sep} } \right) = \frac{{\left( {a - bw} \right)w}}{2} + \frac{{\beta_{l} }}{2}we_{l}^{sep} - ke_{l}^{{sep}^{2}} . $$

Therefore, we have

$$ \begin{aligned} & {{\Pi }}_{lp}^{M} \left( {e^{pool} } \right) - {{\Pi }}_{ll}^{M} \left( {e_{l}^{sep} } \right) \\ & \quad = \frac{{\left( {a - bw} \right)w}}{2} + \frac{{\left( {2\beta_{l} - \mu } \right)^{2} w^{2} }}{16k} - \left[ {\frac{{\left( {a - bw} \right)w}}{2} + \frac{{\beta_{l} }}{2}we_{l}^{sep} - ke_{l}^{sep2} } \right] \\ & = \frac{{\beta_{l}^{2} w^{2} }}{16k}\left\{ {\left( {\theta - 1} \right)\left[ {\left( {7 + \alpha^{2} } \right)\theta - 4\sqrt {1 - 4\theta + 3\theta^{2} } - \alpha^{2} - 2\alpha - 5} \right]} \right\}. \\ \end{aligned} $$

Recall that $\theta > 1$. Thus, to have ${{\Pi }}_{lp}^{M} \left( {e^{pool} } \right) - {{\Pi }}_{ll}^{M} \left( {e_{l}^{sep} } \right) \ge 0$ is equivalent to have

$$ \left( {7 + \alpha^{2} } \right)\theta - \alpha^{2} - 2\alpha - 5 \ge 4\sqrt {1 - 4\theta + 3\theta^{2} } , $$

Recall that $0 \le \alpha \le 1$ and $\theta > 1$, which implies that the left-hand side of the above inequality is no negative. Therefore, the above inequality is equivalent to

$$ \left[ {\left( {7 + \alpha^{2} } \right)\theta - \alpha^{2} - 2\alpha - 5} \right]^{2} \ge 16\left( {1 - 4\theta + 3\theta^{2} } \right), $$

solving which we obtain

$$ \begin{aligned} \theta & \le \frac{{\alpha^{4} + 2\alpha^{3} + 12\alpha^{2} + 14\alpha - 8\sqrt {\alpha + 2\alpha^{2} + \alpha^{3} } + 3}}{{\alpha^{4} + 14\alpha^{2} + 1}}\;{\text{or}} \\ \theta & > \frac{{\alpha^{4} + 2\alpha^{3} + 12\alpha^{2} + 14\alpha + 8\sqrt {\alpha + 2\alpha^{2} + \alpha^{3} } + 3}}{{\alpha^{4} + 14\alpha^{2} + 1}}. \\ \end{aligned} $$

Recall the definition of $\overline{\overline{\theta }} \left( \alpha \right)$, and it is easy to check that $\frac{{\alpha^{4} + 2\alpha^{3} + 12\alpha^{2} + 14\alpha + 8\sqrt {\alpha + 2\alpha^{2} + \alpha^{3} } + 3}}{{\alpha^{4} + 14\alpha^{2} + 1}} > 3 > \bar{\theta }\left( \alpha \right)$. Therefore, the condition to have ${{\Pi }}_{lp}^{M} \left( {e^{pool} } \right) \ge {{\Pi }}_{ll}^{M} \left( {e_{l}^{sep} } \right)$ is $\theta \le \overline{\overline{\theta }} \left( \alpha \right).$ Proposition 4 is proved. □

Proof of Proposition 5

We drive the optimal ex ante wholesale prices according to the value of $\theta$. Case (i): $\theta \le \overline{\overline{\theta }}(\alpha)$. In this case, the manufacturer will pool. Thus, the manufacturer’s ex ante expected profit is

$$ \begin{aligned} {{\Pi }}^{M} \left( w \right) & = E_{i} \left[ { {{\Pi }}_{ip}^{M} \left( w \right)} \right] = \alpha {{\Pi }}_{hp}^{M} \left( w \right) + \left( {1 - \alpha } \right) {{\Pi }}_{lp}^{M} \left( w \right) \\ & = \alpha \left[ {w\left( {a - b\frac{{a + \mu e^{p} + bw}}{2b} + \beta_{h} e^{p} } \right) - ke^{{p}^{2}} } \right] \\ &\quad + \left( {1 - \alpha } \right)\left[ {w\left( {a - b\frac{{a + \mu e^{p} + bw}}{{2b}} + \beta _{l} e^{p} } \right) - ke^{{p} ^{2}} } \right] \\ & = - \frac{1}{2}bw^{2} + \frac{{a - \mu e^{p} }}{2}w + \mu e^{p} w - ke^{{p}^{2}} \\ & = \frac{{\left( {2\beta_{l} - \mu } \right)^{2} w^{2} \left( {k - \mu w} \right)}}{{16k^{2} }} + \frac{{bw^{2} + aw}}{2}. \\ \end{aligned} $$

Taking the first- and second-order derivatives on the above equation, we obtain

$$ \frac{{d{{\Pi }}^{M} \left( w \right)}}{dw} = \frac{a}{2} - bw - \frac{{w\left( {2\beta_{l} - \mu } \right)\left( { - 4\alpha \beta_{h} - 2\beta_{l} + 4\alpha \beta_{l} + \mu } \right)}}{8k}, $$

and

$$ \begin{aligned} \frac{{d^{2} {{\Pi }}^{M} \left( w \right)}}{{dw^{2} }} & = - \frac{{8bk + \left( {2\beta_{l} - \mu } \right)\left( { - 4\alpha \beta_{h} - 2\beta_{l} + 4\alpha \beta_{l} + \mu } \right)}}{8k} \\ & = - \frac{b}{k}\left[ {k - \frac{{\beta_{l}^{2} \left( {1 - \alpha \theta + \alpha } \right)\left( {3\alpha \theta - 3\alpha + 1} \right)}}{8b}} \right] < 0. \\ \end{aligned} $$

The last inequality holds from $k > \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)/8b$, and

$$ \frac{{\beta_{l}^{2} }}{8b}\left( {\alpha \theta^{2} + 1 - \alpha } \right) - \frac{{\beta_{l}^{2} }}{8b}\left( {1 - \alpha \theta + \alpha } \right)\left( {3\alpha \theta - 3\alpha + 1} \right) = \frac{{\beta_{l}^{2} }}{8b}\alpha \left( {1 + 3\alpha } \right)\left( {\theta - 1} \right)^{2} > 0. $$

Thus, ${{\Pi }}^{M} \left( w \right)$ is concave, and the optimal wholesale price can be determined from the first-best condition. We obtain $w = \frac{4ak}{{8bk - \beta_{l}^{2} \left[ {1 + 2\alpha \left( {\theta - 1} \right) - 3\alpha^{2} \left( {\theta - 1} \right)^{2} } \right]}}.$

With the optimal ex ante $w$, it is easy to check that the optimal advertising effort and the optimal retailing price are $e^{pool} = \frac{{a\beta_{l} \left( {1 + \alpha - \alpha \theta } \right)}}{{8bk - \beta_{l}^{2} \left[ {1 + 2\alpha \left( {\theta - 1} \right) - 3\alpha^{2} \left( {\theta - 1} \right)^{2} } \right]}}$ and $p_{p} = \frac{{a\left\{ {6bk + \alpha \beta_{l}^{2} \left( {\theta - 1} \right)\left[ {\alpha \left( {\theta - 1} \right) - 1} \right]} \right\}}}{{b\left\{ {8bk - \beta_{l}^{2} \left[ {1 + 2\alpha \left( {\theta - 1} \right) - 3\alpha^{2} \left( {\theta - 1} \right)^{2} } \right]} \right\}}}$, respectively.

Case (ii): $\bar{\bar\theta}(\alpha) < \theta \le 3$. In this case, the manufacturer achieves costly separating, and the manufacturer’s ex ante expected profit is

$$ \begin{aligned} {{\Pi }}^{M} \left( w \right) & = E_{i} \left[ { {{\Pi }}_{ii}^{M} \left( w \right)} \right] = \alpha {{\Pi }}_{hh}^{M} \left( w \right) + \left( {1 - \alpha } \right){{\Pi }}_{ll}^{M} \left( w \right) \\ & = \alpha \left[ {w\left( {\frac{a - bw}{2} + \frac{{\beta_{h} }}{2}e_{hh} } \right) - ke_{hh}^{2} } \right] + \left( {1 - \alpha } \right)\left[ {w\left( {\frac{a - bw}{2} + \frac{{\beta_{l} }}{2}e_{l}^{sep} } \right) - ke_{l}^{{sep}^{2}}} \right] \\ & = \frac{{\left( {a - bw} \right)w}}{2} + \frac{{w^{2} }}{16k}\left[\alpha \beta_{h}^{2} + \left( {1 - \alpha } \right)\left( {2\beta_{h} - 2\beta_{l} - \sqrt {\left( {3\beta_{h} - \beta_{l} } \right)\left( {\beta_{h} - \beta_{l} } \right)} } \right)\left( {3\beta_{l} - 2\beta_{h} + \sqrt {\left( {3\beta_{h} - \beta_{l} } \right)\left( {\beta_{h} - \beta_{l} } \right)} } \right)\right]. \\ \end{aligned} $$

Taking the first- and second-order derivatives on the above equation, we have

$$ \frac{{d{{\Pi }}^{M} \left( w \right)}}{dw} = \frac{a}{2} - bw + \frac{{w\beta_{l}^{2} \left\{ {\left\{ {\left( {8\alpha - 7} \right)} \right.\theta^{2} + 4\left( {1 - \alpha } \right)\left[ {3\theta - 1 + \left( {\theta - 1} \right)\sqrt {\left( {3\theta - 1} \right)\left( {\theta - 1} \right)} } \right]} \right\}}}{8k} = - bw + \frac{{w\beta_{l}^{2} \gamma }}{8k}, $$

and

$$ \frac{{d^{2} {{\Pi }}^{M} \left( w \right)}}{{dw^{2} }} = - b + \frac{\beta ^{2}_{1} \left\{ (8\alpha - 7) \, \theta ^{2} + 4(1 - \alpha) \left[3 \theta -1 + (\theta -1) \sqrt {(3 \theta -1) (\theta -1)}\right] \right \} } {8k} = \frac{{ - 8bk + \beta_{l}^{2} \gamma }}{8k} < 0, $$

Recall that we assume $k > \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)/8b$, and we can check that

$$ \frac{{\beta_{l}^{2} }}{8b}\left( {\alpha \theta^{2} + 1 - \alpha } \right) - \frac{{\beta_{l}^{2} }}{8b}\gamma = \frac{{\beta_{l}^{2} }}{8b}\left( {1 - \alpha } \right)\left( {\theta - 1} \right)\left( {7\theta - 4\sqrt {1 - 4\theta + 3\theta^{2} } - 5} \right) > 0. $$

Thus, we have $\frac{{d^{2} {{\Pi }}^{M} \left( w \right)}}{{dw^{2} }} < 0$. Then, the optimal wholesale price can be determined from the first-best condition. We obtain $w = \frac{4ak}{{8bk - \beta_{l}^{2} {{\gamma }}}}.$

With the optimal ex ante $w$, it is easy to obtain that the $h$-type manufacturer and the $l$-type manufacturer’s optimal advertising effort are $e_{h}^{sep} = \frac{{a\beta_{l} \theta }}{{8bk - \beta_{l}^{2} \gamma }}$ and $e_{l}^{sep} = \frac{{a\beta_{l} \left( {2\theta - 1 - \sqrt {\left( {\theta - 1} \right)\left( {3\theta - 1} \right)} } \right)}}{{8bk - \beta_{l}^{2} \gamma }}$, and the optimal retailing prices are $p_{h} = \frac{{a\left[ {12bk + \beta_{l}^{2} \left( {\theta^{2} - \gamma } \right)} \right]}}{{2b\left( {8bk - \beta_{l}^{2} \gamma } \right)}}$ and $p_{l} = \frac{{a\left[ {12bk - \beta_{l}^{2} \left( {1 + \gamma - 2\theta + \sqrt {\left( {\theta - 1} \right)\left( {3\theta - 1} \right)} } \right)} \right]}}{{2b\left( {8bk - \beta_{l}^{2} \gamma } \right)}}$.

Case (iii): $\theta > 3$. In this case, the manufacturer will attain costless separating, and the manufacturer’s ex ante expected profit is

$$ \begin{aligned} {{\Pi }}^{M} \left( w \right) & = E_{i} \left[ { {{\Pi }}_{ii}^{M} \left( w \right)} \right] = \alpha {{\Pi }}_{hh}^{M} \left( w \right) + \left( {1 - \alpha } \right) {{\Pi }}_{ll}^{M} \left( w \right) \\ & = \alpha \left[ {w\left( {\frac{a - bw}{2} + \frac{{\beta_{h} }}{2}e_{hh} } \right) - ke_{hh}^{2} } \right] + \left( {1 - \alpha } \right)\left[ {w\left( {\frac{a - bw}{2} + \frac{{\beta_{l} }}{2}e_{ll} } \right) - ke_{ll}^{2} } \right] \\ & = \frac{{\left( {a - bw} \right)w}}{2} + \frac{{w^{2} }}{16k}\left[ {\alpha \beta_{h}^{2} + \left( {1 - \alpha } \right)\beta_{l}^{2} } \right] \\ \end{aligned} $$

Taking the first- and second-order derivatives on the above equation, we have

$$ \frac{{d{{\Pi }}^{M} \left( w \right)}}{dw} = \frac{a}{2} - bw + \frac{w}{8k}\left[ {\alpha \beta_{h}^{2} + \left( {1 - \alpha } \right)\beta_{l}^{2} } \right], $$

and

$$ \frac{{d^{2} {{\Pi }}^{M} \left( w \right)}}{{dw^{2} }} = \frac{{ - 8bk + \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}}{8k} < 0, $$

where the last inequality holds from $k > \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)/8b$. Then, the optimal wholesale price can be determined from the first-best condition. We obtain $w = \frac{4ak}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}}$.

With the optimal ex ante $w$, it is easy to obtain that the $h$-type manufacturer and the $l$-type manufacturer’s optimal advertising effort are $e_{h}^{sep} = \frac{{a\beta_{l} \theta }}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}}$ and $e_{l}^{sep} = \frac{{a\beta_{l} }}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}}$, and the optimal retailing prices are $p_{h} = \frac{{a\left[ {12bk + \beta_{l}^{2} \left( {1 - \alpha } \right)\left( {\theta^{2} - 1} \right)} \right]}}{{2{\text{b}}\left[ {8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)} \right]}}$ and $p_{l} = \frac{{a\left[ {12bk - \alpha \beta_{l}^{2} \left( {\theta^{2} - 1} \right)} \right]}}{{2b\left[ {8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)} \right]}}$. □

Proof of Proposition 8

From (1), the manufacturer’s ex ante profit is

$$ \begin{aligned} {\tilde{{\Pi }}}^{M} \left( w \right) & = E\left[ {{\tilde{{\Pi }}}^{M} \left( w \right)} \right] = \alpha {\tilde{{\Pi }}}_{h}^{M} \left( w \right) + \left( {1 - \alpha } \right){\tilde{{\Pi }}}_{l}^{M} \left( w \right) \\ & = \alpha \left[ {w\left( {\frac{a - bw}{2} + \frac{{\beta_{h} }}{2}e_{hh} } \right) - ke_{hh}^{2} } \right] + \left( {1 - \alpha } \right)\left[ {w\left( {\frac{a - bw}{2} + \frac{{\beta_{l} }}{2}e_{ll} } \right) - ke_{ll}^{2} } \right] \\ & = \frac{{\left( {a - bw} \right)w}}{2} + \frac{{w^{2} }}{16k}\left[ {\alpha \beta_{h}^{2} + \left( {1 - \alpha } \right)\beta_{l}^{2} } \right]. \\ \end{aligned} $$

(A15)

Take the first- and second-order derivatives on the above equation, we have

$$ \frac{{d{\tilde{{\Pi }}}^{M} \left( w \right)}}{dw} = \frac{a}{2} - bw + \frac{w}{8k}\left[ {\alpha \beta_{h}^{2} + \left( {1 - \alpha } \right)\beta_{l}^{2} } \right], $$

and

$$ \frac{{d^{2} {\tilde{{\Pi }}}^{M} \left( w \right)}}{{dw^{2} }} = \frac{{ - 8bk + \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}}{8k} < 0, $$

where the last inequality holds from $k > \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)/8b$. Then, the optimal wholesale price can be determined by letting $\frac{{d{\tilde{{\Pi }}}^{M} \left( w \right)}}{dw} = 0$, which implies that $\tilde{w} = \frac{4ak}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}}$.Substituting $\tilde{w}$ to (A15), we have ${\tilde{{\Pi }}}^{M} = \frac{{a^{2} k}}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}}.$ □

Proof of Proposition 9

We compare ${\tilde{{\Pi }}}^{M}$ and ${{\Pi }}^{M}$ for different values of $\theta$.

If $\theta \le \overline{\overline{\theta }}(\alpha)$, from Proposition 5, ${{\Pi }}^{M} = \frac{{a^{2} k}}{{8bk - \beta_{l}^{2} \left[ {1 + 2\alpha \left( {\theta - 1} \right) - 3\alpha^{2} \left( {\theta - 1} \right)^{2} } \right]}}.$ Thus, we have

$$ \begin{aligned} \frac{{{\tilde{{\Pi }}}^{M} }}{{{{\Pi }}^{M} }} & = \frac{{8bk - \beta_{l}^{2} \left[ {1 + 2\alpha \left( {\theta - 1} \right) - 3\alpha^{2} \left( {\theta - 1} \right)^{2} } \right]}}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}} \\ & = \frac{{8bk - \beta_{l}^{2} \left[ {1 + 2\alpha \left( {\theta - 1} \right) - 3\alpha^{2} \left( {\theta - 1} \right)^{2} } \right] - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right) + \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}} \\ & = 1 + \frac{{\beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right) - \beta_{l}^{2} \left[ {1 + 2\alpha \left( {\theta - 1} \right) - 3\alpha^{2} \left( {\theta - 1} \right)^{2} } \right]}}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}} \\ & = 1 + \frac{{\beta_{l}^{2} \left[ {\left( {\alpha \theta^{2} + 1 - \alpha } \right) - \left( {1 - \alpha \theta + \alpha } \right)\left( {3\alpha \theta - 3\alpha + 1} \right)} \right]}}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}} \\ & = 1 + \frac{{\frac{{\beta_{l}^{2} }}{8b}\alpha \left( {1 + 3\alpha } \right)\left( {\theta - 1} \right)^{2} }}{{k - \frac{{\beta_{l}^{2} }}{8b}\left( {\alpha \theta^{2} + 1 - \alpha } \right)}} > 1. \\ \end{aligned} $$

(A16)

In the right-hand side of (A16), the denominator $k - \frac{{\beta_{l}^{2} }}{8b}\left( {\alpha \theta^{2} + 1 - \alpha } \right) > 0$ from assumption $k > \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)/8b$, and the numerator $\frac{{\beta_{l}^{2} }}{8b}\alpha \left( {1 + 3\alpha } \right)\left( {\theta - 1} \right)^{2} > 0$ has been shown in proof of Proposition 5. Therefore, the right-hand side of (A15) is greater than 1, i.e., $\frac{{{\tilde{{\Pi }}}^{M} }}{{{{\Pi }}^{M} }} > 1$. In this case, we have ${\tilde{{\Pi }}}^{M} > {{\Pi }}^{M} .$

If $\overline{\overline{\theta }}(\alpha) < \theta \le 3$, from Proposition 5, ${{\Pi }}^{M} = \frac{{a^{2} k}}{{8bk - \beta_{l}^{2} \gamma }}$. In this case, we have

$$ \begin{aligned} \frac{{{\tilde{{\Pi }}}^{M} }}{{{{\Pi }}^{M} }} & = \frac{{8bk - \beta_{l}^{2} \gamma }}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}} \\ & = \frac{{8bk - \beta_{l}^{2} \gamma - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right) + \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}} \\ & = 1 + \frac{{\beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right) - \beta_{l}^{2} \gamma }}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}} \\ & = 1 + \frac{{\beta_{l}^{2} \left[ {\left( {\alpha \theta^{2} + 1 - \alpha } \right) - \gamma } \right]}}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}} \\ & = 1 + \frac{{\frac{{\beta_{l}^{2} }}{8b}\left( {1 - \alpha } \right)\left( {\theta - 1} \right)\left( {7\theta - 4\sqrt {1 - 4\theta + 3\theta^{2} } - 5} \right)}}{{k - \frac{{\beta_{l}^{2} }}{8b}\left( {\alpha \theta^{2} + 1 - \alpha } \right)}}. \\ \end{aligned} $$

(A17)

In the right-hand side of (A17), the denominator $k - \frac{{\beta_{l}^{2} }}{8b}\left( {\alpha \theta^{2} + 1 - \alpha } \right) > 0$ from assumption $k > \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)/8b$, and the numerator $\frac{{\beta_{l}^{2} }}{8b}\left( {1 - \alpha } \right)\left( {\theta - 1} \right)\left( {7\theta - 4\sqrt {1 - 4\theta + 3\theta^{2} } - 5} \right) > 0$ has been shown in the proof of Proposition 5. Thus, Therefore, the right-hand side of (A17) is greater than 1. In this case, ${\tilde{{\Pi }}}^{M} > {{\Pi }}^{M}$.

If $\theta > 3$, from Propositions 5 and 7, we have ${\tilde{{\Pi }}}^{M} = {{\Pi }}^{M}$.

To summarize, we always have ${\tilde{{\Pi }}}^{M} \ge {{\Pi }}^{M}$. □

Proof of Proposition 10

We establish the proof by considering the $h$-type manufacturer and the $l$-type manufacturer separately.

First, we consider the $h$-type manufacturer. From Table 1 and Proposition 7, we have

$$ \frac{{\tilde{e}}}{e} = \left\{ {\begin{array}{*{20}l} {\frac{{8bk - \beta_{l}^{2} \left[ {1 + 2\alpha \left( {\theta - 1} \right) - 3\alpha^{2} \left( {\theta - 1} \right)^{2} } \right]}}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}} \cdot \frac{\theta }{{\left( {1 + \alpha - \alpha \theta } \right)}}, } \hfill & {if\; \theta \le \overline{\overline{\theta }}(\alpha),} \hfill \\ {\frac{{8bk - \beta_{l}^{2} \gamma }}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}},} \hfill & {if\;\overline{\overline{\theta }} \left( \alpha \right) < \theta \le 3,} \hfill \\ {1,} \hfill & {if\;\theta > 3.} \hfill \\ \end{array} } \right. $$

Recall that in the proof of Proposition 9, we have shown that $\frac{{8bk - \beta_{l}^{2} \left[ {1 + 2\alpha \left( {\theta - 1} \right) - 3\alpha^{2} \left( {\theta - 1} \right)^{2} } \right]}}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}} > 1$ and $\frac{{8bk - \beta_{l}^{2} \gamma }}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}} > 1$. Also, it is easy to demonstrate that $\theta - \left( {1 + \alpha - \alpha \theta } \right) = \left( {1 + \alpha } \right)\left( {\theta - 1} \right) > 0$, which implies that $\frac{\theta }{{\left( {1 + \alpha - \alpha \theta } \right)}} > 1$. Thus, for the $h$-type manufacturer, we always have $\frac{{\tilde{e}}}{e} \ge 1$, i.e., $e \le \tilde{e}.$

Second, we consider the $l$-type manufacturer. Similarly, from Table 1 and Proposition 7, we have

$$ \frac{{\tilde{e}}}{e} = \left\{ {\begin{array}{*{20}l} {\frac{{8bk - \beta_{l}^{2} \left[ {1 + 2\alpha \left( {\theta - 1} \right) - 3\alpha^{2} \left( {\theta - 1} \right)^{2} } \right]}}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}} \cdot \frac{\theta }{{\left( {1 + \alpha - \alpha \theta } \right)}}, } \hfill & {if\; \theta \le \overline{\overline{\theta }}(\alpha),} \hfill \\ {\frac{{8bk - \beta_{l}^{2} \gamma }}{{8bk - \beta_{l}^{2} \left( {\alpha \theta^{2} + 1 - \alpha } \right)}} \cdot \frac{1}{{2\theta - 1 - \sqrt {\left( {\theta - 1} \right)\left( {3\theta - 1} \right)} }},} \hfill & {if\;\overline{\overline{\theta }} \left( \alpha \right) < \theta \le 3,} \hfill \\ {1,} \hfill & {if\;\theta > 3.} \hfill \\ \end{array} } \right. $$

It is easy to show that $\frac{1}{{\left( {1 + \alpha - \alpha \theta } \right)}} > 1$ and $\frac{1}{{2\theta - 1 - \sqrt {\left( {\theta - 1} \right)\left( {3\theta - 1} \right)} }} \ge 1$ for any $\theta \le 3$. Thus, in this case, $\frac{{\tilde{e}}}{e} \ge 1$, i.e., $e \le \tilde{e}$.

To summarize, we always have $e \le \tilde{e}$. □