SASS: slicing with adaptive steps search method for finding the non-dominated points of tri-objective mixed-integer linear programming problems

Abstract

Multi-objective optimization problems (MOOP) reflect the complexity of many real-world decision problems where objectives are conflicting. The presence of more than one criterion makes finding the non-dominated (ND) points a crucial issue in the decision making process. Tri-objective mixed-integer linear programs (TOMILP) are an important subclass of MOOPs that are applicable to many problems in economics, business, science, and engineering including sustainable systems that must consider economic, environmental, and social concerns simultaneously. The literature on finding the ND points of TOMILPs is limited; there are only a few algorithms published in the literature that do not guarantee generating the entire ND points of TOMILPs. We present a new method, the Slicing with Adaptive Steps Search (SASS), to generate the ND points of TOMILPs. The result of SASS is primarily a superset of the set of ND points in the form of (partially) ND faces. We then perform a post-processing to eliminate the dominated parts of the partially ND faces. We provide a theoretical analysis of SASS and illustrate its effectiveness on a large set of instances.

Appendices

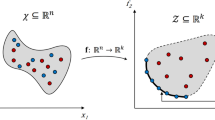
The formulation of the illustrative instance given in Fig. 1

We provide the mathematical formulation for Fig. 1 (note that there can be other formulations that correspond to the same feasible region shown in Fig. 1). Let M be a sufficiently large number (e.g. we use $M=1000$), $x=(x_1,x_2,x_3) \ge 0$, and $y=(y_1,y_2,y_3) \in \{0, 1\}^3$.

$$\begin{aligned}&\hbox {max }z(x,y)=(x_1,x_2,x_3)\\&\hbox {s.t.}\\&5x_1+5x_2+2x_3 \le 66+M(1-y_1),\\&-6-M(1-y_1) \le -x_1+x_2 \le 8+M(1-y_1),\\&x_1+x_2 - x_3 \ge 2-M(1-y_1),\\&-3x_1-3x_2 -4x_3 \le -48+M(1-y_1),\\&1-M(1-y_2) \le x_1 \le 5+M(1-y_2),\\&4-M(1-y_2) \le x_2 \le 7+M(1-y_2),\\&3-M(1-y_2) \le x_3 \le 9+M(1-y_2),\\&5-M(1-y_3) \le x_1+x_2 \le 11+M(1-y_3),\\&-5-M(1-y_3) \le -x_1+x_2 \le -4+M(1-y_3),\\&1-M(1-y_3) \le x_3 \le 5+M(1-y_3),\\&y_1+y_2+y_3 = 1,\\&x_i \ge 0, \; \forall i=1,2,3,\\&y_i \in \{0,1\}, \; \forall i=1,2,3. \end{aligned}$$

The value of $\delta _j$, $j=1,2$

These values are supposed to be very small positive numbers. Their function is to exclude some regions in the objective space which do not include ND points. We set the values of $\delta _j$’s based on the ranges of objective function values. Let $\Delta$ be a sufficiently small positive value between 0 and 1. Then, we set $\delta _j:=\Delta \times$“a value derived from the range of the $j^{th}$ objective function” for $j=1,2$. These ranges differ in different sections of the algorithm. We provide the value of $\delta _j$, $j=1,2$, for constraints EC given in (4), the LOP given in (5), DM2 given in (7), and $\mathrm {LOP}_{sy}$ given in (10).

In (4) and the LOP given in (5), $\delta _j:=\Delta \times \Omega _j$, where $\Omega _j:=max\{z_j(x,y) \; | \; x\in S(y), y \in \mathbb {Z}^q, z_3(x,y)=z_3^{cr}\}-min\{z_j(x,y) \; | \; x\in S(y), y \in \mathbb {Z}^q, z_3(x,y)=z_3^{cr}\}$, for $j=1,2$. Note that $\Omega _j$ is the range of $z_j(x,y)$ in the slice $SL(z_3^{cr})$.

Regarding $\delta _1$-value used in DM2 given in (7), we solve the following problems:

$$\begin{aligned} z^U_2:=\mathrm {max}&z_2(x,y^A) \\ \mathrm {s.t.}&x \in S(y^A), \; z_3(x,y^A)=z_3^A, \nonumber \\ z^L_1:=\mathrm {max}&z_1(x,y^A) \nonumber \\ \mathrm {s.t.}&x \in S(y^A), \; z_3(x,y^A)=z_3^A, \; z_2(x,y^A)=z_2^U\nonumber \end{aligned}$$

(14)

and

$$\begin{aligned} z^U_1:=\mathrm {max}&z_1(x,y^A) \\ \mathrm {s.t.}&x \in S(y^A), \; z_3(x,y^A)=z_3^A.\nonumber \end{aligned}$$

(15)

Then, $\delta _1:=\Delta \times (z_1^U-z_1^L)$. Note that $(z_1^U-z_1^L)$ is equal to the range of $z_1$-value in $NDSSL(z_3^A,y^A)$.

In the $\mathrm {LOP}_{sy}$ given in (10), $\delta _j:=\Delta \times \Omega _j$, where $\Omega _j:=max\{z_j(x,y^A) \; | \; x\in S(y^A)\}-min\{z_j(x,y^A) \; | \; x\in S(y^A)\}$, for $j=1,2$. Note that $\Omega _j$ is the range of $z_j(x,y^A)$ in $x \in S(y^A)$.

No-good constraints

If y is a binary vector, we add constraint (16) to exclude $\bar{y}$ from the feasible region.

$$\begin{aligned} \sum _{i:\bar{y}_i=1} y_i - \sum _{i:\bar{y}_i=0} y_i \le \sum _{i} \bar{y}_i -1. \end{aligned}$$

(16)

Note that if we add (16) to a problem, $\bar{y}$ does not satisfy (16), and then $\bar{y}$ is excluded from the feasible region. However, all binary vectors other than $\bar{y}$ satisfy (16).

Now, suppose that $y_i$’s are general integer such that $1-2^U \le y_i \le 2^U$, for all $i=1,\ldots ,q$, where $(1-2^U)$ and $2^U$ are known lower and upper bounds on the values of $y_i$’s. For example, if $U=3$, then we know $-7\le y_i\le 8$, for all i (note that we can set U such that $1-2^U \le y_i \le 2^U$ is valid for all i). We define binary variables $w_{iu} \in \{0,1\}$, for all $i=1,\ldots ,q$, $u=0,\ldots ,U$. Assume that we want to exclude $\bar{y}$. Consider equations:

$$\begin{aligned} \bar{y}_i = (1-2^U) + \sum _{u=0}^{U}2^{u} \bar{w}_{iu}, \ \forall i, \end{aligned}$$

where $\bar{y}_i$’s are given and $\bar{w}_{iu}$’s are determined based on $\bar{y}_i$’s. We note that these equations map $\bar{y}$ to a unique $\bar{w}$. Hence, we add the following constraints to exclude $\bar{y}$.

$$\begin{aligned}&y_i = (1-2^U)+\sum _{u=0}^{U}2^{u}w_{iu}, \ \forall i, \end{aligned}$$

(17)

$$\begin{aligned}&\sum _{i,u:\bar{w}_{iu}=1}w_{iu}-\sum _{i,u:\bar{w}_{iu}=0}w_{iu}\le \sum _{i,u}\bar{w}_{iu}-1, \end{aligned}$$

(18)

$$\begin{aligned}&w_{iu}\in \{0,1\}, \ \forall i=1,\ldots ,q,\ u=0,\ldots ,U, \end{aligned}$$

(19)

where (17) assigns values to $w_{ui}$’s and (18) excludes $\bar{w}$ (and consequently $\bar{y}$). We acknowledge that there are other types of no-good constraints to exclude integer variables (Soylu and Yıldız 2016).

Generating our instances

In the mathematical formulation of our instances, we have m constraints, q integer variables, and n continuous variables. Moreover, $m=q+n$. $U_I$ is the upper bound on the values of integer variables. Moreover, CF is a real number to enlarge or tighten the feasible region. Boland et al. (2015b) present these instances with $CF=1$. However, to change the size of the feasible regions, we also consider $CF=0.5$ and $CF=2$.

$$\begin{aligned}&max \; \; z_1(x,y)=\sum _{i=1}^{n} c_i^1 x_i + \sum _{j=1}^{q} f_j^1 y_j\\&max \; \; z_2(x,y)=\sum _{i=1}^{n} c_i^2 x_i + \sum _{j=1}^{q} f_j^2 y_j\\&max \; \; z_3(x,y)=\sum _{i=1}^{n} c_i^3 x_i + \sum _{j=1}^{q} f_j^3 y_j\\&\hbox {s.t.}\\&\sum _{i=1}^{n} a_{ij} x_i + a'_j y_j \le b_j, \; \forall j=1, \ldots , q,\\&\sum _{i=1}^{n} a_{ij} x_i \le b_j, \; \forall j=q + 1, \ldots , m-1,\\&\sum _{j=1}^{q} y_j \le \frac{q}{3}CF,\\&x_i \in \mathbb {R}^{+}, \; \forall \; i=1, \ldots , n,\\&y_j \in \{0,1, \ldots , U_I\}, \; \forall \; j=1, \ldots , q,\\ \end{aligned}$$

where in the described benchmarks, the objective function coefficients of the continuous and integer variables, right-hand-side values of the constraints, and the coefficients in the left-hand sides of the constraints (for both continuous and integer variables) are generated using a uniform distribution with domains $[-10, 10], [-200, 200], [50, 100]$, and $[-1, 20]$, respectively.