Robust numerical schemes for time delayed singularly perturbed parabolic problems with discontinuous convection and source terms

Abstract

This article deals with two different numerical approaches for solving singularly perturbed parabolic problems with time delay and interior layers. In both approaches, the implicit Euler scheme is used for the time scale. In the first approach, the upwind scheme is used to deal with the spatial derivatives whereas in the second approach a hybrid scheme is used, comprising the midpoint upwind scheme and the central difference scheme at appropriate domains. Both schemes are applied on two different layer resolving meshes, namely a Shishkin mesh and a Bakhvalov–Shishkin mesh. Stability and error analysis are provided for both schemes. The comparison is made in terms of the maximum absolute errors, rates of convergence, and the computational time required. Numerical outputs are presented in the form of tables and graphs to illustrate the theoretical findings.

1 Introduction

The time delay/lag is not just a mathematical invention, since it is deeply rooted in many natural and man-made systems such as biology, process industries, and mechatronic motions. The lag can capture a wide variety of possible gestures of a simple system [1, 2]. Any system certainly can contain a time lag if it has a feedback control or if it requires prior information about itself to act further.

Time-delayed singularly perturbed parabolic differential equations (SPPDEs) are delayed parabolic differential equations (DPDEs) in which a small perturbation parameter ($0<\varepsilon \ll 1$) is associated along with the time delay parameter. The parameter ($\varepsilon$) is multiplied to the highest-order spatial derivative term, affecting the solution in a larger scale, when $\varepsilon \rightarrow 0$. Some of the main differences between the instantaneous SPPDEs and the time-delayed SPPDEs are mentioned below [3]:

• 1. SPPDEs with time-delay can capture/predict the after-effect of a system that can not be done by conventional instantaneous SPPDEs.

• 2. The delay in time ($\rho$) is large enough and hence the nature of the approximated solution can behave quite differently from the original solution, if approximated by the first few terms of Taylor series expansion.

• 3. SPPDEs without delay have an initial condition as a function of the space variable (x) only i.e., along time (t) at 0, whereas in case of time-delayed SPPDEs, the initial condition is always a function of both x and t.

• 4. Even if the initial condition given in the delayed domain is sufficiently differentiable, in general, the solution may have various discontinuities along the integration interval in the time direction. This is due to the fact that the initial function does not satisfy the DPDE. However, these discontinuities smooth out more and more as time progresses.

It is evident that the introduction of a time delay in a differential model significantly increases the complexity of the model. Undoubtedly, some of the recent developments in theory and applications have enhanced our conception, regarding the mathematical and qualitative behavior of time-delayed SPPDEs. To mention a few, one can refer to Das and Natesan [4] who used the hybrid scheme on a spatial Shishkin mesh (S-mesh) and the implicit Euler scheme on a time uniform mesh. Govindarao and Mohapatra [5] proposed a fourth-order scheme to solve the problems appearing in population dynamics and in [6], Kaushik and Sharma studied the use of an adaptive grid. Again, for time delayed SPPs containing two small parameters in [7], the authors used the implicit Euler scheme in time on a uniform mesh with an upwind scheme in space using both the S-mesh and the Bakhvalov Shishkin mesh (B–S-mesh). Keeping meshes the same, both in time and space for the same class of problems, the authors in [8] used a hybrid scheme in space. Recently, the authors in [9] used the Richardson extrapolation technique in both space and time with three different layer resolving meshes in the spatial direction, to have a global second-order accuracy. For semilinear time-delayed SPPDEs, Priyadarshana et al., in [10] and [11] proposed second-order time accurate schemes with upwind and weighted variable based monotone hybrid scheme in space, respectively. For some recent developments in this regard, one can also go through [12,13,14] and the references therein.

In all the literature discussed above the coefficients associated with the time-delayed SPPDEs are considered to be sufficiently smooth. There is no significant discussion (neither asymptotic analytical nor numerical) for SPPDEs with discontinuous coefficients. Our work comes to fill this gap in the literature. It is worthy enough to mention that the discontinuity in the convection coefficient (especially with alternate sign pattern) can create a solid abrupt change in the solution to any SPPDE, causing layers in the interior to the domain of consideration, as $\varepsilon \rightarrow 0$ [15]. These layers are called the interior layers and the part of this domain is called the interior layer region. Apart from their widespread applications, these problems are of major concern as one has to handle the discontinuity, the sharp change because of $\varepsilon$, and the larger delay in time, all at once. The time-delayed SPPDEs with interior layers need more mathematical maturity than their without-delay counterparts, as the error in each segment of the time domain has to be efficiently handled so that it will be less contributory to the error in subsequent sub-domains. The prime objective of this work is to design some parameter-uniform numerical approximations for these problems, where some minute changes in the parameters highly impact the solutions. Before discussing the model problem, a brief literature survey for numerical approximations of singularly perturbed problems (SPPs) with interior layers is discussed below.

In the literature, several researchers have done some remarkable contributions to the numerical approximations of SPPs with interior layers. Mainly, for the stationary case, Farrell et al. [16, 17], Shanthi et al. [18] and for the parabolic case, O’Riordan and Shishkin [19] and Shishkin [20] are referred to. Mukherjee and Natesan studied problems of the form (1) without any delay by using the Fitted Mesh Methods (FMMs). Initially, in [21] experiments with applying the first-order upwind-based FMM on two different layer resolving meshes namely the S-mesh and the B–S-mesh was considered. Furthermore, in [15] a second-order accurate (up to a logarithmic term) hybrid scheme in the spatial direction on the S-mesh is discussed. Recently, for the same class of problems, Yadav and Mukherjee in [22] used a second-order accurate modified hybrid scheme on an S-mesh in the spatial direction, and also extended their study to the semilinear form of the same model problem.

In this work, a SPPDE with interior layers and a large time lag is discussed. Before that, some basic notations are introduced as follows,

$$\begin{aligned} \left\{ \begin{array}{ll} \overline{{\mathcal {F}}}= {\mathcal {F}} \cup \partial {\mathcal {F}},\quad {\mathcal {F}}={\mathcal {F}}_{x}\times {\mathcal {F}}_{t},\quad \partial {\mathcal {F}} = {\Upsilon _{d}} \cup {\Upsilon _{l}} \cup {\Upsilon _{r}},\\ {\mathcal {F}}^{-}={\mathcal {F}}_{x}^{-}\times {\mathcal {F}}_{t}, \quad {\mathcal {F}}^{+}={\mathcal {F}}_{x}^{+}\times {\mathcal {F}}_{t},\\ {\mathcal {F}}_{x}=(0,1),\quad {\mathcal {F}}_{t}=(0,T],\quad {\mathcal {F}}_{x}^{-}=(0,\eta ), \quad {\mathcal {F}}_{x}^{+}=(\eta ,1),\quad 0<\eta <1,\\ {\Upsilon _{d}}={\mathcal {F}}_{x}\times [-\rho ,0], \quad {\Upsilon _{l}}=0 \times (0,T],\quad {\Upsilon _{r}}=1\times (0,T]. \end{array} \right. \end{aligned}$$

The following time delayed SPPDE is described on ${\mathcal {F}}^{-}\cup {\mathcal {F}}^{+}$

$$\begin{aligned} \left\{ \begin{array}{ll} L_{\varepsilon }z(x,t)\equiv \big (-z_{t}+\varepsilon z_{xx}+a(x)z_{x}-b(x)z\big )(x,t)=-z(x,t-\rho )+f(x,t),\\ z\big |_{\Upsilon _{d}}=\varPhi _{d}(x,t),\quad z\big |_{\Upsilon _{l}}=\varPhi _{l}(t),\quad z\big |_{\Upsilon _{r}}=\varPhi _{r}(t). \end{array} \right. \end{aligned}$$

(1)

$0<\varepsilon \ll 1$ is the perturbation parameter and $\rho > 0$ is the temporal lag. We assume that T is given by $T = k\rho$ for some $k\in {\mathbb {N}}$. All the analysis for (1) in $[0,1]\times [0,\rho ]$ is analogous to SPPDE without time lag having discontinuous convection and source term, as the solution in this domain depends upon the known solution in $[0,1]\times [-\rho ,0]$. So in the present manuscript, all the discussions are done up to $[0,1]\times [\rho ,2\rho ]$. The proofs can be followed in an analogous way for $k>2$. We assume that the convection coefficient a(x) is sufficiently smooth on ${\mathcal {F}}_{x}^{-} \cup {\mathcal {F}}_{x}^{+}$, the source term f(x, t) is sufficiently smooth on ${\mathcal {F}}^{-}\cup {\mathcal {F}}^{+}$ and the coefficient b(x) is sufficiently smooth on $\overline{{\mathcal {F}}}_{x}$. Furthermore, consider that

$$\begin{aligned} \left\{ \begin{array}{ll} b(x)\ge \beta \ge 0,\quad \text {on}\quad \overline{{\mathcal {F}}}_{x},\\ |[a]|\le {\mathcal {C}},\quad |[f]|\le {\mathcal {C}}, \quad \text {at} \quad x=\eta . \end{array} \right. \end{aligned}$$

The solution satisfies the following interface condition $[z]=0,\quad [z_{x}]=0,\quad \text {at} \quad x=\eta ,$ where [z] represents the jump of z across $x=\eta$ (point of discontinuity) and is defined by $[z](\eta ,t)=z(\eta ^{+},t)-z(\eta ^{-},t)$, where $z(\eta ^{\pm },t)=\underset{x\rightarrow \eta \pm 0}{\lim }z(x,t)$. Because of the discontinuity of a(x) at $\eta$, the solution has an interior layer of width $O(\varepsilon )$ in the neighbourhood of $\eta$ [15, 21, 22]. Practically, the nature of the interior layer depends on the sign of a(x) on each side of the line of discontinuity. Therefore, the following assumptions will be considered to ensure the presence of strong interior layers:

$$\begin{aligned} \left\{ \begin{array}{ll} -\alpha _{1}^{*}< a(x)<-\alpha _{1}<0, \quad s<\eta , \\ \alpha _{2}^{*}> a(x)>\alpha _{2}>0, \quad s>\eta . \end{array} \right. \end{aligned}$$

The present work comprises a comparative study of two different finite difference schemes for solving (1). At first, (1) is solved using a combination of the implicit Euler scheme in the time direction and the upwind scheme in the spatial direction (IE-UP scheme). Again, keeping the implicit Euler scheme in time fixed, the second scheme is formed considering a hybrid scheme in the spatial direction (IE-HYB scheme). Both schemes are applied on S-mesh as well as B–S-mesh. The study is extended by solving the semilinear form of (1) using both schemes.

The manuscript is organized as follows. Some analytical aspects of the model problem are given in Sect. 2. The construction of meshes for both space and time direction is described in Sect. 3.1. Fully discrete schemes are discussed separately in Sects. 3.2 and 3.4. In Sects. 3.3 and 3.5, the stability analysis of each scheme is discussed, separately. Section 4 provides the error bounds of both schemes. Section 5 discusses the semilinear form of (1) along with Newton’s linearization technique. To verify the main conclusion in Sect. 7, Sect. 6 provides numerical tests on three different types of examples.

Throughout the manuscript, ${\mathcal {C}}>0$ is considered to be a generic constant, independent of $\varepsilon$, and the number of mesh points. For a real function f(x, t) defined on ${\mathcal {F}}$, the standard supremum norm is defined as $\Vert f \Vert _{\infty }$ = $\sup _{(x, t) \in {\mathcal {F}}} \mid f(x,t)\mid .$

2 Analytical solution of the continuous problem

In this section, the existence of a unique solution and some stability bounds are discussed. The coefficients used in $L_{\varepsilon }$ are time-independent and the discontinuity is only considered in the spatial variable. The sufficient smoothness of $\varPhi _{d}$, $\varPhi _{l}$ and $\varPhi _{r}$ along with the compatibility conditions at the corner points and delay terms are stated as: $\varPhi _{d}(0,0)=\varPhi _{l}(0)$, $\varPhi _{d}(1,0)=\varPhi _{r}(0)$ and

$$\begin{aligned} \left\{ \begin{array}{ll} -\dfrac{d\varPhi _{l}(0)}{d t}+\varepsilon \dfrac{\partial ^{2}\varPhi _{d}(0,0)}{\partial x^{2}}+a(0)\dfrac{\partial \varPhi _{d}(0,0)}{\partial x}-b(0)\varPhi _{d}(0,0)=-\varPhi _{d}(0,-\rho )+f(0,0),\\ -\dfrac{d\varPhi _{r}(0)}{d t}+\varepsilon \dfrac{\partial ^{2}\varPhi _{d}(1,0)}{\partial x^{2}}+a(1)\dfrac{\partial \varPhi _{d}(1,0)}{\partial x}-b(1)\varPhi _{d}(1,0)=-\varPhi _{d}(1,-\rho )+f(1,0). \end{array} \right. \end{aligned}$$

The compatibility conditions at $x=\eta$ follow analogously. The existence of a unique solution $z\in {\mathscr {C}}^{1+\lambda }({\mathcal {F}})\cap {\mathscr {C}}^{2+\lambda }({\mathcal {F}}^{-}\cup {\mathcal {F}}^{+})$ for (1) can be assumed from the results in [19, 23]. The differential operator $L_{\varepsilon }$ satisfies the following maximum principle.

Lemma 1

If a function $\psi \in {\mathscr {C}}^{0}(\overline{{\mathcal {F}}})\cup {\mathscr {C}}^{2}({\mathcal {F}}^{-}\cup {\mathcal {F}}^{+})$ satisfies $\psi (x,t)\le 0$, $(x,t)\in \partial {\overline{{\mathcal {F}}}}$ and $\bigg [\dfrac{\partial \psi }{\partial x}\bigg ](\eta ,t)\ge 0$, $t>0$ together with $L_{\varepsilon }\psi (x,t)\ge 0$, $\forall (x,t)\in {\mathcal {F}}^{-}\cup {\mathcal {F}}^{+}$, then $\psi (x,t)\le 0$ $\forall (x,t)\in \overline{{\mathcal {F}}}$.

Proof

Consider g(x, t) such that

$$\begin{aligned} \psi (x,t)=\exp (-\alpha |x-\eta |/2\varepsilon )g(x,t), \end{aligned}$$

where $\alpha =\min \{\alpha _{1},\alpha _{2}\}$. Assume that $(x^{*},t^{*})$ is a point where g(x, t) attains its maximum value, i.e.,

$$\begin{aligned} g(x^{*},t^{*})=\underset{(x,t)\in {\mathcal {F}}}{\max }g(x,t)>0. \end{aligned}$$

Clearly, $(x^{*},t^{*})\notin \partial \overline{{\mathcal {F}}}$. So, either $(x^{*},t^{*})\in {\mathcal {F}}^{-}\cup {\mathcal {F}}^{+}$ or $(x^{*},t^{*})=(\eta ,t^{*})$. If $(x^{*},t^{*})\in {\mathcal {F}}^{-}$, then

$$\begin{aligned} L_{\varepsilon }\psi (x^{*},t^{*})&=\exp (-\alpha _{1}|\eta -x^{*} |/2\varepsilon )\bigg (\varepsilon \dfrac{\partial ^{2}g}{\partial x^{2}}+(a(x^{*})+\alpha _{1})\dfrac{\partial g}{\partial x}\\&\quad +\bigg (\dfrac{\alpha _{1}}{2\varepsilon } \bigg (\dfrac{\alpha _{1}}{2}+a(x^{*})\bigg )-b(x^{*})\bigg )g-\dfrac{\partial g}{\partial t}\bigg )(x^{*},t^{*})<0. \end{aligned}$$

Similarly, for $(x^{*},t^{*})\in {\mathcal {F}}^{+}$, it is

$$\begin{aligned} L_{\varepsilon }\psi (x^{*},t^{*})&=\exp (-\alpha _{2}|x^{*}-\eta |/2\varepsilon )\bigg (\varepsilon \dfrac{\partial ^{2}g}{\partial x^{2}}+(a(x^{*})-\alpha _{2})\dfrac{\partial g}{\partial x}\\&\quad +\bigg (\dfrac{\alpha _{2}}{2\varepsilon }\bigg (\dfrac{\alpha _{2}}{2} -a(x^{*})\bigg )-b(x^{*})\bigg )g-\dfrac{\partial g}{\partial t}\bigg )(x^{*},t^{*})<0. \end{aligned}$$

Furthermore, if $(x^{*},t^{*})=(\eta ,t^{*})$, then

$$\begin{aligned} \bigg [\dfrac{\partial \psi }{\partial x}\bigg ](x^{*},t^{*})&=\bigg [\dfrac{\partial \psi }{\partial x}\bigg ](\eta ,t^{*})=\bigg [\dfrac{\partial \psi }{\partial x}\bigg ](\eta ^{+},t^{*})-\bigg [\dfrac{\partial \psi }{\partial x}\bigg ](\eta ^{-},t^{*})\\&=\bigg [\dfrac{\partial g}{\partial x}\bigg ](\eta ,t)-\dfrac{\alpha _{1}+\alpha _{2}}{2\varepsilon }g(\eta ,t). \end{aligned}$$

Since a contradiction is obtained in every possible situation, the statement is proved. $\square$

Lemma 2

The following bound holds true for the solution of (1)

$$\begin{aligned} \Vert z(x,t)\Vert _{\overline{{\mathcal {F}}}}\le \Vert z(x,t)\Vert _{\partial \overline{{\mathcal {F}}}}+\dfrac{1}{\gamma }\Vert f\Vert _{\overline{{\mathcal {F}}}}, \quad where\quad \gamma =\min \{\alpha _{1}/\eta ,\alpha _{2}/(1-\eta )\}. \end{aligned}$$

Proof

The proof is similar to the one in [19]. $\square$

2.1 Decomposition of the analytical solution

The solution of (1) is decomposed into its regular (u) and boundary layer (v) components as $z(x,t)=u(x,t)+v(x,t)$, where the regular component u is the solution of the following parabolic problem

$$\begin{aligned} \left\{ \begin{array}{ll} L_{\varepsilon }u(x,t)=-u(x,t-\rho )+f(x,t)\quad \text {for}\quad (x,t) \in {\mathcal {F}}^{-}\cup {\mathcal {F}}^{+},\\ u\big |_{\Upsilon _{d}}=z\big |_{\Upsilon _{d}}(x,t),\quad u\big |_{\Upsilon _{l}}=z\big |_{\Upsilon _{l}}(t),\quad u\big |_{\Upsilon _{r}}=z\big |_{\Upsilon _{r}}(t), \quad t\in {\mathcal {F}}_{t},\\ u(\eta ^{-},t)=\zeta _{1}(t),\quad u(\eta ^{+},t)=\zeta _{2}(t),\quad t\in {\mathcal {F}}_{t}. \end{array} \right. \end{aligned}$$

(2)

The suitable choices for $\zeta _{1}$ and $\zeta _{2}$ will be obtained later. Now, the boundary layer component satisfies

$$\begin{aligned} \left\{ \begin{array}{ll} L_{\varepsilon }v(x,t)=-v(x,t-\rho )\quad \text {for}\quad (x,t) \in {\mathcal {F}}^{-}\cup {\mathcal {F}}^{+},\\ v\big |_{\Upsilon _{d}}=0,\quad v\big |_{\Upsilon _{l}}=0,\quad v\big |_{\Upsilon _{r}}=0,\\ {[}v](\eta ,t)=-[u](\eta ,t),\quad \bigg [\dfrac{\partial v}{\partial x}\bigg ](\eta ,t) =-\bigg [\dfrac{\partial u}{\partial x}\bigg ](\eta ,t). \end{array} \right. \end{aligned}$$

(3)

Since, $v(\eta ^{-},t)=z(\eta ^{-},t)-u(\eta ^{-},t)$ and $v(\eta ^{+},t)=z(\eta ^{+},t)-u(\eta ^{+},t)$, without loss of generality, assuming $z(x,t)|_{\Upsilon _{d}}=0$, the following statement is proved.

Theorem 3

For $l,m\ge 0$ satisfying $0\le l\le 3$ and $0\le l+2\,m\le 4$, there exist smooth functions $\zeta _{1}(t)$, $\zeta _{2}(t)$ such that u(x, t) and v(x, t) defined in (2) and (3), respectively, satisfy the following bounds

$$\begin{aligned} \bigg \Vert \dfrac{\partial ^{l+m}u(x,t)}{\partial x^{l}\partial t^{m}}\bigg \Vert _{{\mathcal {F}}^{-}\cup {\mathcal {F}}^{+}}\le {\mathcal {C}}, \quad \bigg \Vert \dfrac{\partial ^{4}u(x,t)}{\partial x^{4}}\bigg \Vert _{{\mathcal {F}}^{-}\cup {\mathcal {F}}^{+}}\le {\mathcal {C}}\varepsilon ^{-1}, \end{aligned}$$

and

$$\begin{aligned} \bigg |\dfrac{\partial ^{l+m}v(x,t)}{\partial x^{l}\partial t^{m}}\bigg |= \left\{ \begin{array}{ll} {\mathcal {C}}\big (\varepsilon ^{-l}\exp (-(\eta -x)\alpha _{1}/\varepsilon )\big ),\quad (x,t)\in {\mathcal {F}}^{-},\\ {\mathcal {C}}\big (\varepsilon ^{-l}\exp (-(x-\eta )\alpha _{2}/\varepsilon )\big ),\quad (x,t)\in {\mathcal {F}}^{+}, \end{array} \right. \\ \bigg |\dfrac{\partial ^{4}v(x,t)}{\partial x^{4}}\bigg |= \left\{ \begin{array}{ll} {\mathcal {C}}\big (\varepsilon ^{-4}\exp (-(\eta -x)\alpha _{1}/\varepsilon )\big ),\quad (x,t)\in {\mathcal {F}}^{-},\\ {\mathcal {C}}\big (\varepsilon ^{-4}\exp (-(x-\eta )\alpha _{2}/\varepsilon )\big ),\quad (x,t)\in {\mathcal {F}}^{+}. \end{array} \right. \end{aligned}$$

Here, ${\mathcal {C}}$ is the bound for [a] and [f] as mentioned in the Sect. 1.

Proof

The proof will be carried out separately for separate sub-regions i.e., ${\mathcal {F}}^{-}$ and ${\mathcal {F}}^{+}$. To start with ${\mathcal {F}}^{+}$, an extended domain ${\mathcal {F}}^{*}$ is chosen, such that ${\mathcal {F}}^{+}\subset {\mathcal {F}}^{*}$, whereas ${\mathcal {F}}^{*}={\mathcal {F}}_{x}^{*}\times {\mathcal {F}}_{t}$, ${\mathcal {F}}_{x}^{*}=(-1,1)$. Let, $u^{*}$ be the smooth component on ${\mathcal {F}}_{x}^{*}$ defined as

$$\begin{aligned} u^{*}(x,t)=\sum \limits _{j=0}^3\varepsilon ^{j}u^{*}_{j}(x,t), \end{aligned}$$

where the components satisfy the following time delayed parabolic problems

$$\begin{aligned} \left\{ \begin{array}{ll} a^{*}(u_{0}^{*})_{x}-b^{*}(u_{0}^{*})-(u_{0}^{*})_{t} =-u_{0}^{*}(x,t-\rho )+f^{*}(x,t)\quad \text {in}\quad {\mathcal {F}}^{*},\\ u_{0}^{*}\big |_{\Upsilon _{d}}=\varPhi _{d}^{*}(x,t),\quad u_{0}^{*}\big |_{\Upsilon _{r}}=\varPhi _{r}(t), \end{array} \right. \end{aligned}$$

(4)

$$\begin{aligned} \left\{ \begin{array}{ll} a^{*}(u_{j}^{*})_{x}-b^{*}(u_{j}^{*})-(u_{j}^{*})_{t} =-u_{j}^{*}(x,t-\rho )-(u_{j-1}^{*})_{xx}\quad \text {in}\quad {\mathcal {F}}^{*},\\ u_{j}^{*}\big |_{\Upsilon _{d}}=0,\quad u_{j}^{*}\big |_{\Upsilon _{r}}=0,\quad j=1,2, \end{array} \right. \end{aligned}$$

(5)

and

$$\begin{aligned} \left\{ \begin{array}{ll} \varepsilon (u_{3}^{*})_{xx}+a^{*}(u_{3}^{*})_{x}-b^{*}(u_{3}^{*}) -(u_{3}^{*})_{t}=-u_{3}^{*}(x,t-\rho )-(u_{2}^{*})_{xx}\quad \text {in}\quad {\mathcal {F}}^{*},\\ u_{3}^{*}\big |_{\Upsilon _{d}}=0,\quad u_{3}^{*}\big |_{\Upsilon _{r}}=0,\quad u_{3}^{*}(-1,t)=0,\quad t\in {\mathcal {F}}_{t}. \end{array} \right. \end{aligned}$$

(6)

The coefficients $a^{*}$, $b^{*}$ are smooth extensions of the functions a and b from ${\mathcal {F}}_{x}^{+}$ to ${\mathcal {F}}_{x}^{*}$. Similarly, $f^{*}$, $\varPhi _{d}^{*}$ are smooth extensions of f, $\varPhi _{d}$, from ${\mathcal {F}}^{+}$ to ${\mathcal {F}}^{*}$, and are chosen in such a way that $f^{*}=0$, $\varPhi _{d}^{*}=0$ for $x=-1$ and $t\in [-\rho ,T]$. This helps to maintain the compatibility conditions at the corner with $x=-1$. Now, following the approach of (Theorem 3.4, [15]) along with the fact that the solutions of (4)–(5) are independent of $\varepsilon$ and $u_{3}^{*}$ in (6) preserves the nature of z(x, t) in (1), a restriction u can be obtained from ${\mathcal {F}}^{*}$ to ${\mathcal {F}}^{+}$ with $\zeta _{2}(t)=u^{*}(\eta ,t)$. So, $u(x,t)\in {\mathscr {C}}^{4+\lambda }({\mathcal {F}}^{+})$ is the solution of the following problem

$$\begin{aligned} \left\{ \begin{array}{ll} L_{\varepsilon }u(x,t)=-u(x,t-\rho )+f(x,t)\quad \text {for}\quad (x,t) \in {\mathcal {F}}^{+},\\ u\big |_{\Upsilon _{d}}=z\big |_{\Upsilon _{d}}(x,t),\quad u\big |_{\Upsilon _{r}}=z\big |_{\Upsilon _{r}}(t),\quad u(\eta ,t)=u^{*}(\eta ,t),\quad t\in {\mathcal {F}}_{t}. \end{array} \right. \end{aligned}$$

(7)

Thus, the smooth component for $0\le l+2m\le 4$ satisfies,

$$\begin{aligned} \bigg \Vert \dfrac{\partial ^{l+m}u(x,t)}{\partial x^{l}\partial t^{m}}\bigg \Vert _{{\mathcal {F}}^{-}\cup {\mathcal {F}}^{+}}\le {\mathcal {C}}(1+\varepsilon ^{3-l}). \end{aligned}$$

Applying the above arguments to ${\mathcal {F}}^{-}$, one can obtain $\zeta _{1}(t)$, and furthermore, the bounds on the regular component can be easily derived. For the proof of the boundary layer component, see [15]. $\square$

3 Numerical approximation

The construction of meshes for both spatial and temporal directions along with the fully discrete schemes are discussed in this section. The time direction for both schemes is handled using the implicit Euler method. For space, in the IE-UP scheme, an upwind scheme is used and in the IE-HYB scheme, a hybrid scheme is proposed. The stability analysis of the Implicit Euler scheme (used in the temporal direction of any SPP) is well studied in the literature and can be followed from [12]. Furthermore, the matrix criterion for stability analysis is used to show the fully discrete schemes are uniformly stable in the supremum norm. Our main objective is to show that the matrix associated with each difference operator will be M-matrix and hence will satisfy the discrete maximum principle [24].

3.1 Discretization of the domain

Due to the presence of time lag, $[-\rho ,T=2\rho ]$ is split into various subdomains. The proposed numerical procedure approximates the time variable employing a uniform mesh with step length $\Delta t$. The discretized domain on $\overline{{\mathcal {F}}_{t}}^M=[-\rho ,2\rho = T]$ is

$$\begin{aligned} {\mathcal {F}}_{t}^{M_{1}}= & {} \{t_{m-M_{1}}=-\rho +m \Delta t,~ m=0,1,\ldots ,M_{1},~ t_{-M_{1}}=-\rho ,~ \Delta t=\rho /M_{1}\},\\ {\mathcal {F}}_{t}^{M_{2}}= & {} \{t_{m}=m \Delta t,~ m=0,1,\ldots ,M_{2},~ t_{M_{2}}=T,~\Delta t=T/M_{2}\}. \end{aligned}$$

The total number of mesh intervals in time domain $[-\rho , 2\rho =T]$ is $M = (M_{1} + M_{2})$, with $M_{1}$ and $M_{2}$ denoting the number of mesh intervals in $[-\rho ,0]$ and [0, T], respectively.

Concerning the space variable, the total number of mesh intervals in $\overline{{\mathcal {F}}}_{x}$ is taken to be N with non-negative constants ($\vartheta _{1}$ and $\vartheta _{2}$) as the transition parameters, defined as:

$$\begin{aligned} \vartheta _{1} = \min \bigg \{\dfrac{\eta }{2},\vartheta _{0}\varepsilon \ln N\bigg \},&\vartheta _{2} = \min \bigg \{\dfrac{\eta -1}{2},\vartheta _{0}\varepsilon \ln N\bigg \}, \end{aligned}$$

where $\vartheta _{0}=2/\theta$ and $\theta$ is a positive constant. The domain $\overline{{\mathcal {F}}}_{x}$ is split into four sub-domains as follows

$$\begin{aligned} \overline{{\mathcal {F}}}_{x}= [0,\eta -\vartheta _{1}]\cup [\eta -\vartheta _{1},\eta ]\cup [\eta ,\eta +\vartheta _{2}]\cup [\eta +\vartheta _{2},1]. \end{aligned}$$

The intervals are taken in such a way that $x_{0}=0$, $x_{N/4}=(\eta -\vartheta _{1}$), $x_{3N/4}=(\eta +\vartheta _{2})$ and $x_{N}=1$. The meshes in $[0,\eta -\vartheta _{1}]$ and $[\eta +\vartheta _{2},1]$ are uniform with N/4 mesh intervals in each, whereas $[\eta -\vartheta _{1},\eta ]$ and $[\eta ,\eta +\vartheta _{2}]$ are partitioned using two continuous, piecewise differentiable, monotonically increasing mesh generating functions $\Phi _{1}(\chi )$, $\chi \in [1/4,1/2]$ and $\Phi _{2}(\chi )$, $\chi \in [1/2,3/4]$, respectively. The functions are chosen to satisfy,

$$\begin{aligned} \Phi _{1}(1/4)=-\ln N,\quad \Phi _{1}(1/2)=0,\quad \Phi _{2}(1/2)=0\quad \text {and}\quad \Phi _{2}(3/4)=\ln N. \end{aligned}$$

Clearly, $x_{N/2}=\eta$. Let $x_{n}=nh_{n}$ with $h_{n}= x_{n}-x_{n-1}$ and $\hbar _{n}=h_{n}+h_{n+1}$ for $n=1,\ldots ,N-1$. The mesh points are given by:

$$\begin{aligned} x_{n}= {\left\{ \begin{array}{ll} n\dfrac{4(\eta -\vartheta _{1})}{N}&{} \text {if}\quad 0\le n\le \frac{N}{4},\\ \eta +\vartheta _{0}\varepsilon \Phi _{1}(\chi _{n}) &{} \text {for}\quad \chi _{n}=n/N, \quad \text {if}\quad \frac{N}{4}< n \le \frac{N}{2},\\ \eta +\vartheta _{0}\varepsilon \Phi _{2}(\chi _{n}) &{} \text {for}\quad \chi _{n}=n/N, \quad \text {if}\quad \frac{N}{2}< n < \frac{3N}{4},\\ (\eta +\vartheta _{2})+\frac{4(1-\eta -\vartheta _{2})}{N}(n-(3N/4)) &{} \text {if}\quad \frac{3N}{4}\le n \le N. \end{array}\right. } \end{aligned}$$

According to the above, one can observe that

$$\begin{aligned} h_{n}= \left\{ \begin{array}{ll} H_{(l)}=\dfrac{4(\eta -\vartheta _{1})}{N}&{} \text {for}\quad n=1,\ldots ,\frac{N}{4}, \\ H_{(r)}=\dfrac{4(1-\eta -\vartheta _{2})}{N}&{} \text {for}\quad n=\frac{3N}{4}+1,\ldots ,N, \end{array} \right. \end{aligned}$$

(8)

and

$$\begin{aligned} h_{n}= \left\{ \begin{array}{ll} h_{(l)},~ \text {where}~h_{n}\ge h_{n+1}\quad \text {for}\quad n=\frac{N}{4}+1,\ldots ,\frac{N}{2}, \\ h_{(r)},~ \text {where}~h_{n}\le h_{n+1}\quad \text {for}\quad n=\frac{N}{2}+1,\ldots ,\frac{3N}{4}. \end{array} \right. \end{aligned}$$

(9)

Define two functions $\Psi _{1}$ and $\Psi _{2}$ closely related to $\Phi _{1}$ and $\Phi _{2}$ by $\Phi _{1}=\ln \Psi _{1}$ and $\Phi _{2}=-\ln \Psi _{2},$ respectively, where the function $\Psi _{1}$ is monotonically increasing with $\Psi _{1}(1/4)=N^{-1}$, $\Psi _{1}(1/2)=1$ and $\Psi _{2}$ is monotonically decreasing with $\Psi _{2}(1/2)=1$, $\Psi _{2}(3/4)=N^{-1}$. The mesh generating functions for S-mesh and B–S-mesh are

• S-mesh: $\Psi _{1}(\chi )=\exp (-4(1/2-\chi )\ln N),\quad \quad \Psi _{2}(\chi )=\exp (-4(\chi -1/2)\ln N).$

• B–S-mesh: $\Psi _{1}(\chi )=1-4(1-N^{-1})(1/2-\chi ),\quad \Psi _{2}(\chi )=1-4(1-N^{-1})(\chi -1/2).$

In the analysis section, we shall assume that $\vartheta _{1}=\vartheta _{2}=\vartheta _{0}\varepsilon \ln N$. If this condition is discarded then $N^{-1}$ will be exponentially small in comparison to $\varepsilon$, which is quite not so likely in practice. In the numerical section the following notations are used:

$$\begin{aligned} {\mathcal {F}}_{l}=(0,\eta -\vartheta _{1})\times {\mathcal {F}}_{t}, \quad {\mathcal {F}}_{m}=(\eta -\vartheta _{1},\eta +\vartheta _{2}) \times {\mathcal {F}}_{t},\quad {\mathcal {F}}_{r}=(\eta +\vartheta _{2},1) \times {\mathcal {F}}_{t}. \end{aligned}$$

3.2 IE-UP scheme

With N and M as the number of mesh points in ${\mathcal {F}}_{x}$ and ${\mathcal {F}}_{t}$, respectively, ${\mathcal {F}}^{N,M}$ is used to denote the discretized form of ${\mathcal {F}}$. The fully-discrete form of (1) using the implicit Euler scheme in time and an upwind scheme for the space variable, on ${\mathcal {F}}^{N,M}$ at $(x_{n},t_{m+1})$ is

$$\begin{aligned} \left\{ \begin{array}{ll} L_{up}^{N,M}Z_{n}^{m+1}\cong {\widetilde{F}}_{up}\quad \text {for}\quad m=M_{1},M_{1}+1,\ldots , M \quad \text {and}\quad n= 1,\ldots , N-1,\\ Z_{n}^{-m}=\varPhi _{d}(x_{n},-t_{m})\quad \text {for}\quad m=0,1,\ldots , M_{1} \quad \text {and}\quad n= 1,\ldots , N-1, \\ Z_{0}^{m+1}=\varPhi _{l}(t_{m+1}),~~ Z_{N}^{m+1}=\varPhi _{r}(t_{m+1}), \quad m=M_{1},M_{1}+1,\ldots , M, \end{array} \right. \end{aligned}$$

(10)

where

$$\begin{aligned} L_{up}^{N,M}Z_{n}^{m+1}\cong {\left\{ \begin{array}{ll} \varepsilon D_{x}^{+}D_{x}^{-} Z_{n}^{m+1}+a_{n}D_{x}^{-} Z_{n}^{m+1} -b_{n}Z_{n}^{m+1}-D_{t}^{-} Z_{n}^{m+1},\\ \text {if}\quad 1< n<\frac{N}{2}\\ \varepsilon D_{x}^{+}D_{x}^{-} Z_{n}^{m+1}+a_{n}D_{x}^{+} Z_{n}^{m+1} -b_{n}Z_{n}^{m+1}-D_{t}^{-} Z_{n}^{m+1}, \\ \text {if}\quad \frac{N}{2}+1<n\le N,\\ D_{x}^{+}Z_{n}^{m+1}-D_{x}^{-}Z_{n}^{m+1}, \quad \text {if}\quad n=\frac{N}{2}, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\widetilde{F}}_{up}= {\left\{ \begin{array}{ll} f_{n}^{m+1}-Z_{n}^{m+1-M_{1}},\quad \text {if}\quad 1<n <\frac{N}{2}\quad \text {and}\quad \frac{N}{2}+1\le n \le N+1,\\ 0,\quad \text {if}\quad n=\frac{N}{2}, \end{array}\right. } \end{aligned}$$

where $Z_{n}^{m+1}=Z(x_{n},t_{m+1})$ and $Z_{n}^{m+1-M_{1}}=Z(x_{n},t_{m+1-M_{1}})$. The same approach is taken for $a_{n},~b_{n}$ and $f_{n}^{m+1}$. The differential operators are defined as

$$\begin{aligned} \begin{array}{ll} D_{t}^{-}Z^{m}_{n}=\dfrac{Z^{m}_{n}-Z^{m-1}_{n}}{\Delta t}\quad D_{x}^{+}Z^{m}_{n}=\dfrac{Z^{m}_{n+1}-Z^{m}_{n}}{h_{n+1}},\quad D_{x}^{-}Z^{m}_{n}=\dfrac{Z^{m}_{n}-Z^{m}_{n-1}}{h_{n}}, \\ D_{x}^{+}D_{x}^{-}Z^{m}_{n}=\dfrac{2}{\hbar _{n}} \big (D_{x}^{+}Z^{m}_{n}-D_{x}^{-}Z^{m}_{n}\big ),\quad D_{x}^{0}Z^{m}_{n}=\dfrac{Z^{m}_{n+1}-Z^{m}_{n-1}}{\hbar _{n}}. \end{array} \end{aligned}$$

(11)

After using (11), we have the following system of linear difference equations for $m=M_{1},M_{1}+1,\ldots , M,$

$$\begin{aligned} \left\{ \begin{array}{ll} A_{up,n}^{-}Z_{n-1}^{m+1} + A_{up,n}^{c}Z_{n}^{m+1} + A_{up,n}^{+}Z_{n+1}^{m+1} = {\widetilde{F}}_{up}\quad \text {for}\quad n= 1,\ldots , N-1,\\ Z_{n}^{-m}=\varPhi _{d}(x_{n},-t_{m}) \quad \text {for}\quad m=0,\ldots , M_{1} \quad \text {and}\quad n= 1,\ldots , N-1, \\ Z_{0}^{m+1}=\varPhi _{l}(t_{m+1}),\quad Z_{N}^{m+1}=\varPhi _{r}(t_{m+1}),\quad \text {for}\quad m=M_{1},M_{1}+1,\ldots , M, \end{array} \right. \end{aligned}$$

(12)

where the coefficients are given by

$$\begin{aligned} \left\{ \begin{array}{ll} A_{up,n}^{+} =\dfrac{2\varepsilon }{\hbar _{n} h_{n+1}},\quad A_{up,n}^{c} = -\dfrac{2\varepsilon }{h_{n+1} h_{n}} -\dfrac{a_{n}}{h_{n}}-b_{n}-\dfrac{1}{\Delta t},\quad A_{up,n}^{-} =\dfrac{2\varepsilon }{\hbar _{n} h_{n}}-\dfrac{a_{n}}{h_{n}}, \\ \text {for}\quad 1< n < \frac{N}{2},\\ A_{up,n}^{+} =\dfrac{2\varepsilon }{\hbar _{n} h_{n+1}},\quad A_{up,n}^{c} = -\dfrac{2\varepsilon }{h_{n+1} h_{n}} +\dfrac{a_{n}}{h_{n}}-b_{n}-\dfrac{1}{\Delta t},\quad A_{up,n}^{-} =\dfrac{2\varepsilon }{\hbar _{n} h_{n}}-\dfrac{a_{n}}{h_{n}},\\ \text {for}\quad \frac{N}{2}+1\le n \le N,\\ A_{up,n}^{+} =\dfrac{1}{h_{n+1}},\quad A_{up,n}^{c} = -\dfrac{1}{h_{n+1}}-\dfrac{1}{h_{n}},\quad A_{up,n}^{-} =\dfrac{1}{h_{n}},\quad \text {for}\quad n=\frac{N}{2}. \end{array} \right. \end{aligned}$$

3.3 Stability of the IE-UP scheme

$A_{up}$ can be easily proved to be an M-matrix and hence, the operator $L_{up}^{N,M}$ can be proved to satisfy the following discrete maximum principle.

Lemma 4

Suppose that a mesh function $\Theta$ satisfies $\Theta \le 0$ on $\Upsilon _{d}^{N,M}$, $L_{up}^{N,M}\Theta \ge 0$ in $\Theta \in {\mathcal {F}}^{N,M}\cap ({\mathcal {F}}^{-}\cup {\mathcal {F}}^{+})$ and $D_{x}^{+}\Theta _{N/2}^{m+1}-D_{x}^{-}\Theta _{N/2}^{m+1}\ge 0$ for $m=M_{1},M_{1}+1,\ldots , M,$ then $\Theta \le 0$ at each point in $\overline{{\mathcal {F}}}^{N,M}$.

Proof

One can refer to [21] for the complete proof, which leads to the $\varepsilon$-uniform stability of $L_{up}^{N,M}$. $\square$

3.4 IE-HYB scheme

The fully-discrete form of (1) using an appropriate combination of the mid-point upwind and the central difference scheme for the space variable, on ${\mathcal {F}}^{N,M}$ at $(x_{n},t_{m+1})$ is

$$\begin{aligned} \left\{ \begin{array}{ll} L_{\varepsilon }^{N,M}Z_{n}^{m+1}\cong {\widetilde{F}}_{\varepsilon },\quad m=M_{1},M_{1}+1,\ldots , M \quad \text {and}\quad n= 1,\ldots , N-1,\\ Z_{n}^{-m}=\varPhi _{d}(x_{n},-t_{m})\quad \text {for}\quad m=0,\ldots , M_{1} \quad \text {and}\quad n= 1,\ldots , N-1, \\ Z_{0}^{m+1}=\varPhi _{l}(t_{m+1}),\quad Z_{N}^{m+1}=\varPhi _{r}(t_{m+1}),\quad m=M_{1},M_{1}+1,\ldots , M, \end{array} \right. \end{aligned}$$

(13)

where

$$\begin{aligned} L_{\varepsilon }^{N,M}Z_{n}^{m+1}\cong {\left\{ \begin{array}{ll} L_{mid}^{N,M,(-)}Z_{n}^{m+1}= \varepsilon D_{x}^{+}D_{x}^{-} Z_{n}^{m+1}+a_{n-1/2}D_{x}^{-} Z_{n}^{m+1}\\ -b_{n-1/2}Z_{n-1/2}^{m+1}-D_{t}^{-} Z_{n-1/2}^{m+1},\quad \text {if}\quad 1< n \le \frac{N}{4},\\ L_{cen}^{N,M}Z_{n}^{m+1}=\varepsilon D_{x}^{+}D_{x}^{-} Z_{n}^{m+1}+a_{n}D_{x}^{0} Z_{n}^{m+1}\\ -b_{n}Z_{n}^{m+1}-D_{t}^{-} Z_{n}^{m+1},\\ \text {if}\quad \frac{N}{4}+1<n<\frac{N}{2}\quad \text {and}\quad \frac{N}{2}+1\le n \le \frac{3N}{4},\\ L_{mid}^{N,M,(+)}Z_{n}^{m+1}= \varepsilon D_{x}^{+}D_{x}^{-} Z_{n}^{m+1}+a_{n+1/2}D_{x}^{+} Z_{n}^{m+1}\\ -b_{n+1/2}Z_{n+1/2}^{m+1}-D_{t}^{-} Z_{n+1/2}^{m+1},\quad \text {if}\quad \frac{3N}{4}< n \le N,\\ D_{x}^{F}Z_{n}^{m+1}-D_{x}^{B}Z_{n}^{m+1},\quad \text {if}\quad n=\frac{N}{2}, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\widetilde{F}}_{\varepsilon }= {\left\{ \begin{array}{ll} f_{n-1/2}^{m+1}-Z_{n-1/2}^{m+1-M_{1}},\quad \text {if}\quad 1< n \le \frac{N}{4},\\ f_{n}^{m+1}-Z_{n}^{m+1-M_{1}},\\ \text {if}\quad \frac{N}{4}+1<n<\frac{N}{2}\quad \text {and}\quad \frac{N}{2}+1\le n \le \frac{3N}{4},\\ f_{n+1/2}^{m+1}-Z_{n+1/2}^{m+1-M_{1}},\quad \text {if}\quad \frac{3N}{4}< n \le N,\\ 0,\quad \text {if}\quad n=\frac{N}{2}. \end{array}\right. } \end{aligned}$$

In the above equations, at the time level $t_{m+1}$, $a_{n-1/2}=\dfrac{a_{n}+a_{n-1}}{2}$ and $a_{n+1/2}=\dfrac{a_{n}+a_{n+1}}{2}$. The same approach is taken for $b_{n\pm 1/2}$, $f_{n\pm 1/2}$, $Z_{n\pm 1/2}$. Along with (11), using $D_{x}^{F}Z_{n}^{m+1}=(-Z_{n+2}^{m+1}+4Z_{n+1}^{m+1}-3Z_{n}^{m+1})/2h_{(r)}$ and $D_{x}^{B}Z_{n}^{m+1}=(Z_{n-2}^{m+1}-4Z_{n-1}^{m+1}+3Z_{n}^{m+1})/2h_{(l)}$, we have

$$\begin{aligned} \left\{ \begin{array}{ll} A_{\varepsilon ,n}^{-}Z_{n-1}^{m+1} + A_{\varepsilon ,n}^{c}Z_{n}^{m+1} + A_{\varepsilon ,n}^{+}Z_{n+1}^{m+1} = {\widetilde{F}}_{\varepsilon }\quad \text {for}\quad m=M_{1},M_{1}+1,\ldots , M,\\ \text {and}\quad n= 1,\ldots , (N/2)-1, \quad n= (N/2)+1,\ldots ,N-1,\\ A_{\varepsilon ,N/2}^{-2}Z_{n-2}^{m+1}+A_{\varepsilon ,N/2}^{-1}Z_{n-1}^{m+1} + A_{\varepsilon ,N/2}^{c}Z_{n}^{m+1}\\ +A_{\varepsilon ,N/2}^{+1}Z_{n+1}^{m+1}+A_{\varepsilon ,N/2}^{+2}Z_{n+2}^{m+1} = 0\quad \text {for}\quad m=M_{1},M_{1}+1,\ldots , M,\\ Z_{n}^{-m}=\varPhi _{d}(x_{n},-t_{m})\quad \text {for}\quad m=0,\ldots , M_{1} \quad \text {and}\quad n= 1,\ldots , N-1, \\ Z_{0}^{m+1}=\varPhi _{l}(t_{m+1}),\quad Z_{N}^{m+1}=\varPhi _{r}(t_{m+1}),\quad m=M_{1},M_{1}+1,\ldots , M, \end{array} \right. \end{aligned}$$

(14)

where the coefficients for $1< n \le (N/4)$ are

$$\begin{aligned}&A_{\varepsilon ,n}^{+} =\dfrac{2\varepsilon }{\hbar _{n} h_{n+1}},\quad A_{\varepsilon ,n}^{c} = -\dfrac{2\varepsilon }{h_{n+1} h_{n}}+\dfrac{a_{n-1/2}}{h_{n}}-\dfrac{b_{n-1/2}}{2}-\dfrac{1}{2\Delta t},\\&A_{\varepsilon ,n}^{-} =\dfrac{2\varepsilon }{\hbar _{n} h_{n}}-\dfrac{a_{n-1/2}}{h_{n}}-\dfrac{b_{n-1/2}}{2}-\dfrac{1}{2\Delta t}, \end{aligned}$$

for $(3N/4)\le n \le N$,

$$\begin{aligned}&A_{\varepsilon ,n}^{+} =\dfrac{2\varepsilon }{h_{n+1} \hbar _{n}}+\dfrac{a_{n+1/2}}{h_{n+1}}-\dfrac{b_{n+1/2}}{2}-\dfrac{1}{2\Delta t},\\&A_{\varepsilon ,n}^{c} = -\dfrac{2\varepsilon }{h_{n+1} h_{n}}-\dfrac{a_{n+1/2}}{h_{n+1}}-\dfrac{b_{n+1/2}}{2}-\dfrac{1}{2\Delta t},\quad A_{\varepsilon ,n}^{-} =\dfrac{2\varepsilon }{\hbar _{n} h_{n}}, \end{aligned}$$

for $(N/4)+1\le n \le (N/2)-1$ and $(N/2)+1\le n \le (3N/4)-1$,

$$\begin{aligned} A_{\varepsilon ,n}^{+} =\dfrac{2\varepsilon }{\hbar _{n} h_{n+1}}+\dfrac{a_{n}}{\hbar _{n}},\quad A_{\varepsilon ,n}^{c} =-\dfrac{2\varepsilon }{h_{n+1} h_{n}}-b_{n}-\dfrac{1}{\Delta t},\quad A_{\varepsilon ,n}^{-} = \dfrac{2\varepsilon }{\hbar _{n} h_{n}}-\dfrac{a_{n}}{\hbar _{n}}. \end{aligned}$$

For $n=(N/2)$, we have

$$\begin{aligned}&A_{\varepsilon ,N/2}^{-2}=-1/2h_{(l)}, \quad A_{\varepsilon ,N/2}^{-1}=2/h_{(l)},\\&A_{\varepsilon ,N/2}^{c}=-3/2(1/h_{(l)}+1/h_{(r)}),\quad A_{\varepsilon ,N/2}^{+1}=2/h_{(r)},\quad A_{\varepsilon ,N/2}^{+2}=-1/2h_{(r)}. \end{aligned}$$

3.5 Stability of the IE-HYB scheme

It is an easy calculation to show that $L_{\varepsilon }^{N,M}$ defined in (13) does not satisfy the discrete maximum principle and accordingly, the uniform stability criteria can not be established. So, the scheme needs to be transformed at $n=N/2$. Using $L_{\varepsilon }^{N,M}$ at $n=(N/2)-1$ and $n=(N/2)+1$, we get

$$\begin{aligned} \left\{ \begin{array}{ll} Z_{N/2-2}^{m+1} &{}=\dfrac{2h^{2}}{2\varepsilon -ha_{N/2-1}}\bigg [f_{N/2-1}^{m+1} -Z_{N/2-1}^{m+1-M_{1}}-A_{\varepsilon ,N/2-1}^{c}Z_{N/2-1}^{m+1}\\ &{} \quad -A_{\varepsilon ,N/2-1}^{+}Z_{N/2}^{m+1}-\dfrac{1}{\Delta t}Z_{N/2-1}^{m}\bigg ],\\ Z_{N/2+2}^{m+1} &{}=\dfrac{2h^{2}}{2\varepsilon +ha_{N/2+1}}\bigg [f_{N/2+1}^{m+1}-Z_{N/2+1} ^{m+1-M_{1}}-A_{\varepsilon ,N/2+1}^{c}Z_{N/2+1}^{m+1}\\ &{} \quad -A_{\varepsilon ,N/2+1}^{-}Z_{N/2}^{m+1}-\dfrac{1}{\Delta t}Z_{N/2+1}^{m}\bigg ], \end{array} \right. \end{aligned}$$

(15)

where $h=h_{(l)}=h_{(r)}$ (as $\vartheta _{1}=\vartheta _{2}$ is assumed) for $n=(N/4),\ldots ,(3N/4)$. Now, substituting (15) in (14), the following fully discrete scheme satisfying the discrete maximum principle can be obtained as

$$\begin{aligned} \left\{ \begin{array}{ll} L_{hy}^{N,M}Z_{n}^{m+1}\cong {\widetilde{F}}_{hy},\quad m=M_{1},M_{1}+1,\ldots , M \quad \text {and}\quad n= 1,\ldots , N-1,\\ Z_{n}^{-m}=\varPhi _{d}(x_{n},-t_{m})\quad \text {for}\quad m=0,\ldots , M_{1} \quad \text {and}\quad n= 1,\ldots , N-1, \\ Z_{0}^{m+1}=\varPhi _{l}(t_{m+1}),\quad Z_{N}^{m+1}=\varPhi _{r}(t_{m+1}),\quad m=M_{1},M_{1}+1,\ldots , M. \end{array} \right. \end{aligned}$$

(16)

On further rearrangement, the scheme becomes

$$\begin{aligned} \left\{ \begin{array}{ll} A_{hy,n}^{-}Z_{n-1}^{m+1} + A_{hy,n}^{c}Z_{n}^{m+1} + A_{hy,n}^{+}Z_{n+1}^{m+1} = {\widetilde{F}}_{hy},\quad m=M_{1},M_{1}+1,\ldots , M,\\ Z_{n}^{-m}=\varPhi _{d}(x_{n},-t_{m}) \quad \text {for}\quad m=0,\ldots , M_{1} \quad \text {and}\quad n= 1,\ldots , N-1, \\ Z_{0}^{m+1}=\varPhi _{l}(t_{m+1}),~~ Z_{N}^{m+1}=\varPhi _{r}(t_{m+1}), ~~~ m=M_{1},M_{1}+1,\ldots , M, \end{array} \right. \end{aligned}$$

(17)

where for $n\ne (N/2)$, $A_{hy}=A_{\varepsilon }$ and ${\widetilde{F}}_{hy}={\widetilde{F}}_{\varepsilon }$. For $n=(N/2)$, we have

$$\begin{aligned} \left\{ \begin{array}{ll} A_{hy,N/2}^{+} =\dfrac{1}{2h}\bigg [4-\dfrac{2\Bigg(2\varepsilon +h^{2}b_{n+1}+\frac{h^{2}}{\Delta t}\Bigg)}{2\varepsilon +ha_{n+1}}\bigg ],\\ A_{hy,N/2}^{c} =\dfrac{1}{2h}\bigg [-6+\dfrac{2\varepsilon +ha_{n-1}}{2\varepsilon -ha_{n-1}}+\dfrac{2\varepsilon -ha_{n+1}}{2\varepsilon +ha_{n+1}}\bigg ],\\ A_{hy,N/2}^{-} = \dfrac{1}{2h}\bigg [4-\dfrac{2\Bigg(2\varepsilon +h^{2}b_{n-1}+\frac{h^{2}}{\Delta t}\Bigg)}{2\varepsilon -ha_{n-1}}\bigg ], \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} {\widetilde{F}}_{hy}= &\, {} \dfrac{h}{(2\varepsilon -ha_{n-1})}\bigg [-\dfrac{Z_{n-1}^{m}}{\Delta t}+f_{n-1}^{m+1}-Z_{n-1}^{m+1-M_{1}}\bigg ]\\{} & {} +\dfrac{h}{(2\varepsilon +ha_{n+1})}\bigg [-\dfrac{Z_{n+1}^{m}}{\Delta t}+f_{n+1}^{m+1}-Z_{n+1}^{m+1-M_{1}}\bigg ]. \end{aligned}$$

Lemma 5

Assume $N\ge N_{0}$, $\dfrac{N_{0}}{\ln N_{0}}\ge 2\vartheta _{0}\alpha ^{*}$ and $(\Vert b\Vert _{\infty }+\Delta t^{-1})\le \alpha N_{0}/2$, where $\alpha =\min \{\alpha _{1},\alpha _{2}\}$ and $\alpha ^{*}=\min \{\alpha _{1}^{*},\alpha _{2}^{*}\}$. Given a mesh function $\Theta$ satisfying $\Theta \le 0$ on $\Upsilon _{d}^{N,M}$, $L_{hy}^{N,M}\Theta \ge 0$ in ${\mathcal {F}}^{N,M}\cap ({\mathcal {F}}^{-}\cup {\mathcal {F}}^{+})$ then $\Theta \le 0$ at each point in $\overline{{\mathcal {F}}}^{N,M}$.

Proof

One can refer to [15] for the complete proof. $\square$

The Thomas algorithm is used to solve the system of equations formed in any of the schemes above, which in terms of the computational time required, is preferable to the matrix inversion method.

4 Error analysis

From the previous section, it can be concluded that both schemes are stable. Now, this section addresses the error analysis for each scheme, separately. In order to make the paper more readable, the technical and complete proofs of the following theorems have been included in an appendix.

4.1 Error bounds for the IE-UP scheme

Theorem 6

If z and $Z_{n}^{m+1}$ are the solutions of (1) and (10), respectively then the following error bounds can be obtained for the IE-UP scheme on $\overline{{\mathcal {F}}}^{N,M}$

$$\begin{aligned} \big |z(x_{n},t_{m+1})-Z_{n}^{m+1}\big |\le \left\{ \begin{array}{ll} {\mathcal {C}}(N^{-1}\ln N+\Delta t)\quad \text {for S-mesh},\\ {\mathcal {C}}(N^{-1}+\Delta t)\quad {\text {for B}}{-}{\text {S-mesh}}, \end{array} \right. \end{aligned}$$

with $m=M_{1},M_{1}+1,\ldots , M$ and $1\le n \le (N-1)$.

Proof

See appendix. $\square$

4.2 Error bounds for the IE-HYB scheme

Theorem 7

If z and $Z_{n}^{m+1}$ are the solutions of (1) and (16) on $\overline{{\mathcal {F}}}^{N,M}$, respectively, then the error bounds using the IE-HYB scheme are

$$\begin{aligned}{} & {} \big |z(x_{n},t_{m+1})-Z_{n}^{m+1}\big |\le \left\{ \begin{array}{ll} {\mathcal {C}}(N^{-2}+\Delta t)\quad for\quad 1\le n \le (N/4),\\ {\mathcal {C}}(N^{-2}\ln ^2 N+\Delta t)\quad for \quad (N/4) +1\le n \le (3N/4)-1,\\ {\mathcal {C}}(N^{-2}+\Delta t)\quad for\quad (3N/4)\le n\le N -1\quad \text {on}\quad \text {S-mesh}, \end{array} \right. \\{} & {} \big |z(x_{n},t_{m+1})-Z_{n}^{m+1}\big |\le {\mathcal {C}}(N^{-2}+\Delta t)\quad for\quad 1\le n \le (N-1)\quad \text {on}\quad \text {B--S-mesh}, \end{aligned}$$

with $m=M_{1},M_{1}+1,\ldots , M$.

Proof

See appendix. $\square$

5 Extension to time delayed semilinear parabolic SPPs

In this section, the following semi-linear form of our prescribed model problem is considered for $(x,t) \in {\mathcal {F}}$

$$\begin{aligned} \left\{ \begin{array}{ll} L_{\varepsilon }z(x,t)\equiv \big (-z_{t}+\varepsilon z_{xx}+a(x)z_{x}\big )(x,t)=-z(x,t-\rho )+{\tilde{f}}(x,t,z), \\ z\big |_{\Upsilon _{d}}=\varPhi _{d}(x,t),\quad z\big |_{\Upsilon _{l}}=\varPhi _{l}(t),\quad z\big |_{\Upsilon _{r}}=\varPhi _{r}(t), \quad t\in {\mathcal {F}}_{t}. \end{array} \right. \end{aligned}$$

(18)

Following the concept of the upper and lower solutions (see Definition 3.1 in [25]) and using the weaker assumption ${\tilde{f}}_{z}\ge 0$ in ${\mathcal {F}}$, problem (1) has a unique solution (see Lemma 3.4–3.6, Chapter 2 in [25]). The technique of Newton’s linearization can be used to solve (18). $z^{(0)}(x,t)$ is taken as a reasonable initial guess for z(x, t) in the source term ${\tilde{f}}(x,t,z)$. For all $i>0$, expansion of $({\tilde{f}}(x,t,z^{(i+1)})$ around $z^{(i)}$ gives,

$$\begin{aligned} {\tilde{f}}(x,t,z^{(i+1)}(x,t))\approx {\tilde{f}}(x,t,z^{(i)})+\big [z^{(i+1)}-z^{(i)}\big ]\frac{\partial {\tilde{f}}}{\partial z(x,t)}\bigg |_{(x,t,z^{(i)})}+\cdots \end{aligned}$$

(19)

Substituting (19) in (18), we get

$$\begin{aligned} \begin{array}{ll} L_{\varepsilon }z&{}\cong \big [-z_{t}^{(i+1)}+\varepsilon z_{xx}^{(i+1)}+ a(x)z_{x}^{(i+1)}-\frac{\partial {\tilde{f}}}{\partial z}\big |_{(x,t,z^{(i)})}z^{(i+1)}\big ](x,t)\\ &{}= -z^{(i+1)}(x,t-\rho )+ {\tilde{f}}(x,t,z^{(i)})-z^{(i)}\frac{\partial {\tilde{f}}}{\partial z}\big |_{(x,t,z^{(i)})}. \end{array} \end{aligned}$$

After further arrangements we have,

$$\begin{aligned} \begin{array}{ll} L_{\varepsilon }z&{}\cong \big [-z_{t}^{(i+1)}+\varepsilon z_{xx}^{(i+1)}+ a(x)z_{x}^{(i+1)}-b(x,t)z^{(i+1)}\big ](x,t)\\ &{}= -z^{(i+1)}(x,t-\rho )+ F(x,t), \end{array} \end{aligned}$$

(20)

where $b(x,t)=\frac{\partial {\tilde{f}}}{\partial z}\big |_{(x,t,z^{(i)})}$ and $F(x,t)= {\tilde{f}}(x,t,z^{(i)})-z^{(i)}\frac{\partial {\tilde{f}}}{\partial z}\big |_{(x,t,z^{(i)})}$. Afterward, each iteration is solved numerically with a stopping criterion given by

$$\begin{aligned} \underset{(x_{n},~ t_{m})~ \in ~{\mathcal {F}}^{N,M}}{\max } \big \vert Z^{i+1}(x_{n},~ t_{m}) - Z^{i}(x_{n},~ t_{m})\big \vert \le TOL, \end{aligned}$$

where TOL is chosen to be $10^{-6}$ for computations. The numerical approximation and the convergence analysis of (20) can be done in a similar way as discussed for (1).

6 Numerical experiments

Three exemplifying problems are presented in this section to validate the theoretical findings. The model problems mentioned in [15, 21, 22] are modified to prove the efficacy of our algorithm. For the problems, where the exact solutions are not known, the double mesh principle is applied to calculate the errors $(E_{\varepsilon }^{N, \Delta t})$ and rates of convergence $(R^{N, \Delta t})$. $E_{\varepsilon }^{N, \Delta t}$ and $R^{N, \Delta t}$ are computed by,

$$\begin{aligned} E_{\varepsilon }^{N, \Delta t} = \underset{(x_{n},~ t_{m})~ \in ~{\mathcal {F}}^{N,M}}{\max } \big |Z^{N, M}(x_{n},~ t_{m}) - {{\mathcal {Z}}}(x_{n},~ t_{m})\big |,~~R^{N, \Delta t} = \log _{2} \bigg (\dfrac{E_{\varepsilon }^{N, \Delta t}}{E_{\varepsilon }^{2N, \Delta t/2}}\bigg ), \end{aligned}$$

where ${\mathcal {Z}}=z(x_{n},~ t_{m})$ if the exact solution is known or else ${\mathcal {Z}}=Z^{2N,2M}(x_{n},~ t_{m})$. The value of $\rho$ is taken to be 1 for all the problems.

Example 1

Consider the following parabolic IBVP having a large time lag

$$\begin{aligned} \left\{ \begin{array}{ll} -z_{t}+\varepsilon z_{xx}+a(x)z_{x}-x(1-x)z=-z(x,t-\rho )+f(x,t)\quad \text {for}~~ (x,t) \in {\mathcal {F}}, \\ z\big |_{\Upsilon _{d}}=\varPhi _{d}(x,t), \\ z(0,t)=z (1,t)=0\quad \text {for}\quad t \in {\mathcal {F}}_{t}, \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} a(x)=&\left\{ \begin{array}{ll} -(1+x(0.5-x)),&{} \quad 0\le x \le 0.5, \\ (1+x(x-0.5)),&{} \quad 0.5< x \le 1, \end{array} \right. \end{aligned}$$

and f(x, t) and $\varPhi _{d}$ are made to satisfy the exact solution z(x, t) as

$$\begin{aligned} z(x,t)=&\left\{ \begin{array}{ll} \exp (-t)\bigg [\dfrac{1-\exp (-(0.5-x)/\varepsilon )}{1-\exp (-0.5/\varepsilon )}-\cos (\pi x)\bigg ],&{} \quad 0\le x < 0.5,\\ \exp (-t)\bigg [\dfrac{-1-\exp (-(x-0.5)/\varepsilon )}{1-\exp (-0.5/\varepsilon )}-\cos (\pi x)\bigg ],&{} \quad 0.5\le x \le 1. \end{array} \right. \end{aligned}$$

Example 2

Consider the following parabolic IBVP having a large time lag with an unknown solution

$$\begin{aligned} \left\{ \begin{array}{ll} -z_{t}+\varepsilon z_{xx}+a(x)z_{x}=-z(x,t-\rho )+f(x,t)\quad \text {for}~~ (x,t) \in {\mathcal {F}}, \\ z\big |_{\Upsilon _{d}}=0, \\ z(0,t)=z (1,t)=0,\quad \text {for}\quad t \in {\mathcal {F}}_{t}, \end{array} \right. \end{aligned}$$

where

$$\begin{aligned} a(x)=&\left\{ \begin{array}{ll} -2(1+x),&{} \quad 0\le x \le 0.5, \\ (3-2x),&{} \quad 0.5< x \le 1, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} f(x,t)=&\left\{ \begin{array}{ll} 2xt,&{} \quad 0\le x \le 0.5, \\ 2(1-x)t,&{} \quad 0.5< x \le 1. \end{array} \right. \end{aligned}$$

Example 3

Consider the following semilinear parabolic IBVP

$$\begin{aligned} \left\{ \begin{array}{ll} -z_{t}+\varepsilon z_{xx}+a(x)z_{x}=-z(x,t-\rho )+{\tilde{f}}(x,t,z)\quad \text {for}~~ (x,t) \in {\mathcal {F}}, \\ z\big |_{\Upsilon _{d}}=\varPhi _{d}(x,t), \\ z(0,t)=z (1,t)=0\quad \text {for}\quad t \in {\mathcal {F}}_{t}, \end{array} \right. \end{aligned}$$

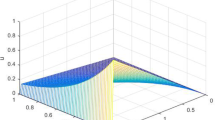
where ${\tilde{f}}(x,t,z)=f(x,t)-\exp (z)$. The exact solution and convection coefficient for Example 3 are the same as defined in Example 1. The numerical results and comparisons are structured in the form of graphs and tables. It is noteworthy that all the examples have discontinuity in the convection coefficients which create the abrupt change in the neighbourhood of $x=0.5$. To show how the gradient of the solution steepens at the point of discontinuity when $\varepsilon$ decreases, the solution profiles in the form of surface-contour plots are given in Figs. 1 and 2 for Examples 1 and 2, respectively. To verify the theoretical estimates, the numerical results for Example 1 are provided in Tables 1 and 2. Table 1 shows a comparison of errors and rates of convergence using the IE-UP scheme on both the S-mesh and the B–S-mesh. Similar kinds of results using the IE-HYB scheme are tabulated in Table 2. From both the tables, it is quite evident that the B–S-mesh provides better accuracy than the S-mesh, irrespective of the schemes used.

The plots in Fig. 4a, b for Example 2 prove the fact that the error inside the layer region is quite high in comparison to the errors outside the layer regions while using both the schemes. This fact is again shown by giving the numerical data in Tables 3, 4, 5 and 6. Table 3 compares the errors and rates of convergence distinctively in all the regions using the IE-UP scheme on S-mesh and the similar outputs on B–S-mesh are provided in Table 4. Though the order of convergence is one, in all the distinct regions, it can be seen that the outputs inside the layer region are less accurate. Again, as the IE-HYB scheme gives second-order accuracy in spatial direction but first order in time, so to match up the accuracy in space, the step-length in time is chosen as $\Delta t=1/N^{2}$, this procedure ensures that the accuracy inside the layer region does not reduces to one [15]. Clearly, outside the layer region, the order of accuracy is two but inside the layer region, the results are less accurate. All the tables and graphs discussed till now prove the efficacy of the IE-HYB scheme over the IE-UP scheme. Again, Table 7 gives a comparison of computational time taken by both the schemes for solving Example 2. It is visible that the IE-HYB scheme requires an almost equal amount of computational time as IE-UP scheme.

Example 3 is an instance of the semilinear form of (1). To visualize the nature of the solution of Example 3 at different time levels, Fig. 3 is plotted. This indicates the presence of an interior layer at the point of discontinuity with smaller values of $\varepsilon$, at each distinct time level. Figure 5a shows the solution profiles while using different values of N, which clearly shows that larger N can provide better approximations with fewer oscillations. Figure 5b shows the log-log plot for the solution of Example 3, from which it is quite evident that the IE-HYB scheme is much more efficient than the IE-UP scheme and the B–S-mesh is more accurate in both the schemes than the S-mesh, even in the semilinear case. The aforesaid results for Example 3 are again shown computationally through Tables 8 and 9 that compare the numerical outputs.

7 Conclusion

The singularly perturbed parabolic problem with time delay and an interior layers is solved using two different parameter uniform finite difference schemes. In both schemes, the time direction is treated with the implicit Euler scheme on a uniform mesh. To resolve the abrupt change that happens due to the presence of the perturbation parameter and the discontinuity in the convection-coefficient, at first, the upwind scheme and then a hybrid scheme on two different layer resolving meshes are applied in space. The efficiency of the schemes is tested over the semilinear form of the same model problem. Both analytically and numerically, the hybrid scheme is shown to be more efficient than the upwind scheme. Again, the B–S-mesh is shown to provide better accuracy than the S-mesh.

Fig. 1

Solution profiles for Example 1

Fig. 2

Solution profiles for Example 2

Fig. 3

Solution profiles at different time levels with $N=64$ for Example 3

Fig. 4

Error plots using S-mesh with $\varepsilon =10^{-2}$ and $N=64$ for Example 2

Fig. 5

Comparison graphs for Example 3

Table 1 Numerical results using the IE-UP scheme with $\Delta t=1/N$ for Example 1

Table 2 Numerical results using the IE-HYB scheme with $\Delta t=0.8/N$ for Example 1

Table 3 Numerical results using the IE-UP scheme on S-mesh for Example 2

Table 4 Numerical results using the IE-UP scheme on B–S-mesh for Example 2

Table 5 Numerical results using the IE-HYB scheme with $M_{1}=N^{2}$ on S-mesh for Example 2

Table 6 Numerical results using the IE-HYB scheme with $M_{1}=N^{2}$ on B–S-mesh for Example 2

Table 7 Time comparison with $\Delta t=1/N$, $\varepsilon =10^{-4}$ for Example 2

Table 8 Comparison of numerical results on S-mesh with $\Delta t=0.8/N$ for Example 3

Table 9 Comparison of numerical results on B–S-mesh with $\Delta t=0.8/N$ for Example 3

Appendix

1.1 Proof of Theorem 6

At the time subinterval $[0,\rho ]$, the right-hand side of our approach (10) is independent of $\varepsilon$ as the initial conditions in the region $\partial \overline{{\mathcal {F}}}$ are known. So, the analysis in this region can be done similarly as it can be done for any SPPDEs without having a time lag. Following the approach in [19] for the region $[0,\rho ]$, the error bounds can be obtained as

$$\begin{aligned} \big |z(x_{n},t_{m+1})-Z_{n}^{m+1}\big |\le \left\{ \begin{array}{ll} {\mathcal {C}}(N^{-1}\ln N+\Delta t)\quad \text {for S-mesh},\\ {\mathcal {C}}(N^{-1}+\Delta t)\quad {\text {for B}}{-}{\text {S-mesh}}, \end{array} \right. \end{aligned}$$

(21)

with $m=M_{1},M_{1}+1,\ldots , M_{1}+(M_{2}/2)$ and $n=0\le n\le N$. For the domain $[\rho ,2\rho ]$, the following delayed parabolic problem is considered

$$\begin{aligned} \left\{ \begin{array}{ll} L_{\varepsilon }z(x,t)\equiv \big (-z_{t}+\varepsilon z_{xx}+a(x)z_{x}-b(x)z\big )(x,t)\\ \quad =-z(x,t-\rho )+f(x,t)\quad \text {for}\quad (x,t) \in ({\mathcal {F}}_{x}^{-}\cup {\mathcal {F}}_{x}^{+})\times [\rho ,2\rho ],\\ z\big |_{\Upsilon _{d}}=z_{\rho }(x,t),\quad z\big |_{\Upsilon _{l}}=\varPhi _{l}(t),\quad z\big |_{\Upsilon _{r}}=\varPhi _{r}(t), \quad \rho \le t\le 2\rho , \end{array} \right. \end{aligned}$$

(22)

where $z_{\rho }$ is the solution obtained in $[0,\rho ]$. All the conditions for the coefficients are similar as in (1). After decomposing the solution of (22), the regular and the boundary layer components satisfy the following differential equations,

$$\begin{aligned} \left\{ \begin{array}{ll} L_{\varepsilon }u(x,t)=-u(x,t-\rho )+f(x,t)\quad \text {for}\quad (x,t) \in ({\mathcal {F}}_{x}^{-}\cup {\mathcal {F}}_{x}^{+})\times [\rho ,2\rho ],\\ u\big |_{\Upsilon _{d}}=z_{\rho }(x,t),\quad u\big |_{\Upsilon _{l}}=z\big |_{\Upsilon _{l}}(t),\quad u\big |_{\Upsilon _{r}}=z\big |_{\Upsilon _{r}}(t),\\ u(\eta ^{-},t)=\zeta _{1}(t),\quad u(\eta ^{+},t)=\zeta _{2}(t),\quad \rho \le t\le 2\rho . \end{array} \right. \end{aligned}$$

(23)

The boundary layer component satisfies

$$\begin{aligned} \left\{ \begin{array}{ll} L_{\varepsilon }v(x,t)=-v(x,t-\rho ),\quad \text {for}\quad (x,t) \in ({\mathcal {F}}_{x}^{-}\cup {\mathcal {F}}_{x}^{+})\times [\rho ,2\rho ],\\ v\big |_{\Upsilon _{d}}=0,\quad v\big |_{\Upsilon _{l}}=0,\quad v\big |_{\Upsilon _{r}}=0,\\ {[}v](\eta ,t)=-[u](\eta ,t)\quad \bigg [\dfrac{\partial v}{\partial x}\bigg ](\eta ,t)=-\bigg [\dfrac{\partial u}{\partial x}\bigg ](\eta ,t),\quad \rho \le t\le 2\rho . \end{array} \right. \end{aligned}$$

(24)

The fully discrete scheme of (22) is given by

$$\begin{aligned} \left\{ \begin{array}{ll} L_{up}^{N,M}Z_{n}^{m+1}\cong {\widetilde{F}}_{up},\\ m=M_{1}+(M_{2}/2),\ldots , M \quad \text {and}\quad n= 1,\ldots , (N-1),\\ Z_{n}^{m+1-M_{1}}=Z_{\rho }(x_{n},t_{m+1-M_{1}}),\\ \text {for}\quad m=M_{1}+(M_{2}/2),\ldots , M \quad \text {and}\quad n= 1,\ldots , (N-1),\\ Z_{0}^{m+1}=\varPhi _{l}(t_{m+1}),~~ Z_{N}^{m+1}=\varPhi _{r}(t_{m+1})\quad \text {for}\quad m=M_{1}+(M_{2}/2),\ldots , M, \end{array} \right. \end{aligned}$$

(25)

where

$$\begin{aligned} L_{up}^{N,M}Z_{n}^{m+1}\cong {\left\{ \begin{array}{ll} \varepsilon D_{x}^{+}D_{x}^{-} Z_{n}^{m+1}+a_{n}D_{x}^{-} Z_{n}^{m+1} -b_{n}Z_{n}^{m+1}-D_{t}^{-} Z_{n}^{m+1},\\ \text {if}\quad 1< n<\frac{N}{2},\\ \varepsilon D_{x}^{+}D_{x}^{-} Z_{n}^{m+1}+a_{n}D_{x}^{+} Z_{n}^{m+1} -b_{n}Z_{n}^{m+1}-D_{t}^{-} Z_{n}^{m+1},\\ \text {if}\quad \frac{N}{2}+1<n\le N,\\ D_{x}^{+}Z_{n}^{m+1}-D_{x}^{-}Z_{n}^{m+1},\quad \text {if}\quad n=\frac{N}{2}, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\widetilde{F}}_{up}= {\left\{ \begin{array}{ll} f_{n}^{m+1}-Z_{n}^{m+1-M_{1}},\quad \text {if}\quad 1 <\frac{N}{2}\quad \text {and}\quad \frac{N}{2}+1\le n \le N+1,\\ 0,\quad \text {if}\quad n=\frac{N}{2}. \end{array}\right. } \end{aligned}$$

To approximate the nodal error throughout the domain, the discrete solution of (25) needs to be decomposed into regular and boundary layer components as $Z_{n}^{m+1}=U_{n}^{m+1}+V_{n}^{m+1}$. Let $U_{l}$ and $U_{r}$ be two functions that approximate u to the left and right ends of the discontinuity $x=\eta$ as

$$\begin{aligned} \left\{ \begin{array}{ll} L_{up}^{N,M}U_{l,n}^{m+1}=-U_{l,n}^{m+1-M_{1}}+f_{n}^{m+1},\\ m=M_{1}+(M_{2}/2),\ldots , M,\quad \quad n=0,1,\ldots ,\frac{N}{2}-1,\\ U_{l,0}^{m+1}=u(x_{0},t_{m+1}),\quad U_{l,N/2}^{m+1}=u(\eta ^{-},t_{m+1}),\quad m=M_{1}+(M_{2}/2),\ldots , M,\\ U_{l,n}^{m+1-M_{1}}=Z_{\rho }(x_{n},t_{m+1-M_{1}}),\quad m=M_{1}+(M_{2}/2),\ldots , M,~ \quad n\le \frac{N}{2}, \end{array} \right. \end{aligned}$$

(26)

and

$$\begin{aligned} \left\{ \begin{array}{ll} L_{up}^{N,M}U_{r,n}^{m+1}=-U_{r,n}^{m+1-M_{1}}+f_{n}^{m+1},\\ m=M_{1}+(M_{2}/2),\ldots , M,\quad \quad n=\frac{N}{2},\ldots ,N,\\ U_{r,N}^{m+1}=u(x_{N},t_{m+1}),\quad U_{r,N/2}^{m+1}=u(\eta ^{+},t_{m+1}),\quad m=M_{1}+(M_{2}/2),\ldots , M,\\ U_{r,n}^{m+1-M_{1}}=Z_{\rho }(x_{n},t_{m+1-M_{1}}),\quad m=M_{1}+(M_{2}/2),\ldots , M,\quad \quad n\ge \frac{N}{2}. \end{array} \right. \end{aligned}$$

(27)

So, the discrete functions approximating the boundary layer component (V) at both sides of $x=\eta$, satisfy the following equations for $m=M_{1}+(M_{2}/2),\ldots , M,$

$$\begin{aligned} \left\{ \begin{array}{ll} L_{up}^{N,M}V_{l,n}^{m+1}=-V_{l,n}^{m+1-M_{1}}\quad \text {for} \quad n=0,1,\ldots ,\frac{N}{2}-1,\\ L_{up}^{N,M}V_{r,n}^{m+1}=-V_{r,n}^{m+1-M_{1}}\quad \text {for} \quad n=\frac{N}{2}+1,\ldots ,N-1,\\ V_{l,0}^{m+1}=0,\quad V_{r,N}^{m+1}=0,\\ V_{l,N/2}^{m+1}+U_{l,N/2}^{m+1}=V_{r,N/2}^{m+1}+U_{r,N/2}^{m+1},\\ D_{x}^{+}V_{l,N/2}^{m+1}+D_{x}^{+}U_{l,N/2}^{m+1} =D_{x}^{-}V_{r,N/2}^{m+1}+D_{x}^{-}U_{r,N/2}^{m+1},\\ V_{l,n}^{m+1-M_{1}}=0,\quad n\le \frac{N}{2},\quad V_{r,n}^{m+1-M_{1}}=0, \quad n\ge \frac{N}{2}. \end{array} \right. \end{aligned}$$

(28)

Thus, when $m=M_{1}+(M_{2}/2),\ldots , M$, $Z_{n}^{m+1}$ can be decomposed as

$$\begin{aligned} Z_{n}^{m+1}= \left\{ \begin{array}{ll} U_{l,n}^{m+1}+V_{l,n}^{m+1}&{}\text {for} \quad n=1,2,\ldots ,\frac{N}{2}-1,\\ U_{l,n}^{m+1}+V_{l,n}^{m+1}=U_{r,n}^{m+1}+V_{r,n}^{m+1}&{} \text {for} \quad n=\frac{N}{2},\\ U_{r,n}^{m+1}+V_{r,n}^{m+1}&{} \text {for} \quad n=\frac{N}{2}+1,\ldots ,N-1. \end{array} \right. \end{aligned}$$

(29)

The error at the node $(x_{n},t_{m+1})$ can be written as

$$\begin{aligned} (z-Z)(x_{n},t_{m+1})=(u-U)(x_{n},t_{m+1})+(v-V)(x_{n},t_{m+1}). \end{aligned}$$

Error in the outer region: In this section, the error for $1\le n \le (N/4)$ and $(3N/4)\le n \le (N-1)$ is discussed for both the regular and boundary layer component. Corresponding to the smooth component for $1\le n \le (N/4)$ and $m=M_{1}+(M_{2}/2),\ldots , M$, we have

$$\begin{aligned} \bigg |L_{up}^{N,M}(U_{l,n}^{m+1}-u_{n}^{m+1})\bigg |&= (U_{l,n}^{m+1-M_{1}}-u_{n}^{m+1-M_{1}})+ \bigg \arrowvert L_{\varepsilon } u_{n}^{m+1}-L_{up}^{N,M}U_{l,n}^{m+1}\bigg \arrowvert \\&=(Z_{\rho }-z_{\rho })(x_{n},t_{m+1-M_{1}}) +\bigg \arrowvert L_{\varepsilon } u_{n}^{m+1}-L_{up}^{N,M}U_{l,n}^{m+1}\bigg \arrowvert . \end{aligned}$$

Now for $1\le n\le (N/4)$ and $m=M_{1}+(M_{2}/2),\ldots , M$, the following truncation error bound can be obtained using (23) and (26):

$$\begin{aligned}&\bigg |L_{up}^{N,M}(U_{l,n}^{m+1}-u_{n}^{m+1})\bigg |\\&\quad \le {\mathcal {C}}(N^{-1}+\Delta t)+\bigg \arrowvert (L_{\varepsilon } -L_{up}^{N,M})u_{n}^{m+1}\bigg \arrowvert \\&\quad \le {\mathcal {C}}(N^{-1}+\Delta t)+ {\mathcal {C}}\bigg [\dfrac{\varepsilon }{12}h_{n}^{2}\bigg \Vert \dfrac{\partial ^{4}u}{\partial x^{4}}\bigg \Vert _{\infty }+\dfrac{h_{n}}{2}a(x_{n})\bigg \Vert \dfrac{\partial ^{2}u}{\partial x^{2}}\bigg \Vert _{\infty }+\dfrac{\Delta t}{2}\bigg \Vert \dfrac{\partial ^{2}u}{\partial t^{2}}\bigg \Vert _{\infty }\bigg ]. \end{aligned}$$

Using the bounds mentioned in Theorem 3, $h_{n}\le {\mathcal {C}}N^{-1}$, the assumption $\varepsilon \le N^{-1}$ and the barrier function

$$\begin{aligned} \Psi _{l,n}=-{\mathcal {C}}(N^{-1}+\Delta t)x_{n},\quad 1\le n\le (N/4), \end{aligned}$$

we get,

$$\begin{aligned} \bigg |L_{up}^{N,M}(U_{l,n}^{m+1}-u_{n}^{m+1})\bigg |\le {\mathcal {C}}(N^{-1}+\Delta t),\quad m=M_{1}+(M_{2}/2),\ldots , M,~ 1\le n\le \dfrac{N}{4}-1. \end{aligned}$$

Since, $L_{up}^{N,M}$ satisfies Lemma 4 and the inverse of this operator is uniformly bounded, this inequality gives

$$\begin{aligned} |(U_{l,n}^{m+1}-u_{n}^{m+1})|\le {\mathcal {C}}(N^{-1}+\Delta t),\quad m=M_{1}+(M_{2}/2),\ldots , M,~ 1\le n\le \frac{N}{4}-1.~~~ \end{aligned}$$

(30)

Likewise, employing a new barrier function for the right-hand side of discontinuity as

$$\begin{aligned} \Psi _{r,n}=-{\mathcal {C}}(N^{-1}+\Delta t)(1-x_{n}),\quad n\ge (N/2), \end{aligned}$$

the error bound with $m=M_{1}+(M_{2}/2),\ldots , M$, can be found to be

$$\begin{aligned} |(U_{r,n}^{m+1}-u_{n}^{m+1})|\le {\mathcal {C}}(N^{-1}+\Delta t),\quad (3N/4)+1\le n \le (N-1).~~ \end{aligned}$$

(31)

Now, since the boundary layer components satisfy the differential equations in (28), following arguments similar to those given in [21, Lemma 4.2], one can have

$$\begin{aligned} \left\{ \begin{array}{ll} |(V_{l,n}^{m+1}-v_{n}^{m+1})|\le {\mathcal {C}}(N^{-1}+\Delta t),\quad 1\le n\le (N/4),\\ |(V_{r,n}^{m+1}-v_{n}^{m+1})|\le {\mathcal {C}}(N^{-1}+\Delta t),\quad (3N/4)\le n \le (N-1), \end{array} \right. \end{aligned}$$

(32)

for $m=M_{1}+(M_{2}/2),\ldots , M$.

Error inside the layer region: From (32), for $m=M_{1}+(M_{2}/2),\ldots , M$, it is straightforward to write

$$\begin{aligned} |Z_{n}^{m+1}-z(x_{n},t_{m+1})|\le {\mathcal {C}}(N^{-1}+\Delta t) \quad \text {for}~ n=(N/4), (3N/4).~~~ \end{aligned}$$

(33)

Now, following the similar arguments used for the regular components outside the layer region, the following truncation error bound can be obtained for $(N/4)+1\le n\le (N/2)-1$ and $m=M_{1}+(M_{2}/2),\ldots , M$,

$$\begin{aligned} \bigg |L_{up}^{N,M}(U_{l,n}^{m+1}-u_{n}^{m+1})\bigg |\le & {} {\mathcal {C}}(N^{-1}\ln N+\Delta t)+\bigg \arrowvert (L_{\varepsilon } -L_{up}^{N,M})u_{n}^{m+1}\bigg \arrowvert \\\le & {} {\mathcal {C}}(N^{-1}\ln N+\Delta t)+{\mathcal {C}}\bigg [\dfrac{\varepsilon }{3}(h_{n} +h_{n+1})\bigg \Vert \dfrac{\partial ^{3}u}{\partial x^{3}}\bigg \Vert _{\infty }\\{} & {} +\dfrac{h_{n}}{2}a(x_{n})\bigg \Vert \dfrac{\partial ^{2}u}{\partial x^{2}}\bigg \Vert _{\infty } +\dfrac{\Delta t}{2}\bigg \Vert \dfrac{\partial ^{2}u}{\partial t^{2}}\bigg \Vert _{\infty }\bigg ]. \end{aligned}$$

Again, using the fact that $h_{n}\le {\mathcal {C}}N^{-1}$, the assumption $\varepsilon \le N^{-1}$, the bounds mentioned in Theorem 3, and the barrier function $\Psi _{l,n}$ along with the discrete maximum principle, we have

$$\begin{aligned} |(U_{l,n}^{m+1}-u_{n}^{m+1})|\le {\mathcal {C}}(N^{-1}\ln N+\Delta t),\quad (N/4)+1\le n \le (N/2)-1, \end{aligned}$$

(34)

for $m=M_{1}+(M_{2}/2),\ldots , M$. Similarly, using $\Psi _{r,n}$ and a similar approach, one can find

$$\begin{aligned} |(U_{r,n}^{m+1}-u_{n}^{m+1})|\le {\mathcal {C}}(N^{-1}\ln N+\Delta t),\quad (N/2)+1\le n \le (3N/4)-1. \end{aligned}$$

(35)

Using Taylor’s formula with the integral form of the remainder as in [26] and Theorem 3, for $n=(N/4)+1,\ldots ,(N/2)-1$ and $m=M_{1}+(M_{2}/2),\ldots , M$, we have

$$\begin{aligned} \bigg |L_{up}^{N,M}(Z_{n}^{m+1}-z_{n}^{m+1})\bigg |&\le {\mathcal {C}}\bigg [\varepsilon \int _{x_{n-1}}^{x_{n+1}}\bigg |\dfrac{\partial ^{3}z}{\partial x^{3}}\bigg |dx+\int _{x_{n}}^{x_{n+1}}\bigg |\dfrac{\partial ^{2}z}{\partial x^{2}}\bigg |dx\bigg ]+{\mathcal {C}}\Delta t\bigg \Vert \dfrac{\partial ^{2}z}{\partial t^{2}}\bigg \Vert _{\infty }\nonumber \\&\le {\mathcal {C}}\bigg [h_{n}+\varepsilon ^{-2}\int _{x_{n-1}} ^{x_{n+1}}\exp (-(\eta -x)\alpha _{1}/\varepsilon ) dx\bigg ]+{\mathcal {C}}\Delta t. \end{aligned}$$

(36)

Similarly, for $n=(N/2)+1,\ldots ,(3N/4)-1$ and $m=M_{1}+(M_{2}/2),\ldots , M$, we have

$$\begin{aligned} \bigg |L_{up}^{N,M}(Z_{n}^{m+1}-z_{n}^{m+1})\bigg |\le {\mathcal {C}}\bigg [h_{n}+\varepsilon ^{-2}\int _{x_{n-1}}^{x_{n+1}} \exp (-(x-\eta )\alpha _{2}/\varepsilon ) dx\bigg ]+{\mathcal {C}}\Delta t. \end{aligned}$$

(37)

Now, for $x_{N/2}=\eta$ and $m=M_{1}+(M_{2}/2),\ldots , M$, it is

$$\begin{aligned} \bigg |(D_{x}^{+}-D_{x}^{-})(Z_{N/2}^{m+1}-z_{N/2}^{m+1})\bigg |&= \bigg |(D_{x}^{-}-D_{x}^{+})z_{N/2}^{m+1}-\bigg [\dfrac{\partial z}{\partial x}\bigg ](x_{N/2},t_{m+1})\bigg |\nonumber \\&\le \bigg |(D_{x}^{-}-\dfrac{\partial z}{\partial x} (x_{N/2},t_{m+1})\bigg |+ \bigg |(D_{x}^{+} -\dfrac{\partial z}{\partial x}(x_{N/2},t_{m+1})\bigg |\nonumber \\&\le {\mathcal {C}}(h_{N/2}+h_{N/2+1})\nonumber \\&\quad +{\mathcal {C}}\varepsilon ^{-2}\bigg (\int _{x_{N/2-1} }^{x_{N/2}}\exp (-(\eta -x)\alpha _{1}/\varepsilon )dx\nonumber \\&\quad +\int _{x_{N/2}}^{x_{N/2+1}}\exp (-(x-\eta )\alpha _{2} /\varepsilon )dx\bigg ). \end{aligned}$$

(38)

In order to obtain bounds for (36), (37) and (38), the approach in [21] can be followed. Now, combining the obtained bounds along with (21) and (30)–(35), the proof is complete.

1.2 Proof of Theorem 7

At the time subinterval $[0,\rho ]$, the right-hand side of our approach (16) is independent of $\varepsilon$, so following the approach in [15] on S-mesh, the error bounds can be obtained as

$$\begin{aligned} \big |z(x_{n},t_{m+1})-Z_{n}^{m+1}\big |\le \left\{ \begin{array}{ll} {\mathcal {C}}(N^{-2}+\Delta t)\quad for\quad 1\le n \le \frac{N}{4},\\ {\mathcal {C}}(N^{-2}\ln ^2 N+\Delta t)\quad for \quad \frac{N}{4}+1\le n \le \frac{3N}{4}-1,~~\\ {\mathcal {C}}(N^{-2}+\Delta t)\quad for\quad \frac{3N}{4}\le n\le (N-1), \end{array} \right. \end{aligned}$$

(39)

and on B–S-mesh is

$$\begin{aligned} \big |z(x_{n},t_{m+1})-Z_{n}^{m+1}\big |\le {\mathcal {C}}(N^{-2}+\Delta t)\quad for\quad 1\le n \le (N-1),~~ \end{aligned}$$

(40)

with $m=M_{1},M_{1}+1,\ldots ,M_{1}+(M_{2}/2)$. For the domain $[\rho ,2\rho ]$, the fully discrete scheme in (22) is given by,

$$\begin{aligned} \left\{ \begin{array}{ll} L_{hy}^{N,M}Z_{n}^{m+1}\cong {\widetilde{F}}_{hy},\\ m=M_{1}+(M_{2}/2),\ldots , M \quad \text {and}\quad n= 1,\ldots , (N-1),\\ Z_{n}^{m+1-M_{1}}=Z_{\rho }(x_{n},t_{m+1-M_{1}}),\\ \text {for}\quad m=M_{1}+(M_{2}/2),\ldots , M \quad \text {and}\quad n= 1,\ldots , (N-1),~~\\ Z_{0}^{m+1}=\varPhi _{l}(t_{m+1}),~~ Z_{N}^{m+1}=\varPhi _{r}(t_{m+1}), \quad m=M_{1}+(M_{2}/2),\ldots , M, \end{array} \right. \end{aligned}$$

(41)

where

$$\begin{aligned} L_{hy}^{N,M}Z_{n}^{m+1}\cong {\left\{ \begin{array}{ll} L_{mid}^{N,M,(-)}Z_{n}^{m+1}= \varepsilon D_{x}^{+}D_{x}^{-} Z_{n}^{m+1}+a_{n-1/2}D_{x}^{-} Z_{n}^{m+1}\\ -b_{n-1/2}Z_{n-1/2}^{m+1}-D_{t}^{-} Z_{n-1/2}^{m+1},\quad \text {if}\quad 1< n \le \frac{N}{4},\\ \\ L_{cen}^{N,M}Z_{n}^{m+1}=\varepsilon D_{x}^{+}D_{x}^{-} Z_{n}^{m+1}+a_{n}D_{x}^{0} Z_{n}^{m+1}\\ -b_{n}Z_{n}^{m+1}-D_{t}^{-} Z_{n}^{m+1},\quad \text {if}\quad \frac{N}{4}+1<n<\frac{N}{2}\quad \\ \text {and}\quad \frac{N}{2}+1\le n <\frac{3N}{4},\\ \\ L_{mid}^{N,M,(+)}Z_{n}^{m+1}= \varepsilon D_{x}^{+}D_{x}^{-} Z_{n}^{m+1}+a_{n+1/2}D_{x}^{+} Z_{n}^{m+1}\\ -b_{n+1/2}Z_{n+1/2}^{m+1}-D_{t}^{-} Z_{n+1/2}^{m+1},\quad \text {if}\quad \frac{3N}{4}\le n \le N,\\ \\ D_{x}^{F}Z_{n}^{m+1}-D_{x}^{B}Z_{n}^{m+1},\quad \text {if}\quad n=\frac{N}{2}, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\widetilde{F}}_{hy}= {\left\{ \begin{array}{ll} f_{n-1/2}^{m+1}-Z_{\rho ,n-1/2}^{m+1-M_{1}},\quad \text {if}\quad 1< n \le \frac{N}{4},\\ f_{n}^{m+1}-Z_{\rho ,n}^{m+1-M_{1}},\quad \text {if}\quad \frac{N}{4}+1<n<\frac{N}{2}\quad \text {and}\quad \frac{N}{2}+1\le n <\frac{3N}{4},\\ f_{n+1/2}^{m+1}-Z_{\rho ,n+1/2}^{m+1-M_{1}},\quad \text {if}\quad \frac{3N}{4}\le n \le N,\\ 0,\quad \text {if}\quad n=\frac{N}{2}. \end{array}\right. } \end{aligned}$$

The decomposition of the discrete solution of (16) is done in the same way as the IE-UP scheme. Now, with $m=M_{1}+(M_{2}/2),\ldots , M$, $U_{l}$ and $U_{r}$ are the solutions to the following equations,

$$\begin{aligned} \left\{ \begin{array}{ll} L_{hy}^{N,M}U_{l,n}^{m+1}=-U_{l,n}^{m+1-M_{1}}+f_{n}^{m+1}\quad \text {for} \quad n=0,1,\ldots ,\frac{N}{2}-1,\\ U_{l,0}^{m+1}=u(x_{0},t_{m+1}),\quad U_{l,N/2}^{m+1}=u(\eta ^{-},t_{m+1}),\\ U_{l,n}^{m+1-M_{1}}=Z_{\rho }(x_{n},t_{m+1-M_{1}}),\quad n\le \frac{N}{2}, \end{array} \right. \end{aligned}$$

(42)

and

$$\begin{aligned} \left\{ \begin{array}{ll} L_{hy}^{N,M}U_{r,n}^{m+1}=-U_{r,n}^{m+1-M_{1}}+f_{n}^{m+1}\quad \text {for} \quad n=\frac{N}{2},\ldots ,N,\\ U_{r,N}^{m+1}=u(x_{N},t_{m+1}),\quad U_{r,N/2}^{m+1}=u(\eta ^{+},t_{m+1}),\\ U_{r,n}^{m+1-M_{1}}=Z_{\rho }(x_{n},t_{m+1-M_{1}}),\quad n\ge \frac{N}{2}. \end{array} \right. \end{aligned}$$

(43)

The discrete functions approximating the boundary layer component (V) at both the sides of $x=\eta$, satisfy the following equations with $m=M_{1}+(M_{2}/2),\ldots , M$.

$$\begin{aligned} \left\{ \begin{array}{ll} L_{hy}^{N,M}V_{l,n}^{m+1}=-V_{l,n}^{m+1-M_{1}}\quad \text {for} \quad n=0,1,\ldots ,\frac{N}{2}-1,\\ L_{hy}^{N,M}V_{r,n}^{m+1}=-V_{r,n}^{m+1-M_{1}}\quad \text {for} \quad n=\frac{N}{2}+1,\ldots ,N-1,\\ V_{l,0}^{m+1}=0,\quad V_{r,N}^{m+1}=0,\\ V_{l,N/2}^{m+1}+U_{l,N/2}^{m+1}=V_{r,N/2}^{m+1}+U_{r,N/2}^{m+1},\\ D_{x}^{F}V_{l,N/2}^{m+1}+D_{x}^{F}U_{l,N/2}^{m+1}=D_{x} ^{B}V_{r,N/2}^{m+1}+D_{x}^{B}U_{r,N/2}^{m+1},\\ V_{l,n}^{m+1-M_{1}}=0,\quad n\le \frac{N}{2}\quad \text {and}\quad V_{r,n}^{m+1-M_{1}}=0,\quad n\ge \frac{N}{2}. \end{array} \right. \end{aligned}$$

(44)

Error in the outer region:

In this section, the error for $1\le n \le (N/4)$ and $(3N/4)\le n \le N-1$ is discussed for both the regular and boundary layer component. Corresponding to the smooth component for $1\le n \le (N/4)$ and $m=M_{1}+(M_{2}/2),\ldots , M$, we have

$$\begin{aligned} \bigg |L_{hy}^{N,M}(U_{l,n}^{m+1}-u_{n}^{m+1})\bigg |&= (U_{l,n}^{m+1-M_{1}}-u_{n}^{m+1-M_{1}})+ \bigg \arrowvert L_{\varepsilon } u_{n}^{m+1}-L_{hy}^{N,M}U_{l,n}^{m+1}\bigg \arrowvert \\&=(Z_{\rho }-z_{\rho })(x_{n},t_{m+1-M_{1}}) +\bigg \arrowvert L_{\varepsilon } u_{n}^{m+1}-L_{hy}^{N,M}U_{l,n}^{m+1}\bigg \arrowvert . \end{aligned}$$

Now, the following truncation error bound can be obtained using (23) and (42) for $m=M_{1}+(M_{2}/2),\ldots , M$ and $1\le n\le \frac{N}{4}$:

$$\begin{aligned} \bigg |L_{hy}^{N,M}(U_{l,n}^{m+1}-u_{n}^{m+1})\bigg |\le & {} {\mathcal {C}}(N^{-2}+\Delta t)+\bigg \arrowvert (L_{\varepsilon } -L_{hy}^{N,M})u_{n}^{m+1}\bigg \arrowvert \\\le & {} {\mathcal {C}}(N^{-2}+\Delta t)+ {\mathcal {C}}\bigg [(\varepsilon +h_{n})(h_{n}+h_{n+1})\bigg \Vert \dfrac{\partial ^{3}u}{\partial x^{3}}\bigg \Vert _{\infty } \\{} & {} +h_{n}^{2}\bigg (\bigg \Vert \dfrac{\partial ^{2}u}{\partial x^{2}}\bigg \Vert _{\infty }+\bigg \Vert \dfrac{\partial u}{\partial x}\bigg \Vert _{\infty }\bigg )+\Delta t\bigg \Vert \dfrac{\partial ^{2}u}{\partial t^{2}}\bigg \Vert _{\infty }\bigg ]. \end{aligned}$$

With a similar approach as the IE-UP scheme and using $\Psi _{l,n}=-{\mathcal {C}}(N^{-2}+\Delta t)x_{n}$, the following can be obtained for $m=M_{1}+(M_{2}/2),\ldots , M$

$$\begin{aligned} \bigg |L_{hy}^{N,M}(U_{l,n}^{m+1}-u_{n}^{m+1})\bigg |\le {\mathcal {C}}(N^{-2}+\Delta t),\quad 1\le n\le (N/4)-1. \end{aligned}$$

Using Lemma 5, one can have

$$\begin{aligned} |(U_{l,n}^{m+1}-u_{n}^{m+1})|\le {\mathcal {C}}(N^{-2}+\Delta t),\quad 1\le n\le (N/4)-1, \end{aligned}$$

(45)

for $m=M_{1}+(M_{2}/2),\ldots , M$. Likewise using $\Psi _{r,n}=-{\mathcal {C}}(N^{-2}+\Delta t)(1-x_{n})$, the error bound can be found to be

$$\begin{aligned} |(U_{r,n}^{m+1}-u_{n}^{m+1})|\le {\mathcal {C}}(N^{-2}+\Delta t),\quad (3N/4)+1\le n \le (N-1). \end{aligned}$$

(46)

Following arguments given in [Lemma 5.8, [15]], we get

$$\begin{aligned} \left\{ \begin{array}{ll} |(V_{l,n}^{m+1}-v_{n}^{m+1})|\le {\mathcal {C}}(N^{-2}+\Delta t),\quad 1\le n\le (N/4),\\ |(V_{r,n}^{m+1}-v_{n}^{m+1})|\le {\mathcal {C}}(N^{-2}+\Delta t),\quad (3N/4)\le n \le (N-1). \end{array} \right. \end{aligned}$$

(47)

Error inside the layer region:

From (47), it is straightforward to write

$$\begin{aligned} |Z_{n}^{m+1}-z(x_{n},t_{m+1})|\le {\mathcal {C}}(N^{-2}+\Delta t) \quad \text {for}\quad n=N/4,~ 3N/4. \end{aligned}$$

(48)

The truncation error bound for $(N/4)+1\le n\le (N/2)-1$ is given by,

$$\begin{aligned} \bigg |L_{hy}^{N,M}(U_{l,n}^{m+1}-u_{n}^{m+1})\bigg |\le & {} {\mathcal {C}}(N^{-2}\ln ^{2} N+\Delta t)+\bigg \arrowvert (L_{\varepsilon } -L_{hy}^{N,M})u_{n}^{m+1}\bigg \arrowvert \\\le & {} {\mathcal {C}}(N^{-2}\ln ^{2} N+\Delta t) \\{} & {} +{\mathcal {C}}\bigg [h^{2}\bigg (\varepsilon \bigg \Vert \dfrac{\partial ^{4}u}{\partial x^{4}}\bigg \Vert _{\infty }+\bigg \Vert \dfrac{\partial ^{3}u}{\partial x^{3}}\bigg \Vert _{\infty }\bigg )+\Delta t\bigg \Vert \dfrac{\partial ^{2}u}{\partial t^{2}}\bigg \Vert _{\infty }\bigg ]. \end{aligned}$$

Again, using the fact that $h_{n}\le {\mathcal {C}}N^{-1}$, the assumption $\varepsilon \le N^{-1}$, the bounds mentioned in Theorem 3, and the baarier function $\Psi _{l,n}$ along with the discrete maximum principle, we have

$$\begin{aligned} |(U_{l,n}^{m+1}-u_{n}^{m+1})|\le {\mathcal {C}}(N^{-2}\ln ^{2} N+\Delta t),\quad (N/4)+1\le n \le (N/2)-1, \end{aligned}$$

(49)

with $m=M_{1}+(M_{2}/2),\ldots , M$. Using $\Psi _{r,n}$ with a similar approach, one can find

$$\begin{aligned} |(U_{r,n}^{m+1}-u_{n}^{m+1})|\le {\mathcal {C}}(N^{-2}\ln ^{2} N+\Delta t),\quad (N/2)+1\le n \le (3N/4)-1. \end{aligned}$$

(50)

For $n=(N/4)+1,\ldots ,(N/2)-1$ and $m=M_{1}+(M_{2}/2),\ldots , M$, we have

$$\begin{aligned}&\bigg |L_{hy}^{N,M}(Z_{n}^{m+1}-z_{n}^{m+1})\bigg |\nonumber \\&\quad \le h\int _{x_{n-1}}^{x_{n+1}}\bigg (\varepsilon \bigg |\dfrac{\partial ^{4}z}{\partial x^{4}}\bigg |dx+\bigg |\dfrac{\partial ^{3}z}{\partial x^{3}}\bigg |dx\bigg )+{\mathcal {C}}\Delta t\bigg \Vert \dfrac{\partial ^{2}z}{\partial t^{2}}\bigg \Vert _{\infty }\nonumber \\&\quad \le {\mathcal {C}}h^{2}+{\mathcal {C}}h\varepsilon ^{-2}\bigg [\exp (-(\eta -x_{n+1}) \alpha _{1}/\varepsilon )-\exp (-(\eta -x_{n-1}) \alpha _{1}/\varepsilon )\bigg ]+{\mathcal {C}}\Delta t\nonumber \\&\quad \le {\mathcal {C}}\bigg [h^{2}+h\varepsilon ^{-2}\exp (-(\eta -x_{n})\alpha _{1} /\varepsilon )\sinh (\alpha _{1}h/\varepsilon )\bigg ]+{\mathcal {C}}\Delta t. \end{aligned}$$

(51)

Similarly, for $n=(N/2)+1,\ldots ,(3N/4)-1$ and $m=M_{1}+(M_{2}/2),\ldots , M$, we have

$$\begin{aligned} \bigg |L_{hy}^{N,M}(Z_{n}^{m+1}-z_{n}^{m+1})\bigg |\le {\mathcal {C}}\bigg [h^{2}+h^{2}\varepsilon ^{-3}\exp (-(x_{n} -\eta )\alpha _{2}/\varepsilon )\bigg ]+{\mathcal {C}}\Delta t. \end{aligned}$$

(52)

Using (17) for $x_{N/2}=\eta$ and $m=M_{1}+(M_{2}/2),\ldots , M$, one can have

$$\begin{aligned} \bigg |{\widetilde{F}}_{hy}-L_{hy}(z_{N/2}^{m+1})\bigg |&\le {\mathcal {C}}\bigg |L_{hy}^{N,M}(Z_{N/2-1}^{m+1}-z(x_{N/2-1},t_{m+1}))\bigg |\\&\quad +{\mathcal {C}}\bigg |L_{hy}^{N,M}(Z_{N/2+1}^{m+1}-z(x_{N/2+1},t_{m+1}))\bigg |\\&\quad +\bigg |(D_{x}^{F}-D_{x}^{B})z_{N/2}^{m+1}-\bigg [\dfrac{\partial z}{\partial x}\bigg ](x_{N/2},t_{m+1})\bigg |. \end{aligned}$$

Now, using (51)–(52), the following can be obtained

$$\begin{aligned} \bigg |{\widetilde{F}}_{hy}-L_{hy}(z_{N/2}^{m+1})\bigg |&\le {\mathcal {C}}(h^{2}\varepsilon ^{-3}+\Delta t),\quad m=M_{1}+(M_{2}/2),\ldots , M. \end{aligned}$$

(53)

The bounds for (51), (52) and (53) can be obtained by following the approach in [15, Theorem 5.12]. The proof is completed by combining the obtained bounds for (51)–(53) along with (39)–(40) and (45)–(50).