Skip to main content
SpringerLink
Log in

Local search genetic algorithm-based possibilistic weighted fuzzy c-means for clustering mixed numerical and categorical data

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

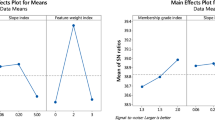
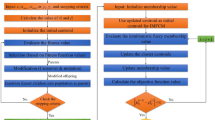
Abstract

Clustering for mixed numerical and categorical attributes has attracted many researchers due to its necessity in many real-world applications. One crucial issue concerned in clustering mixed data is to select an appropriate distance metric for each attribute type. Besides, some current clustering methods are sensitive to the initial solutions and easily trap into a locally optimal solution. Thus, this study proposes a local search genetic algorithm-based possibilistic weighted fuzzy c-means (LSGA-PWFCM) for clustering mixed numerical and categorical data. The possibilistic weighted fuzzy c-means (PWFCM) is firstly proposed in which the object-cluster similarity measure is employed to calculate the distance between two mixed-attribute objects. Besides, each attribute is placed a different important role by calculating its corresponding weight in the PWFCM procedure. Thereafter, GA is used to find a set of optimal parameters and the initial clustering centroids for the PFCM algorithm. To avoid local optimal solution, local search-based variable neighborhoods are embedded in the GA procedure. The proposed LSGA-PWFCM algorithm is compared with other benchmark algorithms based on some public datasets in UCI machine learning repository to evaluate its performance. Two clustering validation indices are used, i.e., clustering accuracy and Rand index. The experimental results show that the proposed LSGA-PWFCM outperforms other algorithms on most of the tested datasets.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Tan P-N, Steinbach M, Kumar V (2006) Introduction to data mining. Pearson education Inc

  2. Kuo R-J, Amornnikun P, Nguyen TPQ (2020) Metaheuristic-based possibilistic multivariate fuzzy weighted c-means algorithms for market segmentation. Appl Soft Comput 96:1–14

    Article  Google Scholar 

  3. Diday E, Govaert G, Lechevallier Y, Sidi J (1981) Clustering in pattern recognition. Digital image processing. Springer, pp 19–58

    Chapter  Google Scholar 

  4. Horn D, Gottlieb A (2001) Algorithm for data clustering in pattern recognition problems based on quantum mechanics. Phys Rev Lett 88:1–4

    Article  Google Scholar 

  5. Allahyari M, Pouriyeh S, Assefi M, Safaei S, Trippe ED, Gutierrez JB, Kochut K (2017) A brief survey of text mining: classification, clustering and extraction techniques. arXiv e-print, arXiv:170702919.

  6. Farhang Y (2017) Face extraction from image based on K-means clustering algorithms. Int J Adv Comput Sci Appl 8:96–107

    Google Scholar 

  7. Taghva K, Veni R (2010) Effects of similarity metrics on document clustering. In: Information technology: 2010 IEEE 7th international conference on new generations (ITNG), pp 222–226

  8. Loohach R, Garg K (2012) Effect of distance functions on k-means clustering algorithm. Int J Comput Appl 49:7–9

    Google Scholar 

  9. Kuo R, Nguyen TPQ (2019) Genetic intuitionistic weighted fuzzy k-modes algorithm for categorical data. Neurocomputing 330:116–126

    Article  Google Scholar 

  10. Esbensen KH, Guyot D, Westad F, Houmoller LP (2002) Multivariate data analysis: in practice: an introduction to multivariate data analysis and experimental design. Aalborg University, Aalborg, Denmark

    Google Scholar 

  11. Behzadi S, Ibrahim MA, Plant C (2018) Parameter free mixed-type density-based clustering. In: International conference on database and expert systems applications. Springer, pp 19–34

  12. Huang Z (1997) Clustering large data sets with mixed numeric and categorical values. In: Proceedings of the 1st Pacific-Asia conference on knowledge discovery and data mining (PAKDD). Singapore, pp 21–34

  13. Ji J, Pang W, Zhou C, Han X, Wang Z (2012) A fuzzy k-prototype clustering algorithm for mixed numeric and categorical data. Knowl Based Syst 30:129–135

    Article  Google Scholar 

  14. Ahmad A, Dey L (2007) A k-mean clustering algorithm for mixed numeric and categorical data. Data Knowl Eng 63:503–527

    Article  Google Scholar 

  15. Chatzis SP (2011) A fuzzy c-means-type algorithm for clustering of data with mixed numeric and categorical attributes employing a probabilistic dissimilarity functional. Expert Syst Appl 38:8684–8689

    Article  Google Scholar 

  16. Jia H, Cheung Y-M (2018) Subspace clustering of categorical and numerical data with an unknown number of clusters. IEEE Trans Neural Netw Learn Syst 29:3308–3325

    Article  MathSciNet  Google Scholar 

  17. Zhang K, Wang Q, Chen Z, Marsic I, Kumar V, Jiang G, Zhang J (2015) From categorical to numerical: multiple transitive distance learning and embedding. In: Proceedings of the 2015 SIAM international conference on data mining. SIAM, pp 46–54

  18. Chen W, Chen Y, Mao Y, Guo B (2013) Density-based logistic regression. In: Proceedings of the 19th ACM SIGKDD international conference on knowledge discovery and data mining. ACM, pp 140–148

  19. Li C, Biswas G (2002) Unsupervised learning with mixed numeric and nominal data. IEEE Trans Knowl Data Eng 14:673–690

    Article  Google Scholar 

  20. Ralambondrainy H (1995) A conceptual version of the K-means algorithm. Pattern Recognit Lett 16:1147–1157

    Article  Google Scholar 

  21. He Z, Xu X, Deng S (2005) Scalable algorithms for clustering large datasets with mixed type attributes. Int J Intell Syst 20:1077–1089

    Article  MATH  Google Scholar 

  22. Luo H, Kong F, Li Y (2006) Clustering mixed data based on evidence accumulation. In: International conference on advanced data mining and applications. Springer, pp 348–355

  23. Hsu C-C, Chen C-L, Su Y-W (2007) Hierarchical clustering of mixed data based on distance hierarchy. Inf Sci 177:4474–4492

    Article  Google Scholar 

  24. Liang J, Zhao X, Li D, Cao F, Dang C (2012) Determining the number of clusters using information entropy for mixed data. Pattern Recognit 45:2251–2265

    Article  MATH  Google Scholar 

  25. Cheung Y-M, Jia H (2013) A unified metric for categorical and numerical attributes in data clustering. In: Pacific-Asia conference on knowledge discovery and data mining. Springer, pp 135–146

  26. Ahmad A, Khan S (2019) A survey of state-of-the-art mixed data clustering algorithms. IEEE Access 7:31883–31902

    Article  Google Scholar 

  27. Pal NR, Pal K, Keller JM, Bezdek JC (2005) A possibilistic fuzzy c-means clustering algorithm. IEEE Trans Fuzzy Syst 13:517–530

    Article  Google Scholar 

  28. Bezdek JC, Ehrlich R, Full W (1984) FCM: The fuzzy c-means clustering algorithm. Comput Geosci 10:191–203

    Article  Google Scholar 

  29. Goldberg DE (1989) Genetic algorithms in search, optimization and machine learning. Addison-Wesley Longman Publishing Co., Inc.

  30. Lee CKH (2018) A review of applications of genetic algorithms in operations management. Eng Appl Artif Intell 76:1–12

    Article  Google Scholar 

  31. Lee NK, Li X, Wang D (2018) A comprehensive survey on genetic algorithms for DNA motif prediction. Inf Sci 466:25–43

    Article  MathSciNet  Google Scholar 

  32. Dai T, Ni L, Luo Q (2020) Diagnosis method of ultrasonic elasticity image of peripheral lung cancer based on genetic algorithm. Neural Comput Appl 32:18315–18325

    Article  Google Scholar 

  33. Guo K, Yang M, Zhu H (2020) Application research of improved genetic algorithm based on machine learning in production scheduling. Neural Comput Appl 32:1857–1868

    Article  Google Scholar 

  34. Mohammadrezapour O, Kisi O, Pourahmad F (2020) Fuzzy c-means and K-means clustering with genetic algorithm for identification of homogeneous regions of groundwater quality. Neural Comput Appl 32:3763–3775

    Article  Google Scholar 

  35. García-Martínez C, Lozano M (2007) Local search based on genetic algorithms. In: Advances in metaheuristics for hard optimization. Springer, pp 199–221

  36. Coello CACC, Pulido GT (2001) A micro-genetic algorithm for multiobjective optimization. In: International conference on evolutionary multi-criterion optimization. Springer, pp 126–140

  37. Kazarlis SA, Papadakis SE, Theocharis J, Petridis V (2001) Microgenetic algorithms as generalized hill-climbing operators for GA optimization. IEEE Trans Evol Comput 5:204–217

    Article  Google Scholar 

  38. Li C-L, Sun Y, Zhang L, Wang X-C (2005) A parallel micro-genetic algorithm and its application. In: 2005 International conference on machine learning and cybernetics. IEEE, pp 2880–2884

  39. Santiago A, Dorronsoro B, Fraire HJ, Ruiz P (2021) Micro-genetic algorithm with fuzzy selection of operators for multi-Objective optimization: μFAME. Swarm Evol Comput 61:100818

    Article  Google Scholar 

  40. Ombuki BM, Ventresca M (2004) Local search genetic algorithms for the job shop scheduling problem. Appl Intell 21:99–109

    Article  MATH  Google Scholar 

  41. Asadzadeh L (2015) A local search genetic algorithm for the job shop scheduling problem with intelligent agents. Comput Ind Eng 85:376–383

    Article  Google Scholar 

  42. Dengiz B, Altiparmak F, Smith AE (1997) Local search genetic algorithm for optimal design of reliable networks. IEEE Trans Evol Comput 1:179–188

    Article  Google Scholar 

  43. Liu D, Jin D, Baquero C, He D, Yang B, Yu Q (2013) Genetic algorithm with a local search strategy for discovering communities in complex networks. Int J Comput Intell Syst 6:354–369

    Article  Google Scholar 

  44. Gharsalli L, Guérin Y (2019) A hybrid genetic algorithm with local search approach for composite structures optimization. In: Proceedings of the European conference for aeronautics and space sciences.

  45. Li X, Gao L (2016) An effective hybrid genetic algorithm and tabu search for flexible job shop scheduling problem. Int J Prod Econ 174:93–110

    Article  Google Scholar 

  46. Yun Y (2006) Hybrid genetic algorithm with adaptive local search scheme. Comput Ind Eng 51:128–141

    Article  Google Scholar 

  47. Baareh A (2013) A hybrid memetic algorithm (genetic algorithm and tabu local search) with back-propagation classifier for fish recognition. Int Rev Comput Softw 8:1287–1293

    Google Scholar 

  48. Mohammadpour T, Bidgoli AM, Enayatifar R, Javadi HHS (2019) Efficient clustering in collaborative filtering recommender system: hybrid method based on genetic algorithm and gravitational emulation local search algorithm. Genomics 111:1902–1912

    Article  Google Scholar 

  49. Derbel H, Jarboui B, Hanafi S, Chabchoub H (2012) Genetic algorithm with iterated local search for solving a location-routing problem. Expert Syst Appl 39:2865–2871

    Article  MATH  Google Scholar 

  50. Sabar NR, Song A, Zhang M (2016) A variable local search based memetic algorithm for the load balancing problem in cloud computing. In: European conference on the applications of evolutionary computation. Springer, pp 267–282

  51. Vavak F, Jukes K, Fogarty TC (1998) Performance of a genetic algorithm with variable local search range relative to frequency of the environmental changes. Genetic Programming, pp 22–25

  52. Vavak F, Jukes K, Fogarty TC (1997) Adaptive balancing of a bank of sugar-beet presses using a genetic algorithm with variable local search range. In: 3rd Intl Mendel Conference on Genetic Algorithms, Citeseer, pp 164–169

  53. Zhang G, Zhang L, Song X, Wang Y, Zhou C (2019) A variable neighborhood search based genetic algorithm for flexible job shop scheduling problem. Cluster Comput 22:11561–11572

    Article  Google Scholar 

  54. Li X, Gao L, Pan Q, Wan L, Chao K-M (2018) An effective hybrid genetic algorithm and variable neighborhood search for integrated process planning and scheduling in a packaging machine workshop. IEEE Trans Syst Man Cybern Syst 49:1933–1945

    Article  Google Scholar 

  55. Xia H, Li X, Gao L (2016) A hybrid genetic algorithm with variable neighborhood search for dynamic integrated process planning and scheduling. Comput Ind Eng 102:99–112

    Article  Google Scholar 

  56. García-Martínez C, Lozano M (2010) Evaluating a local genetic algorithm as context-independent local search operator for metaheuristics. Soft comput 14:1117–1139

    Article  Google Scholar 

  57. Michielssen E, Ranjithan S, Mittra R (1992) Optimal multilayer filter design using real coded genetic algorithms. IEE Proc J-Optoelectron 139:413–420

    Article  Google Scholar 

  58. Hansen P, Mladenović N (2003) Variable neighborhood search. In: Handbook of metaheuristics. Springer, pp 145–184

  59. Lu Y, Cao B, Rego C, Glover F (2018) A Tabu Search based clustering algorithm and its parallel implementation on Spark. Appl Soft Comput 63:97–109

    Article  Google Scholar 

  60. Heloulou I, Radjef MS, Kechadi MT (2017) A multi-act sequential game-based multi-objective clustering approach for categorical data. Neurocomputing 267:320–332

    Article  Google Scholar 

  61. Hoffman M, Steinley D, Brusco MJ (2015) A note on using the adjusted Rand index for link prediction in networks. Soc Networks 42:72–79

    Article  Google Scholar 

  62. Zhao X, Cao F, Liang J (2018) A sequential ensemble clusterings generation algorithm for mixed data. Appl Math Comput 335:264–277

    MathSciNet  MATH  Google Scholar 

  63. Ahmad A, Khan SS (2021) initKmix-A novel initial partition generation algorithm for clustering mixed data using k-means-based clustering. Expert Syst Appl 167:114149

    Article  Google Scholar 

Download references

Acknowledgements

This research is funded by Funds for Science and Technology Development of the University of Danang under Project Number B2020-DN02-83.

Author information

Authors and Affiliations

  1. Faculty of Project Management, The University of Danang–University of Science and Technology, 54 Nguyen Luong Bang, Danang, Vietnam

    Thi Phuong Quyen Nguyen, Thi Cuc Nguyen & Thi Huynh Anh Le

  2. Department of Industrial Management, National Taiwan University of Science and Technology, No. 43, Section 4, Kee-Lung Road, Taipei, 106, Taiwan, ROC

    R. J. Kuo

  3. Faculty of Transportation Mechanical Engineering, The University of Danang–University of Science and Technology, 54 Nguyen Luong Bang, Danang, Viet Nam

    Minh Duc Le

Authors
  1. Thi Phuong Quyen Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. J. Kuo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Minh Duc Le
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Thi Cuc Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Thi Huynh Anh Le
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Thi Phuong Quyen Nguyen.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nguyen, T.P.Q., Kuo, R.J., Le, M.D. et al. Local search genetic algorithm-based possibilistic weighted fuzzy c-means for clustering mixed numerical and categorical data. Neural Comput & Applic 34, 18059–18074 (2022). https://doi.org/10.1007/s00521-022-07411-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-022-07411-1

Keywords

Search

Navigation