Metabolic design of macroscopic bioreaction models: application to Chinese hamster ovary cells

Abstract

The aim of this paper is to present a systematic methodology to design macroscopic bioreaction models for cell cultures based upon metabolic networks. The cell culture is seen as a succession of phases. During each phase, a metabolic network represents the set of reactions occurring in the cell. Then, through the use of the elementary flux modes, these metabolic networks are used to derive macroscopic bioreactions linking the extracellular substrates and products. On this basis, as many separate models are obtained as there are phases. Then, a complete model is obtained by smoothly switching from model to model. This is illustrated with batch cultures of Chinese hamster ovary cells.

Introduction

The metabolism of a cell line is usually represented by a metabolic network (see Fig. 1 for an illustration) which graphically depicts the reactions taking place within the cell as well as the reactions with its environment. It is a well-known fact that the metabolic routes change during the cultivation mainly depending on the availability of the substrates. The aim of this paper is to present a systematic methodology to design macroscopic models for cell cultures based upon metabolic networks. We shall present a global model which is able to describe the cell dynamics for the whole duration of the cultivation. The model will take into account the changes of the metabolism during the cultivation and involve, in an unified framework, the three main successive phases of the cultivation, namely the growth phase, the “transition” phase and the death phase. According to experimental observations a specific and different metabolic map will be used for each phase.

Fig. 1

Metabolic network for the growth of CHO-320 cells. Bold arrows stand for double arrows

The methodology will be illustrated with the particular case of Chinese hamster ovary (CHO) cells. The cell line is the CHO-320 line (see [1]) and the cells are cultivated in a serum-free medium: CHO-BDM S2.2. This medium contains basal defined medium (BDM), 0.1% pluronic F68 and a solution of ITS-S (1%). The media was further supplemented with rice protein hydrolysate (Hypep 5115). Hydrolysate was provided by Quest International (Naarden, The Netherlands). The medium was further supplemented with glutamine (2 mM) to reach a 6 mM final concentration.

The cells were cultivated in 125 ml shake-flasks at 37°C under a water-saturated atmosphere and 5% (v/v) CO₂ on an orbital shaking platform (New Brunswick Scientific, Edison, NJ) at 100 rpm. The experiments have been performed by the staff of the Laboratory of Cellular Biochemistry, UCL.

For these cells, the metabolic networks associated with the three phases—growth, transition and death—are represented in Figs. 1, 6 and 7, respectively.

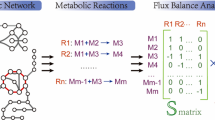
In the first section, the passage from a metabolic network to a general macroscopic model is described. It is shown how the elementary flux modes (EFMs) which are obtained from the convex basis of the network stoichiometric matrix (see e.g. [2–4] for details) are transformed into a set of macroscopic bioreactions involving measurable substrates and products present in the culture medium. The next step is to select a minimal subset of bioreactions among the whole set of macroscopic bioreactions which is sufficient to produce simulation that fully explain the observed data. This is done by computing another convex basis. This one solves a problem involving the EFMs and the substrate and product measurements. On the basis of the examination of these convex basis vectors, the set of macroscopic bioreactions may be further reduced down to a minimal size. Finally, a mass balance dynamical model is derived and validated with the experimental data. This methodology has already been used by the authors to obtain a model for the growth phase (see [5]). Our contribution in this paper is to show how the methodology can be extended, in an unified and systematic way, to the other phases of the cultivation (transition and death phases). Three separate models are obtained, each of them based on a metabolic network specific to its own phase. Finally, the complete model is built up by using the three separate models in their respective time interval, smoothly switching from model to model, on the basis of the availability of the two main substrates: glucose and glutamine.

Principles of metabolic design of macroscopic bioreaction models

When conceiving a macroscopic model, the cell mass in the bioreactor is viewed as a black box device that catalyses the conversion of substrates into products.

The overall conversion mechanism is described by a rather small set of key macroscopic bioreactions that directly connect the substrates to the products. In this paper we are concerned with the design of such macroscopic models when measurements of extra-cellular substrates and products in the culture medium are the only available data besides measurements of the biomass (see also [6] for a different approach). It is assumed that the cells are cultivated in batch mode in a stirred tank reactor. The dynamics of substrates and products are described by the following basic differential equations:

$$\frac{{\hbox{d}s}}{{\hbox{d}t}} = - v_{\rm s} (t)X(t) $$

(1)

$$ \frac{{\hbox{d}p}}{{\hbox{d}t}} = v_{\rm p} (t)X(t) $$

where

• X(t) is the biomass concentration

• s(t) is the vector of substrate concentrations

• p(t) is the vector of product concentrations

• v _s(t) is the vector of specific uptake rates

• v _p(t) is the vector of specific excretion rates

Obviously, the specific rates v _s(t) and v _p(t) are not independent: they are quantitatively related through the intracellular metabolism (see Fig. 1) represented by a metabolic network. A metabolic network is a directed hypergraph encoding a (possibly very large) set of elementary biochemical reactions taking place in the cell. In the graph, the nodes represent the involved metabolites and the arcs represent the fluxes. A typical example of metabolic network that will be considered later in this paper is shown in Fig. 1.

In order to explicit the link between uptake and excretion rates, the quasi steady-state viewpoint of metabolic flux analysis (MFA) is adopted. This means that for each intermediate metabolite, it is assumed that the net sum of production and consumption fluxes, weighted by their stoichiometric coefficients, is zero. This is expressed by an algebraic relation:

$$N v(t) = 0$$

(2)

where v(t) is the vector of the fluxes v _j (t) and N = [n _ij ] is the stoichiometric matrix of the metabolic network. More precisely, the flux v _j denotes the rate of reaction j and a non-zero n _ij is the stoichiometric coefficient of metabolite i in reaction j. The quasi steady-state approximation is justified because the intracellular metabolic transients are much faster than the process transients as represented by Eq. 1.

By definition, the specific uptake and excretion rates v _s and v _p are linear combinations of some of the metabolic fluxes. This is expressed by defining appropriate matrices N _s and N _p such that

$$v_{\rm s} (t) = N_{\rm s} v(t) \quad v_{\rm p} (t) = N_{\rm p} v(t)$$

(3)

As indicated above, our aim is to design a reduced-order macroscopic model in order to link the extracellular substrates and products in a metabolic meaningful way.

The first stage is to compute the EFMs which are the edges of the pointed polyhedral cone that involves all the non-negative solutions of Eq. 2. By definition, these EFMs are obviously also non-negative vectors and they are called the convex basis of the solution set. The non-negative matrix E, whose columns are these vectors, is such that NE =  0

Biochemically speaking, the EFMs encode the simplest metabolic routes that connect the substrates to the products. More precisely, an EFM is a sequence of biochemical reactions starting with one or several substrates and ending with one or several products. Since the intermediate reactions are assumed to be at quasi steady-state, a macroscopic bioreaction is then readily defined from an EFM by considering only the initial substrates and the final products. The stoichiometric matrix K of the set of bioreactions is given by the following expression:

$$K = {\left({\begin{array}{*{20}c} {{- N_{\rm s}}} \\ {{N_{\rm p}}} \\ \end{array}} \right)}E. $$

(4)

Let ξ denote the vector of extracellular species concentrations:

$$ \xi = {\left({\begin{array}{*{20}c} {{s(t)}} \\ {{p(t)}} \\ \end{array}} \right)} $$

Then a dynamical model of the extracellular species governed by the macroscopic bioreactions in the bioreactor is naturally written as follows:

$$ \frac{{\hbox{d}\xi}}{{\hbox{d}t}} = Kw(t)X(t) $$

(5)

where w(t) represents the vector of the rates w _i (t) of the macroscopic bioreactions. From Eqs. 4 and 5, we obtain

$$ \frac{{\hbox{d}\xi}}{{\hbox{d}t}} = Kw(t)X(t) = {\left({\begin{array}{*{20}c} {{- N_{\rm s}}} \\ {{N_{\rm p}}} \\ \end{array}} \right)}Ew(t)X(t) $$

(6)

Moreover, from Eqs. 1 and 3, we obtain

$$ \frac{{\hbox{d}\xi}}{{\hbox{d}t}} = {\left({\begin{array}{*{20}c} {{- N_{\rm s}}} \\ {{N_{\rm p}}} \\ \end{array}} \right)}v(t)X(t) $$

Thus, there is a linear relation between the intracellular fluxes v _i (t) and the macroscopic reaction rates w _i (t):

$$ v(t) = Ew(t) $$

(7)

In biochemical terms, this means that the fluxes v _i are non-negative linear combinations of the specific rates w _i associated with the EFMs of the metabolic network. Equivalently, the vector of fluxes v(t) is a linear combination of EFMs whose non-negative weights are the macroscopic rates w _i (t).

By injecting Eq. 7 into Eq. 3, the specific uptake and excretion rates v _s and v _p can be expressed in terms of the macroscopic reaction rates w _i (t):

$$ \left\{{\begin{array}{*{20}c} {{N_{\rm s} Ew(t) = v_{\rm s} (t)}} \\ {{N_{\rm p} Ew(t) = v_{\rm p} (t)}} \\ \end{array}} \right. \quad \hbox{with}\ w(t) \geqslant 0 $$

(8)

Therefore, the vector of specific rates w can be seen as a non-negative solution of an homogeneous linear system derived from Eq. 8:

$$ {\left({\begin{array}{*{20}c} {{N_{\rm s} E}}& {{- v_{\rm s} (t)}} \\ {{N_{\rm p} E}}& {{- v_{\rm p} (t)}} \\ \end{array}} \right)}{\left({\begin{array}{*{20}c} {{w(t)}} \\ {1} \\ \end{array}} \right)} = {\left({\begin{array}{*{20}c} {0} \\ {0} \\ \end{array}} \right)}\quad {\hbox{with}}\;w(t) \geqslant 0 $$

(9)

In this form, for given values of v _p(t) and v _s(t) at time t, the solution set of system (Eq. 9) can also be analysed in the framework of convex analysis. This means that the set of solutions also forms a convex cone and that every solution is a non-negative combination of convex basis vectors ${\left({\begin{array}{*{20}c} {{h_{i} (t)}} \\ {1} \\ \end{array}} \right)}:$

$$ {\left({\begin{array}{*{20}c} {{w(t)}} \\ {1} \\ \end{array}} \right)} = {\sum\limits_i {{\left({\begin{array}{*{20}c} {{h_{i} (t)}} \\ {1} \\ \end{array}} \right)}}}z_{i} (t) $$

(10)

In matrix form, this yields

$$ \left\{{\begin{array}{*{20}c} {{w = Hz}} \\ {{1 = {\sum\nolimits_i {z_{i}}}}} \\ \end{array}} \right. $$

(11)

where H is the matrix with columns h _i . Remark that here, the convex basis vectors are normalised to have a unit last entry. This is obviously without loss of generality as it is well known that convex basis vectors are always defined up to a real positive scaling factor.

As we will observe in the application (Sect. 3), the vectors h _i have an important and critical property: they have a maximal number of non-zero entries that can be determined beforehand (see [7]). From a biological viewpoint, this means that each vector h _i can be interpreted as a particular solution w of Eq. 9, or equivalently as a particular solution

$$ v = Eh_{i} $$

of Eq. 2 which is fully consistent with the experimental data. As for w, the non-zero entries of h _i can also be interpreted as the weights of the respective contributions of the different EFMs in the computation of the corresponding flux distribution v.

In other words, when only the network topology is taken into account by means of the stoichiometric matrix as in Eq. 2, any flux distribution v that complies with the pseudo-steady-state assumption is defined by Eq. 7. But when the excretion and uptake rates are imposed additionally, the set of solutions is smaller than the cone generated by E (see Fig. 2). Furthermore, not all the EFMs are needed to obtain a model that complies with the pseudo-steady-state assumption (Eq. 2) and the external measurements (Eq. 3).

Fig. 2

Illustration of a cone containing the solutions of Eq. 2 and the subcone containing the solutions of the system (Eq. 2) that complies with the external measurements (Eq. 3)

Hence, each convex basis vector h _i brings two different pieces of information. First, it tells which EFMs, and consequently which macroscopic bioreactions, are sufficient if combined together to build a model that explains the specific rates v _s and v _p. These EFMs are designated by the position of the non-zero entries of h _i .

Secondly, the value of each non-zero entry of h _i is the value of the reaction rate corresponding to the selected EFM or macroscopic bioreaction.

Therefore, the matrix H provides the tool needed to minimise the size of the dynamical macroscopic model by minimising the number of macroscopic bioreactions that are used in the model. This is convenient because in general the number of EFMs may be too large for a practical engineering utilisation.

In the remainder of the paper, we shall illustrate this methodology with an application to CHO cells for each phase of the cell cultivation: growth, transition, death. The procedure is as follows:

• 1. The EFMs are computed and a first dynamical model (Eq. 5) is established.

• 2. Average uptake rates v _s and excretion rates v _p are fitted on the experimental data.

• 3. The convex basis H is computed.

• 4. For each vector h _i , a selection matrix S _i is defined that encodes the corresponding selection of EFMs (or bioreactions). A minimal dynamical model is then written as

  $$ \frac{{\hbox{d}\xi}}{{\hbox{d}t}} = LrX $$

  (12)

  with L =  KS _i the pseudo-stoichiometric matrix of the selected set of bioreactions and r _i the vector of the reaction rates provided by the non-zero entries of h _i . In each phase, we shall present two different models in order to emphasise their equivalence.

Application to CHO cells

In order to illustrate and motivate the methodology presented above, we consider the example of CHO cells cultivated in batch mode in stirred flasks. The measured extracellular species are two substrates (glucose and glutamine) and three excreted products (lactate, ammonia, alanine). The experimental data collected during three experiments are shown in Fig. 3. For this modelling study, three successive phases are considered: the growth phase (marked by green dots in Fig. 3), the transition phase (marked by orange dots) and the death phase (marked by red dots). Let us remark that the three cultures are used at once for the parameter estimation in order to obtain an average simulation model.

Fig. 3

Biomass production and measured extracellular species for three CHO-320 batch cultures. Growth, transition and death phases data are, respectively, represented by green, orange and red dots

The growth phase model

The metabolic network considered for the growth phase is presented in Fig. 1. This metabolic network describes only the part of the metabolism concerned with the utilisation of the two main energetic nutrients (glucose and glutamine). The metabolism of the amino acids provided by the culture medium is not considered. It is assumed that a part of the glutamine is used for the making of purine and pyrimidine nucleotides but is not directly involved in the formation of proteins. This is obviously a simplifying assumption that could be discussed. It must, however, be mentioned that this assumption appears to be quite acceptable since a MFA (reported in reference [3]) based on the network of Fig. 1 gives a production of nucleotides which is in agreement with the data of the literature. Since the goal is to compute the EFMs, all the intermediate species that are not located at branch points are omitted without loss of generality. The stoichiometric matrix N is presented in Table 1, and the vectors coding for the resulting EFMs ¹ are shown in Table 2. As explained above, from these modes nine macroscopic bioreactions are obtained by keeping only the initial substrates and final products. For instance, the first mode (i.e. first column in Table 2) defines a path in the network made up of arcs v ₁, v ₂, v ₃, v ₄, v ₅, v ₆ that connect glucose to lactate. This gives a macroscopic reaction (in moles):

$${\text{glucose }} \to {\text{ 2\ lactate}} $$

with the stoichiometric coefficients given by entry (1,1) of N _s E for glucose and entry (1,1) of N _p E for lactate with

$$ \begin{aligned}\,& \begin{array}{*{20}c} & & & {{v_{1}}}& {{v_{{16}} v_{{17}} v_{{18}}}}& {{v_{{24}}}} \\ \end{array} \\& N_{\rm s} = {\left({\begin{array}{*{20}c} {{1\,\,\, \ldots \,\,\,0\,\,0\,\,0\,\, \ldots \,\,0}} \\ {{0\,\,\, \ldots \,\,\,1\,\,1\,\,2\,\, \ldots \,\,0}} \\ \end{array}} \right)} \\ \end{aligned} $$

$$ \begin{aligned}\,& \begin{array}{*{20}l}&&&& {v_{1}}&& v_{6} v_{7}&& v_{15} v_{16}&& v_{24}\\ \end{array}\\ & N_{\rm p} = {\left({\begin{array}{*{20}l} 0&\ldots&1\; 0&\ldots&0\;0&\ldots&0\\ 0&\ldots&0\;1&\ldots&0\;0&\ldots&0\\ 0& \ldots&0\;0&\ldots&1\;1&\ldots&0\\ \end{array}} \right)} \end{aligned} $$

Table 1 The stoichiometric matrix for the growth phase

Table 2 The 11 elementary flux modes for the growth phase

The 10 macro-reactions for the growth are as follows:

e₁::

$\hbox{G} \xrightarrow{{w_{1}}} 2 \hbox{L}$

e₂ = e₄::

$\hbox{G} \xrightarrow{{w_{2}}} 6 \hbox{CO}_{2}$

e₃::

$3\hbox{G} \xrightarrow{{w_{3}}} 5 \hbox{L} + 3 \hbox{CO}_{2}$

e₅::

$\hbox{Q} \xrightarrow{{w_{5}}} \hbox{A} + 2 \hbox{CO}_{2} + \hbox{N}$

e₆::

$Q \xrightarrow{{w_{6}}} \hbox{L} + 2 \hbox{CO}_{2} + 2 \hbox{N}$

e₇::

$\hbox{Q} \xrightarrow{{w_{7}}} 5 \hbox{CO}_{2} + 2 \hbox{N}$

e₈::

$\hbox{G} + \hbox{Q} \xrightarrow{{w_{8}}} \hbox{Pyr} + 2 \hbox{CO}_{2}$

e₉::

$\hbox{G}+2\hbox{Q} \xrightarrow{{w_{9}}} \hbox{Pur} + \hbox{A} + 3 \hbox{CO}_{2}$

e₁₀::

$\hbox{G}+2\hbox{Q} \xrightarrow{{w_{{10}}}} \hbox{Pur} + 6 \hbox{CO}_{2} + \hbox{N}$

e₁₁::

$\hbox{G}+2\hbox{Q} \xrightarrow{{w_{{10}}}} \hbox{Pur} + \hbox{L} + 3 \hbox{CO}_{2} + \hbox{N}$

where G, Q, L, N, A stand for glucose, glutamine, lactate, ammonia and alanine, respectively. The dynamical model (Eq. 5) for the growth phase is written as follows:

$$ \frac{{\hbox{d}\xi _{g}}}{{\hbox{d}t}} = {\underbrace {{\left({\begin{array}{*{20}c} {{- 1}}& {{- 1}}& {{- 3}}& {{- 3}}& {0}& {0}& {0}& {{- 1}}& {{- 1}}& {{- 1}}& {{- 1}} \\ {0}& {0}& {0}& {0}& {{- 1}}& {{- 1}}& {{- 1}}& {{- 1}}& {{- 2}}& {{- 2}}& {{- 2}} \\ {2}& {0}& {5}& {0}& {0}& {1}& {0}& {0}& {0}& {0}& {1} \\ {0}& {0}& {0}& {0}& {1}& {2}& {1}& {0}& {0}& {1}& {1} \\ {0}& {0}& {0}& {0}& {1}& {0}& {0}& {0}& {1}& {0}& {0} \\ \end{array}} \right)}}_{{K_{g}}}} {w}\,X\quad \hbox{with}\ \xi _{g} = {\left({\begin{array}{*{20}c} {\hbox{G}} \\ {\hbox{Q}} \\ {\hbox{L}} \\ {\hbox{N}} \\ {\hbox{A}} \\ \end{array}} \right)} $$

This model can be reduced by following the procedure described in Sect. 2. From the experimental data of Fig. 3, average constant specific excretion and uptake rates are computed by linear regression (see Fig. 4). A detailed description of this estimation is provided in [5].

Fig. 4

Estimation of the average rates of specific excretion and uptake rates by linear regression

Subsequently, the specific formulation of equation (8) for the growth phase is given as follows:

$$ {\left({\begin{array}{*{20}c} {{N_{\rm s} E- v_{\rm s}}} \\ {{N_{\rm p} E - v_{\rm p}}} \\ \end{array}} \right)}c = {\left({\begin{array}{*{20}c} {1}& {1}& {3}& {3}& {0}& {0}& {0}& {1}& {1}& {1}& {1}& {{- 1.8713{\rm E} - 01}} \\ {0}& {0}& {0}& {0}& {1}& {1}& {1}& {1}& {2}& {2}& {2}& {{- 5.04246{\rm E} - 02}} \\ {2}& {0}& {5}& {0}& {0}& {1}& {0}& {0}& {0}& {0}& {1}& {{- 3.4451{\rm E} - 01}} \\ {0}& {0}& {0}& {0}& {1}& {0}& {0}& {0}& {1}& {0}& {0}& {{- 8.8083{\rm E}-03}} \\ {0}& {0}& {0}& {0}& {1}& {2}& {2}& {0}& {0}& {1}& {1}& {{- 4.5712{\rm E}-02}} \\ \end{array}} \right)}{\left({\begin{array}{*{20}c} {w} \\ {1} \\ \end{array}} \right)} = 0 $$

(13)

where the last column is formed by the average rates. There are 32 resulting convex basis vectors. They are presented in Table 3. To be able to interpret a vector h _i easily in terms of macroscopic bioreactions, a line j of H is labelled with the corresponding EFM e _j . It becomes straightforward to associate the non-zero entries of h _i to macro-reactions by simple inspection. A vector h _i is readily translated into a set of macro-reactions for which the reaction rates are the entries value. It is noteworthy that each column of H shows only five non-zero entries and without any further assumption, any of these columns leads equivalently to a reduced reaction network and hence to a minimal dynamical model.

In order to select some specific models, additional qualitative biological knowledge can be used when available. Indeed, in our example, measurements of purine and pyrimidine nucleotides are not available but these nucleotides are simultaneously necessary for the biomass production. Since the measurements of purine and pyrimidine nucleotides are not involved in the calculations of the convex basis H, nothing ensures that any choice of h _i will lead to model that produces biomass. The only reaction producing pyrimidine nucleotides is e ₈ and the reactions producing purine nucleotides are e ₉, e ₁₀, e ₁₁ in the initial reaction network. So, a vector h _i corresponding to biomass production must contain non-zero entries at least at the following couples: (e ₈, e ₉), (e ₈, e ₁₀), (e ₈, e ₁₁). Hence, the convex basis vectors h ₃, h ₈, h ₁₃, h ₁₅, h ₂₁ and h ₃₀ are valid (see Table 3).

Table 3 The columns of matrix H for the growth phase

As a matter of illustration, let us first consider h ₃ which yields the following bioreaction network:

$$\begin{array}{*{20}l} \hbox{e}_{1}: &\hbox{G} \xrightarrow{{w_{1}}} 2 \hbox{L},\\ \hbox{e}_{5}: &\hbox{Q} \xrightarrow{{w_{5}}} \hbox{A} + 2 \hbox{CO}_{2} + \hbox{N},\\ \hbox{e}_{7}: &\hbox{Q} \xrightarrow{{w_{7}}} 5 \hbox{CO}_{2} + 2 \hbox{N},\\ \hbox{e}_{8}: &\hbox{G} + \hbox{Q} \xrightarrow{{w_{8}}} \hbox{Pyr} + 2 \hbox{CO}_{2},\\ \hbox{e}_{11}: &\hbox{G}+2\hbox{Q} \xrightarrow{{w_{{12}}}} \hbox{Pur} + \hbox{L} + 3 \hbox{CO}_{2} + \hbox{N} \end{array}$$

(14)

The reactions rates of these five reactions are modelled by the following Michaëlis-Menten kinetics:

$$ \begin{array}{*{20}l} {{r_{1} = \mu _{1} \frac{G}{{k_{G} + G}}}} \\ {{r_{2} = \mu _{2} \frac{Q}{{(k_{Q} + Q)}}}} \\ {{r_{3} = \mu _{3} \frac{Q}{{(k_{Q} + Q)}}}} \\ {{r_{4} = \mu _{4} \frac{{GQ}}{{(k_{G} + G)(k_{Q} + Q)}}}} \\ {{r_{5} = \mu _{5} \frac{{GQ}}{{(k_{G} + G)(k_{Q} + Q)}}}} \\ \end{array} $$

where the maximum reaction rates μ _i are given by the entries of h ₃:

• μ₁ =  1.6820 E−01

• μ₂ =  8.8083 E−03

• μ₃ =  1.4396 E−02

• μ₄ =  1.0817 E−02

• μ₅ =  8.1125 E−03

In order to complete the model, it remains to select numerical values for the parameters k _G and k _Q . Under the balanced growth condition, it clearly makes sense to assume that the macro-reactions proceed almost at their maximal rate during the exponential growth phase. The half-saturation constants k _G and k _Q are therefore selected small enough to be ineffective during the growth phase but large enough to avoid stiffness difficulties in the numerical simulation of the model. Here we have set the half-saturation constants at the following values:

$$k_{G} = k_{Q} = 0.1\,\hbox{mM}. $$

Finally, the growth phase model is written as follows:

$$ \frac{{\hbox{d}\xi _{g}}}{{\hbox{d}t}} = L_{g} r_{g} X $$

with

• the state vector

  $$ \xi _{g} = {\left({\begin{array}{*{20}c} {\hbox{G}}\\ {\hbox{Q}}\\ {\hbox{L}}\\ {\hbox{N}}\\ {\hbox{A}}\\ \end{array}} \right)} $$

• the selection matrix S _g corresponding to Eq. 14

  $$ S_{g} = {\left({\begin{array}{*{20}c} {1}& {0}& {0}& {0}& {0}\\ {0}& {0}& {0}& {0}& {0}\\ {0}& {0}& {0}& {0}& {0}\\ {0}& {0}& {0}& {0}& {0}\\ {0}& {1}& {0}& {0}& {0}\\ {0}& {0}& {0}& {0}& {0}\\ {0}& {0}& {1}& {0}& {0}\\ {0}& {0}& {0}& {1}& {0}\\ {0}& {0}& {0}& {0}& {0}\\ {0}& {0}& {0}& {0}& {0}\\ {0}& {0}& {0}& {0}& {1}\\ \end{array}} \right)} $$

• the stoichiometric matrix L _g of Eq. 14:

  $$ L_{g} = K_{g} S_{g} = {\left({\begin{array}{*{20}c} {{- 1}}& {0}& {0}& {{- 1}}& {{- 1}}\\ {0}& {{- 1}}& {{- 1}}& {{- 1}}& {{- 2}}\\ {2}& {0}& {0}& {0}& {1}\\ {0}& {1}& {2}& {0}& {1}\\ {0}& {1}& {0}& {0}& {0}\\ \end{array}} \right)} $$

• the reaction rate vector:

  $$ \begin{array}{*{20}c} {{r_{1} = 1.6820\hbox{E} - 01 \frac{G}{{0.1 +G}}}}\\ {{r_{2} = 8.8083\hbox{E} - 03 \frac{Q}{{(0.1 + Q)}}}}\\ {{r_{3} = 1.4396\hbox{E} - 02 \frac{Q}{{(0.1 + Q)}}}}\\ {{r_{4} = 1.0817\hbox{E} - 02 \frac{{GQ}}{{(0.1 + G)(0.1 + Q)}}}}\\ {{r_{5} = 8.1125\hbox{E} - 03 \frac{{GQ}}{{(0.1 + G)(0.1 + Q)}}}}\\ \end{array} $$

The growth model obtained with these values has been used to produce the simulation result presented in Fig. 5 (left-hand side). Obviously, the model succeeds in describing the concentration of the measured metabolites during the growth. It is noteworthy that all the models that could be similarly established from the vectors h _i of Table 3 are able to provide similar results. This is illustrated in Fig. 5 (right-hand side) with a model corresponding to h ₃₀.

Fig. 5

On the left-hand side, simulation resulting from the growth phase model corresponding to h ₃; on the right, simulation obtained with the growth model corresponding to h ₃₀

The transition phase model

Now that an efficient model is available for the growth phase, a different metabolic network is depicted in Fig. 6 for the transition phase which occurs in the time period just after glucose is exhausted (from about 80 to 120 h). As we can see in Fig. 3, during this period the cell keeps growing while lactate and alanine start to be consumed. Our assumption is then to consider lactate and alanine as new substrates, in addition to glutamine whose consumption is slowed down. Therefore, some of the reactions of the previous network are inverted in order to be in agreement with this assumption and, in particular, to still have a production of the nucleotide precursors. The stoichiometric matrix of the network is given in Table 4. For this network, there are 12 EFMs represented in Table 5. The following nine macro-reactions are subsequently derived:

Fig. 6

Simplified metabolic network proposed for the transition phase

Table 4 The stoichiometric matrix for the transition phase

Table 5 The 12 elementary flux modes for the transition phase

e₁ = e₂::

$\hbox{L} \xrightarrow{{w_{1}}} 3 \hbox{CO}_{2}$

e₃ = e₄::

$\hbox{A} \xrightarrow{{w_{3}}} 3 \hbox{CO}_{2} + \hbox{N}$

e₅::

$2\hbox{L} \xrightarrow{{w_{5}}} \hbox{Pyr} + 2 \hbox{CO}_{2}$

e₆::

$\hbox{L}+2\hbox{Q} \xrightarrow{{w_{6}}} \hbox{Pur} + 3 \hbox{CO}_{2} + \hbox{N}$

e₇::

$2\hbox{A}+\hbox{Q} \xrightarrow{{w_{7}}} \hbox{Pyr} + 2 \hbox{CO}_{2} + 2 \hbox{N}$

e₈::

$\hbox{A}+2\hbox{Q} \xrightarrow{{w_{8}}} \hbox{Pur} + 3 \hbox{CO}_{2} + 2 \hbox{N}$

e₉ = e₁₀::

$Q \xrightarrow{{w_{9}}} 5 \hbox{CO}_{2} + 2 \hbox{N}$

e₁₁::

$\hbox{G}+2\hbox{Q} \xrightarrow{{w_{{11}}}} \hbox{Pyr} + 6 \hbox{CO}_{2} + 4 \hbox{N}$

e₁₂::

$\hbox{G}+2\hbox{Q} \xrightarrow{{w_{{12}}}} \hbox{Pur} + 5 \hbox{CO}_{2} + 3 \hbox{N}$

The corresponding stoichiometry matrix K _t is easily obtained:

$$ K_{t} = {\left({\begin{array}{*{20}c} {0}& {0}& {0}& {0}& {{- 1}}& {{- 2}}& {{- 1}}& {{- 2}}& {{- 1}}& {{- 1}}& {{- 3}}& {{- 3}} \\ {{- 1}}& {{- 1}}& {0}& {0}& {{- 2}}& {{- 1}}& {0}& {0}& {0}& {0}& {0}& {0} \\ {0}& {0}& {1}& {1}& {0}& {1}& {2}& {2}& {2}& {2}& {4}& {3} \\ {0}& {0}& {{- 1}}& {{- 1}}& {0}& {0}& {{- 2}}& {{- 1}}& {0}& {0}& {0}& {0} \\ \end{array}} \right)} $$

Consequently, the combined problem of finding the reduced set of macroscopic bioreactions and the vector of maximal rates is formulated as follows:

$$ {\left({\begin{array}{*{20}c} {0}& {0}& {0}& {0}& {{1}}& {{2}}& {{1}}& {{2}}& {{1}}& {{1}}& {{3}}& {{3}}&{-1.0583\hbox{E}}&{-03} \\ {{1}}&{{1}}& {0}& {0}& {{2}}& {{1}}& {0}& {0}& {0}& {0}& {0}& {0}&{-3.4513\hbox{E}}&{-02} \\ {0}& {0}& {1}& {1}& {0}& {0}& {2}& {1}& {0}& {0}& {0}& {0}&{-4.0125\hbox{E}}&{-03} \\ {0}& {0}&{{1}}& {{1}}& {0}& {1}& {{2}}& {{ 2}}& {2}& {2}& {4}&{3}&{-9.0000\hbox{E}}&{-04}\\ \end{array}} \right)} {\left({\begin{array}{*{20}c} w\\ 1\\ \\ \end{array}} \right)}=0 $$

where the last column is formed by the average rates obtained by linear regression.

The convex basis for this problem is presented in Tables 6 and 7. Here, all the vectors h _i contain exactly four non-zero entries. As for the growth phase, one of the convex basis vectors represented by a column of H has to be taken into consideration. Here again, purine nucleotides and pyrimidine nucleotides must be produced. Therefore, the first column of H, h ₁ is a valid choice. This vector provides the selection matrix S _t :

$$ S_{t} = {\left({\begin{array}{*{20}c} {0}& {0}& {0}& {0} \\ {1}& {0}& {0}& {0} \\ {0}& {1}& {0}& {0} \\ {0}& {0}& {0}& {0} \\ {0}& {0}& {1}& {0} \\ {0}& {0}& {0}& {1} \\ {0}& {0}& {0}& {0} \\ {0}& {0}& {0}& {0} \\ {0}& {0}& {0}& {0} \\ {0}& {0}& {0}& {0} \\ {0}& {0}& {0}& {0} \\ {0}& {0}& {0}& {0} \\ \end{array}} \right)}, $$

and leads to the selection of a reduced set of four macroscopic bioreactions:

e₂::

$\hbox{L} \xrightarrow{{w_{1}}} 3 \hbox{CO}_{2}$

e₃::

$\hbox{A} \xrightarrow{{w_{3}}} 3 \hbox{CO}_{2} + \hbox{N}$

e₅::

$2\hbox{L}+ \hbox{Q} \xrightarrow{{w_{5}}} \hbox{Pyr} + 2 \hbox{CO}_{2}$

e₆::

$\hbox{L}+2\hbox{Q} \xrightarrow{{w_{6}}} \hbox{Pur} + 3 \hbox{CO}_{2} + \hbox{N}.$

Table 6 The 52 vectors of H for the transition phase

Table 7 The 52 vectors of H for the transition phase (continued)

Finally, the transition phase model is written as follows:

$$ \frac{{\hbox{d}\xi _{t}}}{{\hbox{d}t}} = L_{t}r_{t} X $$

where

$$ \xi _{t} = {\left({\begin{array}{*{20}l} {Q} \\ {L} \\ {N} \\ {A} \\ \end{array}} \right)}\quad \hbox{and}\quad L_{t} = K_{t}S_{t} = {\left({\begin{array}{*{20}c} {0}& {0}& {{- 1}}& {{- 2}} \\ {{- 1}}& {0}& {{- 2}}& {{- 1}} \\ {0}& {1}& {0}& {1} \\ {0}& {{- 1}}& {0}& {0} \\ \end{array}} \right)}. $$

Again, Michaëlis–Menten kinetics are used:

$$ \begin{array}{*{20}l} {{r_{1} = \mu _{1} \frac{L}{{k_{L} + L}}}} \\ {{r_{2} = \mu _{2} \frac{A}{{k_{A} + A}}}} \\ {{r_{3} = \mu _{3} \frac{{LQ}}{{(k_{L} + L)(k_{Q} + Q)}}}} \\ {{r_{4} = \mu _{4} \frac{{LQ}}{{(kL + L)(k_{Q} + Q)}}}} \\ {{}} \\ \end{array} $$

with the following numerical values:

$$ k_{L} = k_{A} = k_{Q} = 0.1\,\hbox{mM}. $$

and the maximal rates μ _i are obtained from the non-zero entries of h ₁:

• μ₁ =  3.3896 E−02

• μ₂ =  4.0000 E−04

• μ₃ =  5.8333 E−05

• μ₄ =  5.0000 E−04

The death phase model

During the transition phase, an underlying assumption was to consider that the decrease in biomass production resulted from the fact that even if cells were still produced more cells were dying. During the death phase, it is assumed that the reason of biomass decrease is simply that nucleotides are no longer produced. This phase begins approximately at 120 h. It is concomitant with a change in lactate, alanine and glutamine consumption rates as well as a change in ammonia production rate. These rates are nearly constant during the death phase.

The metabolic network (Fig. 7) is modified to comply with the fact that lactate, alanine and glutamine are used exclusively to sustain the remaining living cells and no longer to produce new ones. The metabolic network for this phase is presented in Fig. 6. The corresponding stoichiometric matrix is presented in Table 8. There are only three EFMs for this phase which are presented in Table 9.

Fig. 7

Simplified metabolic network for the death phase

Table 8 The stoichiometric matrix for the death phase

Table 9 The three elementary flux modes for the death phase

The three corresponding macroscopic bioreactions are as follows:

e₁::

$\hbox{L} \xrightarrow{{w_{1}}} 3 \hbox{CO}_{2}$

e₂::

$\hbox{A} \xrightarrow{{w_{2}}} 3 \hbox{CO}_{2} + \hbox{N}$

e₃::

$\hbox{Q} \xrightarrow{{w_{3}}} 5 \hbox{CO}_{2} + 2\hbox{N}$

According to the experimental data, the reaction rates w _i of these three bioreactions satisfy

$$ {\left({\begin{array}{*{20}c} {0}& {0}& {1}& {{- 2.9167\hbox{E}}}& {{- 05}} \\ {1}& {0}& {0}& {{- 3.4817\hbox{E}}}& {{- 02}} \\ {0}& {1}& {0}& {{- 9.7917\hbox{E}}}& {{- 04}} \\ {0}& {1}& {2}& {{- 1.4708\hbox{E}}}& {{- 03}} \\ \end{array}} \right)}\,\,{\left({\begin{array}{*{20}c} {w} \\ {1} \\ \end{array}} \right)} = {\left({\begin{array}{*{20}c} {0} \\ {0} \\ \end{array}} \right)}\quad \hbox{with}\ w \geqslant 0 $$

(15)

In contrast with the previous phase, we face here a different situation since system (Eq. 15) is overdetermined (four equations with three unknown variables). Owing to measurement noise, it is clear that an exact solution is not available. Therefore, a least square solution is calculated for system (Eq. 15). This solution is presented in Table 10 and is used in the following in the same fashion as a vector of the convex basis would have been.

Table 10 The approximate solution of Eq. 15

The macroscopic reaction rates are modelled by Michaëlis-Menten kinetics:

$$ \begin{array}{*{20}c} {{r_{1} = \mu _{1} \frac{L}{{k_{L} + L}}}} \\ {{r_{2} = \mu _{2} \frac{A}{{k_{A} + A}}}} \\ {{r_{3} = \mu _{3} \frac{Q}{{k_{Q} + Q}}}} \\ {{}} \\ {{}} \\ \end{array} $$

with the following values:

$$ k_{L} = k_{A} = k_{Q} = 0.1\,\hbox{mM}. $$

and where the maximum rates are given by the entries of h ₁:

• μ₁ =  3.4817E − 02

• μ₂ =  1.0514E − 03

• μ₃ =  1.7360E − 04

The death phase model is then formulated as follows:

$$ \frac{{\hbox{d}\xi _{d}}}{{\hbox{d}t}} = L_{d} r_{d} X $$

with

$$ \xi _{d} = {\left({\begin{array}{*{20}c} {\hbox{Q}} \\ {\hbox{L}} \\ {\hbox{N}} \\ {\hbox{A}} \\ \end{array}} \right)}\quad \hbox{and}\quad L_{d} = {\left({\begin{array}{*{20}c} {0}& {0}& {{- 1}} \\ {{- 1}}& {0}& {0} \\ {0}& {1}& {2} \\ {0}& {{- 1}}& {0} \\ \end{array}} \right)} $$

The complete model

In order to finally complete the design of a model describing the cell dynamics for the whole duration of the cultivation, the three models obtained above are used successively. The transition between them is achieved by smoothly switching from model to model (see e.g. [10]). The results are presented in Fig. 9. The complete model is written as a superposition of the three models whose respective influence is controlled by means of weighting functions noted ϕ _g , ϕ _t and ϕ _d , respectively, for the growth ([0–80 h]), transition ([80–120 h]) and death phases ([120–200 h]). The final model is formulated as follows:

$$\begin{array}{*{20}c} \frac{{\hbox{d}\xi}} {{\hbox{d}t}}& = & \phi _{g} \frac{{\hbox{d}\xi _{g}}}{{\hbox{d}t}} + \phi _{t} \frac{{\hbox{d}\xi ^{*}_{t}}}{{\hbox{d}t}} + \phi _{d} \frac{{\hbox{d}\xi ^{*}_{d}}}{{\hbox{d}t}} \\ & =& \phi _{g} L_{g} r_{g} + \phi _{t} L^{*}_{t} r_{t} + \phi _{d} L^{*}_{d} r_{d} \\ \end{array} $$

where the vectors and matrices

$$ \xi ^{*}_{t} = {\left({\frac{0}{{\xi _{t}}}} \right)},\quad \xi ^{*}_{d} = {\left({\frac{0}{{\xi _{d}}}} \right)},\quad L^{*}_{t} = {\left({\frac{0}{{L_{t}}}} \right)},\quad L^{*}_{d} = {\left({\frac{0}{{L_{d}}}} \right)} $$

are augmented in order for the three models to fit in the same framework. The weighting functions ϕ _g , ϕ _t , ϕ _d are functions of time, sliding from 0 to 1 as represented in Fig. 8. When only the growth model is activated, ϕ _g equals one. With the progressive exhaustion of glucose, the function ϕ _g passes from 1 to 0 meaning that the influence of this model begins to fade out. Then the transition model progressively gets into action with the passage of ϕ _t from 0 to 1. The same mechanism controls the second transition. At 120 h, ϕ _d has already switched from 0 to 1 and the value of ϕ _t has become 0. At this point, the death phase model alone accounts for the behaviour of the cells (Fig. 9).

Fig. 8

The smooth switching functions

Fig. 9

Simulations resulting from the complete model with the same growth model but different transition models. The left-hand figure shows the results obtained with the transition model developed from h ₁ (see Sect. 3.2); the right-hand simulations are obtained with a transition model derived from the vector h ₃ in Table 6

Conclusion

We have been concerned in this paper with the design of macroscopic dynamical bioreaction models for biological processes from measurements of extra-cellular species (substrates and products) in the culture medium. Such macroscopic models rely on the category of “unstructured models” and are important for the design of on-line algorithms for process monitoring, control and optimisation. Following a systematic model reduction approach, we have presented a methodology for characterising a family of models that involve a minimal set of macroscopic bioreactions while being compatible with the underlying metabolism and consistent with the experimental data. Moreover, the experimental validation presented in this paper illustrates how the methodology enables to take into account the changes in the metabolism during the cultivation in connection with the availability of the substrates.

For the modelling of a protein such as the γ-interferon which is a product of the CHO-320 cell line, a more complex metabolic network involving amino acids is necessary. In [11], the same methodogy as presented in this paper has been used to derive a model of the γ-interferon. It is shown that it leads to a much more complicated general model and that the reduction part of the methodology is of great interest to derive a practical model.