Analysis of a two-class queueing system with service times dependent on the presence of a certain class

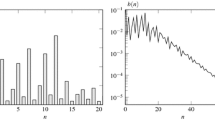
Abstract

Most queueing models and their analysis have a rich history and follow a process of increased generality and complexity. In this paper, we introduce a new model, namely a multiclass queueing model where service times depend on the presence of one of the classes. Our model is motivated by road traffic, where the presence of heavy vehicles in a queue slows down the entire system, or, in contrast, where the presence of emergency vehicles may speed up the service. The specific assumption we impose is that the service time of each customer depends on whether at least one customer of that particular class is present in the system at the time of service. Although we study a fairly simple discrete-time model, we show that analysis is not straightforward. Furthermore, numerical examples expose that the impact of particular customers in the system can lead to a substantial slow down (or, in contrast, speed up) of the entire system.

Stability condition

In this Appendix, we discuss the stability condition for the case $\alpha >0$. When $\alpha =0$, the stability condition is that of a single-class system with only class-1 customers, i.e., $\rho _1<1$.

First, recall that $(T_l,X_l)$, $l\ge 1$ is a DTMC for which both coordinates can go to infinity. Secondly, the second component’s transitions depend on the state of the first component, see Sect. 3.2. The characterization of the stability region of such processes is known to be challenging because of these two observations. Therefore, in order to simplify the stability analysis, we modify the queueing system such that the corresponding DTMC is only unbounded in one coordinate.

Consider the following adapted queuing system which is identical to the original system w.r.t. the arrivals and the FCFS discipline, but where we now only have a type-2 service time if there is a class-2 customer in the first N customers present. To obtain the stability condition of this adapted queueing system, we assume that the system is saturated. This means that there are always enough customers present so that there are at least N customers waiting in the queue. Since the queueing system under consideration is work-conserving, the system reaches a stable regime if and only if the average amount of work—expressed in slots of service time—entering the system per slot is strictly less than one Bruneel and Kim (1993). Since an arriving customer is of class 2 with probability $\alpha$, independent from customer to customer, and since we assume FCFS, the probability of having no class-2 customers in the first N waiting customers—and hence a type-1 service time—is given by $(1-\alpha )^N$. Hence, this leads to the following stability condition for the adapted queueing system:

$$\begin{aligned} (1-\alpha )^N \rho _1 + \left( 1 - (1-\alpha )^N \right) \rho _2 <1 . \end{aligned}$$

(39)

From the equation above it is seen that the first term becomes negligible for large N and vanishes for $N \rightarrow \infty$. Intuitively speaking, for $\alpha >0$, this leads to the stability condition of the original queueing system: $\rho _2<1$. When service times are assumed to be deterministic, we can make this more formal. The modified queueing system becomes either a dominant ($\rho _1\ge \rho _2$ or equivalently $S_1 \ge S_2$) or a dominated ($\rho _1 \le \rho _2$ or equivalently $S_1 \le S_2$) queueing system if the arrivals into both systems occur at exactly the same instants. For instance in the case that $\rho _1\ge \rho _2$, the queue size in the adapted system will never be smaller than its counterpart in the original system, provided that the queues start with identical conditions in both systems. The dominance of the adapted system on the original system implies that the stability condition of the adapted system is a sufficient condition for the original system to be stable. Since this is true for every N, it follows that $\rho _2<1$ is a sufficient condition for stability. To show that $\rho _2<1$ is also a necessary condition, still assuming that $\rho _1\ge \rho _2$, we can compare the original system with the system where every customer has a type-2 service time (see Sect. 4.1.2), which always has a better performance under the assumption that $\rho _1\ge \rho _2$. Clearly, similar reasoning can be made for the case that $\rho _1\le \rho _2$, which also lead to the stability condition $\rho _2<1$. These arguments suggest that $\rho _2 < 1$ is a natural condition for the stability of this system and the existence of a stationary distribution. However, we are at this point not able to prove the existence of the stationary distribution under $\rho _2 < 1$. This remains for future work.