Abstract
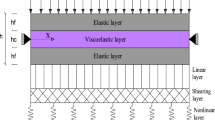
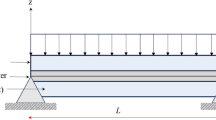
In the present work, the effect of frequency-dependent viscoelastic property on the forced/parametric resonant amplitude of viscoelastic sandwich beam is investigated by deriving a reduced-order finite element model (ROM) in frequency domain. In this concern, the frequency-dependent viscoelasticity is modelled using fractional Zener model and the corresponding responses of sandwich beam are compared with that are derived using an equivalent Kelvin-Voigt model. The ROM in frequency domain is derived by implementing harmonic balance method prior to the finite element discretization and reduced-order transformation. The comparison of frequency responses evaluated using ROM and full-order model revealed that the ROM with reduction basis from modal strain energy method provides the response of frequency-dependent viscoelastic sandwich beam with reasonable accuracy. Further, the frequency-dependent viscoelastic property has shown a significant effect on the resonant amplitudes especially when compared with an equivalent Kelvin-Voigt model in wide-frequency range. Moreover, the results suggest that the nonlinear frequency response analysis of viscoelastic layered beams using Kelvin-Voigt model may be reasonably accurate when the different model parameters are considered around each modal natural frequency.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Jacques, N., Daya, E.M., Potier-Ferry, M.: Nonlinear vibration of viscoelastic sandwich beams by the harmonic balance and finite element methods. J. Sound Vib. 329(20), 4251–4265 (2010)
Zhu, B., Dong, Y., Li, Y.: Nonlinear dynamics of a viscoelastic sandwich beam with parametric excitations and internal resonance. Nonlinear Dyn. 94(4), 2575–2612 (2018)
Reddy, R.S., Panda, S., Gupta, A.: Nonlinear dynamics and active control of smart beams using shear/extensional mode piezoelectric actuators. Int. J. Mech. Sci. 106495 (2021)
Dwivedy, S.K., Sahu, K.C., Babu, S.: Parametric instability regions of three-layered soft-cored sandwich beam using higher-order theory. J. Sound Vib. 304(1–2), 326–344 (2007)
Gupta, A., Panda, S., Reddy, R.S.: Passive control of parametric instability of layered beams using graphite particle-filled viscoelastic damping layers. Mech. Adv. Mater. Struct. 1–16 (2021)
Gupta, A., Panda, S., Reddy, R.S.: Improved damping in sandwich beams through the inclusion of dispersed graphite particles within the viscoelastic core. Compos. Struct. 247, 112424 (2020)
Madeira, J.F.A., Araújo, A.L., Soares, C.M.M., Soares, C.A.M.: Multiobjective optimization for vibration reduction in composite plate structures using constrained layer damping. Comput. Struct. 232, 105810 (2020)
Detroux, T., Renson, L., Masset, L., Kerschen, G.: The harmonic balance method for bifurcation analysis of large-scale nonlinear mechanical systems. Comput. Methods Appl. Mech. Eng. 296, 18–38 (2015)
Litewka, P., Lewandowski, R.: Steady-state non-linear vibrations of plates using Zener material model with fractional derivative. Comput. Mech. 60, 333–354 (2017)
Galucio, A.C., Deü, J.-F., Ohayon, R.: Finite element formulation of viscoelastic sandwich beams using fractional derivative operators. Comput. Mech. 33(4), 282–291 (2004)
Rutzmoser, J.: Model order reduction for nonlinear structural dynamics. Doctoral dissertation, Technische Universität München (2018)
Touzé, C., Vidrascu, M., Chapelle, D.: Direct finite element computation of non-linear modal coupling coefficients for reduced-order shell models. Comput. Mech. 54(2), 567–580 (2014)
Givois, A., Grolet, A., Thomas, O., Deü, J.-F.: On the frequency response computation of geometrically nonlinear flat structures using reduced-order finite element models. Nonlinear Dyn. 97(2), 1747–1781 (2019)
Lv, H.-W., Li, L., Li, Y.-H.: Non-linearly parametric resonances of an axially moving viscoelastic sandwich beam with time-dependent velocity. Appl. Math. Model. 53, 83–105 (2018)
Ray, M.C., Baz, A.: Control of nonlinear vibration of beams using active constrained layer damping. J. Vib. Control. 7(4), 539–549 (2001)
Rouleau, L., Deü, J.-F., Legay, A.: A comparison of model reduction techniques based on modal projection for structures with frequency-dependent damping. Mech. Syst. Signal Process. 90, 110–125 (2017)
Rutzmoser, J.B., Rixen, D.J., Tiso, P., Jain, S.: Generalization of quadratic manifolds for reduced order modeling of nonlinear structural dynamics. Comput. Struct. 192, 196–209 (2017)
Shih, Y.-S., Yeh, Z.-F.: Dynamic stability of a viscoelastic beam with frequency-dependent modulus. Int. J. Solids Struct. 42(7), 2145–2159 (2005)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Shashidhar Reddy, R., Gupta, A., Panda, S. (2022). Nonlinear Frequency Response of Sandwich Beam with Frequency-Dependent Viscoelastic Core Using Reduced-Order Finite Element Method. In: Popat, K.C., Kanagaraj, S., Sreekanth, P.S.R., Kumar, V.M.R. (eds) Advances in Mechanical Engineering and Material Science. ICAMEMS 2022. Lecture Notes in Mechanical Engineering. Springer, Singapore. https://doi.org/10.1007/978-981-19-0676-3_1
Download citation
DOI: https://doi.org/10.1007/978-981-19-0676-3_1
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-19-0675-6
Online ISBN: 978-981-19-0676-3
eBook Packages: EngineeringEngineering (R0)