Skip to main content
SpringerLink
Log in

D-Optimal Design for a Five-Parameter Logistic Model

  • Conference paper
  • First Online:
mODa 9 – Advances in Model-Oriented Design and Analysis

Part of the book series: Contributions to Statistics ((CONTRIB.STAT.))

  • 851 Accesses

Abstract

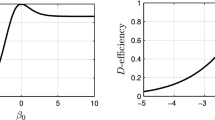
We explore the D-optimal design for a five-parameter logistic model, which includes a shape parameter to handle asymmetries, and two threshold parameters to account for situations where the asymptotes are not at 0 and 1. The optimal design is five points, including points at -∞ and ∞ representing the thresholds. We compare the efficiencies of the optimal designs arising from the two- and five- parameter models. We find a significant loss of efficiency when the two-parameter model is used on data generated from the five-parameter model.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 84.99
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 109.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  • Atkinson, A. C., A.N. Donev, and R. D. Tobias (2007). Optimum Experimental Designs, with SAS. Oxford: Oxford University Press.

    MATH  Google Scholar 

  • Biedermann, S., H. Dette, and A. Pepelyshev (2006). Some robust design strategies for percentile estimation in binary response models. Canadian Journal of Statistics 34, 603–622.

    Article  MATH  MathSciNet  Google Scholar 

  • Haines, L. M., I. Perevozskaya, and W. F. Rosenberger (2003). Bayesian optimal designs for Phase I clinical trials. Biometrics 59, 591–600.

    Article  MathSciNet  Google Scholar 

  • Kalish, L. A. and J. L. Rosenberger (1978). Optimal designs for the estimation of the logistic function. Technical Report 33, Pennsylvania State University.

    Google Scholar 

  • Kiefer, J. and J. Wolfowitz (1960). The equivalence of two extremum problems. Canadian Journal of Mathematics 12, 363–366.

    MATH  MathSciNet  Google Scholar 

  • Manukyan, Z. (2009). Sequential Designs for Estimating Toxicity and Efficacy in a Dose-Response Setting. Ph. D. thesis, George Mason University.

    Google Scholar 

Download references

Acknowledgements

The authors thank two excellent referees for their detailed comments. One of the referees found a major mistake, and the authors are deeply appreciative.

Author information

Authors and Affiliations

  1. The EMMES Corporation, 401 N. Washington St, Rockville, MD, 20850, USA

    Zorayr Manukyan

  2. Department of Statistics, George Mason University, 4400 University Dr., MS 4A7, Fairfax, VA, 22030-4444, USA

    William F. Rosenberger

Authors
  1. Zorayr Manukyan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. William F. Rosenberger
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zorayr Manukyan .

Editor information

Editors and Affiliations

  1. Dipt. di Scienze Statistiche, University of Bologna, Via Belle Arti 41, Bologna, 40126, Italy

    Alessandra Giovagnoli

  2. and Political Science, Department of Statistics, London School Economics, Houghton Street, London, WC2A 2AE, United Kingdom

    Anthony C. Atkinson

  3. Department of Statistics, University of Glasgow, University Gardens 15, Glasgow, G12 8QW, United Kingdom

    Bernard Torsney

  4. , SEMEQ, Università del Piemonte Orientale, via Perrone 18, Novara, 28100, Italy

    Caterina May

Rights and permissions

Reprints and permissions

Copyright information

© 2010 Springer-Verlag Berlin Heidelberg

About this paper

Cite this paper

Manukyan, Z., Rosenberger, W.F. (2010). D-Optimal Design for a Five-Parameter Logistic Model. In: Giovagnoli, A., Atkinson, A., Torsney, B., May, C. (eds) mODa 9 – Advances in Model-Oriented Design and Analysis. Contributions to Statistics. Physica-Verlag HD. https://doi.org/10.1007/978-3-7908-2410-0_15

Download citation

Publish with us

Policies and ethics

Search

Navigation