Abstract
The counter mode (CTR) is a simple, efficient and widely used encryption mode using a block cipher. It comes with a security proof that guarantees no attacks up to the birthday bound (i.e. as long as the number of encrypted blocks \(\sigma \) satisfies \(\sigma \ll 2^{n/2}\)), and a matching attack that can distinguish plaintext/ciphertext pairs from random using about \(2^{n/2}\) blocks of data.
The main goal of this paper is to study attacks against the counter mode beyond this simple distinguisher. We focus on message recovery attacks, with realistic assumptions about the capabilities of an adversary, and evaluate the full time complexity of the attacks rather than just the query complexity. Our main result is an attack to recover a block of message with complexity \(\tilde{\mathcal {O}}(2^{n/2})\). This shows that the actual security of CTR is similar to that of CBC, where collision attacks are well known to reveal information about the message.
To achieve this result, we study a simple algorithmic problem related to the security of the CTR mode: the missing difference problem. We give efficient algorithms for this problem in two practically relevant cases: where the missing difference is known to be in some linear subspace, and when the amount of data is higher than strictly required.
As a further application, we show that the second algorithm can also be used to break some polynomial MACs such as GMAC and Poly1305, with a universal forgery attack with complexity \(\tilde{\mathcal {O}}(2^{2n/3})\).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Block ciphers (such as DES or the AES) are probably the most widely used cryptographic primitives. Formally, a block cipher is just a keyed family of permutations over n-bit blocks, but when combined with a mode of operation, it can provide confidentiality (e.g. using CBC, or CTR), authenticity (e.g. using CBC-MAC, CMAC, or GMAC), or authenticated encryption (e.g. using GCM, CCM, or OCB). A mode of operation defines how to divide a message into blocks, and how to process the blocks one by one with some chaining rule.
The security of block ciphers is studied with cryptanalysis, with classical techniques such as differential [8] and linear [27] cryptanalysis, dedicated techniques like the SQUARE attack [9], and ad-hoc improvements for specific targets. This allows to evaluate the security margin of block ciphers, and today we have a high confidence that AES or Blowfish are as secure as a family of pseudo-random permutations with the same parameters (key size and block size).
On the other hand, modes of operation are mostly studied with security proofs, in order to determine conditions where using a particular mode of operation is safe. However, exceeding those conditions doesn’t imply that there is an attack, and even when there is one, it can range from a weak distinguisher to a devastating key recovery. In order to get a better understanding of the security of modes of operations, we must combine lower bound on the security from security proofs, and upper bounds from attacks.
In particular, most of the modes used today are sensible to birthday attacks because of collisions; those attacks can even be practical with 64-bit block ciphers, as shown in [7], but security proofs don’t tell us how dangerous the attacks are. For instance, the CBC and CTR modes have been proven secure against chosen plaintext attacks up to \(\sigma \ll 2^{n/2}\) blocks of encrypted data [5, 35]. Formally, the security statements bound the maximum advantage of an attacker against the modes as follows:
Both statement are essentially the same, and become moot when \(\sigma \) reaches \(2^{n/2}\), but attacks can actually be quite different.
More precisely, the CBC mode is defined as \(c_i = E(m_i \oplus c_{i-1})\), with E a block cipher. A collision between two ciphertext blocks \(c_i = c_j\) is expected after \(2^{n/2}\) blocks, and reveals the xor of two plaintext blocks: \(m_i \oplus m_j = c_{i-1} \oplus c_{j-1}\). On the other hand, the counter mode is defined as \(c_i = E(i) \oplus m_i\). There are no collisions in the inputs/outputs of E, but this can actually be used by a distinguisher. Indeed, if an adversary has access to \(2^{n/2}\) known plaintext/ciphertext pairs, he can recover \(E(i) = c_i \oplus m_i\) and detect that the values are unique (because E is a permutation), while collisions would be expected with a random ciphertext. Both attacks have the same complexity, and show that the corresponding proofs are tight. However, the loss of security is quite different: the attack against CBC lets an attacker recover message blocks from collisions (as shown in practice in [7]), but the attack against the counter mode hardly reveals any useful information.
In general, there is a folklore belief that the leakage of the CTR mode is not as bad as the leakage of the CBC mode. For instance, Ferguson et al. wrote [15, Sect. 4.8.2] (in the context of a 128-bit block cipher):
CTR leaks very little data. [...] It would be reasonable to limit the cipher mode to \(2^{60}\) blocks, which allows you to encrypt \(2^{64}\) bytes but restricts the leakage to a small fraction of a bit.
When using CBC mode you should be a bit more restrictive. [...] We suggest limiting CBC encryption to \(2^{32}\) blocks or so.
Our Contribution. The main goal of this paper is to study attacks against the counter mode beyond the simple distinguisher given above. This is an important security issue, because uses of the CTR mode with 64-bit block ciphers could be attacked in practice. We consider generic attacks that work for any instance of the block cipher E, and assume that E behaves as a pseudo-random permutation. The complexity of the attacks will be determined by the block size n, rather than the key size, and we focus on the asymptotic complexity, using the Big-O notation \(\mathcal {O}()\), and the Soft-O notation \(\tilde{\mathcal {O}}()\) (ignoring logarithmic factors).
We consider message recovery attacks, where an attacker tries to recover secret information contained in the message, rather than recovering the encryption key k. Following recent attacks against HTTPS [2, 7, 12], we assume that a fixed message containing both known blocks and secret blocks is encrypted multiple times (this is common with web cookies, for instance). As shown by McGrew [28], this kind of attack against the CTR mode can be written as a simple algorithmic problem: the missing difference problem, defined as follows: given two functions \(f, g: X \rightarrow \{0,1\}^n\), with the promise that there exists a unique \(S \in \{0,1\}^n\) such that \(\forall (x,y),~ f(x) \oplus g(y) \ne S\), recover S. We further assume that f and g behave like random functions, and that we are given a set \(\mathcal {S} \subseteq \{0,1\}^n\), such that \(S \in \mathcal {S}\) (\(\mathcal {S}\) represents prior knowledge about the secret). In an attack against the counter mode, f outputs correspond to known keystream blocks, while g outputs correspond to encryptions of S.
In the information theoretic setting, this problem can be solved with \(\tilde{\mathcal {O}}(2^{n/2})\) queries for any set \(\mathcal {S}\), and requires at least \(\varOmega (2^{n/2})\) queries when \(|\mathcal {S}| \ge 2\). However, the analysis is more complex when taking into account the cost of the computations required to recover S. McGrew introduces two algorithms for this problem: a sieving algorithm with \(\tilde{\mathcal {O}}(2^{n/2})\) queries and time \(\tilde{\mathcal {O}}(2^n)\), and a searching algorithm that can be optimized to time and query complexity \(\tilde{\mathcal {O}}(2^{n/2}\sqrt{|\mathcal {S}|})\). Our main contribution is to give better algorithms for this problem:
-
1.
An algorithm with \(\tilde{\mathcal {O}}(2^{n/2})\) queries and time \(\tilde{\mathcal {O}}(2^{n/2} + 2^{\dim \langle \mathcal {S}\rangle })\), in the case where \(\mathcal {S}\) is (a subset of) a linear subspace of \(\{0,1\}^n\). In particular, when \(\mathcal {S}\) is a linear subspace of dimension n / 2, we reach a time and query complexity of \(\tilde{\mathcal {O}}(2^{n/2})\), while the searching algorithm of McGrew has a time and query complexity of \(\tilde{\mathcal {O}}(2^{3n/4})\).
-
2.
An algorithm with time and query complexity \(\tilde{\mathcal {O}}(2^{2n/3})\) for any \(\mathcal {S}\). In particular, with \(\mathcal {S} = \{0,1\}^n\), the best previous algorithm had a time complexity of \(\tilde{\mathcal {O}}(2^{n})\).
We also show new applications of these algorithms. The first algorithm leads to an efficient message recovery attack with complexity \(\tilde{\mathcal {O}}(2^{n/2})\) against the CTR mode, assuming that the adversary can control the position of the secret, by splitting it across block boundaries (following ideas of [12, 32]). The second algorithm can be used to recover the polynomial key in some polynomial based MACs such as GMAC and Poly1305, leading to a universal forgery attack with complexity \(\tilde{\mathcal {O}}(2^{2n/3})\). As far as we know, this is the first universal forgery attack against those MACs with complexity below \(2^n\).
Related Works. There are several known results about the security of mode of operation beyond the birthday bound, when the proof is not applicable. For encryption modes, the security of the CBC mode beyond the birthday bound is well understood: collision attacks reveal the XOR of two message blocks, and can exploited in practice [7]. Other modes that allow collisions (eg. CFB) have the same properties. The goal of this paper is to study the security of modes that don’t have collisions, to get a similar understanding of their security.
Many interesting attacks have also been found against authentication modes. In 1995, Preneel and van Oorschot [31] gave a generic collision attack against all deterministic iterated message authentication codes (MACs), leading to existential forgeries with complexity \(\mathcal {O}(2^{n/2})\). Later, a number of more advanced generic attacks have been described, with stronger outcomes than existential forgeries, starting with a key-recovery attack against the envelop MAC by the same authors [32]. In particular, a series of attack against hash-based MAC [11, 18, 25, 30] led to universal forgery attacks against long challenges, and key-recovery attacks when the hash function has an internal checksum (like the GOST family). Against PMAC, Lee et al. showed a universal forgery attack in 2006 [24]. Later, Fuhr et al. gave a key-recovery attack against the PMAC variant used in AEZv3 [17]. Issues with GCM authentication with truncated tags were also pointed out by Ferguson [14].
None of these attacks contradict the proof of security of the scheme they target, but they are important results to understand the security degradation after the birthday bound.
Organization of the Paper. We introduce the CTR mode and the missing difference problem in Sect. 2, and present our algorithmic contributions in Sect. 3. Then we describe concrete attacks against the CTR mode in Sect. 4, and attacks against Carter-Wegman MACs in Sect. 5. At last we show detailed proofs and simulation results in Sect. 6.
2 Message Recovery Attacks on CTR Mode
The CTR mode was first proposed by Diffie and Hellman in 1979 [10]. It was not included in the first series of standardized modes by NIST [16], but was added later [13]. The CTR mode essentially turns a block cipher into a stream cipher, by encrypting some non-repeating counter. It is now a popular mode of operation, thanks to its parallelizability, speed, and simple design. This led Phillip Rogaway to write in an evaluation of different privacy modes of operation talking about CTR [35]: “Overall, usually the best and most modern way to achieve privacy-only encryption”. In particular, CTR is used as the basic of the authenticated encryption mode GCM, the most widely used mode in TLS today.
2.1 Setting and Notations
In the following we assume that the counter mode is implemented such that the input to the block cipher never repeats. For simplicity we consider a stateful variant of the counter mode with a global counter that is maintained across messages and initialized as 0 (as shown in Fig. 1):
where \(E_k\) is an n-bit block cipher, \(m_i\) an n-bit block of plaintext and \(c_i\) an n-bit block of ciphertext.
Our attacks do not depend on the details of how the input to the block cipher is constructed, and can also be applied to nonce-based variantsFootnote 1; we only require that all inputs are different. Note that some variants of the counter mode can have repetitions in the block cipher inputFootnote 2, but this gives easy attacks because repetitions leak the xor of two plaintext blocks (as in the CBC mode).
We consider a message recovery attack, where the attacker tries to recover some secret message block S. Throughout the attack, the key k will be invariant so we will write \(E_k(i)\) as \(a_i\) to represent the \(i^{th}\) block of CTR keystream. We can immediately notice that if we have partial knowledge of the plaintext, for every known block \(m_i\) we can recover the associated \(a_i\) as \(c_i \oplus m_i = a_i\). Assume further that we have access to the repeated encryption \(b_j\) of the secret S so that \(b_j = a_j \oplus S\). The first property of the CTR mode is that \(E_k(\cdot )\) being a permutation, the keystream \(a_i\) never repeats, thus we have the following inequalities:
From now on we will always assume that we can observe and collect lists of many \(a_i\) and \(b_j\) and use them with the previous inequality to recover S. This setting is similar to the practical attack Sweet32 on the CBC mode mounted by Bhargavan and Leurent, using repeated encryptions of an authentication token to obtain many different ciphertext blocks for the same secret information [7].
Formally, let \(\mathcal {A} \subseteq \{0,1\}^n\) be the set of observed keystream blocks, \(\mathcal {B} \subseteq \{0,1\}^n\) the set of observed encryptions and \(\mathcal {S} \subseteq \{0,1\}^n\) the set of possible secrets (corresponding to some already known information about S). We define the missing difference algorithmic problem in terms of set:
Definition 1
(Missing Difference Problem). Given two sets \(\mathcal {A}\) and \(\mathcal {B}\), and a hint \(\mathcal {S}\), find the value \(S \in \mathcal {S}\) such that:
Alternatively, we can consider that the attacker is given oracle access to \(\mathcal {A}\) and \(\mathcal {B}\) though some functions f and g, so that its running time includes calls to f and g, and computations to recover S. This presentation corresponds to a more active attack, where the adversary can optimize the size of the sets.
Definition 2
(Missing Difference Problem with Functions). Given two functions \(f, g: X \rightarrow \{0,1\}^n\), and a hint \(\mathcal {S}\), find the value \(S \in \mathcal {S}\) such that:
2.2 Previous Work
An attack can only be carried to the end if the secret S is the only value in \(\mathcal {S}\) such that \( \forall (a,b) \in \mathcal {A} \times \mathcal {B},~ S \ne a \oplus b \), or else it will be indistinguishable from the other values that satisfy the same condition (those values could have produced the same sets with same probability). The coupon collector’s problem predicts that N out of N different coupons are found after \(N \cdot H_N \simeq N \ln {N}\) draws (with \(H_N\) the N-th harmonic number), assuming uniform distribution of the draws. In our case we will assume that all the differences \(a \oplus b\) are independent and uniformly distributed over \(\{0,1\}^n \setminus {S}\), which is a reasonable approximation validated by our experiments. To carry the attack to the end we require to collect \(N = |\mathcal {S}|-1\) differences thus we will need \(\mathcal {O}(|\mathcal {S}|\ln |\mathcal {S}|)\) “draws”. A draw is a couple (a, b) s.t. \(a \oplus b \in |\mathcal {S}|\), otherwise we discard it; it happens with probability \((|\mathcal {S}|-1)/(2^n-1)\). Therefore we need to observe enough data to have \(|\mathcal {A}|\cdot |\mathcal {B}|\) in the order of \(\mathcal {O}(2^n\ln |\mathcal {S}|)\); this may be achieved by having both sets in the order of \(\mathcal {O}(2^{n/2}\sqrt{\ln |\mathcal {S}|})\). This size of the observed sets can be understood as the query complexity, that is the number of encrypted messages the attacker will have to intercept in order to carry out the attack. Notice that even for \(|\mathcal {S}| = \mathcal {O}(2^n)\), \(|\mathcal {A}| = |\mathcal {B}| = \mathcal {O}(\sqrt{n} \cdot 2^{n/2})\) is quite close to the theoretical lower bound of \(\mathcal {O}(2^{n/2})\) given by the distinguishing attack and the security proof for the CTR mode. Therefore, message recovery attacks are possible with an (almost) optimal data complexity. The next question is to study the time complexity, i.e. how to efficiently recover S.


A first approach consists in computing all the impossible values of S from the large set of \(\mathcal {A} \times \mathcal {B}\) and discard any new value we encounter as impossible until there’s only one possible plaintext left. This is Algorithm 1. This approach works but requires to actually compute \(\mathcal {O}(2^n\ln |\mathcal {S}|)\) values and maintain in memory a sieve of size \(|\mathcal {S}|\). In the case where the key size is equal to the block size n, like AES-128, this attack is actually worse than a simple exhaustive search of the key. In a 2012 work, McGrew [28] described this sieving algorithm and noticed that when the set \(\mathcal {S}\) is small, the sieving wastes a lot of time computing useless values. Therefore he proposed a second algorithm, Algorithm 2, to test and eliminate values of \(\mathcal {S}\) one by one. This algorithm loops over \(\mathcal {S}\) and \(\mathcal {A}\) to efficiently test whether \(s \oplus a \in \mathcal {B}\); if yes then we sieve the value s out of \(\mathcal {S}\).
Both algorithms act on a sieving set \(\mathcal {S}\) to reduce it, so McGrew proposed a hybrid algorithm switching from one algorithm to the other in order to reduce the searching space as quickly as possible. This improves the attack when \(\mathcal {A}\) and \(\mathcal {B}\) are fixed, but if the adversary can choose the sizes of \(\mathcal {A}\) and \(\mathcal {B}\) (in particular, if he actually has oracle access to functions f and g), then the searching algorithm allows better trade-offs. Indeed, the searching algorithm has a complexity of \(\mathcal {O}(|\mathcal {B}|+|\mathcal {A}| \cdot |\mathcal {S}|)\), and is successful as soon as \(|\mathcal {A}|\cdot |\mathcal {B}| = \varOmega (2^n\ln |\mathcal {S}|)\). To optimize the complexity, we use \(|\mathcal {B}| = |\mathcal {A}| \cdot |\mathcal {S}|\) to obtain an overall complexity of \(\mathcal {O}(2^{n/2}\sqrt{|\mathcal {S}|\ln |\mathcal {S}|})\) in both time and queries. In particular for small \(\mathcal {S}\) (of size polynomial in n) this algorithm is (almost) optimal, reaching the birthday bound \(\tilde{\mathcal {O}}(2^{n/2})\).
Starting from these observations we will show improved algorithms to recover a block of secret information without big exhaustive searches in the next section.
3 Efficient Algorithms for the Missing Difference Problem
We now propose two new algorithms to solve the missing difference algorithmic problem more efficiently in two practically relevant different settings. Our first algorithm requires that the set \(\mathcal {S}\) — or its linear span \(\langle \mathcal {S}\rangle \) — is a vector space of relatively small dimension, and has complexity \(\tilde{\mathcal {O}}(2^{n/2}+|\langle \mathcal {S}\rangle |)\). The second algorithm uses a larger query complexity of \(\tilde{\mathcal {O}}(2^{2n/3})\), to reduce the computation and memory usage to \(\tilde{\mathcal {O}}(2^{2n/3})\).
3.1 Known Prefix Sieving
In many concrete attack scenarios, an attacker knows some bits of the secret message in advance. For instance, an HTTP cookie typically uses ASCII printable characters, whose high order bit is always set to zero. More generally, we assume that \(\mathcal {S}\) is (included in) an affine subspace of \(\{0,1\}^n\) of dimension \(n-z\) for some natural \(z < n\). In order to simplify the attack, we use a bijective affine function \(\phi \) that maps \(\mathcal {S}\) unto \(\{0\}^{z} \times \{0,1\}^{n-z}\), and rewrite the problem as follows:
Therefore, we can reduce the missing difference problem on \(\mathcal {A}\), \(\mathcal {B}\), \(\mathcal {S}\) with \(\dim (\langle \mathcal {S}\rangle ) = n-z\) to the missing difference problem on \(\mathcal {A}'\), \(\mathcal {B}'\), \(\mathcal {S}'\), where the secret is known to start with z zeroes:
We now introduce a known prefix sieving algorithm (Algorithm 3) to solve this problem efficiently. The algorithm is quite straightforward; it looks for a prefix collision before sieving in the same way as before to recover S. The complexity depend on the dimension \(n-z\); the sieving requires \(\mathcal {O}(2^{n-z})\) memory and \(\mathcal {O}((n-z) \cdot 2^{n-z})\) XOR computations in expectation, while looking for collisions only requires to store the prefix keys and to go through one of the set. Looking for collisions allows us to skip the computations of many pairs (a, b) that would be irrelevant as \(a \oplus b \notin \mathcal {S}\).
The expected number of collisions required to isolate the secret is given by the coupon collector problem as \(\ln (2^{n-z})2^{n-z} = \ln 2 \cdot (n-z)\cdot 2^{n-z}\). Therefore the total optimized complexity (with balanced sets \(\mathcal {A}\) and \(\mathcal {B}\)) to recover an \(n-z\) bits secret with this algorithm is:
As we can see from the complexity, when \(z = 0\) this is the naive algorithm with its original complexity. When z nears n, this performs similarly to McGrew’s searching algorithm i.e. the cost of looking for collisions (or storing \(\mathcal {B}\) so that the search is efficient) will dominate the overall cost of the algorithm therefore the time and query complexity will match. Actually, this algorithm improves over previous works for intermediate values of z. With \(z=n/2\), we have an algorithm with complexity \(\tilde{\mathcal {O}}(2^{n/2})\), while McGrew’s searching algorithm would require \(\tilde{\mathcal {O}}(2^{3n/4})\) computations in the same setting. The complexity therefore becomes tractable and we could implement and run this algorithm for \(n=64\) bits with success, as shown in Sect. 6.2.

3.2 Fast Convolution Sieving
Alternatively, we can reduce the complexity of the sieving algorithm by using sets \(\mathcal {A}\) and \(\mathcal {B}\) of size \(2^{m} \gg 2^{n/2}\), rather than \(\tilde{\mathcal {O}}(2^{n/2})\) as required to uniquely identify S. If we consider all the values \(a \oplus b\) for (a, b) in \(\mathcal {A}\times \mathcal {B}\), we expect that they are close to uniformly distributed over \(\{0,1\}^n \setminus S\), so that every value except S is reached about \(2^{2m-n}\) times, while S is never hit. Increasing m makes the gap more visible than with sets of size only \(\tilde{\mathcal {O}}(2^{n/2})\). Therefore, we can consider buckets of several candidates s, and accumulate the number of \(a \oplus b\) in each bucket. If we consider buckets of \(2^t\) values, each bucket receives \(2^{2m+t-n}\) values on average, but the bucket containing S receives only \(2^{2m+t-n} - 2^{2m-n}\) values. If we model this number with random variables following a binomial distribution, the variance \(\sigma ^2\) is about \(2^{m+t/2-n/2}\). Therefore, the bias will be detectable when: \(\sigma \ll 2^{2m-n}\), i.e. when \(t \ll 2m-n\).
Concretely, we use a truncation function T that keeps only \(n-t\) bits of an n-bit word. We consider the values \(T(a \oplus b)\) for all \((a,b) \in \mathcal {A} \times \mathcal {B}\), and count how many times each value is reached. If m is large enough, the value with the lowest counter corresponds to T(S). This attack does not require any prior information on the secret; it can be used with \(\mathcal {S} = \{0,1\}^n\), and once T(S) is known, we can use known-prefix sieving to recover the remaining bits (looking for S in an affine space of dimension t).
We now show an algorithm to quickly count the number of occurrences for each combination. For a given multi-set \(\mathcal {X}\), we consider an array of counters \(C_{\mathcal {X}}\), to represent how many times each value T(x) is reached:

Our goal is to compute \(C_{\mathcal {A} \oplus \mathcal {B}}\) efficiently from \(\mathcal {A}\) and \(\mathcal {B}\), where \(\mathcal {A} \oplus \mathcal {B}\) is the multi-set  . We observe that:
. We observe that:

This is a form of convolution that can be computed efficiently only using the Fast Walsh-Hadamard Transform (Algorithm 4), in the same way we use the Fast Fourier Transform to compute circular convolutions (see Algorithm 5). Therefore the full attack (shown in Algorithm 6) takes time \(\tilde{\mathcal {O}}(2^{n-t})\) using lists of size \(2^m\) with \(m \gg (n+t)/2\) and a sieve of \(2^{n-t}\) elements.
In order to optimize the attack, we select \(t=n/3\) such that the time complexity, data complexity, and memory usage are all roughly \(2^{2n/3}\). A detailed analysis in Sect. 6.1 shows that we reach a constant success rate with \(t=n/3\) using lists of size \(\mathcal {O}(\sqrt{n} \cdot 2^{2n/3})\). This gives the following complexity for the full attack:




As seen in Sect. 6.1, we performed experiments with \(n = 12, 24, 48\), and the correct S was found with the lowest counter in at least 70% of our experiments, using list of size \(\sqrt{n} 2^{2n/3}\). This validates our approach and shows that the constant in the \(\mathcal {O}\) notation is small. We could run this algorithm over \(n=48\) bits in a matter of minutes.
Optimizations. In order to increase the success rate of the algorithm, one can test several candidates for T(S) (using the lowest remaining counters), and use the known-prefix sieving to detect whether the candidate is correct. Another option is to run multiple independent runs of the algorithm with different choices of the n / 3 truncated bits. This would avoid some bad cases we have observed in simulations, where the right counter grows abnormally high and gets hidden in all of the other counters.
For the memory complexity, notice that we don’t need to store all the data but simply to increment a counter. We only need to keep enough blocks for the second part of the algorithm so that the sieving yields a unique result. Initially the counters for \(C_\mathcal {A}\) and \(C_\mathcal {B}\) are quite small, \(\sqrt{n}\) in expectation. However, \(C_{\mathcal {A}\oplus \mathcal {B}}\) will have much bigger entries, \(n \cdot 2^{2n/3}\) in expectation, so that we need \(\mathcal {O}(n)\) bits to store each entry.
4 Application to the CTR Mode
We know show how to mount attacks against the counter mode using the new algorithms for the missing difference problem.
4.1 Attack Using Fast Convolution
Use of the fast convolution algorithm to recover one block of CTR mode plaintext is straightforward. The attacker is completely passive and observes encryptions of S (gathered in set \(\mathcal {B}\)), and keystream blocks recovered from the encryption of known message blocks (gathered in set \(\mathcal {A}\)). When the lists are large enough, he runs the fast convolution algorithm on \(\mathcal {A}\) and \(\mathcal {B}\) to recover S.
4.2 Attacks Using Known Prefix Sieving
Direct Attack. There are many settings where unknown plaintext will naturally lie in some known affine subspace, and the known prefix sieving algorithm can be used directly. For instance a credit card number (or any number) could be encoded in 16 bytes of ASCII then encrypted. Because in ASCII the encoding of any digit starts by 0x3 (0x30 to 0x39), we know half of the bits of the plaintext, and we can use the known-prefix sieving with \(z = n/2\). Other examples are information encoded by uuencode that uses ASCII values 0x20 to 0x5F (corresponding to two known bits) or HTML authentication cookies that are typically encoded to some subset of ASCII numbers and lettersFootnote 3.
Block Splitting. We often assume that the secret is encrypted in its own block, but when the secret is part of the message, it can also be split across block boundaries, depending on how the plaintext is constructed and encrypted by the protocol. In particular, if a message block contains both known bytes and secret bytes, we can apply the known prefix sieving algorithm to this block and recover the secret bytes.
In many protocols, messages start with some low entropy header that can be guessed by an attacker. Moreover, the attacker often has some degree of control over those headers. For instance, in the BEAST attack [12] against HTTPS, an attacker uses Javascript code to generate HTTPS requests, and he can choose the URL corresponding to the requests. Using this control of the length of the header, block splitting attacks have been shown in the BEAST model [12, 20]. The attacker starts with a header length so that a small chunk of the secret message is encrypted together with known information, and recovers this secret chunk. Then he changes the length of the header to recover a second chunk of the message, using the fact that the first chunk is now known. Eventually, the full secret can be recovered iteratively.
In our case, the easiest choice is to recover chunks of n / 2 bits of secret one by one, using the known-prefix sieving algorithm with \(z=n/2\). We illustrate this attack in Table 1, assuming a two-block secret \(S = S_1\Vert S_2 \Vert S_3\Vert S_4\), and a protocol that lets the adversary query an encryption of the secret with an arbitrary chosen prefix:
-
1.
The attacker makes two kind of queries
-
\(Q_1\) with a known half-block header \(H_1\) (\(\mathcal {E}([H_1 \Vert S_1] \Vert [S_2 \Vert S_3 ] \Vert [S_4])\));
-
\(Q_2\) with a known full-block header \(H_1 \Vert H_2\) (\(\mathcal {E}([H_1 \Vert H_2] \Vert [S_1 \Vert S_2 ] \Vert [S_3 \Vert S_4])\)).
-
-
2.
He first recovers \(S_1\) using the known-prefix sieving with the first block of each type of query. More precisely, he uses
 and
and  , so that the missing difference is \(0\, \Vert \,(S_1 \oplus H_2)\).
, so that the missing difference is \(0\, \Vert \,(S_1 \oplus H_2)\). -
3.
When \(S_1\) is known, he can again use known prefix sieving to recover \(S_2\), with the first and second blocks of \(Q_2\) queries:
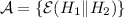 and
and 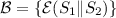 , so that the missing difference is \((S_1 \oplus H_1) \Vert (S_2 \oplus H_2)\). To improve the success rate of this step, he can also consider the first block of \(Q_1\) queries as known keystream.
, so that the missing difference is \((S_1 \oplus H_1) \Vert (S_2 \oplus H_2)\). To improve the success rate of this step, he can also consider the first block of \(Q_1\) queries as known keystream. -
4.
When \(S_2\) is known, another round of known prefix sieving reveals \(S_3\), e.g. with
 and
and  , the missing difference is \((S_2 \oplus H_1) \Vert (S_3 \oplus H_2)\).
, the missing difference is \((S_2 \oplus H_1) \Vert (S_3 \oplus H_2)\). -
5.
Finally, \(S_4\) is recovered with a last round of known prefix sieving using
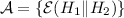 and
and  , with missing difference is \((S_3 \oplus H_1) \Vert (S_4 \oplus ~ H_2)\).
, with missing difference is \((S_3 \oplus H_1) \Vert (S_4 \oplus ~ H_2)\).
This gives an algorithm with query complexity of \(\mathcal {O}(\sqrt{n}2^{n/2}\)) to recover repeated encryption of a secret over multiple blocks in the BEAST attacker model. In Sect. 6.2, we analyze the constants in the \(\mathcal {O}()\) and run experiments with \(n=64\) using locally encrypted data. In particular, we have a success probability higher than 80% using two lists of \(5 \times 2^{32}\) queries with \(n=64\).
More generally, we show that for \(n \ge 32\) the success probability of this attack is at least 99% with lists of size \(\sqrt{n/2} \cdot 2^{n/2}\). With a one block secret, an optimal attack uses two lists of \(\sqrt{n/2} \cdot 2^{n/2}\) two-block queries: queries \([H_1 \Vert S_1] \Vert [S_2]\) with a half-block header, and queries \([H_1 \Vert H_2] \Vert [S_1 \Vert S_2]\) with a full-block header. This translates to a data complexity of \(4 \sqrt{n/2} \cdot 2^{n/2}\) blocks. For comparison, an attack against the CBC mode requires on average \(2 \cdot 2^{n/2}\) blocks of data in the ideal case.
Alternatively, an attacker could recover the secret bit by bit. This leads to a more complex attack in practice, but the complexity is similar, and this variant could use McGrew’s searching algorithm instead of our known-prefix sieving algorithm (because in this scenario, we have  ). We show a detailed analysis of this variant in Sect. 6.2, taking into account the n steps necessary for this attack.
). We show a detailed analysis of this variant in Sect. 6.2, taking into account the n steps necessary for this attack.
4.3 Use of CTR Mode in Communication Protocols
The CTR mode is widely used in internet protocols, in particular as part of the GCM authenticated encryption mode [29], with the AES block cipher. For instance, Mozilla telemetry data show that more than 90% of HTTPS connections from Firefox 58 use AES-GCMFootnote 4. While attacks against modes with a 128-bit block cipher are not practical yet, it is important to limit the amount of data processed with a given key, in order to keep the probability of a successfull attack negligible, following the guidelines of Luykx and Paterson [26].
Surprisingly, there are also real protocols that use 64-bit block ciphers with the CTR mode (or variants of the CTR mode), as shown below. Attacks against those protocols would be (close to) practical, assuming a scenario where an attacker can generate the encryption of a large number of messages with some fixed secret.
SSH. Ciphersuites based on the CTR mode were added to SSHv2 in 2006 [4]. In particular, 3DES-CTR is one of the recommended ciphers, but actual usage of 3DES-CTR seems to be rather low [1]. In practice, 3DES-CTR is optionally supported by the dropbear server, but it is not implemented in OpenSSH. According to a scan of the full IPv4 space by Censys.ioFootnote 5, around 9% of SSH servers support 3DES-CTR, but actual usage is hard to estimate because it depends on client configuration.
The SSH specification requires to rekey after 1 GB of data, but an attack is still possible, although the complexity increases.
3G Telephony. The main encryption algorithm in UMTS telephony is based on the 64-bit blockcipher Kasumi. The mode of operation, denoted as f8, is represented in Fig. 2. While this mode in not the CTR mode and was designed to avoid its weaknesses, our attack can be applied to the first block of ciphertext. Indeed the first block of message i is encrypted as \(c_{i,0} = m_{i,0} \oplus E_k(E_{k'}(i))\), where the value \(E_k(E_{k'}(i))\) is unique for all the messages encrypted with a given key.
There is a maximum of \(2^{32}\) messages encrypted with a given key in 3G, but this only has a small effect on the complexity of attacks.
Because of the low usage of 3DES-CTR in SSH, and the difficulty of mounting an attack against 3G telephony in practice, we did not attempt to demonstrate the attack in practice, but the setting and complexity of our attacks are comparable to recent results on the CBC mode with 64-bit ciphers [7].
4.4 Counter-Measures
As for many modes of operation, the common wisdom to counter this kind of attacks asks for rekeying before the birthday bound, i.e. before \(2^{n/2}\) blocks. However rekeying too close to the birthday bound may not be enough. For example let’s consider an implementation of a CTR based mode of operation that rekeys every \(2^{n/2}\) blocks, Using the same model as previously, and a one-block secret, an optimal attack uses queries \([H_1 \Vert S_1] \Vert [S_2]\) with a half-block header, and queries \([H_1 \Vert H_2] \Vert [S_1 \Vert S_2]\) with a full-block header, where rekeying occurs after \(2^{n/2-2}\) queries of each type. To recover \(S_1\), we use the known prefix sieving algorithm as previously, but we can only use relations between ciphertext blocks encrypted with the same key. In each session of \(2^{n/2}\) blocks, we consider \(2^{n-4}\) pairs of ciphertext blocks; on average there are \(2^{n/2-4}\) pairs with the correct prefix used for sieving. Since we need \(n/2 \cdot 2^{n/2}\) draws to reduce the sieve to a single element with high probability, we use 8n sessions, i.e. \(8n \cdot 2^{n/2}\) blocks of data in total. The same data can be reused to recover \(S_2\) when \(S_1\) is known. This should be compared with the previous data complexity of \(4\sqrt{n/2} \cdot 2^{n/2}\) in the absence of rekeying.
However, rekeying every \(2^{n/2-16}\) blocks makes the data complexity goes up to \(2^{35}n\) sessions or \(n \cdot 2^{19+n/2}\) blocks to recover the secret block. Notice that the security gain of rekeying is comparable with what is gained in CBC, where rekeying every \(2^{n/2-16}\) blocks forces increases the data complexity from \(2 \cdot 2^{n/2}\) to \(2^{18} \cdot 2^{n/2}\).
5 Application to Wegman-Carter MACs
Because the fast convolution algorithm requires fewer assumptions, it can be adapted to other modes of operation based on CTR and particularly to Wegman-Carter type of constructions for MAC. Wegman-Carter MACs use a keyed permutation E and a keyed universal hash function h, with k1 and k2 two private keys. The input is a message M and a nonce N, and the MAC is defined as:
Again, the construction requires that all block cipher inputs are different. To apply our attack, we use two fixed message M and \(M'\), and we capture many values \(\text {MAC}(N,M)\) in a list \(\mathcal {A}\) and values \(\text {MAC}(N',M')\) in a list \(\mathcal {B}\), all using unique nonces. Then we solve the missing difference problem to recover \(h_{k1}(M) - h_{k1}(M')\) as we know that \(\forall N \ne N' : E_{k2}(N) - E_{k2}(N') \ne 0\). It is often sufficient to know this difference and the two messages M and \(M'\) to recover the key \(k_1\). We give two examples with concrete MAC algorithms.
Galois/Counter Mode. GCM is an authenticated encryption mode with associated data, combining the CTR mode for encryption and a Wegman-Carter MAC based on polynomial evaluation in a Galois field for authentication. It takes as input a message M that is encrypted and authenticated, and some associated data A that is authenticated but not encrypted. When used with an empty message, the resulting MAC is known as GMAC. In our attack, we use an empty message with one block of authenticated data A, so that the tag is computed as:
with H the hash key and (\(\cdot \)) the multiplication in a Galois Field defined by a public polynomial. So, for two different blocks of authenticated data A and \(A'\) we collect \(\mathcal {O}(\sqrt{n} \cdot 2^{2n/3}\)) MACs and perform the fast convolution algorithm to recover \(A\cdot H^2 \oplus H \oplus A'\cdot H^2 \oplus H = (A \oplus A') \cdot H^2\). We known \(A \oplus A'\) and the field is known so we invert that value and recover \(H^2\) then compute the square root and recover the hash key H.
 There are several known attacks against GCM and GMAC, but none of them seems to allow universal forgery with just \(2^{2n/3}\) blocks of data and \(2^{2n/3}\) computations. In particular, Handschuh and Preneel [19] gave a weak-key attack, that can also be used to recover the hash key without weak key assumptions, using roughly \(2^{n/2}\) messages of \(2^{n/2}\) blocks. Later work extended these weak key properties [33, 36] but an attack still requires about \(2^n\) blocks in total when no assumptions are made about the key. We also note that these attacks require access to a verification oracle, while our attack only uses a MAC oracle.
There are several known attacks against GCM and GMAC, but none of them seems to allow universal forgery with just \(2^{2n/3}\) blocks of data and \(2^{2n/3}\) computations. In particular, Handschuh and Preneel [19] gave a weak-key attack, that can also be used to recover the hash key without weak key assumptions, using roughly \(2^{n/2}\) messages of \(2^{n/2}\) blocks. Later work extended these weak key properties [33, 36] but an attack still requires about \(2^n\) blocks in total when no assumptions are made about the key. We also note that these attacks require access to a verification oracle, while our attack only uses a MAC oracle.
Some earlier attacks use specific options of the GCM specifications to reach a lower complexity, but cannot be applied with standard-length IV, and tag: Ferguson [14] showed an attack when the tag is truncated, and Joux [23] gave an attack based on non-default IV lengths.
Poly1305. Poly1305 [6] is a MAC scheme following the Wegman-Carter construction, using polynomial evaluation modulo the prime number \(2^{130}-5\). It uses a keyed 128-bit permutation (usually AES), and the hash function key, r, has 106 free bits (22 bits of the key are set to 0, including in particular the 4 most significant ones). The message blocks are first padded to 129-bit values \(c_i\). Then the MAC of a q-block message M with nonce N is defined as:
With the same strategy as above, using two different messages M and \(M'\) we recover the missing difference
Moreover, we chose M and \(M'\) such that \(c_i - c'_i = 0\) and \(c_q - c'_q = 1\); since by design, \(r < 2^{124}\) the value recovered is simply the hash key r.
Notice that Poly1305 doesn’t use the XOR operation but a modular addition, and we have to adapt our algorithms to this case. Luckily, the fast convolution algorithm can easily be tweaked. First, we keep the 2n / 3 least significant bits to avoid issues the carry, something the XOR operation doesn’t have. Then, when the lists of counters are up, we need to compute their cyclic convolution, which is done with a fast convolution algorithm based on the fast Fourier transform (instead of fast Walsh-Hadamard). Then we verify the value suggested by the lowest counter by running the known prefix algorithm looking for collisions on the least significant bits and sieving the modular subtraction of the most significant bits. This adaptation has similar complexities and proofs than the one described earlier. Moreover, in the case of Poly1305, one can further adapt the algorithms to take into account the fact that 22 bits of the key r are fixed at 0 effectively reducing the dimension of \(\mathcal {S}\).
6 Proofs and Simulations
In this section we give some theoretical and simulation results that further support the claims we made thus far.
6.1 About the Fast Convolution Algorithm
Proof of query complexity for the claim made in Sect. 3.2. Consider, without loss of generality and for blocks of size n, that we possess \(a\cdot 2^{2n/3}\) blocks of keystream and the same number of blocks of encrypted secret S with \(a\) a function of n. So in this setting we have \(a^2\cdot 2^{4n/3}\) different XORed-values possible between the two lists, that we will consider as independent and uniformly distributed over \(2^n-1\) values. We will then focus on the \(2n/3\) bits truncation, \(T(\cdot )\), and ignore the rest. We count the number of occurrences for every truncated values and store them in two lists of size \(2^{2n/3}\). Using the fast Walsh-Hadamard transform 3 times, Algorithm 5, we can therefore compute the same counters but for all the XORed-values. We hope that the counter for T(S), the good counter, will be lower than all of the other counters, the bad counters, with probability \(\varOmega (1)\). In which case we say the algorithm succeeds.
Let \(X^c_i\) represents the fact that the \(i^{th}\) value truncates to c, so that \(X^c_i\) follows a Bernoulli distribution and any counter can be written as \(X^c = \sum _{i=1}^{a^22^{4n/3}} X^c_i\). Now we have to discriminate between the distributions of the good and bad counters:

Now we are interested by the probability that a bad counter gets a value below \(\mathbf {E}[X^{T(S)}]\) as a measure of how distinct the distributions are. Using Chernov Bound we get for all \(c \ne T(S)\):
And to compute the probability that no bad counter gets below \(\mathbf {E}[X^{T(S)}]\) we will have to assume their independence, which is wrong, but we will come back later to discuss this assumption.
To conclude, we need to find an \(a = a(n)\) such that this probability remains greater than some positive value as n grows. This is clearly achieved with \( a = \mathcal {O}(\sqrt{n})\) as for example taking \( a = \frac{2\sqrt{n}}{\sqrt{3 \cdot \log _2(e)}} \simeq 0.96\sqrt{n} \) we get:
Therefore we can bound the probability of success by the events ‘\(X^{T(S)} < \mathbf {E}[X^{T(S)}] \)’, probability \(\simeq 1/2\), and ‘\( \forall c \ne T(S) : X^c \ge \mathbf {E}[X^{T(S)}] \)’, probability at least 1/4. Then we indeed have a probability of at least 1/8 of having a successful algorithm. We can conclude that with \( \mathcal {O}(n \cdot 2^{4n/3}) \) XORed-values the algorithm has probability \(\varOmega (1)\) of succeeding.
Notice that this requires lists of size \( \mathcal {O}(\sqrt{n} \cdot 2^{2n/3}) \) but for the proof we only need the total number of pairs between the two lists. So we can break the requirement that the two lists are of comparable sizes as long as the product of their sizes sum up to the order of required values.
On the independence of the counters, this is obviously wrong as they are bound by the relation \( \sum _c X^c = a^22^{4n/3} \). However this relation becomes looser and looser as n grows so the approximation obtained should still be correct asymptotically. Moreover, the covariances implied are negative i.e. knowing one draw is big makes the other draws smaller in expectation to compensate. Small negative covariances will make the distribution look more evenly distributed in the sense that we can’t observe too many extreme events in a particular direction which is good for the success rate of the algorithm. So the assumption of independence may be a conservative one for this complexity analysis.
Simulation Results. We ran simulations for block sizes \(n =\) 12, 24, 32 and 48 bits, so that we could do some statistical estimations of the success probability for this attack. We first create two lists of same size, one of raw keystream output and one XORed with an n-bit secret S. Then we pass the two lists in Algorithm 5 counting over \(n' = 2n/3\) bits (unless specified otherwise) to get a list of counters for each possible XOR outputs on those \(n'\) bits. Then the expected behaviour of the attack would be to look for a solution whose \(n'\) first bits correspond to the position of the lowest counter and test this hypothesis with Algorithm 3. If it returns a unique value then this is S and we are done, if it returns an empty set then test with the position of the second lowest counter, etc. We can therefore know the number of key candidates that would be required to recover S and, over many trials, have an estimation of the probability of success after a given number of candidates in these parameters.
For block sizes of 12 and 24 we simulated a permutation simply by shuffling a range into a list. For bigger sizes of 32 and 48 we used the Simon lightweight cipher from the NSA [3] as that is one of the rare block cipher who can act on 48-bit blocks. We could quickly gather 10 000 runs for each setting except for the 48-bit blocks simulation where we gathered 756 runs.
In general we observe in Fig. 6 that the algorithm has a good chance of success with the first few candidates when using the suggested parameters. Moreover the sensibility with respect to the data complexity (Fig. 4) and to the number of bits counted over (Fig. 5) is fairly high. These results back up our complexity analysis and are a good indication that no big constant is ignored by the \(\mathcal {O}()\) notation.
On the speed at which the probability increases we realized that, despite the log scale on the x axis, the curves take a straight (Fig. 3) or concave shape (Figs. 5 and 6). That means that the probability of success with the next key candidate decreases very quickly with the number of key candidates already tested and proved wrong. For example for \(n=48\) bits (Fig. 6) over 756 trials the right key candidate was in the 2048 lowest counters in 98.1% of the time but the worst case found was 1 313 576 and these “very bad” cases push the mean rank of the right key candidate to 2287 and its sample variance to 2 336 937 008.
For \(n=48\) bits, one simulation took us 40 min over 10 cores (each step is highly parallelizable), and 64 gibibytes of RAM for the counters lists.
6.2 About the Known Prefix Sieving Algorithm
We consider two particular settings for the known prefix sieving algorithm and the corresping block splitting attack, with \(z=n/2\) and \(z=1\).
Theoretical Bound. We first give a theoretical lower bound to the probability of success of the sieving when \(\dim (\mathcal {S})=n/2\) (i.e. \(z=n/2\)), depending on the query complexity. Every partial collision found helps us to sieve. After collecting many blocks of keystream and encryption of S let \(|\mathcal {A}| \cdot |\mathcal {B}| =: \alpha 2^n\) for some \(\alpha \). Thus we get \(\alpha 2^{n}/2^{n/2} = \alpha 2^{n/2}\) partial collisions in expectation. More precisely, the Chernoff bound gives us a lower bound for the probability of finding at least \((1-\delta ) \alpha 2^{n/2}\) collisions:
for any \(\delta > 0\).
We see one partial collision as a draw in the coupon collector problem. One can use the formula in [34] for the tail of coupon collector problem probability distribution to estimate the chance of success after obtaining \(\beta \cdot 2^{n/2}\) partial collisions:
which is positive whenever \(\beta \ge n/2\cdot \ln (2)\).
Therefore we bound the probability of success when collecting \(|\mathcal {A}| \cdot |\mathcal {B}| = \alpha 2^n\) pairs as the probability of obtaining at least \((1-\delta ) \alpha 2^{n/2}\) partial collisions multiplied by the probability of success after sieving \((1-\delta ) \alpha 2^{n/2} \) values:
In particular, with two lists of size \(\sqrt{n/2} \cdot 2^{n/2}\) (i.e. \(\alpha = n/2\)), we get \(p \ge 0.99\) as long as \(n \ge 32\) (using \(\delta = 2^{-8}\)).
Simulation Results. We ran simulations with a block size \(n = 64\) bits, and a secret S of size \(n/2=32\) bits, using the Tiny Encryption Algorithm (TEA [37]) in CTR mode to encrypt the data. We create two lists, the keystream output list \(a_i \in \mathcal {A}\), and the encryptions \(b_j = a_j \oplus (\bar{0} \Vert S) \in \mathcal {B}\). We first produce and sort a list \(\mathcal {B}\) with \(2^{32}\) elements then produce, sort and sieve iteratively several lists \(\mathcal {A}\) with \(2^{32}\) elements, until the secret S is the only one remaining in the sieve.
One simulation runs in around 20 min over 36 cores, as every steps are trivially parallelizable: encryption, sorting and sieving. We ran 3700 simulations and tracked how many chunks of \(2^{n/2} = 2^{32}\) keystream outputs were needed for sieving. The coupon collector problem predicts that one will need on average \(n/2 \cdot \ln (2) \cdot 2^{n/2}\) partial collisions which will be obtained after \(n/2 \cdot \ln (2) \simeq 22.18 < 23\) rounds in expectation. And indeed the simulations showed a 64.5% probability of success after 23 iterations. Figure 7 shows the convergence between the theoretical lower bound and the simulated probabilities. We also noticed that the discrepancy in the number of rounds required is largely due to the last few candidates remaining in the sieve. If we decided the attack is successful when we are left with less than 1000 potential candidates for the secret then the algorithm successfully finishes after 16 rounds every time. In fact after 16 rounds the number of candidates left varies from 419 to 560 in all the simulations we have run.
Bit by Bit Secret Recovery. We also want to study the complexity of recovering the secret S bit by bit as an extreme case of the block splitting scenario described in Sect. 4.2. For simplicity, we consider a setting where one query returns a block of keystream and the encryption of \(0\,\Vert s_{i}\) with an unknown bit \(s_{i}\). We are interested in the query complexity for recovering n bits of secret one bit at a time; that is we need to know the first bit to ask for the second one, etc. Clearly this can be done in \(\mathcal {O}(n \cdot 2^{n/2})\) queries by repeating n times the attack on one bit. But the intuition is that we may need less and less queries to uncover the next bit as we go forward and accumulate blocks of keystream.
Let:
From the definition of a query, the above description and because each time we find a bit of secret we can deduce a range of keystream blocks for the next step we have the relations:
We consider the following proposition:
and, using (2), when \(P_k\) true for all \(k \le i\) we have:
Moreover (1) and (3) imply \(K_1=U_1=2^{n/2}\) so \(P_1\) is true. Now suppose \(P_k\) true for all \(k \le i\), let’s prove it holds for \(P_{i+1}\):
Now that we have a closed form for \(U_i\) we can deduce the expected number of queries needed to recover n bits of secret by summing over as \(\sum _{i=1}^{n} U_i = 2^{n/2}\sqrt{n}.\)
Therefore the query complexity is really \(\mathcal {O}(\sqrt{n} \cdot 2^{n/2})\) ignoring a constant depending on the length of a query. Notice that this complexity is the same as when sieving S as a whole showing that we don’t grow the query complexity by more than a constant with this strategy.
7 Conclusion
In this work, we have studied the missing difference problem and its relation to the security of the CTR mode. We have given efficient algorithms for the missing difference problem in two practically relevant cases: with an arbitrary missing difference, and when the missing difference is known to be in some low-dimension vector space. These algorithms lead to a message-recovery attack against the CTR mode with complexity \(\tilde{\mathcal {O}}(2^{n/2})\), and a universal forgery attack against some Carter-Wegman MACs with complexity \(\tilde{\mathcal {O}}(2^{2n/3})\).
In particular, we show that message-recovery attacks against the CTR mode can be mounted with roughly the same requirements and the same complexity as attacks against the CBC mode. While both modes have similar security proofs, there was a folklore assumption that the security loss of the CTR mode with large amounts of data is slower than in the CBC mode, because the absence of collision in the CTR keystream is harder to exploit than CBC collisions [15, Sect. 4.8.2]. Our results show that this is baseless, and use of the CTR mode with 64-bit block ciphers should be considered unsafe (unless strict data limits are in place). As a counter-measure, we recommend to use larger block sizes, and to rekey well before \(2^{n/2}\) blocks of data. Concrete guidelines for 128-bit block ciphers have been given by Luykx and Paterson [26]. Alternatively, if the use of small block is required, we suggest using a mode with provable security beyond the birthday bound, such as CENC [21, 22].
Our missing difference attacks against CTR and the collision attacks against CBC are two different possible failure of block cipher modes beyond the birthday bound. They exploit different properties of the modes but result in similar attacks. These techniques can be used against other modes of operations (OFB, CFB, ...), and most of them will be vulnerable to at least one the attacks, unless they have been specially designed to provide security beyond the birthday bound.
Notes
- 1.
For instance, GCM concatenates a per-message nonce and a counter within a message.
- 2.
For instance, the treatment of non-default-length nonces in GCM can lead to collisions [23].
- 3.
For example, wikipedia.org encodes cookies with lower case letters and digits, this corresponds to two known bits.
- 4.
https://mzl.la/2GY53Mc, accessed February 8, 2018.
- 5.
https://censys.io/data/22-ssh-banner-full_ipv4, scan performed July 5, 2017.
References
Albrecht, M.R., Degabriele, J.P., Hansen, T.B., Paterson, K.G.: A surfeit of SSH cipher suites. In: Weippl, E.R., Katzenbeisser, S., Kruegel, C., Myers, A.C., Halevi, S. (eds.) ACM CCS 2016, pp. 1480–1491. ACM Press, October 2016
AlFardan, N.J., Bernstein, D.J., Paterson, K.G., Poettering, B., Schuldt, J.C.N.: On the security of RC4 in TLS. In: King, S.T. (ed.) USENIX Security 2013, pp. 305–320. USENIX Association (2013)
Beaulieu, R., Shors, D., Smith, J., Treatman-Clark, S., Weeks, B., Wingers, L.: SIMON and SPECK: Block ciphers for the internet of things. Cryptology ePrint Archive, Report 2015/585 (2015). http://eprint.iacr.org/2015/585
Bellare, M., Kohno, T., Namprempre, C.: The Secure Shell (SSH) Transport Layer Encryption Modes. IETF RFC 4344 (2006)
Bellare, M., Desai, A., Jokipii, E., Rogaway, P.: A concrete security treatment of symmetric encryption. In: 38th FOCS, pp. 394–403. IEEE Computer Society Press, October 1997
Bernstein, D.J.: The Poly1305-AES message-authentication code. In: Gilbert, H., Handschuh, H. (eds.) FSE 2005. LNCS, vol. 3557, pp. 32–49. Springer, Heidelberg (2005). https://doi.org/10.1007/11502760_3
Bhargavan, K., Leurent, G.: On the practical (in-)security of 64-bit block ciphers: collision attacks on HTTP over TLS and OpenVPN. In: Weippl, E.R., Katzenbeisser, S., Kruegel, C., Myers, A.C., Halevi, S. (eds.) ACM CCS 2016, pp. 456–467. ACM Press, October 2016
Biham, E., Shamir, A.: Differential cryptanalysis of DES-like cryptosystems. J. Cryptol. 4(1), 3–72 (1991). https://doi.org/10.1007/BF00630563
Daemen, J., Knudsen, L., Rijmen, V.: The block cipher Square. In: Biham, E. (ed.) FSE 1997. LNCS, vol. 1267, pp. 149–165. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0052343
Diffie, W., Hellman, M.E.: Privacy and authentication: an introduction to cryptography. Proc. IEEE 67(3), 397–427 (1979)
Dinur, I., Leurent, G.: Improved generic attacks against hash-based MACs and HAIFA. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 149–168. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_9
Duong, T., Rizzo, J.: Here come the \(\oplus \) ninjas (2011)
Dworkin, M.: Recommendation for Block Cipher Modes of Operation: Methods and Techniques. NIST Special Publication 800–38A, National Institute for Standards and Technology, December 2001
Ferguson, N.: Authentication weaknesses in GCM. Comment to NIST (2005). http://csrc.nist.gov/groups/ST/toolkit/BCM/documents/comments/CWC-GCM/Ferguson2.pdf
Ferguson, N., Schneier, B., Kohno, T.: Cryptography Engineering: Design Principles and Practical Applications. Wiley, New York (2011)
DES Modes of Operation. NIST Special Publication 81, National Institute for Standards and Technology, December 1980
Fuhr, T., Leurent, G., Suder, V.: Collision attacks against CAESAR candidates. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015, Part II. LNCS, vol. 9453, pp. 510–532. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48800-3_21
Guo, J., Peyrin, T., Sasaki, Y., Wang, L.: Updates on generic attacks against HMAC and NMAC. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 131–148. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_8
Handschuh, H., Preneel, B.: Key-recovery attacks on universal hash function based MAC algorithms. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 144–161. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_9
Hoang, V.T., Reyhanitabar, R., Rogaway, P., Vizár, D.: Online authenticated-encryption and its nonce-reuse misuse-resistance. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part I. LNCS, vol. 9215, pp. 493–517. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_24
Iwata, T.: New blockcipher modes of operation with beyond the birthday bound security. In: Robshaw, M. (ed.) FSE 2006. LNCS, vol. 4047, pp. 310–327. Springer, Heidelberg (2006). https://doi.org/10.1007/11799313_20
Iwata, T., Mennink, B., Vizár, D.: CENC is optimally secure. Cryptology ePrint Archive, Report 2016/1087 (2016). http://eprint.iacr.org/2016/1087
Joux, A.: Authentication failures in NIST version of GCM. Comment to NIST (2006). http://csrc.nist.gov/groups/ST/toolkit/BCM/documents/comments/800-38_Series-Drafts/GCM/Joux_comments.pdf
Lee, C., Kim, J., Sung, J., Hong, S., Lee, S.: Forgery and key recovery attacks on PMAC and Mitchell’s TMAC variant. In: Batten, L.M., Safavi-Naini, R. (eds.) ACISP 2006. LNCS, vol. 4058, pp. 421–431. Springer, Heidelberg (2006). https://doi.org/10.1007/11780656_35
Leurent, G., Peyrin, T., Wang, L.: New generic attacks against hash-based MACs. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part II. LNCS, vol. 8270, pp. 1–20. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_1
Luykx, A., Paterson, K.G.: Limits on authenticated encryption use in TLS, March 2016. http://www.isg.rhul.ac.uk/~kp/TLS-AEbounds.pdf
Matsui, M.: Linear cryptanalysis method for DES cipher. In: Helleseth, T. (ed.) EUROCRYPT 1993. LNCS, vol. 765, pp. 386–397. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48285-7_33
McGrew, D.: Impossible plaintext cryptanalysis and probable-plaintext collision attacks of 64-bit block cipher modes. Cryptology ePrint Archive, Report 2012/623. Accepted to FSE 2013 (2012). http://eprint.iacr.org/2012/623
McGrew, D.A., Viega, J.: The security and performance of the Galois/counter mode (GCM) of operation. In: Canteaut, A., Viswanathan, K. (eds.) INDOCRYPT 2004. LNCS, vol. 3348, pp. 343–355. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30556-9_27
Peyrin, T., Wang, L.: Generic universal forgery attack on iterative hash-based MACs. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 147–164. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_9
Preneel, B., van Oorschot, P.C.: MDx-MAC and building fast MACs from hash functions. In: Coppersmith, D. (ed.) CRYPTO 1995. LNCS, vol. 963, pp. 1–14. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-44750-4_1
Preneel, B., van Oorschot, P.C.: On the security of two MAC algorithms. In: Maurer, U. (ed.) EUROCRYPT 1996. LNCS, vol. 1070, pp. 19–32. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68339-9_3
Procter, G., Cid, C.: On weak keys and forgery attacks against polynomial-based MAC schemes. J. Cryptol. 28(4), 769–795 (2015)
Rajeev, M., Prabhakar, R.: Randomized Algorithms. Cambridge University Press, New York (1995)
Rogaway, P.: Evaluation of some blockcipher modes of operation (2011)
Saarinen, M.-J.O.: Cycling attacks on GCM, GHASH and other polynomial MACs and hashes. In: Canteaut, A. (ed.) FSE 2012. LNCS, vol. 7549, pp. 216–225. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34047-5_13
Wheeler, D.J., Needham, R.M.: TEA, a tiny encryption algorithm. In: Preneel, B. (ed.) FSE 1994. LNCS, vol. 1008, pp. 363–366. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-60590-8_29
Acknowledgement
Part of this work was supported by the French DGA, and the authors are partially supported by the French Agence Nationale de la Recherche through the BRUTUS project under Contract ANR-14-CE28-0015.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Leurent, G., Sibleyras, F. (2018). The Missing Difference Problem, and Its Applications to Counter Mode Encryption. In: Nielsen, J., Rijmen, V. (eds) Advances in Cryptology – EUROCRYPT 2018 . EUROCRYPT 2018. Lecture Notes in Computer Science(), vol 10821. Springer, Cham. https://doi.org/10.1007/978-3-319-78375-8_24
Download citation
DOI: https://doi.org/10.1007/978-3-319-78375-8_24
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-78374-1
Online ISBN: 978-3-319-78375-8
eBook Packages: Computer ScienceComputer Science (R0)






 and
and  , so that the missing difference is
, so that the missing difference is 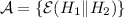 and
and 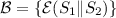 , so that the missing difference is
, so that the missing difference is  and
and  , the missing difference is
, the missing difference is 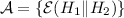 and
and  , with missing difference is
, with missing difference is 





