Defects

Abstract

An ideal crystalline solid has a periodic structure that is based on the chemical properties of its constituent atoms (see Chap. 3). However, real crystals are not perfect. They always have imperfections such as extra/missing atoms or impurities, which are called defects.

Problems

• 1. Give some examples of physical properties that defects can change.

• 2. Identify the types of point defects shown in Fig. 19.1. Please re-sketch the figure.

• 3. Calculate the number of vacancies per cubic meter in iron at 750 °C. The energy for vacancy formation is 1.08 eV/atom. Also, the density and atomic weight for Fe are 7.65 g⋅cm⁻³ and 55.85 g⋅mol⁻¹, respectively. Assume A is unity.

• 4. Find the equilibrium concentration of defects for T = 0, 200, 400, 600, 800, 1000, and 1200 K if the energy to form a defect is 1 eV/atom. Assume A is unity. Graph your results. For T = 1200 K, how many atoms per single vacancy are present?

• 5. The formation energies of vacancy clusters in Si are listed below. Calculate the formation energy of (i) system a (30 single vacancies), (ii) system B (five 6-vacancy clusters), and (iii) system C (three 10-vacancy clusters). Which system has the lowest formation energy? Why?

  

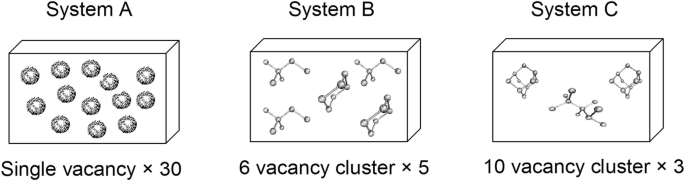
  (Cluster shapes reprinted with permission from Europhys Lett Vol. 43, p. 697, Fig. 1, Bongiorno A, Colombo L, and Diaz de la Rubia T, “Structural and binding properties of vacancy clusters in silicon,” p. 697. Copyright 1998, EPD Sciences.)

Size	1	6	10
Energy (eV)	3.4	11.4	15.6

• 6. Briefly describe the difference between an edge dislocation and a screw dislocation.

• 7. Show how to find the Burgers’ vector for a screw dislocation.

• 8. GaAs/InAs have a 7.2% lattice mismatch. How many monolayers of InAs may be grown on GaAs before a semi-coherent boundary is formed? (a_GaAs = 0.565 nm a_InAs = 0.606 nm, assume $b={a}_{\mathrm{InAs}}/\sqrt{2}$).

• 9. What is preferential etching?

• 10. What have been the goals of the semiconductor industry in silicon crystal growth technology? Why?