Low Cost Constant Round MPC Combining BMR and Oblivious Transfer

Abstract

In this work, we present two new universally composable, actively secure, constant round multi-party protocols for generating BMR garbled circuits with free-XOR and reduced costs.

• 1. Our first protocol takes a generic approach using any secret-sharing based MPC protocol for binary circuits, and a correlated oblivious transfer functionality.

• 2. Our specialized protocol uses secret-sharing based MPC with information-theoretic MACs. This approach is less general, but requires no additional correlated OTs to compute the garbled circuit.

In both approaches, the underlying secret-sharing based protocol is only used for one secure $\mathbb {F}_2$ multiplication per AND gate. An interesting consequence of this is that, with current techniques, constant round MPC for binary circuits is not much more expensive than practical, non-constant round protocols.

We demonstrate the practicality of our second protocol with an implementation, and perform experiments with up to 9 parties securely computing the AES and SHA-256 circuits. Our running times improve upon the best possible performance with previous BMR-based protocols by 60 times.

P. Scholl—Work done whilst at University of Bristol, UK.

1 Introduction

Secure multi-party computation (MPC) protocols allow a group of n parties to compute some function f on the parties’ private inputs, while preserving a number of security properties such as privacy and correctness. The former property implies data confidentiality, namely, nothing leaks from the protocol execution but the computed output. The latter requirement implies that the protocol enforces the integrity of the computations made by the parties, namely, honest parties learn the correct output. Modern, practical MPC protocols typically fall into two main categories: those based on secret-sharing [5, 13, 15, 18, 22, 35], and those based on garbled circuits [2, 11, 25,26,27,28, 32, 39]. When it comes to choosing a protocol, many different factors need to be taken into account, such as the function being evaluated, the latency and bandwidth of the network and the adversary model.

Secret-sharing based protocols such as [5, 15, 18] tend to have lower communication requirements in terms of bandwidth, but require a large number of rounds of communication, which increases with the complexity of the function. In this approach the parties first secret-share their inputs and then evaluate the circuit gate by gate while preserving privacy and correctness. In low-latency networks, they can have an extremely fast online evaluation stage, but the round complexity makes them much less suited to high-latency networks, when the parties may be far apart.

Garbled circuits, introduced in Yao’s protocol [39], are the core behind all practical, constant round protocols for secure computation. In the two-party setting, one of the parties “encrypts” the circuit being evaluated, whereas the other party privately evaluates it. Garbled circuit-based protocols have recently become much more efficient, and currently give the most practical approach for actively secure computation of binary circuits [34, 37]. With more than two parties, the situation is more complex, as the garbled circuit must be computed by all parties in a distributed manner using another (non-constant-round) MPC protocol, as in the BMR protocol from [2]. This still leads to a low depth circuit, hence a constant round protocol overall, because all gates can be garbled in parallel. We note that this paradigm has received very little attention, compared with two-party protocols. The original BMR construction uses generic zero-knowledge techniques for proving correct computation of PRG values, so is impractical. A different protocol, but only for three parties, was designed by Choi et al. [11] in the dishonest majority setting. More practical, actively secure protocols for any number of parties are the recent works of Lindell et al. [29, 31], which use somewhat homomorphic encryption (SHE) or generic MPC to garble a circuit. Ben-Efraim et al. [4] recently presented and implemented an efficient multi-party garbling protocol based on oblivious transfer, but with only semi-honest security. Very recently, Katz et al. introduced in [23] protocols based on authenticated garbling, with a preprocessing phase that can be instantiated based on TinyOT [33].

1.1 Our Contributions

In this work, we present a practical, actively secure, constant round multi-party protocol for generating BMR garbled circuits with free-XOR in the presence of up to $n-1$ out of n corruptions. As in prior constructions, our approach has two phases: a preprocessing phase where the garbled circuit is mutually generated by all parties, and an online phase where the parties obtain the output of the computation. While the online phase is typically efficient and incurs no cost to achieve active security, the focus of recent works was on optimizing the preprocessing complexity, where the main bottleneck is with respect to garbling AND gates. In that context, we present two new constant-round protocols for securely generating the garbled circuit:

• 1. A generic approach using any secret-sharing based MPC protocol for binary circuits, and a correlated oblivious transfer functionality.

• 2. A specialized protocol which uses secret-sharing based MPC with information-theoretic MACs, such as TinyOT [17, 33]. This approach is less general, but requires no additional correlated OTs to compute the garbled circuit.

In both approaches, the underlying secret-sharing based protocol is only used for one secure $\mathbb {F}_2$ multiplication per AND gate.

In the first, more general method, every pair of parties needs to run one correlated OT per AND gate, which costs $O(\kappa )$ communication for security parameter $\kappa$. Combining this with the overhead induced by the correlated OTs in our protocol, we obtain total complexity $O(|C |\kappa n^2)$, assuming only symmetric primitives and $O(\kappa )$ seed OTs between every pair of parties. This gives an overall communication cost of $O(M + |C |\kappa n^2)$ to evaluate a circuit C, where M is the cost of evaluating $|C |$ AND gates in the secret-sharing based protocol, $\varPi$. To realize $\varPi$, we can define a functionality with multiplication depth 1 that computes all the AND gates in parallel (these multiplications can be computed in parallel as they are independent of the parties’ inputs). Furthermore, the [21] compiler can be instantiated with semi-honest [18] as the inner protocol and [12] as the outer protocol. By Theorem 2, Sect. 5 from [21], for some constant number of parties $m\ge 2$, the functionality can be computed with communication complexity O(|C|) plus low order terms that depend on a statistical parameter s, the circuit’s depth and $\log |C|$. As in [21], this extends to the case of a non-constant number of parties n, in which case the communication complexity grows by an additional factor of $|C| \mathsf {poly}(n)$.

Another interesting candidate for instantiating $\varPi$ would be to use an MPC protocol optimized for SIMD binary circuits such as MiniMAC [16]. This is because in our construction, all the AND gates can be computed in parallel. Currently, the only known preprocessing methods [17] for MiniMAC are not practical, but this seems to be an interesting future direction to explore.

TinyOT is currently the most practical approach to secret-sharing based MPC on binary circuits, so the second method leads to a highly practical protocol for constant-round secure computation. The complexity is essentially the same as TinyOT, as here we do not require any additional OTs. However, the protocol is less general and has worse asymptotic communication complexity, since TinyOT costs either $O(|C |B \kappa n^2)$ (with 2 parties or the recent protocol of [38]), or $O(|C |B^2\kappa n^2)$ (with [17]), where $B = O(1 + s/\log {|C |})$ (and in practice is between 3–5), and s is the statistical security parameter.

Our constructions employ several very appealing features. For a start, we embed into the modeling of the preprocessing functionality, which computes the garbled circuit, an additive error introduced into the garbling by the adversary. Concretely, we extend the functionality from [29] so that it obtains a vector of additive errors from the adversary to be applied to each garbled gate, which captures the fact that the adversary may submit inconsistent keys and pseudorandom function (PRF) values. We further strengthen this by allowing the adversary to pick the error adaptively after seeing the garbled circuit (in prior constructions this error is independent of the garbling) and allowing corrupt parties to choose their own PRF keys, possibly not at random. This requires a new analysis and proof of the online phase.

Secondly, we devise a new consistency check to enforce correctness of inputs to correlated OT, which is based on very efficient linear operations similar to recent advances in homomorphic commitments [9]. This check, combined with our improved error analysis for the online phase, allows the garbled circuit to be created without authenticating any of the parties’ keys or PRF values, which removes a significant cost from previous works (saving a factor of $\varOmega (n)$).

Implementation. We demonstrate the practicality of our TinyOT-based protocol with an implementation, and perform experiments with up to 9 parties securely computing the AES and SHA-256 circuits. In a 1 Gbps LAN setting, we can securely compute the AES circuit with 9 parties in just 620 ms. This improves upon the best possible performance that would be attainable using [29] by around 60 times. The details of our implementation can be found in Sect. 6.

Comparison with Other Approaches. Table 1 shows how the communication complexity of our work compares with other actively secure, constant-round protocols. As mentioned earlier, most previous constructions express the garbling function as an arithmetic circuit over a large finite field. In these protocols, garbling even a single AND gate requires computing O(n) multiplications over a large field with SHE or MPC. This means they scale at least cubically in the number of parties. In constrast, our protocol only requires one $\mathbb {F}_2$ multiplication per AND gate, so scales with $O(n^2)$. Previous SHE-based protocols also require zero-knowledge proofs of plaintext knowledge of SHE ciphertexts, which in practice are very costly. Note that the recent MASCOT protocol [24] for secure computation of arithmetic circuits could also be used in [29], instead of SHE, but this still has very high communication costs. We denote by MASCOT-BMR-FX an optimized variant of [29], modified to use free-XOR as in our protocol, with multiplications in $\mathbb {F}_{2^\kappa }$ done using MASCOT. Finally, the recent concurrent work by Katz et al. [23] is based on an optimized variant of TinyOT, with comparable performance to our approach.

None of these previous works have reported implementations at the time of writing, but our implementation of the TinyOT-based protocol improves upon the best times that would be achievable with SPDZ-BMR and MASCOT by up to 60x. This is because our protocol has lower communication costs than [29] (by at least 2 orders of magnitude) and the main computational costs are from standard symmetric primitives, so far cheaper than using SHE.

Overall, our protocols significantly narrow the gap between the cost of constant-round and many-round MPC protocols for binary circuits. More specifically, this implies that, with current techniques, constant round MPC for binary circuits is not much more expensive than practical, non-constant round protocols. Additionally, both of our protocols have potential for future improvement by optimizing existing non-constant round protocols: a practical implementation of MiniMAC [16] would lead to a very efficient approach with our generic protocol, whilst any future improvements to multi-party TinyOT would directly give a similar improvement to our second protocol.

Table 1. Comparison of actively secure, constant round MPC protocols. $B = O(1 + s/\log {|C |})$ is a cut-and-choose parameter, which in practice is between 3–5. Our second protocol can also be based upon optimized TinyOT to obtain the same complexity as [23].

1.2 Technical Overview

Our protocol is based on the recent free-XOR variant of BMR garbling used for semi-honest MPC in [4]. In that scheme, a garbling of the g-th AND gate with input wires u, v and output wire w, consists of the 4n values (where n is the number of parties):

$$\begin{aligned} \tilde{g}^j_{a,b} =&\left( \bigoplus _{i=1}^n F_{k^i_{u,a},k^i_{v,b}}(g \Vert j)\right) \oplus k^j_{w,0} \\ \oplus&\left( R^j ((\lambda _u \oplus a) (\lambda _v \oplus b) \oplus \lambda _w)\right) , \quad (a,b) \in \{0,1\}^2, \; j \in [n]\nonumber \\ \nonumber \end{aligned}$$

(1)

Here, F is a double-key PRF, $R^j \in \{0,1\}^\kappa$ is a fixed correlation string for free-XOR known to party $P_j$, and the keys $k^j_{u,a}, k^j_{v,b} \in \{0,1\}^\kappa$ are also known to $P_j$. Furthermore, the wire masks $\lambda _u,\lambda _v,\lambda _w \in \{0,1\}$ are random, additively secret-shared bits known by no single party.

The main idea behind BMR is to compute the garbling, except for the PRF values, with a general MPC protocol. The analysis of [29] showed that it is not necessary to prove in zero-knowledge that every party inputs the correct PRF values to the MPC protocol that computes the garbling. This is because when evaluating the garbled circuit, each party $P_j$ can check that the decryption of the j-th entry in every garbled gate gives one of the keys $k^j_{w,b}$, and this check would overwhelmingly fail if any PRF value was incorrect. It further implies that the adversary cannot flip the value transmitted through some wire as that would require from it to guess a key.

Our garbling protocol proceeds by computing a random, unauthenticated, additive secret sharing of the garbled circuit. This differs from previous works [29, 31], which obtain authenticated (with MACs, or SHE ciphertexts) sharings of the entire garbled circuit. Our protocol greatly reduces this complexity, since the PRF values and keys (on the first line of Eq. (1)) do not need to be authenticated. The main challenge, therefore, is to compute shares of the products on the second line of (1). Similarly to [4], a key observation that allows efficiency is the fact that these multiplications are either between two secret-shared bits, or a secret-shared bit and a fixed, secret string. So, we do not need the full power of an MPC protocol for arithmetic circuit evaluation over $\mathbb {F}_{2^\kappa }$ or $\mathbb {F}_p$ (for large p), as used in previous works.

To compute the bit product $\lambda _u \cdot \lambda _v$, we can use any actively secure GMW-style MPC protocol for binary circuits. This protocol is only needed for computing one secure AND per garbled AND gate, since all bit products in $\tilde{g}^j_{a,b}$ can be computed as linear combinations of $\lambda _u \cdot \lambda _v$, $\lambda _u$ and $\lambda _v$. We then need to multiply the resulting secret-shared bits by the string $R^j$, known to $P_j$. We give two variants for computing this product, the first one being more general and the second more concretely efficient. In more details,

• 1. The first solution performs the multiplication by running actively secure correlated OT between $P_j$ and every other party, where $P_j$ inputs $R^j$ as the fixed OT correlation. The parties then run a consistency check by applying a universal linear hash function to the outputs and sacrificing a few OTs, ensuring the correct inputs were provided to the OT. This protocol is presented in Sect. 3.

• 2. The second method requires using a ‘TinyOT’-style protocol [6, 17] based on information-theoretic MACs, and allows us to compute the bit/string products directly from the MACs, provided each party’s MAC key is chosen to be the same string $R^i$ used in the garbling. This saves interaction since we do not need any additional OTs. This protocol is presented in Sect. 4.

After creating shares of all these products, the parties can compute shares of the whole garbled circuit. These shares must then be rerandomized, before they can be broadcast. Opening the garbled circuit in this way allows a corrupt party to introduce further errors into the garbling by changing their share, even after learning the correct garbled circuit, since we may have a rushing adversary. Nevertheless, we prove that the BMR online phase remains secure when this type of error is allowed, as it would only lead to an abort. This significantly strengthens the result from [29], which only allowed corrupt parties to provide incorrect PRF values, and is an important factor that allows our preprocessing protocol to be so efficient.

Concurrent Work. Two recent works by Katz, Ranellucci and Wang introduced constant round, two-party [38] and multi-party [23] protocols based on authenticated garbling, with a preprocessing phase that can be instantiated based on TinyOT. At the time of writing, their two-party paper also reports on an implementation, but the multi-party version does not. Our work is conceptually quite similar, since both involve generating a garbled circuit in a distributed manner using TinyOT. The main difference seems to be that our protocol is symmetric, since all parties evaluate the same garbled circuit. With authenticated garbling, the garbled circuit is only evaluated by one party. This makes the garbled circuit slightly smaller, since there are $n-1$ sets of keys instead of n, but the online phase requires at least one more round of interaction (if all parties learn the output). The works of Katz et al. also contain concrete and asymptotic improvements to the two-party and multi-party TinyOT protocols, which improves upon the TinyOT protocol we give in the full version of this paper [20] by a factor of $O(s/\log {|C |})$, where s is a statistical parameter. These improvements can be directly plugged into our second garbling protocol. We remark that the two-party protocol in [38] inspired our use of TinyOT MACs to perform the bit/string multiplications in our protocol from Sect. 4. The rest of our work is independent.

Another difference is that our protocol from Sect. 3 is more generic, since $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$ can be implemented with any secret-sharing based bit-MPC protocol, rather than just TinyOT. This can be instantiated with [21] to obtain a constant-round protocol with complexity $O(|C |(\kappa n^2 + \mathsf {poly}(n)))$ in the OT-hybrid model. The multi-party paper [23] does not have an analogous generic result.

2 Preliminaries

We denote the security parameter by $\kappa$. We say that a function $\mu :\mathbb {N}\rightarrow \mathbb {N}$ is negligible if for every positive polynomial $p(\cdot )$ and all sufficiently large $\kappa$ it holds that $\mu (\kappa )<\frac{1}{p(\kappa )}$. We use the abbreviation PPT to denote probabilistic polynomial-time. We further denote by $a \leftarrow A$ the uniform sampling of a from a set A, and by [d] the set of elements $(1,\ldots ,d)$. We often view bit-strings in $\{0,1\}^k$ as vectors in $\mathbb {F}_2^k$, depending on the context, and denote exclusive-or by “$\oplus$” or “$+$”. If $a, b \in \mathbb {F}_2$ then $a \cdot b$ denotes multiplication (or AND), and if ${\varvec{c}}\in \mathbb {F}_2^\kappa$ then $a \cdot {\varvec{c}}\in \mathbb {F}_2^\kappa$ denotes the product of a with every component of ${\varvec{c}}$.

For vectors ${\varvec{x}}= (x_1,\dots ,x_n) \in \mathbb {F}_2^n$ and ${\varvec{y}}\in \mathbb {F}_2^m$, the tensor product (or outer product) ${\varvec{x}}\otimes {\varvec{y}}$ is defined as the $n \times m$ matrix over $\mathbb {F}_2$ where the i-th row is $x_i \cdot {\varvec{y}}$. We use the following property.

Fact 21

If ${\varvec{x}}\in \mathbb {F}_2^n,{\varvec{y}}\in \mathbb {F}_2^m$ and ${\mathbf {M}}\in \mathbb {F}_2^{m \times n}$ then

$$ {\mathbf {M}}\cdot ({\varvec{x}}\otimes {\varvec{y}}) = ({\mathbf {M}}\cdot {\varvec{x}}) \otimes {\varvec{y}}. $$

Universal composability. We prove security of our protocols in the universal composability (UC) framework [7] (see also [8] for a simplified version of UC).

Communication model. We assume all parties are connected via authenticated communication channels, as well as secure point-to-point channels and a broadcast channel. The default method of communication in our protocols is authenticated channels, unless otherwise specified. Note that in practice, these can all be implemented with standard techniques (in particular, for broadcast a simple 2-round protocol suffices, since we allow abort [19]).

Adversary model. The adversary model we consider is a static, active adversary who corrupts up to $n-1$ out of n parties. This means that the identities of the corrupted parties are fixed at the beginning of the protocol, and they may deviate arbitrarily from the protocol.

2.1 Circular 2-Correlation Robust PRF

The BMR garbling technique from [29] is proven secure based on a pseudorandom function (PRF) with multiple keys. However, since our scheme supports free-XOR, we need to adapt the definition of correlation robustness with circularity from [10] given for hash functions to double-key PRFs. This definition captures the related key and circularity requirements induced by supporting the free-XOR technique. Formally, fix some function $F : \{0,1\}^n \times \{0,1\}^\kappa \times \{0,1\}^\kappa \mapsto \{0,1\}^\kappa$. We define an oracle $\mathsf {Circ}_R$ as follows:

• $\mathsf {Circ}_R(k_1, k_2, g, j, b_1, b_2, b_3)$ outputs $F_{k_1\oplus b_1R,k_2\oplus b_2R}(g\Vert j)\oplus b_3R$.

The outcome of oracle $\mathsf {Circ}$ is compared with the a random string of the same length computed by an oracle $\mathsf {Rand}$:

• $\mathsf {Rand}(k_1, k_2, g, j, b_1, b_2, b_3)$: if this input was queried before then return the answer given previously. Otherwise choose $u \leftarrow \{0,1\}^\kappa$ and return u.

Definition 21

(Circular 2-correlation robust PRF). A PRF F is circular 2-correlation robust if for any non-uniform polynomial-time distinguisher $\mathcal{D}$ making legal queries to its oracle, there exists a negligible function $\mathsf {negl}$ such that:

$$ \big |\Pr [R\leftarrow \{0,1\}^\kappa ; \mathcal{D}^{\mathsf {Circ}_R(\cdot )}(1^\kappa ) = 1] - \Pr [\mathcal{D}^{\mathsf {Rand}(\cdot )}(1^\kappa ) = 1]\big |\le \mathsf {negl}(\kappa ). $$

As in [10], some trivial queries must be ruled out. Specifically, the distinguisher is restricted as follows: (1) it is not allowed to make any query of the form $\mathcal{O}(k_1, k_2, g, j, 0, 0, b_3)$ (since it can compute $F_{k_1,k_2}(g\Vert j)$ on its own) and (2) it is not allowed to query both tuples $\mathcal{O}(k_1, k_2, g, j, b_1, b_2, 0)$ and $\mathcal{O}(k_1, k_2, g, j, b_1, b_2, 1)$ for any values $k_1, k_2, g, j, b_1, b_2$ (since that would allow it to trivially recover the global difference). We say that any distinguisher respecting these restrictions makes legal queries.

2.2 Almost-1-Universal Linear Hashing

We use a family of almost-1-universal linear hash functions over $\mathbb {F}_2$, defined by:

Definition 22

(Almost-1-Universal Linear Hashing). We say that a family $\mathcal{H}$ of linear functions $\mathbb {F}_2^m \rightarrow \mathbb {F}_2^s$ is $\varepsilon$-almost 1-universal, if it holds that for every non-zero ${\varvec{x}}\in \mathbb {F}_2^m$ and for every ${\varvec{y}}\in \mathbb {F}_2^s$:

$$ \mathop {\Pr }\limits _{{\mathbf {H}}\leftarrow \mathcal{H}} [{\mathbf {H}}({\varvec{x}}) = {\varvec{y}}] \le \varepsilon $$

where ${\mathbf {H}}$ is chosen uniformly at random from the family $\mathcal{H}$. We will identify functions ${\mathbf {H}}\in \mathcal{H}$ with their $s \times m$ transformation matrix, and write ${\mathbf {H}}({\varvec{x}}) = {\mathbf {H}}\cdot {\varvec{x}}$.

This definition is slightly stronger than a family of almost-universal linear hash functions (where the above need only hold for ${\varvec{y}}=0$, as in [9]). However, this is still much weaker than 2-universality (or pairwise independence), which a linear family of hash functions cannot achieve, because ${\mathbf {H}}(0) = 0$ always. The two main properties affecting the efficiency of a family of hash functions are the seed size, which refers to the length of the description of a random function ${\mathbf {H}}\leftarrow \mathcal{H}$, and the computational complexity of evaluating the function. The simplest family of almost-1-universal hash functions is the set of all $s \times m$ matrices; however, this is not efficient as the seed size and complexity are both $O(m \cdot s)$. Recently, in [9], it was shown how to construct a family with seed size O(s) and complexity O(m), which is asymptotically optimal. A more practical construction is a polynomial hash based on GMAC (used also in [34]), described as follows (here we assume that s divides m, for simplicity):

• Sample a random seed $\alpha \leftarrow \mathbb {F}_{2^s}$

• Define ${\mathbf {H}}_\alpha$ to be the function:

  $$\begin{aligned} {\mathbf {H}}_\alpha : \mathbb {F}_{2^s}^{m/s} \rightarrow \mathbb {F}_{2^s}, \quad {\mathbf {H}}_\alpha (x_1,\dots ,x_{m/s}) = \alpha \cdot x_1 + \alpha ^2 \cdot x_2 + \dots + \alpha ^{m/s} \cdot x_{m/s} \end{aligned}$$

  Note that by viewing elements of $\mathbb {F}_{2^s}$ as vectors in $\mathbb {F}_2^s$, multiplication by a fixed field element $\alpha ^i \in \mathbb {F}_{2^s}$ is linear over $\mathbb {F}_2$. Therefore, ${\mathbf {H}}_\alpha$ can be seen as an $\mathbb {F}_2$-linear map, represented by a unique matrix in $\mathbb {F}_2^{s \times m}$.

Here, the seed is short, but the computational complexity is $O(m \cdot s)$. However, in practice when $s = 128$ the finite field multiplications can be performed very efficiently in hardware on modern CPUs. Note that this gives a 1-universal family with $\varepsilon =\frac{m}{s} \cdot 2^{-s}$. This can be improved to $2^{-s}$ (i.e. perfect), at the cost of a larger seed, by using m / s distinct elements $\alpha _i$, instead of powers of $\alpha$.

2.3 Commitment Functionality

We require a UC commitment functionality $\mathcal {F}_{\scriptstyle \mathrm {Commit}}$ (Fig. 1). This can easily be implemented in the random oracle model by defining $\mathtt {Commit}(x,P_i) = \mathsf {H}(x, i, r)$, where $\mathsf {H}$ is a random oracle and $r \leftarrow \{0,1\}^\kappa$.

Fig. 1.

Ideal commitments

2.4 Coin-Tossing Functionality

We use a standard coin-tossing functionality, $\mathcal {F}_{\scriptstyle \mathrm {Rand}}$ (Fig. 2), which can be implemented with UC commitments to random values.

Fig. 2.

Coin-tossing functionality

2.5 Correlated Oblivious Transfer

In this work we use an actively secure protocol for oblivious transfer (OT) on correlated pairs of strings of the form $(a_i, a_i \oplus \varDelta )$, where $\varDelta$ is fixed for every OT. The TinyOT protocol [33] for secure two-party computation constructs such a protocol, and a significantly optimized version of this is given in [34]. The communication cost is roughly $\kappa + s$ bits per OT. The ideal functionality is shown in Fig. 3.

Fig. 3.

Fixed correlation oblivious transfer functionality

2.6 Functionality for Secret-Sharing-Based MPC

We make use of a general, actively secure protocol for secret-sharing-based MPC for binary circuits, which is modeled by the functionality $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$ in Fig. 4. This functionality allows parties to provide private inputs, which are then stored and can be added or multiplied internally by $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$, and revealed if desired. Note that we also need the Multiply command to output a random additive secret-sharing of the product to all parties; this essentially assumes that the underlying protocol is based on secret-sharing.

We use the notation $\langle x \rangle$ to represent a secret-shared value x that is stored internally by $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$, and define $x^i$ to be party $P_i$’s additive share of x (if it is known). We also define the $+$ and $\cdot$ operators on two shared values $\langle x \rangle , \langle y \rangle$ to call the Add and Multiply commands of $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$, respectively, and return the identifier associated with the result.

Fig. 4.

Functionality for GMW-style MPC for binary circuits

2.7 BMR Garbling

The [2] garbling technique by Beaver, Micali and Rogaway involves garbling each gate separately using pseudorandom generators while ensuring consistency between the wires. This method was recently improved in a sequence of works [4, 29, 31], where the latter work further supports the free XOR property. The main task of generating the garbled circuit while supporting this property is to compute, for each AND gate g with input wires u, v and output wire w, the 4n values:

$$\begin{aligned} \tilde{g}^j_{a,b} =&\left( \bigoplus _{i=1}^n F_{k^i_{u,a},k^i_{v,b}}(g \Vert j)\right) \oplus k^j_{w,0} \\ \oplus&\left( R^j \cdot ((\lambda _u \oplus a) \cdot (\lambda _v \oplus b) \oplus \lambda _w)\right) , \nonumber \quad (a,b) \in \{0,1\}^2, \; j \in [n] \nonumber \end{aligned}$$

(2)

where the wire masks $\lambda _u, \lambda _v, \lambda _w \in \{0,1\}$ are secret-shared between all parties, while the PRF keys $k^j_{u,a}, k^j_{v,b}$ and the global difference string $R^j$ are known only to party $P_j$.

3 Generic Protocol for Multi-party Garbling

We now describe our generic method for creating the garbled circuit using any secret-sharing based MPC protocol (modeled by $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$) and the correlated OT functionality $\mathcal {F}_{\scriptstyle \mathrm {COT}}$. We first describe the functionality in Sect. 3.1 and the protocol in Sect. 3.2, and then analyse its security in Sect. 3.4.

3.1 The Preprocessing Functionality

The preprocessing functionality, formalized in Fig. 5, captures the generation of the garbled circuit as well as an error introduced by the adversary. The adversary is allowed to submit an additive error, chosen adaptively after seeing the garbled circuit, that is added by the functionality to each entry when the garbled circuit is opened.

Fig. 5.

The preprocessing functionality $\mathcal {F}_{\scriptstyle \mathrm {Prepocessing}}$

3.2 Protocol Overview

The garbling protocol, shown in Fig. 6, proceeds in three main stages. Firstly, the parties locally sample all of their keys and shares of wire masks for the garbled circuit. Secondly, the parties compute shares of the products of the wire masks and each party’s global difference string; these are then used by each party to locally obtain a share of the entire garbled circuit. Finally, the bit masks for the output wires are opened to all parties. The opening of the garbled circuit is shown in Fig. 7.

Concretely, each party $P_i$ starts by sampling a global difference string $R^i \leftarrow \{0,1\}^\kappa$, and for each wire w which is an output wire of an AND gate, or an input wire, $P_i$ also samples the keys $k^i_{w,0}$, $k^i_{w,1} = k^i_{w,0} \oplus R^i$ and an additive share of the wire mask, $\lambda _w^i \leftarrow \mathbb {F}_2$. As in [4], we let $P_i$ input the actual wire mask (instead of a share) for every input wire associated with $P_i$’s input.

In step 3, the parties compute additive shares of the bit products $\lambda _{uv} = \lambda _u \cdot \lambda _v \in \mathbb {F}_2$, and then, for each $j \in [n]$, shares of:

$$\begin{aligned} \lambda _u \cdot R^j, \quad \lambda _v \cdot R^j, \quad \lambda _{uvw} \cdot R^j \in \mathbb {F}_2^\kappa \end{aligned}$$

(3)

where $\lambda _{uvw} := \lambda _{uv} \oplus \lambda _w$, and u, v and w are the input and output wires of AND gate g. We note that (as observed in [4]) only one bit/bit product and 3n bit/string products are necessary, even though each gate has 4n entries, due to correlations between the entries, as can be seen below.

Fig. 6.

The preprocessing protocol that realizes $\mathcal {F}_{\scriptstyle \mathrm {Prepocessing}}$ in the $\{\mathcal {F}_{\scriptstyle \mathrm {COT}}, \mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}, \mathcal {F}_{\scriptstyle \mathrm {Rand}}\, \mathcal {F}_{\scriptstyle \mathrm {Commit}}\}$-hybrid model.

We compute the bit multiplications using the $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$ functionality on the bits that are already stored by $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$. To compute the bit/string multiplications in (3), we use correlated OT, followed by a consistency check to verify that the parties provided the correct shares of $\lambda _w$ and correlation $R^i$ to each $\mathcal {F}_{\scriptstyle \mathrm {COT}}$ instance; see Sect. 3.3 for details.

Using shares of the bit/string products, the parties can locally compute an unauthenticated additive share of the entire garbled circuit (steps 3d–4). First, for each of the four values $(a,b) \in \{0,1\}^2$, each party $P_i, i \ne j$ computes the share

$$ \rho ^i_{j, a, b} = {\left\{ \begin{array}{ll} a \cdot (\lambda _v \cdot R^j)^i \oplus b \cdot (\lambda _{u} \cdot R^j)^i \oplus (\lambda _{uvw}\cdot R^j)^i &{} \text { if } i \ne j \\ a \cdot (\lambda _v \cdot R^j)^i \oplus b \cdot (\lambda _{u} \cdot R^j)^i \oplus (\lambda _{uvw}\cdot R^j)^i \oplus a \cdot b \cdot R^j &{} \text { if } i = j \\ \end{array}\right. } $$

These define additive shares of the values

$$ \begin{aligned} \rho _{j,a,b}&= R^j \cdot (a \cdot \lambda _v \oplus b \cdot \lambda _u \oplus \lambda _{uvw} \oplus a\cdot b) \\&= R^j \cdot ((\lambda _u \oplus a) \cdot (\lambda _v \oplus b) \oplus \lambda _w) \\ \end{aligned} $$

Each party’s share of the garbled circuit is then obtained by adding the appropriate PRF values and keys to the shares of each $\rho _{j,a,b}$. To conclude the Garbling stage, the parties reveal the masks for all output wires using $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$, so that the outputs can be obtained in the online phase.

Fig. 7.

Open garbling stage of the preprocessing protocol.

Before opening the garbled circuit, the parties must rerandomize their shares by distributing a fresh, random secret-sharing of each share to the other parties, via private channels. This is needed so that the shares do not leak any information on the PRF values, so we can prove security. This may seem unnecessary, since the inclusion of the PRF values in the shares should randomize them sufficiently. However, we cannot prove this intuition, as the same PRF values are used to compute the garbled circuit that is output by the protocol, so they cannot also be used as a one-time pad.¹ In steps 1 to 2 of Fig. 7, we show how to perform this extra rerandomization step with $O(n^2 \cdot \kappa )$ communication.

Finally, to reconstruct the garbled circuit, the parties sum up and broadcast the rerandomized shares and add them together to get $\tilde{g}^j_{a,b}$.

3.3 Bit/String Multiplications

Our method for this is in the subrotocol $\varPi _{\scriptstyle \mathrm {Bit\times String}}$ (Fig. 8). It proceeds in two stages: first the Multiply step creates the shared products, and then the Consistency Check verifies that the correct inputs were used to create the products.

Recall that the task is for the parties to obtain an additive sharing of the products, for each $j \in [n]$ and $(a,b) \in \{0,1\}^2$:

$$\begin{aligned} R^j \cdot ((\lambda _u \oplus a) \cdot (\lambda _v \oplus b) \oplus \lambda _w) \end{aligned}$$

(4)

where the string $R^j$ is known only to $P_j$, and fixed for every gate. Denote by x one of the additively shared $\lambda _{(\cdot )}$ bits used in a single bit/string product and stored by $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$. We obtain shares of $x \cdot R^j$ using actively secure correlated OT (cf. Fig. 3), as follows:

• 1. For each $i \ne j$, parties $P_i$ and $P_j$ run a correlated OT, with choice bit $x^i$ and correlation $R^j$. $P_i$ obtains $T_{i,j}$ and $P_j$ obtains $Q_{i,j}$ such that:

  $$\begin{aligned} T_{i,j} = Q_{i,j} + x^i \cdot R^j. \end{aligned}$$

• 2. Each $P_i$, for $i \ne j$, defines the share $Z^i = T_{i,j}$, and $P_j$ defines $Z^j = \sum _{i \ne j} Q_{i,j} + x^j \cdot R^j$. Now we have:

  $$ \begin{aligned} \sum _{i=1}^n Z^i&= \sum _{i \ne j} T_{i,j} + \sum _{i \ne j}Q_{i,j} + x^j \cdot R^j&= \sum _{i \ne j}(T_{i,j} + Q_{i,j}) + x^j \cdot R^j&= x \cdot R^j \end{aligned} $$

  as required.

The above method is performed $3|G |$ times and for each $P_j$, to produce the shared bit/string products $x \cdot R^j$, for $x \in \{\lambda _{u},\lambda _{v},\lambda _{uv}\}$.

Fig. 8.

Subprotocol for bit/string multiplication and checking consistency

3.4 Consistency Check

We now show how the parties verify that the correct shares of x and correlations $R^j$ were used in the correlated OTs, and analyse the security of this check. The parties first create $m+s$ bit/string products, where m is the number of products needed and s is a statistical security parameter, and then open random linear combinations (over $\mathbb {F}_2$) of all the products and check correctness of the opened results. This is possible because the products are just a linear function of the fixed string $R^j$. In more detail, the parties first sample a random $\varepsilon$-almost 1-universal hash function ${\mathbf {H}}\leftarrow \mathbb {F}_2^{m\times s}$, and then open

$${\varvec{c}}_x = {\mathbf {H}}\cdot {\varvec{x}}+ \hat{{\varvec{x}}}$$

using $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$. Here, ${\varvec{x}}$ is the vector of all m wire masks to be multiplied, whilst $\hat{\varvec{x}}\in \mathbb {F}_2^s$ are the additional, random masking bits, used as a one-time pad to ensure that ${\varvec{c}}_x$ does not leak information on ${\varvec{x}}$.

To verify that a single shared matrix ${\mathbf {Z}}_j$ is equal to ${\varvec{x}}\otimes R^j$ (as in Fig. 8), each party $P_i$, for $i \ne j$, then commits to ${\mathbf {H}}\cdot {\mathbf {Z}}_j^i$, whilst $P_j$ commits to ${\mathbf {H}}\cdot {\mathbf {Z}}_j^i + {\varvec{c}}_x \otimes R^j$. The parties then open all commitments and check that these sum to zero, which should happen if the products were correct.

The intuition behind the check is that any errors present in the original bit/string products will remain when multiplied by ${\mathbf {H}}$, except with probability $\varepsilon$, by the almost-1-universal property (Definition 22). Furthermore, it turns out that cancelling out any non-zero errors in the check requires either guessing an honest party’s global difference $R^j$, or guessing the secret masking bits $\hat{{\varvec{x}}}$.

We formalize this, by first considering the exact deviations that are possible by a corrupt $P_j$ in $\varPi _{\scriptstyle \mathrm {Bit\times String}}$. These are:

• 1. Provide inconsistent inputs $R^j$ when acting as sender in the Initialize command of the $\mathcal {F}_{\scriptstyle \mathrm {COT}}$ instances with two different honest parties.

• 2. Input an incorrect share $x^j$ when acting as receiver in the Extend command of $\mathcal {F}_{\scriptstyle \mathrm {COT}}$.

Note that in both of these cases, we are only concerned when the other party in the $\mathcal {F}_{\scriptstyle \mathrm {COT}}$ execution is honest, as if both parties are corrupt then $\mathcal {F}_{\scriptstyle \mathrm {COT}}$ does not need to be simulated in the security proof.

We model these two attacks by defining $R^{j,i}$ and $x^{j,i}$ to be the actual inputs used by a corrupt $P_j$ in the above two cases, and then define the errors (for $j \in I$ and $i \notin I$):

$$\begin{aligned} \varDelta ^{j,i}&= R^{j,i} + R^j \\ \delta ^{j,i}_\ell&= x^{j,i}_\ell + x^j_\ell , \quad \ell \in [3|G |]. \\ \end{aligned} $$

Note that $\varDelta ^{j,i}$ is fixed in the initialization of $\mathcal {F}_{\scriptstyle \mathrm {COT}}$, whilst $\delta ^{j,i}_\ell$ may be different for every OT. Whenever $P_i$ and $P_j$ are both corrupt, or both honest, for convenience we define $\varDelta ^{j,i} = 0$ and $\delta ^{j,i} = 0$.

This means that the outputs of $\mathcal {F}_{\scriptstyle \mathrm {COT}}$ with $(P_i,P_j)$ then satisfy (omitting $\ell$ subscripts):

$$\begin{aligned} t_{i,j} = q_{i,j} + x^i \cdot R^j + \delta ^{i,j} \cdot R^j + \varDelta ^{j,i}\cdot x^i \end{aligned}$$

where $\delta ^{i,j} \ne 0$ if $P_i$ cheated, and $\varDelta ^{j,i} \ne 0$ if $P_j$ cheated.

Now, as in step 1 of the first stage of $\varPi _{\scriptstyle \mathrm {Bit\times String}}$, we can put the $\mathcal {F}_{\scriptstyle \mathrm {COT}}$ outputs for each party into the rows of a matrix, and express the above as:

$$\begin{aligned} {\mathbf {T}}_{i,j} = {\mathbf {Q}}_{i,j} + {\varvec{x}}^i \otimes R^j + {\varvec{\delta }}^{i,j} \otimes R^j + \varDelta ^{j,i}\otimes x^i \end{aligned}$$

where ${\varvec{\delta }}^{j,i} = (\delta ^{j,i}_1, \dots , \delta ^{j,i}_{3|G |})$, and the tensor product notation is defined in Sect. 2.

Accounting for these errors in the outputs of the Multiply step in $\varPi _{\scriptstyle \mathrm {Bit\times String}}$, we get:

$$\begin{aligned} {\mathbf {Z}}_j = \sum _{i=1}^n {\mathbf {Z}}_j^i = {\varvec{x}}\otimes R^j + R^j \cdot \underbrace{\sum _{i\in I} {\varvec{\delta }}^{i,j}}_{={\varvec{\delta }}^j} + \sum _{i \notin I} x_i \cdot \varDelta ^{j,i}. \end{aligned}$$

(5)

The following lemma shows if a party cheated, then to pass the check they must either guess all of the shares $\hat{{\varvec{x}}}^i \in \mathbb {F}_2^s$ for some honest $P_i$, or guess $P_i$’s global difference $R^i$ (except with negligible probability over the choice of the $\varepsilon$-almost 1-universal hash function, ${\mathbf {H}}$).

Lemma 31

If the check in $\varPi _{\scriptstyle \mathrm {Bit\times String}}$ passes, then except with probability $\max (2^{-s}, \varepsilon + 2^{-\kappa })$, all of the errors ${\varvec{\delta }}^{j},\varDelta ^{i,j}$ are zero.

The proof can be found in the full version of the paper [20].

We now give some intuition behind the security of the whole protocol. In the proof, the strategy of the simulator is to run an internal copy of the protocol, using dummy, random values for the honest parties’ keys and wire mask shares. All communication with the adversary is simulated by computing the correct messages according to the protocol and the dummy honest shares, until the final output stage. In the output stage, we switch to fresh, random honest parties’ shares, consistent with the garbled circuit received from $\mathcal {F}_{\scriptstyle \mathrm {Prepocessing}}$ and the corrupt parties’ shares.

Firstly, by Lemma 31, it holds that in the real execution, if the adversary introduced any non-zero errors then the consistency check fails with overwhelming probability. The same is true in the ideal execution; note that the errors are still well-defined in this case because the simulator can compute them by comparing all inputs received to $\mathcal {F}_{\scriptstyle \mathrm {COT}}$ with the inputs the adversary should have used, based on its random tape. This implies that the probability of passing the check is the same in both worlds. Also, if the check fails then both executions abort, and it is straightforward to see that the two views are indistinguishable because no outputs are sent to honest parties (hence, also the environment).

It remains to show that the two views are indistinguishable when the consistency check passes, and the environment sees the outputs of all honest parties, as well as the view of the adversary during the protocol. The main point of interest here is the output stage. We observe that, without the final rerandomization step, the honest parties’ shares of the garbled circuit would not be uniformly random. Specifically, consider an honest $P_i$’s share, $(\tilde{g}^j_{a,b})^i$, where $P_j$ is corrupt. This is computed by adding some PRF value, v, to the $\mathcal {F}_{\scriptstyle \mathrm {COT}}$ outputs where $P_i$ was receiver and $P_j$ was sender (step 2 of $\varPi _{\scriptstyle \mathrm {Bit\times String}}$). Since $P_j$ knows both strings in each OT, there are only two possibilities for $P_i$’s output (depending on the choice bit), so this is not uniformly random. It might be tempting to argue that v is a random PRF output, so serves as a one-time pad, but this proof attempt fails because v is also used to compute the final garbled circuit. In fact, it seems difficult to rely on any reduction to the PRF, since all the PRF keys are included in the output to the environment. To avoid this issue, we need the rerandomization step using a PRG, and the additional assumption of secure point-to-point channels.

Theorem 31

Protocol $\varPi _{\scriptstyle \mathrm {Preprocessing}}$ from Fig. 6 UC-securely computes $\mathcal {F}_{\scriptstyle \mathrm {Prepocessing}}$ from Fig. 5 in the presence of a static, active adversary corrupting up to $n-1$ parties in the $\{\mathcal {F}_{\scriptstyle \mathrm {COT}}, \mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}, \mathcal {F}_{\scriptstyle \mathrm {Rand}},\mathcal {F}_{\scriptstyle \mathrm {Commit}}\}$-hybrid model.

The proof can be found in the full version of the paper [20].

4 More Efficient Garbling with Multi-party TinyOT

We now describe a less general, but concretely more efficient, variant of the protocol in the previous section. We replace the generic $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$ functionality with a more specialized one based on ‘TinyOT’-style information-theoretic MACs. This is asymptotically worse, but more practical, than using [21] for $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$. It also allows us to completely remove the bit/string multiplications and consistency checks in $\varPi _{\scriptstyle \mathrm {Bit\times String}}$, since we show that these can be obtained directly from the TinyOT MACs. This means the only cost in the protocol, apart from opening and evaluating the garbled circuit, is the single bit multiplication per AND gate in the underlying TinyOT-based protocol.

In the full version of this paper [20], we present a complete description of a suitable TinyOT-based protocol. This is done by combining the multiplication triple generation protocol (over $\mathbb {F}_2$) from [17] with a consistency check to enforce correct shared random bits, which is similar to the more general check from the previous section.

4.1 Secret-Shared MAC Representation

For $x \in \{0,1\}$ held by $P_i$, define the following two-party MAC representation, as used in 2-party TinyOT [33]:

$$\begin{aligned}{}[x]_{i,j} = (x, M_j^i, K_i^j), \qquad M_j^i = K_i^j + x \cdot R^j \end{aligned}$$

where $P_i$ holds x and a MAC $M^i_j$, and $P_j$ holds a local MAC key $K_i^j$, as well as the fixed, global MAC key $R^j$.

Similarly, we define the n-party representation of an additively shared value $x = x^1 + \dots + x^n$:

$$\begin{aligned}{}[x] = (x^i, \{M_j^i, K_j^i\}_{j \ne i})_{i \in [n]}, \quad M_j^i = K_i^j + x^i \cdot R^j \end{aligned}$$

where each party $P_i$ holds the $n-1$ MACs $M_j^i$ on $x^i$, as well as the keys $K^i_j$ on each $x^j$, for $j \ne i$, and a global key $R^i$. Note that this is equivalent to every pair $(P_i,P_j)$ holding a representation $[x^i]_{i,j}$.

The key observation for this section, is that a sharing [x] can be used to directly compute shares of all the products $x \cdot R^j$, as in the following claim.

Claim 41

Given a representation [x], the parties can locally compute additive shares of $x \cdot R^j$, for each $j \in [n]$.

Proof

Write $[x] = (x^i, \{M_j^i, K_j^i\}_{j \ne i})_{i \in [n]}$. Each party $P_i$ defines the n shares:

$$ \begin{aligned} Z_i^i&= x^i \cdot R^i + \sum _{j \ne i} K_{j}^{i} \quad \text { and} \quad Z_j^i&= M_{j}^i, \quad \text { for each } j \ne i \end{aligned} $$

We then have, for each $j \in [n]$:

We define addition of two shared values [x], [y], to be straightforward addition of the components. We define addition of [x] with a public constant $c \in \mathbb {F}_2$ by:

• $P_1$ stores: $(x^1 + c, \{M_j^1, K_j^1\}_{j \ne 1})$

• $P_i$ stores: $(x^i, (M_1^i, K_1^i + c \cdot R^i), \{M_j^i,K_j^i\}_{j \in [n] \setminus \{1,i\}})), \quad \text { for } i \ne 1$

This results in a correct sharing of $[x + c]$.

We can create a sharing of the product of two shared values using a random multiplication triple ([x], [y], [z]) such that $z = x \cdot y$ with Beaver’s technique [1].

4.2 MAC-Based MPC Functionality

The functionality , which we use in place of $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$ for the optimized preprocessing, is shown in the full version [20]. It produces authenticated sharings of random bits and multiplication triples. For both of these, first receives corrupted parties’ shares, MAC values and keys from the adversary, and then randomly samples consistent sharings and MACs for the honest parties.

Another important aspect of the functionality is the Key Queries command, which allows the adversary to try to guess the MAC key $R^i$ of any party, and will be informed if the guess is correct. This is needed to allow the security proof to go through; we explain this in more detail in the full version. In that section we also present a complete description of a variant on the multi-party TinyOT protocol, which can be used to implement this functionality.

4.3 Garbling with $\mathcal {F}_{{\text {n}} \text {-} {\text {TinyOT}}}$

Following from the observation in Claim 41, if each party $P_j$ chooses the global difference string in $\varPi _{\scriptstyle \mathrm {Preprocessing}}$ to be the same $R^j$ as in the MAC representation, then given $[\lambda ]$, additive shares of the products $\lambda \cdot R^j$ can be obtained at no extra cost. Moreover, the shares are guaranteed to be correct, and the honest party’s shares will be random (subject to the constraint that they sum to the correct value), since they come directly from the functionality. This means there is no need to perform the consistency check, which greatly simplifies the protocol.

The rest of the protocol is mostly the same as $\varPi _{\scriptstyle \mathrm {Preprocessing}}$ in Fig. 6, using with $[\cdot ]$-sharings instead of $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$ with $\langle \cdot \rangle$-sharings. One other small difference is that because does not have a private input command, we instead sample $[\lambda _w]$ shares for input wires using random bits, and later use a private output protocol to open the relevant input wire masks to $P_i$. This change is not strictly necessary, but simplifies the protocol for implementing —if also had an Input command for sharing private inputs based on , it would be much more complex to implement with the correct distribution of shares and MACs.

In more detail, the Garbling phase proceeds as follows.

• 1. Each party obtains a random key offset $R^i$ by calling the Initialize command of .

• 2. For every wire w which is an input wire, or the output wire of an AND gate, the parties obtain a shared mask $[\lambda _w]$ using the Bit command of .

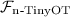• 3. All the wire keys $k^i_{w,0}, k^i_{w,1} = k^i_{w,0} \oplus R^i$ are defined by $P_i$ the same way as in $\varPi _{\scriptstyle \mathrm {Preprocessing}}$.

• 4. For XOR gates, the output wire mask is computed as $[\lambda _w] = [\lambda _u] + [\lambda _v]$.

• 5. For each AND gate, the parties compute $[\lambda _{uv}] = [\lambda _u \cdot \lambda _v]$.

• 6. The parties then obtain shares of the garbled circuit as follows:

  • For each AND gate $g \in G$ with wires (u, v, w), the parties use Claim 41 with the shared values $[\lambda _u], [\lambda _v], [\lambda _{uv} + \lambda _w]$, to define, for each $j \in [n]$, shares of the bit/string products:

    $$\begin{aligned} \lambda _u \cdot R^j, \quad \lambda _v \cdot R^j, \quad (\lambda _{uv} + \lambda _w)\cdot R^j \end{aligned}$$

  • These are then used to define shares of $\rho _{j,a,b}$ and the garbled circuit, as in the original protocol.

• 7. For every circuit-output-wire w, the parties run $\varPi _{\scriptstyle \mathrm {Open}}$ to reveal $\lambda _w$ to all the parties.

• 8. For every circuit input wire w corresponding to party $P_i$’s input, the parties run $\varPi _{\scriptstyle \mathrm {Open}}^i$ to open $\lambda _w$ to $P_i$.

The only interaction introduced in the new protocol is in the multiply and opening protocols, which were abstracted away by $\mathcal {F}_{\scriptstyle \mathrm {Bit MPC}}$ in the previous protocol. Simulating and proving security of these techniques is straightforward, due to the correctness and randomness of the multiplication triples and MACs produced by . One important detail is the Key Queries command of the functionality, which allows the adversary to try to guess an honest party’s global MAC key share, $R^i$, and learn if the guess is correct. To allow the proof to go through, we modify $\mathcal {F}_{\scriptstyle \mathrm {Prepocessing}}$ to also have a Key Queries command, so that the simulator can use this to respond to any key queries from the adversary. We denote this modified functionality by $\mathcal {F}_{\scriptstyle \mathrm {Prepocessing}}^\mathrm{{KQ}}$.

The following theorem can be proven, similarly to the proof of Theorem 31 where we modify the preprocessing functionality to support key queries, and adjust the simulation as described above.

Theorem 41

The modified protocol described above UC-securely computes $\mathcal {F}_{\scriptstyle \mathrm {Prepocessing}}^\mathrm{{KQ}}$ from Fig. 5 in the presence of a static, active adversary corrupting up to $n-1$ parties in the -hybrid model.

5 The Online Phase

Our final protocol, presented in Fig. 9, implements the online phase where the parties reveal the garbled circuit’s shares and evaluate it. Our protocol is presented in the $\mathcal {F}_{\scriptstyle \mathrm {Prepocessing}}$-hybrid model. Upon reconstructing the garbled circuit and obtaining all input keys, the process of evaluation is similar to that of [39], except here all parties run the evaluation algorithm, which involves each party computing $n^2$ PRF values per gate. During evaluation, the parties only see the randomly masked wire values and cannot determine the actual wire values. Upon completion, the parties compute the actual output using the output wire masks revealed from $\mathcal {F}_{\scriptstyle \mathrm {Prepocessing}}$. We conclude with the following theorem.

Fig. 9.

The MPC protocol - $\varPi _{\scriptstyle \mathrm {MPC}}$

Theorem 51

Let f be an n-party functionality $\{0,1\}^{n\kappa }\mapsto \{0,1\}^\kappa$ and assume that F is a PRF. Then Protocol $\varPi _{\scriptstyle \mathrm {MPC}}$ from Fig. 9, UC-securely computes f in the presence of a static, active adversary corrupting up to $n-1$ parties in the $\mathcal {F}_{\scriptstyle \mathrm {Prepocessing}}$-hybrid.

Proof overview. Our proof follows by first demonstrating that the adversary’s view is computationally indistinguishable in both real and simulated executions. To be concrete, we consider an event for which the adversary successfully causes the bit transferred through some wire to be flipped and prove that this event can only occur with negligible probability (our proof is different to the proof in [29] as in our case the adversary may choose its additive error as a function of the garbled circuit). Then, conditioned on the event flip not occurring, we prove that the two executions are computationally indistinguishable via a reduction to the correlation robust PRF, inducing a garbled circuit that is indistinguishable. The complete proof can be found in the full version of the paper [20].

6 Performance

In this section we present implementation results for our protocol from Sect. 4 for up to 9 parties. We also analyse the concrete communication complexity of the protocol and compare this with previous, state-of-the-art protocols in a similar setting.

We have made a couple of tweaks to our protocol to simplify the implementation. We moved the Open Garbling stage to the preprocessing phase, instead of the online phase. This optimizes the online phase so that the amount of communication is independent of the size of the circuit. This change means that our standard model security proof would no longer apply, but we could prove it secure using a random oracle instead of the circular-correlation robust PRF, similarly to [3, 30]. Secondly, when not working in a modular fashion with a separate preprocessing functionality, the share rerandomization step in the output stage is not necessary to prove security of the entire protocol, so we omit this.

6.1 Implementation

We implemented our variant of the multi-party TinyOT protocol (given in the full version) using the libOTe library [36] for the fixed-correlation OTs and tested it for between 3 and 9 parties. We benchmarked the protocol over a 1 Gbps LAN on 5 servers with 2.3 GHz Intel Xeon CPUs with 20 cores. For the experiments with more than 5 parties, we had to run more than one party per machine; this should not make much difference in a LAN, as the number of threads being used was still fewer than the number of cores. As benchmarks, we measured the time for securely computing the circuits for AES (6800 AND gates) and SHA-256 (90825 AND gates).

For the TinyOT bit and triple generation, every pair of parties needs two correlated OT instances running between them (one in each direction). We ran each OT instance in a separate thread with libOTe, so that each party uses $2(n-1)$ OT threads. This gave a small improvement (${\approx }6\%$) compared with running $n-1$ threads. We also considered a multiple execution setting, where many (possibly different) secure computations are evaluated. Provided the total number of AND gates in the circuits being evaluated is at least $2^{20}$, this allows us to generate the TinyOT triples for all executions at once using a bucket size of $B=3$, compared with $B=5$ for one execution of AES or $B=4$ for one execution of SHA-256. Since the protocol scales with $B^2$, this has a big impact on performance. The results for 9 parties, for the different choices of B, are shown in Table 2.

Table 2. Runtimes in ms for AES and SHA-256 evalution with 9 parties

Fig. 10.

AES performance (6800 AND gates).

Fig. 11.

SHA-256 performance (90825 AND gates).

Figures 10 and 11 show how the performance of AES and SHA-256 scales with different numbers of parties, in the amortized setting. Although the asymptotic complexity is quadratic, the runtimes grow relatively slowly as the number of parties increases. This is because in the preprocessing phase, the amount of data sent per party is actually linear. However, the super-linear trend is probably due to the limitations of the total network capacity, and the computational costs.

Comparison with other works. We calculated the cost of computing the SPDZ-BMR protocol [29] using [24] to derive estimates for creating the SPDZ triples (the main cost). Using MASCOT over $\mathbb {F}_{2^\kappa }$ with free-XOR, SPDZ-BMR requires $3n+1$ multiplications per garbled AND gate. This gives an estimated cost of at least 14 s to evaluate AES, which is over 20x slower than our protocol.

The only other implementation of actively secure, constant-round, dishonest majority MPC is the concurrent work of [23], which presents implementation figures for up to 256 parties running on Amazon servers. Their runtimes with 9 parties in a LAN setting are around 200 ms for AES and 2200 ms for SHA-256, which is around 3 times faster than our results. However, their LAN setup has 10Gbps bandwidth, whereas we only tested on machines with 1Gbps bandwidth. Since the bottleneck in our implementation is mostly communication, it seems that our implementation could perform similar to or even faster than theirs in the same environment, despite our higher communication costs. However, it is not possible to make an accurate comparison without testing both implementations in the same environment.

Compared with protocols based solely on secret-sharing, such as SPDZ and TinyOT, the advantage of our protocol is the low round complexity. We have not yet managed to benchmark our protocol in a WAN setting, but since our total round complexity is less than 20, it should perform reasonably fast. With secret-sharing, using e.g. TinyOT, evaluating the AES circuit requires at least 40 rounds in just the online phase (it can be done with 10 rounds [14], but this uses a special representation of the AES function, rather than a general circuit), whilst computing the SHA-256 circuit requires 4000 rounds. In a network with 100 ms delay between parties, the AES online time alone would be at least 4 s, whilst SHA-256 would take over 10 min to securely compute in that setting. If our protocol is run in this setting, we should be able to compute both AES and SHA-256 in just a few seconds (assuming that latency rather than bandwidth is the bottleneck).

6.2 Communication Complexity Analysis

We now focus on analysing the concrete communication complexity of the optimized variant of our protocol and compare it with the state of the art in constant-round two-party and multi-party computation protocols. We have not implemented our protocol, but since the underlying computational primitives are very simple, the communication cost will be the overall bottleneck. As a benchmark, we estimate the cost of securely computing the AES circuit (6800 AND gates, 25124 XOR gates), where we assume that one party provides a 128-bit plaintext or ciphertext and the rest of them have an XOR sharing of a 128-bit AES key. This implies we have $128 \cdot n$ input wires and an additional layer of XOR gates in the circuit to add the key shares together. We consider a single set of 128 output wires, containing the final encrypted or decrypted message.

Table 3. Communication estimates for secure AES evaluation with our protocol and previous works in the two-party setting. Cost is the maximum amount of data sent by any one party, per execution.

Two Parties. In Table 3 we compare the cost of our protocol in the two-party case, with state-of-the-art secure two-party computation protocols. We instantiate our TinyOT-based preprocessing method with the optimized, two-party TinyOT protocol from [38], lowering the previous costs further. For consistency with the other two-party protocols, we divide the protocol costs into three phases: function-independent preprocessing, which only depends on the size of the circuit; function-dependent preprocessing, which depends on the exact structure of the circuit; and the online phase, which depends on the parties’ inputs. As with the implementation, we move the garbled circuit opening to the function-dependent preprocessing, to simplify the online phase.

The online phase of the modified protocol is just two rounds of interaction, and has the lowest online cost of any actively secure two-party protocol.² The main cost of the function-dependent preprocessing is opening the garbled circuit, which requires each party to send $8\kappa$ bits per AND gate. This is slightly larger than the best Yao-based protocols, due to the need for a set of keys for every party in BMR.

In the batch setting, where many executions of the same circuit are needed, protocols such as [37] clearly still perform the best. However, if many circuits are required, but they may be different, or not known in advance, then our multi-party protocol is highly competitive with two-party protocols.

Comparison with Multi-party Protocols. In Table 4 we compare our work with previous constant-round protocols suitable for any number of parties, again for evaluating the AES circuit. We do not present the communication complexity of the online phase as we expect it to be very similar in all of the protocols. We denote by MASCOT-BMR-FX an optimized variant of [29], modified to use free-XOR as in our protocol, with multiplications done using the OT-based MASCOT protocol [24].

Table 4. Comparison of the cost of our protocol with previous constant-round MPC protocols in a range of security models, for secure AES evaluation. Costs are the amount of data sent over the network per party.

As in the previous section, we move the cost of opening the garbled circuit to the preprocessing phase for all of the presented protocols (again relying on random oracles). By applying this technique the online phase of our work is just two rounds, and has exactly the same complexity as the current most efficient semi-honest constant-round MPC protocol for any number of parties [4], except we achieve active security. We see that with respect to other actively secure protocols, we improve the communication cost of the preprocessing by around 2–4 orders of magnitude. Moreover, our protocol scales much better with n, since the complexity is $O(n^2)$ instead of $O(n^3)$. The concurrent work of Katz et al. [23] requires around 3 times less communication than our protocol, which is due to their optimized version of the multi-party TinyOT protocol.