CVA with Wrong-Way Risk in the Presence of Early Exercise

Abstract

Hull–White approach of CVA with embedded WWR (Hull and White, Financ. Anal. J. 68:58-69, 2012, [11]) can be easily applied also to portfolios of derivatives with early termination features. The tree-based approach described in Baviera et al. (Int. J. Financ. Eng. 2015, [1]) allows to deal with American or Bermudan options in a straightforward way. Extensive numerical results highlight the nontrivial impact of early exercise on CVA.

1 Introduction

As a direct consequence of the 2008 financial turmoil, counterparty credit risk has become substantial in OTC derivatives transactions. In particular, the credit value adjustment (CVA) is meant to measure the impact of counterparty riskiness on a derivative portfolio value as requested by the current Basel III regulatory framework. Accounting standards (IFRS 13, FAS 157), moreover, require a CVA¹ adjustment as part of a consistent fair value measurement of financial instruments.

CVA is strongly affected by derivative transaction arrangements: exposure depends on collateral and netting agreement between the two counterparties that have written the derivative contracts of interest. Despite the increased use of collateral, however, a significant portion of OTC derivatives remains uncollateralized. This is mainly due to the nature of the counterparties involved, such as corporates and sovereigns, without the liquidity and operational capacity to adhere to daily collateral calls. In such cases, an institution must consider the impact of counterparty risk on the overall portfolio value and a correct CVA quantification acquires even more importance. Extensive literature has been produced on the topic in recent years, as for example [5] and [9] that give a comprehensive overview of CVA computation and the more general topic of counterparty credit risk management. It seems, however, that attention has been mainly paid to CVA with respect to portfolios of European-style derivatives. Dealing with derivatives with early exercise features is even more delicate. Indeed, as pointed out in [3], for American- and Bermudan-style derivatives CVA computation becomes path-dependent since we need to take into account the exercise strategy and the fact that exposure falls to zero after the exercise.

A peculiar problem that we encounter in CVA computation is the presence of the so-called wrong-way risk (WWR), that is the non-negligible dependency between the value of a derivatives portfolio and counterparty default probability. In particular we face WWR if a deterioration in counterparty creditworthiness is more likely when portfolio exposure increases. Several attempts have been made to deal with WWR. From a regulatory point of view, the Basel III Committee currently requires to correct by a multiplicative factor $\alpha = 1.4$ the CVA computed under hypothesis of market-credit independence. In this way the impact of WWR is considered equivalent to a 40 % increase in standard CVA. However, the Committee leaves room for financial institutions with approved models to apply for lower multipliers (floored at 1.2). This opportunity opens the way for more sophisticated models in order to reach a more efficient risk capital allocation.

Relevant contributions on alternative approaches to manage WWR include copula-based modeling as in [6], introduction of jumps at default as in [13], the backward stochastic differential equations framework developed in [7], and the stochastic hazard rate approach in [11]. In particular [11] introduces the idea to link the counterparty hazard rate to the portfolio value by means of an arbitrary monotone function. The dependence structure is, then, described uniquely by one parameter that controls the impact of exposures on the hazard rate. Additionally, a deterministic time-dependent function is introduced to match the counterparty credit term structure observed on the market. In this framework CVA pricing in the presence of WWR involves just a small adjustment to the pricing machinery already in place in financial institutions. We only need to take into account the randomness incorporated into the counterparty default probabilities by means of the stochastic hazard rate and price CVA with standard techniques. This is probably the most relevant property of the model: as soon as we associate a WWR parameter to a given counterparty–portfolio combination, we are able to deal with WWR using the same pricing engine underlying standard CVA computation. As pointed out in [14], leveraging as much as possible on existing platforms should be one of the principles an optimal risk model should be shaped on. However, the original approach in [11] relies on a Monte Carlo-based technique to determine the auxiliary deterministic function in order to calibrate the model on the counterparty credit structure. Obtaining this auxiliary function is the trickiest part in the calibration procedure, because it involves a “delicate” path-dependent problem that is difficult to implement for realistic portfolios. In [1], it is shown how it is possible to overcome such a limitation by transforming the path-dependent problem into a recursive one with a considerable reduction in the overall computational complexity. The basic idea is to consider discrete market factor dynamics and induce a change of probability such that the new set of (transition) probabilities are computed recursively in time. We presented a straightforward implementation of our approach via tree methods. Trees are also a straightforward and well understood tool to manage the early termination in derivatives pricing. So combining tree-based dynamic programing and the recursive algorithm in [1] leads to a simple and effective procedure to price CVA with WWR when American or Bermudan features are considered. The paper is organized as follows: in Sect. 2 we review the Hull–White model for CVA in the presence of WWR and the recursive approach in [1]. In Sect. 3 we analyze the effects of early termination on CVA adjustments via numerical tests and in Sect. 4 we study the relevant case of a long position on a Bermudan swaption. Finally Sect. 5 reports some final remarks.

2 CVA Pricing and WWR

For a given derivatives portfolio we can define the unilateral CVA² as the risk-neutral expectation of the discounted loss that can be suffered over a given period of time

$$\begin{aligned} CVA = (1-R) \int ^T_{t_0} B(t_{0}, t) \; EE(t) \; PD(dt), \end{aligned}$$

(1)

where usually $t_{0}$ is the value date (hereinafter we set $t_{0} = 0$ if not stated otherwise) and T is the longest maturity date in the portfolio. Here R is the recovery rate, PD(dt) is the probability density of counterparty default between t and $t+dt$ (with no default before t), and $B(t_{0}, t) EE(t)$ is the discounted expected exposure in t. If interest rates are stochastic, the expected exposure is defined

$$ B(t_{0}, t) \; EE(t) \equiv \mathbb {E}[ D(t_{0},t) \; E(t) ] , $$

with $\mathbb {E}[ \cdot ]$ the expectation operator given the information at value date $t_0$, $D(t_{0},t)$ the stochastic discount, and E(t) the (stochastic) exposure at time t. The latter is inherently defined by the collateral agreement that the parties have in place: for example in uncollateralized transactions, E(t) is simply the max w.r.t. zero of v(t), the portfolio value at time t. For practical computation, the integral in (1) is approximated by choosing a discretized set of times $\mathscr {T}=\{ t_i \}_{i=0,\ldots ,n}$ with $t_n=T$. In particular, the Basel III standard approach for CVA valuation is

$$\begin{aligned} CVA = (1-R) \sum ^n_{i=1} \frac{B_i \; EE_i + B_{i-1} \; EE_{i-1}}{2} PD_i, \end{aligned}$$

(2)

with $B_i$ that stands for³ $B(t_{0},t_i)$ and

$$ PD_i \equiv SP_{i-1} - SP_{i}, $$

where $SP_{i}$ is the counterparty survival probability up to $t_i$. Assuming that the default is modeled by means of a generic intensity-based model, we can link survival probabilities to the so-called hazard rate function h(t), (see e.g. [15]):

$$ SP_i = \exp \left( -\int ^{t_{i}}_{t_{0}} h(t) \, dt \right) . $$

A common assumption is to consider h(t) constant between two consecutive dates in the set $\mathscr {T}$. Pricing CVA with (2) holds if there is no “market-credit” dependency. However, in case of wrong-way risk (WWR) a new, more sophisticated, model is needed because exposure and counterparty default probabilities are no more independent: exposure is conditional to default and a positive “market-credit” dependence originates the WWR. Recently Hull and White [11] have proposed an approach to WWR that is financially intuitive: the conditional hazard rate is modeled as a stochastic quantity related to the portfolio value v(t) through a monotonic increasing function. In the following we focus on the specific functional form

$$\begin{aligned} {\tilde{h}}(t) = \exp \biggl ( a(t) + b \, v(t) \biggr ) , \end{aligned}$$

(3)

where $b \in \mathfrak {R}^+$ is the WWR parameter. However, results still hold for an arbitrary order-preserving function. The function a(t) is a deterministic function of time, chosen in such a way that on each date

$$\begin{aligned} SP_i = \mathbb {E} \left[ \exp \left( -\int ^{t_{i}}_{t_{0}} \; {\tilde{h}}(t)\; dt \right) \right] \qquad \forall i = 1,\ldots ,n. \end{aligned}$$

(4)

Combining (3) and (4) we clearly see that function a(t) depends also on the value specified for the parameter b.

The main advantage of this model is that once we know b and a(t), WWR can be implemented easily by means of a simple generalization of (2):

$$\begin{aligned} CVA_W = (1-R) \sum ^n_{i=1} \mathbb {E} \left[ \frac{D_i \; E_i + D_{i-1} \; E_{i-1}}{2} \, {\widetilde{PD}}_i \right] , \end{aligned}$$

(5)

where ${\widetilde{PD}}_i$ is the stochastic probability to default between $t_{i-1}$ and $t_i$ defined in terms of ${\tilde{h}}_{i}$. We want to stress that expectation in (5) can be computed via any feasible numerical method: this fact implies that, given b and a(t), taking into account WWR just requires a slight modification in the payoff of existing algorithms used for the calculation of CVA.

We now briefly recall the recursive approach presented in [1] that avoids the path dependency in the determination of a(t) so that Eq. (4) is satisfied. Hereinafter we refer to the technique to get such a function as either the calibration of a(t) or the “calibration problem”: once the three sets of parameters (the recovery R, the default probabilities PDs, and the WWR parameter b) for dealer’s clients are estimated (e.g. with statistical methods) it is the most complicated issue in the calibration of Hull–White model.

Let us assume that the market risk factors underlying the portfolio are discrete and we indicate with $j_i$ the discrete state variable that describes the market at time $t_i$. In this framework market dynamics is described by a Markov chain with

$$ q_i(j_{i-1}, j_{i}) \quad \forall i = 1,\ldots ,n $$

the transition probability between $j_{i-1}$ at time $t_{i-1}$ and $j_{i}$ at time $t_{i}$. Typical examples where such a discrete approach is natural are lattice models. In particular, in [1], we applied tree methods to the pricing of CVA for linear derivatives portfolios.

Embedding the Hull–White model (3) in our setting, the stochastic survival probability between $t_{i-1}$ and $t_i$ becomes

$$\begin{aligned} {\tilde{P}}_{i} (j) \equiv \exp \left( - (t_i - t_{i-1}) \; {\tilde{h}}_{i}(j) \right) \equiv P_i \; \eta _i (j) \qquad \forall i = 1,\ldots ,n, \end{aligned}$$

(6)

where

$$ P_i \equiv \frac{SP_{i}}{SP_{i-1}} $$

is the forward survival probability between $t_{i-1}$ and $t_i$ valued in $t_0$. For notational convenience, we also set ${\tilde{P}}_{0} (j_0) = \eta _0 (j_0) = 1$. The $\eta$ process introduced in (6) can be seen as the driver of the stochasticity in survival probabilities and it plays a key role in circumventing path-dependency in the calibration of a(t), as shown in the following proposition.

Proposition

In the model with discrete market risk factors, the calibration problem (4) becomes

$$\begin{aligned} \sum _{j_i} p_{i} (j_i) \; \eta _{i} (j_i) = 1 \qquad \forall i = 1,\ldots ,n, \end{aligned}$$

(7)

where $p_{i} (j_i)$ are probabilities and they can be obtained via the recursive equation

$$\begin{aligned} p_{i} (j_i) = \sum _{j_{i-1}} q_i(j_{i-1}, j_{i}) \; \eta _{i-1} (j_{i-1}) \; p_{i-1} (j_{i-1}) \qquad \forall i = 1,\ldots ,n, \end{aligned}$$

(8)

with the initial condition $p_{0} (j_0=0) = 1$.

Proof See [1].

Thus the calibration problem (4) can be solved at each discrete date $t_{i}$ via (7) by simply exploiting the fact that the process $\eta$, non-path-dependent, is a martingale under the probability measure p. Equation (8), in addition, specifies an algorithm to build this new probability measure recursively. In this framework ${\widetilde{PD}}_i$ can be readily obtained from (6). Let us mention that, although this is just one of the viable approaches to solve (4), it turns out to be, as shown in the next section, a natural way to handle the additional complexity induced by early exercises within the Hull–White approach to WWR modeling.

3 The Impact of Early Exercise

As already anticipated in Sect. 1, CVA when early exercise is allowed gives rise to additional features. In this section we want to highlight the differences in CVA figures when both European and American options are considered, implementing the tree-based procedure described in the previous section. It is well known that backward induction and dynamic programing applied on (recombining) trees are, probably, the simplest and most intuitive tool to price derivatives with an early exercise as American options. For these options, indeed, Monte Carlo techniques turn out to be computationally intensive in case of CVA: the exercise date, after which the exposure falls to zero, depends on the path of the underlying asset and on the exercise strategy. In such a case we are asked to describe two random times: the optimal exercise time and the counterparty default time.

3.1 The Pricing Problem

Since our goal is to study the effects of early exercise clauses on CVA, we focus on the case of a dealer that enters into a long position⁴ on American-style derivatives with a defaultable counterparty. That is, the dealer is the holder of the option and she has the opportunity to choose the optimal exercise strategy in order to maximize the option value. In particular, following [3], we would need to differentiate between two possible assumptions depending on the effects of counterparty defaultability on the exercise strategy. The option holder would or would not take into account the possibility of counterparty default when she chooses whether to exercise or not. In the former case, the continuation value (the value of holding the option until the next exercise date) should be adjusted for the possibility of default. However, following the actual practice in CVA computation, we assume that counterparty defaultability plays no role in defining the exercise strategy of the dealer. This means that the pricing problem (before any CVA consideration) is the classical one for American options in a default-free world.

Let us assume to have a tree for the evolution of market risk factors⁵ up to time T. Hereinafter, without loss of generality, we can set a constant time step $\varDelta t$ and denote the time partition on the tree by means of an index i in $\mathscr {T} = \{ t_{i} \}_{i = 0,\ldots ,n}$ with $t_{i} = i\, \varDelta t$. We further introduce an arbitrary set of m exercise dates $\mathscr {E} = \{ e_{k} \}_{k = 1,\ldots ,m}$ with $\mathscr {E} \subseteq \mathscr {T}$ at which the holder can exercise her rights receiving a payoff $\phi _{k}$ that could depend on the specific exercise date $e_{k}$. In this setting we can deal indistinctly with European ($m = 1$), Bermudan ($m \in \mathbb {N}$), and American options ($m \rightarrow \infty$). The standard dynamic programing approach then allows us to compute the derivative value at each node of the tree:

$$\begin{aligned} v_{i}(j_{i})={\left\{ \begin{array}{ll} \phi _{m}(j_{i}) &{} \text {for}\, i \,\text {s.t.}\, t_{i} = e_{m} = T,\\ \max (c_{i}(j_{i}),\,\phi _{k}(j_{i})) &{} \text {for}\, i\,\text {s.t.}\, t_{i} \in \mathscr {E}\backslash \{e_{m}\},\\ c_{i}(j_{i}) &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(9)

with $c_{i}$ the continuation value of the derivative defined as

$$\begin{aligned} c_{i}(j_{i}) = B(i,i+1;j_{i})\, \sum _{j_{i+1}}\, q_{i}(j_{i},j_{i+1})\, v_{i+1}(j_{i+1}), \end{aligned}$$

(10)

where the sum must be considered over all possible $t_{i+1}$-nodes connected to $j_{i}$ at time $t_{i}$ and $B(i,i+1;j_{i})$ is the future discount factor that applies from $t_{i}$ and $t_{i+1}$ possibly depending on the state variable $j_{i}$ on the tree.

We describe in detail the simple 1-dimensional tree; however, extensions to the 2-factor case (as, for example, the G2++ model in [4] or the recent dual curve approach in [12]) are straightforward. Once the derivative value is computed for all nodes and the WWR parameter b is specified,⁶ we can calibrate the auxiliary function a(t) in (3) by means of the recursive approach in [1]. The advantages of such an approach are, in this case, twofold: we avoid path-dependency in the calibration of a(t), as in any other possible application, and we deal with early exercises via (9) and (10) in a very intuitive way.

3.2 The Plain Vanilla Case

We now want to assess the impact of early termination on CVA in order to understand the potential differences that could arise between European and American options from a counterparty credit risk management perspective.

In the first test we study the plain vanilla option case: we assume that the dealer buys a call option from a defaultable counterparty. Counterparty default probabilities are described in terms of a CDS flat curve at 125 basis points as in [11]. More precisely, with a flat CDS curve we can approximate quite well the survival probability between $t_{0}$ and $t_{i}$ as

$$\begin{aligned} SP_{i} =\exp \left( -\frac{s_{i}\,t_{i}}{1-R} \right) , \end{aligned}$$

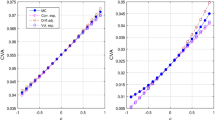
where $s_{i}$ is the credit spread relative to maturity $t_{i}$ and R the recovery rate, equal to 40 %. We further assume that trades are fully uncollateralized.⁷ The underlying asset is lognormally distributed and represented by means of a Cox-Ross-Rubinstein binomial tree. We can thus apply the dynamic programing approach described above to price options on the tree and calibrate the function a(t) recursively via (7). This procedure turns out to be quite fast: the Matlab coded algorithm takes less than 0.1 second to run on a 3.06 GHz desktop PC with 4 GB RAM when $n = m = 500$. Figure 1 shows CVA profile⁸ for both European and American call options as function of WWR parameter b and for different levels of cost of carry. From standard non-arbitrage arguments, we indeed know that the optimality of early exercise for plain vanilla call options is related to the cost of carry (defined as the net cost of holding positions in the underlying asset).⁹

Fig. 1

CVA profiles for European and American options as function of WWR parameter b for several levels of cost of carry (CoC). Parameters are $S_{0} = 100$, $K = 100$, $\sigma = 25\,\%$, $r = 1\,\%$, $T = 1$, $n = m = 500$. Counterparty CDS curve flat at 125 basis points

Fig. 2

The effect of early exercise on exposures. Parameters are $S_{0} = 100$, $K = 100$, $\sigma = 25\,\%$, $r = 1\,\%$, $\text {CoC} = -2\,\%$, $T = 1$, $n = m = 500$. Left hand scale Asset path (black solid line) and optimal exercise boundary (dashed line). Right hand scale European option (light gray line) and American option (dark gray line)

As shown in Fig. 1, CVA profiles are significantly different for European and American options when early exercise can represent the optimal strategy (black and dark gray lines). In particular the impact of WWR is significantly less pronounced for American options compared to the corresponding European ones. On the other hand, when early exercise is no more optimal, the two options are equivalent: light gray lines in Fig. 1 are undistinguishable from each other. In addition, the upward shift in CVA exposures is due to the fact that an increase in cost of carry (e.g. a reduction in the dividend yield) is reflected entirely in an augmented drift of the underlying asset dynamics that makes, ceteris paribus, the call option more valuable.

The effect of early exercise on exposure profiles is depicted in Fig. 2 where a possible underlying asset path is (reconstructed on the binomial tree) and the corresponding value of European and American options. Until the asset value remains within the continuation region (the area below the dashed line), the two options have a similar value with the only difference given by the early exercise premium embedded in the American style derivative. However, if the asset value reaches or crosses the exercise boundary, the exposure due to the American option falls to zero while the European option remains alive until maturity. From the definition of CVA (1), we can see that early exercise, if optimal, reduces the exposure of the holder to the counterparty default by shortening the life of the option. The effect is even more pronounced when we introduce the WWR: early redemption, indeed, would occur as soon as the portfolio value is large enough with the consequence to eliminate the exposure just when counterparty default probabilities become more relevant. It is possible, then, to identify in the early termination clause an important mechanism that limits CVA charges, particularly when market-credit dependency is non-negligible as shown in [8] in the case without WWR. Any change that makes early exercise more likely tends to enhance such a mechanism. We see this effect in Fig. 3 where we display the difference in CVA between European and American options as function of WWR parameter and option moneyness. With a given underlying asset dynamics, potential early exercise date is closer for more in the money options: the right of the holder is more likely to be exercised sooner. This shortens the life of the option and reduces both CVA charge (with respect to European options) and WWR sensitivity (with respect to the corresponding European option and the American options with lower moneyness). In this section we have shown that WWR can play a very different role for European and American options. In our opinion, however, WWR should be analyzed on a case-by-case basis in order to determine its magnitude and the adequate capital charge: a 40 % increase in standard CVA could overestimate the losses for an American option that can be optimally exercised in a short period while could be reductive in cases where early termination is less likely.

Fig. 3

Difference in CVA between European and American options as function of WWR parameter b and moneyness. Parameters are $S_{0} = 100$, $\sigma = 25\,\%$, $r = 1\,\%$, $\text {CoC} = -2\,\%$, $T = 1$, $n = m = 500$. Counterparty CDS curve flat at 125 basis points

4 The Bermudan Swaption Case

Probably the most relevant case of long position on options with early exercise opportunities in the portfolios of financial institutions is represented by Bermudan swaptions. Such exotic derivatives are, indeed, used by corporate entities to enhance the financial structure related to the issue of callable bonds. Often, by selling a Bermudan receiver swaption to a dealer, the callable bond issuer can reduce its net borrowing cost. Usually the swaption is structured such that exercise dates match the callability schedule of the bond.¹⁰ Let $\hat{T}$ be the bond maturity date. The dealer has the right, at any exercise date $e_{k} \in \mathscr {E}\backslash \{e_{m}\}$, to enter into an interest rate swap with maturity $\hat{T}$, where she receives the fixed rate K (equal to the fixed coupon rate of the bond) and pays the floating rate to the bond issuer with first payment made on date $e_{k+1}$. In our test we use the Euro interbank market data as of September 13, 2012 as given in [2]. We assume that the dealer buys a 10-year Bermudan receiver swaption where the underlying swap has, for simplicity, both fixed and floating legs with semiannual payments. The swaption can be exercised semiannually and its notional amount is Eur 100 million. We describe interest rates dynamics with a 1-factor Extended Vasicek model on a trinomial tree as in [10]. Model parameters are calibrated to market prices of European ATM swaptions with overall contract maturity equal to 10 years as shown in Table 1. As done in the previous section, we value the Bermudan swaption on the tree via dynamic programing and calibrate the WWR model function a(t). Once again the combined approach on the tree allows to perform both tasks in a negligible amount of time. Figure 4 reports the WWR impact¹¹ for uncollateralized transactions struck at different levels of moneyness: at the money (swaption strike set equal to the market 10 years spot swap rate) and $\pm 50$ basis points. The upper graph reports the case with no initial lockout period while in the lower one we assume that the option cannot be exercised in the first 2 years. When the option can be exercised with no restrictions, we observe a moderate inverse relationship between moneyness and WWR impact due to the protection mechanism: the opportunity to early exercise when the exposure is large limits the effect of increased counterparty default probabilities. On the other hand, the introduction of a lockout period intensifies the WWR impact. Intuitively, by expanding the lockout period we move toward the limiting case of a European option. In this case the moneyness–WWR effect is reversed: the more in the money the option is, the more relevant the WWR effect becomes. During the lockout period the in-the-money option has a considerably higher exposure to counterparty default that cannot be mitigated via early termination.

Table 1 Diagonal implied volatility of European ATM swaptions used to calibrate the 1-factor Hull–White model

Fig. 4

Impact of WWR on Bermudan receiver swaptions as function of WWR parameter b for several levels of moneyness. Market data as of September 13, 2012. Counterparty CDS curve flat at 125 basis points

5 Concluding Remarks

Nowadays WWR is a crucial concern in OTC derivatives transactions. This is particularly true for uncollateralized trades that a financial institution could have in place with medium-sized corporate clients. The presence of early termination clauses in vulnerable derivatives portfolios makes the CVA computation even more tricky. We have shown a simple and effective approach to deal with calibration and pricing of CVA within the Hull–White framework [11] for American or Bermudan options. We extended the procedure in [1] to the dynamic programing algorithm required to take into account the free boundary problem inherent in the pricing of such derivatives. Numerical tests carried out underline the importance of adequate procedures to differentiate CVA profiles for European and American options. The possibility of early exercise, indeed, plays a remarkable role in mitigating the WWR: an undifferentiated CVA pricing for contingent claims with different exercise styles would then lead to severe misspecification of regulatory capital charges.

An interesting topic for further research would consider the impact of counterparty defaultability in defining the dealer’s optimal exercise strategy. Even if intuitive, this poses nontrivial problems mainly due to the interrelation among derivative pricing, WWR, and calibration of function a(t). It is our opinion, however, that the described framework could be extended in this direction.