Abstract
Classical as well as quantum information is stored in physical systems, or “information is inevitably physical” as Rolf Landauer famously said. These physical systems are ultimately governed by the laws of quantum mechanics. In this chapter we quickly review the relevant mathematical foundations of quantum theory and introduce notational conventions that will be used throughout the book.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
For example, it sheds light on the fact that we use the operator norm for ordinary linear operators and its dual norm, the trace norm, for density operators.
- 2.
The reader is invited to think of \(\log (x)\) as the binary logarithm of x and, consequently, \(\exp (x) = 2^{x}\), as is customary in quantum information theory.
- 3.
Relation to Operator Algebras: Let us note that \(\mathscr {L}(A,B)\) with the norm \(\Vert \cdot \Vert \) is a Banach space over \(\mathbb {C}\). Furthermore, the operator norm satisfies
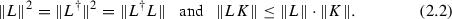
for any \(L \in \mathscr {L}(A, B)\) and \(K \in \mathscr {L}(B, A)\). The inequality states that the norm is sub-multiplicative.
The above properties of the norm imply that the space \(\mathscr {L}(A)\) is (weakly) closed under multiplication and the adjoint operation. In fact, \(\mathscr {L}(A)\) constitutes a (Type I factor) von Neumann algebra or \(C^*\) algebra. Alternatively, we could have started our considerations right here by postulating a Type 1 von Neumann algebra as the fundamental object describing individual physical systems, and then deriving the Hilbert space structure as a consequence.
- 4.
This generalization is quite useful as it, for example, allows us to see the optimal (probabilistic) Neyman-Pearson test as an event.
- 5.
Note also that the norms \(\Vert \cdot \Vert \) and \(\Vert \cdot \Vert _*\) are dual with regards to this form, namely we have
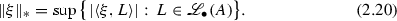
The trace norm is thus sometimes also called the dual norm.
- 6.
Note that \(\varPsi \) is an (unnormalized) maximally entangled state, usually denoted \(\psi \).
- 7.
This convention is very useful to keep the presentation in the following chapters concise, but some care is required. If \(\lim _{\varepsilon \rightarrow 0} f(\varepsilon ) \ne 0\), then \(M \mapsto f(M)\) is not necessarily continuous even if f is continuous on its support.
- 8.
It is noteworthy that the weaker condition that the map be bounded, i.e. \(\Vert \mathcal {E}^{\dag }(L_A) \Vert < \infty \), is not sufficient here and in particular does not imply that the map is completely bounded. In contrast, bounded linear operators in \(\mathscr {L}(A)\) are in fact also completely bounded in the above sense.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2016 The Author(s)
About this chapter
Cite this chapter
Tomamichel, M. (2016). Modeling Quantum Information. In: Quantum Information Processing with Finite Resources. SpringerBriefs in Mathematical Physics, vol 5. Springer, Cham. https://doi.org/10.1007/978-3-319-21891-5_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-21891-5_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-21890-8
Online ISBN: 978-3-319-21891-5
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)