Abstract
Some authors, most notably Luciano Floridi, have recently argued for a notion of “strongly” semantic information, according to which information “encapsulates” truth (the so-called “veridicality thesis”). We propose a simple framework to compare different formal explications of this concept and assess their relative merits. It turns out that the most adequate proposal is that based on the notion of “partial truth”, which measures the amount of “information about the truth” conveyed by a given statement. We conclude with some critical remarks concerning the veridicality thesis in connection with the role played by truth and information as relevant cognitive goals of inquiry.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
As a terminological remark, note that while “misinformation” simply denotes false or incorrect information, “disinformation” is false information deliberately intended to deceive or mislead.
- 2.
- 3.
Nothing substantial, in what follows, depends on such assumption.
- 4.
In the literature, it is usual to say that Eqs. (1) and (2) define the (amount of) “substantive information” or “information content” of \(A\), as opposed to the “unexpectedness” or “surprise value” of \(A\), which is defined as
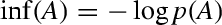[4, p. 20]. On this distinction, see for instance Hintikka [18, p. 313] and Kuipers [22, p. 865]. - 5.
- 6.
This does not mean that this assumption is the only culprit. As noted during discussion at the Trends in Logic XI conference, a way of avoiding BCP would be to adopt a non-classical logic according to which contradictions do not entail everything and hence are not maximally informative. Systems of this kind are provided by those “connexive logics” that reject the classical principle ex contradictione quodlibet (for all \(A\), \(\bot \) entails \(A\)) in favor of the (Aristotelian) intuition that ex contradictione nihil sequitur (cf. [33, Sect. 1.3]).
- 7.
In the following, we replace, without any significant loss of generality, Floridi’s talk of “infons”—“discrete items of factual information qualifiable in principle as either true or false, irrespective of their semiotic code and physical implementation” [10, p. 199]—by talk of sentences or statements in the given language \(\fancyscript{L}_{n}\).
- 8.
In logical parlance, a c-statement is a statement in conjunctive normal form such that each of its clauses is a single literal. Following Oddie [26, p. 86], a c-statement may be also called a “quasi-constituent”, since it can be conceived as a “fragment” of a constituent.
- 9.
- 10.
One may note that measure \( vs _{\phi }\) is not normalized, and varies between \(-\phi \) and \(1\). A normalized measure of the verisimilitude of \(A\) is \(( vs _{\phi }(A)+\phi )/(1+\phi )\), which varies between 0 and 1.
- 11.
Proof note that, among c-statements, \(A\) entails \(B\) iff \( b (A)\supseteq b (B)\). If both are true, this implies \( t (A,C_{\star })\supseteq t (B,C_{\star })\) and hence \( vs _{\phi }(A)= cont _{t}(A,C_{\star })\ge cont _{t}(B,C_{\star })= vs _{\phi }(B)\). For discussion of this Popperian requirement, see [24, pp. 186–187, 233, 235–236]. Note also that \( vs _{\phi }\) satisfies the stronger requirement that among true theories, the one with the greater degree of (true) basic content is more verisimilar than the other; i.e., if \(A\) and \(B\) are true and \( cont _{t}(A,C)> cont _{t}(B,C)\) then \( vs _{\phi }(A)> vs _{\phi }(B)\). \(\square \)
- 12.
Proof if \(A\) entails \(B\) and both are completely false, then \( f (A,C_{\star })\supseteq f (B,C_{\star })\) and hence \( cont _{f}(A,C_{\star })\ge cont _{f}(B,C_{\star })\). Since \(\phi \) is positive, it follows that \( vs _{\phi }(A)=-\phi cont _{f}(A,C_{\star })\le -\phi cont _{f}(B,C_{\star })= vs _{\phi }(B)\). \(\square \)
- 13.
Proof If \(A\) is true, then \( vs _{\phi }(A)= cont _{t}(A,C_{\star })\); if \(B\) is completely false, then \( vs _{\phi }(B)=-\phi cont _{f}(B,C_{\star })\); since \(\phi \) is positive, it follows that \( vs _{\phi }(A)> vs _{\phi }(B)\).
- 14.
Proof sketch When \(A\) is a c-statement, the constituents in its range are \(2^{n-k_A}\); it follows that \( vac (A)=2^{n-k_A} / 2n\), i.e., \(1 / 2^{k_A}\). Thus, among true c-statements, \( cont _{S}(A)=1-1 / 2^{k_A}\) co-varies with the degree of basic content of \(A\), \( b (A)=k_A / n\). As far as false c-statements are concerned, since \( inacc (A)=1- acc (A)\), \( cont _{S}\) co-varies with the accuracy of \(A\). \(\square \)
- 15.
Note that, by definition, a c-statement can not be contradictory; hence, \( cont _{S}^{*}\) is undefined for contradictions. Of course, it is always possible to stipulate, as Floridi does, that contradictions have a minimum degree of SSI.
- 16.
Note again that \( cont _{t}\) is undefined for contradictions, which can be assigned a minimum degree of SSI by stipulation. Interestingly, an argument to this effect was already proposed by Hilpinen [17, p. 30].
- 17.
I thank Gerhard Schurz for raising this point in discussion during the Trends in Logic XI conference.
- 18.
Usually, \(\varDelta _{}(C_i,C_j)\) is identified with the so-called normalized Hamming distance (or Dalal distance, as it is also known in the field of AI), i.e., with the number of literals on which \(C_i\) and \(C_j\) disagree, divided by the total number \(n\) of atomic sentences.
- 19.
Proof Note that, if \(A\) is a c-statement, all constituents \(C_i\) in the range of \(A\) (which are c-statements themselves) are “completions” of \(A\) in the sense that \( b (A)\subset b (C_i)\). The constituent in \(R(A)\) farthest from \(C_{\star }\) will be the one which makes all possible additional mistakes besides the mistakes already made by \(A\): this means that \(\varDelta _{ max }(A,C_{\star })=1-\frac{t_A}{n}\). It follows by (7) that \( pt (A)=1-(1-\frac{t_A}{n})= cont _{t}(A,C_{\star })\). \(\square \)
- 20.
This is still clearer if one consider the generalization of the definition above to arbitrary (non-conjunctive) statements \(A\). Given (18), the misinformation conveyed by \(A\) is given by \(1- pt (A)=\varDelta _{ max }(A,C_{\star })\), that reduces to \( misinf (A)\) as far as c-statements are concerned (the proof is straightforward, see footnote 19).
[References
Barwise, J. (1997). Information and impossibilities. Notre Dame Journal of Formal Logic, 38(4), 488–515.
Bremer, M., & Cohnitz, D. (2004). Information and information flow: An introduction. Frankfurt: Ontos Verlag.
Carnap, R. (1950). Logical foundations of probability. Chicago: University of Chicago Press.
Carnap, R., & Bar-Hillel, Y. (1952). An outline of a theory of semantic information. Technical Report 247, MIT Research Laboratory of Electronics.
Cevolani, G. (2011). Strongly semantic information and verisimilitude. Ethics & Politics, 2, 159–179. http://www2.units.it/etica/
Cevolani, G., Crupi, V., & Festa, R. (2011). Verisimilitude and belief change for conjunctive theories. Erkenntnis, 75(2), 183–202.
D’Agostino, M., & Floridi, L. (2009). The enduring scandal of deduction. Synthese, 167(2), 271–315.
D’Alfonso, S. (2011). On quantifying semantic information. Information, 2(1), 61–101.
Dretske, F. (1981). Knowledge and the flow of information. Cambridge: MIT Press.
Floridi, L. (2004). Outline of a theory of strongly semantic information. Minds and Machines, 14(2), 197–221.
Floridi, L. (2005). Is semantic information meaningful data? Philosophy and Phenomenological Research, 70(2), 351–70.
Floridi, L. (2007). In defence of the veridical nature of semantic information. European Journal of Analytic Philosophy, 3(1), 31–1.
Floridi, L. (2011a). The philosophy of information. Oxford: Oxford University Press.
Floridi, L. (2011b). Semantic conceptions of information. In E. N. Zalta (Ed.), The Stanford encyclopedia of philosophy (Spring 2011 ed.). http://plato.stanford.edu/archives/spr2011/entries/information-semantic/
Frické, M. (1997). Information using likeness measures. Journal of the American Society for Information Science, 48(10), 882–892.
Grice, H. P. (1989). Studies in the way of words. Cambridge: Harvard University Press.
Hilpinen, R. (1976). Approximate truth and truthlikeness. In M. Przełecki, K. Szaniawski & R. Wójcicki (Eds.), Formal methods in the methodology of the empirical sciences (pp. 19–42). Dordrecht: Reidel.
Hintikka, J. (1968). The varieties of information and scientific explanation. In B. V. Rootselaar & J. Staal (Eds.), Logic, methodology and philosophy of science III (Vol. 52, pp. 311–331). Amsterdam: Elsevier.
Hintikka, J. (1970). Surface information and depth information. In J. Hintikka & P. Suppes (Eds.), Information and inference, (pp. 263–297). Dordrecht: Reidel.
Hintikka, J. (1973). Logic, language-games and information. Oxford: Oxford University Press.
Kuipers, T. A. F. (2000). From instrumentalism to constructive realism. Dordrecht: Kluwer Academic Publishers.
Kuipers, T. A. F. (2006). Inductive aspects of confirmation, information and content. In R. E. Auxier & L. E. Hahn (Eds.), The philosophy of Jaakko Hintikka (pp. 855–883). Chicago and La Salle: Open Courts.
Levi, I. (1967). Gambling with truth. New York: Alfred A. Knopf.
Niiniluoto, I. (1987). Truthlikeness. Dordrecht: Reidel.
Niiniluoto, I. (2011). Scientific progress. In E. N. Zalta (Ed.), The Stanford encyclopedia of philosophy (Summer 2011 ed.). http://plato.stanford.edu/entries/scientific-progress/
Oddie, G. (1986). Likeness to truth. Dordrecht: Reidel.
Popper, K. R. (1934). Logik der Forschung. Vienna: Julius Springer [revised edition: The logic of scientific discovery. London: Routledge, 2002 (Hutchinson, London, 1959)].
Popper, K. R. (1963). Conjectures and refutations (3rd ed.). London: Routledge and Kegan Paul.
Schurz, G., & Weingartner, P. (2010). Zwart and franssen’s impossibility theorem holds for possible-world-accounts but not for consequence-accounts to verisimilitude. Synthese, 172, 415–436.
Sequoiah-Grayson, S. (2007). The metaphilosophy of information. Minds and Machines, 17(3), 331–44.
Sequoiah-Grayson, S. (2008). The scandal of deduction. Journal of Philosophical Logic, 37(1), 67–94.
Shannon, C. (1948). A mathematical theory of communication. Bell System Technical Journal, 27, 379–423, 623–656.
Wansing, H. (2010). Connexive logic. In E. N. Zalta (Ed.), The stanford encyclopedia of philosophy (Fall 2010 ed.). http://plato.stanford.edu/entries/logic-connexive/
Acknowledgments
This paper is based on presentations delivered at the Fourth Workshop on the Philosophy of Information (University of Hertfordshire, 10–11 May 2012) and at the Trends in Logic XI conference (Ruhr University Bochum, 3–5 June 2012). I thank the participants in those meetings, and in particular Luciano Floridi and Gerhard Schurz, for valuable feedback. This work was supported by Grant CR 409/1-1 from the Deutsche Forschungsgemeinschaft (DFG) as part of the priority program New Frameworks of Rationality (SPP 1516) and by the Italian Ministry of Scientific Research within the FIRB project Structures and dynamics of knowledge and cognition (Turin unit: D11J12000470001).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Cevolani, G. (2014). Strongly Semantic Information as Information About the Truth. In: Ciuni, R., Wansing, H., Willkommen, C. (eds) Recent Trends in Philosophical Logic. Trends in Logic, vol 41. Springer, Cham. https://doi.org/10.1007/978-3-319-06080-4_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-06080-4_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-06079-8
Online ISBN: 978-3-319-06080-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)
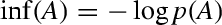