Conformal Mappings onto Nonoverlapping Regions

Abstract

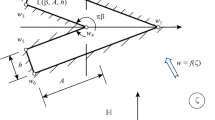
Let f(ζ) = a + dζ… be analytic and univalent in the unit disk |ζ| < 1, mapping it conformally onto some domain D. We shall call a = f(0) the center and |d| = |f′(0)| the inner radius of D with respect to a. Roughly speaking, our problem is to find n functions

$$f_j(\zeta) = a_j+d_j \zeta + \ldots, \quad j=1,2,\ldots,n,$$

((1))

which map the disk conformally onto nonoverlapping regions D _j whose union has prescribed transfinite diameter R, with the centers a _j as far apart as possible and the inner radii |d _j | as large as possible. Here only n and R are specified in advance.