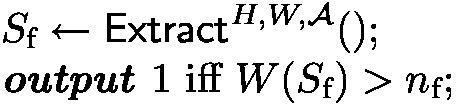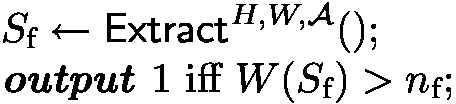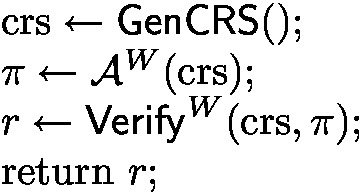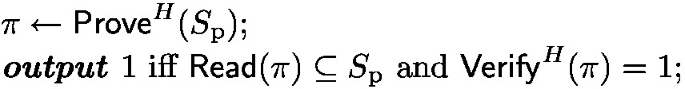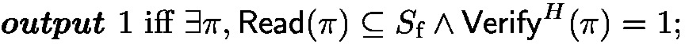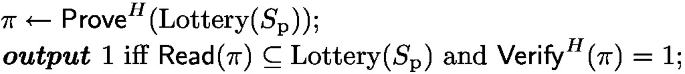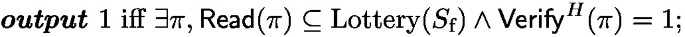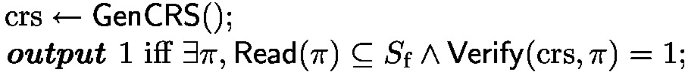Approximate Lower Bound Arguments

Abstract

Suppose a prover, in possession of a large body of valuable evidence, wants to quickly convince a verifier by presenting only a small portion of the evidence.

We define an Approximate Lower Bound Argument, or ALBA, which allows the prover to do just that: to succinctly prove knowledge of a large number of elements satisfying a predicate (or, more generally, elements of a sufficient total weight when a predicate is generalized to a weight function). The argument is approximate because there is a small gap between what the prover actually knows and what the verifier is convinced the prover knows. This gap enables very efficient schemes.

We present noninteractive constructions of ALBA in the random oracle and Uniform Random String models and show that our proof sizes are nearly optimal. We also show how our constructions can be made particularly communication-efficient when the evidence is distributed among multiple provers working together, which is of practical importance when ALBA is applied to a decentralized setting.

We demonstrate two very different applications of ALBAs: for large-scale decentralized signatures and for achieving universal composability in general-purpose succinct proof systems (SNARKs).

L. Reyzin—Work done while visiting the Blockchain Technology Lab at the University of Edinburgh.

1 Introduction

Suppose a prover is in possession of a large body of valuable evidence that is individually verifiable. The evidence is so voluminous that presenting and verifying all of it is very expensive. Instead, the prover wants to convince a verifier by presenting only a small portion of the evidence.

More formally, let R be a predicate. We explore succinct arguments of knowledge for a prover who knows a set $S_\text {p}$ of values that satisfy R such that $|S_\text {p}| \ge n_\text {p}$ and wants to convince a verifier that $|S_\text {p}|>n_\text {f}$, where $n_\text {f}$ is somewhat smaller than $n_\text {p}$. Because $n_\text {f}<n_\text {p}$, the verifier obtains a lower bound approximation to the actual cardinality of $S_\text {p}$; hence we call this primitive an Approximate Lower Bound Argument or ALBA.

This problem has a long history. In 1983, in order to prove that $\textrm{BPP}\subseteq \textrm{RP}^\textrm{NP}$, Sipser and Gács [Sip83, Section V, Corollary to Theorem 6] showed a simple two-round interactive protocol for proving a lower bound on the size of the set S of accepting random strings. Their construction is based on hash collisions: the verifier chooses some number of universal hash functions $h_1, \dots , h_m$ [CW79] and the prover shows $s,s'$ such that $s\ne s'$ and $h_i(s) = h_i(s')$ for some $i\in \{1,\ldots ,m\}$. If S is small (of size at most $n_\text {f}$), then such hash collisions are very unlikely to exist, and if S is big (of size at least $n_\text {p}$), then they must exist by the pigeonhole principle. In 1986, Goldwasser and Sipser [GS86, Section 4.1] used a slightly different approach, based on the existence of inverses rather than collisions, for proving that public coins suffice for interactive proofs (we provide more details in the full version of our paper [CKRZ23]). To the best of our knowledge, the term “approximate lower bound” in the context of proof systems appears first in Babai’s work [Bab85, Section 5.2].

In designing ALBAs, we will aim to minimize communication and computational complexity; these metrics improve as the “gap” $n_\text {p}/n_\text {f}$ increases. The proof size and verifier time in classical techniques above are far from optimal. While this does not affect the classical applications of ALBAs (such as in proving that any IP language can be decided by an Arthur-Merlin protocol, where the gap can be a large constant and the prover has exponential time), as we will see it does become a pressing concern in modern applications of ALBAs.

1.1 Our Setting

The prover and verifier have access to a predicate R and the prover needs to show some elements of $S_\text {p}$ to the verifier so it is convinced that the prover possesses more than $n_\text {f}$ elements that pass R. The goal is to find some property that is unlikely to hold for small sets $S_\text {f}$ of size $n_\text {f}$, likely to hold for large sets $S_\text {p}$ of size $n_\text {p}$, and can be shown with just a few elements.

Generalization to Weighted Sets. We generalize a predicate R that determines validity of set elements, and consider instead a weight function W that takes a set element and outputs its nonnegative integer weight. In that context we wish to explore succinct arguments of knowledge that convince a verifier that the prover knows a set S that satisfies a lower bound $\sum _{s\in S} W(s) > n_\text {f}$. When W is $\{0,1\}$-valued, we are in the setting of a predicate, and we call this case “unweighted.”

We emphasize that R or W are used in a black-box way in our protocols. Thus, our protocols can be used in settings when these functions do not have a known specification—for example, they may be evaluated by human judges who weigh evidence or via some complex MPC protocol that uses secret inputs.

Setup and Interaction Models. Our main focus is on building ALBA protocols that are succinct Non-Interactive Random Oracle Proofs of Knowledge or NIROPK (see Sect. 2 for the definition). If the prover is successful in convincing the verifier, then the knowledge extractor can obtain a set of total weight exceeding $n_\text {f}$ by simply observing the random oracle queries; in other words, the protocol is straight-line extractable in the nonprogrammable random oracle model. Our security is information-theoretic as long as the predicate R (or the weight function W) is independent of the random oracle; by the standard technique of adding a commitment to R (or W) to every random oracle query, we obtain computational security even if this function is adaptively chosen to depend on the oracle.

We also show simple modifications of our protocols that replace random oracles with pseudorandom functions (PRFs). By simply publishing the PRF seed as a shared random string, we obtain a non-interactive proof of knowledge in the Uniform Random String (URS) model, in which extractor works by reprogramming the URS. Alternatively, we can obtain a two-round public coin proof of knowledge by having the verifier send the PRF seed (we would then use rewinding for extraction). Protocols in these two models are non-adaptively secure—i.e., they require that the predicate R is independent of the URS or the verifier’s first message.

Decentralized Setting. The set $S_\text {p}$ may be distributed among many parties. For instance, in a blockchain setting it could be the case that multiple contributing peers hold signatures on a block of transactions and they wish to collectively advance a protocol which approves that block. To capture such settings, we introduce decentralized ALBAs: in such a scheme, the provers diffuse messages via a peer to peer network, and an aggregator (who may be one of the provers themselves) collects the messages and produces the proof. Note that not all provers may decide to transmit a message. In addition to the complexity considerations of regular ALBAs, in the decentralized setting we also wish to minimize the total communication complexity in the prover interaction phase as well as the computational complexity of the aggregator.

1.2 Our Results

Our goal is to design protocols that give the prover a short, carefully chosen, sequence of elements from $S_\text {p}$. We show how to do this with near optimal efficiency.

Let $\lambda$ be the parameter that controls soundness and completeness: the honest prover (who possesses a set of weight $n_\text {p}$) will fail with probability $2^{-\lambda }$ and the dishonest prover (who possesses a set of weight at most $n_\text {f}$) will succeed with, say, also probability $2^{-\lambda }$. Let u be the length of the sequence the prover sends.

The unweighted case. We first show an unweighted ALBA in which the prover sends only

$$\begin{aligned} u=\frac{\lambda +\log \lambda }{\log \frac{n_\text {p}}{n_\text {f}}} \end{aligned}$$

(1)

elements of $S_\text {p}$. Moreover, we show that this number is essentially tight, by proving that at least

$$ u=\frac{\lambda }{\log \frac{n_\text {p}}{n_\text {f}}} $$

elements of $S_\text {p}$ are necessary. (Note that all formulas in this section omit small additive constants for simplicity; the exact formulas are given in subsequent sections.)

Such a protocol is relatively easy to build in the random oracle model if one disregards the running time of the prover: just ask the prover to brute force a sequence of u elements of $S_\text {p}$ on which the random oracle gives a sufficiently rare output. Calibrate the probability $\varepsilon$ of this output so that $\varepsilon \cdot n_\text {f}^u \le 2^{-\lambda }$ for soundness, but $(1-\varepsilon )^{n_\text {p}^u} \le 2^{-\lambda }$ for completeness. A bit of algebra shows that $u= \frac{\lambda +\log \lambda }{\log \frac{n_\text {p}}{n_\text {f}}}$ suffices to satisfy both soundness and completeness constraints, so the proof is short.¹ However, in this scheme, the prover has to do an exhaustive search of $1/\varepsilon$ sequences of length u, and thus the running time is exponential.

It follows that the main technical challenge is in finding a scheme that maintains the short proof while allowing the prover to find one quickly. In other words, the prover needs to be able to find a sequence of u elements with some special rare property (that is likely to occur among $n_\text {p}$ elements but not among $n_\text {f}$ elements), without looking through all sequences. We do so in Sect. 3 by demonstrating the Telescope construction.

Its core idea is to find a sequence of values that itself and also all its prefixes satisfy a suitable condition determined by a hash function (and modeled as a random oracle). This prefix invariant property enables the prover to sieve through the possible sequences efficiently expanding gradually the candidate sequence as in an unfolding telescope. We augment this basic technique further via parallel self composition to match the proof length of the exhaustive search scheme. The resulting prover time (as measured in the number of random oracle queries) is dropped from exponential to $O(n_\text {p}\cdot \lambda ^2)$. We then show how to drop further the prover complexity to $O(n_\text {p}+\lambda ^2)$ by prehashing all elements and expressing the prefix invariant property as a hash collision. We also establish that our constructions are essentially optimal in terms of proof size by proving a lower bound in the number of elements than must be communicated by any ALBA scheme that satisfies the extractability requirements of Definition 4.

Weights and Decentralized Provers. In the case where all elements have an integer weight, the straightforward way to design a weighted scheme is to give each set element a multiplicity equal to its weight and apply the algorithms we described above. However, the prover’s running time becomes linear in the input’s total weight $n_\text {p}$ which could be in the order of $2^{64}$ (number of coins in popular cryptocurrencies). A way to solve this problem is to select (with the help of the random oracle) a reasonably-sized subset of the resulting multiset by sampling, for each weighted element, a binomial distribution in accordance with its weight. Given this precomputation, we can then proceed with the Telescope construction as above and with only a (poly)logarithmic penalty due to the weights. We detail this technique in Sect. 5.

Turning our attention to the decentralized setting we present two constructions. In the first one, each party performs a private random-oracle-based coin flip to decide whether to share her value. The aggregator produces a proof by concatenating a number of the resulting values equal to a set threshold. In the second construction, we combine the above idea with the Telescope construction letting the aggregator do a bit more work; this results in essentially optimal proof size with total communication complexity $O(\lambda ^3)$, or proof size an additive term $\sqrt{\lambda }$ larger than optimal and total communication complexity $O(\lambda ^2)$.

1.3 Applications

Beyond the classical applications of ALBAs in complexity theory described earlier [CW79, Sip83, Bab85, GS86], there are further applications of the primitive in cryptography.

Weighted Multisignatures and Compact Certificates. In a multisignature scheme, a signature is accepted if sufficiently many parties have signed the message (depending on the flavor, the signature may reveal with certainty, fully hide, or reveal partially who the signers are). In consensus protocols and blockchain applications, schemes that accommodate large numbers of parties have been put to use in the context of certifying the state of the ledger. In a “proof-of-stake” setting, each party is assigned a weight (corresponding to its stake), and the verifier needs to be assured that parties with sufficient stake have signed a message.

Most existing approaches to building large-scale multisignatures exploit properties of particular signatures or algebraic structures. For example, the recent results of Das et al. and Garg et al. [GJM+23, DCX+23] are based on bilinear pairings and require a structured setup.

In contrast, our work relies only on random oracles, making it compatible with any complexity assumption used for the underlying signature scheme, including ones that are post-quantum secure. Expectedly, the black box nature of our construction with respect to the underlying signature results in longer proofs (they can be shortened using succinct proof systems, as we discuss in Sect. 1.4).

In more detail, in order to apply an ALBA scheme to the problem of multisignatures, we treat individual signatures as set elements. The underlying signature scheme needs to be unique: it should be impossible (or computationally infeasible) to come up with two different signatures for the same message and public key. Otherwise, it is easy to come up with a set of sufficient total weight by producing multiple signatures for just a few keys². Alternatively, if the knowledge extractor is allowed to rewind (need not be straight-line), one can use an arbitrary (not necessarily unique) signature scheme as follows: treat the public keys as set elements and for every selected public key in the ALBA proof, add its signature. Using an ALBA with decentralized provers is particularly suited to the blockchain setting as signatures will be collected from all participants.

A closely related approach is compact certificates by Micali et al. [MRV+21] who also treat the underlying signature scheme as a black box. In more detail, their construction collects all individual signatures in a Merkle tree, and selects a subset of signatures to reveal via lottery (that can be instantiated via the Fiat-Shamir transform [BR93]). Compared to compact certificates, our Telescope scheme obviates the need for the Merkle tree and hence shaves off a multiplicative logarithmic factor in the certificate length. It is also not susceptible to grinding while in compact certificates the adversary can try different signatures to include in the Merkle tree, and unlike compact certificates that rely inherently on the random oracle, our scheme can be instantiated in the CRS/URS model. Finally, our decentralized prover constructions drastically reduce communication. On the other hand, compact certificates cleverly tie the lottery to public keys rather than signatures and support an arbitrary signature scheme (not necessarily unique) while still providing straight-line knowledge extraction.

Reducing communication complexity was also the focus of Chaidos and Kiayias in Mithril, a weighted threshold multisignature, [CK21], that also uses unique signatures and random-oracle-based selection. In our terminology, Mithril applies a decentralized ALBA scheme to unique signatures (possibly followed by compactification via succinct proof systems, as discussed in Sect. 1.4). In comparison to Mithril, our decentralized prover construction achieves significantly smaller proof sizes (when comparing with the simple concatenation version of [CK21]) at the cost of higher communication. In Sect. 4.1 we present a simple lottery that is asymptotically similar to Mithril with concatenation proofs, and offer a comparison in Sect. 8.

Straight-Line Witness Extraction for SNARKs. Ganesh et al. [GKO+23] addressed the problem of universal composability [Can00] for witness-succinct non-interactive arguments of knowledge. Universal composability requires the ability to extract the witness without rewinding the prover. However, since the proof is witness-succinct (i.e., shorter than the witness), the extractor must look elsewhere to obtain the witness. Building on the ideas of Pass [Pas03] and Fischlin [Fis05], Ganesh et al. proposed the following approach: the prover represents the witness as a polynomial of some degree d, uses a polynomial commitment scheme to commit to it, and then makes multiple random oracle queries on evaluations of this polynomial (together with proofs that the evaluations are correct with respect to the commitment) until it obtains some rare output of the random oracle (much like the Bitcoin proof of work). The prover repeats this process many times, and includes in the proof only the queries that result in the rare outputs. The verifier can be assured that the prover made more than d queries with high probability, because otherwise it would not be able to obtain sufficiently many rare outputs. Thus, the knowledge extractor can reconstruct the witness via polynomial interpolation by simply observing the prover’s random oracle queries.

We observe that this approach really involves the prover trying to convince the verifier that the size of the set of random oracle queries is greater than d. This approach is just an ALBA protocol, but not a particularly efficient one. Applying our scheme instead of the one custom-built by Ganesh et al. results in less work for the prover. To get a proof of size $u\le \lambda$, the protocol of Ganesh et al. requires the prover to compute $d \cdot u \cdot 2^{\lambda /u}$ polynomial evaluations and decommitment proofs,³whereas our Telescope construction from Sect. 3 requires only $d\cdot \lambda ^{1/u} \cdot 2^{\lambda /u}$ of those.⁴ Thus, our approach speeds up this part of prover’s work by a factor of about u (which is close to the security parameter $\lambda$).

1.4 Relation to General-Purpose Witness-Succinct Proofs

In cases where the weight function can be realized by a program, one can use general-purpose witness-succinct proofs to tackle the construction of ALBA schemes via utilizing SNARKs [Gro16, GWC19].

These general purpose tools, however, are quite expensive, especially for the prover. First, the proving time can become impractical when the number of set elements in the witness is large. Second, given that the weight function W must be encoded as a circuit, the proving cost also depends heavily on the complexity of W. Moreover, W cannot always be specified as a circuit, but is evaluated by a more complex process—via a secure multi-party computation protocol or a human judge weighing the strength of the evidence.

On the other hand, these tools can give very short, even constant-size, proofs. To get the best of both worlds—prover efficiency and constant-size proofs—one can combine an ALBA proof with a witness-succinct proof of knowledge of the ALBA proof. This is indeed the approach proposed by Chaidos and Kiayias [CK21]: it first reduces witness size $n_\text {f}$ to u by using very fast random-oracle-based techniques, and then has the prover prove u (instead of $n_\text {f}$) weight computations. We can also apply this technique to our constructions, something that can result in a constant size proof with a computationally efficient prover. And given that our constructions can work in the CRS model, one can avoid heuristically instantiating the random oracle inside a circuit.

2 Definitions

Below we present a definition of ALBA inspired by the non-interactive random oracle proof of knowledge (NIROPK) [BCS16] with straight-line extraction. To introduce arbitrary weights, we use a weight oracle $W : \{0, 1\}^* \rightarrow \mathbb {N}\cup \{0\}$ and denote for a set S, $W(S) = \sum _{s \in S} W(s)$.

Definition 1

The triple $(\textsf{Prove}, \textsf{Verify}, \textsf{Extract})$ is a $(\lambda _\text {sec}, \lambda _\text {rel}, n_\text {p}, n_\text {f})$-NIROPK ALBA scheme if and only if

• $\textsf{Prove}^{H,W}$ is a probabilistic program that has access to the random oracle H and a weight oracle W;

• $\textsf{Verify}^{H,W}$ is a program that has access to the random oracle H and a weight oracle W;

• $\textsf{Extract}^{H,W,\mathcal {A}}$ is a probabilistic program that has access to the random oracle H, a weight oracle W and an adversary program $\mathcal {A}$;

• completeness: for all weight oracles W and all $S_\text {p}$ such that $W(S_\text {p}) \ge n_\text {p}$, $\Pr [\textsf{Verify}^{H,W}(\textsf{Prove}^{H,W}(S_\text {p})) = 1] \ge 1 - 2^{-\lambda _\text {rel}}$;

• proof of knowledge: consider the following experiment $\text {ExtractExp}(\mathcal {A}^{H,W}, W)$:

  

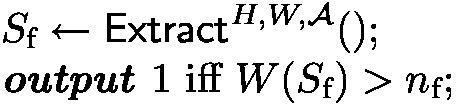
  we require that for all weight oracles W and all probabilistic oracle access programs $\mathcal {A}^{H,W}$,

  $$\begin{aligned} \Pr [\text {ExtractExp}(\mathcal {A}, W) = 1] \ge \Pr \big [\textsf{Verify}^{H,W}\big (\mathcal {A}^{H,W}()\big ) = 1\big ] - 2^{-\lambda _\text {sec}}; \end{aligned}$$

  moreover, $\textsf{Extract}^{H,W,\mathcal {A}}()$ is only allowed to run $\mathcal {A}^{H,W}$ once with the real H and W and only observes the transcript with its oracles (straight-line extraction property), $\textsf{Extract}$ runs in time polynomial in the size of this transcript.

As presented, this definition is non-adaptive; i.e., it does not allow W to depend on H; adaptivity can be added if it is possible to commit to W; see Sect. 6 for further discussion.

The above formulation of ALBAs captures the setting where a prover has the entire set $S_\text {p}$ in its possession. We will also be interested in ALBAs where the prover is decentralized—by this we refer to a setting where a number of prover entities, each one possessing an element $s \in S_\text {p}$ wish to act in coordination towards convincing the verifier. We now define a decentralized ALBA.

Definition 2

The quadruple $(\textsf{Prove}, \textsf{Aggregate}, \textsf{Verify}, \textsf{Extract})$ is a $(\lambda _\text {sec}, \lambda _\text {rel}, n_\text {p}, n_\text {f})$-decentralized NIROPK ALBA scheme if and only if

• $\textsf{Prove}^{H,W}$ is a probabilistic program that has access to the random oracle H and a weight oracle W;

• $\textsf{Aggregate}^{H,W}$ is a probabilistic program that has access to the random oracle H and a weight oracle W;

• $\textsf{Verify}^{H,W}$ is a program that has access to the random oracle H and a weight oracle W;

• $\textsf{Extract}^{H,W,\mathcal {A}}$ is a probabilistic program that has access to the random oracle H, a weight oracle W and an adversary program $\mathcal {A}$;

• completeness: consider the following experiment $\text {CompExp}(S_\text {p}, W)$:

  

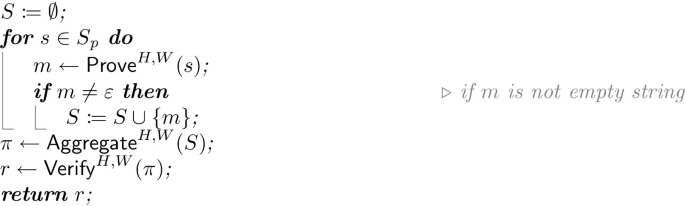
  we require that for all weight oracles W and all $S_\text {p}$ such that $W(S_\text {p}) \ge n_\text {p}$, $\Pr [\text {CompExp}(S_\text {p}, W) = 1] \ge 1 - 2^{-\lambda _\text {rel}}$;

• proof of knowledge: consider the following experiment $\text {ExtractExp}(\mathcal {A}^{H,W}, W)$:

  

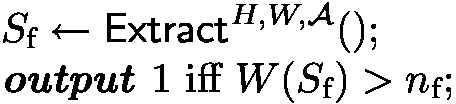
  we require that for all weight oracles W and all probabilistic oracle access programs $\mathcal {A}^{H,W}$,

  $$\begin{aligned} \Pr [\text {ExtractExp}(\mathcal {A}, W) = 1] \ge \Pr \big [\textsf{Verify}^{H,W}\big (\mathcal {A}^{H,W}()\big ) = 1\big ] - 2^{-\lambda _\text {sec}}; \end{aligned}$$

  moreover, $\textsf{Extract}^{H,W,\mathcal {A}}()$ is only allowed to run $\mathcal {A}^{H,W}$ once with the real H and W and only observes the transcript with its oracles (straight-line extraction property), $\textsf{Extract}$ runs in time polynomial in the size of this transcript.

In this model, we would like to minimize not only the proof size, but also the amount of communication characterized by the size of S in $\text {CompExp}$. Note that the above definition can be extended to multiple rounds of communication, but this is not something we explore in this work—all our decentralized constructions are “1-round.”

Finally, we present a proof of knowledge ALBA definition in the CRS model. Unlike for NIROPK, the knowledge extractor here is allowed to rewind the adversary $\mathcal {A}$ and is given it as regular input. Note that the definition crucially requires the CRS to be independent of W; see Sect. 7 for further discussion.

Definition 3

$(\textsf{Prove}, \textsf{Verify}, \textsf{Extract}, \textsf{GenCRS})$ is a $(\lambda _\text {sec}, \lambda _\text {rel}, n_\text {p}, n_\text {f})$-CRS proof of knowledge ALBA scheme if and only if

• $\textsf{Prove}^W$ is a probabilistic program;

• $\textsf{Verify}^W$ is a program having access to a weight oracle W;

• $\textsf{Extract}^W$ is a probabilistic program having access to a weight oracle W;

• $\textsf{GenCRS}$ is a probabilistic program;

• completeness: consider the following experiment $\text {CompExp}(W, S_\text {p})$:

  

  we require that for all weight oracles W and all $S_\text {p}$ such that $W(S_\text {p}) \ge n_\text {p}$, $\Pr [\text {CompExp}(W, S_\text {p}) = 1] \ge 1 - 2^{-\lambda _\text {rel}}$;

• proof of knowledge: consider the following experiment $\text {SoundExp}(\mathcal {A}^W, W)$:

  

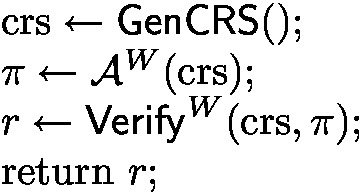
  we require that for all weight oracles W and all probabilistic oracle access programs $\mathcal {A}^W$, if $\mathcal {A}$ runs in time T and $\varepsilon = \Pr [\text {SoundExp}(\mathcal {A}^W, W) = 1] - 2^{-\lambda _\text {sec}} > 0$, then $S_\text {f}\leftarrow \textsf{Extract}^W(\mathcal {A})$ runs in expected time $\text {poly}(T, 1 / \varepsilon )$ and $\Pr \big [W(S_\text {f}) > n_\text {f}\big ] = 1$.

3 Telescope ALBA

In this section we present two ALBA schemes in sequence. We start with a less efficient but simpler construction to illustrate the main idea. We then proceed to optimize the scheme’s efficiency.

For both constructions, we will assume we have three random oracles $H_0, H_1$, and $H_2$ having particular output distributions. We explain how to implement these using a single random oracle which outputs binary strings in the full version [CKRZ23] of this work. Further, we initially restrict weights to be either 0 or 1, and generalize to integers in Sect. 5. Finally, we postpone showing the proof of knowledge property and instead consider a simpler notion of soundness: given $n_\text {f}$ elements fixed in advance, what is the probability that a valid proof exists containing only those elements? Sect. 6 will then show how a knowledge extractor can be constructed.

3.1 Basic Construction

The main idea is as follows. Let d, u and q be parameters. The prover first considers all pairs consisting of an integer in [d] and one of the elements of $S_\text {p}$ and selects each of the $n_\text {p}d$ pairs with probability $1 / n_\text {p}$. In expectation he will have d pairs selected. Now these pairs are treated as single units and they are paired with each element of $S_\text {p}$, resulting in triples that are selected again with probability $1 / n_\text {p}$. This process is repeated u times ending with, in expectation, d tuples consisting of one integer in [d] and u set elements. Now, each of the tuples is selected with probability q and any selected tuple will be a valid proof.

More formally, let $H_1$ and $H_2$ be random functions returning 1 with probability $1 / n_\text {p}$ and q respectively, and returning 0 otherwise. Any tuple $(t, s_1, ..., s_u)$ such that

• $1 \le t \le d$;

• for all $1 \le i \le u$, $H_1(t, s_1, ..., s_i) = 1$;

• $H_2(t, s_1, ..., s_u) = 1$;

is a valid proof (see Sect. 3.3 how to implement $H_1$ efficiently). Define the program $\textsf{Verify}$ accordingly.

Intuitively, this works because the honest prover maintains d tuples in expectation at each stage, while the malicious prover’s tuples decrease $n_\text {p}/ n_\text {f}$ times with each stage. However, to implement and analyze the prover algorithm, it will be convenient to represent all tuples $(t, s_1, ..., s_i)$, where $1 \le t \le d$, $0 \le i \le u$ and $s_1, ..., s_i \in S_\text {p}$, as d trees of height u with $\{(1), ..., (d)\}$ being the roots of the trees and $\{(t, s_1, ..., s_u)\}_{1 \le t \le d, s_1, ..., s_u \in S_\text {p}}$ being the leaves. To implement $\textsf{Prove}$, simply run depth first search (DFS) to find a “valid” path from a root to a leaf.

We will now analyze soundness of this construction. As mentioned above, the soundness error is defined to be the probability that a valid proof exists containing only elements from a fixed set $S_\text {f}$ of size $n_\text {f}$.

Theorem 1

Let

$$\begin{aligned} u \ge \frac{\lambda _\text {sec}+ \log (qd)}{\log \frac{n_\text {p}}{n_\text {f}}}. \end{aligned}$$

Then soundness error is $\le 2^{-\lambda _\text {sec}}$.

Proof

We analyze soundness error, denoted by S, using simple union bound.

$$\begin{aligned} S \le \bigg (\frac{1}{n_\text {p}}\bigg )^u \cdot q \cdot d \cdot n_\text {f}^u = \bigg (\frac{n_\text {f}}{n_\text {p}}\bigg )^u \cdot qd. \end{aligned}$$

Then

$$\begin{aligned} -\log S \ge -\bigg (u \log \frac{n_\text {f}}{n_\text {p}} + \log (qd)\bigg ) = u \log \frac{n_\text {p}}{n_\text {f}} - \log (qd) \ge \lambda _\text {sec}. \end{aligned}$$

We now analyze completeness.

Theorem 2

Let

$$\begin{aligned} d \ge \frac{2u\lambda _\text {rel}}{\log e}; q = \frac{2\lambda _\text {rel}}{d \log e}. \end{aligned}$$

Then completeness error is $\le 2^{-\lambda _\text {rel}}$ and the probability that there exists a valid proof with a particular integer t is at least $q - (u + 1) \cdot \frac{q^2}{2}$.

Proof

Completeness can be described using the following recursive formula. For $0 \le k \le u$, let f(k) be the probability that when fixing a prefix of an integer in [d] and $u-k$ elements $t, s_1, ..., s_{u-k}$, there is no suffix of honest player’s elements that works, meaning there is no $s_{u-k+1}, ..., s_u \in S_\text {p}$ such that for all $u - k + 1 \le i \le u$, $H_1(t, s_1, ..., s_i) = 1$, and $H_2(t, s_1, ..., s_u) = 1$. Then one can see that

• $f(0) = 1 - q$;

• for $0 \le k < u$, $f(k+1) = \big ((1 - \frac{1}{n_\text {p}}) + \frac{1}{n_\text {p}} \cdot f(k)\big )^{n_\text {p}}$;

• the probability that there does not exist a valid proof with a particular integer t is f(u);

• the probability that the algorithm fails in the honest case is $\big (f(u)\big )^d$.

This recursive formula can be approximated:

$$\begin{aligned} f(k+1) = \bigg (1 + \frac{1}{n_\text {p}} \big (f(k) - 1\big )\bigg )^{n_\text {p}} \le \Big (e^{\frac{1}{n_\text {p}} (f(k) - 1)}\Big )^{n_\text {p}} = e^{f(k) - 1}. \end{aligned}$$

(2)

It is convenient to look at the negative logarithm of this expression; we will prove by induction that $-\ln f(k) \ge q - k \cdot \frac{q^2}{2}$.

Basic case: $-\ln f(0) = -\ln (1 - q) \ge -\ln (e^{-q}) = q$.

Inductive step: by Eq. 2,

$$\begin{aligned} -\ln f(k+1) \ge 1 - f(k) \ge 1 - e^{-\big (q - k \cdot \frac{q^2}{2}\big )} [\ge ] \end{aligned}$$

Using the values for d and q, one can see that $k \cdot \frac{q^2}{2} \le u \cdot \frac{q^2}{2} \le q$, then

$$\begin{aligned} & [\ge ] 1 - \Bigg (1 - \bigg (q - k \cdot \frac{q^2}{2}\bigg ) + \frac{\big (q - k \cdot \frac{q^2}{2}\big )^2}{2}\Bigg ) \ge \\ &\qquad \bigg (q - k \cdot \frac{q^2}{2}\bigg ) - \frac{q^2}{2} = q - (k + 1) \cdot \frac{q^2}{2}. \end{aligned}$$

Hence, $-\ln f(u) \ge q - u \cdot \frac{q^2}{2}$ and the probability that the honest prover fails is $\big (f(u)\big )^d \le \exp \Big (-\big (q - u \cdot \frac{q^2}{2}\big ) d\Big )$. Using the values for d and q, one can see that this is at most $2^{-\lambda _\text {rel}}$. Additionally, the probability that there exists a valid proof with a particular integer t is

$$\begin{aligned} &\quad \qquad \qquad \qquad 1 - f(u) \ge e^{-\big (q - u \cdot \frac{q^2}{2}\big )} \ge \\ & 1 - \Bigg (1 - \bigg (q - u \cdot \frac{q^2}{2}\bigg ) + \frac{(q - u \cdot \frac{q^2}{2})^2}{2}\Bigg ) \ge q - (u + 1) \cdot \frac{q^2}{2}. \end{aligned}$$

   $\square$

Corollary 1

Let

$$\begin{aligned} u \ge \frac{\lambda _\text {sec}+ \log \lambda _\text {rel}+ 1 - \log \log e}{\log \frac{n_\text {p}}{n_\text {f}}}; d \ge \frac{2u\lambda _\text {rel}}{\log e}; q = \frac{2\lambda _\text {rel}}{d \log e}. \end{aligned}$$

Then soundness error is $\le 2^{-\lambda _\text {sec}}$ and completeness error is $\le 2^{-\lambda _\text {rel}}$.

It is worth noting that the constant in d, and thus algorithm’s running time, can be reduced. We show how to do this in the full version. Although the scheme still remains less efficient than the improved construction in Sect. 3.2, the optimizations can potentially be transferred over; we leave that for future work.

Running Time. In this section we analyze the prover’s running time.

Assume $S_\text {p}$ is a set with cardinality $n_\text {p}$. As mentioned above, all tuples $(j, s_1, ..., s_i)$ can be represented as d trees. We would like to analyze the number of “accessible” vertices in these trees. Let the indicator random variable

$$\begin{aligned} A_{j, s_1, ..., s_i} = {\left\{ \begin{array}{ll} 1 &{} \text {if for all}\, 1 \le r \le i, H_1(j, s_1, ..., s_r) = 1\\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

If $A_{j, s_1, ..., s_i} = 1$ we say the vertex $(j, s_1, ..., s_i)$ is accessible.

Let us first prove that the expected number of accessible vertices in a single tree at a particular height is 1.

Theorem 3

For any j and $0 \le i \le u$,

We present the proof in the full version [CKRZ23] of this work.

Assuming the prover runs DFS, Theorem 2 gives a bound on the expected number of evaluated trees. And by the above theorem, the algorithm invokes $H_1$ $n_\text {p}u$ times and $H_2$ once in expectation per tree. Thus, the expected total number of hash evaluations shall be the product of the expected number of evaluated trees and $(n_\text {p}u + 1)$. This, however, needs a more careful proof.

Theorem 4

The expected number of hash evaluations is at most

$$\begin{aligned} \bigg (q - (u + 1) \cdot \frac{q^2}{2}\bigg )^{-1} (n_\text {p}u + 1) \end{aligned}$$

We present the proof in the full version [CKRZ23] of this work.

Taking parameter values from Corollary 1 and letting $\lambda = \lambda _\text {sec}= \lambda _\text {rel}$, we thus obtain an expected number of hash evaluations of $O(n_\text {p}\cdot \lambda ^2)$.

We might also wish to have a tighter bound on the running time or on the number of accessible vertices to argue that an adversary cannot exploit an imperfect hash function or a PRF by making too many queries. Below we present a Chernoff style bound on the number of accessible non-root vertices in all d trees

$$\begin{aligned} Z = \sum _{\begin{array}{c} 1 \le j \le d,\\ 1 \le i \le u,\\ s_1, ..., s_i \in S_\text {p} \end{array}} A_{j, s_1, ..., s_i}. \end{aligned}$$

Note that .

Theorem 5

$$\begin{aligned} \Pr [Z \ge (1 + \delta ) du] \le \exp \bigg (-\frac{\delta ^2}{4 (1 + \delta )} \cdot \frac{d}{u}\bigg ). \end{aligned}$$

We present the proof in the full version [CKRZ23] of this work.

Taking parameter values from Corollary 1 and letting $\lambda = \lambda _\text {sec}= \lambda _\text {rel}$, we thus conclude that the algorithm does $O(n_\text {p}\cdot \lambda ^3)$ hash evaluations with overwhelming probability.

3.2 Construction with Prehashing

The basic scheme described above has proving expected time $O(n_\text {p}\cdot \lambda ^2)$ and verification time $O(\lambda )$ if we let $\lambda = \lambda _\text {sec}= \lambda _\text {rel}$. The modification described in this section has proving expected time $O(n_\text {p}+ \lambda ^2)$ and verification time is unchanged.

The improvement is inspired by balls-and-bins collisions. Whereas in the previous scheme for every tuple we tried each of $n_\text {p}$ possible extensions, here we hash tuples to a uniform value in $[n_\text {p}]$ and hash individual set elements to a uniform value in $[n_\text {p}]$, and consider a valid extension to be such that the tuple and the extension both hash to the same value. More formally, we have random functions $H_0$ and $H_1$ producing a uniformly random value in $[n_\text {p}]$ and hash function $H_2$ returning 1 with probability q and 0 otherwise, and consider a tuple $(t, s_1, ..., s_u)$ a valid proof if and only if

• $1 \le t \le d$;

• for all $1 \le i \le u$, $H_1(t, s_1, ..., s_{i-1}) = H_0(s_i)$;

• $H_2(t, s_1, ..., s_u) = 1$;

(see Sect. 3.3 how to implement $H_1$ efficiently). Define the $\textsf{Verify}$ program accordingly.

As before, we have d valid tuples in expectation at each stage but by precomputing $H_0(\cdot )$ (balls to bins) we avoid trying all $n_\text {p}$ extensions for a tuple. The analysis of completeness, however, is more complicated. Before, we assumed in the recursive formula that failure events for each element extension are all independent. Here, it is not true: the fact that one extension eventually succeeds can tell that the balls-to-bins are well distributed. Indeed, if each bin gets exactly one ball, then there will always be a tuple that succeeds except maybe for the requirement that $H_2(\cdot ) = 1$. However, if all balls land in one bin, then the success probability is smaller. To get rid of this dependency, we can however fix the balls-to-bins arrangement. Then such events become independent again.

The proof has two parts: the first one says that if the arrangement of the balls is “nice”, then with high probability the honest player succeeds. The second part proves that we get a “nice” distribution of balls with high probability. The “nice” property itself is artificial, but one can notice that if the number of bins of size s is exactly the expected number of bins of size s if the size of each bin is a Poisson random variable with mean 1, then the analysis of completeness becomes very similar to that of the previous scheme. By using Poisson approximation and Chernoff like analysis, we can show that the property we care about does hold with high probability. We need, however, assume that the number of set elements $n_\text {p}$ is large enough (on the order of $\lambda ^3$). Alternatively, we can generate multiple balls per set element.

We first analyze soundness. As mentioned previosly, we define soundness error to be the probability that a valid proof can be constructed using elements $S_\text {f}$ with $|S_\text {f}| = n_\text {f}$ (simple soundness).

Theorem 6

Let

$$\begin{aligned} u \ge \frac{\lambda _\text {sec}+ \log (qd)}{\log \frac{n_\text {p}}{n_\text {f}}}. \end{aligned}$$

Then soundness error is $\le 2^{-\lambda _\text {sec}}$.

We present the proof in the full version [CKRZ23] of this work.

Theorem 7

Assume

$$\begin{aligned} d \ge \frac{16 u (\lambda _\text {rel}+ \log 3)}{\log e}; q = \frac{2 (\lambda _\text {rel}+ \log 3)}{d \log e}; n_\text {p}\ge \frac{d^2 \log e}{9 (\lambda _\text {rel}+ \log 3)}. \end{aligned}$$

(3)

Then completeness error is $\le 2^{-\lambda _\text {rel}}$.

We present the proof in the full version [CKRZ23] of this work.

Corollary 2

Assume

$$\begin{aligned} & u \ge \frac{ \lambda _\text {sec}+ \log (\lambda _\text {rel}+ \log 3) + 1 - \log \log e}{\log \frac{n_\text {p}}{n_\text {f}}}; d \ge \frac{16 u (\lambda _\text {rel}+ \log 3)}{\log e};\\ &\qquad \qquad \quad q = \frac{2 (\lambda _\text {rel}+ \log 3)}{d \log e}; n_\text {p}\ge \frac{d^2 \log e}{8 (\lambda _\text {rel}+ \log 3)}. \end{aligned}$$

Then soundness is $\le 2^{-\lambda _\text {sec}}$ and completeness error is $\le 2^{-\lambda _\text {rel}}$.

It is worth noting that the $n_\text {p}\ge \varOmega (\lambda ^3)$ requirement can be removed as follows. Instead of doing Chernoff like analysis, that requires large $n_\text {p}$, one can utilize Markov’s inequality to show that the “nice” arrangement of balls into bins happens with moderate probability, e.g. $\frac{3}{4}$, to achieve a scheme with completeness $\frac{1}{2}$. Such a scheme can then be amplified to achieve arbitrary $\lambda _\text {rel}$ by setting $\lambda _\text {sec}{:}{=}\lambda _\text {sec}+ \log \lambda _\text {rel}$ and having the verifier accept any one of $\lambda _\text {rel}$ independent proofs. As a result, the expected running time is no longer $\varOmega (\lambda ^3)$ but $O(n_\text {p}+ \lambda ^2)$, but we need to apply $H_0$ to all elements twice in expectation as opposed to exactly once. Hence, for large $n_\text {p}$ it still makes sense to use the algorithm as described at the beginning of the section. The Markov analysis can be found in the full version [CKRZ23] of this paper.

Running Time. In this section we analyze the prover’s running time. Assume $S_\text {p}$ is a set with cardinality $n_\text {p}$. As described in Sect. 3.1, all tuples $(j, s_1, ..., s_i)$ can be represented as d trees of height u. We would like to analyze the number of “accessible” vertices in these trees. Let the indicator random variable

$$\begin{aligned} A_{j, s_1, ..., s_i} = {\left\{ \begin{array}{ll} 1 &{} \text {if for all}\, 1 \le r \le i, H_1(j, s_1, ..., s_{r-1}) = H_0(s_r)\\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

If $A_{j, s_1, ..., s_i} = 1$ we say the vertex $(j, s_1, ..., s_i)$ is accessible.

Similarly to Sect. 3.1, one can prove that the expected number of accessible vertices in a single tree at a particular height is 1. This holds independently of the value of $H_0$!

Theorem 8

For any j and $0 \le i \le u$,

We will now analyze the expected running time of the prover. The hash function $H_0$ is invoked exactly $n_\text {p}$ times, so we will only upper bound the expected number of invocations of $H_1$ and $H_2$.

Theorem 9

The expected number of invocations of $H_1$ and $H_2$ is at most

$$\begin{aligned} \frac{u + 1}{1 - e^{-q + 4uq^2}} + 2 e^{-\frac{9}{4} n_\text {p}q^2} \cdot d (u + 1). \end{aligned}$$

We present the proof in the full version [CKRZ23] of this work.

Taking parameter values from Corollary 2 and letting $\lambda = \lambda _\text {sec}= \lambda _\text {rel}$, we thus get expected number of evaluations of $H_1$ and $H_2$ $O(\lambda ^2)$. This is dominated by $n_\text {p}$ invocations of $H_0$ since $n_\text {p}$ is assumed to be $\varOmega (\lambda ^3)$.

Below we also present a tight bound on the number of accessible non-root vertices in all d trees

$$\begin{aligned} Z = \sum _{\begin{array}{c} 1 \le j \le d,\\ 1 \le i \le u,\\ s_1, ..., s_i \in S_\text {p} \end{array}} A_{j, s_1, ..., s_i}. \end{aligned}$$

Note that .

Theorem 10

Let

Then

$$\begin{aligned} \Pr [Z \ge \delta du] \le 2^{-\lambda }. \end{aligned}$$

We present the proof in the full version [CKRZ23] of this work.

Taking parameter values from Corollary 2 and letting $\lambda = \lambda _\text {sec}= \lambda _\text {rel}$, we thus conclude that the prover algorithm evaluates $H_1$ and $H_2$ $O(\lambda ^3)$ times with overwhelming probability.

3.3 Implementing Random Oracles with Long Inputs

We describe our protocols assuming a random oracle $H_1$ that can accommodate inputs of any length, which, in particular, implies independence of outputs for inputs of different lengths. However, to have an accurate accounting for running times, one has to charge for the cost of running a random oracle in proportion to the input length. Because the Telescope construction runs $H_1(j)$, $H_1(j, s_1)$, $H_1(j, s_1, s_2)$, $H_1(j, s_1, s_2 \dots , s_u)$, the cost of just one u-tuple is quadratic in u. To reduce this cost to linear (thus saving a factor of u in running time), we will implement $H_1(j, s_1, \dots , s_{i+1})$ to reuse most of the computation of $H_1(j, s_1, \dots , s_i)$. The most natural way to do so is to slightly modify the Merkle-Damgård construction: use a two-input random oracle f (“compression function”) with a sufficiently long output and a function g that maps the range of f to the distribution needed by $H_1$. We present the details of implementing g in the full version of this work. Inductively define $H'_1(j, s_1, \dots , s_{i+1})=f(H'_1(j, s_1, \dots , s_i), s_{i+1})$ and let $H_1(x)=g(H'_1(x))$.

While not indifferentiable from a random oracle (see Coron et al. [CDMP05] for similar constructions that are), this construction suffices for our soundness and extractability arguments, because those arguments need independence only for a single chain (they handle multiple different chains by the union bound). Neither length extension attacks nor collisions are important. Completeness suffers very slightly by the probability of f-collisions, which can be made negligible by making the output of f large enough and using the bound on the number of queries made by the honest prover (Theorems 5 and 10).

3.4 Optimality of the Certificate Size

In this section, we show that the number of set elements u included in a proof is essentially optimal for our constructions. Because our construction works for a black-box weight function that formally is implemented via an oracle (and in reality may be implemented by MPC, a human judge, etc.), the verifier must query the weight function on some values; else the verifier has no knowledge of whether any values in the prover’s possession have any weight.

Thus, for the sake of proving optimality, we consider only protocols that make this part of verification explicit. We define an algorithm $\textsf{Read}$ (see the definition below) that takes a proof and returns set elements; these set elements must have been in the prover’s possession. We bound the proof size in terms of the number of set elements returned by $\textsf{Read}$, showing that if it is too small, the protocol cannot be secure. We also note that the following definition can be used for upper bound results too, as demonstrated in Sect. 7 for the CRS model.

Definition 4

$(\textsf{Prove}, \textsf{Read}, \textsf{Verify})$ is a $(\lambda _\text {sec}, \lambda _\text {rel}, n_\text {p}, n_\text {f})$-ALBA scheme if and only if

• $\textsf{Prove}^H$ is a probabilistic random oracle access program;

• $\textsf{Verify}^H$ is a random oracle access program;

• $\textsf{Read}$ is a program;

• completeness: consider the following experiment $\text {CompExp}(S_\text {p})$:

  

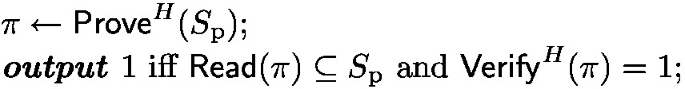
  we require that for all sets $S_\text {p}$ with size $\ge n_\text {p}$, $\Pr [\text {CompExp}(S_\text {p}) = 1] \ge 1 - 2^{-\lambda _\text {rel}}$.

• soundness: consider the following experiment $\text {SoundExp}(S_\text {f})$:

  

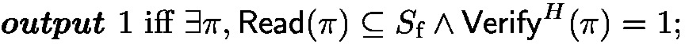
  we require that for all sets $S_\text {f}$ with size $\le n_\text {f}$, $\Pr [\text {SoundExp}(S_\text {f}) = 1] \le 2^{-\lambda _\text {sec}}$;

We now prove a lower bound for a scheme satisfying this definition.

Theorem 11

Assume $\lambda _\text {rel}\ge 1$, define $\alpha = \frac{\lambda _\text {sec}- 3}{\log (n_\text {p}/ n_\text {f})}$, assume $n_\text {f}\ge 3 \alpha ^2$, let $S_\text {p}$ be an arbitrary set of size $n_\text {p}$, and let $(\textsf{Prove}, \textsf{Read}, \textsf{Verify})$ be a $(\lambda _\text {sec}, \lambda _\text {rel}, n_\text {p}, n_\text {f})$-ALBA scheme. Then

$$\begin{aligned} \Pr \Big [\big |\textsf{Read}(\textsf{Prove}^H(S_\text {p}))\big | > \alpha \Big ] \ge \frac{1}{4}. \end{aligned}$$

We present the proof in the full version [CKRZ23] of this work.

4 ALBAs with Decentralized Prover

In the previous section we assumed the ALBA prover has all the set elements at hand. In many applications however, such as threshold signatures, this is not the case. The set elements may be spread across numerous parties who will then jointly compute a proof. A trivial solution is to use a centralized protocol, by designating one of the parties as the lead prover and have all other parties communicate their set elements to that party. However, this incurs a communication cost equal to the size of the set, which we would rather avoid.

In this section we present protocols where the various parties holding set elements start out by performing computations locally and only conditionally communicate their elements to a designated prover or aggregator. Whilst our constructions we present in this section still use weights of 0 or 1, they can be generalized to integer weights as explained in Sect. 5. Finally, as in Sect. 3, instead of proof of knowledge we consider a simpler notion of soundness: the probability that a valid proof exists containing only elements from set $S_\text {f}$ of size $n_\text {f}$. Section 6 demonstrates how to do knowledge extraction.

4.1 Simple Lottery Construction

The simple lottery scheme is parametrized by the expected number of network participants $\mu$. Let H be a random oracle that outputs 1 with probability $p = \frac{\mu }{n_\text {p}}$ and 0 otherwise. Each set element s is sent to the aggregator over the network if and only if $H(s)=1$. Now let $r_\text {s}, r_\text {c}> 1$ such that $r_\text {s}r_\text {c}= \frac{n_\text {p}}{n_\text {f}}$ and set $u = r_\text {s}\cdot pn_\text {f}$ (or equivalently $u = \frac{pn_\text {p}}{r_\text {c}}$). The aggregator needs to collect and concatenate u set elements and the verifier accepts if it receives u values that each hash to 1.

Lemma 1

Assuming

$$ u \ge \frac{\lambda _\text {sec}\cdot \ln 2}{\ln r_\text {s}- 1 + \frac{1}{r_\text {s}}}\,, $$

soundness error of the scheme is $\le 2^{-\lambda _\text {sec}}$.

We present the proof in the full version [CKRZ23] of this work.

Lemma 2

Assuming

$$ u \ge \frac{\lambda _\text {rel}\cdot \ln 2}{r_\text {c}- 1 - \ln r_\text {c}}\,, $$

completeness error of the scheme is $\le 2^{-\lambda _\text {rel}}$.

We present the proof in the full version [CKRZ23] of this work.

Thus, to minimize u, we need to minimize

$$\begin{aligned} \max \bigg \{ \frac{\lambda _\text {sec}\cdot \ln 2}{\ln r_\text {s}- 1 + \frac{1}{r_\text {s}}}, \frac{\lambda _\text {rel}\cdot \ln 2}{r_\text {c}- 1 - \ln r_\text {c}} \bigg \}. \end{aligned}$$

Noting that the first term is decreasing with respect to $r_\text {s}$ and the second term is decreasing with respect to $r_\text {c}$, the minimum is achieved when the two terms are equal. If $\lambda _\text {sec}=\lambda _\text {rel}=\lambda$, then setting $r_\text {c}=\frac{n_\text {p}}{n_\text {p}-n_\text {f}}\cdot \ln \frac{n_\text {p}}{n_\text {f}}$ and $r_\text {s}=\frac{n_\text {p}-n_\text {f}}{n_\text {f}}\cdot \frac{1}{\ln \frac{n_\text {p}}{n_\text {f}}}$ gives the smallest u.

We note the interesting fact that choosing $r_\text {s}$ and $r_\text {c}$ that minimize u also minimizes $\mu$. Since $\mu = pn_\text {p}= ur_\text {c}$, we have

$$\begin{aligned} \mu \ge \max \bigg \{ \frac{\lambda _\text {sec}\cdot \ln 2}{\ln r_\text {s}- 1 + \frac{1}{r_\text {s}}} \cdot r_\text {c}, \frac{\lambda _\text {rel}\cdot \ln 2}{r_\text {c}- 1 - \ln r_\text {c}} \cdot r_\text {c}\bigg \}. \end{aligned}$$

The first term is decreasing with respect to $r_\text {s}$ since $r_\text {c}$ is, and it can be seen that the second term is decreasing with respect to $r_\text {c}$. Hence, $\mu$ is minimized when the two terms are equal which is the same as the condition for minimizing u.

4.2 Decentralized Telescope

The next logical step to minimize the size of the proof is to run a smarter aggregator, Telescope, and calculate an appropriate increase to the security and reliability parameters. While combining a simple lottery with an ALBA aggregator is a generic technique, the generic analysis requires one to calculate two lottery tail bounds: one for soundness and one for completeness. By using Telescope for the aggregator, we benefit from omitting the soundness tail bounds from analysis; this section has all details.

As previously, we have parameter $\mu$ and select each element to be transmitted over the network with probability $\mu / n_\text {p}$. After receiving enough elements selected by the simple lottery, the aggregator runs the algorithm from Sect. 3.2. Note that it assumes that the number of set elements is large enough, see a bound on $n_\text {p}$ in Theorem 7. Since $\mu$ can be much smaller than said bound, we artificially increase the number of set elements by producing k sub-elements for each element, for an appropriate k. This is a purely technical hindrance that goes away in the full version [CKRZ23] of this paper which describes an ALBA scheme without this requirement.

We employ threshold analysis here: calculate the number of set elements selected by the simple lottery such that 1) this number is achievable with probability $1 - \frac{1}{4} \cdot 2^{-\lambda _\text {rel}}$ and 2) the Telescope aggregator will produce a valid certificate with probability $1 - \frac{3}{4} \cdot 2^{-\lambda _\text {rel}}$.

For all $1 \le i \le n_\text {p}$, let $X_i$ be 1 if and only if element $s_i$ is selected and 0 otherwise. Let $X = \sum _{i=1}^{n_\text {p}} X_i$; then . Assume $\rho \in \mathbb {N}$ satisfies $\Pr [X \ge \rho ] \ge 1 - 2^{-\lambda _\text {rel}- 2}$. Reducing the honest-malicious gap from $\frac{n_\text {p}}{n_\text {f}}$ to $\frac{\rho }{\frac{\mu }{n_\text {p}} \cdot n_\text {f}} = \frac{n_\text {p}}{n_\text {f}} \cdot \frac{\rho }{\mu }$ results in increasing the certificate size to

$$\begin{aligned} \frac{\lambda _\text {sec}+ \log (\lambda _\text {rel}+ 2) + 1 + \log e - \log \log e}{\log \frac{n_\text {p}}{n_\text {f}} + \log \frac{\rho }{\mu }} \end{aligned}$$

(we have $\lambda _\text {sec}+ \log (\lambda _\text {rel}+ 2) + 1 + \log e - \log \log e$ instead of $\lambda _\text {sec}+ \log (\lambda _\text {rel}+ \log 3) + 1 - \log \log e$ in Theorem 2 because we instantiate it with $\lambda _\text {sec}:= \lambda _\text {sec}+ \log e$ and $\lambda _\text {rel}:= \lambda _\text {rel}+ \log \frac{4}{3}$ for technical reasons).

One can think of the gap $\frac{\rho n_\text {p}}{\mu n_\text {f}}$ as $\frac{(1 - \delta ) n_\text {p}}{n_\text {f}}$ if we set $\rho = (1 - \delta ) \mu$. Note that we only decrease $n_\text {p}$ in the $\frac{n_\text {p}}{n_\text {f}}$ gap. $n_\text {f}$ remains the same since the union bound argument for soundness still works, but with some modifications. Particularly, it requires $\mu$ to be on the order of $u^2$. If we wanted to decrease $\mu$ even further, we could improve the proof below or employ a two-sided threshold analysis as well.

Let $\text {Lottery}: \{0, 1\}^* \rightarrow \{0, 1\}$ be an oracle returning 1 with probability $\frac{\mu }{n_\text {p}}$ and assume $H = (H_0, H_1, H_2, \text {Lottery})$ where $H_0$, $H_1$, $H_2$ are as defined in Sect. 3.2. Also let $A.\textsf{Prove}^H$, $A.\textsf{Verify}^H$ be as in Sect. 3.2 and define the following.

Theorem 12

Assume

$$\begin{aligned} k \ge \frac{d^2 \log e}{9 \rho (\lambda _\text {rel}+ 2)} \end{aligned}$$

and instantiate the algorithm in Sect. 3.2 with $d \ge \frac{16 u (\lambda _\text {rel}+ 2)}{\log e}$, $q := \frac{2 (\lambda _\text {rel}+ 2)}{d \log e}$, and $n_\text {p}:= k \rho$. Then completeness error is $\le 2^{-\lambda _\text {rel}}$.

Proof

As assumed above, the simple lottery chooses at least $\rho$ set elements with probability at least $1 - 2^{-\lambda _\text {rel}- 2}$. Given this event, by Theorem 7, the algorithm outputs a valid certificate with probability at least $1 - 2^{-\lambda _\text {rel}- \log \frac{4}{3}}$. Therefore, completeness error is $\le 2^{-\lambda _\text {rel}}$.    $\square$

We now calculate soundness error defined as the probability that a valid proof can be constructed using elements $S_\text {f}$ with $|S_\text {f}| = n_\text {f}$.

Theorem 13

Assume

$$\begin{aligned} &\qquad \qquad \mu \ge \frac{n_\text {p}u^2}{n_\text {f}};\quad \quad \quad \frac{\rho n_\text {p}}{\mu n_\text {f}} > 1;\\ &u \ge \frac{\lambda _\text {sec}+ \log (\lambda _\text {rel}+ 2) + 1 + \log e - \log \log e}{\log \frac{n_\text {p}}{n_\text {f}} + \log \frac{\rho }{\mu }}. \end{aligned}$$

Then soundness error is $\le 2^{-\lambda _\text {sec}}$.

We present the proof in the full version [CKRZ23] of this work.

Theorem 12 and 13 give

Corollary 3

Assume

$$\begin{aligned} \mu \ge \frac{n_\text {p}u^2}{n_\text {f}};\quad \quad \quad \frac{\rho n_\text {p}}{\mu n_\text {f}} > 1; \quad \quad \quad k \ge \frac{d^2 \log e}{9 \rho (\lambda _\text {rel}+ 2)};\\ u \ge \frac{\lambda _\text {sec}+ \log (\lambda _\text {rel}+ 2) + 1 + \log e - \log \log e}{\log \frac{n_\text {p}}{n_\text {f}} + \log \frac{\rho }{\mu }} \end{aligned}$$

and instantiate the algorithm in Sect. 3.2 with $u := u$, $d \ge \frac{16 u (\lambda _\text {rel}+ 2)}{\log e}$, $q := \frac{2 (\lambda _\text {rel}+ 2)}{d \log e}$, and $n_\text {p}:= k \rho$. Then soundness error is $\le 2^{-\lambda _\text {sec}}$ and completeness error is $\le 2^{-\lambda _\text {rel}}$.

Using this, we can see how big $\mu$ needs to be if we increase $u \log \frac{n_\text {p}}{n_\text {f}}$ only by some amount C. To calculate a suitable $\rho$, we just use a Chernoff bound: $\Pr [X \le (1 - \delta ) \mu ] \le e^{-\frac{\mu \delta ^2}{2}}$. Setting this to $2^{-\lambda _\text {rel}- 2}$, we get . We now set $\rho = \big \lceil (1 - \delta ) \mu \big \rceil$.

Corollary 4

Assume

and instantiate the algorithm in Sect. 3.2 just like in corollary 3. Then soundness error is $\le 2^{-\lambda _\text {sec}}$ and completeness error is $\le 2^{-\lambda _\text {rel}}$.

We present the proof in the full version [CKRZ23] of this work.

Thus, if we let $\lambda = \lambda _\text {sec}= \lambda _\text {rel}$ and let u only be a constant larger than optimal, we have $\mu = O(\lambda ^3)$ as well as the time complexity of the centralized algorithm also $O(\lambda ^3)$. Moreover, $\mu$ is proportional to $\frac{1}{C^2}$. We note, however, that setting $\lambda _\text {rel}{:}{=}1$ and $\lambda _\text {sec}{:}{=}\lambda _\text {sec}+ \log \lambda _\text {rel}$ and amplifying the completeness via parallel repetitions as mentioned in Sect. 3.2 lets us reduce the expected communication complexity to $O(\lambda ^2)$. However, it requires some network engineering to avoid redundant communication, specifically delaying repetitions until the previous ones have certainly failed.

In the full version [CKRZ23], we also present a different corollary showing what u needs to be in terms of $\mu$.

4.3 Optimality of the Certificate Size - Communication Tradeoff

We can attempt to find a lower bound for the tradeoff between the certificate size u and $\mu$. For this purpose, we use the following definition.

Definition 5

$(\textsf{Prove}, \textsf{Read}, \textsf{Verify})$ is a $(\lambda _\text {sec}, \lambda _\text {rel}, n_\text {p}, n_\text {f}, \mu )$-lottery based ALBA scheme if and only if

• $\textsf{Prove}^H$ is a probabilistic random oracle access program;

• $\textsf{Verify}^H$ is a random oracle access program;

• $\textsf{Read}$ is a program;

• if L is a random function such that for all x, $\Pr [L(x) = 1] = \frac{\mu }{n_\text {p}}$ and we define $\text {Lottery}(S) = \{x \in S : L(x) = 1\}$, then

  • completeness: consider the following experiment $\text {CompExp}(S_\text {p})$:

    

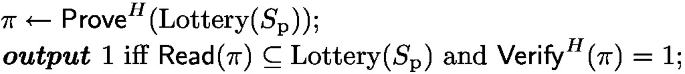
    we require that for all sets $S_\text {p}$ with size $\ge n_\text {p}$, $\Pr [\text {CompExp}(S_\text {p}) = 1] \ge 1 - 2^{-\lambda _\text {rel}}$.

  • soundness: consider the following experiment $\text {SoundExp}(S_\text {f})$:

    

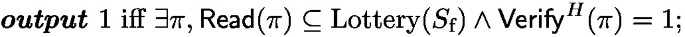
    we require that for all sets $S_\text {f}$ with size $\le n_\text {f}$, $\Pr [\text {SoundExp}(S_\text {f}) = 1] \le 2^{-\lambda _\text {sec}}$;

The following theorem presents our lower bound.

Theorem 14

Assume $\rho$ satisfies $\Pr \big [B(n_\text {p}, \frac{\mu }{n_\text {p}}) \le \rho \big ] \ge 2^{-\lambda _\text {rel}+ 1}$ where B(n, p) is a binomial random variable with n experiments each with probability of success p. Also assume

$$\begin{aligned} \frac{\rho n_\text {p}}{\mu n_\text {f}} > 1; \quad \mu \ge \frac{3 u^2 n_\text {p}\log e}{2 n_\text {f}}; \quad n_\text {f}\ge \rho , \end{aligned}$$

let $S_\text {p}$ be an arbitrary set of size $n_\text {p}$ and let $(\textsf{Prove}, \textsf{Read}, \textsf{Verify})$ be a $(\lambda _\text {sec}, \lambda _\text {rel}, n_\text {p},n_\text {f}, \mu )$-lottery based ALBA scheme such that

$$\begin{aligned} \Pr \Big [\big |\textsf{Read}(\textsf{Prove}^H(\text {Lottery}(S_\text {p})))\big | \le u\Big ] = 1. \end{aligned}$$

Then

$$\begin{aligned} u > \frac{\lambda _\text {sec}- 4}{\log \frac{n_\text {p}}{n_\text {f}} + \log \frac{\rho }{\mu }}. \end{aligned}$$

We present the proof in the full version [CKRZ23] of this work.

Using this, we can establish a lower bound similar to the upper bound Corollary 4.

Corollary 5

Let $C > 0$, define

$$\begin{aligned} \alpha = \frac{\lambda _\text {sec}- 4 + C}{\log \frac{n_\text {p}}{n_\text {f}}}; u = \lfloor \alpha \rfloor \end{aligned}$$

and assume

$$\begin{aligned} \max \bigg \{\frac{4}{\lambda _\text {rel}}, \frac{\lambda _\text {rel}}{(1 - \frac{n_\text {f}}{n_\text {p}})^2}, \frac{3 u^2 n_\text {p}\log e}{2 n_\text {f}}\bigg \} \le \mu \le \min \bigg \{\frac{\alpha ^2 \lambda _\text {rel}\log ^2 e}{4\,C^2}, \frac{(\frac{4}{e})^{\lambda _\text {rel}}}{4 e^{10}}\bigg \};\\ n_\text {f}\ge 2 \mu . \end{aligned}$$

Let $S_\text {p}$ be an arbitrary set of size $n_\text {p}$ and let $(\textsf{Prove}, \textsf{Read}, \textsf{Verify})$ be a $(\lambda _\text {sec}, \lambda _\text {rel}, n_\text {p}, n_\text {f}, \mu )$-lottery based ALBA scheme. Then

$$\begin{aligned} \Pr \Big [\big |\textsf{Read}(\textsf{Prove}^H(\text {Lottery}(S_\text {p})))\big | > \alpha \Big ] > 0. \end{aligned}$$

We present the proof in the full version [CKRZ23] of this work.

Alternatively, in the full version we also present a corollary showing a lower bound on the certificate size as of function of $\mu$.

5 Adding Weights

We will assume, without loss of generality, that the weight function W outputs integers. A naive way to handle weights other than 0 and 1 is to interpret each set element s as W(s) elements $(s, 1), \dots , (s, W(s))$ and apply schemes designed for the unweighted case to (s, i) pairs. Unfortunately, this approach makes the prover running time linear in the total weight which could be in the order of $2^{64}$.

Fortunately, any lottery-based scheme in which the number of lottery winners is independent of $n_\text {p}$ (or at most polylogarithmic in $n_\text {p}$) is amenable to a more efficient solution (and the Telescope scheme in Sect. 3 can be turned into a lottery-based scheme first using Sect. 4.2). We simply view $(s, 1), \dots , (s, W(s))$ pairs as W(s) different lottery participants. For efficiency, instead of having each of them play the lottery individually with probability p, we sample the number of winners from the binomial distribution $\textrm{Binom}(W(s),p)$ (similar to the sortition algorithm used in Algorand [GHM+17]). We do so because it does not matter which i values win—what matters is only the number of winners. If the binomial sampling returns k, then $(s, 1), \dots , (s, k)$ are considered winners. This does not increase the complexity compared to the unweighted-lottery-based scheme, except for binomial sampling rather than lottery applied to each element.

Using Corollary 4 with $\lambda _\text {sec}{:}{=}\lambda _\text {sec}+ \log \lambda _\text {rel}$, $\lambda _\text {rel}{:}{=}1$ and $C {:}{=}1$, we achieve a weighted $(\lambda _\text {sec}, \lambda _\text {rel}, n_\text {p}, n_\text {f})$-ALBA scheme with proof size

$$\frac{\lambda _\text {sec}+ \log \lambda _\text {rel}+ 2 + \log 3 + \log e - \log \log e}{\log \frac{n_\text {p}}{n_\text {f}}}$$

and expected prover running time $O(n + \lambda _\text {sec}^2)$, where n is the number of weighted elements in the input.

6 Knowledge Extraction for NIROPK

In this section we show how Definitions 1 and 2 can be realized. While Sects. 3 and 4 provide intuitive constructions with clean combinatorial analysis, they have a missing piece — a knowledge extractor. As we will see, the simple soundness proven there does not immediately imply proof of knowledge, and more reasoning is needed. We also remind that the knowledge extractor must be straight-line; i.e., rewinding of the prover is not allowed but observing its queries to the oracles is. Here we describe the full NIROPK scheme including its knowledge extactor for the case of the basic Telescope construction from Sect. 3.1 while other Telescope constructions can be made NIROPK in a similar fashion. For $H = (H_1, H_2)$, define

Theorem 15

Define parameters as in Theorem 1. Then algorithms $\textsf{Verify}^{H,W}$ with $\textsf{Extract}^{H,W,\mathcal {A}}$ satisfy the proof of knowledge property of Definition 1.

Proof

The extractor succeeds whenever $\mathcal {A}$ succeeds, unless $\mathcal {A}$ succeeds after querying fewer than $n_\text {f}$ elements of S, which happens with probability at most $2^{-\lambda _\text {sec}}$ by the following lemma. Thus, the proof of knowledge property follows by the union bound.

We present the proof in the full version [CKRZ23] of this work.

The following lemma resembles the simple soundness result in Theorem 1, but unfortunately is harder to prove. Whereas the proof of Theorem 1 is a simple application of union bound, the fact that the adversary can choose what weight-1 elements to query adaptively based on past RO responses makes the “vanilla” union bound argument inapplicable. Fortunately, there exists a way around this problem.

Lemma 3

Define parameters as in Theorem 1 and let E be the event that a valid proof can be made from the first $n_\text {f}$ (or less) weight-1 elements that $\mathcal {A}_1^{H,W}$ queries to H. Then $\Pr [E] \le 2^{-\lambda _\text {sec}}$.

We present the proof in the full version [CKRZ23] of this work.

Combining the proof of knowledge property with completeness proven in Sect. 3.1, we now state the main result of this section.

Corollary 6

Using parameters from Corollary 1, $(\textsf{Prove}, \textsf{Verify}, \textsf{Extract})$ is a $(\lambda _\text {sec}, \lambda _\text {rel}, n_\text {p}, n_\text {f})$-NIROPK ALBA scheme.

In summary, we achieve information-theoretic but non-adaptive security; i.e., additional computational power does not help the adversary avoid knowledge extraction but he is not allowed to choose the predicate/weight function based on the random oracle. Adaptive security can be achieved the traditional way: rerandomize the random oracle by including a commitment to the weight function as additional input to the random oracle. However, the security downgrades to computational: assuming that adversary makes at most $2^q$ RO queries, we need to increase ALBA’s $\lambda _\text {sec}$ parameter by q.

7 Replacing the Random Oracle with PRF

In this section we show how to remove the need for the random oracle and instantiate our scheme in the Common Reference String model (or alternatively, the Uniform Random String model). This is a novel feature of our scheme in comparison to compact certificates which inherently rely on the random oracle because of Fiat-Shamir. We utilize a PRF for the hash function H with the CRS being a random PRF key (or alternatively, uniformly random bits sufficient to generate one). We note that although the PRF is only secure against computationally bounded distinguishers, our ALBA scheme retains information-theoretic security.

Assume $(\textsf{GenKey}, F)$ is a PRF such that for any oracle access program $\mathcal {A}^O$ with running time bounded by T,

$$\begin{aligned} \bigg |\Pr \big [\mathcal {A}^H() = 1\big ] - \Pr \Big [\mathcal {A}^{F(\textsf{GenKey}(), \cdot )}() = 1\Big ]\bigg | \le \varepsilon _\text {prf}(T). \end{aligned}$$

(4)

We will assume the unweighted case, but the following can extended to support weights as well. Combining the improved Telescope construction from Sect. 3.2 with the tight bound on the number of accessible vertices (Theorem 10) and instantiating the scheme with the standard (binary) random oracle (the latter is described in the full version) one can build a Telescope scheme such that for some $B \in O(\lambda ^3)$,

• the honest prover’s DFS visits at most B vertices and outputs a valid proof with probability $\ge 1 - 2^{-\lambda }$;

• there exists a valid proof containing elements from $S_\text {f}$ or the number of accessible vertices exceeds B with probability $\le 2^{-\lambda }$.

Implement $\textsf{Prove}^H(S_\text {p})$ as the standard DFS that visits at most B vertices and define $\textsf{Verify}^H(\pi )$ in a natural way. We show an ALBA scheme under Definition 4 where the random oracle is replaced with CRS. Below is the new definition and a Telescope construction for it.

Definition 6

$(\textsf{Prove}, \textsf{Read}, \textsf{Verify}, \textsf{GenCRS})$ is a $(\lambda _\text {sec}, \lambda _\text {rel}, n_\text {p}, n_\text {f})$-CRS ALBA scheme if and only if

• $\textsf{Prove}$ is a probabilistic program;

• $\textsf{Verify}$ is a program;

• $\textsf{Read}$ is a program;

• $\textsf{GenCRS}$ is a probabilistic program;

• completeness: consider the following experiment $\text {CompExp}(S_\text {p})$: we require that for all sets $S_\text {p}$ with size $\ge n_\text {p}$, $\Pr [\text {CompExp}(S_\text {p}) = 1] \ge 1 - 2^{-\lambda _\text {rel}}$.

• soundness: consider the following experiment $\text {SoundExp}(S_\text {f})$:

  

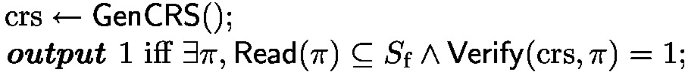
  we require that for all sets $S_\text {f}$ with size $\le n_\text {f}$, $\Pr [\text {SoundExp}(S_\text {f}) = 1] \le 2^{-\lambda _\text {sec}}$;

Theorem 16

R is a $(\lambda _\text {sec}', \lambda _\text {rel}', n_\text {p}, n_\text {f})$-CRS ALBA scheme where $\lambda _\text {sec}' = \lambda _\text {rel}' = -\log \big (2^{-\lambda } + \varepsilon _\text {prf}(O(n_\text {p}+ \lambda ^3))\big )$.

Proof

Completeness follows from the fact that $\textsf{Prove}$’s running time is bounded by $O(n_\text {p}+ B) = O(n_\text {p}+ \lambda ^3)$ steps and that $\textsf{Prove}^H(S_\text {p})$, when instantiated with the random oracle H, finds a valid proof with probability $\ge 1 - 2^{-\lambda }$. Acting as a PRF distinguisher, we conclude that $\textsf{Prove}^{F(\textsf{GenKey}(), \cdot )}$ outputs a valid proof with probability $\ge 1 - 2^{-\lambda } - \varepsilon _\text {prf}(O(n_\text {p}+ \lambda ^3))$.

To prove soundness, we can observe whether a DFS on set $S_\text {f}$ finds a valid proof or does not terminate after visiting B vertices. In the random oracle case, one or both happen with probability $\le 2^{-\lambda }$, so in the PRF case it is $\le 2^{-\lambda } + \varepsilon _\text {prf}(O(n_\text {p}+ \lambda ^3))$. But the probability that there exists a valid proof in the PRF case cannot be larger.    $\square$

We present the complete version of the proof in the full version [CKRZ23] of this work.

7.1 Knowledge Extraction For Definition 6/4

In this section we show how to generically convert an ALBA scheme under Definition 6 to a proof of knowledge scheme under Definition 3. We still assume the unweighted scenario ($W : \{0, 1\}^* \rightarrow \{0, 1\}$) but the following can be generalized to add weights. Sometimes it will be convenient to treat W as a set: $\{s : W(s) = 1\}$.

Let $X = (X.\textsf{Prove}, X.\textsf{Read}, X.\textsf{Verify}, X.\textsf{GenCRS})$ be a $(\lambda _\text {sec}, \lambda _\text {rel}, n_\text {p}, n_\text {f})$-CRS ALBA scheme (as in Definition 6) and define $Y = (Y.\textsf{Prove}, Y.\textsf{Verify}, Y.\textsf{Extract},Y.\textsf{GenCRS})$ as follows.

Theorem 17

Y is $(\lambda _\text {sec}, \lambda _\text {rel}, n_\text {p}, n_\text {f})$-CRS proof of knowledge ALBA scheme.

Proof

It is easy to see that Y satisfies the completeness property. We are left to prove the proof of knowledge property.

First, notice that $Y.\textsf{Extract}$ can only output a set $S_\text {f}$ such that $S_\text {f}\subseteq W$ and $|S_\text {f}| > n_\text {f}$. Now examine a single loop iteration in $Y.\textsf{Extract}$. We know that $\varepsilon = \Pr \big [Y.\textsf{Verify}^W(\text {crs}, \pi ) = 1\big ] - 2^{-\lambda _\text {sec}} > 0$ and $Y.\textsf{Verify}^W(\text {crs}, \pi ) = 1$ implies that $S \subseteq W$ and $X.\textsf{Verify}(\text {crs}, \pi ) = 1$. So,

$$\begin{aligned} 2^{-\lambda _\text {sec}} + \varepsilon = \Pr [Y.\textsf{Verify}^W(\text {crs}, \pi ) = 1] \le \Pr [S \subseteq W \wedge X.\textsf{Verify}(\text {crs}, \pi ) = 1]. \end{aligned}$$

At the same time, since $|S_\text {f}| \le n_\text {f}$, by the soundness of X (considering the experiment $\text {SoundExp}(S_\text {f})$ from Definition 6), $\Pr [S \subseteq S_\text {f}\wedge X.\textsf{Verify}(\text {crs}, \pi ) = 1] \le 2^{-\lambda _\text {sec}}$. Therefore,

$$\begin{aligned} &\qquad \qquad \qquad \qquad \quad \varepsilon = (2^{-\lambda _\text {sec}} + \varepsilon ) - 2^{-\lambda _\text {sec}} \le \\ & \Pr [S \subseteq W \wedge X.\textsf{Verify}(\text {crs}, \pi ) = 1] - \Pr [S \subseteq S_\text {f}\wedge X.\textsf{Verify}(\text {crs}, \pi ) = 1] \le \\ & \Pr [(S \subseteq W \wedge X.\textsf{Verify}(\text {crs}, \pi ) = 1) \wedge \lnot (S \subseteq S_\text {f}\wedge X.\textsf{Verify}(\text {crs}, \pi ) = 1)] =\\ & \qquad \qquad \qquad \Pr [S \subseteq W \wedge S \not \subseteq S_\text {f}\wedge X.\textsf{Verify}(\text {crs}, \pi ) = 1] \le \\ & \qquad \qquad \qquad \qquad \qquad \quad \Pr [S \subseteq W \wedge S \not \subseteq S_\text {f}] \le \\ &\qquad \qquad \qquad \qquad \qquad \quad \Pr [\exists x \in (S \cap W) \setminus S_\text {f}]. \end{aligned}$$

So, a single iteration of the loop adds at least one new element of W to $S_\text {f}$ with probability at least $\varepsilon$. Therefore, in expectation, the loop runs for at most $(n_\text {f}+ 1) \cdot \frac{1}{\varepsilon }$ iterations. Then it is easy to see that $Y.\textsf{Extract}$ runs in expected time $\text {poly}(T, 1 / \varepsilon )$ (treating $n_\text {f}$ as constant).    $\square$

In summary, we achieve information-theoretic but non-adaptive security; i.e., additional computational power does not help the adversary avoid knowledge extraction but he is not allowed to choose the predicate/weight function based on the CRS. Even then, this can be useful; one example is applications where PRF seed is chosen by a randomness beacon after the statement to be proven is already decided. As a last resort, adaptive security can be achieved by rerandomizing the PRF using the random oracle: let the CRS be the output of the random oracle on the description of the weight function. This can be beneficial to instantiating ALBA purely in the random oracle model, for example, when the knowledge of an ALBA proof is proven by a SNARK. In that case, calculating the CRS outside of the SNARK circuit and using PRF inside the circuit lets one avoid heuristically instantiating RO in the circuit.

Fig. 1.

Certificate sizes and expected communication cost, expressed in revealed/sent set elements ($\sigma$) and, in the case of [MRV+21], secondary reveals of the same elements in the form of Merkle Tree paths ($\eta$). The parameters $\lambda _\text {sec},\lambda _\text {rel}$ are set to 128 unless otherwise indicated.

8 Performance Comparisons

In terms of prover computation, the Simple Lottery scheme requires negligible effort from the aggregator (apart from verifying membership and eligibility of the received set elements). Compact certificates require the prover to build a commitment to the set of received set items in the form of a Merkle tree, requiring O(n) hash evaluations, where n is the number of weighted elements in prover’s input. Telescope in turn requires $O(n + \lambda ^2)$ hashes in expectation and Goldwasser-Sipser requires $O(n_\text {p}\cdot \lambda )$ hashes.

In terms of number of revealed elements, compact certificates need to reveal at least $\frac{\lambda _\text {sec}}{\log (n_\text {p}/ n_\text {f})}$ set elements (denoted by $\sigma$) but they additionally need to reveal the Merkle tree path of each element (denoted by $\eta$) with regards to the commitment constructed by the prover. The Simple Lottery scheme only reveals set elements and the number of reveals has the same, linear dependency on $\lambda _\text {sec}$, but has a more complex (and more costly) dependency on $(n_\text {p}/ n_\text {f})$. Telescope combines the best of both worlds, as it only needs to reveal close to $\frac{\lambda _\text {sec}}{\log (n_\text {p}/ n_\text {f})}$ set elements and the integer t with no need for secondary openings. Goldwasser-Sipser requires $8 \lambda \cdot (n_\text {p}/n_\text {f})^4 \cdot (n_\text {p}/n_\text {f}-1)^{-4}$ reveals.

In Fig. 1 we compare proof sizes and communication costs of our constructions with those of existing protocols: compact certificates [MRV+21] and the Goldwasser-Sipser [GS86] scheme. Our analysis of the simple lottery scheme of Sect. 4.1 is also applicable to Mithril [CK21] as the combinatorics are very similar. Compact certificates have computational security and we provide proof sizes secure against adversaries making $2^{80}$ and $2^{128}$ queries; Telescope, on the other hand, has information-theoretic security and smaller number of revealed elements, but becomes computationally secure with number of revealed elements similar to compact certificates when the adversary is allowed to choose the weight function.

We consider communication costs only where they are meaningful, i.e. in decentralized schemes. We note that these costs may be significantly lower in the case of weighted sets where the same element may appear multiple times with different indices. For compact certificates, we derive values using the formula from [MRV+21]. For the simple lottery we use direct calculation, slightly improving on the bounds of Sect. 4.1, for Goldwasser-Sipser we use the analysis performed in the full version, and for Telescope and Decentralized Telescope we use the bounds from Corollaries 2 and 5. For the weighted Telescope scheme we use the formula in Sect. 5.