1 Introduction

Category theory is a branch of mathematics that studies higher-dimensional typed algebraic structures. Originally developed for applications to homological algebra, it was quickly discovered that categorical structures were common in logic and computer science. Formal systems like logics, type theories and programming languages typically have sound and complete models given by notions of structured categories [30, 31, 34]. This Curry-Howard-Lambek correspondence  applies to simply typed lambda calculus [30], computational lambda calculus [34], linear logic [24] dependent type theory [14, 45], and many other type theories designed based on category-theoretic semantics. The syntax of a type theory should present an initial object in its category of models, a category-theoretic reformulation of logical soundness and completeness.

While this research program has been quite successful, category-theoretic notions can be overwhelming for beginners. In a traditional set-theoretic formulation, notions such as adjoint functors and limits produce a proliferation of “naturality” and “functoriality” side-conditions that must be discharged. For example, when constructing an adjoint pair of functors between two categories, a naïve approach would define all of the data of the action on objects, action on arrows, prove the functoriality of such actions, as well as construct two families of transformations, prove they are natural and then finally proving a pair of equalities relating compositions of natural transformations. Carrying out these proofs explicitly is quite tedious and many newcomers are left with the impression that category theory is full of long, but ultimately trivial constructions. This complexity is compounded when moving from ordinary category theory to enriched and internal category theory, where constructions must be additionally proven continuous, monotone, etc, in addition to natural or functorial. However, these generalizations are often exactly what is needed for programming language applications; for example, domain-, metric- and step-index-enriched categories have been used to model recursive programming languages and internal categories have been used to model parametricity and gradual typing [9, 36, 44, 53].

Fortunately, the tools of category theory itself can be employed to simplify this complexity, specifically the tools of higher category theory. As an analogy in differential calculus, when an adept analyst writes down a function, they do not expand out the \(\epsilon \mathord {-}\delta \) definition of continuity for a function and proceed from first principles, but rather use certain syntactic principles for defining functions that are continuous by construction — e.g. that composition of continuous functions is continuous. Similar principles apply to category theory itself: functors and natural transformations are closed under composition and whiskering operations, and experienced category theorists rely on these syntactic principles to eliminate the tedium of explicit proofs. In the case of category theory, these principles can be formalized using algebraic structures such as 2-categories, bicategories, Yoneda structures, (virtual) double categories, pro-arrow equipments [6, 17, 32, 49, 56], an approach known as formal category theory. In these structures, rather than defining notions of category, functor and natural transformation from first principles, they are axiomatized in a manner similar to how a category axiomatizes a notion of space and homomorphism. Proofs in formal category theory apply to enriched and internal settings, which are instances of the formal axioms. A downside is that these algebraic structures are quite complicated, and practitioners typically employ either an algebraic combinator syntax (formalized in [18]) or a 2-dimensional diagrammatic language that can be quite beautiful and elegant, but is also somewhat removed from the traditional formulation of category theory in terms of sets and functions.

In this work, we apply the techniques of categorical logic to define a more familiar logical syntax for carrying out constructions and proofs in formal category theory. We call the resulting theory virtual equipment type theory (VETT) as (hyperdoctrines of) virtual equipments [17, 32], a particular semantic model of formal category theory, provide a sound and complete notion of model for the theory. VETT provides syntax for categories, functors, profunctors, and natural transformations, which are defined using familiar term syntax and \(\beta \eta \) reasoning principles for \(\lambda \)-functions, bound variables, tuples, etc. By adhering to a syntactic discipline, the logic guarantees that all functor terms are automatically functorial, and all natural transformation terms are natural. More specifically, the syntax for transformations is a kind of indexed, ordered linear lambda calculus, where the indexing ensures that transformations are correctly natural and the ordering and linearity ensure that the proofs are valid in a large class of enriched and internal categories, such as enrichment in a non-symmetric monoidal category. VETT provides an alternative to algebraic and string-diagram syntaxes for working with virtual equipments, similar to how the lambda calculus provides an alternative to categorical combinators and string diagram calculi for cartesian closed categories.

The syntax of VETT is an indexed, ordered linear, proof-relevant variant of predicate logic over a unary type theory. Just as a predicate logic has a notion of type, term, relation and implication, VETT is based on four analogous category-theoretic concepts: categories, functors, profunctors and natural transformations of profunctors. Categories are treated like types, and the unary functors we consider in this paper are each represented by a term whose type is a category and whose one free variable ranges over a category. The analog of a relation is a profunctor (defined below), which is written like a set with free category variables. Like the restriction to unary functors, we restrict to profunctors with two free variables. The logic is proof-relevant in that the implications of relations are generalized to natural transformations of profunctors, and we use a \(\lambda \)-calculus notation to describe these “proof terms”. This analogy to predicate logic can be made formal: any construction in VETT can be erased to a corresponding construction or proof in predicate logic, as sets, functions, relations, and implication of relations define a (somewhat degenerate) virtual equipment.

While the restricted syntax developed in this paper does not express some important concepts such as functor categories or opposite categories, the restriction is natural in that it corresponds exactly to virtual equipments, a well-understood notion of model that can express a great deal of fundamental results and constructions in category theory [43, 47]. Moreover, we can work around these unary/binary restrictions to some extent by viewing the type theory as a domain-specific language embedded in a metalanguage. For example, while we cannot talk about functor categories, we can state a theorem that quantifies over functors using the meta-language’s “external” universal quantifier (which does not have automatic functoriality/naturality properties). To support this, VETT includes a third layer, an extensional dependent type theory in the style of Martin-Löf type theory. All of our ordered predicate logic judgments are also indexed by a context from this dependent type theory, and the type theory includes universe types for categories, functors, profunctors and natural transformations. This allow us to formalize theorems the object logic is too restrictive to encode, analogous to 2-level [2, 39, 51] or indexed type theories [15, 27, 29, 52].

While we emphasize the applications to enriched and internal category theory in this work, there is potential for more direct application to programming language semantics. Ordinary predicate logic is the foundation for proof-theoretic presentations of logical relations, such as Abadi-Plotkin logic for parametricity and LSLR and Iris for step-indexed logical relations proofs [20, 28, 40]. We conjecture that VETT might similarly serve as the foundation for a logic of ordered structures, which abound in applications: rewriting and approximation relations can both be modeled as orderings and logical relations involving these structures are proven to respect orderings; operational logical relations must be downward-closed and approximation relations should satisfy transitivity. Just as LSLR and Iris release the user from the syntactic burden of explicit step-indexing, VETT may be used to release the user from the syntactic burden of proving downward-closure or transitivity side-conditions. Additionally, VETT may serve as the basis of a future domain specific proof assistant for category-theoretic proofs. To pilot-test this, we have formalized the syntax of VETT in Agda 2.6.2.2, using the rewrite mechanism to make VETT’s substitution and \(\beta \)-reduction rules definitional equalities.Footnote 1 We have used this lightweight implementation to check a number of examples.

Basics of Profunctors. While we assume the reader has some background knowledge of category theory, we briefly define profunctors, which are not included in many introductory texts. Recall that a category \(\mathbbm {C}\) has a collection of objects and morphisms with identity and composition, and a functor \(F : \mathbbm {C} \rightarrow \mathbbm {D}\) is a function on objects and a function on morphisms that preserves identity and composition. A category can be thought of as a generalization of a preordered set, which has a set of elements and a binary relation on its objects satisfying reflexivity and transitivity. A category is then a proof-relevant preorder, where morphisms are the proofs of ordering, and the reflexivity and transitivity proofs must satisfy identity and unit equations. A functor is then a proof-relevant monotone function. Given categories \(\mathcal C\) and \(\mathcal D\), a profunctor R from \(\mathcal C\) to \(\mathcal D\), written \(R : \mathbbm {C} \nrightarrow \mathbbm {D}\) is a functor \(R : {\mathbbm {C}}^{o} \times {\mathbbm {D}} \rightarrow \text {Set}\)Footnote 2. Because a profunctor outputs a \(\text {Set}\) rather than a proposition, it is itself a proof-relevant relation. Thinking of categories as proof-relevant preorders, functoriality says that the profunctor is downward-closed in \(\mathbbm {C}\) and upward-closed in \(\mathbbm {D}\). Given profunctors \(R, S : \mathbbm {C} \nrightarrow \mathbbm {D}\), a homomorphism from R to S is a natural transformation, which in the preordered setting is simply an implication of relations.

Profunctors are very useful for formalizing category theory, but an additional reason we make them a basic concept of VETT is that they allow us to give a universal property for the type of “morphisms in a category \({\mathbbm {C}}\)”. This is analogous to how the J elimination rule for the identity type in Martin-Löf type theory gives a universal property for morphisms in a groupoid (the special case of a category where all morphisms are invertible) [5, 26, 50]. The reason profunctors are useful for this purpose is that, for any category \(\mathbbm {C}\), \(\text {Hom}_{\mathbbm {C}} : \mathbbm {C} \nrightarrow \mathbbm {C}\) is a profunctor. On preorders this is just the preorder’s ordering relation itself. Moreover, the hom profunctor is the unit for a composition of profunctors \(R \odot S\) which is defined as a co-end. The composition of profunctors is a generalization of the composition of relations, and just as the equality relation is the identity for the composition of relations, the hom profunctor is the identity for this composition. The unit law for the hom profunctor can be seen as a “morphism induction” principle, analogous to the “path induction” used in homotopy type theory (though in this paper we consider only ordinary 1-dimensional categories, not higher generalizations).

Outline. In Section 2 we introduce the syntax of VETT. In Section 3 we demonstrate how to use our syntax for formal category theory. In Section 4, we develop some model theory for VETT, including a sound and complete notion of categorical model and sound interpretation in virtual equipments modeling ordinary, enriched and internal category theory. In Section 5, we discuss related type theories and potential extensions.

2 Syntax of VETT

In Figure 1 we give a table summarizing the relationship between the judgments and connectives of higher-order predicate logic with our ordered variant. Due to the incorporation of variance, some unordered concepts generalize to multiple different ordered notions. For instance, covariant and contravariant presheaf categories generalize the power set. Further, because we only have binary relations rather than relations of arbitrary arity, we have only restricted forms of universal and existential quantification which come combined with implications and conjunctions.

Fig. 1.
figure 1

Analogy between Higher-Order Logic and VETT Judgments and Connectives

Full size image

The syntactic forms of VETT are given in Figure 2. First, we have categories, which are analogous to sorts in a first-order theory. We have M a base sort, product and unit sorts, as well as the graph of a profunctor and the negative and positive presheaf categories. Next, objects a, b, c are the syntax for the functors between categories. We call them objects rather than functors, because in type-theoretic style, a functor is viewed as a “generalized object” parameterized by an input variable \(\alpha : \mathbbm {C}\). Next, sets P, Q, R are the syntax for sets. These sets denote profunctors, i.e., a categorification of relations. Similar to functors, rather than writing profunctors as functions \({\mathbbm {C}}^o\times {\mathbbm {D}} \rightarrow \text {Set}\), we write them as sets with a contravariant variable \(\alpha :\mathbbm {C}\) and a covariant variable \(\beta :\mathbbm {D}\). The sets we can define are the Hom-set, the tensor and internal hom, as well as products of sets, profunctors applied to two objects and elements of positive and negative presheaves. Finally we have elements of sets, which correspond to natural transformations of multiple inputs, where again we view natural transformations valued in a profunctor as generalized elements of profunctors.

After these forms we have types and terms, which represent the meta-language that we use to talk about categories/profunctors/natural transformations. In addition to standard dependent type theory with \(\varPi \) and \(\varSigma \) and identity types, we have universes of categories, functors, profunctors and natural transformations.

Finally we have several forms of context which are used in the theory. The contexts \(\varGamma \) of term variables with their types are as usual; we write “\({\varGamma \,\,\text {type context}}\)” to indicate that a context is well-formed. We name the remaining contexts after the judgements that they are used by. The set contexts \(\varXi \), which will be used to type-check sets, contain object variables with their categories. The two forms of set context are \(\alpha : \mathbbm {C}\), containing one variable that can be used both contravariantly and covariantly, and \(\alpha : \mathbbm {C} ; \beta : \mathbbm {D}\), containing a contravariant variable \(\alpha \) and covariant variable \(\beta \). Finally, the transformation contexts \(\varPhi \) contain element variables with their sets, alternating with those sets’ object variables with their categories. A typical \(\varPhi \) has the shape

$$ \alpha _1 : \mathbbm {C}_1, x_1:R_1(\alpha _1,\alpha _2), \alpha _2 : \mathbbm {C}_2, x_2:R_2(\alpha _2,\alpha _3), \ldots , R_n(\alpha _n,\alpha _{n+1}), \alpha _{n+1} : \mathbbm {C}_{n+1} $$

and represents the composition of the “relations” \(R_1, R_2, R_3, \ldots , R_n\). We write \(d^-(\varPhi )\) for the first category variable in \(\varPhi \) (which we regard as the negative or contravariant position), \(d^+(\varPhi )\) for the last category variable in \(\varPhi \) (which we regard as the positive or covariant position) and use the notation \(d^\pm \varXi \) with the same meaning. We write for the append of two transformation contexts, which is only well-formed when the last variable in \(\varPhi _1\) is equal to the first variable in \(\varPhi _2\). Formal inductive definitions are in the appendix, but intuitively:

figure b

Next, we overview our basic judgement forms. We have

  • Categories: \({\varGamma \vdash \mathbbm {C} \,\,\text {Cat}}\), where \({\varGamma \,\,\text {type context}}\).

  • Objects/functors: \({\varGamma \mathrel {|}\alpha : \mathbbm {C} \vdash a : \mathbbm {D}}\), where \(\varGamma \vdash \mathbbm {C}\,\,\text {Cat}\) and \(\varGamma \vdash \mathbbm {D} \,\,\text {Cat}\). Objects are typed with an input object variable \(\alpha : \mathbbm {C}\) and an output category \(\mathbbm {D}\); in the semantics, objects are modeled as functors \(\mathbbm {C} \rightarrow \mathbbm {D}\).

  • Sets/profunctors: \({\varGamma \mathrel {|}\varXi \vdash S \,\,\text {Set}}\), where \(\varGamma \vdash \varXi \,\,\text {set context}\). A set S is typed with respect to a set context \(\varXi \) to describe its covariant/contravariant dependence on some input objects. Sets are semantically modeled as profunctors.

  • Elements/natural transformations: \({\varGamma \mathrel {|}\varPhi \vdash s : R}\), where \({\varGamma \vdash \varPhi \,\,\text {trans. context}}\) and \(\varGamma \mathrel {|}\underline{\varPhi }\vdash R \,\,\text {Set}\). A transformation s has a context \(\varPhi \) of transformation variables and a single output set R. To be well-formed, the context and set must be parameterized by the same contravariant and covariant object variables. To ensure this, we use a coercion operation \(\underline{\varPhi }\) from transformation contexts to set contexts that erases everything in the context but the left-most and right-most object variables (\(\underline{\alpha : \mathbbm {C}} = \alpha : \mathbbm {C}\) and \(\underline{\varPhi } = d^-(\varPhi );d^+(\varPhi )\)).

  • Meta-language types and terms: \(\varGamma \vdash A \,\,\text {Type}\) and \(\varGamma \vdash M : A\) as in standard dependent type theory.

Fig. 2.
figure 2

VETT Syntactic Forms

Full size image

The variable rules for objects and elements are

figure c

As when using variables in linear logic, the latter rule applies only when the context contains a single set R. All syntactic forms typed in context admit an action of substitution. For types and terms, this is as usual. Objects \(\alpha :\mathbbm {C} \vdash a : \mathbbm {D}\) can be substituted for object variables \(\beta : \mathbbm {D}\) in other objects. We can also substitute objects into sets, that is, if we have a set P parameterized by a contravariant variable \(\alpha : \mathbbm {C}\) and a covariant variable \(\beta : \mathbbm {D}\), then we can substitute objects \(a : \mathbbm {C}\) and \(b : \mathbbm {D}\) for these variables \(P[a/\alpha ;b/\beta ]\). This generalizes the ordinary precomposition of a relation by a function. Semantically this is the “restriction” of a profunctor along two functors, which is just composition of functors if a profunctor is viewed as a functor to \(\text {Set}\). Modeling this operation as a substitution considerably simplifies reasoning using profunctors. Finally we have the action of substitution on elements/natural transformations. First, we can substitute elements/natural transformations for the set variables in elements, denoting the composition of natural transformations. Second, an element is also parameterized by a contravariant and a covariant category variable \(\alpha ;\beta \). We can think of natural transformations as polymorphic in the categories involved, and so when we make a transformation substitution, we also instantiate the polymorphic category variables with objects. The full syntactic details of substitution are included in the appendix.

2.1 Category Connectives

In this section we discuss some connectives for constructing categories, which are specified by introduction and elimination rules in Figure 3 (the \(\beta \eta \) equality and substitution rules are included in the appendix). The introduction and elimination rules make use of functors, profunctors, and natural transformations. First we introduce the additive connectives: the unit category 1 and product category \(\mathbbm {C} \times \mathbbm {D}\) have the usual introduction and elimination rules defining functors to/from them. Next, we introduce the graph of a profunctor \(\sum _{{\alpha };{\beta }} P\). Just as a relation \(R : A \times B \rightarrow \text {Set}\) can be viewed as a subset \(\{ (a,b) \in A\times B | R(a,b)\}\), any profunctor \(P : {\mathbbm {C}}_-^o\times {\mathbbm {D}}_+ \rightarrow \text {Set}\) can be viewed as a category with a functor to \({\mathbbm {C}}_- \times {\mathbbm {D}}_+\) (no op), specifically a two-sided discrete fibration. In set-based category theory, the objects of \(\sum _{{\alpha };{\beta }} P\) are triples \((a_-, a_+, s : P(a_-,a_+))\) and morphisms from \((a_-,a_+, s)\) to \((a_-',a_+', s')\) are pairs of morphisms \(f_- : a_- \rightarrow a_-'\) and \(f_+ : a_+ \rightarrow a_+'\) such that \(P(\text {id},f_+)(s) = P(f_-,\text {id})(s')\). With various choices of P, this connective can be used to define the arrow category, slice category, comma category and category of elements. In our syntax we define it as the universal category \(\mathbbm {C}\) equipped with functors to \(\mathbbm {C}_-\) and \(\mathbbm {C}_+\) and a natural transformation to P.

Lastly, we define the negative and positive presheaf categories \(\mathcal P^{-}\mathbbm {C}\) and \(\mathcal P^{+}\mathbbm {D}\). These are given a syntax suggestive of the fact that they generalize the notion of a powerset, and so can be thought of as “power categories”. Note that we include a restriction that the input category is small, which is an inductively defined by saying all base categories are small, the unit is small, product of small categories is small and the graph of a profunctor over small categories is small. Notably, the presheaf categories themselves are not small. The negative presheaf category is defined by its universal property that a functor into it \(\mathbbm {D} \rightarrow \mathcal P^{-}\mathbbm {C}\) is equivalent to a profunctor \(\mathbbm {C}^o \times \mathbbm {D} \rightarrow \text {Set}\). The introduction rule constructs an object of the negative presheaf category from such a profunctor and the elimination rule inverts it. We use the notation \(p\in a\) for the elements of the induced profunctor. Since a occurs in a negative position, it must depend only on the contravariant variable \(d^-\varXi \) and vice-versa for p. The positive presheaf category is then the dual. In ordinary set-theoretic category theory the negative presheaf category is the usual presheaf category \(\text {Set}^{\mathbbm {C}^o}\), and the positive presheaf category is the opposite of the dual presheaf category \((\text {Set}^{\mathbbm {D}})^o\).

Fig. 3.
figure 3

Category Conectives

Full size image

2.2 Set Connectives

Next, in Figure 4, we cover the connectives for the sets/profunctors, which classify elements/natural transformations (the \(\beta /\eta \)-rules are in the appendix). First, the unit set \(a \mathop {\rightarrow _{\mathbbm {C}}} b\) is our syntax for the profunctor of morphisms in \(\mathbbm {C}\) instantiated at generalized objects a and b. Its introduction and elimination rules are analogous to the usual rules for equality in intensional Martin-Löf type theory. The introduction rule is the identity morphism (reflexivity) and the elimination rule is an induction principle: we can use a term of \(s : a \mathop {\rightarrow _{\mathbbm {C}}} b\) by specifying the behavior when s is of the form \(\text {id}_{\alpha }\) in the form of a continuation \(\alpha . t\). Like the J elimination rule for equality in Martin-Löf type theory, P must be “fully general”, i.e. well-typed for variables \(\alpha \) and \(\beta \). This is because for distinct variables \(\alpha \) and \(\beta \), \(\alpha \mathop {\rightarrow _{\mathbbm {C}}} \beta \) denotes the unit in a virtual double category, which has a universal property, but \(a \mathop {\rightarrow _{\mathbbm {C}}} b\) denotes a restriction of the unit, which in general does not. Those familiar with linear logic as in e.g. [41] might expect a more general rule, where the continuation t is allowed to use variables that are not used in s, i.e., have a context and the conclusion of the rule to have a context . Because of dependency, this is not necessarily well-formed in cases where the endpoints a and b of \(a \mathop {\rightarrow _{\mathbbm {C}}} b\) are not distinct variables. However, the instances of this more general rule that do type check are derivable from our more restricted rule using right/left-hom types.

The tensor product of sets is a kind of combined existential quantifier and monoidal product, which we combine into a single notation \(P \mathop {\overset{\exists \beta }{\odot }} Q\), where \(\beta \) is the covariant variable of P and the contravariant variable of Q. Then the covariant variable of the tensor product is the covariant variable of Q and the contravariant variable similarly comes from P. In ordinary category theory, this is the composition of profunctors, and is defined by a coend of a product. We require that the variable \(\beta \) quantifies over a small category \(\mathbbm {D}\), as in general this composite doesn’t exist for large categories. The introduction and elimination are like those for a combined tensor product and existential type: the introduction rule is a pair of terms, with an appropriate instantiation of \(\beta \), and the elimination rule says to use a term of a tensor product, it is sufficient to specify the behavior on two elements typed with an arbitrary middle object \(\beta \).

Next, we introduce the contravariant ( ) and covariant (\(R \mathop {\triangleright ^{\forall \alpha }} P\)) homs of sets, which are different from each other because we are in an ordered logic. These are a kind of universally quantified function type, where the universally quantified variable must occur with the same variance in domain and codomain. In the contravariant case, it occurs as the contravariant variable in both, and vice-versa for the covariant case. To highlight this, the notation for the contravariant dependence puts the quantified variable on the left of the triangle, as contravariant variables occur to the left of the covariant variable, and similarly the covariant hom has the quantified variable on the right. Similar to ordered lambda calculus, the covariant hom is right-associative while the contravariant hom is left-associative. Then the covariant variable of the contravariant hom set is the covariant variable of the codomain and, and the contravariant variable of the hom set is the covariant variable of the domain, as the two contravariances cancel. The covariant hom is dual. Semantically, in ordinary category theory these are known as the hom of profunctors and are adjoint to the composition of profunctors [7]. The two connectives have similar introduction and elimination rules in the form of \(\lambda \) terms abstracting over both the object of the category and the element of the set, and appropriate application forms. To keep with our invariant that the variable occurrences occur left to right in the term syntax in a manner matching the context, we write the covariant application in the usual order \(s \mathop {\triangleright ^{a}} t\) where the function is on the left and the argument is on the right, and the contravariant application in the flipped order. We also write the instantiating object as a superscript to de-emphasize it, as in practice it can often be inferred.

Finally, we have the cartesian unit and product sets, which are analogous to the normal unit and product of types. The most notable point to emphasize is that in the formation rule for the product, the two subformulae should have the same covariant and contravariant dependence (as with linear logic, some constructions can syntactically use a variable more than once and still be “linear”).

2.3 Type Connectives

Finally, we briefly describe the connectives for the “meta-logic”, which extends Martin-Löf type theory with \(\varPi \)/\(\varSigma \) and extensional identity types (with their standard rules) (Fig. 5). We use extensional identity types so that the description of models is simpler, but intensional identity types could be used instead. The types we include are universes for the object categorical logic: types of small categories and locally small categories, functors, profunctors and natural transformations. The rule for the types of small categories and (large) categories are very similar: any definable category defines an element of type \(\text {Cat}\), and any element of that type can be reflected back into a category. The only difference for \(\text {SmallCat}\) is that the categories involved additionally satisfy \(\mathbbm {C} \,\,\text {Small}\). Again we elide the \(\beta \eta \) principles, which state that \(\lceil {} {-}\rceil {}\) and \(\lfloor {} {-}\rfloor {}\) are mutually inverse. Since every small category \(\mathbbm {C} \,\,\text {Small}\) is a category \(\mathbbm {C} \,\,\text {Cat}\), there is a definable inclusion function from \(\text {SmallCat}\) to \(\text {Cat}\) and the \(\beta \eta \) properties ensure that this is a monomorphism.

Fig. 4.
figure 4

Set Connectives

Full size image

Next, we have the types of all functors and profunctors between any two fixed categories. The introduction and elimination forms are those for unary and binary function types respectively, where metalanguage terms of type \(\text {Fun}\,{\mathbbm {C}}\,{\mathbbm {D}}\) can be used to construct an object/functor, while metalanguage terms of type \(\text {Prof}\,{\mathbbm {C}}\,{\mathbbm {D}}\) can be used to construct a set/profunctor.

Finally we include a type \(\forall \alpha :\mathbbm {C}. P\) which we call the set of “natural elements” of P. The name comes from the case that P is of the form \(F(\alpha ) \mathop {\rightarrow _{}} G(\alpha )\) in which case the type \(\forall \alpha :\mathbbm {C}. F(\alpha ) \mathop {\rightarrow _{}} G(\alpha )\) can be interpreted as the set of all natural transformations from F to G. More generally this is modeled as an end, and we notate it with a universal quantifier (just as we do for the quantifiers in left/right hom types). Syntactically, \(\forall \alpha . P\) is a meta-language type that represents elements/natural transformations with exactly one free variable.

3 Formal Category Theory in VETT

To demonstrate what formal category theory in VETT looks like, we demonstrate some basic definitions and theorems. While it is well known that much category theory can be formalized in virtual equipments, we show these examples to demonstrate how the VETT syntax gives a more familiar syntax to these constructions, while still avoiding the need for explicit naturality and functoriality side conditions. We have mechanized some of the results in this section (e.g. Lemma 2 and Lemma 3 and the maps in Lemma 4) in Agda.Footnote 3

Fig. 5.
figure 5

Type Connectives

Full size image

First, we using the elimination for the unit set, we can see that all constructions are (pro-)functorial:

Construction 1

For any small category \(\mathbbm {C}\), we can construct natural elements

  1. 1.

    Identity: \(\forall \alpha :\mathbbm {C}. \alpha \mathop {\rightarrow _{\mathbbm {C}}} \alpha \)

  2. 2.

    Composition: \(\forall \alpha _1:\mathbbm {C}. (\alpha _1 \mathop {\rightarrow _{\mathbbm {C}}} \alpha _2) \mathop {\triangleright ^{\forall \alpha _2:\mathbbm {C}}} (\alpha _2 \mathop {\rightarrow _{\mathbbm {C}}} \alpha _3) \mathop {\triangleright ^{\forall \alpha _3:\mathbbm {C}}} (\alpha _1 \mathop {\rightarrow _{\mathbbm {C}}} \alpha _3)\)

  3. 3.

    Functoriality: for any \(F : \text {Fun}\,{\mathbbm {C}}\,{\mathbbm {D}}\), \(\forall \alpha _1:\mathbbm {C}. (\alpha _1 \mathop {\rightarrow _{\mathbbm {C}}} \alpha _2) \mathop {\triangleright ^{\forall \alpha _2:\mathbbm {C}}} (F(\alpha _1) \mathop {\rightarrow _{\mathbbm {D}}} F(\alpha _2))\).

  4. 4.

    Profunctoriality: for any \(R : \text {Prof}\,{\mathbbm {C}}\,{\mathbbm {D}}\) if \(\mathbbm {D}\) is small then \(\forall \alpha _1:\mathbbm {C}. (\alpha _1 \mathop {\rightarrow _{\mathbbm {C}}} \alpha _2) \mathop {\triangleright ^{\forall \alpha _2:\mathbbm {C}}} R{\alpha _2}{\beta _2} \mathop {\triangleright ^{\forall \beta _2:\mathbbm {D}}} (\beta _2 \mathop {\rightarrow _{\mathbbm {D}}} \beta _1) \mathop {\triangleright ^{\forall \beta _1:\mathbbm {D}}} R\alpha _1\beta _1\)

Identity and Composition generalize the reflexivity and transitivity properties of equality, respectively, with the lack of symmetry being a key feature of the generalization. In addition, we can prove that the (pro)-functoriality axioms commute with the composition proof by the \(\eta \) principle for the unit. (Pro-)Functoriality generalizes the statement that all functions and relations respect equality. Naturality is more complex to state, and it is a statement about the proofs so it has no analog in ordinary higher-order logic. The following version is stated for any profunctor, with the usual case of naturality arising when \(R \alpha \beta = F \alpha \mathop {\rightarrow _{\mathbbm {C}}} G \beta \).

Lemma 1 (Naturality)

For any \(t : \forall \alpha :\mathbbm {C}. R(\alpha ;\alpha )\), by composing with profunctoriality, we can construct terms \(\alpha _1:{\mathbbm {C}}, f : \alpha _1 \mathop {\rightarrow _{\mathbbm {C}}} \alpha _2, \alpha _2:{\mathbbm {C}} \vdash \text {lcomp}(f,t^{\alpha _2})\) and \(\text {rcomp}(t^{\alpha _1}, f) : R(\alpha _1;\alpha _2)\) that are both equal to \(\text {ind}_{\rightarrow }(f,t)\).

Next, we turn to some of the central theorems of category theory, the Yoneda and Co-Yoneda lemmas. Despite being ultimately quite elementary, these are notoriously abstract. In VETT, we view these as ordered generalizations of some very simple tautologies about equality. For instance, the Yoneda lemma generalizes the equivalence between the formulae \(\forall y. x = y \Rightarrow P y\) and Px for any x.

Lemma 2

Let \(\alpha : \mathbbm {C}\) and \(\pi : \mathcal P^{+}{\mathbbm {C}}\). Then

  1. 1.

    (Yoneda) The profunctor \((\alpha \mathop {\rightarrow _{\mathbbm {C}}} \alpha ') \mathop {\triangleright ^{\forall \alpha '}} (\pi \ni \alpha ')\) is isomorphic to \(\pi \ni \alpha \)

  2. 2.

    (Co-Yoneda) The profunctor \((\pi \ni \alpha ') \mathop {\overset{\exists \alpha '}{\odot }} (\alpha ' \mathop {\rightarrow _{}} \alpha )\) is isomorphic to \(\pi \ni \alpha \)

The proofs both follow from the unit elimination rule, which is essentially the Yoneda lemma—the two cases of showing (1) is an isomorphism are precisely the \(\beta \) and \(\eta \) rules for the unit.

Next, we have the “Fubini” theorems, which relate the tensor and hom types. The statement and proofs for these theorems are analogous to proofs relating tensor and hom in ordered logic. For instance, the second isomorphism below is analogous to the equivalence \((P \odot Q) \multimap R \cong P \multimap Q \multimap R\) in ordered logic.

Lemma 3 (Fubini)

The following isomorphisms hold when the corresponding profunctors are well typed.

  1. 1.

    \(P(\alpha ;\beta ) \mathop {\overset{\exists \beta }{\odot }} (Q(\beta ;\gamma ) \mathop {\overset{\exists \gamma }{\odot }} R(\gamma ;\delta )) \cong (P(\alpha ;\beta ) \mathop {\overset{\exists \beta }{\odot }} Q(\beta ;\gamma )) \mathop {\overset{\exists \gamma }{\odot }} R(\gamma ;\delta )\)

  2. 2.

    \((P(\delta ;\beta ) \mathop {\overset{\exists \beta }{\odot }} Q(\beta ;\gamma )) \mathop {\triangleright ^{\forall \gamma }} S(\alpha ;\gamma ) \cong P(\delta ;\beta ) \mathop {\triangleright ^{\forall \beta }} Q(\beta ;\gamma ) \mathop {\triangleright ^{\forall \gamma }} S(\alpha ;\gamma )\)

  3. 3.
  4. 4.
  5. 5.

Proof

We show one case as an example, the forward direction of (1) is given by \(\lambda \alpha . \lambda ^\triangleright (x, \delta ). \text {ind}_{\odot }(p,\beta ,y. \text {ind}_{\odot }(q,\gamma ,r. ((p,\beta ,q),\gamma ,r);y);x)\)

Next, we can prove that two definitions of an adjunction are equivalent:

Lemma 4

For \(R : \text {Fun}\,{\mathbbm {D}}\,{\mathbbm {C}}\) and \(L : \text {Fun}\,{\mathbbm {C}}\,{\mathbbm {D}}\), the following are in bijection:

  1. 1.

    An isomorphism of profunctors \((L \alpha \mathop {\rightarrow _{\mathbbm {D}}} \beta ) \cong (\alpha \mathop {\rightarrow _{\mathbbm {C}}} R \beta )\)

  2. 2.

    A unit \(\eta : \forall \alpha . \alpha \mathop {\rightarrow _{\mathbbm {C}}} R(L\alpha )\) and co-unit \(\varepsilon : \forall \beta . L(R(\beta )) \mathop {\rightarrow _{\mathbbm {D}}} \beta \) satisfying triangle identities.

Proof

Given the forward homomorphism \(\text {lr}\), we can construct \(\eta = \lambda \alpha . \text {lr}^{\alpha } \mathop {\triangleright ^{L \alpha }} \text {id}_{\alpha }\). Given the unit we can reconstruct the forward homomorphism using \(\text {comp}\) (composition) and \(\text {fctor}\) (functoriality) from Construction 1 as

\(\text {comp}^{\alpha } \mathop {\triangleright ^{R(L\alpha )}} \eta ^{\alpha } \mathop {\triangleright ^{R \beta }} (\text {fctor}(R)^{L \alpha } \mathop {\triangleright ^{\beta }} f)\).

We can define weighted limits, which as special cases include ordinary limits and Kan extensions.

Definition 1

For a functor \(D : \text {Fun}\,{\mathbbm {J}}\,{\mathbbm {C}}\) and a profunctor \(W : \text {Prof}\,{\mathbbm {K}}\,{\mathbbm {J}}\), the limit of D weighted by W is (if it exists) a functor \(\text {lim}^{W}{D}\, : \text {Fun}\,{\mathbbm {K}}\,{\mathbbm {C}}\) with an isomorphism \(\alpha \mathop {\rightarrow _{\mathbbm {C}}} (\text {lim}^{W}{D}\,) k \cong W k j \mathop {\triangleright ^{\forall j}} (\alpha \mathop {\rightarrow _{\mathbbm {C}}} D j)\)

This generalizes the usual definition that a morphism into a limit is a cone over the diagram \((\alpha \mathop {\rightarrow _{\mathbbm {C}}} D j)\) to be parameterized by a weight Wkj. Then we can prove the well-known theorem that right adjoints preserve (weighted) limits:

Theorem 1

If \(\text {lim}^{W}{D}\,\) exists and is a limit and \(R : \text {Fun}\,{\mathbbm {C}}\,{\mathbbm {C}'}\) has a left adjoint L, then \(\lambda \kappa . R((\text {lim}^{W}{D}\,) \kappa )\) is the limit of \(\lambda j. R(D j)\) weighted by W.

Proof

$$ \gamma \mathop {\rightarrow _{}} R ((\text {lim}^{W}{D}\,) \kappa ) \cong L \gamma \mathop {\rightarrow _{}} (\text {lim}^{W}{D}\,) \kappa \cong W k j \mathop {\triangleright ^{\forall j}} L \gamma \mathop {\rightarrow _{}} D j \cong W k j \mathop {\triangleright ^{\forall j}} \gamma \mathop {\rightarrow _{}} R(D j) $$

This is a high level proof in terms of isomorphisms that may be written in VETT. The first two steps are the instantiation of assumptions (adjointness, weighted limits). The last step uses the fact that a natural isomorphisms lift to natural isomorphism of homs of profunctors. The construction of this isomorphism illustrates how naturality need not be proved explicitly in VETT. For any \(\phi : \forall \alpha . R' \alpha \beta \mathop {\triangleright ^{\forall \beta }} R \alpha \beta \) and \(\psi : \forall \gamma . S \gamma \beta \mathop {\triangleright ^{\forall \beta }} S' \gamma \beta \) we can construct a natural transformation \(\phi \triangleright \psi : \forall \gamma . (R \alpha \beta \mathop {\triangleright ^{\forall \beta }} S \gamma \beta ) \mathop {\triangleright ^{\forall \alpha }} R'\alpha \beta \mathop {\triangleright ^{\forall \beta }} S'\gamma \beta \) as

\(\lambda \gamma . \lambda ^\triangleright (f, \alpha ). \lambda ^\triangleright (r, \beta ). \psi ^{\gamma } \mathop {\triangleright ^{\beta }} (f \mathop {\triangleright ^{\beta }} (\phi ^{\alpha } \mathop {\triangleright ^{\beta }} r))\). Furthermore if \(\phi \) and \(\psi \) have inverses, then \(\phi ^{-1} \triangleright \psi ^{-1}\) is the inverse of \(\phi \triangleright \psi \).

4 Semantics

Next, we develop the basics of the model theory for VETT. First, we define a sound and complete notion of categorical model based on hyperdoctrines of virtual equipments. Then we instantiate this general notion of model to show that the VETT can be interpreted in ordinary category theory as well as enriched, internal and indexed notions.

First, we can model the judgmental structure of the unary type theory and predicate logic in virtual double categories that are split fibrant and have a notion of small object [17, 32]. We briefly recount the structure present in a virtual double category, but see [17] for a precise definition of the composition rules for 2-cells and functor of virtual double categories.

Definition 2

A virtual double category \(\mathcal V\) consists of

  1. 1.

    A category \(V_o\) of “objects and vertical arrows”

  2. 2.

    A set \({\mathcal V}_h\) of “horizontal arrows” with source and target functions \(s,t : {\mathcal V}_h \rightarrow {\mathcal V_o}^2\)

  3. 3.

    Sets of 2-cells of the following form, with appropriate “multi-categorical” notions of identity and composition:

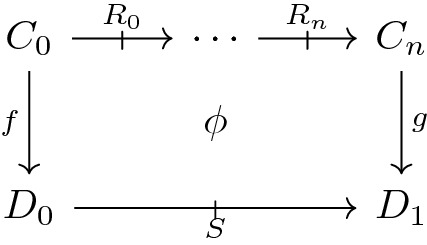
    figure j

    We say that the 2-cell \(\phi \) has S as codomain, the sequence \(R_0 \ldots R_n\) as domain and call f and g the left and right “frames”, or that \(\phi \) is framed by f and g.

We say a virtual double category is split fibrant when it has a choice of restrictions, that is, for any horizontal arrow \(R : C \nrightarrow D\) and vertical arrows \(f : C' \rightarrow C\) and \(g : D' \rightarrow D\) there is a chosen horizontal arrow \(R(f,g) : C' \nrightarrow D'\) with a cartesian 2-cell to R framed by f, g and these chosen cartesian lifts are functorial in f, g ([46]). A choice of small objects is a subset of the objects \(V_s \subseteq V_o\). A morphism of split fibrant virtual double categories with small objects is a functor of the virtual double categories that additionally preserves the restrictions and smallness of objects. This defines a category \(\text {fVDCs}\).

In the presence of restrictions, every 2-cell can be represented as a “globular” 2-cell where the left and right frame are identities [46]. For example the 2-cell \(\phi \) above can be represented as one with the same domain but whose codomain is S(f, g). This property is crucial for the completeness of our semantics as we only include a syntax for these globular terms (proof of Construction 2). Each component of this definition has a direct correspondence to a syntactic structure in VETT. The objects of \(\mathcal V_o\) models the category judgment and the morphisms model the functor judgment. The set \(\mathcal V_h\) models the profunctor judgment. A composable string \(R_0 \cdots R_n\) models the profunctor contexts. The 2-cells correspond to the natural transformation judgment where we have taken the restriction S(F, G) of the codomain. Note that Cruttwell and Shulman define a virtual equipment to be a virtual double category with all restrictions and all units. The units are the model of the unit of profunctors connective and so all of our models with the unit will be virtual equipments, hence the name VETT.

To model the dependent type theory and indexing of category-theoretic judgments by a \(\varGamma \) with an action of substitution, we use a variation on Lawvere’s notion of hyperdoctrine for modeling predicate logic[31]Footnote 4:

Definition 3 (VETT Judgmental model)

A VETT judgmental model (\(\text {VM}_J\)) is a pair of a category with families \(\mathcal C\) and a functor \(V^{(-)} : \mathcal C^o \rightarrow \text {fVDCs}\).

Categories with families \(\mathcal C\) model dependent type theory [22] and for each semantic context \(\varGamma \), \(V^\varGamma \) models the VETT judgments in context \(\varGamma \), with the functoriality modeling the fact that all of these judgments admit a well-behaved action of substitution. A \(\text {VM}_J\) is then precisely the structure corresponding to the judgments and actions of substitution in VETT.

Construction 2

(Syntactic Model). The syntax of VETT with with any subset of connectives are included presents a \(\text {VM}_J\).

Proof

Define the category of families using the dependent type structure and the virtual equipment structure having (\(\alpha \)-equivalence classes of) syntactic categories as objects, functors/sets as vertical/horizontal arrows and interpreting compositions/restrictions as substitutions. The biggest gap between syntax and semantics is in the definition of the 2-cells. A 2-cell from

\((\alpha _1:\mathbbm {C}_1\mathord {;}\alpha _2:\mathbbm {C}_2\vdash R_1),(\alpha _2:\mathbbm {C}_2;\alpha _3:\mathbbm {C}_3 \vdash R_2),\ldots \) to \((\beta _1:\mathbbm {D}_1;\beta _2 : \mathbbm {D}_2\vdash S)\) with frames \(\alpha _1:\mathbbm {C}_1\vdash b_1 : \mathbbm {D}_1\) and \(\alpha _n:\mathbbm {C}_n\vdash b_2 : \mathbbm {D}_2\) is given by a term \(x_1:R_1,x_2:R_2\ldots \vdash s : S[b_1/\beta _1;b_2/\beta _2]\). Composition is defined by substitution.

Then the connectives of VETT each precisely correspond to a universal construction in a \(\text {VM}_J\). The \(\varPi ,\varSigma ,\text {Id}\) types correspond to their standard semantics in a CwF and the connectives for categories and profunctors correspond to universal constructions in the virtual double categories. Products of categories are interpreted as products in the vertical category, and products of sets as products in the category of pro-arrows and 2-cells. The units, tensor and covariant and contravariant homs are modeled by the universal properties of the same names, as described in [46]. The graph of a profunctor is modeled by tabulators [25]. Finally, the covariant and contravariant presheaf categories can be described as a weakening of the definition of a Yoneda equipment from [19] to virtual double categories. More detailed descriptions of these universal properties are included in the extended version [37]. Then the soundness and completeness of this notion of categorical model is formalized by the following initiality theorem.

Theorem 2 (Initiality)

The syntax of VETT with any subset of connectives that includes the hom types presents a \(\text {VM}_J\) that is initial in the category of \(\text {VM}_J\) with the chosen instances of the universal properties and functors that preserve such chosen instances.

Proof

The construction 2 can be extended for any connective modularly, with the exception that the unit relies on the presence of hom sets in order to satisfy the “distributivity” requirement that its elimination can occur in any context. Then we can construct the unique morphism to any HVE induction on syntax.

Now that we have a category-theoretic notion of model, we give some model construction theorems that can be used to justify our intuitive notion of semantics in (enriched, internal, indexed) category theory. First, we can extend any set-theoretic model of the category theoretic judgments to a hyperdoctrine of models where the category of families is the category of sets:

Construction 3

Given a \(\mathcal V \in \text {fVDCs}\), we can construct a \(\text {VM}_J\) \(\mathcal V^{-}: \text {Set}\rightarrow \text {vDbl}_r\) by defining of \((\mathcal V^\varGamma )_o\) to be functions \(\mathcal V_o^\varGamma \), and similarly for morphisms and 2-cells with all operations given pointwise.

Then to define a model of VETT with a collection of connectives it is sufficient to construct a virtual equipment with the corresponding universal properties. The “standard model” is the virtual double category of locally small categories where the small objects are the small categories.

Construction 4

Fix a cardinal \(\kappa \). The virtual double category \(\text {Cat}_{\kappa }\) is defined to have as objects locally \(\kappa \)-small categories, small objects as \(\kappa \)-small categories, vertical morphisms as functors, horizontal arrows as functors \(\mathbbm {C}^o \times \mathbbm {D} \rightarrow \kappa Set\) and 2-cells as morphisms of profunctors. Restriction of profunctors is given by composition, which is strictly associative and unital. \(\text {Cat}_{U}\) has objects satisfying the universal properties of all connectives in VETT.

More generally, categories internal to, enriched in and/or indexed by sufficiently nice categories define a virtual equipment that model the connectives of VETT. We highlight one example from the literature that is highly general: Shulman’s enriched indexed categories [47]. Shulman’s construction defines a virtual double category of large and small \(\mathcal V\)-categories for any pseudofunctor \(\mathcal V : S^o \rightarrow \text {MonCat}\) where S is a category with finite products. He gives examples that show that this subsumes ordinary internal, enriched and indexed categories for suitable choices of \(\mathcal V\), as well as more general categories that can be thought of as both indexed and enriched. This is slightly weaker then what we require: to have split restrictions, we need that \(\mathcal V\) be a strict functor, not merely a pseudo-functor. This is analogous to the situation for dependent type theory, where syntactic substitution is strictly associative, but semantic substitution is typically given by pullback, which is only associative up to unique isomorphism. Shulman’s construction carries over when the functor is strict but some of their example instances would require a strictification theorem.

Construction 5

(Shulman [47]). Given any functor \(\mathcal V : S^o \rightarrow \text {SymMonCat}\) such that S and \(\mathcal V\) have sufficiently well-behaved (indexed) \(\kappa \)-products, then there is a virtual equipment \(\mathcal V-\text {Cat}\) whose objects are locally \(\kappa \)-small \(\mathcal V\)-categories, small objects are \(\kappa \)-small \(\mathcal V\)-categories etc. This virtual equipment has objects satisfying all of the universal properties needed for a model of VETT.

A final model that uses a CwF that is not \(\text {Set}\) would be given by taking extensional dependent type theory as the CwF and interpreting the category-theoretic constructions by their definitions inside type theory.

5 Related and Future Work

We now compare VETT with other calculi for formal category theory.

Cáccamo and Winskel [12] develop a formal language for defining categories, functors (of many variables) and proving existence of natural equivalences between them. Their system can encode profunctors as functors into \(\text {Set}\). Their natural equivalence judgment does not have proof terms or equality between equivalences and they do not support natural transformations. Additionally, they only consider ordinary categories as the intended model and do not develop a more general semantics. Riehl and Verity [43] use a formal language of virtual equipments to prove results valid for \(\infty \)-categories without concrete manipulation of model categories. They formalize this language as a theory in Makkai’s framework of first-order logic with dependent sorts (FOLDS). While this previous work has the same models as VETT, we believe that the syntax we propose in this paper formalizes informal arguments more directly, as shown in Section 3. This is because FOLDS approach approach is entirely relational, whereas we formalize concepts like restriction of a profunctor or composition of natural transformations as functional operations (substitution). In particular, this means that our calculus requires only vertically degenerate squares (elements/natural transformations) as a “user-facing” notion, with general squares occurring only in the admissible substitution operations.

The coend calculus [33] is an informal syntax for manipulating profunctors involving ends and coends; an extension of VETT to treat profunctors of many variables of different variances may provide a formal treatment of it.

Myers [35] provides a string diagram calculus for double categories and pro-arrow equipments, generalizing string diagrams for monoidal categories. These are an alternative approach to type-theoretic calculi, with the string diagrams typically making tensor products simpler to work with, while a type-theoretic calculus like VETT makes the closed structure \(P \mathop {\triangleright ^{\forall \alpha }} Q\) simpler to work with by using bound variables.

Cartesian bicategories are similar to equipments but they axiomatize the bicategory of profunctors rather than the full double category of functors and profunctors [13]. Frey [23] describes preliminary work on a proof system for Cartesian bicateogires. Their profunctors are more general than in VETT in as they may have 0, 1 or more covariant or contravariant variables. But they do not have a term syntax for functors or natural transformations.

Our work in this paper fits broadly into a line of work on directed dependent type theories, a type theory where the identity type is interpreted as morphisms in a (possibly \(\infty \)-)category. In directed type theories based on a bisimplicial model [11, 42, 54, 55], morphism types are defined using an interval object, like in cubical type theory [3, 4, 8, 16], and universal properties like “morphism induction” are an internally definable property of certain types. Other type theories [1, 38] define morphism types via an induction principle, corresponding to the lifting properties of certain kinds of fibrations of categories. While these previous works can express some constructions on \(\text {Cat}\) that are not expressible in VETT, because VETT is more restricted, VETT contrariwise has more models, for instance categories enriched in non-cartesian monoidal categories, so the theorems that are provable in VETT apply in more settings.

Finally, some variations on double categories have been used to model the structure of certain program logics. GTT [36] is a logic for vertically thin pro-arrow equipments, where there is at most one vertical arrow or 2-cell of any tyepe, so their calculus does not include functor or transformation judgments. Another similar calculus is System P [21] which is an internal language of reflexive graph categories, which are like double categories without horizontal composition.

In future work, VETT could incorporate functor categories by generalizing the unary type theory of functors to functors of many variables, in which case ordinary \(\lambda \) calculus can be used to define functor categories as function types, and incorporate multi-variable profunctors as in [23]. This would require to the models to have a monoidal structure. Ideas from coeffects and enriched category theory may be useful for defining opposite categories [10, 48].