Preservation and Reflection of Bisimilarity via Invertible Steps

Abstract

In the theory of coalgebras, distributive laws give a general perspective on determinisation and other automata constructions. This perspective has recently been extended to include so-called weak distributive laws, covering several constructions on state-based systems that are not captured by regular distributive laws, such as the construction of a belief-state transformer from a probabilistic automaton, and ultrafilter extensions of Kripke frames.

In this paper we first observe that weak distributive laws give rise to the more general notion of what we call an invertible step: a pair of natural transformations that allows to move coalgebras along an adjunction. Our main result is that part of the construction induced by an invertible step preserves and reflects bisimilarity. This covers results that have previously been shown by hand for the instances of ultrafilter extensions and belief-state transformers.

1 Introduction

Distributive laws between a monad T and a functor B are ubiquitous in the theory of coalgebras. They capture various forms of interaction between algebras and coalgebras, including structural operational semantics [33, 45], efficient proof techniques [9] and a general coalgebraic determinisation procedure which applies to a wide range of automata and other state-based systems [15, 29, 43].

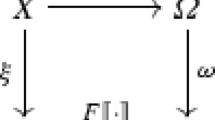
The central idea of this general determinisation procedure is to interpret coalgebras in the Eilenberg-Moore category , as coalgebras for a lifting of B that arises from the distributive law. Behavioural equivalence in then amounts to desired notions of equivalence. For instance: language equivalence of non-deterministic automata; weighted automata [7]; Mealy and Moore machines with side-effects [43]; or various types of trace equivalence of transition systems [8].

An illustrative non-example of this general determinisation procedure is in a natural construction of belief-state transformers from probabilistic automata, which feature both non-determinism and probabilities. From a categorical perspective, the problem is related to the classical result that there is no suitable distributive law of the probability distribution monad $\mathcal {D}$ over the powerset monad $\mathcal {P}$ [46] (also see [34, 47] for other non-existence results of distributive laws). Hence, general determinisation via distributive laws seems not applicable here.

Nevertheless, in [12] a concrete coalgebraic account of the construction of belief-state transformers is given, in terms of a two-stage process:

• 1. from probabilistic automata to coalgebras in , which are a type of labelled transition systems over convex algebras;

• 2. from these coalgebras in back to plain transition systems in $\textsf{Set}$, yielding the belief-state transformer.

A key result in op. cit. is that the second stage preserves and reflects behavioural equivalence. This shows that behavioural equivalence of coalgebras in coincides with distribution bisimilarity on the belief-state transformer.

In [12, 21] it was shown that this construction, in fact, arises from a canonical weak distributive law of $\mathcal {D}$ over $\mathcal {P}$ [22]. Weak distributive laws correspond to so-called weak liftings [19], and—as shown in [22]—these yield a new generalised determinisation procedure which covers the above example, and precisely instantiates to the two stages above. Further examples are the treatment of alternating automata via weak distributive laws in [23], and weak distributive laws for combining non-determinism with semimodules in [10].

However, the result for probabilistic automata that the second stage above preserves and reflects behavioural equivalence has not yet been accounted for in the abstract theory of determinisation via weak distributive laws.

In this paper we provide such an account, starting from a more general setting than weak distributive laws: what we call invertible steps. These basically replace the Eilenberg-Moore adjunction inherent in the weak liftings approach by a general adjunction. In this context, a step allows one to lift the left adjoint to coalgebras—this is a widely occurring phenomenon, for instance in the semantics of coalgebraic modal logic, testing semantics and trace semantics (see [41] for an overview). The key idea here is to assume a right inverse, allowing the lifting of the right adjoint, such that we generalise the two-stage construction above.

We show that, in this setting of an invertible step, the second stage of the two-stage construction preserves and reflects bisimilarity, under mild conditions. As a consequence, we recover the above-mentioned results on preservation and reflection of behavioural equivalence for probabilistic automata [12] for free from the abstract theory.¹ Another motivating example is that of coalgebras for the Vietoris functor on the category of Stone spaces: we obtain that bisimilarity is preserved and reflected by the forgetful functor, recovering the main result in [5].

In fact, the latter example is related to a coalgebraic presentation [36] of ultrafilter extensions, a standard construction in modal logic [6]. It fits within the general setting of invertible steps, but not directly in weak liftings, as it involves the category of Stone spaces (for the duality with Boolean algebras). However, if we move from Stone spaces to compact Hausdorff spaces, then the relevant weak lifting (or invertible step) arises precisely from the weak distributive law constructed by Garner [19]. The weak distributive law in loc. cit. thus gives rise to ultrafilter extensions in modal logic.

Finally, we include an example of an invertible step involving $\textsf{Set}^\textsf{op}$ instead of an Eilenberg-Moore category. Steps for adjunctions with opposite categories are a standard way of presenting the semantics of coalgebraic modal logic [32, 40]. The included example shows the generality of the approach.

Outline. Section 2 presents (invertible) steps, the relation to weak liftings and distributive laws, and a range of examples. In Section 3 we recall the standard notion of coalgebraic bisimilarity, defined via relation lifting. Section 4 contains the main results on preservation and reflection of bisimilarity. In Section 5 we discuss applications and instances of these results. We discuss other notions of bisimulation, and future work, in Section 6.

2 Forward and Backward Steps

We briefly present the required theory of steps, first termed as such in [41]. This structure occurs already in work on coalgebraic modal logic [14, 17, 32, 35, 38, 40] where a step gives the one-step semantics of a logic. In existing work, only what we call a forward step is considered. Here, we also speak of backward steps, being arrows in the opposite direction. In the sequel, such forward and backward steps will usually be each other’s (one-sided) inverses, referred to as invertible steps.

Next, we recall how such steps give rise to liftings of functors between categories of coalgebras and further, when the adjunction underlying the steps can also be lifted to coalgebras [27]. Finally, we present examples of invertible steps from the literature, which we return to in later sections.

For a functor $B :\mathcal {C}\rightarrow \mathcal {C}$, a coalgebra is a pair (X, f) consisting of an object X and an arrow $f :X \rightarrow BX$. A homomorphism from (X, f) to (Y, g) is an arrow $h :X \rightarrow Y$ such that $g \circ h = Bh \circ f$. Coalgebras and homomorphisms between them form a category, denoted by ${\textsf{Coalg}}(B)$, or ${\textsf{Coalg}}_{\mathcal {C}}(B)$ if we wish to make the underlying category explicit.

The category of sets and functions is denoted by $\textsf{Set}$. For a monad T, we write for the category of Eilenberg-Moore algebras. The powerset monad is denoted by $\mathcal {P} :\textsf{Set}\rightarrow \textsf{Set}$, given on objects by $\mathcal {P}(X) = \{S \mid S \subseteq X\}$, and the finitely-supported distribution monad by $\mathcal {D} :\textsf{Set}\rightarrow \textsf{Set}$, given by $\mathcal {D}(X) = \{\varphi :X \rightarrow [0,1] \mid \sum _{x \in X} \varphi (x) = 1,\ \textrm{supp}(\varphi ) \text { finite}\}$ (see also [12]).

2.1 Invertible Steps

The basic setting of interest in this work consists of the following:

Definition 2.1

Given an adjunction $P \dashv Q :\mathcal {D}\rightarrow \mathcal {C}$ and endofunctors $B :\mathcal {C}\rightarrow \mathcal {C}$ and $L :\mathcal {D}\rightarrow \mathcal {D}$ as in the diagram

(1)

a (forward) step is a natural transformation $\delta :BQ \rightarrow QL$. A backward step is simply a natural transformation $\iota :QL \rightarrow BQ$ going the other way. If, moreover, $\delta \circ \iota = \textsf{id}$ then we call $\delta$ an invertible step (with right inverse $\iota$). Finally, if $\delta$ witnesses an isomorphism then we call it an isomorphic step.

Notice the asymmetry in the definition of invertible step: $\iota$ is always assumed to be a right inverse of $\delta$. These invertible steps are the main focus of this paper. Examples are given below in Section 2.2.

Step-induced liftings There is a bijective correspondence between a step and its mate $\hat{\delta } :PB \rightarrow LP$ given by (see [31, 37]). This mate and the backward step allow us to define liftings of $P$ and $Q$ to the categories of coalgebras for $B$ and $L$.

Definition 2.2

Given steps $\delta :BQ \rightarrow QL$ and $\iota :QL \rightarrow BQ$, the step-induced coalgebra liftings $\overline{P} :{\textsf{Coalg}}(B) \rightarrow {\textsf{Coalg}}(L)$ and $\overline{Q} :{\textsf{Coalg}}(L) \rightarrow {\textsf{Coalg}}(B)$ of $P$ and $Q$ are defined by

$$\begin{aligned} f :X \rightarrow BX \quad&\mapsto \quad \hat{\delta }_X \circ Pf :PX \rightarrow LPX \end{aligned}$$

(2)

$$\begin{aligned} g :Y \rightarrow LY \quad&\mapsto \quad \iota _Y \circ Qg :QY \rightarrow BQY \end{aligned}$$

(3)

on objects and act as $P$ and $Q$ on arrows. This is well-defined due to functoriality of $P$ and $Q$ and naturality of $\hat{\delta }$ and $\iota$.

It is shown in [27, Theorem 2.14] that, when $\delta$ and $\iota$ form an isomorphism, the adjunction $P \dashv Q$ lifts to an adjunction $\overline{P} \dashv \overline{Q}$ between the step-induced liftings. For our purposes it will be useful to split the isomorphism condition into the cases where $\iota$ is the left or right inverse of $\delta$.

Lemma 2.3

If $\delta \circ \iota = \textsf{id}$, then the counit $\varepsilon :PQ \rightarrow \textsf{Id}$ of the adjunction $P \dashv Q$ lifts to a natural transformation $\overline{\varepsilon }:\overline{P}\,\overline{Q} \rightarrow \textsf{Id}$. If $\iota \circ \delta = \textsf{id}$, then the unit $\eta :\textsf{Id}\rightarrow QP$ of the adjunction lifts to a natural transformation $\overline{\eta }:\textsf{Id}\rightarrow \overline{Q}\,\overline{P}$.

The combination of these two liftings gives us the lifting of the adjunction.

Corollary 2.4

If $\delta$ and $\iota$ form an isomorphism, then $\overline{P} \dashv \overline{Q}$.

In such a situation, $\overline{Q}$ (being a right adjoint) preserves the final coalgebra for $L$ (the limit of the empty diagram) when this exists. However, there are a number of known examples where the step is not an isomorphism; instead we only have a one-sided inverse. We consider, in particular, these invertible steps, and in the next subsection give a number of examples of this setting.

2.2 Steps from weak liftings, and other examples

Example 2.5

Our first example arises from the work of Garner, who shows that the Vietoris monad $\mathcal {V}$ on the category $\textsf{CHaus}$ of compact Hausdorff spaces arises as a so-called weak lifting of the powerset monad [19] (we discuss weak liftings in general after this example). For the definition of the Vietoris monad the reader is referred to [19, Sec. 2.3]. The category $\textsf{CHaus}$ is equivalent to the Eilenberg-Moore category of the ultrafilter monad $\beta$ [39]. The weak lifting provided by Garner consists of natural transformations $\iota , \delta$, satisfying $\delta \circ \iota = \textsf{id}$:

(4)

where $\mathcal {F} \dashv U$ is the Eilenberg-Moore adjunction of $\beta$. Notice that $\delta$ is an invertible step, with right inverse $\iota$. As shown by Garner, a component $\delta _X :\mathcal {P} U X \rightarrow U \mathcal {V} X$, sends each subset $S \in \mathcal {P} U X$ to its topological closure. The components of $\iota$ simply include the closed subsets into the powerset.

It turns out that this invertible step gives rise to ultrafilter extensions of Kripke frames. In modal logic, ultrafilter extensions [4, 6, 20] are a construction taking a Kripke frame (which we can see as a coalgebra for the powerset functor $\mathcal {P}$) with state space $W$ and forming a new Kripke frame with states being ultrafilters over $W$. The central motivation for this is in “bisimilarity-somewhere-else” results: two states are modally equivalent iff they are bisimilar in the ultrafilter extension.

Now, the composition of the step-induced coalgebra liftings $\overline{\mathcal {F}} :{\textsf{Coalg}}(\mathcal {P}) \rightarrow {\textsf{Coalg}}(\mathcal {V})$ and $\overline{U} :{\textsf{Coalg}}(\mathcal {V}) \rightarrow {\textsf{Coalg}}(\mathcal {P})$, precisely yields the ultrafilter extension of a Kripke frame. The first stage $\overline{\beta }$ is the actual extension, which turns the Kripke frame into a $\mathcal {V}$-coalgebra. The second stage $\overline{U}$ turns this back into a Kripke frame, i.e., a powerset coalgebra in $\textsf{Set}$.

In [36], ultrafilter extensions are developed more generally for coalgebras for a functor $B :\textsf{Set}\rightarrow \textsf{Set}$, via the duality between Boolean algebras and Stone spaces. In fact, since both $\mathcal {V}$ and the left adjoint $\mathcal {F}$ restrict to the category $\textsf{Stone}$ of Stone spaces, the invertible step $\delta , \iota$ restricts to an invertible step in the restriction of the above adjunction to $\textsf{Stone}$.

In general, for monads $S,T$ on a category $\mathcal {C}$, Garner [19] defines to be a weak lifting of $S$ if there are natural transformations

(5)

with $\delta \circ \iota = \textsf{id}$ and satisfying further axioms, where U denotes the forgetful functor from to $\mathcal {C}$. They show that there is a bijective correspondence between weak distributive laws of $T$ over $S$, and weak liftings of $S$ to , in case idempotents in $\mathcal {C}$ split (which holds for $\textsf{Set}$). Here, we do not assume a monad structure on $S$ (which is why the additional axioms are not relevant). In this case, a weak lifting is precisely an invertible step, where the underlying adjunction is an Eilenberg-Moore adjunction.

Example 2.6

In [11, 12], a procedure is given for “determinising” probabilistic automata (PAs), which model systems with both non-determinism and probabilities, into belief state transformers. It was shown in [22] that this is an instance of a more general determinisation procedure induced by a weak lifting, which in turn corresponds to a canonical weak distributive law.

Stated for a general monad T with the usual Eilenberg-Moore adjunction , this general determinisation procedure thus starts from an invertible step (weak lifting) $\delta :B U \rightarrow U \overline{B}$. This gives rise to a two-step process:

(6)

where the second functor $\overline{U}$ is simply the step-induced lifting of U. The first is a variation of a step-induced lifting (notice that it takes BT-coalgebras rather than B-coalgebras as input), mapping a coalgebra $f :X \rightarrow BTX$ to , where $\varepsilon$ is the counit of the Eilenberg-Moore adjunction. In fact, this can be viewed as a step-induced lifting for BT which arises by composing $\delta$ and the counit, see [41].

We instantiate this to the Eilenberg-Moore adjunction of the distribution monad $\mathcal {D}$, where $\mathcal {P}_c$ is the convex powerset monad:

(7)

We take $\mathcal {P}_c(X)$ to have as underlying set $\{S \subseteq X \mid S \text { convex}\}$ following [22]. This matches the usage of and in [12], where and are defined to exclude the empty set. A subset is convex if it is closed under convex combinations (see [12] for details). Further, the category is equivalent to the category of convex algebras and convex maps.

It is explained in [22, Sec. 5] that we have an invertible step in the setting of Eq. (7), which sends a subset $X$ to its convex hull (the smallest convex set containing $X$) and that the lifting $\overline{\mathcal {F}}$ of (6) then gives the transformation of a probabilistic automaton into a belief state transformer in the category . The second step is then to transfer the obtained belief state transformer back to $\textsf{Set}$ with the step-induced lifting of $U$. As shown in [12] and later recovered from our abstract theory (Section 5), this yields a system with the same behaviour. In fact, this is done for automata with labels, i.e., for the functors $\mathcal {P}^L$ and $\mathcal {P}_c^L$ with $L$ a set of labels. The weak lifting we will require in this context is given in [21].

Example 2.7

The following example from automata and languages considers a dual adjunction $P\dashv Q :\mathcal {D}^\textsf{op}\rightarrow \mathcal {C}$. One motivation to discuss this kind of example stems from coalgebraic modal logic where $\mathcal {C}$ commonly is some category of ‘spaces’ and $\mathcal {D}$ commonly is a category of ‘algebras’ [32]. The setup is as follows:

(8)

Here, we have $BX = 2\times (\mathcal {P}X)^\varSigma$ and $LX = 1 + \varSigma \times X$ for a fixed alphabet $\varSigma$. The step $\delta$ is given by

$$\begin{aligned} \delta (i, \xi ) = \{\textsf{inl}(*)\mid i = 1\}\cup \{\textsf{inr}( a,x) \mid a\in \varSigma ,x\in \bigcup \xi (a)\} \end{aligned}$$

(9)

This step $\delta$ is invertible, e.g., by $\iota$ as in Eq. (10).

$$\begin{aligned} \iota (u) = ( 1 \ \textsf{iff} \ \textsf{inl}(*)\in u,a\mapsto \{v\mid \{(a,x)\mid x \in v\}\subseteq u\}) \end{aligned}$$

(10)

A B-coalgebra is a non-deterministic automaton. An L-coalgebra in $\textsf{Set}^{\textsf{op}}$ is an algebra $X\leftarrow 1 + \varSigma \times X$ in $\textsf{Set}$, which can be seen as specifying the initial state and transition structure of a deterministic automaton. From this point of view, the coalgebra lifting $\overline{Q}:{\textsf{Coalg}}(L)\rightarrow {\textsf{Coalg}}(B)$ can be seen as first reversing, and then performing a powerset construction. The specific powerset construction might depend on the chosen right inverse $\iota$, as it is not unique. For $\iota$ as in (10), for example, $u\overset{a}{\rightarrow }\ v$ in $\overline{Q}(\mathcal {A})$ if and only if each state in v is reachable from a state in u via an a-transition in the reverse of $\mathcal {A}$.

In Section 5 we return to these examples and show how we can apply the techniques from Section 4 to obtain preservation and reflection of bisimilarity.

3 Relations, Liftings and Coalgebraic Bisimulations

We recall the standard notion of coalgebraic bisimulation defined via relation lifting, broadly following [28, 30]. Note, we will use some terminology from the theory of fibrations to allow us to be more concise and many of the coming results can be generalised to a larger class of fibrations, but knowledge of fibrations is not required as we give a self-contained presentation of the fibration of relations.

We make the following assumptions for the remainder of the paper:

Assumption 3.1

We assume categories $\mathcal {C}, \mathcal {D}$ with all finite limits, and factorisation systems $(\mathcal {E}_1,\mathcal {M}_1)$, $(\mathcal {E}_2,\mathcal {M}_2)$ respectively for which $\mathcal {M}_1=\textsf{Mono}_\mathcal {C},\mathcal {M}_2=\textsf{Mono}_\mathcal {D}$ and for any left adjoint functor $P :\mathcal {C}\rightarrow \mathcal {D}$ we have $P(\mathcal {E}_1) \subseteq \mathcal {E}_2$.

We assume finite limits mainly for binary products and pullbacks to allow the definitions of relations and inverse images. The assumptions that maps in $\mathcal {M}$ are mono means that pullbacks of abstract monos and factorisation both yield monos, which represent subobjects. The final condition specifies that left adjoints preserve abstract epis. This is required in Section 4.2 and holds, e.g., when the involved categories possess a $(\textsf{RegEpi},\textsf{Mono})$-factorisation system [2, 16], as in all our examples from Section 2.2 and Section 5.

For a category $\mathcal {C}$ satisfying the above, the category ${\textsf{Rel}}(\mathcal {C})$ consists of:

• Objects of ${\textsf{Rel}}(\mathcal {C})$ are subobjects $R \rightarrowtail X \times X$ of the binary product of the object $X$ with itself;

• A map $R \rightarrowtail X \times X \rightarrow S \rightarrowtail Y \times Y$ in ${\textsf{Rel}}(\mathcal {C})$ consists of a map $u :X \rightarrow Y$ in $\mathcal {C}$ such that there is the following commutative diagram

  

  (11)

In $\textsf{Set}$, these are subsets of the binary product of underlying sets as usual, and maps between relations constitute maps between the products sending $R$ to $S$, i.e., $x\,R\,y$ implies $u(x)\,S\,u(y)$. Objects of ${\textsf{Rel}}(\textsf{Stone})$ are closed relations, as the image of a mono representing a subobject is homeomorphic to its domain, and images of continuous functions are compact and thus closed. In the case of an Eilenberg-Moore category for a monad T, objects of are congruences, as the map into the product is an algebra morphism.

Remark 3.2

A note on notation: we use for epis and for monos and the subobjects they represent. We use for abstract epis and for abstract monos, i.e., maps in $\mathcal {E}$ and $\mathcal {M}$ respectively.

Using the factorisation system on $\mathcal {D}$, we lift a functor $F :\mathcal {C}\rightarrow \mathcal {D}$ to a functor ${\textsf{Rel}}(F) :{\textsf{Rel}}(\mathcal {C}) \rightarrow {\textsf{Rel}}(\mathcal {D})$. The action on objects is given by the factorisation

(12)

The action on arrows is defined by orthogonality. The resulting functor ${\textsf{Rel}}(F)$ is a lifting in the sense that the following diagram commutes

(13)

where $p :{\textsf{Rel}}(\mathcal {C}) \rightarrow \mathcal {C}$ sends a relation $R \rightarrowtail X \times X$ to the object $X$, and similarly for q. We say (following the terminology of fibrations) that the relation $R$ is above the object $X$ and a map between relations is above the map $u$ from Eq. (11). Note that commutativity of diagram (13) expresses that ${\textsf{Rel}}(F)$, applied to a relation $R \rightarrowtail X \times X$ on X, yields a relation on FX.

Given a category of relations ${\textsf{Rel}}(\mathcal {C})$, called the total category, the subcategory (also called a fibre) ${\textsf{Rel}}_X$ consists of objects $R \rightarrowtail X \times X$ and maps above the identity on $X$. For relations in $\textsf{Set}$, such maps are inclusions of relations. In general, these maps are unique, and writing $R \le S$ iff there is an arrow from $R$ to $S$ turns the fibre into a poset. A relation lifting ${\textsf{Rel}}(F)$ can be restricted to the fibres to give a functor ${\textsf{Rel}}(F)_X :{\textsf{Rel}}_X \rightarrow {\textsf{Rel}}_{FX}$. Since ${\textsf{Rel}}_X$ and ${\textsf{Rel}}_{FX}$ are posetal categories, ${\textsf{Rel}}(F)_X$ can be viewed as a monotone map.

For a map $f :X \rightarrow Y$ in $\mathcal {C}$, we have the direct image and inverse image functors $\coprod _f :{\textsf{Rel}}_X \rightarrow {\textsf{Rel}}_Y$ and $f^* :{\textsf{Rel}}_Y \rightarrow {\textsf{Rel}}_X$. For relations on sets, we have $\coprod _f(R \subseteq X \times X) = \{(f(x),f(y)) \mid (x,y) \in R\}$ and $f^*(S \subseteq Y \times Y) = \{(x,y) \in X \times X \mid (f(x),f(y)) \in S\}$. More generally, they are obtained as the factorisation and pullback in the left and right diagram below respectively

(14)

It can further be shown that $\coprod _f \dashv f^*$. We say that ${\textsf{Rel}}(F) :{\textsf{Rel}}(\mathcal {C}) \rightarrow {\textsf{Rel}}(\mathcal {D})$ preserves inverse images if ${\textsf{Rel}}(F)_X \circ f^* = (Ff)^* \circ {\textsf{Rel}}(F)_{Y}$.

In this context, a bisimulation for a $B$-coalgebra $f :X \rightarrow BX$ is a post-fixed point of the endofunctor $f^* \circ {\textsf{Rel}}(B)_X :{\textsf{Rel}}_X \rightarrow {\textsf{Rel}}_X$, i.e., a relation $R \rightarrowtail X \times X$ such that $R \le f^* \circ {\textsf{Rel}}(B)_X(R)$. Bisimilarity is then obtained as the greatest fixed point $\nu (f^* \circ {\textsf{Rel}}(B)_X)$, if it exists. In $\textsf{Set}$ a bisimulation is a relation $R$ such that $R \subseteq (f \times f)^{-1} ({\textsf{Rel}}(B)(R))$, i.e., if $x\,R\,y$ then $f(x)\,{\textsf{Rel}}(B)(R)\,f(y)$.

4 Preserving and Reflecting Bisimilarity

In this section we show that, in the presence of an invertible step, bisimilarity is preserved and reflected by the step-induced lifting of the right adjoint, given some further mild conditions. This allows us to recover a number of existing results for concrete instances (Section 5).

Our approach is as follows:

• In Section 4.1, we make precise what it means for a monotone map to preserve and reflect bisimulations;

• In Section 4.2, we obtain conditions which ensure that the step-induced lifting of the right adjoint to bisimulations preserves and reflects bisimulations/bisimilarity.

Throughout this section we assume categories $\mathcal {C}$ and $\mathcal {D}$ as in Assumption 3.1, and an invertible step $\delta :BQ \rightarrow QL$ with right inverse $\iota :QL \rightarrow BQ$ (and P, Q, B, L as in Definition 2.1).

4.1 Preservation and reflection

We now make precise what it means for a monotone map $h$ to preserve and reflect bisimulations. This will be instantiated to bisimulations, captured abstractly as post-fixed points of a monotone map $f :\varGamma \rightarrow \varGamma$ on a poset $\varGamma$, which typically consists of relations (Section 3). These are compared against a second type of bisimulations, modelled as post-fixed points of another monotone map $g :\varDelta \rightarrow \varDelta$. This motivates the following definition.

Definition 4.1

Let $\varGamma$ and $\varDelta$ be posets, and $f :\varGamma \rightarrow \varGamma$, $g :\varDelta \rightarrow \varDelta$ monotone maps. A monotone map $h :\varGamma \rightarrow \varDelta$ preserves post-fixed points if $x \le f(x)$ implies $h(x) \le g(h(x))$. It reflects post-fixed points if the converse implication holds.

In the step setting of Eq. (1), bisimulations for $B$- and $L$-coalgebras can be represented as post-fixed points of monotone maps on posets of relations as in Section 3. More concretely:

• Bisimulations for an $L$-coalgebra $f :X \rightarrow LX$ are post-fixed points of the monotone map $f^* \circ {\textsf{Rel}}(L)_X :{\textsf{Rel}}_X \rightarrow {\textsf{Rel}}_X$;

• Bisimulations for the $B$-coalgebra $\iota _X \circ Qf :QX \rightarrow BQX$ resulting from the application of the step-induced lifting of $Q$ are post-fixed points of $(\iota _X \circ Qf)^* \circ {\textsf{Rel}}(B)_{QX} :{\textsf{Rel}}_{QX} \rightarrow {\textsf{Rel}}_{QX}$.

The two can be compared via the restriction ${\textsf{Rel}}(Q)_X :{\textsf{Rel}}_X \rightarrow {\textsf{Rel}}_{QX}$ of the functor ${\textsf{Rel}}(Q)$. Indeed, our main objective is to show that in the presence of an invertible step, ${\textsf{Rel}}(Q)_X$ preserves and reflects post-fixed points representing bisimulations, and that it maps the greatest fixed point in ${\textsf{Rel}}_X$ (bisimilarity on $f$) to the greatest fixed point in ${\textsf{Rel}}_{QX}$ (bisimilarity on $\iota _X \circ Qf$). In this context we speak about preservation and reflection of bisimulations/bisimilarity.

4.2 Proof of preservation and reflection

We are now ready to prove preservation and reflection of bisimilarity, in the sense described in the previous subsection. First, the following basic lemma provides a method of showing preservation and reflection of post-fixed points, which will be useful for our purposes.

Lemma 4.2

Let $\varGamma$ and $\varDelta$ be posets, and $f :\varGamma \rightarrow \varGamma$, $g :\varDelta \rightarrow \varDelta$ and $h :\varGamma \rightarrow \varDelta$ monotone maps. Suppose that $h$ has a left (lower) adjoint $k :\varDelta \rightarrow \varGamma$, and the equality $gh = hf$ holds. Then $h$ maps the greatest fixed point of $f$ to the greatest fixed point of $g$, when these exist; h preserves post-fixed points; and if h is order-reflecting, then $h$ reflects post-fixed points.

Categorically speaking, the equality $gh = hf$ is an isomorphic step. Instantiated to our setting of interest, Lemma 4.2 gives us a method for proving preservation and reflection of bisimilarity: it suffices to show each of the following.

• 1. A left adjoint for ${\textsf{Rel}}(Q)_X$ (Lemma 4.7).

• 2. The equality $(\iota _X \circ Qf)^* \circ {\textsf{Rel}}(B)_{QX} \circ {\textsf{Rel}}(Q)_X = {\textsf{Rel}}(Q)_X \circ f^* \circ {\textsf{Rel}}(L)_X$ (Theorem 4.9).

• 3. Order-reflection of ${\textsf{Rel}}(Q)_X$ (assumption; discussed at the end of this section).

To obtain the required adjunction between the fibres ${\textsf{Rel}}_X$ and ${\textsf{Rel}}_{QX}$, we first establish the adjunction ${\textsf{Rel}}(P) \dashv {\textsf{Rel}}(Q)$ between the total relation categories. Given Assumption 3.1, we can lift the unit and counit of the adjunction $P \dashv Q$, using the transformations constructed in the following lemma.

Lemma 4.3

Let $F :\mathcal {C}\rightarrow \mathcal {D}$ and $G :\mathcal {D}\rightarrow \mathcal {E}$ be functors, with ${\textsf{Rel}}(F) :{\textsf{Rel}}(\mathcal {C}) \rightarrow {\textsf{Rel}}(\mathcal {D})$ and ${\textsf{Rel}}(G) :{\textsf{Rel}}(\mathcal {D}) \rightarrow {\textsf{Rel}}(\mathcal {E})$ the corresponding relation liftings. Then we have a natural transformation ${\textsf{Rel}}(GF) \rightarrow {\textsf{Rel}}(G) {\textsf{Rel}}(F)$. Further, if $G$ preserves abstract epis, then there is also a natural transformation ${\textsf{Rel}}(G) {\textsf{Rel}}(F) \rightarrow {\textsf{Rel}}(GF)$. Also, the constructed transformations are above the identity.

We note that the first part is in [28, Exercise 4.4.6] and the result is proved for $\textsf{Set}$ endofunctors in [9, Lemma 14.1]. This allows the lifting of the adjunction, which we note may also be obtainable from results on fibred adjunctions in [26, 30], but a direct proof is quite straightforward; the main idea is to use Lemma 4.3 together with preservation of abstract epis by $P$.

Lemma 4.4

The adjunction $P \dashv Q :\mathcal {D}\rightarrow \mathcal {C}$ lifts to relations, i.e., the following diagram is commutative, and the unit and counit of the upper adjunction are above the unit and counit of $P \dashv Q$.

(15)

The relation lifting defined in Section 3 allows us to define endofunctors ${\textsf{Rel}}(B)$, ${\textsf{Rel}}(L)$ in the context of the above adjunction:

(16)

In this setting, we may try to lift the step $\delta$ or its converse $\iota$ to this adjunction. It turns out that $\delta$ always lifts. For $\iota$, there is a sufficient condition which is independent of $\iota$ itself: that Q preserves abstract epis. In both cases, this result follows essentially from Lemma 4.3.

Proposition 4.5

For a forward step $\delta$ and backward step $\iota$, we have:

• 1. $\delta$ lifts to relations, i.e., there exists a natural transformation $\overline{\delta } :{\textsf{Rel}}(B) \circ {\textsf{Rel}}(Q) \rightarrow {\textsf{Rel}}(Q) \circ {\textsf{Rel}}(L)$ above $\delta$.

• 2. If $Q$ preserves abstract epis, then $\iota$ lifts to relations, i.e., there exists a natural transformation $\overline{\iota } :{\textsf{Rel}}(Q) \circ {\textsf{Rel}}(L) \rightarrow {\textsf{Rel}}(B) \circ {\textsf{Rel}}(Q)$ above $\iota$.

The condition that $Q$ preserves abstract epis holds, e.g., in case it is the forgetful functor in an adjunction monadic over $\textsf{Set}$. This is because Eilenberg-Moore categories of monads on $\textsf{Set}$ have $(\textsf{RegEpi},\textsf{Mono})$-factorisation systems, and the forgetful functor sends regular epis to epis in $\textsf{Set}$ as discussed in [13, Example 2.3]. It also holds in the $\textsf{Stone}$-$\textsf{Set}$ case, as $\textsf{Stone}$ is a reflective subcategory of $\textsf{CHaus}$ (which is equivalent to the category of algebras for the ultrafilter monad).

The lifted steps $\overline{\delta }$ and $\overline{\iota }$ give step-induced liftings of ${\textsf{Rel}}(P)$ and ${\textsf{Rel}}(Q)$ between ${\textsf{Coalg}}({\textsf{Rel}}(B))$ and ${\textsf{Coalg}}({\textsf{Rel}}(L))$. Since bisimulations can be equivalently presented as coalgebras for ${\textsf{Rel}}(B)$ and ${\textsf{Rel}}(L)$, these liftings can be used to capture preservation of bisimulations. But it is less obvious what reflection means in this context and how to prove it. For reflection of bisimulations by ${\textsf{Rel}}(Q)$, we turn our attention to the fibres, as described in the beginning of this section.

As a consequence of Proposition 4.5 and of $\delta \circ \iota = \textsf{id}$, we obtain the following result, which will later be used in the construction of a step on the fibres.

Lemma 4.6

Let $\delta$ be an invertible step with right inverse $\iota$, and suppose Q preserves abstract epis. Then ${\textsf{Rel}}(Q)_{LX} \circ {\textsf{Rel}}(L)_X = \iota _X^* \circ {\textsf{Rel}}(B)_{QX} \circ {\textsf{Rel}}(Q)_X$.

Adjoining the fibres Next, we construct an adjunction between the fibres ${\textsf{Rel}}_X$ and ${\textsf{Rel}}_{QX}$. The usual restriction ${\textsf{Rel}}(Q)_X$ of ${\textsf{Rel}}(Q)$ to the fibre ${\textsf{Rel}}_X$ will be the right adjoint, similarly to the adjunction obtained earlier. To map back into the fibre ${\textsf{Rel}}_X$, we post-compose ${\textsf{Rel}}(P)_{QX}$ with $\coprod _\varepsilon$, the direct image functor obtained from the counit of the adjunction ${\textsf{Rel}}(P) \dashv {\textsf{Rel}}(Q)$. We note the similarity with results on fibred adjunctions in [30], where only adjunctions over a single base category are considered.

Lemma 4.7

We have an adjunction $\coprod _\varepsilon \circ {\textsf{Rel}}(P)_{QX} \dashv {\textsf{Rel}}(Q)_X :{\textsf{Rel}}_X \rightarrow {\textsf{Rel}}_{QX}$.

The above lemma fulfils the first proof obligation stated in the beginning of Section 4.2. It now remains to show the second proof obligation, i.e., that we have an isomorphic step in the following setting:

(17)

To this end, we first show that ${\textsf{Rel}}(Q)$ preserves inverse images, using the fact that we can obtain inverse images as pullbacks inside the category of relations. Since ${\textsf{Rel}}(Q)$ is a right adjoint, it preserves these pullbacks.

Lemma 4.8

${\textsf{Rel}}(Q)$ preserves inverse images.

We are now ready to show the existence of the required isomorphic step.

Theorem 4.9

If $Q$ preserves abstract epis, then for any L-coalgebra (X, f):

$$\begin{aligned} (\iota _X \circ Qf)^* \circ {\textsf{Rel}}(B)_{QX} \circ {\textsf{Rel}}(Q)_X = {\textsf{Rel}}(Q)_X \circ f^* \circ {\textsf{Rel}}(L)_X \end{aligned}$$

(18)

Proof

We have

$$\begin{aligned} (\iota _X \circ Qf)^* \circ {\textsf{Rel}}(B)_{QX} \circ {\textsf{Rel}}(Q)_X&= (Qf)^* \circ \iota _X^* \circ {\textsf{Rel}}(B)_{QX} \circ {\textsf{Rel}}(Q)_X \end{aligned}$$

(19)

$$\begin{aligned}&= (Qf)^* \circ {\textsf{Rel}}(Q)_{LX} \circ {\textsf{Rel}}(L)_X \end{aligned}$$

(20)

$$\begin{aligned}&= {\textsf{Rel}}(Q)_X \circ f^* \circ {\textsf{Rel}}(L)_X \end{aligned}$$

(21)

where Eq. (19) is an application of a basic fact on inverse images (technically, that the poset fibration of relations is split), Eq. (20) holds by Lemma 4.6, and Eq. (21) holds by Lemma 4.8.    $\square$

We now reach our main result on preservation and reflection of bisimulations and bisimilarity by ${\textsf{Rel}}(Q)_X$.

Theorem 4.10

Let (X, f) be an L-coalgebra. Suppose that Q preserves abstract epis. Then $\overline{{\textsf{Rel}}(Q)_X}$ maps bisimilarity on (X, f) (when it exists) to bisimilarity on $\overline{Q}(X,f)$. Further, ${\textsf{Rel}}(Q)_X$ preserves bisimulations and, if it is order-reflecting, also reflects bisimulations.

Proof

We have seen in Lemma 4.7, that ${\textsf{Rel}}(Q)_X$ has a left adjoint, and in Theorem 4.9, that in this setting we have an isomorphic step. The result now follows from Lemma 4.2.    $\square$

While this result is formulated in terms of ${\textsf{Rel}}(Q)_X$, we will also speak of simply $\overline{Q}$ preserving and reflecting both bisimulations and bisimilarity.

As a special case of Theorem 4.10, we recover (a version of) the following existing result found in [3, 11, 12, 42].

Lemma 4.11

Assume functors $B,L :\mathcal {C}\rightarrow \mathcal {C}$, and a natural transformation $\iota :L \rightarrow B$. Then the functor $\overline{\textsf{Id}} :{\textsf{Coalg}}(L) \rightarrow {\textsf{Coalg}}(B)$ defined by $(X, f) \mapsto (X, \sigma _X \circ f)$ on objects and identity on morphisms, preserves bisimulations. If additionally $\iota$ has a left inverse, $\overline{\textsf{Id}}$ reflects bisimulations.

We briefly turn to the condition of order-reflectingness. As we are often interested in cases where the right adjoint is a forgetful functor in the context of an Eilenberg-Moore adjunction, it is useful to state the following.

Lemma 4.12

For a monad T with forgetful functor , the (restricted) lifting ${\textsf{Rel}}(U)_X$ is an order-reflecting map.

If $\mathcal {C}=\textsf{Set}$ in the above lemma, then ${\textsf{Rel}}(U)_X$ is just the inclusion of the poset of congruences ${\textsf{Rel}}_X$ on an algebra X into the poset of all relations on its carrier.

In that case, we can also use the above to show preservation and reflection of behavioural equivalence. Two states of a coalgebra (in $\textsf{Set}$) are behaviourally equivalent if they can be identified by some coalgebra homomorphism. This can be captured more abstractly using kernel bisimulations (see, e.g., [44]). Since U is assumed to be a forgetful functor to $\textsf{Set}$, we simply define preservation and reflection of behavioural equivalence by $\overline{U}$ to mean that for any two states x, y of an L-coalgebra (X, f), x and y are behaviourally equivalent (for (X, f)) if and only if they are behaviourally equivalent for $\overline{U}(X,f)$.

It turns out that, in our setting, coincidence of bisimilarity and behavioural equivalence for L-coalgebras reduces to coincidence for B-coalgebras. This is stated in the following lemma; the essence is that $\overline{U}$ is easily shown to preserve behavioural equivalence.

Lemma 4.13

For a monad T, consider the Eilenberg-Moore adjunction with functors and $B :\textsf{Set}\rightarrow \textsf{Set}$, and an invertible step $\delta :BU \rightarrow UL$. Further suppose that $\overline{U}$ preserves and reflects bisimilarity, and that B preserves weak pullbacks. Then bisimilarity and behavioural equivalence for L-coalgebras coincide (and hence, $\overline{U}$ preserves and reflects behavioural equivalence).

Remark 4.14

We conclude with a brief exploration of preservation and reflection by the restriction of the left adjoint ${\textsf{Rel}}(P)_X$, in the setting of

(22)

with $f :X \rightarrow BX$ a $B$-coalgebra in this case. Here, we can obtain a backward step ${\textsf{Rel}}(P)_X \circ f^* \circ {\textsf{Rel}}(B)_X \le (\hat{\delta }_X \circ Pf)^* \circ {\textsf{Rel}}(L)_{PX} \circ {\textsf{Rel}}(P)_X$ which means that we can lift ${\textsf{Rel}}(P)_X$ to bisimulations, so that these are preserved. However, we cannot obtain a forward step in this context, thus reflection will not hold. This is illustrated, e.g., by the example of ultrafilter extensions, where the ultrafilter monad $\beta$ certainly does not reflect bisimulations: in general, in the ultrafilter extension more states will be bisimilar.

5 Applications

Now that we have obtained conditions for the preservation and reflection of bisimilarity, we return to the examples of Section 2.2. We will show how a number of existing non-trivial results can be recovered in a concise way. Further, the $\textsf{Set}$-$\textsf{Stone}$ adjunction used in the first example is known to not be monadic, and so outside the scope of weak liftings, which indicates the generality of our results.

Ultrafilter Extensions and Vietoris bisimulations In Example 2.5, we have seen how the construction of ultrafilter extensions can be obtained from an invertible step, which arises from a weak lifting described by Garner. In the current treatment of reflection and preservation of bisimilarity, we focus on the restriction of this invertible step to the category $\textsf{Stone}$.

This brings us in line with [5], where a comparison is made between bisimilarity for the Vietoris functor $\mathcal {V} :\textsf{Stone}\rightarrow \textsf{Stone}$ and bisimilarity for the powerset functor $\mathcal {P} :\textsf{Set}\rightarrow \textsf{Set}$, called Vietoris-bisimilarity and Kripke-bisimilarity respectively in op. cit. More precisely, for a $\mathcal {V}$-coalgebra (X, f), Kripke bisimilarity is bisimilarity on $\overline{U}(X,f)$, where $\overline{U}$ is the step-induced lifting of the forgetful functor $U :\textsf{Stone}\rightarrow \textsf{Set}$. Vietoris bisimilarity is simply bisimilarity on the coalgebra (X, f) itself.

We consider the following results from [5]:

• 1. The relation liftings of $\mathcal {P}$ and $\mathcal {V}$ coincide for closed subsets [5, Prop 3.4]

• 2. Vietoris bisimulations are equivalently closed Kripke bisimulations [5, Thm 3.6]

• 3. The closure of a Kripke bisimulation is a Vietoris bisimulation [5, Thm 5.2]

• 4. Vietoris- and Kripke-bisimilarity are equivalent [5, Cor 3.10]

From the above discussion, we see that these results fit into the setting of Section 4, so that they can be recovered using our results on the preservation and reflection of bisimilarity as follows:

• 1. This follows from the equality of Lemma 4.6, as the action of $\iota ^*$ is exactly the restriction to closed subsets. We can apply this lemma as $U$ preserves abstract epis, due to the same argument as for adjunctions monadic over $\textsf{Set}$ (see the discussion after Proposition 4.5), as $\textsf{Stone}$ is also a regular category.

• 2. For this, we use preservation and reflection of bisimulations by the (restricted) relation lifting ${\textsf{Rel}}(U)_X :{\textsf{Rel}}_X \rightarrow {\textsf{Rel}}_{UX}$ of the forgetful functor, which is simply the inclusion of the poset of closed relations on a Stone space X to that of all relations on the underlying set.

  Indeed, preservation and reflection by ${\textsf{Rel}}(U)_X$ follows from Theorem 4.10. We have seen that $U :\textsf{Stone}\rightarrow \textsf{Set}$ preserves abstract epis, so it only remains to check that ${\textsf{Rel}}(U)_X$ is order-reflecting. This holds because $\textsf{Stone}$ is a reflective (i.e. full) subcategory of $\textsf{CHaus}$, which is monadic over $\textsf{Set}$.

• 3. The left adjoint $\coprod _\varepsilon \circ {\textsf{Rel}}(\beta )_{UX}$ of Lemma 4.7 gives the closure of a relation. Its lifting to bisimulations (cf. Remark 4.14) yields the desired result.

• 4. This holds since ${\textsf{Rel}}(U)_X$ maps the greatest fixed point of $(\iota _X \circ Uf)^* \circ {\textsf{Rel}}(\mathcal {P})_{UX}$ to that of $f^* \circ {\textsf{Rel}}(\mathcal {V})_X$, i.e., it preserves and reflects bisimilarity.

PAs and Belief State Transformers As discussed in Example 2.6, we can determinise a PA to a coalgebra for the convex powerset functor using a lifting of . The step-induced lifting of the corresponding forgetful functor maps the $\mathcal {P}_c$-coalgebra back into $\textsf{Set}$, but we must take care that this does not change its behaviour. What we can do now, is show that bisimilarity is preserved and reflected.

Once we know this, we can apply Lemma 4.13 to show the coincidence of bisimilarity and behavioural equivalence in the case of the convex powerset functor on and the powerset functor on $\textsf{Set}$ as this preserves weak pullbacks. This coincidence is relevant for the generalisation of the corresponding results of [12] (restricted to the convex powerset functor), which are formulated in terms of behavioural equivalence. As mentioned in Example 2.6, the weak lifting we require to cover automata with labels can be found in [21]. Consider the following:

• 1. The lifting of the forgetful functor preserves and reflects behavioural equivalence on $\mathcal {P}_c^L$-coalgebras [12, Proposition 6.6].

• 2. A relation $R$ is a kernel bisimulation for a $\mathcal {P}_c^L$-coalgebra $(\mathbb {S},c)$ in iff it is a kernel bisimulation for $\overline{U}(\mathbb {S},c)$ and also a congruence.

Again, we can apply the results of Section 4 to recover these results. In fact, in [12, Proposition 6.5], the second result is proved more generally, namely for settings where a so-called lax lifting exists rather than the weak lifting we require.

• 1. We have seen that $U$ preserves abstract epis as the adjunction in question is monadic over $\textsf{Set}$. This allows us to apply Theorem 4.10 so that $\overline{U}$ indeed preserves and reflects bisimulations, and the relevant lifting preserves and reflects bisimilarity. From Lemma 4.13, it follows that $\overline{U}$ also preserves and reflects behavioural equivalence.

• 2. Assuming $(\mathbb {S},c)$ is a $\mathcal {P}_c^L$-coalgebra, this follows from Lemma 4.13 together with the previous item, and the fact that bisimulations in Eilenberg-Moore categories are congruences.

Automata For a different instance, we revisit Example 2.7 and consider the basic adjunction $P\dashv Q :\mathcal {D}^\textsf{op}\rightarrow \mathcal {C}$. As a general remark, we note that if $\mathcal {D}$ admits a factorization system $(\mathcal {E}, \mathcal {M})$ with $\mathcal {E}$ a class of epis, and $\mathcal {M}$ a class of monos, then $(\mathcal {M},\mathcal {E})$ forms a factorization system for $\mathcal {D}^\textsf{op}$, with $\mathcal {M}$ a class of epis in $\mathcal {D}^\textsf{op}$, and $\mathcal {E}$ a class of monos in $\mathcal {D}^\textsf{op}$. We can explicitly describe ${\textsf{Rel}}(\mathcal {D}^\textsf{op})$ as follows:

• Objects of ${\textsf{Rel}}(\mathcal {D}^\textsf{op})$ are quotients $X+X\twoheadrightarrow E$ of $X+X$;

• A map $X+X\twoheadrightarrow E \rightarrow Y + Y\twoheadrightarrow F$ consists of a map $u:Y\rightarrow X$ in $\mathcal {D}$ such that there is the following commutative diagram

  

  (23)

In the case $\mathcal {D} = \textsf{Set}$, $\mathcal {E} = \textsf{Epi}$ and $\mathcal {M} = \textsf{Mono}$. Further, every epi $e :X+X\twoheadrightarrow E$ is isomorphic to an epi of the form $X+X\twoheadrightarrow (X+X)/{\sim }$ with $\sim$ an equivalence relation on $X+X$. This gives us an equivalent description of ${\textsf{Rel}}(\textsf{Set}^\textsf{op})$:

• Objects of ${\textsf{Rel}}(\textsf{Set}^\textsf{op})$ are equivalence relations $\sim$ on $X+X$ for a set X;

• A map ${\sim } \subseteq (X+X)^2\rightarrow {\approx } \subseteq (Y+Y)^2$ consists of a map $u:Y\rightarrow X$ such that if $j(y)\approx j'(y')$, then $j(u(y))\sim j'(u(y'))$, with $j, j'$ arbitrary coproduct inclusions.

In particular, we see that the fibre over a set X consists of all equivalence relations on $X+X$, ordered by reverse inclusion. Reindexing along a map $u :X\leftarrow Y$ maps an equivalence relation ${\approx }$ on $Y+Y$ to the least equivalence relation ${\sim }$ on $X+X$, such that $j(u(y))\sim j'(u(y'))$ for all $j(y)\approx j'(y')$.

Focusing on the setting of (8) in Example 2.7, the lifting ${\textsf{Rel}}(L)$ is given by

$$\begin{aligned} \textsf{inl}(*)\ {\textsf{Rel}}(L)(\sim )\ \textsf{inr}(*)&\end{aligned}$$

(24)

$$\begin{aligned} j(( a, x)) \ {\textsf{Rel}}(L)(\sim ) \ j'(( b,x))&\iff a = b\text { and }j(x)\sim j'(y) \end{aligned}$$

(25)

If $f :X\leftarrow 1 + \varSigma \times X$ is an L-coalgebra, we see that $f^*\circ {\textsf{Rel}}(L)_X$ maps an equivalence relation ${\sim }$ on $X+X$ to the least equivalence relation $\approx$ satisfying

$$\begin{aligned} \textsf{inl}(f(*))\approx \textsf{inr}(f(*))&\end{aligned}$$

(26)

$$\begin{aligned} j(f(a,x)) \approx j'(f(a,y))&\text { whenever }j(x)\sim j'(y) \end{aligned}$$

(27)

A post-fixed point of this map is an equivalence relation $\sim$ which relates $\textsf{inl}(f(*))$ and $\textsf{inr}(f(*))$ and is closed under the action of $\varSigma$ on $X+X$. The greatest post-fixed point is the least such relation, as relations in ${\textsf{Rel}}_X$ are ordered by reverse inclusion. It is easy to see that this is exactly the relation which identifies $\textsf{inl}(x)$ and $\textsf{inr}(x)$ for those x reachable from $f(*)$.

${\textsf{Rel}}(Q)$, meanwhile, maps an equivalence relation $\sim$ on $X+X$ to the relation R on $2^X$ given by

$$\begin{aligned} uRv\iff \textsf{inl}[u]\cup \textsf{inr}[v]\text { is }{\sim }\text {-closed} \end{aligned}$$

(28)

If $X'$ is the set of reachable states, we conclude that ${\textsf{Rel}}(Q)$ maps the greatest bisimulation $\sim$ to the relation

$$\begin{aligned} uRv\iff u\cap X' = v\cap X' \end{aligned}$$

(29)

The functor $Q$ preserves (abstract) epis, as all epis in $\textsf{Set}^\textsf{op}$ are regular. Now, Theorem 4.10 tells us that the relation (29) coincides with bisimilarity on the automaton $\overline{Q}(X,f)$ from Example 2.7. It follows that the subautomaton on $2^{X'}$ is minimal, and is the minimal automaton equivalent to $\overline{Q}(X,f)$.

6 Discussion and Future Work

We studied the notion of an invertible step, which provides several constructions on coalgebras via functor liftings. We showed that the lifting of the right adjoint, induced by such an invertible step, preserves and reflects bisimilarity. This abstract result instantiates to several concrete results from the literature, in examples related to ultrafilter extensions and weak distributive laws.

We have focused on preservation and reflection of bisimilarity, defined in terms of relation lifting. There are several other coalgebraic notions of behavioural equivalence and bisimilarity [44]—we discuss these in the next subsection. Finally, in Section 6.2 we list directions for future work.

6.1 Remarks on other notions of bisimulation

Aczel-Mendler bisimulations For a coalgebra $f :X \rightarrow LX$, an Aczel-Mendler bisimulation $R \rightarrowtail X \times X$ is defined by the existence of an $L$-coalgebra structure $R \rightarrow LR$ on $R$ such that the projection maps are coalgebra homomorphisms [1].

In the invertible step setting, applying a lifting $\overline{Q}$ to such a bisimulation, yields a structure $QR \rightarrow BQR$. However, this is not immediately a bisimulation, as $QR$ may not be a relation. We can obtain a relation by taking the image of $\langle Q \pi _1, Q \pi _2 \rangle$ as we do to define relation lifting, but in general this is a Hermida-Jacobs bisimulation [28, Exercise 4.5.2], rather than an Aczel-Mendler one.

On the other hand, if we wish to speak of reflection of Aczel-Mendler bisimulations, we start with a span $QX \leftarrow R \rightarrow QX$ and try to construct a relation on $X$. Using the adjunction of the step setting, we can transpose the projections to obtain a span $X \leftarrow PR \rightarrow X$. Again $PR$ is not immediately a relation in general, and taking the image yields a ${\textsf{Rel}}(L)$-coalgebra (not an $L$-coalgebra) as the projections and the counit $\varepsilon$ are coalgebra homomorphisms (see also [28, Exercise 4.5.4]). This in fact comes down to the same as the left adjoint ${\coprod _\varepsilon \circ {\textsf{Rel}}(P)_{QX}}$ constructed earlier. There we factorise to obtain the relation lifting and factorise again for the direct image of $\varepsilon$, instead of factorising the paired transposes defined using $\varepsilon$. We also do not explicitly use that $\varepsilon$ is a coalgebra homomorphism (although this follows from the step with right inverse and Lemma 2.3); instead we lift the adjunction at the level of relations to give a map between bisimulations. This is part of the motivation for the use of relation liftings and the corresponding notion of bisimulations.

Going further, it is shown in [5] that there exists a Vietoris bisimulation which is not an Aczel-Mendler bisimulation and, stronger, that there exist Vietoris coalgebras with states which can be related by a Vietoris but not an Aczel-Mendler bisimulation. Thus, the correspondences between bisimulations on $\textsf{Set}$ and $\textsf{Stone}$ we have discussed in the previous sections are not obtainable when we consider Aczel-Mendler bisimulations.

Kernel bisimulations/behavioural equivalence In applying our results to the preservation and reflection of behavioural equivalence, we currently work concretely; considering sets of states and identification of elements.

We prefer to work more abstractly, as we have done for bisimilarity. To this end, we may consider kernel bisimulations. A relation $R \rightarrowtail X \times X$ is a kernel bisimulation on a coalgebra $(X,f :X \rightarrow LX)$ in a category $\mathcal {D}$, if it is the pullback of morphisms $X \rightarrow Z \leftarrow X$ in $\mathcal {D}$ forming a cospan of coalgebra homomorphisms $(X,f) \rightarrow (Z,z) \leftarrow (X,f)$ in ${\textsf{Coalg}}_{\mathcal {D}}(L)$. In a concrete setting this coincides with behavioural equivalence, as such a pullback contains exactly the pairs of elements of $X$ which are identified in $Z$ by the morphisms forming the cospan. We can thus view this as a generalisation of behavioural equivalence as defined earlier.

Assuming an invertible step $\delta :BQ \rightarrow QL$, we would like to relate $R$ to a kernel bisimulation on the coalgebra $\overline{Q}(X,f)$ obtained by applying the step-induced lifting of $Q$. Applying $Q$ to the pullback square for $R$ yields a pullback square as $Q$ is a right adjoint. However, as in our discussion of Aczel-Mendler bisimulations, this may not be a relation. We may try to also use relation liftings here, and take ${\textsf{Rel}}(Q)(R)$ instead of $Q(R)$, however this may no longer be a pullback. It is not currently clear to us how to resolve these problems in general.

6.2 Future work

There are several further directions for future work. First, in this paper we focused primarily on fibrations of relations, which suffice for our purposes of studying bisimilarity. However, we expect that some of our results can be generalised to arbitrary (posetal) fibrations. Such a generalisation could be the basis to study preservation and reflection of other coinductive predicates and relations than bisimilarity, which can be formulated in terms of fibrations and liftings (e.g., [25]).

Secondly, while we have shown in Section 5 how our results can be used to recover the central results from [5], the latter have been generalised in two directions: the recent [24] considers bisimulations for Vietoris coalgebras on the category of arbitrary topological spaces, while [18] develops a notion of neighbourhood bisimulation for coalgebras that allows to generalise the results from [5] to a large variety of functors on the category of Stone spaces and their corresponding functors on $\textsf{Set}$. We would like to understand whether or not our framework is able to recover these generalisations.

Finally, the examples that we have studied in this paper do not yet exploit the full generality of invertible steps: our main motivating examples are based on an Eilenberg-Moore adjunction (or close, as in the example based on Stone spaces). In [41] it is shown that steps are relevant in a much wider setting, for instance when based on a Kleisli adjunction or on contravariant adjunctions and dualities. The latter type of steps are relevant for coalgebraic modal logics—we have studied a first instance in our example of deterministic and non-deterministic automata. Investigating the meaning of invertible steps in these other types of adjunctions is left for future work.