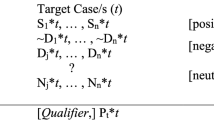Black Holes and Analogy

Abstract

It is generally accepted that science sometimes involves reasoning with analogies. Often, this simply means that analogies between disparate objects of study might be used as heuristics to guide theory development. Contemporary black hole physics, however, deploys analogical reasoning in a way that seems to overreach this traditional heuristic role. In this chapter, I describe two distinct pieces of analogical reasoning that are quite central to the contemporary study of black holes. The first underpins arguments for the existence of astrophysical Hawking radiation, and the second underpins arguments for black holes being ‘genuinely’ thermodynamical in nature. I argue that while these are distinct analogical arguments, they depend on one another in an interesting way: the success of the second analogical argument presupposes the success of the first. This induces a tension for those who wish to take black hole thermodynamics seriously, but who are sceptical of the evidence provided for astrophysical Hawking radiation by the results of analogue gravity. I consider three ways to resolve this tension, and show that each fails.

1 Introduction

To put it flippantly, the trouble with black holes is that they are black, and that they are holes. This makes direct empirical contact with black hole systems an intrinsically troublesome business, since by definition the (classical) black hole necessarily has no optical signature and the fact that its conventional definition—in terms of an event horizon—makes reference to future null infinity means that it has no well-defined location in spacetime. But the experimental astrophysicist’s loss is the philosopher’s gain: the difficulties that hinder straightforward empirical access to black holes have necessitated the use of less conventional epistemic techniques by physicists, and it is precisely these difficulties that make the epistemology of black hole physics such a fertile ground for philosophical scrutiny. Some of these techniques are comparatively quotidian: indirect detection of black holes by the observation of their interaction (gravitational or electromagnetic) with ordinary matter, for instance.¹ But others are more philosophically interesting, and perhaps controversial. One example is the use of analogical reasoning in black hole physics.

That there is analogical reasoning in contemporary black hole physics is, by now, an uncontroversial point. Indeed, there is a burgeoning literature on the epistemology of analogue experiments, and analogue gravity (as we shall examine in greater detail below) is a central case study in this literature (Dardashti et al. 2017, 2019; Thébault 2019; Evans and Thébault 2020; Crowther et al. 2021; Field 2022). Similarly, black hole thermodynamics (BHT)—which takes as its departure point the striking analogy between the laws of black hole mechanics and those of ordinary thermodynamics—has been of great interest to physicists since its discovery by Bardeen et al. (1973). Recent years have seen a growing interest in—and dispute over—how we should interpret this unexpected correspondence between two pillars of modern physics by philosophers (Curiel 2014; Wallace 2018, 2019; Wüthrich 2019; Prunkl and Timpson 2019; Dougherty and Callender 2016).

Relatively little attention, however, has been paid to BHT qua a piece of analogical reasoning. The literature that does exist focuses almost exclusively on the conceptual difficulties that arise from attempting to interpret various black hole mechanical quantities as genuinely equivalent to their thermodynamical analogues, and the attendant difficulties for the claim that black holes are capable of genuinely thermodynamical behaviour. But it does not explicitly apply the philosophical literature on analogical reasoning to the BHT analogy. This leaves two blind spots in the literature on analogical reasoning in black hole physics. First, there is the need for precisely this kind of focused analysis of BHT qua a piece of analogical reasoning. Second, although philosophers have scrutinised both analogue gravity and BHT in isolation, scant philosophical work has been done on the connection between them.²

And yet such a connection clearly exists: on the standard view, it is Hawking’s (1974) prediction of radiative flux from a black hole’s event horizon that “removes the blemishes in BHT and transforms it from a suggestive analogy to a full equivalence” (Wallace 2018, p. 60).³ Because direct empirical detection of the Hawking flux borders on the impossible, however, it is analogue gravity research that provides the closest thing to empirical evidence for the Hawking effect. Here, then, the two instances of analogical reasoning clearly make contact. I shall argue that their doing so creates an interesting tension for those who are compelled by BHT and yet remain skeptical about analogue gravity epistemology.

This chapter is primarily intended to clarify the structure of the instances of analogical reasoning in contemporary black hole physics, and to clarify how they make contact with one another, rather than intended to directly evaluate whether those instances of analogical reasoning succeed. In a sense, then, this chapter plays the role of prelude to both the existing philosophy of physics literature that seeks to defend or downplay the physical significance of the analogue gravity or BHT analogies, and the existing philosophy of science literature that examines the possibility of confirmation via analogue experimentation in black hole physics.

The structure of this piece is as follows: The first half of the paper (Sect. 14.2) provides a survey of the two central instances of analogical reasoning in contemporary black hole physics: analogue gravity and black hole thermodynamics. I begin with some groundwork on analogical reasoning (Sect. 14.2.1), and then survey, and explicitly reconstruct analogical arguments for, analogue gravity (Sect. 14.2.2) and BHT (Sect. 14.2.3). The second half of the paper (Sect. 14.3) examines what the relationship between these two analogical arguments might be, arguing that they are distinct but nevertheless importantly interdependent, and teasing out an important tension that this implies. I then consider three possible ways to resolve this tension and argue that each will fail. In Sect. 14.4 I conclude.

2 Two Analogies in Contemporary Black Hole Physics

2.1 Analogical Reasoning

Before we examine the ways in which analogies and analogical reasoning are invoked in contemporary black hole physics, we should make explicit exactly what is meant by these terms in the round. In this chapter, I adopt a broadly Hessean picture of analogy, following in particular Keynes (1921), Hesse (1966), and Bartha (2010), since these works build, sequentially, on one another and I take them collectively to constitute the mainstream orthodoxy in the analogical reasoning literature. It is worth noting, however, that plenty of dissenting accounts of analogical reasoning exist.⁴ My concern, then, is with specifically Hessean analogical reasoning in contemporary black hole physics. Whether the problems I describe in this chapter are remedied or exacerbated by adopting an alternative account of analogy is a question that must be left for another time.⁵

Bartha (2010, p. 1) takes an analogy to be “a comparison between two objects, or systems of objects, that highlights respects in which they are thought to be similar”. The conventional way of formalising this idea appeals to the notion of a mapping. Given a source domain, S, and a target domain, T, an analogy is a one-to-one mapping, ϕ, that maps elements of S to elements of T. Here, ‘elements’ can be construed quite broadly: elements could be properties, relations, objects, or functions depending on the nature of the domains in question (p. 13).

$$\displaystyle \begin{aligned} a \in S \leftrightarrow_{\phi} a^* \in T \end{aligned}$$

$$\displaystyle \begin{aligned} b \in S \leftrightarrow_{\phi} b^* \in T\end{aligned}$$

$$\displaystyle \begin{aligned} c \in S \leftrightarrow_{\phi} c^* \in T\end{aligned}$$

Starred and unstarred elements are ‘analogues’ of one another under ϕ. From here on I drop the ‘∈’ notation and take it as understood that elements on either side of the horizontal relation are from different domains (as a convention, I shall stick to ‘source’ being left, and ‘target’ being right).

It is worth making two useful terminological refinements to our account of analogy:

• 1. Following Keynes (1921), we can distinguish between ‘positive’, ‘negative’ and ‘neutral’ parts of an analogy. For expositional simplicity, let the elements of our source and target domains be propositions. The positive analogy is the set P of propositions in S whose images under ϕ hold in T. The negative analogy is the set N of propositions in S whose images under ϕ do not hold in T. The neutral analogy is the set of propositions in S for whom it is not known whether their images under ϕ hold in T, i.e. S ∖ P ∪ N.

• 2. Following Hesse (1966), we can make a further distinction between ‘horizontal’ and ‘vertical’ relations in an analogy. Horizontal relations are, according to Hesse (1966, p. 59), those concerned with the similarity of counterparts determined by the mapping, ϕ. The horizontal relation is the relation of identity or difference between an element of S and its image under ϕ in T. What makes a and a ^∗ analogues is the fact that ϕ picks them out as identical with respect to, e.g., function, property, mathematical structure, and so on. By contrast, vertical relations, for Hesse are the causal relations that obtain between elements of a single domain. For example, how a relates to b, and so forth.

It is worth noting that this definition sets the bar trivially low for the existence of analogies in black hole physics. One can always propose a comparison between any two systems (black holes and thermodynamical systems, for example) that moots certain similarities, and as such one can always trivially assert the existence of analogies more or less anywhere. This makes the question of whether there are analogies in black hole physics somewhat uninteresting. The answer is yes, for the same reason that there are analogies everywhere—we are pattern-seeking beings, and we are apt to propose patterns or similarities wherever we like. Our concern, rather than with analogy simpliciter, is with the earnest deployment of analogical reasoning in black hole physics.

Analogical reasoning, Bartha suggests, is “any type of thinking that relies upon an analogy” (2010, p. 1, my emphasis). In formal terms, this usually comprises conjecturing that an element currently in the neutral analogy belongs in the positive analogy, with the chosen element of the neutral analogy being referred to by Keynes as the ‘hypothetical analogy’. An ‘analogical argument’ is simply an explicit representation, by way of premise and conclusion, of a piece of analogical reasoning, conforming roughly to the general schema below:

General Schema

• (i) P ↔_ϕ P ^∗ [Positive Analogy]

• (ii) Q ↔_ϕ Q ^∗ [Positive Analogy]

• (iii) R ↔_ϕ R ^∗ [Positive Analogy]

  __________________________________________________________

• $$\therefore$$∴ S ↔_ϕ S ^∗ [Hypothetical Analogy]

The rest of this section applies this schema to the two cases of analogical reasoning in contemporary black hole physics, identifying the salient positive analogies, the types of horizontal relationships involved, and any critical disanalogies that appear to block the conclusion. Section 14.2.2 discusses and formalises the analogical argument that underpins analogue gravity research; Sect. 14.2.3 does the same for BHT.

2.2 Analogue Gravity

Analogue gravity research exploits a precise mathematical isomorphism, first discovered by Unruh (1981), between the behaviour of sound waves in a convergent fluid flow, and the behaviour of light in black hole spacetimes. Because our understanding of the propagation of sound in a fluid is so much better than our understanding of quantum field theory in curved spacetime, the primary benefit of analogue gravity is that a system whose microphysics is well understood can be used as an empirical surrogate for a system whose microphysics is incredibly poorly understood (since we expect a complete description to require an adequate theory of quantum gravity), and almost entirely inaccessible. To return to the comment I made at the start of this chapter, analogue gravity’s ingenuity stems from the fact that it seems to offer a way to study systems that are not black, and not holes, but are—in some sense—still black holes.

2.2.1 The Positive Analogy

Crudely put, the positive analogy between analogue black holes and astrophysical black holes is that in both cases we can describe them well mathematically by “[taking] some sort of ‘excitation’, travelling on some sort of ‘background’, and [analysing] its propagation in terms of the tools and methods of differential geometry” (Visser 2013, p. 31). For present purposes, it is not necessary to delve too much further into the technical details of semiclassical or analogue gravity.⁶ Rather, we can simply note (as Unruh 1981 originally did) that sound waves in a converging fluid flow can be modelled as the excitations of a minimally-coupled massless scalar field propagating in a (3 + 1)-dimensional Lorentzian geometry with the covariant acoustic metric:

$$\displaystyle \begin{aligned} g^{\text{acoustic}}_{\mu\nu} = \frac{\rho_0}{c_{\text{sound}}} \begin{bmatrix} -(c_{\text{sound}}^2-v_0^2) & \vdots & -v_0^j\\ \dots & \cdot & \dots \\ -v_0^i & \vdots & \delta_{ij} \end{bmatrix}{} \end{aligned} $$

(14.1)

Which bears a striking resemblance to the Painlevé-Gullstrand form of the Schwarzschild metric:

$$\displaystyle \begin{aligned} g^{\text{Schwarzschild}}_{\mu\nu} = \begin{bmatrix} -(c_{0}^2-\frac{2GM}{r}) & \vdots & -\sqrt{\frac{2GM}{r}}{\mathbf{r}}_j\\ \dots & \cdot & \dots \\ -\sqrt{\frac{2GM}{r}}{\mathbf{r}}_i & \vdots & \delta_{ij} \end{bmatrix} \end{aligned} $$

(14.2)

Thus, the Schwarzschild spacetime and the converging fluid flow share the same effective geometry, encoded by these isomorphic metrics. Using the tools of quantum field theory of curved spacetime, we approximate quantum gravity by propagating quantum fields across this curved but classical spacetime background. In much the same way, sound waves moving in the fluid medium described by (14.1) can be modelled as scalar fields propagating across this geometry.

Despite the numerous ways in which analogue black holes remain radically dissimilar to their astrophysical counterparts,⁷ the thought is that this underlying mathematical isomorphism is nevertheless strong enough to capture at least kinematic similarity between acoustic black holes and their astrophysical counterparts. Thus, the thinking goes, the positive analogy between the mathematics of analogue black holes and astrophysical black holes can support certain inferences about the behaviour of astrophysical black holes from the behaviour of their analogue counterparts.

In principle, there could be many different candidates for what these inferences might be. To put it in Keynes’ terms, any property of analogue black holes in the ‘neutral analogy’ could, in principle, be proposed as the ‘hypothetical analogy’ (i.e. the property that we are suggesting astrophysical black holes might have, based on the strength of the existing ‘positive analogy’). This flexibility is simultaneously analogical reasoning’s greatest strength and greatest weakness. But in practice, the inference most commonly made from analogue gravity research has to do with the Hawking effect.

The Hawking effect is the result that at asymptotically late times, particles of a quantum field in a stationary black hole spacetime are radiated from the event horizon out to infinity in precisely the same way as radiation from a perfect blackbody at the Hawking temperature, $T=\frac {\kappa }{2\pi }$.⁸ But because surface gravity scales inversely with mass, and because black holes are typically very massive objects, the Hawking temperature for even solar mass black holes is minuscule (of the order 10⁻⁸ K) which makes astrophysical Hawking radiation nigh on impossible to detect empirically. The inference that analogue gravity research is commonly taken to support is that direct observation of the analogue Hawking effect in analogue black holes allows us to infer (at least analogically) that astrophysical Hawking radiation does, indeed, exist.⁹

We might worry that because there remain so many differences between analogue and astrophysical black holes, this inference is a spurious one. There are two ways to allay this concern, which both appeal to the robustness of the Hawking effect. First, we can appeal to the fact that various universality arguments have been given to support the idea that the Hawking effect will be robust under changes in the microphysics of the system in which it appears.¹⁰ It is worth noting, however, that Gryb et al. (2020) argue forcefully that none of the available universality arguments for Hawking radiation are entirely convincing (especially in light of the fact that none provide a fully satisfactory response to the trans-Planckian problem, which we shall see in more detail in Sect. 14.3.2). Field (2022) goes one step further, questioning whether the epistemic situation in analogue gravity is even one that can be ameliorated by universality arguments. On Field’s view, “our state of knowledge with respect to Hawking radiation is not currently universality-argument-apt” (2022, p. 25). A safer option, then, is the second: we can note that because the Hawking effect is entirely kinematic and depends only on the existence of a Lorentzian metric and an appropriate horizon (Visser 2003), it would seem to be the kind of thing that is determined by the isomorphism we saw above. Thus, analogue gravity advocates suggest, the existence of the Hawking effect in analogue black hole systems would support the existence of the Hawking effect in astrophysical black hole systems. And furthermore, since researchers have demonstrated the existence of both stimulated and spontaneous phononic Hawking radiation from acoustic horizons in fluids (Weinfurtner et al. 2011), and from optical horizons in Bose-Einstein condensates (Steinhauer 2016; de Nova et al. 2019; Drori et al. 2019; Kolobov et al. 2021), the antecedent in this conditional seems to be satisfied.¹¹ Thus, the results of analogue gravity experiments may be considered to indirectly confirm Hawking’s (1974; 1975) prediction of thermalised radiation from astrophysical black holes.

2.2.2 Formalisation

Here is a reasonable first pass at formalising the analogical argument for astrophysical Hawking radiation:

Analogue Gravity (Mathematical Similarity)

• (i) Mathematics of analogue black holes ↔_ϕ Mathematics of astrophysical black holes

  __________________________________________________________________________________________

• $$\therefore$$∴ Radiation from analogue black holes ↔_ϕ Radiation from astrophysical black holes

This is, of course, not deductively valid. No analogical arguments are. But it is also not sufficiently detailed. For a start, we need to be more precise about the nature of ϕ. In what sense is the mathematics of the two systems similar? After all, the mathematics used to describe analogue black holes is not entirely similar to the mathematics used to describe astrophysical black holes—gravitation is not fluid flow.¹² So which parts of the mathematics for the two types of systems are we interested in, and in what sense are these parts connected? Whichever mathematical commonality (i) is picking out will have to be appropriately related to the proposed physical commonality in the conclusion.

If Visser is correct that Hawking radiation requires only the existence of a Lorentzian geometry and a suitable horizon, then the relevant parts of the mathematics are the (3 + 1)-dimensional Lorentzian metric we saw for both systems in Sect. 14.2.2.1, and a horizon within that geometry (i.e. some region that excitations of the scalar field may enter but not leave). This also takes care of the question of vertical relations: Visser’s argument explains why these two parts of the mathematics are sufficient to license an inference to the existence of Hawking radiation. And since we are dealing with mathematical structures, the relevant type of mapping is an isomorphism such that ‘↔_ϕ’ denotes ‘is isomorphic to’. Here is a second pass:

Analogue Gravity (Isomorphic Kinematics)

• (i) Lorentzian geometry for analogue black holes ↔_ϕ Lorentzian geometry for astrophysical black holes

• (ii) Horizons in analogue black holes ↔_ϕ Horizons in astrophysical black holes

• (iii) Hawking radiation requires only a suitable Lorentzian geometry and the existence of a horizon

  __________________________________________________________________________________________

• $$\therefore$$∴ Radiation from analogue black holes ↔_ϕ Radiation from astrophysical black holes

But this is too quick, because we can actually read off a deductive argument for astrophysical Hawking radiation by only looking at the right hand side: if astrophysical black holes have a suitable Lorentzian geometry and suitable horizon structure, then the addition of (iii) entails that astrophysical Hawking radiation exists. But if this were the case, there would be no need for analogue gravity! What has gone wrong here is that Visser’s argument, i.e. (iii), is fundamentally an argument about differential geometry, not about empirical physics. What I mean here is that Visser’s assertion about the ‘essential’ features of Hawking radiation concerns the derivation of the Hawking effect from within a particular theoretical framework—either semiclassical gravity, or hydrodynamics, or condensed matter. It is not—nor does it purport to be—an argument about the existence of Hawking radiation in any empirical sense. This version therefore states Visser’s argument too strongly. A third pass:

Analogue Gravity (Derivation from Isomorphic Kinematics)

• (i) Lorentzian geometry for analogue black holes ↔_ϕ Lorentzian geometry for astrophysical black holes

• (ii) Horizons in analogue black holes ↔_ϕ Horizons in astrophysical black holes

• (iii) The derivation of Hawking radiation requires only a suitable Lorentzian geometry and the existence of a horizon

  __________________________________________________________________________________________

• $$\therefore$$∴ Radiation from analogue black holes ↔_ϕ Radiation from astrophysical black holes

This seems to capture the thinking behind analogue gravity without overreaching it.

2.3 Black Hole Thermodynamics

2.3.1 The Positive Analogy

BHT hinges upon the recognition that there is a remarkable mathematical similarity between the laws of classical black hole mechanics derived by Bardeen et al. (1973) and the ordinary laws of thermodynamics (Table 14.1).

Table 14.1 The formal analogy between the laws of black hole mechanics and ordinary thermodynamics

The formal analogy between (a) surface gravity and thermodynamical temperature, and (b) horizon area and thermodynamical entropy suggests, as Wald (1994, p. 133) puts it, “a close—and, undoubtedly, deep—relationship between the laws of black hole physics and the laws of ordinary thermodynamics”. The basis for this suggestion is that a black hole’s surface gravity behaves, mathematically, as if it were the temperature of a thermodynamical system, and the area of a black hole’s event horizon behaves, mathematically, as if it were the entropy of a thermodynamical system. This follows from the fact that these quantities occupy structurally equivalent positions in each set of laws. But it does not follow from the formal analogy alone that surface gravity and horizon area physically are a black hole’s thermodynamical temperature and entropy respectively. Indeed, there are many good reasons to resist this conclusion in the classical regime, with two of the most obvious being precisely those that make empirical access to black holes so difficult in the first place: (i) there are severe problems when it comes to even delineating where a black hole is, which makes it difficult to see how to distinguish ‘the system’ in a thermodynamical context; and (ii) in classical relativity, a black hole is a perfect absorber, and thus, if it has a thermodynamical temperature at all, that temperature could only ever be absolute zero. These are seemingly critical disanalogies between the two domains that prevent the analogy from being taken seriously.¹³

The fundamental idea of BHT is that the analogy between the laws of black hole mechanics and the laws of ordinary thermodynamics is more than just a formal coincidence in spite of these disanalogies. According to BHT, the analogy in Table 14.1 is physically significant, which is to say that it broadly indicates that black holes are thermodynamical systems in the fullest sense of the term. At least part of the case for this physical significance comes from addressing critical disanalogies like those above, and thereby extending the positive analogy such that black holes and thermodynamical systems are more plausibly equivalent in some sense. In the next section, I consider the disanalogies (i) and (ii), and show how the responses to these problems bolster the analogical argument for BHT.

2.3.2 The Negative Analogy

2.3.2.1 System Boundaries

One critical part of the negative analogy between the physics of classical black holes and the physics of ordinary thermodynamical systems is that while ordinary thermodynamical systems are local systems that exist in some region of spacetime, classical black holes are not. Classical black holes are typically defined as the region bounded by an event horizon, and the standard definition of an event horizon is the boundary of the causal past of future null infinity (Hawking and Ellis 1973, pp. 311–312; Wald 1984, pp. 299–300).¹⁴ But as Erik Curiel remarks:

This definition is global in a strong and straightforward sense: the idea that nothing can escape the interior of a black hole once it enters makes implicit reference to all future time—the thing can never escape no matter how long it tries. Thus, in order to know the location of the event horizon in spacetime, one must know the entire structure of the spacetime, from start to finish, so to speak, and all the way out to infinity. As a consequence, no local measurements one can make can ever determine the location of an event horizon. That feature is already objectionable to many physicists on philosophical grounds: one cannot operationalize an event horizon in any standard sense of the term.

(Curiel 2019a, p. 29)

It is extraordinarily difficult to see how global spacetime structures like the event horizon could ever number among the things treated by the theory of thermodynamics, itself a fundamentally operational theory that makes crucial use of the distinction between system and environment. Prima facie, this poses a severe challenge for any argument to the effect that we should take BHT seriously.

Any practically-minded physicist would rightly baulk at the idea that the global nature of event horizons in classical relativity somehow prohibits us from believing BHT, however. For example: Astrophysicists routinely speak about the ‘location’ of black holes (Sagittarius-A* being at the centre of the Milky Way for instance); the LIGO collaboration are credited with detecting black hole mergers for the first time (Abbott et al. 2016); and scientists from the Event Horizon Telescope were lauded for producing the first direct image of the shadow of what is thought to be a 6.5 × 10⁹ M _⊙ black hole at the centre of the elliptical galaxy M87 (The EHT Collaboration et al. 2019). There is clearly a sense in which these fabulous achievements presuppose that black holes are entities occupying a well-defined region of spacetime—how else would the EHT team have known where to point their telescope? Thus, we might object, that to argue that black holes cannot be local, dynamical entities because their classical definition is non-local is to fixate on a technicality. If anything, the objection would go, this problematic global nature of the event horizon speaks to a deficiency of classical relativity as a tool for describing the universe, not to an intrinsic deficiency of astrophysical black holes that prevents them from being thermodynamical systems.¹⁵ But an objection such as this, that suggests that classical relativity should not be the final arbiter of the physical nature of black holes, also suggests, a fortiori, that an analogy between classical relativity and ordinary thermodynamics is equally deficient as a guide to the physical nature of black holes.

As such, there are good pragmatic arguments against allowing the global nature of the event horizon to block the argument for BHT. But there are also more principled arguments, which draw from the wide variety of locally-definable alternatives to the global event horizon to argue that BHT can be made suitably ‘local’. The most well-known of these is the trapping horizon, which takes as its departure point the notion of a ‘trapped surface’ (Penrose 1965).¹⁶ A trapped surface is a closed, spacelike surface with normal, future-directed null vectors that have an expansion parameters, θ ₊ and θ ₋, which are both negative (Nielsen 2009). Loosely put, this means that not just inward but also outward lightlike vectors are infalling, toward the interior of the trapped surface (Fig. 14.1). A trapping horizon is an extremal trapped surface such that θ ₊ = 0.¹⁷

Fig. 14.1

A closed spacelike surface (dotted) with two future-directed null vectors. The surface is trapped when both θ ₊ and θ ₋ are negative (Color figure online)

Whether BHT can be localised in terms of trapping horizons is a matter of dispute. Nielsen (2009) identifies them as the forerunner in a sizeable group of locally-defined alternatives to the event horizon, for a number of reasons whose technical details go beyond the scope of this paper (pp. 39–40).¹⁸ While the suitability of the trapping horizon for truly ‘localising’ BHT has been questioned by Dougherty and Callender (2016, Sect. 4), others have come to its defence (Wallace 2018, A.2). Insofar as the jury remains out on this question, it seems reasonable to treat it as a live and promising strategy for reformulating BHT without the global event horizon. For our purposes, all that matters is that there are viable local alternatives to the event horizon that take the sting out the critical analogy discussed above.

2.3.2.2 Hawking Radiation

Taking the mathematical similarity between surface gravity and thermodynamic temperature seriously would mean assigning a black hole a thermodynamic temperature of T = ακ, where α is some constant to be determined. In classical general relativity this stands in direct contradiction to the fact that a black hole is a perfect absorber, prevented by its very definition from emitting radiation. The only thermodynamic temperature that it makes sense to assign to a black hole is zero, and yet such black holes generically have nonzero surface gravity. This rules out taking the formal analogy between surface gravity and temperature seriously.

In the semiclassical framework, however, this is no longer the case. In semiclassical gravity, we approximate quantum corrections to classical relativity by propagating quantum fields on a classical but curved spacetime background (a modelling framework that will be familiar from Sect. 14.2.2). And in this framework, as Hawking’s (1975) celebrated result shows, black holes emit radiation with a perfect thermal spectrum corresponding to the Hawking temperature (setting G = c = ħ = 1):

$$\displaystyle \begin{aligned} T_{H}=\frac{\kappa}{2\pi} \end{aligned} $$

(14.3)

Which is exactly what the formal analogy suggests.

The precise role of Hawking radiation in bolstering the analogy between black hole physics and ordinary thermodynamics is not always entirely clear, but prima facie it achieves at least the following two things. First, it remedies the numerical disagreement between the classical black hole’s surface gravity and its temperature, since if black holes are no longer perfect absorbers, they need not have zero temperature. Second, it provides a way to make sense of the notion of thermal contact between black holes. Let two black holes of surface gravity κ ₁ and κ ₂, respectively, occupy a box that is sufficiently large so as to allow us to neglect their gravitational interaction with one another. Radiation from each will cause the box to reach a temperature κ ₁∕2π > T _Box > κ ₂∕2π, resulting in the movement of heat from the hotter black hole to the colder (Wallace 2018). Thus, Hawking radiation moves two important elements of the negative analogy (numerical disagreement between T and κ; the lack of a well-defined notion of thermal contact between black holes) into the positive analogy.

Two problems hamper Hawking radiation’s role in substantiating the BHT analogy, however. The first problem is that for a solar mass black hole, T _H is of the order 10⁻⁸ K, making it some 100 million times smaller than the 2.7 K cosmic microwave background temperature, and a thousand times smaller than the ∼10⁻⁵ K fluctuations in the cosmic microwave background alone (Smoot et al. 1992). The prospect of direct detection of astrophysical Hawking radiation is therefore incredibly poor. As Thébault (2019, pp. 185–186) vividly puts it: “Trying to detect astrophysical Hawking radiation in the night sky is thus like trying to see the heat from an ice cube against the background of an exploding nuclear bomb.” Indeed, as we saw in Sect. 14.2.2, the entire field of analogue gravity research can be understood as a reaction to the astonishingly dim prospects for the direct detection of astrophysical Hawking radiation. The second problem is that there are a battery of fairly severe conceptual problems with Hawking’s theoretical derivation. Some of these have been resolved in more modern derivations of the Hawking effect by other means,¹⁹ but some remain unresolved and are therefore cause for concern over the existence of astrophysical Hawking radiation. I discuss both of these problems in more detail in Sect. 14.3, but for now we have enough to sketch a formalisation of the analogical argument for BHT.

2.3.3 The Hypothetical Analogy?

Together, local alternatives to the event horizon, the existence of astrophysical Hawking radiation and the generalised second law substantially strengthen the analogical argument for BHT. But towards which conclusion? There are two plausible candidates. On the one hand, the conclusion might be that the formal analogy between the specific mathematics under comparison in Table 14.1 is now endowed with physical significance. On the other hand, the conclusion might be that the formal analogy between black holes and ordinary thermodynamical systems is complete—that is, that it extends far beyond what is already encoded in the similarities of Table 14.1, to all the physical quantities of black holes and thermodynamical systems. The first conclusion can be understood as attempting to deepen the purported connection between black holes and ordinary thermodynamical systems; the second as attempting to broaden that connection.

There are reasons both for and against each interpretation. If the connection between black holes and thermodynamical systems is to be deepened by an appeal to ‘physical significance’, then we owe an account of what this mysterious property might be.²⁰ But similarly, if the scope of this connection is to be broadened by extending the formal analogy, we soon run into problems. For instance: How are we to account for the missing pdV  term in the first law of black hole mechanics (Dolan 2012)? What about the fact that the Hawking temperature generically disagrees with the Tolman temperature, which is the canonical measure of temperature in relativistic thermodynamics, since the two only coincide at future null infinity?²¹ And how are we to understand the fact that the laws of black hole mechanics are theorems, while the laws of ordinary thermodynamics admit of no analytic proof (Curiel 2014)?

I shall adopt the ‘deepening’ interpretation, going forward, since the problems with it are problems of clarification rather than problems of contradiction. That is to say: it seems more feasible to provide a satisfactory account of physical significance than it does to provide an exhaustive argument resolving all of the myriad possible mathematical disanalogies that the broadening approach would require.²²

2.3.4 Formalisation

The most coarse-grained version of the analogical argument for BHT is simply to state that the positive analogy between the laws in Table 14.1 suggests that the systems described by these laws are really and truly the same kinds of systems. A schematisation of this coarse-grained argument would then be:

Black Hole Thermodynamics (Nomic Isomorphism)

• (i) Laws of black hole mechanics $\leftrightarrow _{\phi _1}$ Laws of ordinary thermodynamics

  __________________________________________________________________________________________

• $$\therefore$$∴ Black holes $\leftrightarrow _{\phi _2}$ Thermodynamical systems

Modulo some minor discrepancies—notably the absence of a pdV  term—ϕ ₁ is a horizontal relationship of isomorphism, since we are comparing structurally identical mathematical equations. ϕ ₂, following the discussion in Sect. 14.2.3.3, has two plausible interpretations, but the better of the pair is that black hole quantities are physically, not just mathematically, equivalent to thermodynamical quantities.²³ But as we have seen, this argument seems nevertheless to fail due to the critical negative analogy between various aspects of black hole physics and various aspects of thermodynamics, namely the global nature of event horizons, and the lack of radiation from classical black holes. As we saw above, however, local alternatives to the event horizon, coupled with the derivation of Hawking radiation in the semiclassical framework allow us to smooth over two of the most pressing disanalogies. The result is a stronger and more detailed analogical argument:

Black Hole Thermodynamics (Nomic Isomorphism + Boundaries and Radiation)

• (i) Laws of black hole mechanics $\leftrightarrow _{\phi _1}$ Laws of ordinary thermodynamics

• (ii) System boundaries for astrophysical black holes $\leftrightarrow _{\phi _1}$ System boundaries for thermodynamical systems

• (iii) Radiation from astrophysical black holes $\leftrightarrow _{\phi _1}$ Radiation from thermodynamical systems

  __________________________________________________________________________________________

• $$\therefore$$∴ Black holes $\leftrightarrow _{\phi _2}$ Thermodynamical systems

3 What Is the Relationship Between Them?

We have arrived at plausible formalisations for the analogical arguments for astrophysical Hawking radiation and for the physical significance of BHT. These arguments are distinct from one another. Primarily, because they appeal to different premises to draw different conclusions. But also because the conclusions they seem to license are of a fundamentally different kind. On the one hand, analogue gravity concerns the ability of one type of physical system to serve as an experimental surrogate for another type of physical system. This is an epistemic matter: it concerns the validity of certain kinds of experiments that scientists might conduct in order to gain indirect access to empirically inaccessible systems. On the other hand, BHT concerns the physical nature of black holes. The upshot of taking BHT seriously is, to quote the physicist Robert Wald, “that the laws of black hole mechanics truly are the ordinary laws of thermodynamics applied to a system containing a black hole” (1994, p. 163, my emphasis). Whereas nobody appears to think that analogue gravity evinces some profound and hitherto unappreciated connection between waterfalls and black holes, precisely that kind of connection is being claimed in the case of BHT—in its more extreme form, the claim is that “gravity […] is a fundamentally thermodynamical phenomenon” (Curiel 2014, p. 3, see also Curiel 2019b, Sect. 5.5). Not only do the two analogical arguments invoked in contemporary black hole physics concern different premises in support of different conclusions, those conclusions also constitute fundamentally different kinds of claim.

It would be too hasty, however, to conclude that the two analogical arguments can be divorced from one another completely. Because a large part of our evidence for astrophysical Hawking radiation comes from the impressive results of analogue gravity research, and because the existence of astrophysical Hawking radiation in turn constitutes such a crucial part of the analogical argument for BHT, there is a clear sense in which these two analogical arguments bear on one another. Indeed, if the analogical argument for Hawking radiation fails, so too must the analogical argument for BHT. One way to see this is to note that one side of the conclusion in the final version of the analogical argument for Hawking radiation appears as one side of premise (iii) in the final version of the analogical argument for BHT. Consequently, the analogical argument for astrophysical Hawking radiation appears as a component of the analogical argument for BHT.

Why is this interesting? Because it appears to tie together, in a very specific way, the epistemic legitimacy of the BHT analogy, the basis of a research programme that is “as widely accepted an idea in theoretical physics as an idea with no direct empirical substantiation can be” (Curiel 2019b), with that of analogue gravity, which some have dismissed as little more than an “amusing feat of engineering [that] won’t teach us anything about black holes” (Daniel Harlow, quoted in Wolchover 2016). If the analogical argument for BHT presupposes the success of the analogical argument for astrophysical Hawking radiation, then it is difficult, prima facie, to see how these two attitudes can be reconciled. That is, it is hard to see how it is consistent to (a) interpret the connection between black hole mechanics and ordinary thermodynamics as having genuine physical significance while (b) remaining skeptical about the epistemic warrant that analogue gravity gives us for astrophysical Hawking radiation. Yet it is exactly this combination of attitudes that some wish to adopt: Harlow himself, for instance, is actively engaged in research on BHT while remaining openly skeptical about the results of analogue gravity. Similarly, Wüthrich (2019, p. 221) claims that BHT certainly has “some support”, but elsewhere concludes starkly that analogue confirmation “does not work” (Crowther et al. 2021, p. 3723).

I can see three plausible strategies for resolving this tension. In the rest of this section, I shall examine each in turn.

3.1 Naïve Formalism

I take it to be uncontroversial that there is a clear distinction to be drawn between saying “that is a black hole” while pointing one’s finger at the Schwarzschild metric, and saying “that is a black hole” while pointing one’s finger into the night sky in the direction of Sagittarius-A*. The former identifies a black hole as a type of mathematical entity, while the latter identifies a black hole as a type of astrophysical entity. Of course, we should expect that there is some connection between the two things (indeed, the use of mathematics in physics presupposes such a connection) but the fact remains that they are distinct: the mathematics is not the physical system it describes.

One way to resolve the tension for those who wish to combine belief in the physical significance of BHT with scepticism about analogue experimentation might be to try to interpret the conclusions of the two analogical arguments as being conclusions about mathematical—rather than astrophysical—entities. On this view, the term ‘black holes’ is to be understood as referring to certain classes of spacetime models in general relativity, rather than as referring to real physical systems in our universe, which may be reasonably well described by certain mathematical models under certain idealisations. Call this strategy ‘naïve formalism’, in recognition of its wholesale focus on the formalism of relativity.

When the naïve formalist says ‘black holes are thermodynamical systems’, roughly what they mean is that black holes (qua particular solutions to the Einstein field equation) have certain mathematical properties in common with thermodynamical systems.²⁴ One of these mathematical properties will be that which corresponds to their tendency to produce a thermally distributed radiative flux in certain situations: blackbody radiation in the case of ordinary thermodynamical systems, and Hawking radiation from black holes.²⁵ But this mathematical property can obtain for black holes—and so can be shared with thermodynamical systems—completely irrespective of any empirical confirmation of astrophysical Hawking radiation. Matters of mathematical similarity are to be settled by the mathematics alone.

For the naïve formalist, then, the claim that BHT presupposes the epistemic legitimacy of analogue experimentation fails. This is because if we are only interested in black holes as mathematical entities, we need only be interested in Hawking radiation as a mathematical entity, too. And since Hawking radiation can be derived for black hole spacetimes in semiclassical gravity without any assumptions about whether acoustic black holes can serve as legitimate empirical surrogates for astrophysical black holes, black holes (qua mathematical entities) can be said to have the correct mathematical properties so as to be considered ‘thermodynamical’ without any recourse to analogue gravity. To put the same point slightly differently, this objection would say that claims about the thermodynamical nature of black holes and claims about the existence of Hawking radiation are, at bottom, claims about the mathematical machinery of our physical theories. The same claims could be made about astrophysical black holes, and indeed then one would need a story about the empirical warrant for astrophysical Hawking radiation. But, the objection might go, this is a separate claim.

There are two arguments against the naïve formalist, however. The first is a straightforward sociological observation: nobody actually seems to interpret BHT this way. Presumably, we are interested in formal properties of mathematical entities only insofar as we expect those properties to manifest in the physical world—that is the essence of ‘physical significance’. It should not be surprising that nobody interprets BHT in this extremely narrow sense, since to do so is perhaps to fixate on the mathematics at the expense of the physics. While naïve formalism could plausibly resolve the tension for those willing to adopt it, the cost is an unfamiliar and arguably myopic interpretation of BHT.

A second argument is that naïve formalism is simply too weak to capture the central thesis of BHT. If the central idea of BHT is supposed to be that “black holes are thermodynamical systems in the fullest sense” (Wallace 2018, p. 52, emphasis added), it stands to reason that this sense includes not just shared mathematical properties of the two kinds of systems, but shared non-mathematical properties too. Black holes must actually be thermodynamical systems (whatever that means), not just be mathematically equivalent to them. Thus, we might worry, the naïve formalist fails to actually demonstrate anything beyond formal analogy between black hole mechanics and ordinary thermodynamics. Rather, they smuggle in the physical significance of that analogy by simply moving the goalposts, redefining what physical significance means in flat-footed, mathematical terms. It would, of course, be entirely possible to parry this second objection to naïve formalism by adopting a kind of Pythagoreanism about physics, such that there is nothing to being a certain kind of thing over and above having the appropriate mathematical properties. But this kind of radical Pythagoreanism is surely an inordinately heavy price for the naïve formalist to pay.

3.2 Sophisticated Formalism

A second strategy is to break with the naïve formalist approach by maintaining that ‘black holes’ are to be understood as astrophysical entities, and therefore to maintain that astrophysical Hawking radiation must exist in more than just a mathematical sense, but to argue that the theoretical basis for astrophysical Hawking radiation is already strong enough to justify this without the results of analogue gravity. Broadly stated, the animating idea for this second strategy is that the absence of empirical evidence for the thermodynamical behaviour of black holes need not be a severe problem so long as we can fall back on non-empirical evidence for that behaviour, including non-empirical evidence for Hawking radiation.

Call this view ‘sophisticated formalism’. Like naïve formalism, it retains a focus on the importance of theory, in the sense that it takes a sufficiently strong theoretical basis for astrophysical Hawking radiation to render confirmation of astrophysical Hawking radiation by analogue experimentation redundant. Unlike naïve formalism, however, sophisticated formalism does not limit attention to theory completely. Rather, it maintains that theory can be strong enough to support inferences about the empirical world, even in the absence of experiment. Sophisticated formalism can be seen as a refinement of the ideas of naïve formalism: both identify the importance of theory for decoupling the two analogical arguments, but where the naïve formalist attempted to achieve this by radically reinterpreting BHT as a thesis about mathematical entities, their sophisticated counterpart attempts to achieve this by instead lowering the evidential bar for the existence of astrophysical Hawking radiation.

Something like sophisticated formalism is what underpins pre-analogue gravity attempts to endow BHT with physical significance. This extends to black hole entropy, too: Bekenstein’s (1972) arguments for black hole entropy on the basis of information theory, for instance, are one such attempt, and these are (trivially) independent of any analogue gravity results, predating Unruh’s seminal work by a whole decade.²⁶ As Wüthrich (2019, p. 203) notes, to the extent that non-empirical theory confirmation is legitimate, “the fact that thermodynamic behaviour of black holes has not been observed to date may not be a worry as long as we have convincing non-empirical reasons for believing the Bekenstein-Hawking formula”. This is an elegant statement of the sophisticated formalist position. However, Wüthrich’s own conclusion is that Bekenstein’s information-theoretic reasons fail to provide such convincing non-empirical reasons.²⁷

Although Bekenstein’s original arguments for the physical significance of BHT have failed to convince contemporary philosophers of physics, Wallace (2018) has argued forcefully that the contemporary theoretical arguments for the existence of astrophysical Hawking radiation are, in fact, “very powerful” (p. 61), and have only been strengthened in the 50 years since Hawking’s original work. Now, we have at least five independent means of deriving the Hawking effect, each with their own strengths and weaknesses. This consilience is, itself, evidence for the robustness of the Hawking effect, but the theoretical case is not entirely watertight, as we shall see in a moment. It is, however, nevertheless true that the prima facie strength of the arguments for the Hawking effect make the prospects for the sophisticated formalist seem initially promising, and this is bolstered further by the sociological observation that many physicists seem to espouse this view (one need only look at the huge literature on the information loss paradox to be persuaded that physicists are sufficiently convinced of the existence of Hawking radiation to be concerned about its consequences for unitarity).

But there are two problems for the sophisticated formalist. The first is that despite the theoretical basis for astrophysical Hawking radiation from black holes being very strong, it is not perfect. For example, it is a matter of some delicacy determining what the Hawking temperature should actually be attributed to. Giddings (2016) has argued that Hawking radiation originates not from the black hole horizon but from a region “well outside the horizon” (p. 40).²⁸ If Giddings is correct, then it is not quite right to say that the horizon is the source of the thermalised radiation. This poses a challenge for the sophisticated formalist’s claim that the theory unequivocally militates in favour of Hawking radiation from black holes, since that radiation in fact comes from a region in the black hole exterior. This is a pedantic point, of course—we might think that the quantum region Giddings describes is close enough for the sophisticated formalist’s purposes, or that the production of Hawking radiation in that region can nevertheless be causally attributed to the presence of the black hole. But even if these objections succeed, there are other technical challenges beyond that posed by Giddings. The most notorious is the so-called ‘trans-Planckian problem’, which refers to the fact that the finite wavelengths of the Hawking radiation particles measured at future null infinity, which have been gravitationally redshifted to a drastic extent by their journey away from the black hole, must correspond to particles originating from the black hole with wavelengths arbitrarily shorter than the Planck length. Intuitively, this strongly suggests that the physics giving rise to the Hawking effect near the black hole is beyond Planck scale, i.e. from a regime where we should expect quantum gravitational corrections to relativity to become non-negligible.²⁹ Polchinski (1995) has argued that the trans-Planckian problem can be finessed by the so-called ‘nice slice argument’, which roughly says that the Hawking effect can be derived using only ‘nice’ spacetime slices upon which only low-energy (i.e. cis-Planckian) physics is happening. Polchinski’s argument is echoed by Wallace (2018), but Gryb et al. (2020, Sect. 2.3) argue that certain assumptions in the nice slice argument make it essentially question-begging. The extent to which the trans-Planckian problem remains an issue for the sophisticated formalist is therefore unclear, but generally, it seems prudent to tread carefully. As Wallace himself rightly notes at the end of his defence of the theoretical basis for the Hawking effect, “as good scientists we should remind ourselves that [the Hawking effect] remains purely theoretical, and that tests of quantum field theory itself in the curved-spacetime regime to date have been much less precise and numerous than in the flat-spacetime regime” (2018, p. 62).

Technical worries about the theoretical basis for Hawking radiation aside, there is a second argument against sophisticated formalism. Namely, that upon closer inspection, the position seems inconsistent. At bottom, to be a sophisticated formalist is to try to rid BHT of any dependence on analogue gravity, and to be motivated to do so by a skepticism about the epistemology of analogue experimentation in general. But this seems necessarily to involve replacing one dubious epistemic technique with another. Is bare theory really more capable than analogue gravity when it comes to providing evidence for the existence of Hawking radiation? In thinking so, the sophisticated formalist seems to be trying to use one hand to set the bar for empirical confirmation so high that analogue experimentation cannot reach it, while using the other hand to remove the bar completely. If theory is strong enough to confirm, on its own, then so too should analogue experimentation be, a fortiori. While it would be consistent to maintain either (a) full-blooded empiricism, such that we have reason to believe that astrophysical Hawking radiation exists if and only if we have suitable empirical evidence of astrophysical Hawking radiation; or (b) or full-blooded anti-empiricism, such that a belief in the existence of astrophysical Hawking radiation can be justified even by non-empirical (e.g. theoretical or analogical) evidence, the sophisticated formalist tries to be both and arguably achieves neither.³⁰ It seems plainly inconsistent for the sophisticated formalist to demand that the existence of astrophysical Hawking radiation requires, empirically, more than the evidence provided by analogue gravity, but no more than the evidence provided by bare theory alone.

3.3 Classicalism

The third strategy is the least fiddly, but the most radical. Rather than entering the treacherous ground of attempting to describe how non-empirical evidence of astrophysical Hawking radiation may nevertheless justify belief in the empirical existence of that radiation, the third strategy de-couples the two analogical arguments by severing all ties between the physical significance of BHT and the existence of astrophysical Hawking radiation. It does so by arguing that classical BHT—BHT without, inter alia, Hawking radiation—is already physically significant. Call this strategy ‘classicalism’.

The clearest statement of the classicalist position is given in Curiel (2014). For a black hole to be considered a thermodynamical system, Curiel tells us, what surely matters is only that “surface gravity and area couple to ordinary thermodynamical systems in the same way as temperature and entropy, respectively, do”, and that counterpart quantities are introduced using into the theory using the same “constructions and arguments” (2014, p. 3). Curiel goes on to argue that since one can, indeed, construct a Carnot cycle operating between a black hole and a thermodynamic fluid, and since κ appears in place of the black hole’s ‘temperature’ when one defines the efficiency of that Carnot cycle, there is little room to doubt that surface gravity really is a temperature. On the classicalist view, one need not wait for Hawking radiation to establish the physical significance of the analogy between the two quantities. Insofar as Curiel’s arguments succeed, they establish that BHT need not presuppose the epistemic legitimacy of analogue gravity in the way that I have described, simply by virtue of the fact that premise (iii) in the second formalisation of the analogical argument for BHT above is doing no work. The conclusion—the classicalist would have it—follows immediately from (i) and (ii).

There are at least two reasons to think that the classicalist response fails, however. The first is that Curiel’s Carnot cycle fails to be reversible in the standard thermodynamical sense: it results in an increase in the black hole’s irreducible mass, and thus an increase in its horizon area, which in classical relativity cannot be reversed on pain of violating the second law of BHT—Hawking’s area theorem (Curiel 2014, pp. 16–17). One could reasonably question whether this cycle can be considered sufficiently similar to a thermodynamical Carnot cycle to justify the very strong conclusion of the analogical argument for BHT.³¹

The second is that while the classicalist response may be viable for establishing the physical significance of the analogy between surface gravity and temperature, it seems impossible—in principle—to establish the physical significance of the analogy between horizon area and entropy with the same logic. This is because, as Curiel notes (2014, p. 10, fn. 20) thermodynamic entropy mediates no known physical processes, and so there is, ipso facto, no process one could construct so as to demonstrate that it is mediated by horizon area in the same way it would have been mediated by entropy in the thermodynamical case. Thus, while classicalism may succeed in removing the reliance of BHT on the analogical argument for astrophysical Hawking radiation, it seems to do so at the price of only recovering, at best, a partial equivalence between black holes and thermodynamical systems.

4 Conclusion

Contemporary black hole physics is an interesting case study for the epistemology of science because it deploys analogical reasoning in a way that seems to overreach the traditional heuristic role of analogy. There are two distinct ways in which it does so. First, it relies on analogue experimentation and the observation of analogue Hawking radiation in acoustic and optical black holes to justify the existence of astrophysical Hawking radiation. Second, it relies on the analogy between the laws of black hole mechanics and the laws of ordinary thermodynamics to justify the claim that black holes are genuinely thermodynamical systems.

The analogical arguments in favour of these two claims are distinct. Each one appeals to different premises in order to draw different conclusions, and those conclusions seems to be fundamentally different in kind. But because the BHT analogy is typically only considered physically significant with the inclusion of Hawking radiation, there is an important sense in which the two analogical arguments are linked. Indeed, the first can be nested inside the other in such a way that the analogical argument for BHT cannot succeed without the analogical argument for the existence of astrophysical Hawking radiation. This connection, I argued in Sect. 14.3, leads to a tension for those who wish to combine an optimism about the physical significance of BHT with a pessimism about the epistemic warrant provided by analogue experiments.

I considered three strategies for resolving this tension, and showed that each one fails. The naïve formalist (Sect. 14.3.1) and the classicalist (Sect. 14.3.3) strategies may succeed in decoupling the two analogical arguments, but they do so at the cost of settling for impoverished versions of BHT: one nakedly mathematical; the other only partially complete. The sophisticated formalist (Sect. 14.3.2), on the other hand, seems to replace the tension between optimism about BHT and skepticism about analogue gravity with another, new tension. The sophisticated formalist is committed to the contradictory idea that analogical evidence is inadequate to the task of justifying the existence of astrophysical Hawking radiation, and yet that same justification may be amply provided by bare theory—something weaker, not stronger, than analogical evidence.

If these three strategies exhaust the space of possibilities, then the tension I pointed out at the start of Sect. 14.3 remains: the analogical argument for BHT presupposes the success of the analogical argument for the existence of astrophysical Hawking radiation. Thus, it presupposes the epistemic legitimacy of analogue gravity. It is difficult to see how Harlow’s assertion that analogue gravity is no more than an amusing feat of engineering can be reconciled with the belief that black holes are, nevertheless, genuinely thermodynamical systems.

Perhaps the best prospects for resolving this tension come from a retreat to the ‘traditional’ role of analogy: as heuristic. If there are reasons to believe that these analogical arguments will, in time, be superseded by robust non-analogical arguments, then there are, eo ipso, reasons to believe that this tension will, in time, dissipate. It is far from clear, however, that the analogical arguments discussed here are even capable of being replaced by non-analogical arguments. Insofar as the magnitude of Hawking radiation from an astrophysical black hole and the magnitude of CMB fluctuations are fixed by the nature of physical law, the impossibility of direct detection of Hawking radiation seems fixed with at least nomological necessity. One way around this, which we have not considered in this chapter, would be the discovery of primordial black holes, whose low mass would result in a Hawking temperature sufficiently high to admit direct detection. Until such a discovery, it seems we should make peace with the fact that black hole physics seems destined to continue depending upon analogical reasoning in this unusually strong way.