Visual Proofs as Counterexamples to the Standard View of Informal Mathematical Proofs?

Abstract

A passage from Jody Azzouni’s article “The Algorithmic-Device View of Informal Rigorous Mathematical Proof” in which he argues against Hamami and Avigad’s standard view of informal mathematical proof with the help of a specific visual proof of $1/2+1/4+1/8+1/16+\dots =1$ is critically examined. By reference to mathematicians’ judgments about visual proofs in general, it is argued that Azzouni’s critique of Hamami and Avigad’s account is not valid. Nevertheless, by identifying a necessary condition for the visual proof to be considered a proper proof in the first place, and suggesting an appropriate way to establish its correctness, it is shown how Azzouni’s assessment of the epistemic process associated with the visual proof can turn out to be essentially correct. From this, it is concluded that although visual proofs do not constitute counterexamples to the standard view in the sense suggested by Azzouni, at least the visual proof mentioned above shows that this view does not cover all the ways in which mathematical truth can be justified.

1 Introduction

The relation between informal mathematical proofs and formal derivations in (suitable) formal systems is a much debated topic in the philosophy of mathematics in general and the philosophy of mathematical practice in particular. Here I concentrate on the epistemological side of the topic and am concerned with the question whether and, if so, to what extent this relation has something to do with how mathematicians’ informal proofs secure mathematical knowledge. The focus is on a specific “derivational account of informal mathematical proof” together with a particular critique of it. According to the derivationists, as named by Tanswell [25], the rigor and correctness of informal proofs depend (in some sense) on associated formal derivations.

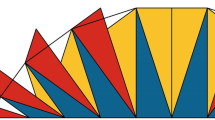
While Jody Azzouni has defended a derivational account of informal mathematical proof himself [4], he has developed an alternative approach to informal rigorous proof in his recent article [7] which he calls “the algorithmic-device view.” In this article, he explains why derivational accounts of mathematical proofs do not work and argues for the “superiority” of his algorithmic-device view. He argues explicitly against a specific derivational account, namely Hamami and Avigad’s standard view of informal mathematical rigor and proof, among other things with the help of the visual/diagrammatic proof of the fact that $1/2+1/4+1/8+1/16+\cdots =1$ shown in Fig. 1.¹ Note that when the talk is of “Hamami and Avigad’s standard view” I am referring to two separate papers, namely [20] and [3]. Insofar as Avigad’s work can be understood as an augmentation of Hamami’s model of the “standard view of mathematical rigor” which we will see later, and for the purposes of this text, it is convenient to talk about “Hamami and Avigad’s derivational account/standard view,” as sometimes Azzouni himself does.

Fig. 1.

A visual proof of $1/2+1/4+1/8+1/16+\cdots =1$.

In the following, I will critically examine Azzouni’s account of the visual proof and the conclusions he draws regarding Hamami and Avigad’s standard view. In particular, using mathematicians’ evaluations of visual proofs in general, which play a fundamental role in Hamami and Avigad’s standard view, I will argue that Azzouni’s criticism of their account is not valid. Nevertheless, by identifying a necessary condition for the visual proof to be considered a proper proof in the first place, and suggesting an appropriate way to establish its correctness, I will argue that his assessment of the epistemic process associated with the visual proof proves to be essentially correct. From this, I will conclude that although visual proofs do not constitute “counterexamples” to the standard view in the sense suggested by Azzouni, at least the one presented in Fig. 1 shows that this view does not cover all the ways in which mathematical truth can be justified.

After having introduced, in Sect. 2, Azzouni’s account of the visual proof and his critique towards Hamami and Avigad’s standard view, their work is briefly discussed in Sect. 3. Section 4 is about how mathematicians themselves regard visual proofs. This is followed by a critical examination of Azzouni’s critique in Sect. 5, which discusses, inter alia, the conditions under which the visual proof can turn out to be a proper proof (5.1) and what this means for the standard view (5.2).

2 Azzouni’s Counterexample to the Standard View

In [7], Azzouni uses the visual proof of $1/2+1/4+1/8+1/16+\cdots =1$ shown in Fig. 1 to argue against Hamami and Avigad’s standard view. In particular, he argues that this proof constitutes a counterexample to the “normativity thesis” which is “in a way” part of Avigad’s standard view. We will see to what extent this is true in Sect. 3, where I will discuss their standard view in more detail. In Azzouni’s own words:

I’ve suggested in earlier work [5] – in a way related to Avigad’s [3] approach to a normative role for formal derivations – that transcribability to a formal derivation has, in the contemporary setting, become a norm for informal rigorous proof. I want to end this section by revisiting considerations that cut against that idea. The problem is that there are informal rigorous mathematical proofs that are counterexamples to the normativity thesis. [7, p. 77]

Besides in this passage, he does not mention the expression “normativity thesis” again. Since he writes shortly after that whether “derivations correspond to informal proofs” is actually a norm is “ultimately, a sociological matter” [7, pp. 77f.], I take him to mean by the normativity thesis something like “the transcribability to a formal derivation should be considered a norm for informal rigorous proof.” In the earlier work he is referring to in the indented quote above, he explains that

The first point to observe is that formalized proofs have become the norms of mathematical practice. And that is to say: should it become clear that the implications (of assumptions to conclusion) of an informal proof cannot be replicated by a formal analogue, the status of that informal proof as a successful proof will be rejected. [...] The norm is this: There is a formal analogue of a purported informal mathematical proof or else the latter fails to be a proof. [5, p. 14]

Based on this passage, I present the following characterization as a first attempt to specify what this thesis might amount to:

• (NT*) Should it become clear that the implications (of assumptions to conclusion) of an informal rigorous proof cannot be replicated by a formal analogue, the status of that informal rigorous proof as a successful proof should be rejected.

His reasoning for the visual proof being a counterexample to the normativity thesis is as follows (cf. [7, p. 77]): (i) “Phenomenologically – notice – this proof is utterly convincing as it stands” and (ii) “there is no sense in which it looks like it needs to be completed or filled in” from which he concludes that (iii) “neither epistemically nor normatively does this proof and many other informal rigorous proofs [...] need supplementation of any sort.” Finally, he states that (iv) this and many other informal rigorous mathematical proofs do not themselves “indicate the existence of formalizations that, in turn, justify why they’re true: their content, that is, does nothing of this sort.”²

Because of this—especially because of his statement (iv) —and the fact that the implications of the visual proof can in fact be captured and to a certain degree replicated by a formal analogue, which is also admitted by Azzouni himself,³ the following appears to be a more appropriate characterization of the normativity thesis:

• (NT) The transcribability to a formal derivation should be considered a norm for informal rigorous proof, i.e., an informal rigorous proof should indicate the existence of a formal counterpart that, in turn, justifies why it is true.

Besides the reference to an “indication relation” between informal rigorous proofs and their formal counterparts in the sense that an informal proof should indicate the existence of a formal analogue, there is a second essential component of Azzouni’s “normativity thesis,” namely that it deals exclusively with informal rigorous proofs. In accordance with this, he describes the visual proof shown in Fig. 1 as a rigorous one. With respect to the (alleged) rigorousness of visual proofs, Azzouni explains in [6] that

it’s been quite common, historically, to describe diagrammatic proofs as lacking ‘in rigor’. This is so to the extent that, in the nineteenth century, if not before, it seemed reasonable to expunge diagrams altogether from mathematical proof along with reliance on ‘intuition’. [6, p. 324]

In this article, however, Azzouni argues that it is false to claim that diagrammatic proofs lack in rigor. He identifies several factors which people mistakenly regard as reasons to deny rigor to them. In particular, he argues against the suggestion that these proofs are not rigorous or defective because they involve unarticulated mathematical content. Although he does not give a very detailed account of mathematical rigor, I take him to implicitly assume something like the following sufficient condition for (informal) rigorousness that is related to his statement (ii)  from above (cf. [6, p. 333], where also the following expressions in quotation marks come from): If there are no missing steps in the mathematical content of a proof—where the content does not need to be “explicit” (e.g. “explicated by axioms”), but which is nevertheless “playing a role enabling the proof procedure”—then this proof should count as rigorous. Except for one qualification, I think that statements (ii)  and (iii)  show that Azzouni in [7] still holds on to this view. Since he states in footnote 142 on page 77 of [7], that if “language-based transcriptions of something we see visually” are treated to be more explicit or as making something explicit in the first place, then only by fiat, let me reformulate the condition as follows:

• (R) If there are no missing steps in the content of a proof—where the content does not necessarily have to be presented in a language-based form, but which is nevertheless playing a role enabling the proof-procedure—then this proof counts as rigorous.

Furthermore, with respect to the visual proof, Azzouni argues that (v)

The epistemic process, rather, is the exact reverse of what normative and descriptive derivational accounts hypothesize. The intuitively effective procedures such proofs exhibit right on their surfaces, when preserved formally, simultaneously preserve the epistemic qualities (the phenomenology) of those informal proofs. The formalization inherits, that is, what it is about the informal proof that convinces us – what justifies our being convinced of the result of the proof. It’s not, that is, that the formalization reveals what’s convincing about that proof or that the formalization justifies that proof. [7, p. 77]

He concludes that (vi) this “is enough to show that – at least with respect to many informal rigorous mathematical proofs – derivation accounts are intrinsically misleading” (ibid.).

The “intuitively effective (recognition) procedures” which are mentioned in statement (v), lie at the heart of Azzouni’s algorithmic-device view of informal rigorous mathematical proofs. These are procedures that “mathematicians grasp directly and not via formal transcriptions of those procedures into the medium of formal languages” [7, p. 20]. The notion of “intuitive” involved in the characterization is meant to refer to something which is computable or executable by a human being while an “effective procedure” or “effective method” which is expressible as a finite set of precise instructions is closely related to the notion of an algorithm [7, pp. 11–17].

Let us now take a closer look at Hamami and Avigad’s account(s).

3 The Standard View of Mathematical Rigor and Proof

In a recent article, Yacin Hamami [20] offers an elaborated formulation of, what he calls, “the standard view of mathematical rigor” [20, p. 411]. He traces this view back to the work by Saunders Mac Lane and Bourbaki. Hamami differentiates between a descriptive and a normative part of the standard view. The descriptive part—which might be called an account of informal mathematical rigor—is meant to “provide a characterization of the process by which mathematical proofs are judged to be rigorous in mathematical practice, i.e., by which the quality of being rigorous is attributed to mathematical proofs in mathematical practice” [20, p. 420]. His general characterization of a descriptive account of mathematical rigor is given as follows [20, pp. 420f.]:

A mathematical proof P is rigorous$_\mathcal {M}$

$\Leftrightarrow$

P can be verified by a typical agent in mathematical practice $\mathcal {M}$, using the resources commonly available to the agents engaged in $\mathcal {M}$.

$\Leftrightarrow$

Every mathematical inference I in P can be verified by a typical agent in mathematical practice $\mathcal {M}$, using the resources commonly available to the agents engaged in $\mathcal {M}$.

Hamami’s particular description of the descriptive part of the standard view expresses the last specification of the characterization above in terms of decomposition and verification processes. That is to say that when confronted with a proof P, agents in a practice $\mathcal {M}$ verify specific proof steps by decomposing these steps into smaller steps (if needed) until they can verify them with the help of mathematical inference rules that were acquired during their former studies [20, pp. 422ff.].

Hamami explains that in general, “a normative account of mathematical rigor stipulates one or more conditions that a mathematical proof ought to satisfy in order to qualify as rigorous” [20, p. 411]. The specific normative part of the standard view is now given by the following characterization [20, p. 428]: A mathematical proof P is rigorous in the normative sense if and only if it “can be routinely translated into a formal proof.” It is with respect to this part of the view that Hamami claims that it is “almost an orthodoxy among contemporary mathematicians” [20, p. 409]. He develops in his article a precise conception of the notion of “routine translation” by first differentiating between four “levels of granularity” and then elaborating three successive translations, i.e., algorithmic procedures, each from one level of granularity to the next finer level. At the coarsest level, which he calls the “vernacular level,” the mathematical proof “is a sequence of inferences as commonly presented in the ordinary mathematical texts of mathematical practice $\mathcal {M}$” [20, p. 429].

With the help of the machinery presented in his article, Hamami can show that if a proof is informally rigorous, it is also rigorous in the normative sense, i.e., it can be routinely translated into a formal proof [20, pp. 433f.].

In [3], in which the philosopher and mathematician Jeremy Avigad defends the standard view, he explains that according to this view, “an informal mathematical statement is a theorem if and only if its formal counterpart has a formal derivation” and that a judgment as to the correctness of a mathematical proof “is tantamount to a judgment as to the existence of a formal derivation, and whatever psychological processes the mathematician brings to bear, they are reliable insofar as they track the correspondence” [3, p. 7379, emphasis added]. Avigad further explains that informal proof texts are “high-level sketches that are intended to indicate the existence of formal derivations” [3, p. 7381, emphasis original] and that informal proofs “work” in this way [3, p. 7394]. To be sure, when Avigad talks about “informal proofs” he is referring to informal mathematical proofs that are in line with mathematicians’ contemporary proof practice. Since he explicitly mentions Hamami’s work, among others, as an example in which his general viewpoint has been articulated [3, p. 7379] (another example is Burgess’s account expressed in [13] where he characterizes rigor as, among other things, “[t]he quality whose presence in a purported proof makes it a genuine proof by present-day journal standards” [13, p. 2]), we may take him to be talking about informal rigorous proofs. Together with Avigad’s statements above, one can see that the normativity thesis ( NT )  is indeed—at least “in a way”—part of his standard view, which is in accordance with Azzouni’s assessment. (Notice the subtle difference that while Avigad speaks of the existence of formal derivations, Hamami (only) speaks of the existence of a routine translation which is able to turn a proof P into a formal one (cf. [20, p. 432, footnote 25]).)

Now, with respect to Hamami’s model of informal rigor, i.e., the descriptive part of the standard view, Avigad, while broadly accepting it, nevertheless has some reservations. He believes that

Hamami’s model is essentially correct: when we read an informal mathematical proof, we really do try to expand inferences in order to gain confidence that a much more detailed version could be given, down to the kinds of basic inferences that twentieth century logic has shown can be reduced to axiomatic primitives. At the same time, we can be convinced by an informal proof without carrying out a fully detailed expansion, and it is too much to ask that we reach the point where each inference is an instance of a known theorem or an explicit rule we have stored in memory. [3, pp. 7393f.]

In order to bridge this gap with respect to Hamami’s criterion of informal rigor, Avigad discusses in his article several strategies, such as modularize, generalize and visualize, which are employed by mathematicians to ensure reliable and robust assessments concerning the correctness of informal mathematical proofs. In fact, he presents these “common features of mathematical practice” as “normative dictates, strategies that one might urge upon an aspiring young mathematician” [3, p. 7388].

Since the judgments and evaluations of (contemporary) mathematicians play a fundamental role in Hamami’s (and Avigad’s) descriptive part of the standard view, we will now have a look at how mathematicians themselves regard visual proofs such as the one shown in Fig. 1.

4 Mathematicians on Visual Proofs

How do (contemporary) mathematicians regard visual proofs? Roger Nelsen, for instance, who has edited three volumes on “proofs without words” (PWWs) (as visual proofs are often referred to in the mathematical literature), states in the introduction of the first volume in which Fig. 1 can be found on page 118, that “[o]f course, ‘proofs without words’ are not really proofs” [21, p. vi]. This statement is somewhat weakened in the introduction of the second volume, where he explains that “[o]f course, some argue that PWWs are not really ‘proofs’” but goes on by quoting a passage by James Brown from his “Philosophy of Mathematics – An Introduction to the World of Proofs and Pictures” [12] in which Brown states that “pictures can prove theorems” [22, p. x]. However, this is again relativized in [2], where Nelsen and his co-author Claudi Alsina describe PWWs as “pictures or diagrams that help the reader see why a particular mathematical statement may be true, and also to see how one might begin to go about proving it true” [2, p. 118].

As another example, consider the two mathematicians Peter Borwein and Loki Jörgenson who write in their article “Visible Structures in Number Theory” (for which they won a “Paul R. Halmos – Lester R. Ford Award” from the “Mathematical Association of America” which recognizes “authors of articles of expository excellence published in The American Mathematical Monthly” [24]) that

The value of visualization hardly seems to be in question. The real issue seems to be what it can be used for. Can it contribute directly to the body of mathematical knowledge? Can an image act as a form of “visual proof”? Strong cases can be made to the affirmative [they mention two references, one of which is an article again by James Brown; S.W.] (including in number theory), with examples typically in the form of simplified, heuristic diagrams such as Fig. [2 a) (see below); S.W.]. These carefully crafted examples call into question the epistemological criteria of an acceptable proof. [10, pp. 898f.]

Note that although Borwein and Jörgenson seem inclined to grant specific diagrams the status of “visual proofs” (“strong cases can be made”), they nevertheless refer to them as “heuristic diagrams.”

Besides what these individual mathematicians have to say about visual proofs, there is also a survey study conducted by Weber and Czocher [26] in which the executors asked ninety-four mathematicians from universities in the United Kingdom to judge the visual proof shown in Fig. 2 b)—in addition to an empirical, a computer-based and two “prototypical” proofs—regarding its validity. When the participants were asked “If you were forced to choose, would you say that this argument is a valid proof?,” 38% chose “This is not a valid proof” [26, pp. 259f.]. Note that this visual proof is quite different from the proofs shown in Fig. 1 and 2 a) which raises the question whether the evaluations of mathematicians concerning this specific visual proof should be considered representative of a whole class of proofs. However, the general handling of visual proofs, especially the fact that they are almost all listed in the mathematical literature under the heading of PWWs, suggests this.⁴

Fig. 2.

a) A visual proof of $(1/2)^2+(1/4)^2+(1/8)^2+(1/16)^2+\cdots =1/3$.

b) A visual proof that n odd implies $n^2\equiv 1\pmod {8}$ [23, p. 8].

These findings suggest that the general status of visual proofs, i.e., whether they should count as “proper” or “valid” proofs, is (at least to some degree) controversial among (contemporary) mathematicians. Obviously, whether these “proofs” should count as “rigorous proofs”—insofar as one can legitimately (or wants to in the first place) distinguish between valid and rigorous proofs—is then not less controversial.⁵ This assessment is consistent with Azzouni’s own statement which we have already seen in Sect. 2 that “it’s been quite common, historically, to describe diagrammatic proofs as lacking ‘in rigor’” [6, p. 324].⁶

5 Azzouni’s Critique Towards the Standard View Revisited

In this section, I have a closer look at Azzouni’s critique of the normativity thesis and Hamami and Avigad’s standard view in general. Before I go into more detail on this, however, let me give one possible description of what is going on in Fig. 1, which will play a role later on.

The numbers written on the rectangles suggest that these rectangles stem from a successive bisecting process. We might imagine two squares with the same area (for convenience, we may assume that they have an edge length of 1) where we use parts of the first square to cover parts of the second square. The process starts by bisecting the first square in order to get two rectangles and using one of them to cover the left side of the second square (this square is meant to be positioned as the one in Fig. 1). Now, we halve the remaining rectangle of the first “square” to get two smaller squares, and use one of them to cover the lower right corner of the second square, and so on and so forth, so that the second square is covered more and more by the parts of the first “square.” By referring to the areas of the rectangles, this process can be represented as follows (where the last summand in each case denotes the area of the remaining part of the first “square,” respectively the part of the second square that is not yet covered):

$$\begin{aligned} \begin{aligned} 1&=\frac{1}{2}+\frac{1}{2} \\&=\frac{1}{2}+\frac{1}{4}+\frac{1}{4}\\&=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{8}\\&=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{16}\\&=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{32} \end{aligned} \end{aligned}$$

(1)

and so forth, so that in the nth step we have $1=(\sum _{k=1}^n(1/2)^k)+(1/2)^n$ or, equivalently, $1-(1/2)^n=\sum _{k=1}^n(1/2)^k$. That is, in each step, the last summand of the previous step is expressed as the summation of its bisection with its bisection. This process could in principle be performed infinitely often, so that the last summand (or the remaining area of the first “square,” respectively the part of the second square that is not yet covered) becomes infinitesimally small and the series $1/2+1/4+1/8+1/16+\dots$ should be assigned the value 1 (if any at all). Note that I propose here “to make the jump to an infinite summation” as a “modern reader is inclined to” do, as expressed by David Bressoud in his “radical approach” to real analysis [11, p. 11], while this would have been avoided, for instance, by the Greeks of the classical era, such as Archimedes [11, pp. 9ff.].

5.1 Figure 1 and the Corresponding Epistemic Process

I think that Azzouni’s characterization of the epistemic process with respect to the visual proof shown in Fig. 1 which he gives in (v), in particular that it is not the case that a formalization would reveal what is convincing about the visual proof in the first place or that it justifies this proof, is essentially correct. However, I think there is an implicit assumption by Azzouni that needs to be made explicit and argued for in a proper way to give a full explanation of why his characterization in (v)  is appropriate.

With that in mind, let us distinguish between an intuitive, pre-formal notion of something that could in principle be repeated infinitely often or that refers to infinity in one way or another and an exact, i.e., “rigorous” (with respect to modern standards) mathematical definition thereof, such as the modern definition of an infinite series or the sum of a convergent infinite series. Let us write the “mathematical theorem” suggested by the visual proof which corresponds to the first, pre-formal understanding as “$1/2+1/4+1/8+\dots =1$,” where the dots “...” are referring to the involved (potential) infinite process, and let “$\sum _{k=1}^{\infty }(1/2)^k=1$” denote the theorem which appears in modern mathematical textbooks or exercise sheets. The description of what is going on in Fig. 1 which I gave above shows that it is quite reasonable to judge the figure as a proof of “$1/2+1/4+1/8+\dots =1$” or why one is inclined to judge it as “utterly convincing” as Azzouni does in (i). But of course Azzouni wants the visual proof to be understood as a proof of “$\sum _{k=1}^{\infty }(1/2)^k=1$” and his comments (v)  and (vi)  are to be interpreted in this sense (see also [6, pp. 329f.]). This means that he has to assume some sort of link between these two interpretations, probably something like the following:

• (Lim) The (an) intuitive notion of the sum of the series involved in the intuitively effective procedure that Fig. 1 exhibits right on its surface is compatible with the now-standard, “rigorous” definition of the sum as the limit of the sequence of partial sums using the $\epsilon$-$\delta$ terminology.

By “compatible with” I mean that the now-standard definition should not rule out the (an) intuitive notion of the sum of the series which one is inclined to read into the diagram.

So I claim that the correctness of ( Lim )  is a necessary condition for Fig. 1 to constitute a (visual) proof of the mathematical theorem “$\sum _{k=1}^{\infty }(1/2)^k=1$.” If there were no such connection between the visual proof and the mathematical theorem that appears in current textbooks, I cannot see how the former could ever constitute a proof of the latter.

Now, how can we know that ( Lim )  is correct? One way would be to simply verify that the now-standard $\epsilon$-$\delta$ technique proves this series to be convergent. Azzouni claims in (v), however, that it is not the formalization of the visual proof that justifies it, but the diagram itself. This would not follow if we justified ( Lim )—which, as I have just pointed out, is a necessary condition for the visual proof to constitute a proof of the mathematical theorem “$\sum _{k=1}^{\infty }(1/2)^k=1$”—with reference to the semi-formal version of it. Note that if this were the only way to establish ( Lim ), the visual proof could not be considered a real proof either, since one would have to prove the theorem by another method before one could prove it using the diagram. I submit, however, that there is another way of justifying ( Lim )  which does not lead to this result so that Azzouni’s evaluation of the epistemic process in (v)  can still turn out to be valid: One can also establish ( Lim )  by showing that mathematicians in the development of the calculus tried to capture the (main) intuitions underlying the visual proof shown in Fig. 1—possibly in the form of the equations (1)—with their definitions of the sum of a series.

Even though the following two excerpts from the history of mathematics might not necessarily prove the correctness of ( Lim )  themselves, they strongly suggest that one can justify ( Lim )  in the way just described: For instance, in his “De seriebus divergentibus” from 1760 (which was roughly a century before “[w]ith Weierstrass, the now-accepted $\epsilon$-$\delta$ terminology became part of the language of rigorous analysis” [14, p. 620]), Leonhard Euler refers to the series $1+1/2+1/4+1/8+\dots =2$ in his characterization of a convergent series as a clear example of this “phenomenon”:

And now, series are said to be convergent when their terms steadily become smaller and at length completely vanish, such as this one: $1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32$ + etc., whose sum is in fact $= 2$, without any doubt. For as you add in more terms, you draw closer to 2; thus the sum of 100 terms falls short of 2 by a very small amount, indeed a fraction with numerator 1 and a denominator made up of 30 digits. Therefore, with such a series, there is no doubt that it indeed has a sum and that the sum which is assigned in analysis is correct. [8, p. 143]

As another example, consider Cauchy’s still “unrigorous” definition (with respect to modern standards) of the convergence of series presented in his “Cours d’Analyse” from 1821. Especially when the calculations or relations indicated by the visual proof are written as in (1), one can see how they fit nicely with this definition: Cauchy calls a series convergent if and only if its sequence of partial sums $s_n$ “tends to a certain limit s for increasing values of n” [9, p. 3] where by “limit” he means that “[w]hen the values successively attributed to the same variable approach indefinitely a fixed value, eventually differing from it by as little as one could wish, that fixed value is called the limit of all the others” [9, p. 2]. Immediately after the presentation of his definition of the convergence of series, Cauchy briefly discusses “one of the simplest sequences” which is the geometric progression $1, x, x^2, x^3, \dots$ for which one finds that

$$\begin{aligned} 1+x+x^2+\cdots +x^{n-1}=\frac{1}{1-x}-\frac{x^n}{1-x} \end{aligned}$$

and whose sum is $1/(1-x)$ if the magnitude of x is less than unity [9, p. 3]. If we start with the term $u_1=x$ (or subtract the value 1) and set $x=1/2$, we of course get the series that is currently being discussed.

Let me conclude this section with a comment on Azzouni’s statement (vi). Insofar as mathematicians throughout history tried to capture with their definitions of the convergence of series the intuitive notion of the sum of the series involved in the intuitively effective procedure that Fig. 1 exhibits right on its surface as the historical findings from above suggest (at least to a certain degree), I think that an account of informal mathematical proof would in fact be “intrinsically misleading”—as Azzouni states in (vi)—if it suggested that the truth of the visual proof can be justified only by its formalization. However, that Hamami and Avigad’s account is not susceptible to the accusation of being “intrinsically misleading” in this respect will be shown, inter alia, in the next section.

5.2 Visual Proofs as Counterexamples to the Standard View?

As we have already seen in Sect. 2, Azzouni argues in [7] against the normativity thesis ( NT )  with the help of the visual proof shown in Fig. 1 which is meant to constitute a counterexample towards it. Insofar as ( NT )  is part of the standard view (which it actually appears to be as indicated in Sect. 3), does this imply that the visual proof constitutes a counterexample to this view itself? I claim that the answer is no, even if one were to agree with Azzouni’s estimation expressed in (iv), that the visual proof does not indicate a formalization—which seems not to be uncontroversial, since it is a general statement about all possible “indication relations” (where his own from his earlier work [4] and Hamami’s “routine translation” are only two of them).

The reason for this is that crucial to Hamami and Avigad’s models of informal rigor is the assessment of proofs by mathematicians themselves (keyword “descriptive part”). The findings of Sect. 4—especially the quotations of the individual mathematicians—suggest that even the general status of visual proofs among mathematicians is controversial, i.e., whether Fig. 1, for example, qualifies as a proof of “$\sum _{k=1}^{\infty }(1/2)^k=1$” (referring to the interpretation introduced in Sect. 5.1) in the first place, not to mention whether they should be considered rigorous.⁷

As we have seen in Sect. 3, Hamami’s descriptive part of the standard view is meant to characterize the process by which “a typical agent in mathematical practice $\mathcal {M}$” attributes the quality of being rigorous to mathematical proof. But even if one granted that the creation of PWWs constituted one of these practices, Nelsen’s statements above suggest that “a typical agent” of this practice would not characterize these proofs as rigorous. Due to Avigad’s generally affirmative attitude towards Hamami’s account and his own focus on contemporary mathematical practice and its practitioners, I take this to mean that the visual proof shown in Fig. 1 does not constitute a counterexample to ( NT )  from the perspective of the standard view, since this view is simply not concerned with this genre of proofs. This also means that if Fig. 1 would indeed constitute a counterexample to ( NT )  as claimed by Azzouni, this interpretation of the normativity thesis would not be part of the standard view, since it would deal with a different notion of informal rigorous proof, (partially) expressed, for instance, in ( R ).

As I have argued in Sect. 5.1, the visual proof shown in Fig. 1 can indeed be seen as a proper proof of the mathematical theorem “$\sum _{k=1}^{\infty }(1/2)^k=1$,” although one has to establish the correctness of the necessary condition ( Lim )  first without having to confirm that the now-standard $\epsilon$-$\delta$ technique proves this series to be convergent. In light of this, the corresponding epistemic process as described by Azzouni in (v)  turns out to be essentially correct. However, this does not imply that Hamami and Avigad’s account of the standard view is intrinsically misleading. This is due to the same reason that the visual proof is not a counterexample to the normativity thesis from the point of view of their account: It is not intrinsically misleading with respect to visual proofs, because it does not deal with that type of proof. What it shows, however, is that the standard view does not cover all the ways in which mathematical truth can be justified. Hamami starts his investigation with the words

Mathematical proof is the primary form of justification of mathematical knowledge. But in order to count as a proper mathematical proof, and thereby to function properly as a justification for a piece of mathematical knowledge, a mathematical proof must be rigorous. [20, p. 409]

However, as the discussion of the “epistemic process” of the visual proof of Fig. 1 has shown, an informal mathematical proof can be proper—in the sense that it functions properly as a justification for a piece of mathematical knowledge—without being rigorous (in Hamami’s descriptive sense).⁸

6 Conclusion

We have seen that, according to Azzouni, the visual proof shown in Fig. 1 constitutes a counterexample to the “normativity thesis” that is part of Avigad’s standard view and which says that the transcribability to a formal derivation should be considered a norm or standard of correctness for informal rigorous proof. It has been argued, however, that from the point of view of Hamami and Avigad’s standard view, the visual proof does not constitute a counterexample to this thesis and thereby no counterexample to their standard view in general. This is the case, because the standard view is not concerned with this genre of proofs: Crucial to the view are the judgments about the rigorousness of a mathematical argument by the mathematicians themselves. And many comments made by mathematicians and a survey study suggested that even the general status of visual proofs is controversial, not to mention whether they should be considered rigorous.

Furthermore, we have seen that from an evaluation of the epistemic process associated with the visual proof, Azzouni concludes that with respect to this specific one and many other informal proofs the standard view is “intrinsically misleading.” This conclusion was rejected for the same reason that the visual proof is not a counterexample to the normativity thesis from the perspective of the standard view: It is not intrinsically misleading with respect to visual proofs, because it does not deal with that type of proof. I further identified the need for a connection between the intuitive notion of the sum of the series one is inclined to read into the diagram and the now-standard, rigorous definition of it, as a necessary condition for the visual proof to constitute a proper proof, and suggested a way in which one can establish its correctness, namely with the help of the history of mathematics, that also proves Azzouni’s assessment of the epistemic process to be essentially correct. From this, I concluded that although visual proofs do not show that the standard view is intrinsically misleading, at least the one mentioned above shows that this view does not cover all the ways in which mathematical truth can be justified.