Life Events that Cascade: An Excursion into DALY Computations

Abstract

A problem frequently encountered in point process modeling is that event times are usually not known. The only available information is the number of events over a given interval. Calculus and regularization present a convenient framework to perform inference in these circumstances through explicit formulas for this class of mixed doubly point processes. As an application, we present a novel way of dealing with uncertainties in the computation of disability-adjusted life year, which is a measure of overall disease burden in populations.

1 Introduction

Background and motivation of the study. In most applications concerning point processes, we are generally confronted with the problem that we do not have the times at which events have taken place. In such cases, the only information we have is the number of events over a given interval, but the event times are unknown. For example, since there can be many automobile accidents per day in the USA, it is common to record the number of accidents for that day, rather than the exact times at which these events happened.

The purpose of the present article is to spell out closed-form solutions for some functionals of the number of events over a given interval within a class of point processes that exhibit self and externally excitatory interactions. Intuitively, a process is self-exciting if the occurrence of past events makes the occurrence of future events more probable.

The origin of point processes incorporating both self- and external excitations date back to 2002, when the authors Brémaud and Massoulié (2002) introduced this model under very general conditions. In this paper, we perform inference on a model that combines both self-exciting behavior and externally exciting components as set forth in Dassios and Zhao (2011), where they incorporated the shot-noise Cox processes (Mohler 2013) as the external component while maintaining the Hawkes process (Hawkes 1971) for self-excitations. We shall henceforth call this process the Hawkes–Cox model.

Related work. Inference for point processes with the combined elements of endogenous and exogenous components have been studied in the machine learning community. Linderman and Adams (2014) introduced a multidimensional counting process combining a sparse log Gaussian Cox process (Møller et al. 1998) and a Hawkes component to uncover latent networks in the point process data. They showed how the superposition theorem of point processes enables the formulation of a fully Bayesian inference algorithm. Mohler (2013) considered a self-exciting process with background rate driven by a log Gaussian Cox process and performed inference based on an efficient Metropolis adjusted Langevin algorithm for filtering the intensity. Simma and Jordan (2010) proposed an expectation–maximization inference algorithm for Cox-type processes incorporating self-excitations via marked point processes and applied to a very large social network data.

We note that a variety of methods have been developed for the estimation of self or external excitations for point processes: variational flavors (Mangion et al. 2011), expectation propagation (Cseke and Heskes 2011), and the usage of thinning points and uniformization for non-stationary renewal processes, (Gunter et al. 2014; Teh and Rao 2011).

Perhaps the most intimately related work to ours is that of Da Fonseca and Zaatour (2014) where the authors looked at the functionals of event counts over an interval for a Hawkes process (Hawkes 1971). In this work, we proposed an inference procedure for the Hawkes–Cox model which captures both the self and external excitatory relationships over a given interval. As a by product, we extend some theoretical calculations needed to give explicit higher moments to calculate the covariance structure while generalizing the results of Da Fonseca and Zaatour (2014).

Contributions. Consider the scenario where we do not know the exact times at which events happen, but we have the number of events that have occurred in a given interval. We propose an inference procedure to learn the Hawkes–Cox model that can capture both self- and external excitatory relationships under these circumstances. Our major contributions are as follows: (i) We develop closed-form solutions of some functionals for the Hawkes–Cox process. (ii) Special attention is given to the covariance function of event counts over an interval. We show that the covariance structure over the number of jumps in an interval enjoys analytical tractability. This measure is extremely important as it supports the clustering property of the self-exciting property of the Hawkes process and the external excitation features of the Cox process. (iii) We developed an inference procedure through $L_2$ regularization to learn parameters where estimation is almost instantaneous. (iv) We finally conclude by demonstrating the usefulness of applying Hawkes–Cox to model financial trade volumes.

2 The Hawkes–Cox Framework

Background on point processes. This section introduces some pieces of counting process theory needed in what follows. The homogeneous Poisson process $\hat{N}=\{\hat{N}(t):t\ge 0\}$ with intensity m has the following properties: (a) The process starts at 0 with $\hat{N}=0$; (b) the process has independent increments, i.e., for any $t_i,i=0,...,n$ the increments $\hat{N}_{t_1}-\hat{N}_{t_{i-1}}$ are mutually independent; (c) there exists a non-decreasing right continuous function $m:[0,\infty )\rightarrow [0,\infty )$ with $m(0)=0$ such that the increments $\hat{N}_t-\hat{N}_s$ for $0<s<t<\infty$ have a Poisson distribution with mean value function $m(t)-m(s)$.

The Hawkes–Cox Model. We are interested in a counting process N(t) whose behavior is affected by past events, which contains both self- and externally excitation elements. Our point process N(t) has a non-negative $\mathcal {F}_t-$ stochastic intensity function $\lambda (t)$ of the form:

$$\begin{aligned} \lambda (t)&\!=\!\mathcal {B}_0(t)+\sum _{i:t>T_i}\mathcal {H}(Y_i,t\!-\!T_i)\!+\!\sum _{i:t>S_i}\mathcal {C}(X_i,t\!-\!S_i), \end{aligned}$$

(1)

where $\mathcal {B},\mathcal {H}$ and $\mathcal {C}$ are functions whose definitions will be made precise in Definition 1 below. The sequence $(T_i)_{i\ge 1}$ denotes the event times of N, where the occurrence of an event induces the intensity to grow by an amount $\mathcal {H}(Y_i,t\!-\!T_i)$: this element captures self-excitation. At the same time, external events can occur at times $S_i$ and stimulate with a portion of $\mathcal {C}(X_i,t\!-\!T_i)$: this is the externally excited part. The quantities X and Y are positive random elements describing the amplitudes by which $\lambda$ increases during event times. The quantity $\mathcal {B}_0:\mathbb {R}_+\mapsto \mathbb {R}_+$ denotes the deterministic base intensity. We write $N_t:=N(t)$ and $\lambda _t:=\lambda (t)$ to ease notation and $\{\mathcal {F}_t\}$ being the history of the process and contains the list of times of events up to and including t, i.e. $\{T_1,T_2,...,T_{N_t}\}$.

Fig. 1

A sample of a Hawkes–Cox process. In the top plot, the blue line corresponds to the counting process of interested event times, while the black line shows the counting process of the external event times. The bottom graph plots the realized intensity function $\lambda _t$

We now give specific forms for $\mathcal {B},\mathcal {H}$ and $\mathcal {C}$ through the definition of the Hawkes–Cox model.

Definition 1

The Hawkes–Cox process is a point process N on ${\mathbb {R}}^{+}$ with the non-negative $\mathcal {F}_t$ conditional random intensity

$$\begin{aligned} \lambda _t \!=\! a \!+\! (\lambda _0\!-\!a)e^{-\delta t} \!+\! \sum _{i=1}^{N_t} Y_i e^{-\delta (t \!-\! T_i)} \!+\! \sum _{i=1}^{J_t} X_i e^{-\delta (t \!-\! S_i)}, \end{aligned}$$

(2)

for $t\ge 0$, where we have the following features:

• Deterministic background. $a\ge 0$ is the constant mean-reverting level, $\lambda _0>a$ is the initial intensity at time $t=0$, $\delta >0$ is the constant rate of exponential decay. $\mathcal {B}_0(t)=a+(\lambda _0-a)e^{-\delta t}$;

• External excitations. $X_i$ are levels of excitation from an external factor. They form a sequence of independent and identically distributed positive elements with distribution function $H(c),c>0$. $S_i$ are the times at which external events happen and it follows a Poisson process $J_t$ of constant rate $\rho >0$. Similar kernel types are used in Fisher and Banerjee (2010); Du et al. (2015), to name a few. Note that $\mathcal {C}(X_i,t-S_i):=X_i e^{-\delta (t-S_i)}$.

• Self-excitations. $Y_i$ are levels of self-excitation, a sequence of independent and identically distributed positive elements with distribution function $G(h),h>0$, occurring at random $T_i$. Following the occurrence of events, the impact of these events will saturate and the rate at which this occurs is determined by the constant $\delta$. Note that $\mathcal {H}(Y_i,t-T_i):=Y_i e^{-\delta (t-T_i)}$.

For illustration, we present a sample simulation path obtained from the above parameterization in Fig. 1, showing generated event times. From this figure, we can see that the intensity process is excited by both the event times of interest (in crosses $\times$) and the external events (in circle $\circ$).

Note that from Definition 1, if we set $X\equiv 0$ and Y to be a constant, we retrieve the model proposed by Hawkes (1971). If we set $Y\equiv 0$ and X to be a positive random elements, we get the model proposed by Cox and Isham (1980). In addition, setting $X=Y=0$ returns us the inhomogeneous Poisson process, Daley and Vere-Jones (2003). Furthermore, letting $X=Y=0$ and $\lambda _0=a$ simplify to the Poisson process.

2.1 The Choice of Kernel and the Rôle of $\delta$

The kernel for the externally excited component is known as the shot noise (Cox and Isham 1980; Møller 2003) where $\mathcal {C}(X_i,t-S_i)=X_i e^{-\delta (t-S_i)}.$ This is a deliberate choice with $\delta$ being shared between the background rate $\mathcal {B}_0$ $\mathcal {H}$ and $\mathcal {C}$ to ensure that the process inherits the Markov property, see Brémaud and Massoulié (2002); Blundell et al. ( 2012). This property is essential to the derivation of the functionals in Sect. 3. The term $\delta$ determines the rate at which the process decays exponentially from following arrivals of self-excited and externally excited events.

3 Dynkin’s Formula

The Markov property is the key property that allows one to invoke certain tools to obtain the moments for the number of events in an interval, rather than the number of events at a current time $t>0$. Among these tools are the infinitesimal generator and martingale techniques. For a Markov process $X_t$, consider a function $f : D \rightarrow \mathbb {R}$. The infinitesimal generator of the process denoted $\mathcal {A}$, is defined by

$$\begin{aligned} \mathcal {A}f(x)=\lim _{h\rightarrow 0} \frac{\mathbb {E}\left[ f(X_{t+h})|X_t=x\right] -f(x)}{h}. \end{aligned}$$

For every function f in the domain of the infinitesimal generator, the process

$$\begin{aligned} M_t:=f(X_t)-f(X_0)-\int ^t_0\mathcal {A}f(X_u)du \end{aligned}$$

is a martingale (Øksendal and Sulem 2007). Thus, for $t > s$, we have

$$\begin{aligned} \mathbb {E}\left[ f(X_t)\!-\!\int _0^s\mathcal {A}f(X_u)du\Big |\mathcal {F}_s\right] =f(X_s)\!-\!\int _0^s\mathcal {A}f(X_u)du \end{aligned}$$

by the martingale property of M. Rearranging, we finally obtain Dynkin’s formula (see, Øksendal and Sulem (2007))

$$\begin{aligned} \mathbb {E}\left[ f(X_t)|\mathcal {F}_s\right] =f(X_s)+\mathbb {E}\left[ \int _s^t\mathcal {A}f(X_u)du\Big |\mathcal {F}_s\right] . \end{aligned}$$

(3)

In the following section, we will heavily rely on this formula to compute some distributional properties of the Hawkes–Cox process.

4 Theoretical Moments

Our aim is to compute the following quantities: mean, variance and covariance of the number of events in an interval $\tau$, rather than at a fixed time t, as investigated by Dassios and Zhao (2011). To do so, we appeal to the techniques and manipulations presented in the previous section.

To ease notations, the first and second moments of levels of self- and external excitations X and Y, respectively, are denoted by

$$\begin{aligned}&\mu _{1G}:=\int _0^\infty h dG(h),\,\, \mu _{2G}:=\int _0^\infty h^2 dG(h),\\&\mu _{1H}:=\int _0^\infty c dH(c),\,\, \mu _{2H}:=\int _0^\infty c^2 dH(c) \end{aligned}$$

as well as the constant

$$\begin{aligned} k:=\delta -\mu _{1G}. \end{aligned}$$

First note that the joint process of $\{(\lambda _t,N_t)\}_{t\ge 0}$ is a Markov process. This can be seen by proving that the expression $\lambda _{T_k}$ only depends on $\lambda _{T_{k-1}}$ and $\{N_t:T_{k-1}\le t\le T_k\}$. By the Markov property and using the results in Øksendal and Sulem (2007); Davis (1984), the infinitesimal generator of the process $(t,\lambda _t,N_t)$ acting on a function $f(t,\lambda ,n)$ is given by

$$\begin{aligned}&\mathcal {A}f(t,\lambda ,n)=-\delta (\lambda -a)\frac{df}{d\lambda }+\lambda \left( \int _0^\infty f(t,\lambda +y,n+1)dG(y)-f(t,\lambda ,n)\right) \\&+\rho \left( \int _0^\infty f(t,\lambda +c,n)dH(c)-f(t,\lambda ,n)\right) . \end{aligned}$$

4.1 The Moments of Counts in an Interval

In order to obtain the expected number of jumps for an interval (s, t], we apply Dynkin’s formula as in Eq. (3). By setting $f(t,\lambda ,n)=n$, we have that $\mathcal {A}n = \lambda$. Since $N_t-N_s-\int _s^t \lambda _u du$ is a martingale, we have $\mathbb {E}[N_t-N_s-\int _s^t\mathcal {A}N_u du|\mathcal {F}_s]=0$. Rearranging, we get

$$\begin{aligned} \mathbb {E}\left[ N_t|\mathcal {F}_s\right] =N_s+\mathbb {E}\left[ \int _s^t\lambda _udu\right] . \end{aligned}$$

(4)

Due to Fubini’s Theorem, we interchange the order of expectation and the integral subsequently yields

$$\begin{aligned} \mathbb {E}\left[ N_t|\mathcal {F}_s\right] =N_s+\int _s^t\mathbb {E}\left[ \lambda _u|\mathcal {F}_s\right] du. \end{aligned}$$

(5)

Remark that this equation could have been obtained by recalling that $(N_t-\int ^t_0\lambda _sds)_{t\in [0,T]}$ is a martingale, by definition of the intensity of a point process, Daley and Vere-Jones (2003).

We can now give an explicit expression for the expectation of the number of events in an interval.

Proposition 1

The expectation of the number of jumps over an interval $\tau$ is given by

$$\begin{aligned}&\lim _{t\rightarrow \infty } \mathbb {E}\left[ N_{t+\tau }-N_t\right| \lambda _0]=\frac{a\delta }{\delta -\mu _{1G}}\tau =:h^{\tau }_1 \end{aligned}$$

(6)

Proof

An application of tower property of expectation yields

$$\begin{aligned}&\mathbb {E}\left[ N_{t}-N_s\right| \lambda _0]=\mathbb {E}[\mathbb {E}\left[ N_t-N_s|\mathcal {F}_s\right] |\mathcal {F}_0]\\&=\mu _1(t\!-\!s)+\frac{1}{k}(1\!-\!e^{-k(t\!-\!s)})(\mathbb {E}[\lambda _s|\mathcal {F}_0]\!-\!\mu _1)\\&=\mu _1(t-s)-\frac{1}{k}(\lambda _0-\mu _1)(e^{-kt}-e^{ks}), \end{aligned}$$

for $s<t$. Setting $t\!\leftarrow \! t\!+\!\tau$ and $s\!\leftarrow \! t$ and letting $t \!\rightarrow \! \infty$ and under the stationary condition $\mu _{1G} < \delta$, we obtain the expression in Eq. (6). $\blacksquare$

We interpret this quantity as the long-run expectation of the number of events during a given time interval of length $\tau$.

We now calculate the long-run variance of the number of jumps during an interval of length $\tau$. We first note that

$$\begin{aligned}&\textrm{Var}[N_t - N_s|\mathcal {F}_0]\nonumber \\&=\mathbb {E}[(N_t - N_s)^2|\mathcal {F}_0]-(\mathbb {E}[N_t-N_s|\mathcal {F}_0])^2. \end{aligned}$$

(7)

We proceed by calculating the first quantity on the RHS in Eq. (7). First, note that

$$\begin{aligned} \mathbb {E}[(N_t\!-\!N_s)^2|\mathcal {F}_0]&=\mathbb {E}[\mathbb {E}[(N_t-N_s)^2|\mathcal {F}_s]|\mathcal {F}_0]. \end{aligned}$$

Given the previous two results, we can now state the expression for the variance of the number of events in an interval of length $\tau$:

Proposition 2

The variance of the number of jumps over an interval $\tau$ is given by

$$\begin{aligned}&\lim _{t\rightarrow \infty }\textrm{Var}(N_{t+\tau }-N_{t}|\mathcal {F}_0)\nonumber \\&=\lim _{t\rightarrow \infty }\mathbb {E}([N_{t+\tau }-N_{t})^2|\mathcal {F}_0]-\lim _{t\rightarrow \infty }(\mathbb {E}[N_{t+\tau }-N_{t}|\mathcal {F}_0])^2\nonumber \\&=\frac{\theta }{k}+\frac{2}{k}\left( \mu _{1G}\mu _1-\mu _1^2+\frac{(2\theta +\mu _{2G})\theta }{2k^2}+\frac{\rho \mu _{2H}}{2k}\right) \tau -\frac{2}{k^2}\left( \frac{(2\theta +\mu _{2G})\theta }{2k^2}+\frac{\rho \mu _{2H}}{2k}+\mu _{1G}\mu _1+\mu _1^2\right) \nonumber \\&:=h^{\tau }_2. \end{aligned}$$

(8)

4.2 The Covariance

We now turn to perhaps the most important quantity: the covariance function which carries information regarding the clustering nature of Hawkes–Cox. To calculate this cross-expectation of the number of events during different time intervals, we first need to determine the following expression:

$$\begin{aligned}&\mathbb {E}[(N_{t_1}-N_t)(N_{t_3}-N_{t_2})|\mathcal {F}_0]-\mathbb {E}[(N_{t_1}-N_t)|\mathcal {F}_0]\mathbb {E}[(N_{t_3}-N_{t_2})|\mathcal {F}_0], \end{aligned}$$

where $t_0<t<t_1<t_2<t_3$. For simplicity, we let $\tau :=t_1-t$ and $\tau =t_3-t_2$. We further define the lag of Hawkes–Cox as $\tilde{\tau }:=t_2-t_1$. We state the following:

Proposition 3

The covariance of the number of jumps in a given interval $\tau$ with lag $\tilde{\tau }$ can be explicitly expressed as

$$\begin{aligned} \textrm{Cov}(\tau ,\tilde{\tau })&=\lim _{t\rightarrow \infty }\Bigg (\mathbb {E}[(N_{t+\tau }-N_{t})(N_{t+2\tau +\tilde{\tau }}-N_{t+\tau +\tilde{\tau }})]-\mathbb {E}[(N_{t+\tau }-N_{t})]\mathbb {E}[(N_{t+2\tau +\tilde{\tau }}-N_{t+\tau +\tilde{\tau }})]\Bigg )\nonumber \\&=(\mu _1\tau )^2+\Bigg [\left( \frac{1-e^{-k\tau }}{k}\right) ^2 e^{-k\tilde{\tau }}\left( \frac{(2\theta +\mu _{2G})\theta }{2k^2}+\frac{\rho \mu _{2H}}{2k}+\mu _1\mu _{1G}-\mu _1^2\right) \Bigg ]=:h^{\tau }_3. \end{aligned}$$

(9)

5 Learning and Optimization

We present an optimization technique to learn the parameters of the Hawkes–Cox process. Consider the cost function $\mathcal {J}$ of the following form:

$$\begin{aligned}&\mathcal {J}(\varphi )=\sum _{i=1}^{3}\Big |\lim _{t\rightarrow \infty } C^{\varphi }_i(t)-C_i\Big |^2 + \lambda _{reg} F(\varphi ), \end{aligned}$$

where $C^{\varphi }_i(t)$ denotes the theoretical function of moments for Hawkes–Cox. $C^{\varphi }_1(t)=\mathbb {E}(N_{t+\tau }-N_{t})$, $C^{\varphi }_2(t)=\textrm{Var}(N_{t+\tau }-N_{t})$ and

$$\begin{aligned}&C^{\varphi }_3(t)=\mathbb {E}[(N_{t+\tau }-N_{t})(N_{t+2\tau +\tilde{\tau }}-N_{t+\tau +\tilde{\tau }})]-\mathbb {E}[(N_{t+\tau }-N_{t})]\mathbb {E}[(N_{t+2\tau +\tilde{\tau }}-N_{t+\tau +\tilde{\tau }})] \end{aligned}$$

and $C_i$ being the corresponding empirical function of moments in a given interval $\tau$ and lag $\tilde{\tau }$ where $\lambda _{reg}$ is a parameter that controls the level of regularization in the optimization scheme with F being the regularization term. The first role of the penalization term F is to ensure uniqueness of the solution. Indeed, if F is convex in the $\varphi$, then for $\lambda _{reg}$ large enough, the entire functional $\mathcal {J}$ will be convex and the solution will be unique. Note that the difference in the square terms are deviations of the theoretical functions of moments against the corresponding empirical values. Let the parameters of interest be $\varphi$. The learned parameter $\hat{\varphi }$ is obtained from

$$\begin{aligned} \hat{\varphi }= \arg \min _{\varphi } \mathcal {J}(\varphi ), \end{aligned}$$

where $\varphi$ is the parameter of interest. The details of optimization tools are presented in the experiment section.

6 Synthetic Experiments

We evaluate our proposed optimization method using both simulated and real-world data, and show that our approach significantly outperforms the baseline.

With estimation being almost instantaneous, we demonstrate the usefulness of Hawkes–Cox to model financial trade volumes. Empirical evidence have shown that trading activity is not a random process but rather produces time sequences that exhibit clustering behavior (Filimonov and Sornette 2012). If it was the case, a homogeneous Poisson process would have been a suitable candidate to model trade arrival times. Possible exogenous liquidity and news shocks are being capture through the external excitation component of Hawkes–Cox.

We show that our model achieves better accuracy in the prediction compared to MLE and also a homogeneous Point process (HPP).

6.1 Calibration

The experiments on assessing the stability and accuracy of the learned parameters from the Hawkes–Cox process are studied. First, we illustrate the generation of the synthetic data. Then we briefly review the MLE method before presenting the calibration results obtained with the proposed optimization method.

6.1.1 Synthetic Data Generation

For simplicity, we assume the levels of excitation $X_\cdot$ and $Y_\cdot$ be drawn from random elements of exponential distribution with mean parameter $\psi$. One reason is that this makes the data generation process simple since an efficient simulation algorithm is available (Dassios and Zhao 2011). To avoid giving more weight to some parameters over others, we simply assume the following ground truth parameters for the simulation of the synthetic data. All parameters are set to a value of 1 except for the decay $\delta$ and the initial intensity $\lambda _0$. The decay parameter $\delta$ is set to a value of 2 because it has to be greater than $\psi$ to respect the stationarity condition (Brémaud and Massoulié 1996; Brémaud et al. 2002), while $\lambda _0$ is set to 2 such that $(\lambda _0 - a)$ is non-zero. In addition, we arbitrarily set the maturity time T to 5,000 to allow for long-term stationary conditions to be achieved. We spell out the values of the parameters in Table 2 for ease of reading.

6.1.2 Maximum Likelihood Estimation

For practical applications, the MLE method has frequently been employed as the standard for parameter estimation on statistical models due to the lack of efficient and fast inference algorithms for large datasets. Presumably, the popularity of using MLE is due to Ozaki (1979) who first applied MLE procedures to estimate parameters of a Hawkes process. For example, despite the Markov chain Monte Carlo (MCMC) methods giving exact solutions in the limiting cases, they may be too slow for many practical applications (Kuss and Rasmussen 2005). Other inference techniques, albeit faster than MCMC, are still comparatively slower compared to MLE for practical purposes. Here, we use MLE to learn the set of parameters $\varphi = \{a , \delta , \psi , \rho \}$.

To account for randomness from the simulations, the MLE result is obtained from 100 samples of Hawkes–Cox processes simulated with the ground truth parameters described in Sect. 6.1.1 or Table 2. The technical approach for computing the minimum is by using a bounded constrained optimizer built upon MATLAB function fminsearch, which in turn employs the Nelder–Mead simplex method (Nelder and Mead 1965). We bound our search space from 0 to 10.

We find that the learned MLE parameters, presented in the first row of Table 3, are close to the ground truth parameters, where their standard errors are displayed in the corresponding brackets. However, a careful inspection of their 95 % confidence intervals (i.e., ± two standard errors from the estimates) suggests that the estimates are not adequate, as the confidence intervals for a, $\delta$ and $\psi$ failed to contain the true values. Additionally, in Table 3, we compute the mean absolute difference (MAD) of the learned parameters against their ground truth values. This MAD value for MLE suggests that the learned parameters only deviate from (on average) the true values by 0.13.

We report that the MLE method takes quadratic time to run due to the evaluation of the loglikelihood function. In our case, we find that each MLE took around 846 s to complete.

Table 1 The mean absolute differences for the learned parameters against their true values, obtained with our inference technique over various configurations of $\tau$ and $\lambda _{reg}$. The MADs are computed by averaging over 1,000 simulation paths. The results, for which the lower MAD the better, that are lower than 0.01 are highlighted in bold. Observe that as the interval $\tau$ increases, the stronger the regularization parameter $\lambda _{reg}$ required for better parameter estimations

Table 2 Ground truth parameters used in simulating the synthetic data

Table 3 The learned parameters $\{a, \delta , \psi , \rho \}$ and their standard errors (enclosed in brackets) associated with the MLE method and the proposed inference technique. For the proposed optimization method, the results with the best MAD correspond to each $\tau$ are shown. We note that, with the exception of the MLE, the confidence intervals of the learned estimates contain the true parameters

Table 4 The learned parameters $\{a, \delta , \psi , \rho \}$ and their standard errors (enclosed in brackets) associated with the MLE method and our inference technique. For the proposed optimization method, the results with the best MAD in prediction correspond to each $\tau$ are shown. Further, the Hawkes–Cox process is shown to perform much better than the Homogeneous Poisson Process

6.1.3 $L_2-$Regularization

We replicate the above experiments but now with the proposed $L_2-$regularization method described Sect. 5. Since estimation is almost instantaneous, we perform the assessment by simulating 1,000 sample paths of Hawkes–Cox processes. We repeat the experiments for different configurations of the tuning parameters, that is, interval $\tau$ in the range of 0.5–10.0, and regularization parameter $\lambda _{reg}$ in the range of 0.0–1.0.

We present the MAD of the learned parameters against the true values corresponding to various configurations in Table 1, and the most accurately learned parameters from varying the $\lambda _{reg}$ is tabulated in Table 3. Interestingly, we find that the higher the interval $\tau$, we require a higher regularization parameter $\lambda _{reg}$ to obtain the best results. Additionally, we also observe that the best parameter fitting gets worse (in terms of MAD) the higher the $\tau$, this is most likely due to information loss as we aggregate over counts over a coarser granularity. Similarly, note that the standard errors increase as well.

We conclude that our method produces estimations that are very close to the true values as compared to the MLE method, as illustrated in Table 3. Further, in contrast to the MLE method, our regularization technique only took 1.2 s (175 times faster than MLE) for parameter estimations, on average (Table 4).

7 Disability Adjusted Life Years

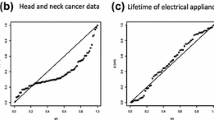
DALY. The notion of the disability-adjusted life year (DALY) has been introduced in the 1990s. DALYs are important measurements that link the burden of disease in populations with the degree of morbidity, disability, and long-term survival. They were initially developed to gauge the global burden of disease and to determine a strategy for the evaluation of health benefits and its associated cost-effectiveness. One DALY is the equivalent of a year of healthy life lost if a person had not experienced a particular disease. Different theoretical and methodological challenges persist, which are likely to affect both the computation and interpretation of DALY estimates (Mathers et al. 2008).

The computation of DALY and its challenges. DALY calculations consist of two smaller estimates: (i) the number of years lived with disability (YLD); and (ii) the number of years of life lost (YLL) associated with the condition of interest. DALYs are estimated as the sum of the YLD and YLL pillars. YLD for different diseases is calculated using disease-specific disability weights that range between 0 (perfect health) and 1 (death) and the duration of disability. YLL is calculated using estimates of mortality associated with the condition of interest when untreated, life expectancy, and age at death.

At times, scarce, reliable population-based data on disease parameters, specifically incidence of deaths and diseases, make estimating DALY of a specific disease difficult, especially in lower middle-income economies (Kularatna et al. 2013; Wyber et al. 2015). Hence, standard techniques to deal with this uncertainty is to employ a sampling-based estimation procedure. In this approach, each parameter is modeled by a probability distribution centered upon the optimal estimate of the parameter with a range reflecting uncertainty (Puett et al. 2019; Noguera Zayas et al. 2021). Typically, disability weights were modeled using the continuous uniform distribution and the expected number of deaths were modeled using the Poisson distribution.

Proposed methodologies. Standard methods dictate the use of Poisson distribution to obtain estimates for the expected number of deaths and specific diseases. Recall that in a Poissonian framework, the probability of the number of deaths occurring in an age group happens with a fixed average rate, and is independent of the time since the last event. We propose the use of the intensity function in Eq. (2), for modeling purposes, which relaxes the Poisson assumption of stationary increments. It allows for the possibility that the rates need not be constant but can vary with time. This choice of intensity is general enough to encapsulate certain stylized facts of rates of deaths and diseases, such as nonlinear trend characteristics. Here, we illustrate the estimation procedure by applying the techniques presented earlier to obtain an estimate for the parameters for Hawkes–Cox process model, generalizing the Poissonian feature that is widely used in the literature. We first suppose that we observe the number of deaths (or number of diseases) across age groups, as tabulated in Table 5. For simplicity, we further suppose that there are three parameters to estimate, absorbed in $\theta \in \mathbb {R}^3$. Define the function $\mathcal {A}_{\theta }$ which takes the form

Table 5 Number of deaths or diseases, stratified by age

$$\begin{aligned} \mathcal {A}_{\theta }=\begin{pmatrix} m_1 - h^{\tau }_1 \\ m_2 - h^{\tau }_2 \\ m_3 - h^{\tau }_3 \end{pmatrix} \end{aligned}$$

where $m_1$, $m_2$, and $m_3$ denote the observed mean, variance, and covariance of the number of events within an interval with a predetermined specification of $\tau$ and $\delta$ given in (10), (11), and (12), respectively. The quantities $h^{\tau }_1$, $h^{\tau }_2$, and $h^{\tau }_3$ given in (6), (8), and (9), respectively, are functions of the parameters. Let $R_i$ denote the number of deaths (or number of diseases) falling in age group i. Furthermore, let N be the number of age groups remaining. In this case, we have

$$\begin{aligned} m_1&= \frac{1}{N}\sum _{i=1}^{N}R_i \end{aligned}$$

(10)

$$\begin{aligned} m_2&=\frac{1}{N}\sum _{i=1}^{N}R_i^2-m_1^2 \end{aligned}$$

(11)

$$\begin{aligned} m_3&= \frac{1}{N}\sum _{i=1}^{N} \Big (R_i\times R_{i+\Delta }\Big ) - \left( \frac{1}{N}\sum _{i=1}^{N} R_i\right) \times \left( \frac{1}{N} \sum _{i=1}^{N}R_{i+\Delta }\right) \end{aligned}$$

(12)

where $\Delta = \lceil \delta /\tau \rceil$. One can then evaluate $\hat{\theta }$ such that $\mathcal {A}_{\hat{\theta }}=0$ using standard methods of moment matching (Hall 2004). With the estimated parameters, one can then obtain distributions related to the number of deaths and specific diseases. By a similar token, the same procedures may be applied to obtain suitable distributional properties for different age groups. This framework gives a natural way to deal with uncertainties in DALY computations, which subsumes the Poissonian assumptions.

8 Concluding Remarks

In this paper, we derive explicit moments and the covariance function of the number of events over an interval for the Hawkes–Cox process. The future evolution of this point process is influenced by the timing of past events whose intensities are affected by a self-exciting mechanism and an exogenous component. We develop an inference procedure through regularizations taking into account the theoretical functionals and showing that estimation is almost immediate. Empirical experiments on real data sets demonstrate its superior scalability and predictive performance.