Abstract
In this chapter, we start by giving an overview of quantum (locally) compact metric spaces. Then, we show that we can associate quantum compact metric spaces to some Markov semigroups of Fourier multipliers satisfying additional conditions: an injectivity and a gap condition on the cocycle which represents the semigroup, and the finite dimensionality (with explicit control on p) of the cocycle Hilbert space. We show a similar result for semigroups of Schur multipliers and obtain a quantum locally compact metric space. We further explore the connections of our gap condition between Fourier multipliers and Schur multipliers with some examples. In the sequel, we introduce spectral triples (= noncommutative manifolds) associated to Markov semigroups of Fourier multipliers or Schur multipliers satisfying again some technical conditions, and in all we investigate four different settings. Along the way, we introduce a Banach space variant of the notion of spectral triple suitable for our context. Finally, we investigate the bisectoriality and the functional calculus of some Hodge-Dirac operators which are crucial in the noncommutative geometries which we introduce here.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Recall that D is an unbounded operator acting on the Hilbert space of L2-spinors and that the functions of C(M) act on the same Hilbert space by multiplication operators.
- 2.
Indeed, \( \operatorname {{\mathrm {Lip}}}(X)\) contains the constant functions. Moreover, \( \operatorname {{\mathrm {Lip}}}(X)\) separates points in X. If x 0, y 0 ∈ X with x 0 ≠ y 0, we can use the lipschitz function \(f \colon X\to \mathbb {R}\), x↦dist(x, y 0) since we have f(x 0) > 0 = f(y 0).
- 3.
- 4.
It is not clear if the support must be in addition open in [143] since the indicator 1A of a subset A is continuous if and only if A is both open and closed.
- 5.
Recall that a family (x s)s ∈ I vanishes at infinity means that for any ε > 0, there exists a finite subset J of I such that for any s ∈ I − J we have |x s| < ε.
- 6.
Write \(x=A^{-\frac {1}{2}}A_p^{\frac {1}{2}}x\).
- 7.
More generally, if 1 < p < ∞ the operator space \(\mathrm {L}^p(\mathbb {T}^2)\) has CCAP by Junge and Ruan [121, Proposition 3.5] since an abelian group is weakly amenable with Cowling-Haagerup constant equal to 1.
- 8.
If \(\eta \in \big ( \xi _1 + \frac {\sqrt {\mathrm {Gap}_\alpha }}{2} \mathrm {B}_n \big ) \cap \big ( \xi _2 + \frac {\sqrt {\mathrm {Gap}_\alpha }}{2} \mathrm {B}_n \big )\) then \(|\xi _1-\xi _2| \leqslant |\xi _1-\eta |+|\eta -\xi _2| < \frac {\sqrt {\mathrm {Gap}_\alpha }}{2}+\frac {\sqrt {\mathrm {Gap}_\alpha }}{2}=\sqrt {\mathrm {Gap}_\alpha }\) which is impossible.
- 9.
Since I is finite, we have \( \operatorname {\mathrm {dom}} A_p^{\frac {1}{2}}=S^p_I\). Write \(x=A^{-\frac {1}{2}}A_p^{\frac {1}{2}}x\).
- 10.
Since I is finite, we have \( \operatorname {\mathrm {dom}} A_{p_0}^{\frac {1}{2}}=S^{p_0}_I\).
- 11.
For any \(n,m \in \mathbb {Z}\), we have the cocycle law
$$\displaystyle \begin{aligned} \begin{array}{rcl} b(n)& +&\displaystyle \pi_n(b_m) =\big(\mathrm{e}^{2 \pi \mathrm{i} \alpha n},\mathrm{e}^{2 \pi \mathrm{i} \beta n}\big) - (1,1) +\pi_n\big[\big(\mathrm{e}^{2 \pi \mathrm{i} \alpha m},\mathrm{e}^{2 \pi \mathrm{i} \beta m}\big) - (1,1) \big] \\ & =&\displaystyle \big(\mathrm{e}^{2 \pi \mathrm{i} \alpha n},\mathrm{e}^{2 \pi \mathrm{i} \beta n}\big) - (1,1) + \big(\mathrm{e}^{2 \pi \mathrm{i} \alpha (n+m)},\mathrm{e}^{2 \pi \mathrm{i} \beta (n+m)}\big) -\big(\mathrm{e}^{2 \pi \mathrm{i} \alpha n},\mathrm{e}^{2 \pi \mathrm{i} \beta n}\big) \\ & =&\displaystyle \big(\mathrm{e}^{2 \pi \mathrm{i} \alpha (n+m)},\mathrm{e}^{2 \pi \mathrm{i} \beta (n+m)}\big) - (1,1) =b(n+m). \end{array} \end{aligned} $$ - 12.
It may perhaps be possible to replace the reflexivity by an assumption of weak compactness, see [110, p. 361].
- 13.
In the sense of [136, p. 167].
- 14.
Recall that the term ∂ ψ,q,p(a)x is by definition equal to
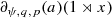 .
. - 15.
For any x ∈ Γq(H) and any s ∈ G, we have
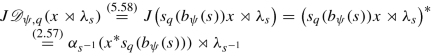
and
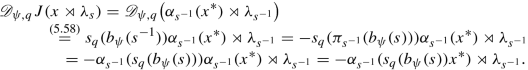
.
- 16.
For t > 0, let μ t(b) denote the generalized singular number of |b|, so that
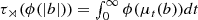 for any continuous function \(\mathbb {R}_+ \to \mathbb {R}\) of bounded variation [227, p. 30]. If b were unbounded, then μ
t(b) →∞ as t → 0. Taking ξ = ϕ(|b|) ≠ 0 with ϕ a smoothed indicator function of an interval [x, y] with large x, it is not difficult to see that \(\left \Vert b\xi \right \Vert { }_p \geqslant x \left \Vert \xi \right \Vert { }_p\), which is the desired contradiction.
for any continuous function \(\mathbb {R}_+ \to \mathbb {R}\) of bounded variation [227, p. 30]. If b were unbounded, then μ
t(b) →∞ as t → 0. Taking ξ = ϕ(|b|) ≠ 0 with ϕ a smoothed indicator function of an interval [x, y] with large x, it is not difficult to see that \(\left \Vert b\xi \right \Vert { }_p \geqslant x \left \Vert \xi \right \Vert { }_p\), which is the desired contradiction. - 17.
Recall that the term ∂ α,q,p(a)x is by definition equal to ∂ α,q(a)(1 ⊗ x).
- 18.
Recall that a family (x i)i ∈ I vanishes at infinity means that for any ε > 0, there exists a finite subset J of I such that for any i ∈ I − J we have \(|x_i| \leqslant \varepsilon \).
- 19.
The entries are 1 on the j-row and zero anywhere else.
- 20.
Note that since \(\Gamma _{-1}(H) \overline \otimes \mathrm {B}(\ell ^2_I)\) is then finite-dimensional, the spaces \(\mathrm {L}^p(\Gamma _{-1}(H) \overline \otimes \mathrm {B}(\ell ^2_I))\) are all isomorphic for different values of p, \(\overline { \operatorname {\mathrm {Ran}} \mathscr {D}_{\alpha ,-1,2}} = \overline { \operatorname {\mathrm {Ran}} \mathscr {D}_{\alpha ,-1,p}}\) for all 1 < p < ∞ and thus, \(|\mathscr {D}_{\alpha ,-1,2}|{ }^{-1}\) extends to a compact operator on \(\overline { \operatorname {\mathrm {Ran}} \mathscr {D}_{\alpha ,-1,p}}\), too.
- 21.
We have
$$\displaystyle \begin{aligned} \begin{array}{rcl} & &\displaystyle \sum_{k,l} J_{kl} R(\lambda,\mathrm{L}_{s_q(\alpha_k -\alpha_l)})Q_{kl} \left( \lambda - \sum_{i,j} J_{ij} \mathrm{L}_{s_q(\alpha_i - \alpha_j)} Q_{ij} \right) \\ & &\displaystyle \qquad \quad = \sum_{k,l}J_{kl} \lambda R(\lambda,\mathrm{L}_{s_q(\alpha_k - \alpha_l)})Q_{kl} - \sum_{k,l,i,j} J_{kl}R(\lambda,\mathrm{L}_{s_q(\alpha_k - \alpha_l)})Q_{kl}J_{ij} \mathrm{L}_{s_q(\alpha_i - \alpha_j)}Q_{ij} \\ & &\displaystyle \qquad \quad = \sum_{k,l} J_{kl}\lambda R(\lambda,\mathrm{L}_{s_q(\alpha_k - \alpha_l)})Q_{kl}- \sum_{k,l,i,j} \delta_{k=i} \delta_{l = j} J_{kl}R(\lambda,\mathrm{L}_{s_q(\alpha_k - \alpha_l)}) \mathrm{L}_{s_q(\alpha_i - \alpha_j)} Q_{ij} \\ & &\displaystyle \qquad \quad = \sum_{k,l}J_{kl} R(\lambda,\mathrm{L}_{s_q(\alpha_k - \alpha_l)})(\lambda - \mathrm{L}_{s_q(\alpha_k-\alpha_l)}) Q_{kl} \\ & &\displaystyle \qquad \quad = \sum_{k,l}J_{kl}\mathrm{Id}_{\mathrm{L}^p(\Gamma_q(H))} Q_{kl} = \mathrm{Id}_{\mathrm{L}^p(\Gamma_q(H) \overline\otimes \mathrm{B}(\ell^2_I))}, \end{array} \end{aligned} $$and similarly the other way around.
References
E.M. Alfsen, Compact Convex Sets and Boundary Integrals. Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 57 (Springer, New York, 1971)
E.M. Alfsen, F.W. Shultz, Geometry of state spaces of operator algebras, in Mathematics: Theory & Applications (Birkhauser Boston, Inc., Boston, 2003)
C. Arhancet, On Matsaev’s conjecture for contractions on noncommutative L p-spaces. J. Operator Theory 69(2), 387–421 (2013)
C. Arhancet, Dilations of markovian semigroups of Fourier multipliers on locally compact groups. Proc. Amer. Math. Soc. 148(6), 2551–2563 (2020)
C. Arhancet, Dilations of markovian semigroups of measurable Schur multipliers. Preprint online on https://arxiv.org/abs/1910.14434
C. Arhancet, C. Kriegler, Projections, multipliers and decomposable maps on noncommutative Lp-spaces. Submitted, Preprint online on https://arxiv.org/abs/1707.05591
B. Bekka, P. de la Harpe, Pierre, A. Valette, Kazhdan’s Property (T). New Mathematical Monographs, vol. 11 (Cambridge University Press, Cambridge, 2008)
J.V. Bellissard, M. Marcolli, K. Reihani, Dynamical Systems on Spectral Metric Spaces. Preprint online on https://arxiv.org/abs/1008.4617
D. Blecher, C. Le Merdy, Operator Algebras and Their Modules-An Operator Space Approach. London Mathematical Society Monographs. New Series, vol. 30 (Oxford Science Publications, The Clarendon Press, Oxford University Press, Oxford, 2004)
V.I. Bogachev, Measure Theory, vol. II (Springer, Berlin, 2007)
M. Bożejko, R. Speicher, Completely positive maps on Coxeter groups, deformed commutation relations, and operator spaces. Math. Ann. 300(1), 97–120 (1994)
N.P. Brown, N. Ozawa, C ∗-algebras and finite-dimensional approximations. Graduate Studies in Mathematics, vol. 88 (American Mathematical Society, Providence, 2008)
A.L. Carey, V. Gayral, A. Rennie, F.A. Sukochev, Index theory for locally compact noncommutative geometries. Mem. Amer. Math. Soc. 231(1085) (2014)
I. Chatterji, Introduction to the rapid decay property, in Around Langlands Correspondences. Contemporary Mathematics, vol. 691 (American Mathematical Society, Providence, 2017), pp. 53–72
F. Cipriani, D. Guido, T. Isola, J.-L. Sauvageot, Spectral triples for the Sierpinski gasket. J. Funct. Anal. 266(8), 4809–4869 (2014)
A. Connes, Compact metric spaces, Fredholm modules, and hyperfiniteness. Ergodic Theory Dynam. Systems 9(2), 207–220 (1989)
A. Connes, Noncommutative Geometry (Academic Press, Inc., San Diego, 1994)
J. De Cannière, U. Haagerup, Multipliers of the Fourier algebras of some simple Lie groups and their discrete subgroups. Amer. J. Math. 107(2), 455–500 (1985)
J. Dieudonné, Treatise on Analysis, vol. II. Enlarged and corrected printing. Translated by I. G. Macdonald. With a loose erratum. Pure and Applied Mathematics, 10-II (Academic Press [Harcourt Brace Jovanovich, Publishers], New York, 1976)
R.M. Dudley, Real Analysis and Probability (CRC Press, Boca Raton, 2018)
M. Egert, On Kato’s conjecture and mixed boundary conditions. PhD (2015)
K.-J. Engel, R. Nagel, One-Parameter Semigroups for Linear Evolution Equations. Graduate Texts in Mathematics, vol. 194 (Springer, New York, 2000)
I. Forsyth, B. Mesland, A. Rennie, Dense domains, symmetric operators and spectral triples. New York J. Math. 20, 1001–1020 (2014)
V. Gayral, J.M. Gracia-Bondía, B. Iochum, T. Schücker, J.C. Varilly, Moyal planes are spectral triples. Comm. Math. Phys. 246(3), 569–623 (2004)
S. Ghorpade, B.V. Limaye, A course in multivariable calculus and analysis, in Undergraduate Texts in Mathematics (Springer, New York, 2010)
J.M. Gracia-Bondía, J.C. Varilly, H. Figueroa, Elements of noncommutative geometry, in Birkhäuser Advanced Texts: Basler Lehrbücher (Birkhäuser Boston, Inc., Boston, 2001)
M. Haase, The functional calculus for sectorial operators, in Operator Theory: Advances and Applications, vol. 169 (Birkhäuser Verlag, Basel, 2006)
T. Hytönen, J. van Neerven, M. Veraar, L. Weis, Analysis in Banach Spaces, vol. II. Probabilistic Methods and Operator Theory (Springer, Berlin, 2018)
M. Junge, T. Mei, Noncommutative Riesz transforms–a probabilistic approach. Amer. J. Math. 132(3), 611–680 (2010)
M. Junge, Z.-J. Ruan, Approximation properties for noncommutative L p-spaces associated with discrete groups. Duke Math. J. 117(2), 313–341 (2003)
M. Junge, D. Sherman, Noncommutative L p modules. J. Operator Theory 53(1), 3–34 (2005)
M. Junge, C. Le Merdy, Q. Xu, H ∞ functional calculus and square functions on noncommutative L p-spaces. Astérisque No. 305 (2006)
M. Junge, T. Mei, J. Parcet, Smooth Fourier multipliers on group von Neumann algebras. Geom. Funct. Anal. 24(6), 1913–1980 (2014)
M. Junge, T. Mei, J. Parcet, Noncommutative Riesz transforms–dimension free bounds and Fourier multipliers. J. Eur. Math. Soc. (JEMS) 20(3), 529–595 (2018)
R.V. Kadison, A representation theory for commutative topological algebra. Mem. Amer. Math. Soc. (7), 39 (1951)
T. Kato, Perturbation Theory for Linear Operators, 2nd edn. Grundlehren der Mathematischen Wissenschaften, Band 132 (Springer, Berlin, 1976)
F. Latrémolière, Quantum locally compact metric spaces. J. Funct. Anal. 264(1), 362–402 (2013)
F. Latrémolière, Convergence of fuzzy tori and quantum tori for the quantum Gromov-Hausdorff propinquity: an explicit approach. Münster J. Math. 8(1), 57–98 (2015)
F. Latrémolière, The dual Gromov-Hausdorff propinquity. J. Math. Pures Appl. (9) 103(2), 303–351 (2015)
F. Latrémolière, Equivalence of quantum metrics with a common domain. J. Math. Anal. Appl. 443(2), 1179–1195 (2016)
F. Latrémolière, Quantum metric spaces and the Gromov-Hausdorff propinquity, in Noncommutative Geometry and Optimal Transport. Contemporary Mathematics, vol. 676 (American Mathematical Society, Providence, 2016), pp. 47–133
F. Latrémolière, The quantum Gromov-Hausdorff propinquity. Trans. Amer. Math. Soc. 368(1), 365–411 (2016)
F. Latrémolière, Heisenberg Modules over Quantum 2-tori are metrized quantum vector bundles. Preprint online on https://arxiv.org/abs/1703.07073
F. Latrémolière, The Gromov-Hausdorff propinquity for metric Spectral Triples. Preprint online on https://arxiv.org/abs/1811.10843
A. McIntosh, S. Monniaux, Hodge-Dirac, Hodge-Laplacian and Hodge-Stokes operators in L p spaces on Lipschitz domains. Rev. Mat. Iberoam. 34(4), 1711–1753 (2018)
R.E. Megginson, An introduction to Banach space theory, in Graduate Texts in Mathematics, vol. 183 (Springer, New York, 1998)
J.v. Neerven, The Adjoint of a Semigroup of Linear Operators. Lecture Notes in Mathematics, vol. 1529 (Springer, Berlin, 1992), x+195 pp.
N. Ozawa, M. Rieffel, Hyperbolic group C ∗-algebras and free-product C ∗-algebras as compact quantum metric spaces. Canad. J. Math. 57(5), 1056–1079 (2005)
V. Paulsen, Completely Bounded Maps and Operator Algebras (Cambridge University Press, Cambridge, 2002)
G. Pisier, Regular operators between non-commutative L p-spaces. Bull. Sci. Math. 119(2), 95–118 (1995)
G. Pisier, Introduction to Operator Space Theory (Cambridge University Press, Cambridge, 2003)
G. Pisier, Q. Xu, Non-commutative L p-spaces, in Handbook of the Geometry of Banach Spaces, vol. II, ed. by W.B. Johnson, J. Lindenstrauss (Elsevier, Amsterdam, 2003), pp. 1459–1517
J.G. Ratcliffe, Foundations of Hyperbolic Manifolds. Graduate Texts in Mathematics, vol. 149 (Springer, New York, 1994)
M. Reed, B. Simon, Methods of Modern Mathematical Physics. I. Functional Analysis, 2nd edn. (Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York, 1980)
M.A. Rieffel, Metrics on state spaces. Doc. Math. 4, 559–600 (1999)
M.A. Rieffel, Compact quantum metric spaces, in Operator Algebras, Quantization, and Noncommutative Geometry. Contemporary Mathematics, vol. 365 (American Mathematical Society, Providence, 2004), pp. 315–330
M.A. Rieffel, Gromov-Hausdorff distance for quantum metric spaces. Appendix 1 by Hanfeng Li. Gromov-Hausdorff distance for quantum metric spaces. Matrix algebras converge to the sphere for quantum Gromov-Hausdorff distance. Mem. Amer. Math. Soc. 168(796), 1–65 (2004)
K. Schmüdgen, Unbounded self-adjoint operators on Hilbert space, in Graduate Texts in Mathematics, vol. 265 (Springer, Dordrecht, 2012)
F. Sukochev, D. Zanin, The Connes character formula for locally compact spectral triples. Preprint online on https://arxiv.org/abs/1803.01551
J.C. Varilly, Dirac operators and spectral geometry. Lecture notes on noncommutative geometry and quantum groups edited by P. M. Hajac. https://www.mimuw.edu.pl/~pwit/toknotes/
C. Villani, Optimal transport. Old and new, in Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 338 (Springer, Berlin, 2009)
N. Weaver, Lipschitz algebras and derivations of von Neumann algebras. J. Funct. Anal. 139(2), 261–300 (1996)
N. Weaver, Lipschitz Algebras, 2nd edn. (World Scientific Publishing Co. Pte. Ltd., Hackensack, 2018)
Q. Xu, Non-commutative L p-spaces. Script not available
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Arhancet, C., Kriegler, C. (2022). Locally Compact Quantum Metric Spaces and Spectral Triples. In: Riesz Transforms, Hodge-Dirac Operators and Functional Calculus for Multipliers. Lecture Notes in Mathematics, vol 2304. Springer, Cham. https://doi.org/10.1007/978-3-030-99011-4_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-99011-4_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-99010-7
Online ISBN: 978-3-030-99011-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


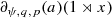 .
.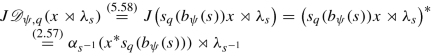
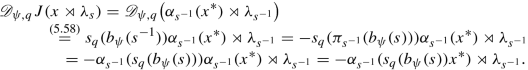
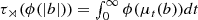 for any continuous function
for any continuous function