Boundary Value Problems and Boundary Value Spaces

Abstract

This chapter is devoted to the study of inhomogeneous boundary value problems. For this, we shall reformulate the boundary value problem again into a form which fits within the general framework of evolutionary equations. In order to have an idea of the type of boundary values which make sense to study, we start off with a section that deals with the boundary values of functions in the domain of the gradient operator defined on a half-space in $\mathbb {R}^d$ (for d = 1 we have $L_2(\mathbb {R}^{d-1})=\mathbb {K}$).

This chapter is devoted to the study of inhomogeneous boundary value problems. For this, we shall reformulate the boundary value problem again into a form which fits within the general framework of evolutionary equations. In order to have an idea of the type of boundary values which make sense to study, we start off with a section that deals with the boundary values of functions in the domain of the gradient operator defined on a half-space in $\mathbb {R}^d$ (for d = 1 we have $L_2(\mathbb {R}^{d-1})=\mathbb {K}$).

12.1 The Boundary Values of $H^{1}(\mathbb {R}^{d-1}\times \mathbb {R}_{>{0}})$

In this section we let and f ∈ H ¹( Ω); our aim is to make sense of the function . Note that this makes no sense if we only assume f ∈ L ₂( Ω) since $\mathbb {R}^{d-1}\times \{0\}=\partial \Omega$ is a set of (d-dimensional) Lebesgue-measure zero. However, if we assume f to be weakly differentiable, something more can be said and the boundary values can be defined by means of a continuous extension of the so-called trace map. In order to properly formulate this, we need the following density result.

Theorem 12.1.1

The set is dense in the space H ¹( Ω).

We will need a density result for $H^1(\mathbb {R}^d)$ first.

Lemma 12.1.2

$C_{\mathrm {c}}^\infty (\mathbb {R}^{d})$ is dense in $H^{1}(\mathbb {R}^{d})$.

Proof

Let $f\in H^{1}(\mathbb {R}^{d})$. We first show that f can be approximated by functions with compact support. For this let $\phi \in C_{\mathrm {c}}^\infty (\mathbb {R}^{d})$ with the properties $0\leqslant \phi \leqslant 1$, ϕ = 1 on $B\left (0,1/2\right )$ and ϕ = 0 on $\mathbb {R}\setminus B\left (0,1\right )$. For all $k\in \mathbb {N}$ we put and . Then f _k has support contained in $B\left [0,k\right ]$. The dominated convergence theorem implies that f _k → f in $L_2(\mathbb {R}^{d})$ as k →∞. Next, let $\psi \in C_{\mathrm {c}}^\infty (\mathbb {R}^{d})^{d}$ and compute for all $k\in \mathbb {N}$

which shows that $f_{k}\in \operatorname {dom}( \operatorname {\mathrm {grad}})=H^{1}(\mathbb {R}^{d})$ and

$$\displaystyle \begin{aligned} \operatorname{\mathrm{grad}} f_{k}=(\operatorname{\mathrm{grad}} f)\phi_{k}+\frac{1}{k} f\left(\operatorname{\mathrm{grad}}\phi\right)(\cdot/k).\end{aligned} $$

From this expression of $\operatorname {\mathrm {grad}} f_k$ we observe $\operatorname {\mathrm {grad}} f_k\to \operatorname {\mathrm {grad}} f$ in $L_2(\mathbb {R}^d)^d$ by dominated convergence. Hence, f _k → f in $\operatorname {dom}( \operatorname {\mathrm {grad}})=H^1(\mathbb {R}^d)$.

To conclude the proof of this lemma it suffices to revisit Exercise 3.2. For this, let (ψ _k)_k in $C_{\mathrm {c}}^\infty (\mathbb {R}^{d})$ be a δ-sequence. Then, by Exercise 3.2, we infer ψ _k ∗ f → f in $L_2(\mathbb {R}^{d})$ as k →∞ and hence, by Exercise 12.1, it follows also that $\operatorname {\mathrm {grad}}\left (\psi _{k}\ast f\right )=\psi _{k}\ast \operatorname {\mathrm {grad}} f\to \operatorname {\mathrm {grad}} f$ (note the component-wise definition of the convolution). A combination of the first part of this proof together with an estimate for the support of the convolution (see again Exercise 3.2) yields the assertion. □

Proof of Theorem 12.1.1

Let f ∈ H ¹( Ω). The approximation of f by functions in $\mathcal {D}$ is done in two steps. First, we shift f in the negative e _d-direction to avoid the boundary, and then we convolve the shifted f to obtain smooth approximants in $\mathcal {D}$.

Let $\widetilde {f}\in L_2(\mathbb {R}^{d})$ be the extension of f by zero. Put , the d-th unit vector. Then for all τ > 0 we have Ω + τe _d ⊆ Ω and, thus by Exercise 12.2, we deduce in H ¹( Ω) as τ → 0. Thus, it suffices to approximate f _τ for τ > 0.

Let τ > 0 and let $\left (\psi _{k}\right )_{k}$ in $C_{\mathrm {c}}^\infty (\mathbb {R}^d)$ be a δ-sequence. Then $\psi _{k}\ast \widetilde {f}(\cdot +\tau e_{d})\in H^{1}(\mathbb {R}^{d})$, by Exercise 12.1. Define . Then we obtain that f _k,τ → f _τ in H ¹( Ω) as k →∞. Indeed, the only thing left to prove is that $\operatorname {\mathrm {grad}} f_{k,\tau }\to \operatorname {\mathrm {grad}} f_{\tau }$ in L ₂( Ω)^d as k →∞. For this, we denote by g the extension of $\operatorname {\mathrm {grad}} f$ by 0. Since $g\in L_2(\mathbb {R}^{d})^{d}$ it suffices to show that $\operatorname {\mathrm {grad}} f_{k,\tau }=\psi _{k}\ast g_{\tau }$ on Ω for all large enough $k\in \mathbb {N},$ where g _τ = g(⋅ + τe _d). Let $k>\frac {1}{\tau }$. Then for all x ∈ Ω and $y\in \operatorname {\mathrm {spt}}\psi _{k}\subseteq \left [-1/k,1/k\right ]^{d}$ we infer x − y + τe _d ∈ Ω. In particular, f(⋅− y + τe _d) ∈ H ¹( Ω) and $\operatorname {\mathrm {grad}} f(\cdot -y+\tau e_{d})=g(\cdot -y+\tau e_{d})$. Take $\eta \in C_{\mathrm {c}}^\infty (\Omega )^{d}$ and compute

As $\psi _{k}\ast \widetilde {f}(\cdot +\tau e_{d})\in H^{1}(\mathbb {R}^{d})$, we conclude the proof using Lemma 12.1.2. □

With these preparations at hand, we can define the boundary trace of H ¹( Ω).

Theorem 12.1.3

The operator

is continuous, densely defined and, thus, admits a unique continuous extension to H ¹( Ω) again denoted by γ. Moreover, we have

$$\displaystyle \begin{aligned} \left\Vert \gamma f \right\Vert {}_{L_2(\mathbb{R}^{d-1})}\leqslant\left(2\left\Vert f \right\Vert {}_{L_2(\Omega)}\left\Vert \operatorname{\mathrm{grad}} f \right\Vert {}_{L_2(\Omega)^{d}}\right)^{\frac{1}{2}}\leqslant\left\Vert f \right\Vert {}_{H^{1}(\Omega)} \quad (f\in H^1(\Omega)). \end{aligned}$$

Proof

Note that γ is densely defined by Theorem 12.1.1. Let $f\in C_{\mathrm {c}}^\infty (\mathbb {R}^{d})$ and . Let R > 0 be such that $\operatorname {\mathrm {spt}} f\subseteq B\left (0,R\right )$. Then

The remaining inequality follows from $2ab\leqslant a^{2}+b^{2}$ for all $a,b\in \mathbb {R}$. □

Except for one spatial dimension, where the boundary trace can be obtained by point evaluation, the boundary trace γ does not map onto the whole of $L_2(\mathbb {R}^{d-1})$. Hence, in order to define the space of all possible boundary values for a function in H ¹ one uses a quotient construction: we set

and endow $H^{1/2}(\mathbb {R}^{d-1})$ with the norm

It is not difficult to see that $H^{1/2}(\mathbb {R}^{d-1})$ is unitarily equivalent to $\left (\operatorname {ker}\gamma \right )^{\bot }$, where the orthogonal complement is computed with respect to the scalar product in H ¹( Ω). Thus, $H^{1/2}(\mathbb {R}^{d-1})$ is a Hilbert space.

Remark 12.1.4

The norm defined on the space $H^{1/2}(\mathbb {R}^{d-1})$ given above is not the standard norm defined on this space. Indeed, following [72, Section 2.3.8] the usual norm is given by

$$\displaystyle \begin{aligned} \left(\left\Vert u \right\Vert {}_{L_2(\mathbb{R}^{d-1})}^2+\int_{\mathbb{R}^{d-1}}\int_{\mathbb{R}^{d-1}} \frac{|u(x)-u(y)|{}^2}{|x-y|{}^{d}}\,\mathrm{d} x\,\mathrm{d} y\right)^{1/2} \end{aligned}$$

for $u\in H^{1/2}(\mathbb {R}^{d-1})$. However, this norm turns out to be equivalent to the norm given above, see e.g. [115, Section 4].

As the notation of this space suggests, it can also be defined as an interpolation space between $H^1(\mathbb {R}^{d-1})$ and $L_2(\mathbb {R}^{d-1})$, see [60, Theorem 15.1].

12.2 The Boundary Values of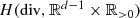

Let $\Omega :=\mathbb {R}^{d-1}\times \mathbb {R}_{>{0}}$. There is also a space of corresponding boundary traces for the divergence operator. Similarly to the boundary values for the domain of the gradient operator, H ¹( Ω), the construction of the boundary trace for -vector fields rests on a density result. The proof can be done along the lines of Theorem 12.1.1 and will be addressed in Exercise 12.3.

Theorem 12.2.1

$\mathcal {D}^{d}$ is dense in , where $\mathcal {D}$ is defined as in Theorem 12.1.1.

Equipped with this result, we can describe all possible boundary values of . It will turn out that vector fields in have a well-defined normal trace, which for $\Omega =\mathbb {R}^{d-1}\times \mathbb {R}_{>0}$ is just the negative of the last coordinate of the vector field.

Theorem 12.2.2

The operator

is densely defined, continuous with norm bounded by 1 and has dense range. Thus γ _n admits a unique extension to again denoted by γ _n . Here, − q _d is the negative of the d-th component of q pointing into the outward normal direction of Ω and − q _d is identified with the linear functional

$$\displaystyle \begin{aligned} H^{1/2}(\mathbb{R}^{d})\ni\gamma f\mapsto\left\langle -q_{d}(\cdot,0) ,\gamma f\right\rangle _{L_2(\mathbb{R}^{d-1})}. \end{aligned}$$

Moreover, for all $f\in \operatorname {dom}( \operatorname {\mathrm {grad}})$ and we have

(12.1)

Proof

Let $f\in \mathcal {D}$ and $q\in \mathcal {D}^{d}$. Then integration by parts yields

Hence,

Since $\mathcal {D}$ is dense in H ¹( Ω), the inequality remains true for all f ∈ H ¹( Ω). Thus,

Computing the infimum over all g ∈ H ¹( Ω) with γg = γf, we deduce

Therefore $\gamma _{\mathrm {n}}q\in H^{-1/2}(\mathbb {R}^{d-1})$ and , which shows continuity of γ _n. It is left to show that γ _n has dense range. For this, take $\gamma f\in H^{1/2}(\mathbb {R}^{d-1})$ for some f ∈ H ¹( Ω) such that

$$\displaystyle \begin{aligned} \left\langle \gamma_{\mathrm{n}}g ,\gamma f\right\rangle _{L_2(\mathbb{R}^{d-1})}=0 \end{aligned}$$

for all $g\in \mathcal {D}^{d}$. Next, take $\widetilde {g}\in C_{\mathrm {c}}^\infty (\mathbb {R}^{d-1})$ and $\psi \in C_{\mathrm {c}}^\infty (\mathbb {R})$ with ψ(0) = 1. Then we set and note that $\gamma _{\mathrm {n}}g=\widetilde {g}$. Hence

$$\displaystyle \begin{aligned} \left\langle \gamma f ,\widetilde{g}\right\rangle _{L_2(\mathbb{R}^{d-1})}=0\quad (\widetilde{g}\in C_{\mathrm{c}}^\infty (\mathbb{R}^{d-1})). \end{aligned}$$

Thus, γf = 0, which implies that the range of γ _n is dense, as $H^{-1/2}(\mathbb {R}^{d-1})$ is a Hilbert space. The remaining formula (12.1) follows by continuously extending both the left- and right-hand side of the integration by parts formula from the beginning of the proof. Note that for this, we have used both Theorems 12.1.1 and 12.2.1. □

Corollary 12.2.3

Let f ∈ H ¹( Ω), . Then $f\in \operatorname {dom}( \operatorname {\mathrm {grad}}_0)$ if and only if γf = 0, and if and only if γ _n q = 0.

Proof

We only show the statement for q. The proof for f is analogous. If , then there exists a sequence (ψ _n)_n in $C_{\mathrm {c}}^\infty (\Omega )^{d}$ such that ψ _n → q in as n →∞. Thus, by continuity of γ _n, we infer 0 = γ _n ψ _n → γ _n q. Assume on the other hand that with γ _n q = 0. Using (12.1), we obtain for all $f\in \operatorname {dom}( \operatorname {\mathrm {grad}})$

This equality implies that , which shows the remaining assertion. □

The remaining part of this section is devoted to showing that the continuous extension of γ _n maps onto $H^{-1/2}(\mathbb {R}^{d-1})$. For this we require the following observation, which will also be needed later on.

Proposition 12.2.4

Let $U\subseteq \mathbb {R}^{d}$ be open. Then

Proof

Let . Then if and only if for all we have

The latter, in turn, is equivalent to and . □

Theorem 12.2.5

γ _n maps onto $H^{-1/2}(\mathbb {R}^{d-1})$ . In particular, we have

for all .

Proof

By Theorem 12.2.2 it suffices to show that γ _n has closed range. For this, it suffices to show that there exists c > 0 such that

for all . By Corollary 12.2.3, we obtain . Hence, by Proposition 12.2.4, we deduce that if and only if and . So, assume that with . Then (12.1) applied to and yields

where we used . Hence

where we again used that . This yields the assertion. □

12.3 Inhomogeneous Boundary Value Problems

Let . With the notion of traces we now have a tool at hand that allows us to formulate inhomogeneous boundary value problems. Here we focus on the scalar wave type equation for given Neumann data $\widetilde {g}\in H^{-1/2}(\mathbb {R}^{d-1})$. We shall address other boundary value problems in the exercises. Let $M\colon \operatorname {dom}(M)\subseteq \mathbb {C}\to L\big (L_2(\Omega )\times L_2(\Omega )^{d}\big )$ be a material law with $\mathrm {s}_{\mathrm {b}}\left ( M \right )<\nu _0$ for some $\nu _0\in \mathbb {R}$. We assume that M satisfies the positive definiteness condition in Theorem 6.2.1; that is, we assume there exists c > 0 such that for all $z\in \mathbb {C}_{\operatorname {Re} \geqslant \nu _0}$ we have $\operatorname {Re} zM(z) \geqslant c$. For $\nu \geqslant \nu _0$ we want to solve

Let us reformulate this problem. Let $\phi \in C^{\infty }(\mathbb {R})$ such that $0\leqslant \phi \leqslant 1$ with ϕ = 1 on $\left [0,\infty \right )$ and ϕ = 0 on $\left (-\infty ,-1\right ]$. We define the function

and consider

(12.2)

instead.

Theorem 12.3.1

Let $\nu \geqslant \max \{\nu _0,0\},\nu \neq 0$ . Then (12.2) admits a unique solution .

Proof

We start with the existence part. By Theorem 12.2.5, we find such that $\gamma _{\mathrm {n}}\widetilde {G}=\widetilde {g}$; set . Consider the following evolutionary equation

Note that the right-hand side is in $H_{\nu }^{2}(\mathbb {R};L_2(\Omega )\times L_2(\Omega )^d)$. By Theorem 6.2.1, we obtain

Indeed, since the solution operator commutes with ∂ _t,ν and the right-hand side lies in $H_\nu ^2$, it even follows that $\begin {pmatrix} u\\ r \end {pmatrix} \in H_\nu ^2(\mathbb {R};L_2(\Omega )\times L_2(\Omega )^d)$. From the equality

it follows that

Hence,

where the resolvent is well-defined since is skew-selfadjoint. Also, we deduce that

Since , by Corollary 12.2.3 and Theorem 4.1.2 we obtain

$$\displaystyle \begin{aligned} \gamma_{\mathrm{n}}\left((r+G)(t)\right)=\gamma_{\mathrm{n}}G(t)=g(t) \quad (t\in \mathbb{R}). \end{aligned}$$

Hence, (u, r + G) solves (12.2).

Next we address the uniqueness result. For this we note that a straightforward computation shows

which coincides with the formula for (u, r + G). □

The upshot of the rationale exemplified in the proof is that inhomogeneous boundary value problems can be reduced to an evolutionary equation of the standard form with non-vanishing right-hand side. The treatment of inhomogeneous Dirichlet data works along similar lines.

12.4 Abstract Boundary Data Spaces

Of course inhomogeneous boundary value problems can be addressed for other domains Ω than the half-space $\mathbb {R}^{d-1}\times \mathbb {R}_{>{0}}$. Classically, some more specific properties need to be imposed on the description of the boundary ∂ Ω. In this section, however, we deviate from the classical perspective in as much as we like to consider arbitrary open sets $\Omega \subseteq \mathbb {R}^{d}$. For this we introduce

By Proposition 12.2.4 and Exercise 6.7, these spaces are closed subspaces of and H ¹( Ω), respectively, and therefore Hilbert spaces. Indeed,

and

$$\displaystyle \begin{aligned} \mathrm{BD}(\operatorname{\mathrm{grad}})=H^1_{0}(\Omega)^{\bot_{H^1(\Omega)}}. \end{aligned}$$

Now, we are in a position to solve inhomogeneous boundary value problems, where the trace mappings γ and γ _n are replaced by the canonical orthogonal projections $\pi _{\mathrm {BD}( \operatorname {\mathrm {grad}})}$ and respectively; see Exercise 12.4. We devote the rest of this section to describe the relationship between the classical trace spaces introduced before and the BD-spaces. In the perspective outlined here, there is not much of a difference between Neumann boundary values and Dirichlet boundary values. The next result is an incarnation of this.

Proposition 12.4.1

We have

Moreover, the mappings

and

are unitary, and .

Proof

Let $\phi \in \mathrm {BD}( \operatorname {\mathrm {grad}})$. Then and . This implies and which yields . Thus, $\operatorname {\mathrm {grad}}_{\mathrm {BD}}$ is defined everywhere; interchanging the roles of $\operatorname {\mathrm {grad}}$ and , we obtain is also defined everywhere. We infer and and thus $\operatorname {\mathrm {grad}}_{\mathrm {BD}}$ is bijective with . It remains to show that $\operatorname {\mathrm {grad}}_{\mathrm {BD}}$ preserves the norm. For this we compute

which implies that $\operatorname {\mathrm {grad}}_{\mathrm {BD}}$ is unitary. Hence, . □

It is also possible to show an ‘integration by parts’ formula analogous to (12.1) for the abstract situation:

Proposition 12.4.2

Let u ∈ H ¹( Ω) and . Then

Proof

We decompose u = u ₀ + u ₁ and q = q ₀ + q ₁ with $u_{0}\in H_{0}^{1}(\Omega )$, , $u_{1}=\pi _{\mathrm {BD}( \operatorname {\mathrm {grad}})}u$ and . Then we obtain

The remaining equality follows from by Proposition 12.4.1. □

In view of Proposition 12.4.2 the proper replacement of γ _n appears to be instead of just . Next, we show the equivalence of the trace spaces for the half-space and the abstract ones introduced in this section.

Theorem 12.4.3

Let . Then $\gamma |{ }_{\mathrm {BD}( \operatorname {\mathrm {grad}})}\colon \mathrm {BD}( \operatorname {\mathrm {grad}})\to H^{1/2}(\mathbb {R}^{d-1})$ and are unitary mappings.

Proof

We begin with γ _n. We have shown in Theorem 12.2.2 that is continuous and in Theorem 12.2.5 it has been shown that is continuous. Also the two norm inequalities have been established.

The injectivity of $\gamma |{ }_{\mathrm {BD}( \operatorname {\mathrm {grad}})}$ follows from $\operatorname {ker}\gamma =H_{0}^{1}(\Omega )$ by Corollary 12.2.3. All that remains simply relies upon recalling that $H^{1/2}(\mathbb {R}^{d-1})$ is isomorphic to $\left (\operatorname {ker}\gamma \right )^{\bot }$ with the orthogonal complement computed in H ¹( Ω). □

12.5 Robin Boundary Conditions

The classical Robin boundary conditions involve both traces, the Dirichlet trace γ and the Neumann trace γ _n. To motivate things, let us again have a look at the case $\Omega =\mathbb {R}^{d-1}\times \mathbb {R}_{>{0}}$. We consider the boundary condition for given and u ∈ H ¹( Ω)

$$\displaystyle \begin{aligned} \gamma_{\mathrm{n}}q+\mathrm{i}\gamma u=0, \end{aligned}$$

in the sense that

$$\displaystyle \begin{aligned} (\gamma_{\mathrm{n}}q)(v)= \left\langle -\mathrm{i} \gamma u ,v\right\rangle _{L_2(\mathbb{R}^{d-1})} \quad (v\in H^{1/2}(\mathbb{R}^{d-1})). \end{aligned}$$

Note that this is an implicit regularity statement as $\gamma _{\mathrm {n}}q\in H^{-1/2}(\mathbb {R}^{d-1})$ is representable as an $L_2(\mathbb {R}^{d-1})$ function. The next result asserts that an evolutionary equation with a spatial operator of the type with the above Robin boundary condition fits into the setting rendered by Theorem 6.2.1. In other words:

Theorem 12.5.1

Let $\Omega =\mathbb {R}^{d-1}\times \mathbb {R}_{>{0}}$ . Then the operator $A\colon \operatorname {dom}(A)\subseteq L_2(\Omega )^{d+1}\to L_2(\Omega )^{d+1}$ with with domain

is skew-selfadjoint.

Proof

Let . Then, by (12.1) we obtain

If, in addition, $(u,q)\in \operatorname {dom}(A)$, we obtain

Since for every $u\in \mathcal {D}$, we find $q\in \mathcal {D}^{d}$ such that $(u,q)\in \operatorname {dom}(A)$,

Thus, the set on the right-hand side is dense in $H^{1/2}(\mathbb {R}^{d-1})$. This in turn implies that $(v,r)\in \operatorname {dom}(A^{*})$ if and only if iγv + γ _n r = 0, and in this case we have A ^∗(v, r) = −A(v, r). This implies that A is skew-selfadjoint. □

Remark 12.5.2

The factor i in front of γu is chosen as a mere convenience in order to render the corresponding operator A in Theorem 12.5.1 skew-selfadjoint. It is also possible to choose β ∈ L(H ^1∕2(∂ Ω)) with $-\operatorname {Re}\beta \geqslant 0$ instead of i. Then one obtains for all $U\in \operatorname {dom}(A)$ and $V\in \operatorname {dom}(A^*)$ the estimates $\operatorname {Re}\left \langle U ,AU\right \rangle \geqslant 0$ and $\operatorname {Re}\left \langle V ,A^*V\right \rangle \geqslant 0$. Appealing to Remark 6.3.3, it can be shown that the corresponding evolutionary equation

$$\displaystyle \begin{aligned} (\partial_{t,\nu}M(\partial_{t,\nu})+A)U=F \end{aligned}$$

for a suitable material law M as in Theorem 6.2.1 is well-posed.

Next, one could argue that in the case of arbitrary Ω, the condition

(12.3)

amounts to a generalisation of the Robin boundary condition just considered. However, this is not true as the following proposition shows.

Proposition 12.5.3

Let u ∈ H ¹( Ω), and . Moreover, we set $\kappa \colon \mathrm {BD}( \operatorname {\mathrm {grad}})\to L_2(\mathbb {R}^{d-1})$ with κv = γv for $v\in \mathrm {BD}( \operatorname {\mathrm {grad}})$ . Then γ _n q + iγu = 0 if and only if

Proof

We first observe that $\kappa \pi _{\mathrm {BD}( \operatorname {\mathrm {grad}})} w=\gamma w$ for each w ∈ H ¹( Ω).Assume now that γ _n q + iγu = 0 and let $v\in \mathrm {BD}( \operatorname {\mathrm {grad}})$. Then we compute, using Proposition 12.4.2 and (12.1)

which proves one of the asserted implications.

Assume that and let $v\in H^{1/2}(\mathbb {R}^{d-1})$. We take w ∈ H ¹( Ω) with γw = v and compute

which shows the remaining implication. □

12.6 Comments

The concept of abstract trace spaces has been introduced in [86] in order to study a multi-dimensional analogue for port-Hamiltonian systems. Also concerning differential equations at the boundary (so-called impedance type boundary conditions), the concept of abstract boundary value spaces has been employed, see [91].

A comparison between abstract and classical trace spaces has been provided in [37, 115] particularly concerning $H^{-1/2}(\mathbb {R}^{d-1})$. A good introduction for trace mappings for more complicated geometries can be found e.g. in [5]. The trace operator can also be suitably established for $H( \operatorname {\mathrm {curl}},\Omega )$-regular vector fields given that Ω is a so-called Lipschitz domain, see [18].

Exercises

Exercise 12.1

Let $\phi \in C_{\mathrm {c}}^\infty (\mathbb {R}^{d})$, $f\in L_2(\mathbb {R}^{d})$. Show that

$$\displaystyle \begin{aligned} \phi\ast f\colon x\mapsto\int_{\mathbb{R}^{d}}\phi(x-y)f(y)\,\mathrm{d} y \end{aligned}$$

belongs to $H^{1}(\mathbb {R}^{d})$ and that $\operatorname {\mathrm {grad}}\left (\phi \ast f\right )=\left ( \operatorname {\mathrm {grad}}\phi \right )\ast f$. If, in addition, $f\in H^{1}(\mathbb {R}^{d})=\operatorname {dom}( \operatorname {\mathrm {grad}})$, then $\operatorname {\mathrm {grad}}(\phi \ast f)=\phi \ast \operatorname {\mathrm {grad}} f$, where the convolution is always taken component wise.

Exercise 12.2

Let $\Omega \subseteq \mathbb {R}^{d}$ be open. Let f ∈ L ₂( Ω) and denote by $\widetilde {f}\in L_2(\mathbb {R}^{d})$ the extension of f by zero. Let $v\in \mathbb {R}^{d}$, τ > 0 and define .

• (a) Show that f _τ → f in L ₂( Ω) as τ → 0.

• (b) Let now f ∈ H ¹( Ω) and Ω + τv ⊆ Ω for all τ > 0. Show that f _τ → f in H ¹( Ω) as τ → 0.

Exercise 12.3

Prove Theorem 12.2.1.

Exercise 12.4

Let $\Omega \subseteq \mathbb {R}^{d}$ be open, $M\colon \operatorname {dom}(M)\subseteq \mathbb {C}\to L\big (L_2(\Omega )\times L_2(\Omega )^d\big )$ with $\mathrm {s}_{\mathrm {b}}\left ( M \right )<\nu _0$ for some $\nu _0\in \mathbb {R}$, c > 0 such that for all $z\in \mathbb {C}_{\operatorname {Re} \geqslant \nu _0}$ we have $\operatorname {Re} zM(z) \geqslant c$, $\nu \geqslant \max \{\nu _0,0\}$ and ν ≠ 0. Show that there exists a unique

satisfying

for some bounded $\phi \in C^{\infty }(\mathbb {R})$ with $\inf \operatorname {\mathrm {spt}}\phi >-\infty$ and $f\in \mathrm {BD}( \operatorname {\mathrm {grad}})$.

Exercise 12.5

Let $\Omega =\mathbb {R}^{d-1}\times \mathbb {R}_{>{0}}$. Show that there exists a continuous linear operator $E\colon H^{1}(\Omega )\to H^{1}(\mathbb {R}^{d})$ such that E(ϕ)|_Ω = ϕ for each ϕ ∈ H ¹( Ω).

Exercise 12.6 (Korn’s Second Inequality)

Let $\Omega =\mathbb {R}^{d-1}\times \mathbb {R}_{>{0}}$. Using Exercise 12.5 show that there exists c > 0 such that for all ϕ ∈ H ¹( Ω)^d we have

$$\displaystyle \begin{aligned} \left\Vert \phi \right\Vert {}_{H^{1}(\Omega)^{d}}\leqslant c\left(\left\Vert \phi \right\Vert {}_{L_2(\Omega)^{d}}+\left\Vert \operatorname{\mathrm{Grad}}\phi \right\Vert {}_{L_2(\Omega)^{d\times d}}\right). \end{aligned}$$

Thus, describe the space of boundary values of $\operatorname {dom}( \operatorname {\mathrm {Grad}})$.

Hint: Prove a corresponding result for $\Omega =\mathbb {R}^{d}$ first after having shown that $C_{\mathrm {c}}^\infty (\mathbb {R}^{d})^{d}$ forms a dense subset of both H ¹( Ω)^d and $\operatorname {dom}( \operatorname {\mathrm {Grad}})$.

Exercise 12.7

Let $\Omega \subseteq \mathbb {R}^{3}$ be open. Compute and show that $\operatorname {\mathrm {curl}}\colon \mathrm {BD}( \operatorname {\mathrm {curl}})\to \mathrm {BD}( \operatorname {\mathrm {curl}})$ is well-defined, unitary and skew-selfadjoint.