Designing of an Anti Roll Bar to Adjust the Balance and Stability of a Formula Student Car

Abstract

This paper focuses on the designing procedure of an adjustable anti-roll bar (ARB) for a Formula Student Car. ARB is a component in suspension assembly which can provide a specific understeering effect to the vehicle depending on its roll stiffness. Different drivers prefer different understeering effects on the car depending on their driving style. For this project, Adjustability in ARB leads to 4 roll rate distribution and 3 roll gradients in the car hence overall 12 settings from one ARB assembly. The ARB has been designed using software like MATLAB and MS Excel to obtain the geometric dimensions and specific orientation of the ARB blade pertaining to different balance and stability. This paper also demonstrates the effect of ARB on suspension travel. The proposed method can help drivers to choose the vehicle dynamics according to their driving style in different tracks.

Appendices

Appendix 1: Weight Transfer Equations

• 1. Gyroscopic Load transfer

  Gyroscopic Moment = $2 \times \left( {lx~ \times ~wy~ \times ~wz} \right)/1.35~$

  Gyroscopic Load transfer = $\left( {2 \times \left( {l~x~ \times wy~ \times ~wz} \right)/1.35} \right)/Tf\,{=}\,\boldsymbol{6.88}\, {\textbf{pounds}}$

  

  where, $wy = \sqrt {\frac{{AyRc}}{R}\quad wz = \sqrt {\frac{{Ay}}{{Rc}}} }$

  R:

  Radius of wheel  =  0.228 m.

  Rc:

  Radius of track curvature  =  3 m.

  I_x:

  Area MOI of wheel  =  0.278 kg m².

  wy:

  Angular velocity of wheel about lateral y-axis  =  29.13 rad/s.

  wz:

  Yawing velocity of wheel about vertical z-axis  =  2.214 rad/s.

  Note: Gyroscopic Load transfer is positive for outer wheel and negative for inner wheel.

• 2. Load Transfer Due To Overturning Moment

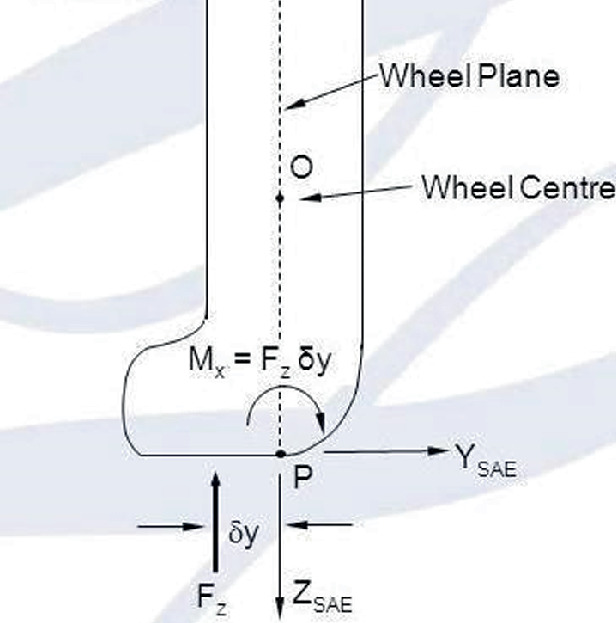
  The equivalency has been drawn overturning moment at wheel center patch and a force has been assumed at wheel center on its behalf, which is formulated as:$Ff = \frac{{Mxf}}{R}$

  $$ Fr = \frac{{Mxr}}{R} $$

  where,

  Mx:

   =  Overturning Moment.

  • The weight transfer due to F has been taken into similar fashion as for un-sprung mass.

Total Load Transfer = Sprung mass Load transfer + Unsprung Mass Load Transfer + Direct load transfer of Front and Rear + Gyroscopic Load transfer + Load transfer due to overturning moment.

W = Weight of Car	b = Distance of CG from rear axle
Wfu = Front Un-sprung mass	L = wheelbase
Ay = Cornering Acceleration	Hs = sprung cg height
Ws = total sprung weight	Tf = Front Track
WRU = Rear un-sprung Mass	Zub = Height of Rear un-sprung mass
r = Roll Rate Distribution	Wsb= Sprung mass rear
Tr= Rear Track	a = distance of CG from front axle
Wsa= Sprung Mass Front	Kϕ= Roll rate
Zrf = Height Of front roll centre	Zrr = Height of Rear roll centre
Zua = Height of front unsprung mass

$$ \begin{aligned} \therefore {\text{Load Transfer}} & = \frac{{Wfu~ \times ~Zua~ \times ~Ay}}{{Tf}}~ + ~\frac{{Wru~ \times ~Zub~ \times ~Ay}}{{Tr}} \\ ~ & \quad + ~\frac{{Wsa~ \times Zrf~ \times ~Ay}}{{Tf}}~ + ~\frac{{Wsb~ \times ~Zrr~ \times ~Ay}}{{Tr}} \\ & \quad + \user2{~}\frac{{\user2{Ws~} \times \user2{~Hs~} \times \user2{~Ay}}}{{\user2{Tf}}}\left[ {\frac{{\user2{K}\phi \user2{~r~} + \user2{~}\frac{\user2{b}}{\user2{l}}\user2{~WsHs}}}{{\user2{K}\phi \user2{~} - \user2{~WsHs}}}} \right] \\ & \quad + ~\frac{{Ws~ \times ~Hs~ \times ~Ay}}{{Tr}}\left[ {\frac{{K\phi \left( {1 - ~r} \right)~ + ~\frac{a}{l}WsHs}}{{K\phi ~ - ~WsHs}}} \right] \\ & \quad + ~\left( {2 \times \left( {l~x~ \times wy~ \times ~wz} \right)/1.35} \right)/Tf \\ & \quad + \left( {2 \times \left( {l~x~ \times wy~ \times ~wz} \right)/1.35} \right)/Tr~ + ~\frac{{Ff~ \times ~Zua}}{{Tf}} \\ & \quad + ~\frac{{Fr~ \times ~Zub}}{{Tf}} \\ \end{aligned} $$

Here,

$$ Hs~ = ~\frac{{W~ \times ~h~ - ~Zfu~~ \times ~Wtu}}{{Wts}} $$

For the start, spring of 26 N/mm was used for both front and rear respectively.

Where, Aero load on the car = 78.6 lbs = W_haero.

$$ \begin{aligned} {\text{W}}_{{{\text{fo}}}} & = {\text{W}}_{{{\text{fsts}}}} + {\text{W}}_{{\text{f}}} + {\text{W}}_{{{\text{haero}}}} /{\text{4 }}\quad \quad {\text{W}}_{{{\text{fi}}}} = {\text{W}}_{{{\text{fsts}}}} - {\text{W}}_{{\text{f}}} {\text{ + W}}_{{{\text{haero}}}} /{\text{4}} \\ {\text{W}}_{{{\text{ro}}}} & = {\text{W}}_{{{\text{rsts}}}} + {\text{W}}_{{\text{r}}} + {\text{W}}_{{{\text{haero}}}} /{\text{4}}\quad \quad {\text{W}}_{{{\text{ri}}}} = {\text{ W}}_{{{\text{rsts}}}} - {\text{ W}}_{{\text{r}}} + {\text{ W}}_{{{\text{haero}}}} /{\text{4}} \\ \end{aligned} $$

Appendix 2: MATLAB Code to Determine the Geometric Dimensions of ARB

%Input force at droop link from Table 38.5

Fwc = 96.542;

% Force at Wheel Centre, N

%Blade angle adjustment to get the desired deflection from ARB

a = pi/62.3;	% Angle in radian for left blade
b = pi/62.3;	% Angle in radian for right blade

%User defined parameters, they can be tweaked to get the desired deflection for a given input % force

%Calculating the deflection at ARB droop link due to right ARB blade

%Calculating the deflection at ARB droop link due to left ARB blade

%Calculating the deflection at ARB droop link due to twist of ARB tube

%Total deflection of ARB droop link due to individual deflection of 2 blades and 1 hollow tube

Twc = ( ( Travel(1) + Travel(2) + Travel(3))/MRarb)