Influence of the Inert Gas Flow on the Laser Powder Bed Fusion (LPBF) Process

Abstract

The inert gas flow is known to have a significant impact on the laser powder bed fusion (LPBF) process in terms of process stability and consistent process results across the whole build platform. Thus, the optimization of the inert gas flow leads to both direct and indirect improvements of the part quality as follows. If the gas flow can steadily and efficiently remove soot particles emerging from the melting process, scattering and attenuation of the laser beam or debris on the laser windows can be avoided, which would indirectly impair the quality of the built parts. Spatter particles should be removed as well because they can directly lead to bonding defects inside the produced parts. Therefore, the gas flow in a self-constructed LPBF machine has been optimized systematically based on computational fluid dynamics (CFD), particle tracking and experimental studies. Herein the effect of the process gas flow and gas type on spatter and soot particles is presented in detail. According to the simulation results, the soot removal is improved by a smaller shielding gas inlet height at the cost of a potential deterioration of the soot removal at extreme process parameters. The simulation results have been validated by measurements of the gas flow velocity and of the density of the built parts. The advantages and disadvantages of different process gas types are shown and recommendations for the gas flow design are derived.

1 Introduction and State of Research

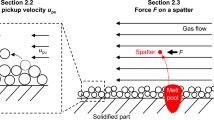
The LPBF process is based on an iterative procedure to manufacture parts in layers inside a powder bed. Once a layer of powder has been spread by the coater on a plane surface, one or several laser beams are guided by laser scanners over the areas which are to become molten and form a single layer of the additively manufactured parts after solidification. Within the immediate environment of its interaction with powder, molten metal and solidified metal, each laser beam creates a melt pool, which follows the scan path. Upon completion of each layer, the build plate is lowered, a new powder layer is spread and the next layer of the parts to be manufactured is molten. The final parts consist of a multitude of overlapping weld seams. In the build chamber, a shielding gas flow prevents the metal from oxidation. Moreover, the shielding gas flow shall carry away process by-products such as spatter or soot and it shall protect the laser windows from contamination with soot. If the shielding gas flow is not suitably designed to perform these tasks, the laser windows are contaminated with debris leading to an attenuation of the laser beam, defocusing of the laser beam or even damage to the laser windows. Furthermore, airborne particles inside the build chamber likewise attenuate the laser beam and provoke scattering or defocusing of the laser beam so that the LPBF process becomes instable. LPBF is used for applications in aerospace, energy, tool and mold making such as lightweight structures with topology optimization, turbine blades or forging tools. Nevertheless, according to the National Institute of Standards and Technology (NIST) [1], the Additive Manufacturing Special Interest Group [2] and Caltanisetta et al. [3], a broader application is limited by the relative instability and poor repeatability of the process and by the low productivity in current LPBF machines. Therefore, multi-laser systems have been developed and high power lasers are increasingly employed for enhanced productivity. However, more lasers and higher laser power lead to an increase in process by-products such as spatter and soot, which impaired the process stability already before. Consequently, it has become even more important to efficiently remove soot and spatter from the build chamber by an optimized shielding gas flow. Because of this reason, herein the interaction between the shielding gas flow and spatter or soot particles is investigated in order to optimize the shielding gas flow in terms of the gas type and the shielding gas flow design. Prior to these investigations, it was observed with the shielding gas flow settings of Table 3, that the density of the parts produced with both parameter sets of Table 1 was 0.5% points lower in the case of build setup 1 according to Fig. 2 in comparison to a build job where only seven cubes were built at once. This effect can be explained by the accumulation of soot particles inside the build chamber, when the ratio of scan time to recoating time is high. Therefore, the successful approaches shown in the following sections had to be found to improve the soot removal from the build chamber.

Table 1. Process parameters.

Several authors have already shown an influence of the shielding gas flow on spatter and soot particles by experimental studies and simulations. Anwar and Pham [4] observed an increased amount of spatter at the gas outlet when the shielding gas flow velocity was increased because then the gas flow was able to carry the spatter particles further and less particles fell into the powder bed. Furthermore, when the scanning direction was against the gas flow, more spatter particles could be seen at the gas outlet as the spatter particles are presumably ejected from the rear of the melt pool in the opposite direction of the scanning direction, i.e. towards the shielding gas outlet. In a further study, Anwar and Pham [5] could measure a higher ultimate tensile strength in the aforementioned cases with more spatter particles deposited close to the gas outlet. Moreover, they could detect a higher number of sparks and other particles interacting with the laser beam when scanning in the gas flow direction, leading to an attenuation of the laser beam and thus to bonding defects. Renishaw [6] showed that the airborne by-products of the LPBF process have a negative effect on a laser beam that is scanning in the gas plume of another laser, where it is attenuated so that the mechanical properties of the built parts are impaired.

There is also an influence of different gas types on the LPBF process. Pauzon et al. [7] could not detect a significant difference in the mechanical properties of parts built from 316L stainless steel when comparing argon with nitrogen as the shielding gas. But Pauzon et al. [8] could achieve an increase by 44% in the build rate of Ti-6Al-4 V when using a mixture of 50% argon and 50% helium. This mixture combines the beneficial properties of both gases. The high thermal conductivity and heat capacity of helium reduces the accumulation of process by-products, while the latter are removed more efficiently thanks to the high density of argon.

Anwar [9] developed a simulation model to investigate the influence of the shielding gas flow on the trajectories of the spatter particles, which showed a limited influence of the shielding gas flow on the spatter particles in accordance with the experimental data. However, the influence of different gas flow designs and gas types was not investigated. The behavior of smaller particles such as soot particles inside the build chamber was not considered either.

When the movement of process by-products inside the build chamber has to be investigated, the gas flow velocity in the process region, i.e. the velocity of the evaporated metal has to be known especially for the simulation of the trajectories of small particles. Bidare et al. [10] developed a 2D axisymmetric simulation model to investigate the gas flow velocity in the vicinity of the LPBF process. Accordingly, a laser beam with a spot size of 50 µm can induce a velocity up to 1200 m/s (300 m/s) at a laser power of 200 W (50 W). Similar 2D simulations of Mayi et al. [11] show results in the same order of magnitude. However, the indicated velocities seem rather high, which might be caused by the neglect of the feed motion of the laser beam as Jakumeit et al. [12] found a velocity of 100 m/s when processing IN718 in their advanced 3D simulation. Masmoudi et al. [13] even state a velocity as low as 40 m/s in an argon atmosphere with a pressure of 1.0 bar for 316L stainless steel.

2 Materials and Methods

A self-developed, modularly constructed, ready for various measurement equipment and vacuum suitable LPBF laboratory machine with a build plate size of 400 × 400 mm² was used for the experiments. A small build plate for reduced quantities can also be inserted. The machine can be equipped with up to two lasers. For the herein mentioned experiments, only one 1 kW continuous wave fiber laser type IPG YLR-1000-WC with a wavelength of 1070 nm was used. Nitrogen was employed as the shielding gas, which was kept at room temperature by a cooling system.

The produced samples were evaluated by Archimedean density measurements to see the influence of process by-products and thus the effect of the shielding gas flow, which is visualized in Fig. 1. The shielding gas flow consists of a purge gas flow from the ceiling and a horizontal flow from an inlet nozzle with a cross sectional area of 78 × 578 mm², which can be reduced. Due to geometrical constraints, the flow direction of the inlet nozzle is 6.8° inclined downwards. In the beginning, 40% of the total shielding gas flow was assigned to the purge gas flow based on the findings of Chen et al. [14]. A Testo Ø 16 mm vane probe anemometer was used for gas flow velocity measurements.

Fig. 1.

Shielding gas flow inside the LPBF machine.

Stainless steel 1.4404 powder from LPW with a particle size of 10-45 µm was processed using the process parameters listed in Table 1. For the experimentally investigated shielding gas flow settings, build jobs with the build setups shown in Fig. 2 were run, which cover the whole build plate. These build setups consisted of several cuboids with a size of 10 × 10 × 10 mm³ or 20 × 20 × 10 mm³ with the 200 W or 500 W parameters of Table 1, where the parameter set with high laser power produced a significant amount of fume. As it was already possible to achieve a high density of the produced parts in build setup 1 after the first modifications of the shielding gas setup, further experiments were carried out with the build setup 2, where a significantly higher amount of fume is generated, so that the shielding gas flow system is put under more strain.

Fig. 2.

Build setup 1 (left) and build setup 2 (right) for experimental investigations.

3 Modeling

The simulation model was set up in ANSYS Fluent using the k-ω shear stress transport (SST) turbulence model with the default values for the turbulence model parameters and assuming an incompressible fluid. Additionally, the temperature field and the concentration of gas contaminated with fume is calculated. The velocity field, the temperature field and the concentration field are calculated in the steady state. The discrete phase model (DPM) is applied to investigate the influence of the shielding gas flow on spatter and soot particles. The drag force is calculated according to the spherical drag law by Morsi and Alexander [15]. Only a 150 mm thick center slice of the volume inside the build chamber is considered in the developed simulation model to investigate the effect of the shielding gas flow on spatter and soot particles as shown in Fig. 3. Symmetry boundary conditions are applied at the front and backside of this slice. It is assumed that the plume is generated during the process on the build plate in a circle with a radius of 5 mm similar to an island and with its center at the indicated position of the plume velocity towards the front of the model. Due to its symmetry boundary condition, the model comprises only a half circle. The plume is emulated by hot gas streaming into the build chamber at this position. The plume velocity indicates the speed of the gas rising from the process zone. The aforementioned literature data for the velocity of an undisturbed gas plume vary in a broad range and it is not known, how the unsteady movement of the gas plume e.g. on an island influences its velocity in the upper spheres. Therefore, the plume velocity was set to $u_{pl} = 10\;{\text{m}}/{\text{s}}$ so that the behavior of the soot particles in the simulation corresponds to the observations at the initial machine configuration, where some smoke clouds bounced against the rear wall of the build chamber and were deflected upward. The gas is assumed to obey the ideal gas law

Fig. 3.

Simulation model geometry.

$$ p \cdot V = n \cdot R \cdot T $$

(1)

with the pressure $p$, volume $V$, number of moles $n$, gas constant $R = 8.31\;{\text{J}}/\left( {{\text{mol}} \cdot {\text{K}}} \right)$ and temperature $T$. While the shielding gas enters the process chamber at ambient temperature $T = T_{0} = 293\;{\text{K}}$, the plume gas is assumed to emerge with the evaporation temperature $T_{v} = 3130\;{\text{K}}$ of the powder material.

Two kinds of particles were considered in the investigations. The soot particles inside the fume are very small so that their behavior is dominated by surface forces such as the drag force due the high surface to volume ratio. On the contrary, spatter particles show a comparably low surface to volume ratio. Therefore, they mainly follow the inertial forces. In the simulation model, the particles are injected at the plume inlet in the upward direction with the ejection velocity $u_{e}$. The initial velocity of the soot particles is equal to the plume velocity, whereas the spatter particles with a size of 50–200 μm are injected with a velocity of 3 ± 1.5 m/s based on the experimental measurement data of Gunenthiram et al. [16]. Barrett et al. [17] indicate higher velocities up to 50 m/s, but these high velocities can be attributed to small particles entrained by the plume. The physical properties of the considered gases according to the ANSYS Fluent database are summarized in Table 2. Nitrogen is commonly used due to its comparably low price, the high thermal conductivity of helium can be beneficial to remove fumes from the process chamber and the high density of argon leads to a comparably high drag force exerted upon the spatter particles to blow them away.

Table 2. Physical properties of considered gases.

The default and initial settings of the simulation model are listed in Table 3. The shielding gas velocity $u_{s} = 0.93 \;{\text{m}}/{\text{s}}$ is equivalent to a shielding gas flow rate of 150 m³/h, while the purge gas velocity $u_{p} = 0.11 \;{\text{m}}/{\text{s}}$ results from a purge gas flow rate of 100 m³/h.

Table 3. Default and initial settings of the simulation model.

4 Results and Discussion

Initially, the influence of the purge gas flow rate was investigated by increasing it by 50% as shown in Fig. 4, where the gas flow velocity field and the soot particle tracks are depicted in the symmetry plane that goes through the plume inlet. The vortex at the rear wall is obviously suppressed when the purge gas flow rate is increased. The plume gas percentage is reduced from 0.40% to 0.34%, which describes the volume percentage of gas in the symmetry plane that has entered the chamber through the plume inlet.

Fig. 4.

Gas flow velocity and soot particle tracks at a purge gas velocity of 0.11 m/s (left) and 0.165 m/s (right).

The reduced accumulation of soot inside the process chamber is confirmed by the results of the Archimedean density measurements in Fig. 5, which shows the achieved density in the three experiments for the two process parameter sets, which can primarily be distinguished by the laser power. For both laser powers, the density is increased when the purge gas flow rate is raised by 50%, even though the corresponding build setup generates more soot. The increase in density can be traced back to less fume inside the build chamber, which scatters and attenuates the laser beam.

Fig. 5.

Influence of shielding gas flow setting on density of produced parts.

The aforementioned finding raises the question, if the purge gas flow rate can also be increased at the expense of a reduced horizontal shielding gas flow rate. Therefore, the purge gas flow rate was increased from 100 m³/h to 150 m³/h, while the shielding gas flow rate was reduced from 150 m³/h to 100 m³/h. Both simulations were carried out with the optimized inlet height of 39 mm. The results are depicted in Fig. 6 and show that the inverted ratio of shielding gas flow rate to purge gas flow rate leads to a higher amount of soot particles inside the process chamber. Thus, the plume gas percentage increases from 0.394% to 0.428%.

Fig. 6.

Gas flow velocity and soot particle tracks at a shielding and purge gas flow rate of 150 m³/h and 100 m³/h (left) or vice versa (right).

If the shielding gas flow rate is limited or fixed, a trade-off has to be found between the inlet height and the shielding gas flow velocity. An increased inlet height means a more homogeneous shielding gas flow velocity field across the build plate and a wider gas jet has a higher capability to carry away the soot particles. Furthermore, a high shielding gas flow velocity is also beneficial as it can transmit a higher momentum to the plume in the direction towards the outlet. According to the results presented in Fig. 7, more soot is removed from the process chamber, if the inlet height is decreased while the volume flow rate is kept constant, leading to an increased shielding gas flow velocity. However, at the inlet height of 25 mm the gas flow becomes more turbulent, which can be seen from some soot tracks that extend to the upper region of the process chamber. This means that there is an increased risk in temporary vortices occurring, which carry soot particles into the upper region of the process chamber or that the plume even passes partially through the thin gas jet. This can occur especially when processing special materials or when using extreme process parameters such as a small spot size combined with a high laser power and a low scan speed, which lead to significantly more evaporation and thus higher plume velocities as compared to the situation that was assumed in the simulations. Therefore, an inlet height of 39 mm was chosen as a conservative compromise, which was tested during the validation experiments. The shielding gas inlet height was reduced from 78 mm to 39 mm by an insert in the shielding gas nozzle. This also allows for the upkeep of a sufficiently high gas flow rate when other powder materials such as aluminum or comparably small powder particles are processed, which are carried away by the shielding gas at lower velocities compared to the herein considered stainless steel powder. According to Fig. 5, the halving of the inlet height leads to an increase of the part density by 0.4–0.5% points. This means that the same density is achieved as if only seven cubes are produced at once and there is no significant accumulation of soot particles inside the process chamber any more.

Fig. 7.

Gas flow velocity and soot tracks at different inlet heights with same volume flow rate.

The comparison between nitrogen and helium as shielding gas does not indicate a significant difference in Fig. 8. The plume gas percentage is also similar with 0.4011% in the case of nitrogen and 0.4009% for helium. The advantage of helium thanks to its high thermal conductivity, which leads to a faster cooling and therefore reduced buoyancy of the plume gas, is used up by the disadvantage of its low density and thus the low momentum that can be transferred to the plume gas. That is also the reason, why Pauzon et al. [8] employed gas mixtures that represent a compromise regarding the physical properties of the different gases.

Fig. 8.

Gas flow velocity and soot tracks with nitrogen (left) and helium (right) as shielding gas.

In Fig. 9 the spatter particle tracks are depicted for three different ejection velocities $u_{e}$. According to the simulation results, the spatter particles can hardly be removed and kept away from the powder bed, even if argon is the process gas, if the inlet height is 78 mm and the shielding gas flow velocity is 3.5 m/s. 3.5 m/s is the experimentally determined maximum velocity, above which the herein used powder is carried away from the powder bed. Only the smaller spatter particles with the lower ejection velocity $u_{e}$ are carried away by the shielding gas flow. It has to be admitted, that the ejection angle was not taken into account. If the spatter particles are already ejected from the melt pool towards the outlet, there is a higher chance that they do not land in the powder bed. Nevertheless, if the spatter particles are ejected towards the shielding gas inlet, it becomes almost impossible to prevent them from landing in the powder bed. Therefore, the vertical ejection at least does not make the problem worse than it really is and it is sufficient to investigate the principal mechanisms of spatter removal from the powder bed area. However, the simulation model represents a worst case scenario as the spatter particles are ejected close to the shielding gas inlet and have to fly over the whole powder bed. It is so that in practice the particles ending in the powder bed are reduced, but still considerable in volume.

Fig. 9.

Tracks of spatter particles with an ejection velocity $u_{e}$ of 1.5, 3.0 and 4.5 m/s in an argon atmosphere.

In order to validate the simulation results further, the gas flow velocity of nitrogen 10 mm above the build plate was measured at 9 points evenly distributed across the whole build plate at a shielding gas flow rate of 150 m³/h and with an inlet height of 78 mm. Accordingly, the difference between measurement and simulation data is in the range of ±10%.

5 Conclusion

A simulation model has been developed in order to investigate the influence of the shielding gas flow in a LPBF machine on soot and spatter particles. It can be concluded from the simulation results that a trade-off has to be found for the shielding gas inlet height at a given maximum shielding gas flow rate. In general, a larger inlet height leads to a more homogeneous velocity field across the powder bed. Soot is however more efficiently removed with a smaller inlet height, which leads to higher shielding gas flow velocities. But at the same time, the shielding gas flow becomes more turbulent and there is an increasing risk, that the plume passes through the gas jet. Furthermore, it has to be taken into account, that powder is carried away from the powder bed if the shielding gas velocity exceeds the limit, which is determined by the size and weight of the powder particles as well as by the density and viscosity of the gas.

The simulations did not reveal any advantages in the use of pure helium shielding gas with regard to its ability in removing soot particles from the process chamber.

According to the simulation results, the shielding gas flow has only a limited capability to carry away spatter particles; especially the critically large ones usually end up in the powder bed.