ASTEROID and the Replica-Aware Co-scheduling for Mixed-Criticality

Abstract

The ASTEROID project developed a cross-layer fault-tolerance solution to provide reliable software execution on unreliable hardware under soft errors. The approach is based on replicated software execution with hardware support for error detection that exploits future many-core platforms to increase reliability without resorting to redundancy in hardware. This chapter gives an overview of ASTEROID and then focuses on the performance of replicated execution and the proposed replica-aware co-scheduling for mixed-criticality. The performance of systems with replicated execution strongly depends on the scheduling. Standard schedulers, such as Partitioned Strict Priority Preemptive (SPP) and Time-Division Multiplexing (TDM)-based ones, although widely employed, provide poor performance in face of replicated execution. By exploiting co-scheduling, the replica-aware co-scheduling is able to achieve superior performance.

1 The ASTEROID Project

1.1 Motivation

Technology downscaling has increased the hardware’s overall susceptibility to errors to the point where they became non-negligible [17, 21, 22]. Hence, current and future computing systems must be appropriately designed to cope with errors in order to provide a reliable service and correct functionality [17, 21]. That is a challenge, especially in the real-time mixed-criticality domain where applications with different requirements and criticalities co-exist in the system, which must provide sufficient independence and prevent error propagation (e.g., timing, data corruption) between criticalities [24, 42]. Recent examples are increasingly complex applications such as flight management systems (FMS), advanced driver assistance systems (ADAS), and autonomous driving (AD) in the avionics and automotive domains, respectively [24, 42]. A major threat to the reliability of such systems is the so-called soft errors.

Soft errors, more specifically Single Event Effects (SEEs), are transient faults abstracted as bit-flips in hardware and can be caused by alpha particles, energetic neutrons from cosmic radiation, and process variability [15, 22]. Soft errors are comprehensively discussed in chapter “Reliable CPS Design for Unreliable Hardware Platforms”. Depending on where and when they occur, their impact on software execution range from masked (no observable effect) to a complete system crash [3, 12, 13]. Soft errors are typically more frequent than hard errors (permanent faults) and often remain undetected, also known as latent error or silent data corruption, because they cannot be detected by testing. Moreover, undetected errors are a frequent source of later system crashes [12]. To handle soft errors, the approaches can vary from completely software-based to completely hardware-based. The former are able to cover only part of the errors [12, 13] and the latter result in costly redundant hardware [22], as seen in lock-step dual-core execution [29]. Cross-layer solutions can be more effective and efficient by distributing the tasks of detecting errors, handling them and recovering from them in different layers of software and hardware [12, 13, 22].

1.2 Overview

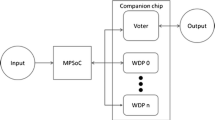
The ASTEROID project [5] developed a cross-layer fault-tolerance solution to provide reliable software execution on unreliable hardware. The approach is based on replicated software execution and exploits the large number of cores available in modern and future architectures at a higher level of abstraction without resorting to hardware redundancy [5, 12]. That concentrates ASTEROID’s contributions around the architecture and operating system (OS) abstraction layers, as illustrated in Fig. 1. ASTEROID’s architecture is illustrated in Fig. 2. The reliable software execution is realized by the OS service Romain [12]. Mixed-critical applications may co-exist in the system and are translated into protected and unprotected applications. Romain replicates the protected applications, which are mapped to arbitrary cores, and manages their execution. Error detection is realized by a set of mechanisms whose main feature is the hardware assisted state comparison, which compares the replicas’ state at certain points in time [5, 12]. Error recovery strategies can vary depending on whether the application is running in dual modular redundancy (DMR) or triple modular redundancy (TMR) [3, 5].

Fig. 1

Main abstraction layers of embedded systems and this chapter’s major (green, solid) and minor (yellow, dashed) cross-layer contributions

Fig. 2

ASTEROID’s architecture

ASTEROID comprised topics ranging from system-level conceptual modeling, to the OS and all the way down to Application-Specific Integrated Circuit (ASIC) synthesis and gate-level simulation. We summarize selected work that were developed in the project next. An initial overview of the ASTEROID approach was introduced in [5]. Romain, the OS service that provides replicated execution for unmodified binary applications, was introduced in [12]. The vulnerabilities of the system were assessed in [9, 13], giving rise to the reliable computing base (RCB), the minimum set of software and hardware components on which the approach relies. The runtime overheads related with the OS-assisted replication were investigated in [10]. Later, RomainMT extends Romain in [11] to support unmodified multithreaded applications. A systematic design process was investigated in [28], followed by the definition of a trusted component ecosystem in [19].

In terms of modeling, the reliability of replicated execution was modeled and evaluated in [3]. The approach was modeled in Compositional Performance Analysis (CPA), a worst-case performance analysis framework, as fork-join tasks and the performance evaluated in [6] and revised in [2]. Later, co-scheduling was employed to improve the worst-case performance of replicated execution with the replica-aware co-scheduling for mixed-criticality [34]. Off-chip real-time communication under soft errors was modeled in [4] with a probabilistic response-time analysis. On-chip real-time communication with and without soft errors were modeled in CPA and evaluated in [33] and [38], where Automatic Repeat reQuest (ARQ)-based protocols were employed in a real-time Network-on-Chip (NoC). As part of the RCB, the NoC’s behavior under soft errors was further researched with thorough Failure Mode and Effects Analyses (FMEAs) in [35,36,37]. Based on those findings, a resilient NoC architecture was proposed in [32, 39, 40], which is able to provide a reliable and predictable service under soft errors.

The remainder of this chapter focuses on the performance of replicated execution under real-time constraints, first published in [34]. It is organized as follows. Section 2 introduces the replica-aware co-scheduling for mixed-criticality and its related work. Section 3 describes the system, task, and error models. Section 4 introduces the formal response-time analysis. Experimental results are reported in Sect. 5. Finally, Sect. 6 ends the chapter with the conclusions.

2 Replica-Aware Co-scheduling for Mixed-Criticality

2.1 Motivation

Replicated software execution is a flexible and powerful mechanism to increase the reliability of the software execution on unreliable hardware. However, the scheduler has a direct influence on its performance. The performance of replicated execution for real-time applications has been formally analyzed in [6] and revised in [2]. The work considers the well-known Partitioned Strict Priority Preemptive (SPP) scheduling, where tasks are mapped to arbitrary cores, and assumes a single error model. The authors found that SPP, although widely employed in real-time systems, provides very pessimistic response-time bounds for replicated tasks. Depending on the interfering workload, replicated tasks executing serially (on the same core) present much better performance than when executing in parallel (on distinct cores). That occurs due to the long time that replicated tasks potentially have to wait on each core to synchronize and compare states before resuming execution. That leads to very low resource utilization and prevents the use of replicated execution in practice.

The replica-aware co-scheduling for mixed-criticality explores co-scheduling to provide short response times for replicated tasks without hindering the remaining unprotected tasks. Co-scheduling is a technique that schedules interacting tasks/threads to execute simultaneously on different cores [30]. It allows tasks/threads to communicate more efficiently by reducing the time they are blocked during synchronization. In contrast to SPP [2, 6], the proposed replica-aware co-scheduling approach drastically minimizes delays due to the implicit synchronization found in state comparisons. In contrast to gang scheduling [14], it rules out starvation and distributes the execution of replicas in time to achieve short response times of unprotected tasks. The proposed approach differs from standard Time-Division Multiplexing (TDM) and TDM with background partition [25] in that all tasks have formal guarantees. In contrast to related work, it supports different recovery strategies and accounts for the NoC communication delay and overheads due to replica management and state comparison. Experimental results with benchmark applications show an improvement on taskset schedulability of up to 6.9× when compared to SPP, and 1.5× when compared to a TDM-based scheduler.

2.2 Related Work

L4/Romain [12] is a cross-layer fault-tolerance approach that provides reliable software execution under soft errors. Romain provides protection at the application-level by replicating and managing the applications’ executions as an operating system service. The error detection is realized by a set of mechanisms [5, 12, 13] whose main feature is the hardware assisted state comparison, which allows an effective and efficient comparison of the replicas’ states. Pipeline fingerprinting [5] provides a checksum of the retired instructions and the pipeline’s data path in every processor, detecting errors in the execution flow and data. The state comparison, reduced to comparing checksums instead of data structures, is carried out at certain points in time. It must occur at least when the application is about to externalize its state, e.g., in a syscall [12]. The replica generated syscalls are intercepted by Romain, have their integrity checked, and their replicas’ states compared before being allowed to externalize the state [12].

Mixed-criticality, in the context of the approach, is supported with different levels of protection for applications with different criticalities and requirements (unprotected, protected with DMR¹ or TMR) and by ensuring that timing constraints are met even in case of errors. For instance, Romain provides different error recovery strategies [3, 5]:

• DMR with checkpoint and rollback: to recover, the replicas rollback to their last valid state and re-execute;

• TMR with state copy: to recover, the state of the faulty replica is replaced with the state of one of the healthy replicas.

This chapter focuses on the system-level timing aspect of errors affecting the applications. We assume thereby the absence of failures in critical components [13, 32], such as the OS/hypervisor, the replica manager/voter (e.g., Romain), and interconnect (e.g., NoC), which can be protected as in [23, 39].

The Worst-Case Response Time (WCRT) of replicated execution has been analyzed in [6], where replicas are modeled as fork-join tasks in a system implementing Partitioned SPP. The work was later revised in [2] due to optimism in the original approach. The revised approach is used in this work. In that approach, with deadline monotonic priority assignment, where the priority of tasks decreases as their deadlines increase, replicated tasks perform worse when mapped in parallel than when mapped to the same core. This is due to the state comparisons during execution, which involves implicit synchronization between cores. With partitioned scheduling, in the worst-case, the synchronization ends up accumulating the interference from all cores to which the replicated task is mapped, resulting in poor performance at higher loads. On the other hand, mapping replicated tasks to the highest priorities results in long response times for lower priority tasks and rules out deadline monotonicity. The latter causes the unschedulability of all tasksets with at least one regular task whose deadline is shorter than the execution time of a replicated task.

Gang scheduling [14] is a co-scheduling variant that schedules groups of interacting tasks/threads simultaneously. It increases performance by reducing the inter-thread communication latency. The authors in [26] present an integration between gang scheduling and Global Earliest Deadline First (EDF), called the Gang EDF. They provide a schedulability analysis derived from the Global EDF’s based on the sporadic task model. In another work, [16] shows that SPP Gang schedulers in general are not predictable, for instance, due to priority inversions and slack utilization. In the context of real-time systems, gang scheduling has not received much attention.

TDM-based scheduling [25] is widely employed to achieve predictability and ensure temporal-isolation. Tasks are allocated to partitions, which are scheduled to execute in time slots. Partitions can span across several (or all) cores and can be executed at the same time. The downside of TDM is that it is not work-conserving and underutilizes system resources. A TDM variant with background partition [25] tackles this issue by allowing low priority tasks to execute in other partitions whenever no higher priority workload is executing. Yet, in addition to the high cost to switch between partitions, no guarantees can be given to tasks in the background partition.

In the proposed approach, we exploit co-scheduling with SPP to improve the performance of the system. The proposed approach differs from [6] in that replicas are treated as gangs and are mapped with highest priorities, and are hence activated simultaneously on different cores. In contrast to gang scheduling [14, 16] and to [6], the execution of replicas is distributed in time with offsets to compensate for the lack of deadline monotonicity, thus allowing the schedulability of tasks with short deadlines. We further provide for the worst-case performance of lower priority tasks by allowing them to execute whenever no higher priority workload is executing. However, in contrast to [25], all tasks have WCRT guarantees. Moreover, we also model the state comparison and the on-chip communication overheads.

3 System, Task, and Error Models

In this work, we use the CPA [20] to provide formal response-time bounds. Let us introduce the system, task, and error models.

3.1 System Model

The system consists of a standard NoC-based many-core composed of processing elements, simply referred to as cores.

There are two types of tasks in our system, as in [2]:

• independent tasks τ _i: regular, unprotected tasks; and

• fork-join tasks Γ_i: replicated, protected tasks.

The system implements partitioned scheduling, where the operating system manages tasks statically mapped to cores. The mapping is assumed to be given as input. The scheduling policy is a combination of SPP and gang scheduling. When executing only independent tasks, the system’s behavior is identical to Partitioned SPP, where tasks are scheduled independently on each core according to SPP. It differs from SPP when scheduling fork-join tasks.

Fork-join tasks are mapped with highest priorities, hence do not suffer interference from independent tasks, and execute simultaneously on different cores, as in gang scheduling. Note that deadline monotonicity is, therefore, only partially possible. To limit the interference to independent tasks, the execution of a fork-join task is divided in smaller intervals called stages, whose executions are distributed in time. At the end of each stage, the states of the replicas are compared. In case of an error, i.e. states differ, recovery is triggered.

Fork-join stages are executed with static offsets [31] in execution slots. One stage is executed per slot. On a core with n fork-join tasks, there are n + 1 execution slots: one slot for each fork-join task Γ_i and one slot for recovery. The slots are cyclically scheduled in a cycle Φ. The slot for Γ_i starts at offset ϕ( Γ_i) relative to the start of Φ and ends after φ( Γ_i), the slot length. The recovery slot is shared by all fork-join tasks on that core and is where error recovery may take place under a single error assumption (details in Sects. 3.3 and 4.3). The recovery slot has an offset ϕ(recovery) relative to Φ and length φ(recovery). Lower priority independent tasks are allowed to execute whenever no higher priority workload is executing.

An example is shown in Fig. 3, where two fork-join tasks Γ₁ and Γ₂ and two independent tasks τ ₃ and τ ₄ are mapped to two cores. Γ₁ and Γ₂ execute in their respective slots simultaneously in both cores. When an error occurs, the recovery of Γ₂ is scheduled and the recovery of the error-affected stage occurs in the recovery slot. The use of offsets enables the schedulability of independent tasks with short periods and deadlines, such as τ ₃ and τ ₄. Note that, without the offsets, Γ₁ and Γ₂ would execute back-to-back leading to the unschedulability of τ ₃ and τ ₄.

Fig. 3

Execution example with two fork-join and two independent tasks on two cores [34]

3.2 Task Model

An independent task τ _i is mapped to core σ with a priority p. Once activated, it executes for at most C _i, its worst-case execution time (WCET). The activations of a task are modeled with arbitrary event models. Task activations in an event model are given by arrival curves η ⁻( Δt) and η ⁺( Δt), which return the minimum and maximum number of events arriving in any time interval Δt. Their pseudo-inverse counterparts δ ⁺(q) and δ ⁻(q) return the maximum and minimum time interval between the first and last events in any sequence of q event arrivals. Conversion is provided in [41]. Periodic events with jitter, sporadic events, and others can be modeled with the minimum distance function $\delta ^{-}_{i}(q)$ as follows [41]:

$$\displaystyle \begin{aligned} \delta^{-}_{i}(q) = \max ( (q-1) \cdot d^{min}, (q-1) \cdot \mathcal{P} - \mathcal{J} ) \end{aligned} $$

(1)

where $\mathcal {P}$ is the period, $\mathcal {J}$ is the jitter, d ^min is the minimum distance between any two events, and the subscript i indicates the association with a task τ _i or Γ_i.

Fork-join tasks are rigid parallel tasks, i.e. the number of processors required by a fork-join task is fixed and specified externally to the scheduler [16], and consist of multiple stages with data dependencies, as in [1, 2]. A fork-join task Γ_i is a Directed Acyclic Graph (DAG) G(V, E), where vertices in V  are subtasks and edges in E are precedence dependencies [2]. In the graph, tasks are partitioned in segments and stages, as illustrated in Fig. 5a. A subtask $\tau ^{\sigma ,s}_{i}$ is the s-th stage of the σ-th segment and is annotated with its WCET $C^{\sigma ,s}_{i}$. The WCET of a stage is equal across all segments, i.e. $\forall x,y \!: C_{i}^{x,s} \! \! = \! C_{i}^{y,s}$. Each segment σ of Γ_i is mapped to a distinct core. A fork-join task Γ_i is annotated with the static offset ϕ( Γ_i), which marks the start of its execution slot in Φ. The offset also admits a small positive jitter j _ϕ, to account for a slight desynchronization between cores and context switch overhead.

The activations of a fork-join task are modeled with event models. Once Γ_i is activated, its stages are successively activated by the completion of all segments of the previous stage, as in [1, 2]. Our approach differs from them in that it restricts the scheduling of at most one stage of Γ_i in a cycle Φ, and the stage receives service at the offset ϕ( Γ_i). Note that the event arrival at a fork-join task is not synchronized with its offset. The events at a fork-join task are queued at the first stage and only one event at a time is processed (FIFO) [2]. A queued event is admitted when the previous event leaves the last stage.

The interaction with Romain (the voter) is modeled in the analysis as part of the WCET $C^{\sigma ,s}_{i}$, as depicted in Fig. 4a. The WCET includes the on-chip communication latency and state comparison overheads, as the Romain instance may be mapped to an arbitrary core. Those can be obtained, e.g., with [38] along with task mapping and scheduler properties to avoid over-conservative interference estimation and obtain tighter bounds.

Fig. 4

The composition of WCET of fork-join subtasks [34]. (a) WCET of a fork-join subtask. (b) WCET of recovery

3.3 Error Model

Our model assumes a single error scenario caused by SEEs. We assume that all errors affecting fork-join tasks can be detected and contained, ensuring integrity. The overhead of error detection mechanisms is modeled as part of the WCET (cf. Fig. 4a). Regarding independent tasks, we assume that an error immediately leads to a task failure and assume also that its failure will not violate the WCRT guarantees of the remaining tasks. Those assumptions are met, e.g., by Romain.² Moreover, we assume the absence of failures in critical components [13, 32], such as the OS, the replica manager/voter Romain, and the interconnect (e.g., the NoC), which can be protected as in [23, 39].

Our model provides recovery ^Fn2 for fork-join tasks, ensuring their availability. With a recovery slot in every cycle Φ, our approach is able to handle up to one error per cycle Φ. However, the analysis in Sect. 4.3 assumes at most one error per busy window for the sake of a simpler analysis (the concept will be introduced in Sect. 4). The assumption is reasonable since the probability of a multiple error scenario is very low and can be considered as an acceptable risk [24]. A multiple error scenario occurs only if an error affects more than one replica at a time or if more than one error occurs within the same busy window.

3.4 Offsets

The execution of fork-join tasks in our approach is based on static offsets, which are assumed to be provided as input to the scheduler. The offsets form execution slots whose size do not vary during runtime, as seen in Fig. 3. Varying the slots sizes would substantially increase the timing analysis complexity without a justifiable performance gain. The offsets must satisfy two constraints:

Constraint 1

A slot for a fork-join task Γ _i must be large enough to fit the largest stage of Γ _i . That is, $\forall s, \sigma \! \!: \varphi (\Gamma _{i}) \geq C^{\sigma ,s}_{i} + j_{\phi }$.

Constraint 2

The recovery slot must be large enough to fit the recovery of the largest stage of any fork-join task mapped to that core. That is, $\forall i,s,\sigma \!\!: \varphi (recovery) \! \geq \! C_{i,rec}^{\sigma ,s} + j_{\phi }$.

where a one error scenario per cycle is assumed and $C_{i,rec}^{\sigma ,s}$ is the recovery WCET of subtask $\tau _{i}^{\sigma ,s}$ (cf. Sect. 4.3).

We provide basic offsets that satisfy Constraints 1 and 2. The calculation must consider only overlapping fork-join tasks, i.e. fork-join tasks mapped to at least one core in common. Offsets for non-overlapping fork-join tasks are computed separately as they do not interfere directly with each other. The indirect interference, e.g., in the NoC, is accounted for in the WCETs. First we determine the smallest slots that satisfy Constraint 1:

$$\displaystyle \begin{aligned} \forall \, \Gamma_{i}: \varphi(\Gamma_{i}) = \max_{\forall \sigma,s} \left\{ C^{\sigma,s}_{i} \right\} + j_{\phi} \end{aligned} $$

(2)

and the smallest recovery slot that satisfies Constraint 2:

$$\displaystyle \begin{aligned} \varphi(recovery) = \max_{\forall \Gamma_{i}, \tau_{j}^{\sigma,s} \in \Gamma_{i}} \left\{ C^{\sigma,s}_{i,rec} \right\} + j_{\phi} \end{aligned} $$

(3)

The cycle Φ is then the sum of all slots:

$$\displaystyle \begin{aligned} \Phi = \sum_{\forall \Gamma_{i}} \left\{ \varphi(\Gamma_{i}) \right\} + \varphi(recovery) \end{aligned} $$

(4)

The offsets then depend on the order in which the slots are placed inside Φ. Assuming that the slots ϕ( Γ_i) are sorted in ascending order on i and that the recovery slot is the last one, the offsets are obtained by

$$\displaystyle \begin{aligned} \phi(x) = \begin{cases} 0 & \quad \text{if } x = \Gamma_{1} \\ \phi(\Gamma_{i-1}) + \varphi(\Gamma_{i-1}) & \quad \text{if } x = \Gamma_{i} \text{ and } i > 1 \\ \Phi - \varphi(recovery) & \quad \text{if } x = recovery \\ \end{cases} \end{aligned} $$

(5)

4 Response-Time Analysis

The analysis is based on CPA and inspired by Axer [2] and Palencia and Harbour [31]. In CPA, the WCRT is calculated with the busy window approach [43]. The response time of an event of a task τ _i (resp. Γ_i) is the time interval between the event arrival and the completion of its execution. In the busy window approach [43], the event with the WCRT can be found inside the busy window. The busy window w _i of a task τ _i (resp. Γ_i) is the time interval where all response times of the task depend on the execution of at least one previous event in the same busy window, except for the task’s first event. The busy window starts at a critical instant corresponding to the worst-case scheduling scenario. Since the worst-case scheduling scenario depends on the type of task, it will be derived individually in the sequel.

Before we derive the analysis for fork-join and for independent tasks, let us introduce the example in Fig. 5 used throughout the section. The taskset consists of four independent tasks and two fork-join tasks, mapped to two cores. The task priority on each core decreases from top to bottom (e.g., $\tau _{1}^{1,1}$ has the highest priority and τ ₄ the lowest).

Fig. 5

A taskset with 4 independent tasks and 2 fork-join tasks, and its mapping to 2 cores. Highest priority at the top, lowest at the bottom [34]. (a) Taskset. (b) Mapping

4.1 Fork-Join Tasks

We now derive the WCRT for an arbitrary fork-join task Γ_i. To do that, we need to identify the critical instant leading to the worst-case scheduling scenario. In case of SPP, the critical instant is when all tasks are activated at the same time and the tasks’ subsequent events arrive as early as possible [43]. In our case, the critical instant must also account for the use of static offsets [31].

The worst-case scheduling scenario for Γ₂ on core 1 is illustrated in Fig. 6. Γ₂ is activated and executed at the same time on cores 1 and 2 (omitted). Note that, by design, fork-join tasks do not dynamically interfere with each other. The critical instant occurs when the first event of Γ₂ arrives just after missing Γ₂’s offset. The event has to wait until the next cycle to be served, which takes time Φ + j _ϕ when the activation with offset is delayed by a jitter j _ϕ. Notice that the WCETs of fork-join tasks already account for the inter-core communication and synchronization overhead (cf. Fig. 4a).

Fig. 6

Worst-case schedule for fork-join gang Γ₂ on core 1 (cf. Fig. 5) [34]

Lemma 1

The critical instant leading to the worst-case scheduling scenario of a fork-join task Γ _i is when the first event of Γ _i arrives just after missing Γ _i ’s offset ϕ( Γ _i).

Proof

A fork-join task Γ_i does not suffer interference from independent tasks or other fork-join tasks. The former holds since independent tasks always have lower priority. The latter holds due to three reasons: an arbitrary fork-join task Γ_j always receives service in its slot ϕ( Γ_j); the slot ϕ( Γ_j) is large enough to fit Γ_j’s largest subtask (Constraint 1); and the slots in a cycle Φ are disjoint. Thus, the critical instant can only be influenced by Γ_i itself.

We prove by contradiction. Suppose that there is another scenario worse than Lemma 1. That means that the first event can arrive at a time that causes a delay to Γ_i larger than Φ + j _ϕ. However, if the delay is larger than Φ + j _ϕ, then the event arrived before a previous slot ϕ( Γ_i) and Γ_i did not receive service. Since that can only happen if there is a pending activation of Γ_i and thus violates the definition of a busy window, the hypothesis must be rejected. □

Let us now derive the Multiple-Event Queueing Delay Q _i(q) and Multiple-Event Busy Time B _i(q) on which the busy window relies. Q _i(q) is the longest time interval between the arrival of Γ_i’s first activation and the first time its q-th activation receives service, considering that all events belong to the same busy window [2, 27]. For Γ_i, the q-th activation can receive service at the next cycle Φ after the execution of $q\!-\!1$ activations of Γ_i lasting s _i ⋅ Φ each, a delay Φ (cf. (cf. Lemma 1), and a jitter j _ϕ. This is given by

$$\displaystyle \begin{aligned} Q_{i}(q) = (q-1) \cdot s_{i} \cdot \Phi + \Phi + j_{\phi} \end{aligned} $$

(6)

where s _i is the number of stages of Γ_i and Φ is the cycle.

Lemma 2

The Multiple-Event Queueing Delay Q _i(q) given by Eq. 6 is an upper bound.

Proof

The proof is by induction. When $q\!=\!1$, Γ_i has to wait for service at most until the next cycle Φ plus an offset jitter j _ϕ to get service for its first stage, considering that the event arrives just after its offset (Lemma 1). In a subsequent q + 1-th activation in the same busy window, Eq. 6 must also consider q entire executions of Γ_i. Since Γ_i has s _i stages and only one stage can be activated and executed per cycle Φ, it takes additional s _i ⋅ Φ for each activation of Γ_i, resulting in Eq. 6. □

The Multiple-Event Busy Time B _i(q) is the longest time interval between the arrival of Γ_i’s first activation and the completion of its q-th activation, considering that all events belong to the same busy window [2, 27]. The q-th activation of Γ_i completes after a delay Φ (cf. Lemma 1), a jitter j _ϕ, and the execution of q activations of Γ_i. This is given by

$$\displaystyle \begin{aligned} B_{i}(q) = q \cdot s_{i} \cdot \Phi + j_{\phi} + C_{i}^{\sigma,s} \end{aligned} $$

(7)

where $C_{i}^{\sigma ,s}$ is the WCET of Γ_i’s last stage.

Lemma 3

The Multiple-Event Busy Time B _i(q) given by Eq. 7 is an upper bound.

Proof

The proof is by induction. When $q\!=\!1$, Γ_i has to wait for service at most until the next cycle Φ plus an offset jitter j _ϕ to get service for its first stage (Lemma 1), plus the completion of the last stage of the activation lasting $(s_{i}\!-\!1) \cdot \Phi + C_{i}^{\sigma ,s}$. This is given by

$$\displaystyle \begin{aligned} B_{i}(1) &= (s_{i} - 1) \cdot \Phi + \Phi + j_{\phi} + C_{i}^{\sigma,s} \\ &= s_{i} \cdot \Phi + j_{\phi} + C_{i}^{\sigma,s} \end{aligned} $$

(8)

In a subsequent q + 1-th activation in the same busy window, Eq. 7 must consider q additional executions of Γ_i. Since Γ_i has s _i stages and only one stage can be activated and executed per cycle Φ, it takes additional s _i ⋅ Φ for each activation of Γ_i. Thus, Eq. 7. □

Now we can calculate the busy window and WCRT of Γ_i. The busy window w _i of a fork-join task Γ_i is given by

$$\displaystyle \begin{aligned} w_{i} = \max_{q \geq 1, \, q \in \mathbb{N}}\{ B_{i}(q) \, | \, Q_{i}(q+1) \geq \delta^{-}_{i}(q+1) \} \end{aligned} $$

(9)

Lemma 4

The busy window is upper bounded by Eq. 9.

Proof

The proof is by contradiction. Suppose there is a busy window w̆_i longer than w _i. In that case, w̆_i must contain at least one activation more than w _i, i.e. q̆ ≥ q + 1. From Eq. 9, we have that $Q_{i}(\breve {q}) < \delta ^{-}_{i}(\breve {q})$, i.e. q̆ is not delayed by the previous activation. Since that violates the definition of a busy window, the hypothesis must be rejected. □

The response time R _i(q) of the q-th activation of Γ_i in the busy window is given by

$$\displaystyle \begin{aligned} R_{i}(q) = B_{i}(q) - \delta_{i}^{-}(q) \end{aligned} $$

(10)

The worst-case response time $R^{+}_{i}$ is the longest response time of any activation of Γ_i observed in the busy window.

$$\displaystyle \begin{aligned} R^{+}_{i} = \max_{1 \leq q \leq \eta^{+}_{i}(w_{i})} R_{i}(q) \end{aligned} $$

(11)

Theorem 1

$R_{i}^{+}$ (Eq. 11) provides an upper bound on the worst-case response time of an arbitrary fork-join task Γ _i.

Proof

The WCRT of a fork-join task Γ_i is obtained with the busy window approach [43]. It remains to prove that the critical instant leads to the worst-case scheduling scenario, that the interference captured in Eqs. 6 and 7 are upper bounds, and that the busy window is correctly captured by Eq. 9. These are proved in Lemmas 1, 2, 3, and 4, respectively. □

4.2 Independent Tasks

We now derive the WCRT analysis of an arbitrary independent task τ _i. Two types of interference affect independent tasks: interference caused by higher priority independent tasks and by fork-join tasks. Let us first identify the critical instant leading to the worst-case scheduling scenario where τ _i suffers the most interference.

Lemma 5

The critical instant of τ _i is when the first event of higher priority independent tasks arrives simultaneously with τ _i ’s event at the offset of a fork-join task.

Proof

The worst-case interference caused by a higher priority (independent) task τ _j under SPP is when its first event arrives simultaneously with τ _i’s and continue arriving as early as possible [43].

The interference caused by a fork-join task Γ_j on τ _i depends on Γ_j’s offset ϕ( Γ_j) and subtasks $\tau _{j}^{\sigma ,s}$, whose execution times vary for different stages s. Assume a critical instant that occurs at a time other than at the offset ϕ( Γ_j). Since a task Γ_j starts receiving service at its offset, an event of τ _i arriving at time t > ϕ( Γ_j) can only suffer less interference from Γ_j’s subtask than when arriving at t = 0. □

Fork-join subtasks have different execution times for different stages, which leads to a number of scheduling scenarios that must be evaluated [31]. Each scenario is defined by the fork-join subtasks that will receive service in the cycle Φ and the offset at which the critical instant supposedly occurs. The scenario is called a critical instant candidate S. Since independent tasks participate in all critical instant candidates, they are omitted in S for the sake of simplicity.

Definition 1

Critical Instant Candidate S: the critical instant candidate S is an ordered pair (a, b), where a is a critical offset and b is a tuple containing one subtask $\tau _{j}^{\sigma ,s}$ of every interfering fork-join task Γ_j.

Let us also define the set of candidates that must be evaluated.

Definition 2

Critical Instant Candidate Set $\mathcal {S}$: the set containing all possible different critical instant candidates S.

The worst-case schedule of the independent task τ ₄ from the example in Fig. 5 is illustrated in Fig. 7. In fact, the critical instant leading to τ ₄’s WCRT is at ϕ( Γ₁) when $\tau _{1}^{1,2}$ and $\tau _{2}^{1,1}$ receive service at the same cycle Φ, i.e. $S=(\phi (\Gamma _{1}), (\tau _{1}^{1,2}, \tau _{2}^{1,1})$). Events of the independent task τ ₃ start arriving at the critical instant and continue arriving as early as possible.

Fig. 7

The worst-case schedule for independent task τ ₄ on core 1 (cf. Fig. 5) [34]

Let us now bound the interference $I_{i}^{I}({\Delta t})$ caused by equal or higher priority independent tasks in any time interval Δt. The interference $I_{i}^{I}({\Delta t})$ can be upper bounded as follows [27]:

$$\displaystyle \begin{aligned} I_{i}^{I}({\Delta t}) = \sum_{\forall \tau_{j} \in hp_{I}(i)} \eta_{j}^{+}({\Delta t}) \cdot C_{j} \end{aligned} $$

(12)

where hp _I(i) is the set of equal or higher priority independent tasks mapped to the same core as τ _i.

To derive the interference caused by fork-join tasks we need to define the Critical Instant Event Model. The critical instant event model $\check {\eta }_{i}^{\sigma ,s}({\Delta t},S)$ of a subtask $\tau _{i}^{\sigma ,s} \in \Gamma _{i}$ returns the maximum number of activations observable in any time interval Δt, assuming the critical instant S. It can be derived from Γ_i’s input event model $\eta _{i}^{+}({\Delta t})$ as follows:

$$\displaystyle \begin{aligned} \check{\eta}_{i}^{\sigma,s}({\Delta t},S) = \min \left \{ \eta_{i}^{+}\big(\Delta t_{S} + \Phi - \phi(\Gamma_{i})\big), \psi \right \} - gt\big(s^{S},s,\phi^{S},\phi(\Gamma_{i})\big) \end{aligned} $$

(13)

$$\displaystyle \begin{aligned} \psi = \left\lfloor {\frac{\Delta t_{S}}{\Phi \cdot s_{i}}\!} \right\rfloor + ge\big(\Delta t_{S} \bmod (\Phi \cdot s_{i}) \, , \, \Phi \cdot (s-1)\big) \end{aligned} $$

(14)

$$\displaystyle \begin{aligned} \Delta t_{S} = {\Delta t} + \underbrace{\Phi \cdot (s^{S}\!-\!1)}_{\substack{\text{critical instant} \\ \text{stage}}} + \underbrace{\phi^{S}}_{\substack{\text{critical instant} \\ \text{offset}}} \end{aligned} $$

(15)

where s is the stage of subtask $\tau _{i}^{\sigma ,s}$; s _i is the number of stages in Γ_i; ϕ ^S is the offset in S; s ^S is the stage of Γ_i in S; gt(a, b, c, d) is a function that returns 1 when (a > b) ∨ (a = b ∧ c > d), 0 otherwise; and ge(a, b) is a function that returns 1 when a ≥ b, 0 otherwise.

Lemma 6

$\check {\eta }_{i}^{\sigma ,s}({\Delta t},S)$ (Eq. 13) provides a valid upper bound on the number of activations of $\tau _{i}^{\sigma ,s}$ observable in any time interval Δt, assuming the critical instant S.

Proof

The proof is by induction, in two parts. First let us assume $s^{S}\!=\!1$ and $\phi ^{S}\!=\!0$, neutral values resulting in Δt _S  =   Δt and $gt(s^{S},s,\phi ^{S},\phi (\Gamma _{i}))\!=\!0$. The maximum number of activations of $\tau _{i}^{\sigma ,s}$ seen in the interval Δt is limited by the maximum number of activations of the fork-join task Γ_i because a subtask $\tau _{i}^{\sigma ,s}$ is activated once per Γ_i’s activation, and limited by the maximum number of times that $\tau _{i}^{\sigma ,s}$ can actually be scheduled and served in Δt. This is ensured in Eq. 13 by the minimum function and its first and second terms, respectively.

When $s^{S}\!>\!1$ and/or $\phi ^{S}\!>\!0$, the time interval [0,  Δt) must be moved forward so that it starts at stage s ^S and offset ϕ ^S. This is captured by Δt _S in Eq. 15 and by the last term of Eq. 13. The former extends the end of the time interval by the time it takes to reach the stage s ^S and the offset ϕ ^S, i.e. [0,  Δt _S). The latter pushes the start of the interval forward by subtracting an activation of $\tau _{i}^{\sigma ,s}$ if it occurs before the stage s ^S and the offset ϕ ^S, resulting in the interval [ Δt _S − Δt,  Δt _S). Thus Eq. 13. □

The interference $I_{i}^{FJ}({\Delta t},S)$ caused by fork-join tasks on the same core in any time interval Δt, assuming a critical instant candidate S, can then be upper bounded as follows:

$$\displaystyle \begin{aligned} I_{i}^{FJ}({\Delta t},S) = \sum_{\forall \tau_{j}^{\sigma,s} \in hp_{FJ}(i)} \check{\eta}_{j}^{\sigma,s}({\Delta t},S) \cdot C_{j}^{\sigma,s} \end{aligned} $$

(16)

where hp _FJ(i) is the set of fork-join subtasks mapped to the same core as τ _i.

The Multiple-Event Queueing Delay Q _i(q, S) and Multiple-Event Busy Time B _i(q, S) for an independent task τ _i, assuming a critical instant candidate S, can be derived as follows:

$$\displaystyle \begin{aligned} Q_{i}(q,S) = (q-1) \cdot C_{i} + I_{i}^{I}( Q_{i}(q,S) ) + I_{i}^{FJ}( Q_{i}(q,S), S ) \end{aligned} $$

(17)

$$\displaystyle \begin{aligned} B_{i}(q,S) = q \cdot C_{i} + I_{i}^{I}( B_{i}(q,S) ) + I_{i}^{FJ}( B_{i}(q,S), S ) \end{aligned} $$

(18)

where q ⋅ C _i is the time required to execute q activations of task τ _i.

Equations 17 and 18 result in fixed-point problems, similar to the well-known busy window equation (Eq. 9). They can be solved iteratively, starting with a very small, positive 𝜖.

Lemma 7

The Multiple-Event Queueing Delay Q _i(q, S) given by Eq. 17 is an upper bound, assuming the critical instant S.

Proof

The proof is by induction. When $q\!=\!1$, τ _i has to wait for service until the interfering workload is served. The interfering workload is given by Eqs. 12 and 16. Since $\eta _{j}^{+}({\Delta t})$ and C _j are upper bounds by definition, Eq. 12 is also an upper bound. Similarly, since $\check {\eta }_{j}^{\sigma ,s}({\Delta t},S)$ is an upper bound (cf. Lemma 6) and $C_{j}^{\sigma ,s}$ is an upper bound by definition, 16 is an upper bound for a given S. Therefore, Q _i(1, S) is also an upper bound, for a given S.

In a subsequent q + 1-th activation in the same busy window, Q _i(q, S) also must consider q executions of τ _i. This is captured in Eq. 17 by the first term, which is, by definition, an upper bound on the execution time. From that, Lemma 7 follows. □

Lemma 8

The Multiple-Event Busy Time B _i(q, S) given by Eq. 18 is an upper bound, assuming the critical instant S.

Proof

The proof is similar to Lemma 7, except that B _i(q, S) in Eq. 18 also captures the completion of the q-th activation. It takes additional C _i, which is an upper bound by definition. Thus Eq. 18 is an upper bound, for a given S. □

The busy window w _i(q, S) of an independent task τ _i is given by

$$\displaystyle \begin{aligned} w_{i}(S) = \max_{q \geq 1, \, q \in \mathbb{N}}\{ B_{i}(q,S) \,\, | \,\, Q_{i}(q\!+\!1,S) \geq \delta^{-}_{i}(q\!+\!1) \} \end{aligned} $$

(19)

Lemma 9

The busy window is upper bounded by Eq. 19.

Proof

The proof is by contradiction. Suppose there is a busy window w̆_i(S) longer than w _i(S). In that case, w̆_i(S) must contain at least one activation more than w _i(S), i.e. q̆ ≥ q + 1. From Eq. 19, we have that $Q_{i}(\breve {q},S) < \delta ^{-}_{i}(\breve {q})$, i.e. q̆ is not delayed by the previous activation. Since that violates the definition of a busy window, the hypothesis must be rejected. □

The response time R _i of the q-th activation of a task in a busy window is given by

$$\displaystyle \begin{aligned} R_{i}(q,S) = B_{i}(q,S) - \delta^{-}_{i}(q) \end{aligned} $$

(20)

Finally, the worst-case response time $R_{i}^{+}$ is found inside the busy window and must be evaluated for all possible critical instant candidates $S \in \mathcal {S}$. The worst-case response time $R_{i}^{+}$ is given by

$$\displaystyle \begin{aligned} R_{i}^{+} = \max_{S \in \mathcal{S}} \bigg\{ \max_{1 \leq q \leq \eta^{+}_{i}(w_{i}(S))} \{ R_{i}(q,S) \} \bigg\} \end{aligned} $$

(21)

where the set $\mathcal {S}$ is given by the following Cartesian products:

$$\displaystyle \begin{aligned} \mathcal{S} = \big\{ \phi(\Gamma_{j}) , \phi(\Gamma_{k}) , \, \ldots \big\} \times \big\{ \sigma_{i}(\Gamma_{j}) \times \sigma_{i}(\Gamma_{k}) \times \ldots \big\} \end{aligned} $$

(22)

where Γ_j, Γ_k, … are all fork-join tasks mapped to the same core as τ _i and σ _i( Γ_j) is the set of subtasks of Γ_j that are mapped to that core. When no fork-join tasks interfere with τ _i, the set $\mathcal {S} = \{(0, ())\}$.

Theorem 2

$R_{i}^{+}$ (Eq. 21) returns an upper bound on the worst-case response time of an independent task τ _i.

Proof

We must first prove that, for a given S, $R_{i}^{+}$ is an upper bound. $R_{i}^{+}$ is obtained with the busy window approach [43]. It returns the maximum response time R _i(q, S) among all activations inside the busy window. From Lemmas 7 and 8 we have that Eqs. 17 and 18 are upper bounds for a given S. From Lemma 9 we have that the busy window is captured by Eq. 19. Since the first term of Eq. 20 is an upper bound and the second term is a lower bound by definition, R _i(q, S) is an upper bound. Thus $R_{i}^{+}$ is an upper bound for a given S. Since Eq. 21 evaluates the maximum response time over all $S \in \mathcal {S}$, $R_{i}^{+}$ is an upper bound on the response time of τ _i. □

4.3 Error Recovery

Designed for mixed-criticality, our approach supports different recovery strategies for different fork-join tasks (cf. Sect. 2.2). For instance, in DMR augmented with checkpointing and rollback, recovery consists in reverting the state and re-executing the error-affected stage in both replicas. In TMR, recovery consists in copying and replacing the state of the faulty replica with the state of a healthy one. The different strategies are captured in the analysis by the recovery execution time, which depends on the strategy and the stage to be recovered. The recovery WCET $C_{i,rec}^{\sigma ,s}$ of a fork-join subtask $\tau _{i}^{\sigma ,s}$ accounts for the adopted recovery strategy as illustrated in Fig. 4b. Once an error is detected, error recovery is triggered and executed in the recovery slot of the same cycle Φ. Figure 3 illustrates the recovery of the s-th stage of Γ₂’s i-th activation.

Let us incorporate the error recovery into the analysis. For a fork-join task Γ_i, we must only adapt the Multiple-Event Busy Time B _i(q) (Eq. 7) to account for the execution of the recovery:

$$\displaystyle \begin{aligned} B_{i}^{rec}(q) = q \cdot s_{i} \cdot \Phi + j_{\phi} + \phi(recovery) - \phi(\Gamma_{i}) + C_{i,rec}^{\sigma,s} \end{aligned} $$

(23)

where $C_{i,rec}^{\sigma ,s}$ is the WCET of the recovery of last subtask of Γ_i. The recovery of another task Γ_j does not interfere with Γ_i’s WCRT. Only the recovery of one of Γ_i’s subtasks can interfere with Γ_i’s WCRT. Moreover, since the recovery of a subtask occurs in the recovery slot of the same cycle Φ and does not interfere with the next subtask, only the recovery of the last stage of Γ_i actually has an impact on its response time. This is captured by the three last terms of Eq. 23.

For an independent task τ _i, the worst-case impact of recovery of a fork-join task Γ_j is modeled as an additional fork-join task Γ_rec with one subtask $\tau _{rec}^{\sigma ,1}$ mapped to the same core as τ _i and that executes in the recovery slot. The WCET $C_{rec}^{\sigma ,1}$ of $\tau _{rec}^{\sigma ,1}$ is chosen as the maximum recovery time among the subtasks of all fork-join tasks mapped to that core:

$$\displaystyle \begin{aligned} C_{rec}^{\sigma,1} = \max_{\forall \tau_{j}^{\sigma,s} \in hp_{FJ}(i)} \left \{ C_{i,rec}^{\sigma,s} \right \} \end{aligned} $$

(24)

with Γ_rec mapped, Eq. 21 finds the critical instant, where the recovery $C_{rec}^{\sigma ,1}$ has the worst impact on the response time of τ _i.

5 Experimental Evaluation

In our experiments we evaluate our approach with real as well as synthetic workloads, focusing on the performance of the scheduler. First we characterize MiBench applications [18] and evaluate them as fork-join (replicated) tasks in the system. Then we evaluate the performance of independent (regular) tasks. Finally we evaluate the approach with synthetic workloads when varying parameters of fork-join tasks.

5.1 Evaluation with Benchmark Applications

5.1.1 Characterization

First we extract execution times and number of stages from MiBench automotive and security applications [18]. They were executed with small input on an ARMv7@1 GHz and a memory subsystem including a DDR3-1600 DRAM [8]. Table 1 summarizes the total WCET, observed number of stages, and WCET of the longest stage (max). A stage is delimited by syscalls (cf. Sect. 2.2). We report the observed execution times as WCETs. As pointed out in [2], stages vary in number and execution time depending on the application and on the current activity in that stage (computation/IO). This is seen, e.g., in susan, where 99% of the WCET is concentrated in one stage (computation) while the other stages perform mostly IO and are on average 3.34 μs long.

Table 1 MiBench applications’ profile [34]

In our approach, the optimum is when all stages of a fork-join task have the same WCET. There are two possibilities to achieve that: to aligned very long stages in shorter ones or to group short, subsequent stages together. We exploit the latter as it does not require changes to the error detection mechanism or to our model. The results with grouped stages are shown on the right-hand side of Table 1. We have first grouped stages without increasing the maximum stage length. The largest improvement is seen in bitcount, where the number of stages reduces by one order of magnitude. In cases where all stages are very short, we increase the maximum stage length. When increasing the maximum stage length by two orders of magnitude, the number of stages of basicmath reduces by four orders of magnitude. We have manually chosen the maximum stage length. Alternatively the problem of finding the maximum stage length can be formulated as an optimization problem that, e.g., minimizes the overall WCRT or maximizes the slack. Next, we map the applications as fork-join tasks and evaluate their WCRTs.

5.1.2 Evaluation of Fork-Join Tasks

Two applications at a time are mapped as fork-join tasks with two segments (i.e., replicas in DMR) to two cores (cf. Fig. 5). On each core, 15% load is introduced by ten independent tasks generated with UUniFast [7]. We compare our approach with a TDM-based scheduler and Axer’s Partitioned SPP [2]. In TDM, each fork-join task executes (and recovers) in its own slot. Independent tasks execute in a third slot, which replaces the recovery slot of our approach. The size of the slots is derived from our offsets. For all approaches, the priority assignment for independent tasks is deadline monotonic and considers that deadline equals period. In SPP, the deadline monotonic priority assignment also includes fork-join tasks.

The results are plotted in Fig. 8, where ba.bi gives the WCRT of basicmath when mapped together with bitcount. Despite the low system load, our approach also outperforms SPP in all cases, with bounds 58.2% lower, on average. Better results with SPP cannot be obtained unless the interfering workload is removed or highest priority is given to the fork-join tasks [2], which violates DM. Despite the similarity of how our approach handles fork-join tasks with TDM, the proposed approach outperforms TDM in all cases, achieving, on average, bounds 13.9% lower. This minor difference is because TDM slots must be slightly longer than our offsets to fit an eventual recovery. Nonetheless, not only our approach can guarantee short WCRT for replicated tasks but also provides for the worst-case performance of independent tasks.

Fig. 8

WCRT of fork-join tasks with two segments derived from MiBench [34]

5.1.3 Evaluation of Independent Tasks

In a second experiment we fix bitcount and rijndael as fork-join tasks and vary the load on both cores. The generated task periods are in the range [20, 500] ms, larger than the longest stage of the fork-join tasks. The schedulability of the system as the load increases is shown in Fig. 9. Our approach outperforms TDM and SPP in all cases, scheduling 1.55× and 6.96× more tasksets, respectively. Due to its non-work conserving characteristic, TDM’s schedulability is limited to medium loads. SPP provides very short response times with lower loads but, as the load increases, the schedulability drops fast due to high interference (and thus high WCRT) suffered by fork-join tasks. For reference purposes, we also plot the schedulability of SPP when assigning the highest priorities to the fork-join tasks (SPP/hp). The schedulability in higher loads improves but losing deadline monotonicity guarantees renders the systems unusable in practice. Moreover, when increasing the jitter to 20% (relative to period), schedulability decreases 14.2% but shows the same trends for all schedulers.

Fig. 9

Schedulability as a function of the load of the system. Basicmath and rijndael as fork-join tasks with two segments [34]

Figure 10 details the tasks’ WCRTs when the system load is 20.2%. Indeed, when schedulable, SPP provides some of the shortest WCRTs for independent tasks, and SPP/hp improves the response times of fork-join tasks at the expense of the independent tasks’. Our approach provides a balanced trade-off between the performance of independent tasks and of fork-join tasks, and achieves high schedulability even in higher loads.

Fig. 10

Basicmath and rijndael as replicated tasks in DMR running on a dual-core configuration with 20.2% load (5% load from independent tasks) [34]. (a) WCRT of independent tasks [ms]. (b) WCRT of FJ tasks

5.2 Evaluation with Synthetic Workload

We now evaluate the performance of our approach when varying parameters such as stage length and cycle Φ.

5.2.1 Evaluation of Fork-Join Tasks

Two fork-join tasks Γ₁ and Γ₂ with two segments each (i.e., replicas in DMR) are in DMR) are mapped to two cores. The total WCETs³ of Γ₁ and Γ₂ are 15 and 25ms, respectively. Both tasks are sporadic, with a minimum distance of 1s between activations. The number of stages of Γ₁ and Γ₂ is varied as a function of the maximum stage WCET, as depicted in Fig. 11a. The length of the cycle Φ, depicted in Fig. 11b, varies with the maximum stage WCET since it is derived from them (cf. Sect. 3.4).

Fig. 11

Parameters of two fork-join tasks Γ₁ and Γ₂ with two segments running on a dual-core configuration [34]. (a) Stages of Γ₁ and Γ₂. (b) Cycle Φ

The system performance as the maximum stage lengths of Γ₁ and Γ₂ increase is reported in Fig. 12. The WCRT of Γ₁ increases with the stage length (Fig. 12a) as it depends on the number of stages and Φ’s length. In fact, the WCRT of Γ₁ is longest when the stages of Γ₁ are the shortest and the stages of the interfering fork-join task ( Γ₂) are the longest. Conversely, WCRT of Γ₁ is shortest when its stages are the longest and the stages of the interfering fork-join task are the shortest. The same occurs to Γ₂ in Fig. 12b. Thus, there is a trade-off between the response times of interfering fork-join tasks. This is plotted in Fig. 13 as the sum of the WCRTs of Γ₁ and Γ₂. As can be seen in Fig. 13, low response times can be obtained next and above to the line segment between the origin (0, 0, 0) and the point (15, 25, 0), the total WCETs ^Fn1 of Γ₁ and Γ₂, respectively.

Fig. 12

Performance of fork-join tasks Γ₁ and Γ₂ as a function of the maximum stage WCET [34]. (a) WCRT of Γ₁. (b) WCRT of Γ₂

Fig. 13

WCRT trade-off between interfering fork-join tasks [34]

5.2.2 Evaluation of Independent Tasks

To evaluate the impact of the parameters on independent tasks, we extend the previous scenario introducing 25% load on each core with ten independent tasks generated with UUniFast [7]. The task periods are within the interval [15, 500] ms for the first experiment, and the interval [25, 500] ms for the second. The priority assignment is deadline monotonic and considers that the deadline is equal to the period.

The schedulability as a function of the stage lengths is shown in Fig. 14. Sufficiently long stages cause the schedulability to decrease as independent tasks with short periods start missing their deadlines. This is seen in Fig. 14a when the stage length of either fork-join task reaches 15 ms, the minimum period for the generated tasksets. Thus, when increasing the minimum period of generated tasks to 25 ms, the number of schedulable tasksets also increases (Fig. 14b).

Fig. 14

Schedulable tasksets as a function of the maximum stage WCET of fork-join tasks Γ₁ and Γ₂ with 25% load from independent tasks [34]. (a) Task period interval [15–500] ms. (b) Task period interval [25–500] ms

The maximum stage length of a fork-join task has direct impact on the response times and schedulability of the system. For the sake of performance, shorter stage lengths are preferred. However, that is not always possible because it would result in a large number of stages or because of the application, which restricts the minimum stage length (cf. Sect. 5.1.1). Nonetheless, fork-join tasks still are able to perform well with appropriate parameter choices. Additionally, one can formulate the problem of finding the stage lengths according to an objective function, such as minimize the overall response time or maximize the slack. The offsets can also be included in the formulation, as long as Constraints 1 and 2 are met.

6 Conclusion

This chapter started with an overview of the project ASTEROID. ASTEROID developed a cross-layer fault-tolerance approach to provide reliable software execution on unreliable hardware. The approach is based on replicated software execution and exploits the large number of cores available in modern and future architectures at a higher level of abstraction without resorting to the inefficient hardware redundancy. The chapter then focused on the performance of replicated execution and the replica-aware co-scheduling, which was developed in ASTEROID.

The replica-aware co-scheduling for mixed-critical systems, where applications with different requirements and criticalities co-exist, overcomes the performance limitations of standard schedulers such as SPP and TDM. A formal WCRT analysis was presented, which supports different recovery strategies and accounting for the NoC communication delay and overheads due to replica management and state comparison. The replica-aware co-scheduling provides for high worst-case performance of replicated software execution on many-core architectures without impairing the remaining tasks in the system. Experimental results with benchmark applications showed an improvement on taskset schedulability of up to 6.9× when compared to Partitioned SPP and 1.5× when compared to a TDM-based scheduler.