Abstract
Uncertain data are observations that cannot be uniquely mapped to a referent. In the case of uncertainty due to incompleteness, possibility theory can be used as an appropriate model for processing such data. In particular, granular counting is a way to count data in presence of uncertainty represented by possibility distributions. Two algorithms were proposed in literature to compute granular counting: exact granular counting, with quadratic time complexity, and approximate granular counting, with linear time complexity. This paper extends approximate granular counting by computing bounds for exact granular count. In this way, the efficiency of approximate granular count is combined with certified bounds whose width can be adjusted in accordance to user needs.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Data uncertainty may arise as a consequence of several conditions and require proper management [1]. The simplest approach is to ignore uncertainty by estimating a precise value for each observation, but this simplistic approach, though of very simple application, can lead to a distortion in the subsequent processing stages that is difficult to detect. A more comprehensive approach should take into account data uncertainty and propagate its footprint throughout the entire data processing flow. In this way, the results of data processing reveal their uncertainty, which can be evaluated to assess their ultimate usefulness.
Several theories can be applied to represent and process uncertainty, such as Probability Theory [2], which is however a particular case falling in the Granular Computing paradigm. Granular Computing also includes classical Set Theory [3], Rough Sets Theory [4], Evidence Theory [5] and Possibility Theory [6]. The choice of a particular theory depends on the nature of uncertainty; in particular, possibility theory deals with uncertainty due to incomplete information, e.g. when the value of an observation cannot be precisely determined: we will use the term uncertain data to denote data characterized by this specific type of uncertainty, therefore we adopt the possibilistic framework in this paper.
A common process on data is counting, which searches for the number of data samples with a specific value. Data counting is often a preliminary step for different types of analysis, such as descriptive statistics, comparative analysis, etc. It is a fairly simple operation when data are accurate, but it becomes non-trivial when data are uncertain. In fact, the uncertainty in the data should propagate in the count, so that the results are granular rather than precise.
Recently, a definition of granular count through Possibility Theory was proposed [7]. It was shown that the resulting counts are fuzzy intervals in the domain of natural numbers. Based on this result, two algorithms for granular counting were defined: an exact granular counting algorithm with quadratic-time complexity and an approximate counting algorithm with linear-time complexity. Approximate granular counting is appealing in applications dealing with large amounts of data due to its low complexity, but a compromise must be accepted in terms of accuracy of the resulting fuzzy interval. In particular, it is not immediate to know how far is the result of the approximate count from the fuzzy interval resulting from the exact granular count.
In this paper an algorithm is proposed for bounded granular counting, which computes an interval-valued fuzzy set representing the boundaries in which the exact granular count is located. In this way, the efficiency of approximate granular count is combined with certified bounds whose width can be adjusted in accordance to user needs.
The concept of granular count and related algorithms are briefly described in Sect. 2, while the proposal of bounded granular count is introduced in Sect. 3. Section 4 reports some numerical experiments to assess the efficiency of the proposed algorithm, as well as an outline of an application in Bioinformatics.
2 Granular Count
A brief summary of Granular Counting is reported in this Section. Further details can be found in the original papers [7, 8].
We assume that data are manifested through observations, which refer to some objects or referents. The relation between observations and referents—which is called reference—may be uncertain in the sense that an unequivocal reference of the observation to one of the referents is not possible. We model such uncertainty with Possibility Theory [6] as we assume that uncertainty is due to the imprecision of the observation, i.e. the observation is not complete enough to make reference unequivocal.
Given a set R of referents and an observation \(o\in O\), a possibility distribution is a mapping
such that \(\exists r\in R:\pi _{o}\left( r\right) =1\). The value \(\pi _{o}\left( r\right) =0\) means that it is impossible that the referent r is referred by the observation, while \(\pi _{o}\left( r\right) =1\) means that the referent r is absolutely possible (though not certain). Intermediate values of \(\pi _{o}\left( r\right) \) stand for gradual values of possibility, which quantify the completeness of information resulting from an observation. (More specifically, the lower the possibility degree, the more information we have to exclude a referent.) The possibility distributions of all observations can be arranged in a possibilistic assignment table, as exemplified in Table 1.
2.1 Definition of Granular Count
By using the operators of Possibility Theory, as well as the assumption that observations are non-interactive (i.e. they do not influence each other), the possibility degree, that a subset \(O_{x}\subseteq O\) of \(x\in \mathbb {N}\) observations is exactlyFootnote 1 the set of observations referring to a reference \(r_{i}\in R\), is defined as:
with the convention that \(\min \emptyset =1\). Informally speaking, Eq. (1) defines the possibility degree that \(O_{x}\) is the subset of all and only the observations of \(r_{i}\) by computing the least possibility degree of two simultaneous events: (i) all observations of \(O_{x}\) refer to \(r_{i}\), and (ii) all the other observations refer to a different referent.
In order to compute the possibility degree that the number of observations referring to a referent \(r_{i}\) is \(N_{i}\), we are not interested in a specific set \(O_{x}\), but in any set of x elements. We can therefore define the possibility value that the number of observations for a referent \(r_{i}\) is x as:
for \(x\le m\) and \(\pi _{N_{i}}\left( x\right) =0\) for \(x>m\). Equation (2) provides a granular definition of count. Counting is imprecise because observations are uncertain.
It is possible to prove that a granular count as in Eq. (2) is a fuzzy interval in the domain of natural numbers. A fuzzy interval is a convex and normal fuzzy set on a numerical domain (in our case, it is \(\mathbb {N}\)). Convexity of a fuzzy set can be established by proving that all \(\alpha \)-cuts are intervals, while normality of the granular count is guaranteed because of the normality of the possibility distributions \(\pi _{o}\) for all \(o\in O\). Figure 1 depicts an example of granular count.
Exact granular count of referent \(r_{1}\) as in Table 1
2.2 Algorithms for Granular Counting
The direct application of Eq. (2) leads to an intractable counting procedure as all possible subsets of O must be considered. On the other hand, a polynomial-time algorithm can be devised by taking profit of the representation of a granular count as a fuzzy interval. In particular, the granular counting algorithm builds the fuzzy interval by considering the \(\alpha \)-cut representation of fuzzy sets. On such basis, two variants of granular counting algorithms can be devised:
-
Exact granular counting uses all the values of \(\alpha \) that correspond to some possibility degree in the possibilistic assignment table;
-
Approximate granular counting uses the values of \(\alpha \) taken from a finite set of evenly spaced numbers over
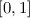 . The number of such values depend on a user-defined parameter \(n_{\alpha }\).
. The number of such values depend on a user-defined parameter \(n_{\alpha }\).
The approximate granular counting is more efficient than the exact version because it does not require to scan the possibilistic assignment table, though at the price of a new required parameter.
Exact granular counting (Algorithm 1) and approximate granular counting (Algorithm 2) share the same core algorithm (Algorithm 3) and only differ by how the set of \(\alpha \)-values are computed. In essence, the core algorithm computes the granular count in an incremental way, by reckoning the \(\alpha \)-cuts of the fuzzy interval for each \(\alpha \) value provided in input.
In brief, the core algorithm works as follows. Given the possibilistic assignment table \(\mathbf {R}\), the index i of the referent and the set A of \(\alpha \)-cuts, the array \(\mathbf {r}\) represents the possibility degrees that an observation refers to \(r_{i}\), i.e. \(\mathbf {r}_{j}=\pi _{o_{j}}\left( r_{i}\right) \) (line 1), while \(\mathbf {\bar{r}}\) represents the possibility degrees that an observation refers to any other referent different from \(r_{i}\) (line 2). N is the array representing the granular count (line 3). The main cycle (lines 4–17) loops over each \(\alpha \in A\) and computes the bounds \(x_{\min }\) and \(x_{\max }\) of the corresponding \(\alpha \)-cut (line 5). These bounds are calculated by looping over all observations (lines 6–13), so that \(x_{\max }\) is incremented if the possibility degree that the current observation refers to \(r_{i}\) is greater than or equal to \(\alpha \) (lines 7–8), while \(x_{\min }\) further requires that the possibility degree that the observation refers to any other referent is less than \(\alpha \) (lines 9–10). When both \(x_{\min }\) and \(x_{\max }\) are computed, the degrees of membership of the granular count are updated accordingly (lines 14–16).
For a fixed referent, the time-complexity of exact granular count is \(\mathcal {O}\left( nm^{2}\right) \) (being n the number of referents and m the number of observations), while the time-complexity of approximate granular count drops to \(\mathcal {O}\left( m\left( n+n_{\alpha }\right) \right) \). In consideration that, in typical scenarios, the number of observations is very large (i.e., \(m\gg n\)), especially in comparison with the number of referents, it is deduced that approximate granular counting is the preferred choice in the case of very large amounts of uncertain data.



3 Bounding the Exact Granular Count
The time-complexity of approximate granular count linearly depends on the number of \(\alpha \) values which, in turn, depend on the value of the parameter \(n_{\alpha }\). On one hand, low values of \(n_{\alpha }\) lead to fast computation of granular counts; on the other hand, low values of \(n_{\alpha }\) may lead to a rough estimate of the possibility degrees of the exact granular count.
In Fig. 2 the Jaccard similarityFootnote 2 measure between approximate granular count and exact granular count is reported for \(n_{\alpha }\) between 2 and 100: even though similarity values close to 1 are reached for  , for smaller values a significant dissimilarity can be observed. In order to assess whether the discrepancy between approximate and exact granular counts is acceptable for a problem at hand, it is important to identify some bounds for the exact granular count when only an approximate count is available.
, for smaller values a significant dissimilarity can be observed. In order to assess whether the discrepancy between approximate and exact granular counts is acceptable for a problem at hand, it is important to identify some bounds for the exact granular count when only an approximate count is available.
Similarity of approximate count to exact granular count for referent \(r_{1}\) in Table 1
3.1 \(\alpha \)-Cut Computation
In order to identify such bounds, a closer look at Algorithm 3 is necessary. The algorithm computes the granular count for the i-th referent given a possibilistic assignment table \(\mathbf {R}\) and a set A of \(\alpha \)-values. The main cycle within the algorithm computes the \(\alpha \)-cut of the granular count, which is represented by the array N and corresponds to the possibility distribution \(\pi _{N}\). For a given value of \(\alpha \), the variable \(x_{\max }\) counts the number of observations that refer to \(r_{i}\) with a possibility degree \(\ge \alpha \); on the other hand, the variable \(x_{\min }\) counts the number of observations that refer to \(r_{i}\) with a possibility degree \(\ge \alpha \) and refer to any other referent with possibility degree \(<\alpha \). As a consequence, \(x_{\min }\le x_{\max }\). Since in our analysis we will consider different values of \(\alpha \), we shall denote the two variables as \(x_{\min }^{\left( \alpha \right) }\) and \(x_{\max }^{\left( \alpha \right) }\) respectively.
By construction, the value \(x_{\max }^{\left( \alpha \right) }\) corresponds to the cardinality of the set
while the value \(x_{\min }^{\left( \alpha \right) }\) is the cardinality of the set
with the obvious relation that \(O_{\min }^{\left( \alpha \right) }\subseteq O_{\max }^{\left( \alpha \right) }\). On this basis, it is possible to prove the following lemmas:
Lemma 1
If \(x_{\min }^{\left( \alpha \right) }>0\), then for all \(x<x_{\min }^{\left( \alpha \right) }\): \(\pi _{N}\left( x\right) <\alpha \).
Proof
By Definition (1), we can write
where \(P=\min _{o\in O_{x}}\pi _{o}\left( r_{i}\right) \) and \(Q=\min _{o\notin O_{x}}\max _{r\ne r_{i}}\pi _{o}\left( r\right) \). We focus on Q.
Let \(O_{x}\subset O\) be a subset of x observations. Since \(x<x_{\min }^{\left( \alpha \right) }\), there exists at least one observation \(o'\) belonging to \(O_{\min }^{\left( \alpha \right) }\) but not to \(O_{x}\), i.e. \(o'\in O_{\min }^{\left( \alpha \right) }\setminus O_{x}\). Since \(o'\in O_{\min }^{\left( \alpha \right) }\), by definition \(\max _{r\ne r_{i}}\pi _{o'}\left( r\right) <\alpha \), therefore \(Q<\alpha \) because \(o'\notin O_{x}\). As a consequence, \(\pi _{O_{x}}\left( r_{i}\right) <\alpha \). This is true for all subsets of cardinality \(x<x_{\min }^{\left( \alpha \right) }\), therefore:
Lemma 2
For all \(x>x_{\max }^{\left( \alpha \right) }\): \(\pi _{N}\left( x\right) <\alpha \).
Proof
Let \(O_{x}\subseteq O\) be a subset of x observations. If \(x_{\max }^{\left( \alpha \right) }=m\) then \(O_{x}=\emptyset \) because there is not a number of observations greater than m; in such a case, \(\pi _{N}\left( x\right) =0<\alpha \).
Similarly to the proof of the previous lemma, we split Definition (1) as in Eq. (5) but now we focus on P. Since \(x>x_{\max }^{\left( \alpha \right) }\) there exists an observation \(o'\in O_{x}\) that does not belong to \(O_{\max }^{\left( \alpha \right) }\), therefore \(\pi _{o'}\left( r_{i}\right) <\alpha \). As a consequence, \(P<\alpha \), thus \(\pi _{O_{x}}\left( r_{i}\right) <\alpha \). This is true for all subsets of cardinality \(x>x_{\max }^{\left( \alpha \right) }\), thus proving the thesis.
Lemma 3
For all \(x_{\min }^{\left( \alpha \right) }\le x\le x_{\max }^{\left( \alpha \right) }\), \(\pi _{N}\left( x\right) \ge \alpha \)
Proof
Obvious from Definitions (3) and (4).
The previous lemmas show that, for a given value of \(\alpha \), the exact granular count must satisfy the following relations:

that is:
Theorem 1
The interval \(\left[ x_{\min }^{\left( \alpha \right) },x_{\max }^{\left( \alpha \right) }\right] \) is the \(\alpha \)-cut of \(\pi _{N}\).
In Fig. 3 the 0.3- and 0.7- cuts are used to depict the regions that bound the values of \(\pi _{N}\). Notice that such regions have been computed without knowing the actual values of the exact granular count.
3.2 Bounds for Exact Granular Count
Thanks to the properties of \(\alpha \)-cuts, it is possible to identify tight bounds for an exact granular count by using the results of an approximate granular count. In fact, given two values \(\alpha '<\alpha ''\), the \(\alpha ''\)-cut is included in the \(\alpha '\)-cut, therefore
and it is easy to verify the following properties:
The previous relations suggest a strategy for computing the bounds of an exact granular count: supposing that, for some x, it is known that \(\alpha _{1}\le \pi _{N}\left( x\right) \le \alpha _{2}\) and a new value \(\alpha \) is considered: if \(x_{\min }^{\left( \alpha \right) }\le x\le x_{\max }^{\left( \alpha \right) }\) than it is possible to assert that \(\pi _{N}\left( x\right) \ge \alpha \), therefore \(\max \left\{ \alpha ,\alpha _{1}\right\} \le \pi _{N}\left( x\right) \le \alpha _{2}\); if x is outside this interval, then \(\pi _{N}\left( x\right) <\alpha \) therefore \(\alpha _{1}\le \pi _{N}\left( x\right) \le \min \left\{ \alpha ,\alpha _{2}\right\} \).
On the basis of such strategy, it is possible to define a bounded granular counting algorithm to compute bounds of the exact granular count when a set A of \(\alpha \)-cuts is given, which is reported in Algorithm 4. In this algorithm the bounds are represented by the arrays \(N_{l}\) and \(N_{u}\) (lines 3–4) and they are updated for each \(\alpha \in A\) so as to satisfy the above-mentioned relations (lines 15–22).

The resulting bounded granular count is an Interval-Valued Fuzzy Set (IVFS) [9] which assigns, to each \(x\in \mathbb {N}\), an interval \(\left[ \pi _{N_{L}}\left( x\right) ,\pi _{N_{U}}\left( x\right) \right] \) representing the possibility distribution of \(\pi _{N}\left( x\right) \), which may be unknown. In Fig. 4 it is shown an example of bounded granular count by generating the set of \(\alpha \)-values as in approximate granular count with \(n_{\alpha }=5\). It is possible to observe that the core of the granular count (i.e. the set of x values such that \(\pi _{N}\left( x\right) =1\)) is precisely identified because the approximate granular counting algorithm includes \(\alpha =1\) in the set of \(\alpha \)-values to be considered. Also, since a value of \(\alpha \) very close to 0 is also included (namely, \(10^{-12}\)), the impossible counts (i.e. the values of x such that \(\pi _{N}\left( x\right) =0\)) are also detected. Finally, since the values of \(\alpha \) are equally spaced in ]0, 1], the lengths of the bounding intervals are constant.
It also possible to set \(n_{\alpha }\) in order to achieve a desired precision. By looking at Algorithm 2, it is possible to observe that the values of \(\alpha \) are equally spaced at distance
where the value \(\varDelta \alpha \) coincides with the maximum length of the intervals computed by the bounded granular counting algorithm. By reversing the problem, it is possible to set the value of \(n_{\alpha }\) so that the maximum length is less than a desired threshold \(\beta \). Since \(\varepsilon \approxeq 0\), it suffices to set
4 Experimental Results
4.1 Efficiency Evaluation
The evaluation of efficiency has been performed on synthetically generated data. In particular, a number of random possibilistic assignment tables have been generated by varying the number of observations on a geometrical progression with common ratio 10 but keeping the number of referents fixed to three.Footnote 3
For each possibilistic assignment table, both exact and bounded granular counting algorithms (with \(n_{\alpha }=10\)) have been applied on the first referent, and the time required to complete operations has been recorded.Footnote 4 Each experiment has been repeated 7 times and average time has been recorded. For each repetition, the experiment has been looped for 10 times and the best timing has been retained. The average execution time is reported in Table 2 and depicted in Fig. 5.
A linear regression in the log-log scale confirms the quadratic trend of the time required for exact granular counting and the linear trend for bounded granular counting algorithm. Noticeably, the change of complexity is most exclusively due to the way the set of \(\alpha \)-values have been generated: the selection of all values occurring in the possibilistic assignment table—which is required for exact granular counting—determines a significant reduction of the overall efficiency. On the other hand, bounded granular counting takes profit of the advantages of approximate granular counting for light-weight computations but, at the same time, it offers certified bounds on the possibility degrees of the exact granular count.
4.2 Application: Gene Expression Estimation
In Bioinformatics, RNA-Seq is a protocol that allows to examine the gene expression in a cell by sampling fragments of RNA called “reads”. When RNA-Seq output is mapped against a reference database of known genes, a high percentage of reads—called multireads—map to more than one gene [10]. Multireads are a source of uncertainty in the quantification of gene expression, which should be managed in order to provide significant results. To this end, the mapping procedure provides a quality index that is a biologically plausible estimate of the possibility that a read can be associated to a gene [11]. However, a high quality index does not mean certainty in association: two or more genes can be candidate for mapping a read because they can be mapped with similar high quality.
Granular counting finds a natural application in the specific problem of counting the number of reads that are possibly associated to a gene. (Reads are considered as observations, while genes are referents.) However, the amount of data involved in such process may be overwhelming. For example, the public dataset SRP014005 downloaded from NCBI-SRA archiveFootnote 5, contains a case-control study of the Asthma disease with 55,579 reads mapped on 14,802 genes (16% are multireads). Nonetheless, accurate granular counting can be achieved by the use of the proposed algorithm. As an example, in Fig. 6 the bounded granular count has been computed for gene OTTHUMG00000189570|HELLPAR with \(n_{\alpha }=10\). It is noteworthy observing how imprecise is the count of this gene, which is due to a large number of multireads (with different quality levels).
5 Conclusions
The proposed bounded granular counting algorithm is an extended version of approximate granular counting where efficient computation is combined with the ability of bounding the exact granular count within intervals whose granularity can be decided by the user. In most cases, it is more than enough that the exact possibility degrees of exact granular count are assured to be within a small range from some approximate values. When such type of imprecision is tolerated, a significant speed-up in calculations can be achieved, thus opening the door of granular counting to big-data problems.
Notes
- 1.
In the sense that any observation non belonging to \(O_{x}\) does not refer to \(r_{i}\).
- 2.
Given the exact granular count \(\pi _{N}\) and an approximate count \(\widetilde{\pi }_{N}\), the Jaccard similarity index is computed as
$$ S=\frac{\sum _{x=0}^{m}\min \left\{ \pi _{N}\left( x\right) ,\widetilde{\pi }_{N}\left( x\right) \right\} }{\sum _{x=0}^{m}\max \left\{ \pi _{N}\left( x\right) ,\widetilde{\pi }_{N}\left( x\right) \right\} } $$.
- 3.
Each possibilistic assignment table has been generated by taking care that each row corresponds to a normal possibility distribution.
- 4.
Experiments have been executed on a machine equipped by an Intel i7 CPU, 16GiB RAM, Linux SO. Scripts were written in Python 3.7 and executed in Jupyter Notebook. The NumPy library has been used for fast numerical computations, but the scripts were not implemented with the objective of maximizing performance.
- 5.
References
Boukhelifa, N., Perrin, M.-E., Huron, S., Eagan, J.: How data workers cope with uncertainty: a task characterisation study. In: Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems, pp. 3645–3656. ACM (2017)
Aggarwal, C.C., Yu, P.S.: A survey of uncertain data algorithms and applications. IEEE Trans. Knowl. Data Eng. 21(5), 609–623 (2009)
Hüllermeier, E., Beringer, J.: Learning from ambiguously labeled examples. In: Advances in Intelligent Data Analysis VI, p. 739 (2005)
Lin, T.Y., Cercone, N.: Rough Sets and Data Mining. Springer, Boston (1996). https://doi.org/10.1007/978-1-4613-1461-5
Vannoorenberghe, P.: Reasoning with unlabeled samples and belief functions. In: The 12th IEEE International Conference on Fuzzy Systems. FUZZ 2003, vol. 2, pp. 814–818. IEEE (2003)
Dubois, D., Prade, H.: Possibility theory. In: Computational Complexity, pp. 2240–2252. Springer, Boston (2012). https://doi.org/10.1007/978-1-4684-5287-7
Mencar, C., Pedrycz, W.: Granular counting of uncertain data. Fuzzy Sets Syst. 387, 108–126 (2019)
Mencar, C., Pedrycz, W.: GrCount: counting method for uncertain data. MethodsX 6, 2455–2459 (2019)
Dubois, D., Prade, H.: Interval-valued fuzzy sets, possibility theory and imprecise probability. In: Proceedings - 4th Conference of EUSFLAT-LFA 2005, pp. 314–319 (2005)
Consiglio, A., Mencar, C., Grillo, G., Liuni, S.: Managing NGS differential expression uncertainty with fuzzy sets. In: Angelini, C., Rancoita, P.M.V., Rovetta, S. (eds.) CIBB 2015. LNCS, vol. 9874, pp. 42–53. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-44332-4_4
Consiglio, A., Mencar, C., Grillo, G., Marzano, F., Caratozzolo, M.F., Liuni, S.: A fuzzy method for RNA-Seq differential expression analysis in presence of multireads. BMC Bioinform. 17(S12:345), 167–182 (2016). https://doi.org/10.1186/s12859-016-1195-2
Acknowledgments
This work was partially funded by the INdAM - GNCS Project 2019 “Metodi per il trattamento di incertezza ed imprecisione nella rappresentazione e revisione di conoscenza”.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Mencar, C. (2020). Possibilistic Bounds for Granular Counting. In: Lesot, MJ., et al. Information Processing and Management of Uncertainty in Knowledge-Based Systems. IPMU 2020. Communications in Computer and Information Science, vol 1239. Springer, Cham. https://doi.org/10.1007/978-3-030-50153-2_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-50153-2_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-50152-5
Online ISBN: 978-3-030-50153-2
eBook Packages: Computer ScienceComputer Science (R0)



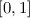 . The number of such values depend on a user-defined parameter
. The number of such values depend on a user-defined parameter 



