Abstract
OR-proofs enable a prover to show that it knows the witness for one of many statements, or that one out of many statements is true. OR-proofs are a remarkably versatile tool, used to strengthen security properties, design group and ring signature schemes, and achieve tight security. The common technique to build OR-proofs is based on an approach introduced by Cramer, Damgård, and Schoenmakers (CRYPTO’94), where the prover splits the verifier’s challenge into random shares and computes proofs for each statement in parallel.
In this work we study a different, less investigated OR-proof technique, highlighted by Abe, Ohkubo, and Suzuki (ASIACRYPT’02). The difference is that the prover now computes the individual proofs sequentially. We show that such sequential OR-proofs yield signature schemes which can be proved secure in the non-programmable random oracle model. We complement this positive result with a black-box impossibility proof, showing that the same is unlikely to be the case for signatures derived from traditional OR-proofs. We finally argue that sequential-OR signature schemes can be proved secure in the quantum random oracle model, albeit with very loose bounds and by programming the random oracle.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Sequential-OR proofs
- Zero-knowledge
- Signatures
- Non-programmable random oracle model
- Quantum random oracle model
1 Introduction
In a zero-knowledge \(\varSigma \)-protocol between a prover \({\textsf {P}}\) and a verifier \({\textsf {V}}\), the prover holds a statement \(x\) and a witness \(w\) for \(x\), and the verifier only \(x\). Both parties engage in an interactive execution, resulting in an initial commitment \(\mathsf {com}\) sent by the prover, a verifier random challenge \(\mathsf {ch}\), and a final response \(\mathsf {resp}\) computed by the prover. With such a proof, \({\textsf {P}}\) shows to \({\textsf {V}}\) that \(x\) is true (in proof systems), or that it knows a witness \(w\) for \(x\) (in proofs of knowledge). At the same time, the zero-knowledge property guarantees that nothing beyond this fact is revealed.
1.1 OR-Proofs
Now assume that one has two interactive proof systems of the above form for two statements \(x_0\) and \(x_1\), and a witness \(w_b\) for \(x_b\), \(b\in \{0,1\}\). The goal is to combine them into a single protocol which proves the logical OR of \(x_0\) and \(x_1\); that is, the prover should be able to convince a verifier that it holds a witness for one of the two statements, ideally without revealing which one. The first instantiation of such general OR-proofs, sometimes called CDS-OR proofs, was given by Cramer, Damgård, and Schoenmakers [23]. Their construction works under the assumption that the two protocols are special honest-verifier zero-knowledge, meaning that a simulator \(\mathsf {S}\), given \(x\) and a random challenge \(\mathsf {ch}\) at the outset, is able to generate a verifier view \((\mathsf {com},\mathsf {resp},\mathsf {ch})\) without knowing a witness for \(x\), in such a way that this view is indistinguishable from a genuine interaction between the real prover and an honest verifier using the given challenge. The prover in the CDS-OR protocol from [23] is described in Fig. 1. For reasons that will become apparent soon, we call such CDS-OR proofs also parallel-OR proofs.
Description of the prover algorithm \({\textsf {P}}_{\mathsf {par}\text {-}\mathsf {OR}}\) from the parallel-OR construction by Cramer et al. [23] in the standard model. On the left, generation of the first message \(\mathsf {com}=(\mathsf {com}_0,\mathsf {com}_1)\). On the right, computation of the final response \(\mathsf {resp}=(\mathsf {ch}_0,\mathsf {ch}_1,\mathsf {resp}_0,\mathsf {resp}_1)\) answering the verifier challenge \(\mathsf {ch}\).
An important observation is that the resulting protocol is witness indistinguishable, i.e., it does not reveal for which statement the prover holds a witness. Moreover, since the resulting protocol is again a \(\varSigma \)-protocol, one can apply the Fiat-Shamir transform [32] to it and obtain a non-interactive version or a signature scheme in the random oracle model. Also, the construction easily generalizes to the case of 1-out-of-n proofs.
1.2 Applications of OR-Proofs
OR-proofs have turned out to be a very powerful tool in the design of efficient protocols. Early on they have been identified as a means to thwart man-in-the-middle attacks [22] and, similarly in spirit, to give designated-verifier proofs [43]. The idea in both cases is to have the verifier send its public key to the prover, who then shows that the statement \(x\) it originally wanted to prove is true or that it knows the verifier’s secret key. This proof is still convincing for the verifier (who knows it is the only holder of its secret key), but not transferable to other parties. Garay et al. [38] apply the same idea to make zero-knowledge proofs simulation-sound and non-malleable, by putting a verification key into a common reference string (CRS). The prover then shows that the original statement \(x\) is true or that it knows the secret to the verification key in the CRS.
The idea of giving a valid proof when knowing a witness for only one of several statements can also be used in the context of group signatures [19] and ring signatures [56]. Given a set of public keys \(x_1,\dots ,x_n\), where the signer knows only one witness \(w_i\) (their own secret key), an OR-proof allows to sign anonymously on behalf of the entire group, and witness indistinguishability implies that the identity of the signer remains hidden. This design strategy appears explicitly for example in the group signature scheme of Camenisch [13].
The OR-technique has also proved very useful in deriving tightly-secure schemes. This approach has appeared in several works in the literature [6, 39, 42]. The idea is to first derive tightly-secure signature schemes from the OR-combination of some \(\varSigma \)-protocols. These schemes are then used within higher-level solutions (like key exchange protocols), passing on the tight security guarantees to these protocols.
1.3 Non-programmable Random Oracles
Another important feature of the OR-technique is that it facilitates the design of schemes in the non-programmable random oracle model. The general random oracle model comes with several remarkable technical properties, rooted in the formalization of the hash function as a truly random, oracle-based function. One of the most extraordinary consequences of this formalization is the programmability property of the random oracle, saying that one can adaptively choose the answers to random oracle queries made by the adversary. Indeed, the ability to change answers on the fly is a necessary feature of security proofs of some signature schemes [33, 35, 37, 61]. In practice, however, hash functions are not programmable and their values are fixed. Therefore, one would ideally prefer to forgo the programming of random oracle replies.
The fact that the OR-technique can be used to bypass the programmability issues with the random oracle model can already be observed in the early constructions of \(\varSigma \)-protocols, namely, the Okamoto variant [52] of the Schnorr signature scheme [57] and the Guillou-Quisquater variant [41] of the Fiat-Shamir signature protocol [32]. In these variants, based on number-theoretic specifics, one uses “embedded” OR-proofs which allow to simulate signatures without having to program the random oracle, as opposed to [32, 57] and explicitly carried out in [55]: One can then simply use the known witness to generate signatures.
Unfortunately, the security proofs of the signature schemes in [41, 52] still need programming at another step. Namely, in order to show that the adversary cannot forge signatures, one rewinds the execution and re-programs the random oracle in order to extract a witness (a technique called forking in [55]). This also comes with a loose security bound. Abdalla et al. [1] overcome the forking technique by considering passively-secure identification schemes, where the adversary is allowed to see transcripts of honest executions. Still, they program the random oracle when simulating signatures.
Later, Abdalla et al. [2] used the notion of lossy identification schemes to give non-forking security proofs for signatures derived via the Fiat-Shamir heuristic. Lossiness here roughly means that valid statements \(x\) are indistinguishable from so-called lossy ones, for which it is statistically impossible to find convincing proofs. This idea has later been adopted by lattice-based and LWE-based signature schemes such as [7, 49] (in the classical random oracle model) or the TESLA signature scheme [4] (in the quantum random oracle model [10]). Still, all approaches program the random oracle in order to be able to simulate signatures.
1.4 Sequential-OR Proofs
The above construction is the classical technique to combine \(\varSigma \)-protocols and prove OR-statements, but it is not the only possible solution. Indeed, there is at least one other way to prove the disjunction of two or more statements in the random oracle model, which in its spirit already appears in a work by Rivest, Shamir, and Tauman [56]. Here, we follow the exposition given by Abe, Ohkubo, and Suzuki [3] in the context of group signature schemes, and call this approach the sequential-OR technique.
In this construction, the non-interactive prover computes the individual proofs sequentially, starting with the commitment \(\mathsf {com}_b\) for the statement \(x_b\) for which it knows the witness \(w_b\). Next it derives the challenge \(\mathsf {ch}_{1-b}\) for the proof of \(x_{1-b}\) (with unknown witness) as the hash value of \(\mathsf {com}_b\). This in turn allows the OR-prover to simulate a view \((\mathsf {com}_{1-b},\mathsf {resp}_{1-b},\mathsf {ch}_{1-b})\) for \(x_{1-b}\) with this predetermined challenge, as done in parallel-OR proofs. The simulated commitment \(\mathsf {com}_{1-b}\) again yields the challenge \(\mathsf {ch}_b\) for the first proof through the hash function, which the prover now can answer with a valid response \(\mathsf {resp}_b\) since it knows the witness \(w_b\). The details of the prover in the sequential-OR protocol from [3] are described in Fig. 2.
Note that this technique generalizes to the 1-out-of-n case (we provide all details in the full version [34]). In fact, Abe et al. [3] and follow-up works like [8, 47], use this more general version of the sequential-OR technique to build group signature schemes, yet still programming the random oracle to fork and extract. The paradigm proposed by Abe et al. has also been applied in the area of cryptocurrencies, in particular Monero [58] and Mimblewimble [44, 54]. There, in order to prevent overflow attacks, it is necessary to prove that committed values fall within a specific range. One instance of such range proofs uses a special type of ring signature, called borromean ring signature [50], which is based on ideas presented in [3]. Observe that, in the aforementioned range proofs, borromean signatures have since been superseded by more efficient bulletproofs [12].
Description of the prover algorithm \({\textsf {P}}_{\mathsf {seq}\text {-}\mathsf {OR}}\) from the sequential-OR construction by Abe et al. [3] in the random oracle model.
1.5 Our Results
At first glance, the sequential-OR technique does not seem to give any significant advantage over the parallel version. Both protocols are based on the idea that one can easily give a proof for a statement for which the witness is known, and simulate the proof for the other statement where the challenge is known in advance. This, however, misses one important point if we combine these two approaches with the idea of lossy statements as in the work by Abdalla et al. [2]: We show that signatures derived from sequential-OR proofs are secure in the non-programmable random oracle model, whereas those originating from parallel-OR proofs do not seem to have a security proof in this model.
The signature scheme in the sequential-OR case is based on two valid statements \(x_0\) and \(x_1\) (the public keys), for which we know one of the two witnesses \(w_b\) (one of the secret keys). A signature for a message m is basically a sequential-OR proof, where m is included in the hash evaluations. In contrast to the proof in [3], which is based on forking, we can now reduce unforgeability to a decisional problem about the languages. This allows us to avoid rewinding and re-programming the random oracle.
The idea of our proof in the sequential-OR case can be illustrated by looking at the honest signer first. If one was able to observe the signer’s random oracle queries, then their order reveals which witness the signer is using: The signer first queries the commitment \(\mathsf {com}_b\) of the instance \(x_b\) for which it knows the witness \(w_b\). We will use the same idea against the adversary, helping us to decide if some random input \(x_{1-b}\) is in the language or not. If \(x_{1-b}\) is not in the language, and thus does not have a witness, the special soundness of the \(\varSigma \)-protocol guarantees that the adversary will never make the first query about this part, since it will then not be able to answer the random challenge.Footnote 1 Hence, by merely observing the adversary’s queries, we can decide membership of \(x_{1-b}\). We use the other part \(x_b\) in the key and its witness \(w_b\) to simulate signatures without programming the random oracle. But we need to make sure that the adversary is not biased by our signatures. This follows from the witness indistinguishability of the proofs (against an adversary who cannot observe random oracle queries).
We next argue that it is in general hard to show that the parallel-OR technique of Cramer et al. [23] yields a secure signature scheme in the non-programmable random oracle model. Our result assumes a black-box reduction \(\mathsf {R}\) transforming any (PPT or unbounded) adversary against the signature scheme into a solver of some hard problem, and makes a mild assumption about the zero-knowledge simulators of the languages (namely, that they work independently of how the statements \(x\) are generated). Remarkably, we do not make any stipulations about the reduction’s executions of the adversary instances: The reduction can run an arbitrary (bounded) number of instances of the adversary, and there are no restrictions on the inputs of these instances or their scheduling. However, the reduction \(\mathsf {R}\) can only use the external random oracle.
Our approach is based on the meta-reduction technique [11, 40, 53]. That is, we start with an unbounded adversary \(\mathsf {A}\), who breaks the signature scheme easily with its super-polynomial power by computing a secret key and signing as the honest prover would. This means that the reduction \(\mathsf {R}\) also solves the underlying problem when interacting with \(\mathsf {A}\). Afterwards, we show how to simulate \(\mathsf {A}\) efficiently, resulting in an efficient algorithm solving the problem directly. This implies that there cannot exist such a reduction \(\mathsf {R}\) in the first place.
The crucial difference between the sequential and the parallel version of the OR-technique is that in the latter case observing the random oracle queries of the adversary does not reveal which witness is being used. By the zero-knowledge property one cannot distinguish real and simulated sub-proofs in the parallel case. Indeed, our negative result relies exactly on this zero-knowledge property, taking advantage of the fact that the random oracle is external to the reduction.
1.6 Further Related Work
The issue of non-programmability of random oracles also appears in recent works related to Canetti’s universal composability (UC) framework [15]. In this model, random oracles can be cast as an ideal functionality \(\mathcal {F}_\textsf {RO}\), and protocols can be developed in the hybrid setting where \(\mathcal {F}_\textsf {RO}\) is present. A technical consequence of this design choice is that the random oracle is programmable, and a compositional consequence is that one would need a fresh random oracle for each protocol instance. Therefore, the global random oracle model [18], based on ideas of global set-ups [16, 26], defines a random oracle functionality \(\mathcal {G}_\textsf {sRO}\) which can be used by all protocols, obliterating also the programmability of the random oracle in this model.
We stress, however, that protocols designed in the global random oracle model are not necessarily secure for non-programmable random oracles. The discrepancy lies in the distinction between the model and the security proof: In the global random oracle model, one may no longer be able to program the random oracle when devising a simulator in the model, but a reduction may still program the random oracle in the security proof showing that the simulator is good. Indeed, this can be observed in the security reductions in [14] proving that all signature schemes which have a stand-alone proof of unforgeability in the “isolated” random oracle model, including schemes with a security reduction via programming, remain secure in the strict global random oracle model \(\mathcal {G}_\textsf {sRO}\).
The impossibility of proving the security of specific types of signatures derived via the Fiat-Shamir transform in the non-programmable random oracle model has already been discussed in prior works, e.g., [33, 36]. These works usually make some restrictions on the reduction being ruled out (like key preservation or being single-instance) , whereas we do not need any such condition. We remark here that our impossibility result for parallel-OR signatures does likely not follow in a general way from these results, since the same approach fails in the sequential-OR case.
In terms of OR-proofs, Ciampi et al. [20], based on an earlier approach by Lindell [46], use the OR-technique to build non-interactive zero-knowledge proofs from \(\varSigma \)-protocols in the non-programmable random oracle model. For technical reasons they also need a common reference string, which is used to form the OR-language. Note that this is orthogonal to our goal here, where we aim to build OR-proofs for two languages in the non-programmable random oracle model. In another work, Ciampi et al. [21] consider extensions of parallel-OR proofs where (some of) the languages are not specified yet when the execution starts. This includes the solution in the common reference string model in [20].
1.7 Extension to the Quantum Random Oracle Model
The results discussed so far are in the classical random oracle model. In terms of the quantum random oracle model (QROM), introduced by Boneh et al. [10], the situation regarding OR-proofs is less scrutinized. Our approach in the (classical) sequential-OR case is based on the observability of queries to the random oracle, a technique that usually does not carry over to the QROM because of superposition queries. In the parallel-OR case, we have seen that observability may not even help in the classical setting.
Fortunately, there have been two recent results regarding the security of Fiat-Shamir protocols in the QROM [27, 48], bypassing previous negative results concerning the Fiat-Shamir transform in this model [5, 24]. These works both yield a non-tight bound, but give an immediate solution for the parallel-OR case in the QROM. There, one first combines the two interactive proofs via the parallel-OR construction to get an interactive Fiat-Shamir proof, and then applies these techniques. We show in Sect. 6 that one can also prove security of signatures derived from the sequential-OR construction in the QROM via the measure-and-reprogram technique described in [27]. The price we pay is that we inherit the loose security bound from the solution in [27] and we, like all currently known constructions in the QROM, need to program the quantum random oracle.
2 Preliminaries
2.1 Basic Notation
We denote by \(\mathbb {N}=\mathbb {Z}_{\ge 0}\) the set of non-negative integers, and by \(\lambda \in \mathbb {N}\) the security parameter (often written in unary notation as \(1^\lambda \)). A function \(\mu :\mathbb {N}\rightarrow \mathbb {R}\) is called negligible if, for every constant \(c\in \mathbb {R}_{>0}\), there exists \(\lambda _c\in \mathbb {N}\) such that, for every \(\lambda \in \mathbb {N}\) with \(\lambda \ge \lambda _c\), we have \(\mu (\lambda )\le \lambda ^{-c}\). For a random variable X, we write  to denote that x is a random variate of X. For a finite set \(S\) of size \(\left|S \right|\), we use
to denote that x is a random variate of X. For a finite set \(S\) of size \(\left|S \right|\), we use  as a shorthand for
as a shorthand for  , where \(U_S\) is a random variable uniformly distributed over \(S\). The arrow \(\leftarrow \) will be used for assignment statements. We denote the length of a string \(x\in \{0,1\}^*\) by \(\left|x \right|\), and we write \(\varepsilon \) for the empty string. We consider an injective, efficiently computable, efficiently reversible, and length-increasing encoding function \((\{0,1\}^*)^*\rightarrow \{0,1\}^*\). This allows us to represent sequences of strings again as strings, and will be tacitly used throughout the paper.
, where \(U_S\) is a random variable uniformly distributed over \(S\). The arrow \(\leftarrow \) will be used for assignment statements. We denote the length of a string \(x\in \{0,1\}^*\) by \(\left|x \right|\), and we write \(\varepsilon \) for the empty string. We consider an injective, efficiently computable, efficiently reversible, and length-increasing encoding function \((\{0,1\}^*)^*\rightarrow \{0,1\}^*\). This allows us to represent sequences of strings again as strings, and will be tacitly used throughout the paper.
In this work we use the computational model of probabilistic oracle Turing machines, also called algorithms. We assume that they are equipped with a separate security parameter tape containing the value \(1^\lambda \). The running time of algorithms, which is intended to be bounded by the worst case, is a function of the security parameter input length only. A uniform algorithm is called probabilistic polynomial-time (PPT) if its running time is bounded by a polynomial, whereas a non-uniform algorithm is PPT if it corresponds to an infinite sequence of Turing machines, indexed by the security parameter \(\lambda \), whose description sizes and running times are bounded by a polynomial in \(\lambda \). Queries to the oracles always count as one operation each. For an algorithm \(\mathsf {A}\), we denote by \(\mathsf {A}^{\mathcal {O}}(1^\lambda ;x)\) the random variable representing the output of \(\mathsf {A}\) when run on security parameter \(\lambda \) and input \(x\in \{0,1\}^*\), with access to oracles \(\mathcal {O}=(\mathcal {O}_1,\dots ,\mathcal {O}_t)\).
We use \(\bot \) as a special symbol to denote rejection or an error, and we assume that \(\bot \notin \{0,1\}^*\). Both inputs and outputs of algorithms can be \(\bot \), and we convene that if any input to an algorithm is \(\bot \), then its output is \(\bot \) as well. Double square brackets \([\![{\cdot }]\!]\) enclosing boolean statements return the bit 1 if the statement is true, and 0 otherwise.
2.2 Random Oracle Model
Let \(\ell :\mathbb {N}\rightarrow \mathbb {N}\) be a polynomial-time computable function. For a security parameter \(\lambda \in \mathbb {N}\), a random oracle (RO) [9, 17] is an oracle \(\mathcal {H}\) that implements a function randomly chosen from the space of all functions \(\{0,1\}^*\rightarrow \{0,1\}^{\ell (\lambda )}\), to which all parties have access. In other words, it is an oracle that answers every query with a truly random response chosen from the range \(\{0,1\}^{\ell (\lambda )}\). For every repeated query the random oracle consistently returns the same output.
Constructions established and statements proved in the presence of a RO are said to hold in the random oracle model (ROM). Throughout the paper, whenever a security game is set in the ROM, we assume that at the beginning of the experiment a random oracle is sampled uniformly from the aforementioned function space, and then used throughout the experiment. In this setting, it will sometimes be necessary to record queries to the random oracle \(\mathcal {H}\), and we will do so via a set \(Q_{\mathcal {H}}\): If \((i,x)\in Q_{\mathcal {H}}\), this means that the i-th query to \(\mathcal {H}\) was x.
We also define the “zero oracle” as a function \(\mathcal {Z}:\{0,1\}^*\rightarrow \{0,1\}^{\ell (\lambda )}\), with \(\mathcal {Z}(x)= 0^{\ell (\lambda )}\) for all \(x\in \{0,1\}^*\). This allows us to state our definitions simultaneously in the standard model and in the ROM: Parties will be given access to a generic oracle \(\mathcal {O}\), and it is understood that \(\mathcal {O}\,{:}{=}\,\mathcal {Z}\) if the definition is formulated in the standard model, and \(\mathcal {O}\,{:}{=}\,\mathcal {H}\) if it is in the ROM.
The quantum analogue of the above is the so-called quantum random oracle model (QROM), introduced by Boneh et al. [10]. Here, a quantum algorithm may query the random oracle \(\mathcal {H}\) in superposition, i.e., submit superposition queries of the form \(\sum _{x} \alpha _x{|}x{\rangle }{|}0{\rangle }\) and obtain the output \(\sum _{x} \alpha _x {|}x{\rangle }{|}\mathcal {H}(x){\rangle }\). We refer to [51] for further background and conventions regarding quantum information.
2.3 Languages and Relations
A language is a subset \(L\subseteq \{0,1\}^*\). In this work, we assume that every language \(L\) is equipped with a uniform PPT algorithm \(\mathsf {G}_L\) (called instance generator) which, on input \((1^\lambda ;b)\) with \(b\in \{0,1\}\), returns an element \(x\in L\) if \(b=1\) (yes-instance), and an element \(x\notin L\) if \(b=0\) (no-instance). Usually, the complexity of \(x\) is closely related to the security parameter \(\lambda \), e.g., \(\left|x \right|=\lambda \), but we can allow for other (polynomial) dependencies as well.
A binary relation is a subset \(R\subseteq \{0,1\}^*\times \{0,1\}^*\) which is polynomially bounded, i.e., there exists a polynomial p such that, for every \((x,w)\in R\), we have \(\left|w \right|\le p(\left|x \right|)\). If \((x,w)\in R\), we call \(x\) an \(R\)-instance and \(w\) an \(R\)-witness of \(x\). For every \(x\in \{0,1\}^*\), we denote the set of all \(R\)-witnesses of \(x\) by  (if \(x\) is not an \(R\)-instance, then \(W_R(x)=\emptyset \)). Note that every binary relation \(R\) defines a language
(if \(x\) is not an \(R\)-instance, then \(W_R(x)=\emptyset \)). Note that every binary relation \(R\) defines a language  . Just like before for languages, we also assume that every binary relation \(R\) is equipped with a uniform PPT algorithm \(\mathsf {G}_R\) (called instance generator) which, on input \((1^\lambda ;b)\) with \(b\in \{0,1\}\), returns a pair \((x,w)\in R\) if \(b=1\) (yes-instance), and an element \(x\notin L_R\) if \(b=0\) (no-instance). Observe that from an instance generator \(\mathsf {G}_R\) for a binary relation \(R\) we get an instance generator \(\mathsf {G}_{L_R}\) for \(L_R\) by simply running \(\mathsf {G}_R\) and returning the first component only if \(b=1\).
. Just like before for languages, we also assume that every binary relation \(R\) is equipped with a uniform PPT algorithm \(\mathsf {G}_R\) (called instance generator) which, on input \((1^\lambda ;b)\) with \(b\in \{0,1\}\), returns a pair \((x,w)\in R\) if \(b=1\) (yes-instance), and an element \(x\notin L_R\) if \(b=0\) (no-instance). Observe that from an instance generator \(\mathsf {G}_R\) for a binary relation \(R\) we get an instance generator \(\mathsf {G}_{L_R}\) for \(L_R\) by simply running \(\mathsf {G}_R\) and returning the first component only if \(b=1\).
An \(\mathcal {NP}\)-relation is a binary relation that is polynomial-time recognizable, i.e., \(R\in \mathcal {P}\). Observe that if \(R\) is an \(\mathcal {NP}\)-relation, then \(L_R\in \mathcal {NP}\), and vice-versa if \(L\in \mathcal {NP}\), then the set \(R_L\) of all string pairs \((x,w)\in \{0,1\}^*\times \{0,1\}^*\) with \(x\in L\) and \(w\) an \(\mathcal {NP}\)-witness for \(x\) (w.r.t. a fixed polynomial and Turing machine) is an \(\mathcal {NP}\)-relation. In this situation, we have of course \(L_{R_L}=L\) and \(R_{L_R}\supseteq R\).
We next define the OR-combination of two relations and its instance generator. Here and in the following, we present all definitions and constructions with respect to the OR of two relations only, but all results extend to the more general 1-out-of-n case. A yes-instance of the OR-relation is a pair of values \((x_0,x_1)\), each in its respective language, together with a witness \(w\) of either value. A no-instance of the OR-relation is again a pair of values, where at least one is not in the corresponding language, while the other may or may not belong to its language. The convention that a yes-instance has both inputs in their respective languages corresponds to the setting of group signature schemes, where all parties choose their public keys honestly; only in security reductions one may diverge from this. It is also in general necessary to ensure completeness of the OR-protocol, since the simulator for \(x_{1-b}\) is only guaranteed to output a valid transcript for yes-instances.
Definition 1
Let \(R_0\) and \(R_1\) be two binary relations. Define the OR-relation of \(R_0\) and \(R_1\) as the binary relation

equipped with the instance generator \(\mathsf {G}_{R_{\mathsf {OR}}}\) defined in Fig. 3. We denote the corresponding OR-language by \(L_{\mathsf {OR}}\,{:}{=}\, L_{R_{\mathsf {OR}}}\).
Observe that, for binary relations \(R_0\) and \(R_1\), the relation \(R_{\mathsf {OR}}\) is indeed a binary relation, and that \(L_{\mathsf {OR}}=L_{R_0}\times L_{R_1}\).
We now recall two hardness notions a binary relation \(R\) may satisfy. Intuitively, \(R\) is decisionally hard if no PPT distinguisher can decide if it is given an \(R\)-instance or a no-instance. It is computationally hard if no PPT adversary can efficiently compute an \(R\)-witness \(w\) for a given \(R\)-instance \(x\).
Definition 2
Let \(R\) be a binary relation. We say that \(R\) is:
-
1.
Decisionally Hard if, for every PPT distinguisher \(\mathsf {D}\), there exists a negligible function \(\mu :\mathbb {N}\rightarrow \mathbb {R}\) such that, for every \(\lambda \in \mathbb {N}\) and every \(z\in \{0,1\}^*\),

where \(\mathbf {Exp}^{\mathsf {DHR},0}_{\mathsf {D},R}(\lambda ,z)\) and \(\mathbf {Exp}^{\mathsf {DHR},1}_{\mathsf {D},R}(\lambda ,z)\) are defined in Fig. 3.
-
2.
Computationally Hard if, for every PPT algorithm \(\mathsf {A}\), there exists a negligible function \(\mu :\mathbb {N}\rightarrow \mathbb {R}\) such that, for every \(\lambda \in \mathbb {N}\) and every \(z\in \{0,1\}^*\),

where \(\mathbf {Exp}^{\mathsf {CHR}}_{\mathsf {A},R}(\lambda ,z)\) is defined in Fig. 3.
It is readily verified that two binary relations \(R_0\) and \(R_1\) are computationally hard if and only if \(R_\mathsf {OR}\) is computationally hard. Furthermore, if an \(\mathcal {NP}\)-relation \(R\) is decisionally hard, it is also computationally hard.
2.4 Interactive Protocols
An interactive protocol \(\varPi \) between two parties, called prover and verifier, is a pair of uniform algorithms \(\varPi =({\textsf {P}},{\textsf {V}})\). We write \({\textsf {P}}^{\mathcal {O}}(1^\lambda ;x,w)\leftrightarrows {\textsf {V}}^{\mathcal {O}}(1^\lambda ;x,z)\) to denote the interaction between \({\textsf {P}}\) and \({\textsf {V}}\) on security parameter \(\lambda \), common input x, respective auxiliary inputs w and z, and with access to oracle \({\mathcal {O}}\).
Definition of the instance generator \(\mathsf {G}_{R_{\mathsf {OR}}}\) of the relation \(R_{\mathsf {OR}}\), and of the experiments \(\mathbf {Exp}^{\mathsf {DHR},b}_{\mathsf {D},R}(\lambda ,z)\) and \(\mathbf {Exp}^{\mathsf {CHR}}_{\mathsf {A},R}(\lambda ,z)\) from Definition 2. Recall that \(\mathcal {O}\) is either a random oracle or the trivial all-zero oracle.
Algorithms \({\textsf {P}}\) and \({\textsf {V}}\) compute the next-message function of the corresponding party. In more detail, \({\textsf {P}}^{\mathcal {O}}(1^\lambda ;\beta _i,\mathsf {st}_{{\textsf {P}}})\) is the random variable which returns the prover’s next message \(\alpha _{i+1}\) and its updated state \(\mathsf {st}_{{\textsf {P}}}\), both computed on input the security parameter \(\lambda \), the last incoming message \(\beta _i\), and the current state \(\mathsf {st}_{{\textsf {P}}}\). Here we assume that \(\mathsf {st}_{{\textsf {P}}}\) contains all the information necessary for \({\textsf {P}}\) to perform its computation, including at least the common input, its auxiliary input, and the messages exchanged thus far. Similar considerations hold for \({\textsf {V}}\).
We write  for the transcript of the interaction between \({\textsf {P}}\) and \({\textsf {V}}\). This is the random variable which returns a sequence of messages \((\alpha _1,\beta _1,\dots ,\alpha _t,\beta _t,\alpha _{t+1})\), where
for the transcript of the interaction between \({\textsf {P}}\) and \({\textsf {V}}\). This is the random variable which returns a sequence of messages \((\alpha _1,\beta _1,\dots ,\alpha _t,\beta _t,\alpha _{t+1})\), where  and
and  for every \({0\le i\le t}\) and \(1\le j\le t\). Here we assume that \(\mathsf {st}_{{\textsf {P}}}\), \(\mathsf {st}_{{\textsf {V}}}\) and \(\beta _0\) are initialized to \(\mathsf {st}_{{\textsf {P}}}\leftarrow (x,w)\), \(\mathsf {st}_{{\textsf {V}}}\leftarrow (x,z)\) and \(\beta _0\leftarrow \varepsilon \). The view of \({\textsf {V}}\) in the interaction with \({\textsf {P}}\), denoted
for every \({0\le i\le t}\) and \(1\le j\le t\). Here we assume that \(\mathsf {st}_{{\textsf {P}}}\), \(\mathsf {st}_{{\textsf {V}}}\) and \(\beta _0\) are initialized to \(\mathsf {st}_{{\textsf {P}}}\leftarrow (x,w)\), \(\mathsf {st}_{{\textsf {V}}}\leftarrow (x,z)\) and \(\beta _0\leftarrow \varepsilon \). The view of \({\textsf {V}}\) in the interaction with \({\textsf {P}}\), denoted  , is the random variable \(\mathopen {}\left( A_1,A_2,\dots ,A_t,A_{t+1},R_{{\textsf {V}}}\right) \mathclose {}\), where \(R_{{\textsf {V}}}\) is the random variable representing \({\textsf {V}}\)’s random coins.
, is the random variable \(\mathopen {}\left( A_1,A_2,\dots ,A_t,A_{t+1},R_{{\textsf {V}}}\right) \mathclose {}\), where \(R_{{\textsf {V}}}\) is the random variable representing \({\textsf {V}}\)’s random coins.
The interaction between prover and verifier terminates with \({\textsf {V}}\) computing a decision  , where \(v \in \{0,1\}\), on whether to accept or reject the transcript. This is also called \({\textsf {V}}\)’s local output, and the corresponding random variable will be denoted by \(\mathrm {out}_{{\textsf {V}}}\!\!\big [{\textsf {P}}^{\mathcal {O}}(1^\lambda ;x,w)\leftrightarrows {\textsf {V}}^{\mathcal {O}}(1^\lambda ;x,z)\big ]\).
, where \(v \in \{0,1\}\), on whether to accept or reject the transcript. This is also called \({\textsf {V}}\)’s local output, and the corresponding random variable will be denoted by \(\mathrm {out}_{{\textsf {V}}}\!\!\big [{\textsf {P}}^{\mathcal {O}}(1^\lambda ;x,w)\leftrightarrows {\textsf {V}}^{\mathcal {O}}(1^\lambda ;x,z)\big ]\).
We say that a protocol \(\varPi =({\textsf {P}},{\textsf {V}})\) is efficient if \({\textsf {V}}\) is a PPT algorithm. For a binary relation \(R\), we say that \(\varPi \) has an efficient prover w.r.t. \(R\) if \({\textsf {P}}\) is a PPT algorithm and, on security parameter \(\lambda \), it receives common and auxiliary inputs \(x\) and \(w\) such that  . Note that we will only consider protocols which are efficient, have an efficient prover w.r.t. a specified binary relation \(R\), and where the honest verifier is independent of its auxiliary input (we can therefore assume \(z=\varepsilon \) in this case). We call these protocols w.r.t. \(R\).
. Note that we will only consider protocols which are efficient, have an efficient prover w.r.t. a specified binary relation \(R\), and where the honest verifier is independent of its auxiliary input (we can therefore assume \(z=\varepsilon \) in this case). We call these protocols w.r.t. \(R\).
We call \(\varPi \) public-coin (PC) if all the messages the honest verifier sends to \({\textsf {P}}\) consist of disjoint segments of its random tape, and if \({\textsf {V}}\)’s local output is computed as a deterministic function of the common input and the transcript, that is \(v\leftarrow {\textsf {V}}^{\mathcal {O}}(1^\lambda ;x,\alpha _1,\beta _1,\dots ,\alpha _t,\beta _t,\alpha _{t+1})\). In this situation we say that a transcript is accepting for x if \(v=1\).
We now recall the notion of computational witness indistinguishability [31], which is the property of general interactive protocols that is most relevant to our work. Intuitively, this notion captures the idea that protocol runs for a fixed \(R\)-instance but different witnesses should be indistinguishable. For the sake of completeness, we state the precise definitions of the completeness, soundness, honest-verifier zero-knowledge (HVCZK), and computational witness hiding (CWH) properties in the full version [34].
Definition 3
Let \(R\) be a binary relation, and let \(\varPi \,=\,\) ( P, V ) be a protocol w.r.t. \(R\). We say that \(\varPi \) is Computationally Witness Indistinguishable (CWI) if, for every uniform PPT algorithm V \(^*\) and every PPT distinguisher \(\mathsf {D}\), there exists a negligible function \(\mu :\mathbb {N}\rightarrow \mathbb {R}\) such that, for every \(\lambda \in \mathbb {N}\), every  , every \(w,w'\in W_R(x)\), and every \(z,z'\in \{0,1\}^*\),
, every \(w,w'\in W_R(x)\), and every \(z,z'\in \{0,1\}^*\),

where \(\mathbf {Exp}^{\mathsf {CWI},b}_{{\mathsf {V}}^*,\mathsf {D},\varPi }(\lambda ,x,w,w',z,z')\) is defined in Fig. 4.
Note that we will later require a stronger version of CWI, which we term multi-query computational witness indistinguishability (mqCWI) and define formally in the full version [34]. This is basically an oracle extension of ordinary CWI, where the distinguisher can query arbitrarily many protocol executions before guessing which witness was used to generate them. One can prove via a simple hybrid argument that CWI and mqCWI are equivalent, albeit with a polynomial loss in the distinguishing advantage.
2.5 3PC-Protocols and \(\varSigma \)-Protocols
Let \(R\) be a binary relation. We will be mainly interested in so-called 3PC-protocols w.r.t. \(R\), i.e., protocols w.r.t. \(R\) which are public-coin, and where the two parties exchange exactly three messages. We also assume that, on security parameter \(\lambda \), the only message sent by the verifier to the prover has fixed length \(\ell (\lambda )\), for a function \(\ell :\mathbb {N}\rightarrow \mathbb {N}\) called the length function associated to the protocol. A graphical representation of such a protocol is given in Fig. 5.
In this particular context, we call the three messages exchanged between prover and verifier the commitment, the challenge, and the response, and denote them by \(\mathsf {com}\,{:}{=}\,\alpha _1\), \(\mathsf {ch}\,{:}{=}\,\beta _1\), and \(\mathsf {resp}\,{:}{=}\,\alpha _2\), respectively. Furthermore, we say that two accepting transcripts \((\mathsf {com},\mathsf {ch},\mathsf {resp})\) and \((\mathsf {com}',\mathsf {ch}',\mathsf {resp}')\) for an element \(x\) constitute a transcript collision for \(x\) if \(\mathsf {com}=\mathsf {com}'\) and \(\mathsf {ch}\ne \mathsf {ch}'\).
We now recall the critical notion of special computational zero-knowledge. Intuitively, it means that there exists a simulator which, for any maliciously chosen challenge given in advance, is able to create an authentic-looking transcript.
Definition 4
Let \(R\) be a binary relation, and let \(\varPi \,=\,\) ( P, V ) be a 3PC protocol w.r.t. \(R\). We say that \(\varPi \) is Special Computational Zero-Knowledge (SCZK), if there exists a uniform PPT algorithm \(\mathsf {S}\) with the following property: For every two-stage PPT distinguisher \(\mathsf {D}=(\mathsf {D}_0,\mathsf {D}_1)\), there exists a negligible function \(\mu :\mathbb {N}\rightarrow \mathbb {R}\) such that, for every \(\lambda \in \mathbb {N}\), every  , and every \(z\in \{0,1\}^*\),
, and every \(z\in \{0,1\}^*\),

where \(\mathbf {Exp}^{\mathsf {SCZK},b}_{\mathsf {D},\varPi }(\lambda ,x,w,z)\) is defined in Fig. 4.
The definitions of other properties of 3PC protocols, like optimal and special soundness, are included in the full version [34]. Roughly, optimal soundness says that for every \(x\notin L\) and every commitment, there is at most one challenge which can lead to a valid response. Special soundness says that for \(x\in L\), any transcript collision yields a witness, and for \(x\notin L\) no collisions can be found. We are now in a position to define the notion of a \(\varSigma \)-protocol.
Definition 5
Let \(R\) be a binary relation. A \(\varSigma \)-protocol w.r.t. \(R\) is a 3PC protocol \(\varPi \) w.r.t. \(R\) which is complete, specially sound, and SCZK.
3 Parallel-OR Proofs
In this section we recall the classical parallel-OR construction of Cramer et al. [23], which works for two arbitrary 3PC HVCZK protocols.
Details of the parallel-OR construction by Cramer et al. [23]. Parts specific to the case where both \(\varPi _0\) and \(\varPi _1\) are SCZK (in comparison to HVCZK) are highlighted in
 .
.
Let \(R_0\) and \(R_1\) be binary relations, and consider two 3PC HVCZK protocols \(\varPi _0=({\textsf {P}}_0,{\textsf {V}}_0)\), \(\varPi _1=({\textsf {P}}_1,{\textsf {V}}_1)\) w.r.t. \(R_0\) and \(R_1\) (with HVCZK-simulators \(\mathsf {S}_0\) and \(\mathsf {S}_1\)), such that the two length functions \(\ell _0=\ell _1\,{=}{:}\,\ell \) coincide (this is no real restriction, as the challenge length of such a protocol can be increased via parallel repetition). The construction, first presented in [23] and depicted in Fig. 6, allows to combine \(\varPi _0\) and \(\varPi _1\) into a new 3PC HVCZK protocol \(\mathsf {par}\text {-}\mathsf {OR}\mathopen {}\left[ \varPi _0,\varPi _1,\mathsf {S}_0,\mathsf {S}_1\right] \mathclose {}=({\textsf {P}}_{\mathsf {par}\text {-}\mathsf {OR}},{\textsf {V}}_{\mathsf {par}\text {-}\mathsf {OR}})\) w.r.t. the binary relation \(R_{\mathsf {OR}}\). Note that the simulators of the two protocols become an integral part of the scheme.
The key idea of the construction is to split the challenge \(\mathsf {ch}\) sent by \({\textsf {V}}_{\mathsf {par}\text {-}\mathsf {OR}}\) into two random parts, \(\mathsf {ch}=\mathsf {ch}_0\oplus \mathsf {ch}_1\), and to provide accepting transcripts for both inputs \(x_0\) and \(x_1\) with the corresponding challenge share. If the prover knows a witness \(w\) for \(x_b\), it can use the HVCZK-simulator \(\mathsf {S}_{1-b}\) of \(\varPi _{1-b}\) to generate a simulated view \((\mathsf {com}_{1-b},\mathsf {resp}_{1-b},\mathsf {ch}_{1-b})\) for \(x_{1-b}\), and then compute a genuine transcript \((\mathsf {com}_b,\mathsf {ch}_b,\mathsf {resp}_b)\) for \(x_b\) using the witness \(w\) it knows.
Observe that the same idea works with minor changes if \(\varPi _0\) and \(\varPi _1\) are both SCZK w.r.t. \(R_0\) and \(R_1\) (instead of HVCZK). The only difference is that \({\textsf {P}}_{\mathsf {par}\text {-}\mathsf {OR}}\) must now sample a random challenge \(\mathsf {ch}_{1-b}\) before running the SCZK-simulator \(\mathsf {S}_{1-b}\) in the first step. The main properties of \(\mathsf {par}\text {-}\mathsf {OR}\mathopen {}\left[ \varPi _0,\varPi _1,\mathsf {S}_0,\mathsf {S}_1\right] \mathclose {}\) are summarized in the following.
Theorem 6
Let \(R_0\) and \(R_1\) be binary relations, and let \(\varPi _0\) and \(\varPi _1\) be two 3PC HVCZK protocols w.r.t. \(R_0\) and \(R_1\), such that the length functions satisfy \(\ell _0=\ell _1\,{=}{:}\,\ell \). Consider the protocol \(\varPi =\mathsf {par}\text {-}\mathsf {OR}\mathopen {}\left[ \varPi _0,\varPi _1,\mathsf {S}_0,\mathsf {S}_1\right] \mathclose {}\). Then:
-
1.
\(\varPi \) is a 3PC CWI HVCZK protocol w.r.t. \(R_{\mathsf {OR}}\).
-
2.
If \(\varPi _0\) and \(\varPi _1\) are complete, then \(\varPi \) is also complete.
-
3.
If \(R_0\) and \(R_1\) are \(\mathcal {NP}\)-relations and \(R_{\mathsf {OR}}\) is computationally hard, then \(\varPi \) is CWH.
Furthermore, if both \(\varPi _0\) and \(\varPi _1\) are SCZK, then \(\varPi \) is SCZK.
The proof of the above can be found in a slightly different syntactical version in [25], whereas the particular proof of the CWH property can be found in [59]. Note that one can build a secure signature scheme \(\mathsf {sFS}\mathopen {}\left[ \varPi ,\mathcal {H}\right] \mathclose {}\) in the ROM from the protocol \(\varPi \) applying the Fiat-Shamir transform, which we discuss in more detail in the full version [34].
4 Sequential-OR Proofs
In this section, we discuss an alternative OR-proof technique which we call sequential-OR. This technique was first used in the context of group signature schemes by Abe et al. [3]. On a high level, in the sequential-OR variant the prover derives two sub-proofs, where data from one proof is used to derive the challenge for the other one.
4.1 Protocol
Similarly to Sect. 3, we denote by \(R_0\) and \(R_1\) two binary relations, and consider two 3PC SCZK protocols \(\varPi _0=({\textsf {P}}_0,{\textsf {V}}_0)\) and \(\varPi _1=({\textsf {P}}_1,{\textsf {V}}_1)\) w.r.t. \(R_0\) and \(R_1\) and simulators \(\mathsf {S}_0\) and \(\mathsf {S}_1\), such that the two length functions \(\ell _0\,=\,\ell _1\,{=}{:}\,\ell \) coincide. Furthermore, let \(\mathcal {H}\) be a random oracle. The sequential-OR construction enables one to merge the two protocols \(\varPi _0\) and \(\varPi _1\) into a non-interactive protocol \(\mathsf {seq}\text {-}\mathsf {OR}[\varPi _0, \varPi _1, \mathsf {S}_0,\mathsf {S}_1,\mathcal {H}] = ({\textsf {P}}_{\mathsf {seq}\text {-}\mathsf {OR}}, {\textsf {V}}_{\mathsf {seq}\text {-}\mathsf {OR}})\) w.r.t. the binary relation \(R_\mathsf {OR}\). The formal details of the protocol are summarized in Fig. 7.
Details of the sequential-OR construction by Abe et al. [3].
The key idea of the construction is to compute the challenge for the instance the prover indeed does know the witness of, based on the commitment for which it does not know the witness (derived via the SCZK-simulator). In more detail, on input the security parameter \(\lambda \in \mathbb {N}\), consider a yes-instance for the OR-relation  . The protocol \(\mathsf {seq}\text {-}\mathsf {OR}[\varPi _0, \varPi _1, \mathsf {S}_0,\mathsf {S}_1,\mathcal {H}]\) starts with the prover \({\textsf {P}}_{\mathsf {seq}\text {-}\mathsf {OR}}\) and verifier \({\textsf {V}}_{\mathsf {seq}\text {-}\mathsf {OR}}\) receiving \((x_0,x_1)\) as common input. Additionally, \({\textsf {P}}_{\mathsf {seq}\text {-}\mathsf {OR}}\) receives the witness \((b,w)\) as auxiliary input. The protocol then proceeds in the following way:
. The protocol \(\mathsf {seq}\text {-}\mathsf {OR}[\varPi _0, \varPi _1, \mathsf {S}_0,\mathsf {S}_1,\mathcal {H}]\) starts with the prover \({\textsf {P}}_{\mathsf {seq}\text {-}\mathsf {OR}}\) and verifier \({\textsf {V}}_{\mathsf {seq}\text {-}\mathsf {OR}}\) receiving \((x_0,x_1)\) as common input. Additionally, \({\textsf {P}}_{\mathsf {seq}\text {-}\mathsf {OR}}\) receives the witness \((b,w)\) as auxiliary input. The protocol then proceeds in the following way:
-
1.
\({\textsf {P}}_{\mathsf {seq}\text {-}\mathsf {OR}}\) sets \(\mathsf {st}_{{\textsf {P}}_b}\leftarrow (x_b,w)\) and computes
 . It then computes the challenge \(\mathsf {ch}_{1-b}\) evaluating the random oracle \({\mathcal {H}}\) on the common input \((x_0,x_1)\) and the previously generated commitment \(\mathsf {com}_b\). It also includes the bit b from the witness for domain separation. Next, it runs the SCZK-simulator \(\mathsf {S}_{1-b}\) to obtain a simulated view
. It then computes the challenge \(\mathsf {ch}_{1-b}\) evaluating the random oracle \({\mathcal {H}}\) on the common input \((x_0,x_1)\) and the previously generated commitment \(\mathsf {com}_b\). It also includes the bit b from the witness for domain separation. Next, it runs the SCZK-simulator \(\mathsf {S}_{1-b}\) to obtain a simulated view 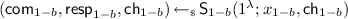 . It then obtains the challenge \(\mathsf {ch}_{b}\) for the first proof by evaluating \({\mathcal {H}}\) on the common input \((x_0,x_1)\), the commitment \(\mathsf {com}_{1-b}\) from the simulator, and the bit \(1-b\). Finally, \({\textsf {P}}_{\mathsf {seq}\text {-}\mathsf {OR}}\) computes
. It then obtains the challenge \(\mathsf {ch}_{b}\) for the first proof by evaluating \({\mathcal {H}}\) on the common input \((x_0,x_1)\), the commitment \(\mathsf {com}_{1-b}\) from the simulator, and the bit \(1-b\). Finally, \({\textsf {P}}_{\mathsf {seq}\text {-}\mathsf {OR}}\) computes 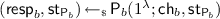 using the witness for \(x_b\), and sends \(\mathsf {resp}\leftarrow (\mathsf {com}_0, \mathsf {com}_1, \mathsf {resp}_0, \mathsf {resp}_1)\) to \({\textsf {V}}_{\mathsf {seq}\text {-}\mathsf {OR}}\).
using the witness for \(x_b\), and sends \(\mathsf {resp}\leftarrow (\mathsf {com}_0, \mathsf {com}_1, \mathsf {resp}_0, \mathsf {resp}_1)\) to \({\textsf {V}}_{\mathsf {seq}\text {-}\mathsf {OR}}\). -
2.
\({\textsf {V}}_{\mathsf {seq}\text {-}\mathsf {OR}}\) first re-computes both challenge values using the random oracle \(\mathcal {H}\). It then accepts the proof if and only if both transcripts verify correctly, i.e., \({\textsf {V}}_0(1^\lambda ;x_0,\mathsf {com}_0,\mathsf {ch}_0,\mathsf {resp}_0)=1\) and \({\textsf {V}}_1(1^\lambda ;x_1,\mathsf {com}_1,\mathsf {ch}_1,\mathsf {resp}_1)=1\).
In the following theorem, we establish the main properties of the protocol \(\mathsf {seq}\text {-}\mathsf {OR}[\varPi _0, \varPi _1,\mathsf {S}_0,\mathsf {S}_1, \mathcal {H}]\).
Theorem 7
Let \(R_0\) and \(R_1\) be binary relations, and let \(\varPi _0\) and \(\varPi _1\) be two 3PC SCZK protocols w.r.t. \(R_0\) and \(R_1\), such that the length functions satisfy \(\ell _0=\ell _1\,{=}{:}\,\ell \). Consider the protocol \(\varPi =\mathsf {seq}\text {-}\mathsf {OR}\mathopen {}\left[ \varPi _0,\varPi _1,\mathsf {S}_0,\mathsf {S}_1,\mathcal {H}\right] \mathclose {}\). Then the following holds in the ROM:
-
1.
\(\varPi \) is a 1-move CWI protocol w.r.t. \(R_{\mathsf {OR}}\).
-
2.
If \(\varPi _0\) and \(\varPi _1\) are complete, then \(\varPi \) is also complete.
-
3.
If \(R_0\) and \(R_1\) are \(\mathcal {NP}\)-relations and \(R_{\mathsf {OR}}\) is computationally hard, then \(\varPi \) is CWH.
A detailed proof of Theorem 7 as well as an extension of the above technique to the more general 1-out-of-n case can be found in the full version [34].
Description of the signature scheme \(\varGamma =(\mathsf {KGen},\mathsf {Sign},\mathsf {Verify})\) obtained from the protocol \(\mathsf {seq}\text {-}\mathsf {OR}\mathopen {}\left[ \varPi _0,\varPi _1,\mathsf {S}_0,\mathsf {S}_1,\mathcal {H}\right] \mathclose {}\) by appending the message m being signed to all random oracle queries.
4.2 Sequential-OR Signatures
We now show how one can use the sequential-OR proof technique (see Fig. 7) to build a secure signature scheme \(\varGamma =(\mathsf {KGen},\mathsf {Sign},\mathsf {Verify})\) in the non-programmable ROM. On a high level, the signer runs a normal execution of the protocol \(\mathsf {seq}\text {-}\mathsf {OR}\mathopen {}\left[ \varPi _0,\varPi _1,\mathsf {S}_0,\mathsf {S}_1,\mathcal {H}\right] \mathclose {}\), but always includes the message m being signed when it queries the random oracle to obtain the challenges. Signatures in this scheme consist of the commitments and responses generated during the protocol execution, and verification can be achieved by re-computing the challenges (again, including the message) and checking whether the two transcripts verify. The formal details of the scheme can be found in Fig. 8, and we provide a detailed description in the following.
The signature scheme’s key generation algorithm runs the instance generator  of the relation \(R_{\mathsf {OR}}\), which returns an \(R_{\mathsf {OR}}\)-instance \((x_0, x_1)\) and a witness \(w\) for \(x_b\). The pair \((x_0, x_1)\) then constitutes the public verification key, and \((b,w)\) is set to be the secret signing key.
of the relation \(R_{\mathsf {OR}}\), which returns an \(R_{\mathsf {OR}}\)-instance \((x_0, x_1)\) and a witness \(w\) for \(x_b\). The pair \((x_0, x_1)\) then constitutes the public verification key, and \((b,w)\) is set to be the secret signing key.
Signing a message m starts with running \({\textsf {P}}_b\) on the instance \(x_b\) with the corresponding known witness (contained in the signing key), which results in a commitment \(\mathsf {com}_b\). The next step is to compute the challenge \(\mathsf {ch}_{1-b}\) for the instance the prover does not know the witness for, and this is done querying the random oracle \(\mathcal {H}\), as done before. The only difference is that now the message m is appended to the oracle’s input. Next, the signer runs the SCZK-simulator of \(\varPi _{1-b}\) on the instance \(x_{1-b}\) and this challenge, generating a simulated view \((\mathsf {com}_{1-b},\mathsf {resp}_{1-b},\mathsf {ch}_{1-b})\). To complete the signature, it is still necessary to derive the missing response \(\mathsf {resp}_{b}\). In order to do so, first the random oracle is invoked to output \(\mathsf {ch}_b\) from \(\mathsf {com}_{1-b}\) (again, the message m is appended to its argument), and on input this challenge the prover computes the response \(\mathsf {resp}_{b}\). Finally, the signature is \((\mathsf {com}_0, \mathsf {com}_1,\mathsf {resp}_0, \mathsf {resp}_1)\).
The verification algorithm checks whether the signature is valid for the given message. The signature is parsed in its components, and the algorithm queries the random oracle twice (including the message) to obtain the challenges \(\mathsf {ch}_0\) and \(\mathsf {ch}_1\), as computed by the signing algorithm. It then verifies whether \((\mathsf {com}_0,\mathsf {ch}_0,\mathsf {resp}_0)\) and \((\mathsf {com}_1,\mathsf {ch}_1,\mathsf {resp}_1)\) are accepting transcripts for \(x_0\) and \(x_1\), respectively. If both transcripts verify correctly then the verification algorithm accepts the signature, and rejects otherwise.
Theorem 8
Let \(R_0\) and \(R_1\) be decisional hard relations, and let \(\varPi _0\) and \(\varPi _1\) be two 3PC optimally sound SCZK protocols w.r.t. \(R_0\) and \(R_1\), such that the length functions satisfy \(\ell _0=\ell _1\,{=}{:}\,\ell \). Consider the signature scheme \(\varGamma \) obtained from the protocol \(\varPi =\mathsf {seq}\text {-}\mathsf {OR}\mathopen {}\left[ \varPi _0,\varPi _1,\mathsf {S}_0,\mathsf {S}_1,\mathcal {H}\right] \mathclose {}\) as depicted in Fig. 8. Then \(\varGamma \) is an \(\mathsf {UF}\text {-}\mathsf {CMA}\)-secure signature scheme in the non-programmable random oracle model. More precisely, for any PPT adversary \(\mathsf {A}\) against the \(\mathsf {UF}\text {-}\mathsf {CMA}\)-security of \(\varGamma \) making at most \(q_{\mathcal {H}}\) queries to the random oracle \(\mathcal {H}\), there exist PPT algorithms \(\mathsf {C}\), V \(^*\), \(\mathsf {D}_0\) and \(\mathsf {D}_1\) such that
In particular, for a perfectly witness indistinguishable proof system, where \(\mathbf {Adv}^{\mathsf {mqCWI}}_{{\textsf {V}}^*,\mathsf {C}, \varPi }(\lambda )\le q_s(\lambda )\cdot \mathbf {Adv}^{\mathsf {CWI}}_{{\textsf {V}}^*,\mathsf {C}, \varPi }(\lambda )=0\) (here and in the following, \(q_s\) denotes the number of queries the adversary makes to the signature oracle), the bound becomes tightly related to the underlying decisional problem. This holds for example if we have a perfect zero-knowledge simulator. We remark that our proof also works if the relations are not optimally sound but instead c-optimally sound, i.e., for every \(x\notin L_R\) and every commitment, there is a small set of at most c challenges for which a valid response can be found. In this case we get the term \(c(\lambda )\cdot 2^{-\ell (\lambda )}\) in place of \(2^{-\ell (\lambda )}\) in the above bound.
The complete proof of Theorem 8 can be found in the full version [34], but we still give a proof sketch here. We show that the obtained signature scheme \(\varGamma \) is secure via a sequence of game hops. The general approach is based on the following idea:
-
1.
Assume that we have an adversary \(\mathsf {A}\) which creates a forgery \((\mathsf {com}_0^*,\mathsf {com}_1^*,\mathsf {resp}_0^*,\mathsf {resp}_1^*)\) for message \(m^*\). We can modify \(\mathsf {A}\) into an adversary \(\mathsf {B}\) which will always query both \((0, x_0, x_1, \mathsf {com}_0^*, m^*)\) and \((1, x_0, x_1, \mathsf {com}_1^*, m^*)\) to the random oracle when computing the forgery, simply by making the two additional queries if necessary.
-
2.
Since the adversary is oblivious about which witness \(w_b\) is being used to create signatures, \(\mathsf {B}\) will submit the query \((1-b,x_0,x_1,\mathsf {com}^*_{1-b},m^*)\) first, before making any query about \((b,x_0,x_1,\mathsf {com}^*_b,m^*)\), with probability roughly 1/2, and will still succeed with non-negligible probability.
-
3.
If we next replace \(x_{1-b}\) with a no-instance (which is indistinguishable for \(\mathsf {B}\) because \(R_{1-b}\) is decisionally hard) we obtain the contradiction that \(\mathsf {B}\)’s advantage must be negligible now, because finding a forgery when querying \(\mathsf {com}^*_{1-b}\) first should be hard by the optimal soundness property of \(\varPi _{1-b}\), since \(x_{1-b}\) is a no-instance.
In more detail, in the first step we transition from the classical unforgeability game \(\mathsf {G}_0\) for the signature scheme \(\varGamma \) to a game \(\mathsf {G}_1\) where the adversary is additionally required to query both \((0, x_0, x_1, \mathsf {com}_0^*, m^*)\) and \((1, x_0, x_1, \mathsf {com}_1^*, m^*)\) to the random oracle. It is always possible to make this simplifying assumption: Indeed, given any adversary \(\mathsf {A}\) against the \(\mathsf {UF}\text {-}\mathsf {CMA}\)-security of \(\varGamma \), we can modify it into an adversary \(\mathsf {B}\) which works exactly like \(\mathsf {A}\), but whose last two operations before returning the forgery as computed by \(\mathsf {A}\) (or aborting) are the two required oracle queries, in the order given above. It is clear that \(\mathsf {B}\) is a PPT algorithm, that it makes at most \(q_{\mathcal {H}}+2\) random oracle queries, and that the probabilities of adversaries \(\mathsf {A}\) winning game \(\mathsf {G}_0\) and \(\mathsf {B}\) winning game \(\mathsf {G}_1\) are the same.
We remark that it is also possible, albeit a bit lengthy, to prove that a successful adversary \(\mathsf {A}\) against \(\mathsf {G}_0\) would already make both oracle queries with overwhelming probability, so that one could replace this first step with a more cumbersome security proof ruling out adversaries that do not make both queries. We choose here not to do so, because it would make the proof much longer and worsen the overall bound on the advantage of \(\mathsf {A}\).
Next, we define a game \(\mathsf {G}_2\) which is the same as game \(\mathsf {G}_1\), with the change that the adversary is required to query \((1-b, x_0, x_1, \mathsf {com}_{1-b}^*, m^*)\) to the random oracle before submitting any query of the form \((b, x_0, x_1, \mathsf {com}_b^*, m^*)\). By witness indistinguishability this should happen with roughly the same probability as the other case (with the opposite order), because from the adversary’s perspective the signatures do not reveal which witness \(w_b\) is used by the signer. Indeed, we show that the difference between both games is (up to a factor \(\tfrac{1}{2}\)) negligibly close. This is shown by building a distinguisher against a multi-query extension of the CWI property (see the full version [34] for its definition), and proving that the difference coincides with the distinguishing advantage of this distinguisher in the mqCWI experiment. As a result, the winning probability of \(\mathsf {B}\) in game \(\mathsf {G}_1\) is approximately twice its winning probability in game \(\mathsf {G}_2\).
Finally, we move to a game \(\mathsf {G}_3\) which is identical to \(\mathsf {G}_2\), with the difference that the \((1-b)\)-th instance is switched to a no-instance. Since the relations are decisionally hard, we can build another distinguisher playing the DHR experiment, showing that the winning probabilities are again roughly the same.
To conclude the proof we argue that the probability of the adversary winning game \(\mathsf {G}_3\) can be bounded using the fact that \(\varPi _{1-b}\) is optimally sound. Indeed, by the winning condition in the game, the adversary needs to provide the commitment \(\mathsf {com}_{1-b}^*\) early on. By the fact that the \((1-b)\)-th instance is a no-instance, we know that for every such commitment there exists at most one challenge (derived querying \(\mathcal {H}\) on \(\mathsf {com}^*_b\) later in the game) for which there exists a response such that the transcript for \(x_{1-b}\) verifies correctly. Since the adversary must ask \(\mathsf {com}_{1-b}^*\) in one of the random oracle queries, there are at most \(q_{\mathcal {H}}+2\) commitments \(\mathsf {com}_{1-b}^*\) it can check. For every such commitment it can try at most \(q_{\mathcal {H}}+2\) other oracle queries to find the matching challenge, so that we can bound \(\mathsf {B}\)’s winning probability in \(\mathsf {G}_3\) by \(\mathopen {}\left( q_{\mathcal {H}}(\lambda )+2\right) \mathclose {}^2\cdot 2^{-\ell {(\lambda )}+1}\).
4.3 Example: Post-Quantum Ring Signatures
We discuss here briefly that our sequential-OR technique can be applied to build lattice-based ring signatures. We exemplify this for the case of the Dilithium signature scheme [28]. We stress that our solution may be less efficient than optimized lattice-based constructions such as [30] (but which, again, relies on programming the random oracle and yields a loose reduction). Our aim is to demonstrate that one can use the sequential-OR approach in principle to immediately obtain a solution with security guarantees in the non-programmable classical ROM (with tight security relative to the underlying lattice problem) and also in the QROM (with loose security at this point).
We briefly recall the Dilithium signature scheme [29]. The scheme works over a ring \(R_q=\mathbb {Z}_q[X]/(X^n+1)\). The public key consists of (a size-reduced version of) \(t=As_1+s_2\), where the matrix \(A\in R_q^{k\times \ell }\) and the vectors \(s_1,s_2\) become part of the secret key. The signature \(\sigma =(z,h,c)\) of a message m consists of a short response value \(z=y+cs_1\), where y is chosen randomly and \(c=\mathsf {H}(\mu ,w_1)\) is a (deterministically post-processed) hash value of a salted hash \(\mu \) of the message m and the commitment of \(w=Ay\) in form of its higher-order bits \(w_1\). The value h is a hint required for verification. When generating a signature, the process may not always create a sufficiently short value z, in which case the generation is started from scratch.
The security proof of Dilithium [45] is based on the presumably hard problem to distinguish genuine public keys \((A,As_1+s_2)\) from (A, t) for random t. As such we have our required decisional hard relation. Optimal soundness, in the sense that for random public keys there exists at most one challenge for which one can find a valid answer for a given commitment, has been also shown to hold with overwhelming probability in [45]. The zero-knowledge property in [45] reveals, by inspecting the construction of the simulator, that the construction is special zero-knowledge with perfectly indistinguishable distribution. The witness indistinguishability of the sequential-OR protocol hence follows from Theorem 7.
We can now apply Theorem 8 to conclude that the sequential-OR version is a secure signature scheme (in the non-programmable random oracle model). Note that it is irrelevant for us how many trials the signature generation takes, since we are merely interested in the point in time when we actually observe the right random oracle queries. With Theorem 10 we can also conclude that the protocol is secure in the quantum random oracle model.
5 Impossibility of Parallel-OR Signatures in the Non-programmable Random Oracle Model
In this section we show that it may be hard to prove the unforgeability of the parallel-OR signature scheme \(\varGamma =\mathsf {sFS}\mathopen {}\left[ \mathsf {par}\text {-}\mathsf {OR}\mathopen {}\left[ \varPi _0,\varPi _1,\mathsf {S}_0,\mathsf {S}_1\right] \mathclose {},\mathcal {H}\right] \mathclose {}\) in the non-programmable ROM (all formal details about the definition of \(\varGamma \) can be found in the full version [34]). On a high level, this means that we must rule out the existence of an efficient reduction \(\mathsf {R}\) which has access to a random oracle but is not allowed to program it, and which transforms any (bounded or unbounded) successful adversary \(\mathsf {A}\) against the unforgeability of \(\varGamma \) into an algorithm \(\mathsf {C}\) solving some problem \(\mathsf {G}\) assumed to be hard with non-negligible advantage.
Our proof will proceed in two steps. First, assuming by contradiction that such a reduction \(\mathsf {R}\) indeed does exist, we will construct a specific unbounded adversary \(\mathsf {A}\) which breaks the unforgeability of \(\varGamma \) with overwhelming probability. By the properties of \(\mathsf {R}\), this means that the unbounded algorithm \(\mathsf {C}\) resulting from the interaction between \(\mathsf {R}\) and \(\mathsf {A}\) must successfully break instances of \(\mathsf {G}\) in the non-programmable ROM with non-negligible probability. Then, we show how to efficiently simulate to \(\mathsf {R}\) its interaction with \(\mathsf {A}\), thereby yielding an efficient algorithm \(\mathsf {B}\) against \(\mathsf {G}\) in the standard model with roughly the same advantage as \(\mathsf {C}\). This is impossible by the hardness of \(\mathsf {G}\), which means that \(\mathsf {R}\) cannot exist.
In the following paragraphs we discuss which kinds of reductions \(\mathsf {R}\) we are able to rule out, define what types of problems \(\mathsf {G}\) the algorithms \(\mathsf {B}\) and \(\mathsf {C}\) play against, and discuss a pointwise version of zero-knowledge which the base protocols must satisfy for our result to work. We then come to the main result of this section.
Reduction. The efficient reductions \(\mathsf {R}\) we consider have oracle access to the random oracle \(\mathcal {H}\), as well as a (bounded) number of adversary instances \(\mathsf {A}_i\) which themselves have oracle access to \(\mathcal {H}\). The latter guarantees that the reduction cannot program the random oracle for the adversarial instances, but we stress that \(\mathsf {R}\) gets to see all the queries made by any instance \(\mathsf {A}_i\). We let each adversarial instance be run on the same security parameter \(\lambda \) as the reduction itself.
Recall that, in the first step of our proof, the adversary \(\mathsf {A}\) is unbounded. Therefore, we can assume that \(\mathsf {A}\) incorporates a truly random function which it uses if random bits are required. With this common derandomization technique, we can make some simplifying assumptions about the reduction: Without loss of generality, \(\mathsf {R}\) runs the instances of the adversary in sequential order, starting with \(\mathsf {A}_1\). It also never revisits any of the previous instances \(\mathsf {A}_1,\dots ,\mathsf {A}_i\) once it switches to the next instance \(\mathsf {A}_{i+1}\) by inputting a verification key \(\mathsf {vk}_{i+1}\). Furthermore, we can disallow any resets of the adversarial instances: The reduction can simply re-run the next instance up to the desired reset point and then diverge from there on.
Games. The hard problems that algorithms \(\mathsf {B}\) and \(\mathsf {C}\) are trying to solve are non-interactive (“oracle-free”) problems, like distinguishing between different inputs. Formally, we consider games of the form \(\mathsf {G}=(\mathsf {I},\mathsf {V},\alpha )\) consisting of an instance generation algorithm \(\mathsf {I}\) and a verification algorithm \(\mathsf {V}\), where  generates a challenge \(\mathsf {inst}\) of the game and some state information \(\mathsf {st}\). On input a potential solution \(\mathsf {sol}\) computed by some algorithm, the deterministic algorithm \(\mathsf {V}(1^\lambda ;\mathsf {inst},\mathsf {sol},\mathsf {st})\) returns 0 or 1, depending on whether \(\mathsf {sol}\) is a valid solution of \(\mathsf {inst}\). The constant \(\alpha \) allows to measure the advantage of an algorithm trying to win the game over some trivial guessing strategy (e.g., \(\alpha =\frac{1}{2}\) for distinguishing games). We say that an algorithm \(\mathsf {B}\) has advantage \(\epsilon \) winning the game \(\mathsf {G}=(\mathsf {I},\mathsf {V},\alpha )\) if
generates a challenge \(\mathsf {inst}\) of the game and some state information \(\mathsf {st}\). On input a potential solution \(\mathsf {sol}\) computed by some algorithm, the deterministic algorithm \(\mathsf {V}(1^\lambda ;\mathsf {inst},\mathsf {sol},\mathsf {st})\) returns 0 or 1, depending on whether \(\mathsf {sol}\) is a valid solution of \(\mathsf {inst}\). The constant \(\alpha \) allows to measure the advantage of an algorithm trying to win the game over some trivial guessing strategy (e.g., \(\alpha =\frac{1}{2}\) for distinguishing games). We say that an algorithm \(\mathsf {B}\) has advantage \(\epsilon \) winning the game \(\mathsf {G}=(\mathsf {I},\mathsf {V},\alpha )\) if

For us, the canonical problem to reduce security of the signature scheme to would be the distinguishing game against the hard instance generator for the underlying language. However, our theorem holds more generally for other problems.
The All-Powerful Adversary. In our setting, the reduction \(\mathsf {R}^{\mathcal {H},\mathsf {A}_1^\mathcal {H},\mathsf {A}_2^\mathcal {H},\dots }(1^\lambda ;\mathsf {inst})\) has black-box access to a successful adversary \(\mathsf {A}\) against \(\varGamma \), receives as input some instance \(\mathsf {inst}\) of a game \(\mathsf {G}=(\mathsf {I},\mathsf {V},\alpha )\), and is supposed to output a valid solution \(\mathsf {sol}\), winning the game with non-negligible advantage \(\epsilon \), while interacting with \(\mathsf {A}\). Recall that \(\mathsf {R}\) must be able to convert any (efficient or unbounded) adversary \(\mathsf {A}\) into a solver for \(\mathsf {G}\); in particular, this must be the case for the following all-powerful forger \(\mathsf {A}\), which we will consider throughout the proof:
-
1.
Upon receiving a verification key \(\mathsf {vk}=(x_0,x_1)\) as input, the adversary first queries its singing oracle for a signature on the message \(m_\mathsf {vk}=\mathsf {vk}\).
-
2.
When receiving the signature \(\sigma \), adversary \(\mathsf {A}\) verifies the signature and aborts if this check fails.
-
3.
Else, adversary \(\mathsf {A}\) uses its power to compute the lexicographic first witness \(w\) of \(x_0\) (if it exists), or of \(x_1\) (if it exists, and no witness for \(x_0\) has been found). If no witness can be found, then \(\mathsf {A}\) aborts. Otherwise, let \(b\in \{0,1\}\) be such that \(\mathsf {A}\) has found a witness for \(x_b\).
-
4.
Adversary \(\mathsf {A}\) picks a random \(\lambda \)-bit message \(m^*\) and runs the signing algorithm with secret key \(\mathsf {sk}=(b,w)\) to create a signature \(\sigma ^*\). This requires one random oracle query over the message \((x_0,x_1,\mathsf {com}_0^*,\mathsf {com}_1^*,m^*)\). The randomness necessary to create the signature and the message \(m^*\) is computed by applying the inner random function to \((\mathsf {vk},\sigma )\).
-
5.
The adversary outputs \((m^*,\sigma ^*)\) as its forgery.
Note that since the adversary includes the public key \(\mathsf {vk}\) in the messages \(m_\mathsf {vk}\), our result would also hold if the signing process itself did not include \(\mathsf {vk}\); according to our specification it currently does.
We observe that \(\mathsf {A}\) obviously wins the \(\mathsf {UF}\text {-}\mathsf {CMA}\) experiment of \(\varGamma \) with overwhelming probability. We denote by \(\mathsf {C}^\mathcal {H}(1^\lambda ;\mathsf {inst})\) the adversary against \(\mathsf {G}\) in the non-programmable ROM obtained by letting \(\mathsf {R}\) interact with \(\mathsf {A}\) (see the left-hand side of Fig. 9). By the properties of \(\mathsf {R}\), the advantage of \(\mathsf {C}\) against \(\mathsf {G}\) in the non-programmable ROM must be non-negligible.
Zero-Knowledge. Recall that we defined the zero-knowledge property for protocols w.r.t. relations \(R\) that have an efficient instance generator. Here, we need a stronger notion: Zero-knowledge must hold pointwise for every \((x,w)\in R\). The reason is that we will rely on the zero-knowledge property to argue that the reduction \(\mathsf {R}\) does not learn any useful information from the signatures created by the all-powerful adversary \(\mathsf {A}\). The problem here is that the reduction may choose the instance \(\mathsf {vk}_i=(x_0,x_1)\) in the execution of the i-th adversary adaptively and in dependence of the behavior of \(\mathsf {A}\) in previous instances. The reduction may then also base its final output on this choice.
We therefore say that a protocol \(\varPi =({\textsf {P}},{\textsf {V}})\) w.r.t. a relation \(R\) is pointwise HVCZK, if there exist a uniform PPT algorithm \(\mathsf {S}\) and a polynomial p with the following property: For every PPT distinguisher \(\mathsf {D}\), there exists a negligible function \(\mu :\mathbb {N}\rightarrow \mathbb {R}\) such that, for every \(\lambda \in \mathbb {N}\), every \((x,w)\in R\) with \(\left|x \right|,\left|w \right|\le p(\lambda )\), and every \(z\in \{0,1\}^*\), \(\mathsf {D}\) can distinguish verifier views \(\mathrm {view}_{{\textsf {V}}}\!\!\big [{\textsf {P}}^\mathcal {O}(1^\lambda ;x,w)\leftrightarrows {\textsf {V}}^{\mathcal {O}}(1^\lambda ;x)\big ]\) in the honest interaction between \({\textsf {P}}\) and \({\textsf {V}}\) from the simulator’s output \(\mathsf {S}(1^\lambda ;x)\) with advantage at most \(\mu (\lambda )\), even if \(\mathsf {D}\) receives z as auxiliary input.
Note that in the definition above, the relation and the language are still fixed, only the sampling process may vary. This seems to be a reasonable assumption which applies to known protocols, as the zero-knowledge simulator is usually independent of the generation process for the statement.
Impossibility Result. We now show that, if there exists a black-box reduction \(\mathsf {R}\) as described above, our all-powerful adversary \(\mathsf {A}\) induces an efficient algorithm \(\mathsf {B}\) winning the game directly, such that the advantages of \(\mathsf {B}\) and \(\mathsf {C}\) are roughly the same. This is impossible by the assumed hardness of \(\mathsf {G}\), so that \(\mathsf {R}\) cannot exist.
Theorem 9
Let \(R_0\) and \(R_1\) be binary relations, and let \(\varPi _0\) and \(\varPi _1\) be two 3PC optimally sound pointwise HVCZK protocols w.r.t. \(R_0\) and \(R_1\), such that the length functions satisfy \(\ell _0=\ell _1\,{=}{:}\,\ell \). Denote by \(\varPi =\mathsf {par}\text {-}\mathsf {OR}\mathopen {}\left[ \varPi _0,\varPi _1,\mathsf {S}_0,\mathsf {S}_1\right] \mathclose {}\) the corresponding parallel-OR protocol, and let \(\varGamma =\mathsf {sFS}\mathopen {}\left[ \varPi ,\mathcal {H}\right] \mathclose {}\) be the parallel-OR signature scheme derived from \(\varPi \) in the ROM.
Assume that there exists a PPT black-box reduction \(\mathsf {R}\) from the unforgeability of \(\varGamma \) to winning a game \(\mathsf {G}=(\mathsf {I},\mathsf {V},\alpha )\). Then there exists a PPT algorithm \(\mathsf {B}\) which wins the game \(\mathsf {G}\) with non-negligible advantage in the standard model.
Representation of the reduction \(\mathsf {R}\) interacting with adversarial instances \(\mathsf {A}_i\) in the ROM (left) and of the efficient solver \(\mathsf {B}\) running \(\mathsf {R}\) (right). The components simulated by \(\mathsf {B}\) are dashed, and the queries of which \(\mathsf {R}\) gets informed are highlighted in
 .
.
The idea is as follows. Algorithm \(\mathsf {B}\) receives as input a challenge \(\mathsf {inst}\) of the game \(\mathsf {G}\), and must compute a valid solution \(\mathsf {sol}\) with non-negligible probability. The strategy of \(\mathsf {B}\) is to run the reduction \(\mathsf {R}\) on \(\mathsf {inst}\) as a subroutine, and to efficiently simulate to \(\mathsf {R}\) its interaction with \(\mathsf {A}\). To do so, \(\mathsf {B}\) must be able to answer the two types of queries that \(\mathsf {R}\) can make: Random oracle evaluations and forgery queries to \(\mathsf {A}\). The former are handled via lazy sampling, i.e., \(\mathsf {B}\) simulates a random oracle to \(\mathsf {R}\). If on the other hand \(\mathsf {R}\) requests a forgery for a verification key \(\mathsf {vk}=(x_0,x_1)\), \(\mathsf {B}\) at first follows the definition of \(\mathsf {A}\) and requests a signature for \(m_\mathsf {vk}\). This initial signature request ensures that the verification key \(\mathsf {vk}\) must be such that \(x_0\in L_0\) or \(x_1\in L_1\) or both. Indeed, the reduction cannot program the random oracle (which is controlled by \(\mathsf {B}\)) and, by special soundness of \(\varPi _0\) and \(\varPi _1\), finding a valid signature when both \(x_0\notin L_0\) and \(x_1\notin L_1\) is infeasible for parallel-OR signatures. Hence, in the original experiment \(\mathsf {A}\) will always be able to find a witness \((b,w)\) for \(\mathsf {vk}\) if it receives a valid signature.
Next, \(\mathsf {A}\) will compute a forgery for the message \(m^*\). Here \(\mathsf {B}\), instead of using \(w\) from the witness \((b,w)\) to run \({\textsf {P}}_b\) and compute \(\mathsf {com}_b^*\) and \(\mathsf {resp}_b^*\) in its forgery, uses the zero-knowledge simulator \(\mathsf {S}_b\) for this part as well. Now both parts of the signature of \(m^*\) are independent of the actual witness. The algorithm \(\mathsf {B}\) can now program the random oracle \(\mathcal {H}\) it is simulating to \(\mathsf {R}\), so that \(\mathcal {H}(\mathsf {vk},\mathsf {com}^*,m^*)\) matches the XOR of the two challenges obtained from the two simulators.Footnote 2 By the strong zero-knowledge property of the base protocols, and since \(m^*\) contains sufficient randomness to make sure that we can still set the random oracle for \(\mathsf {R}\) at this point, this is indistinguishable for the reduction. Finally, if at some point \(\mathsf {R}\) returns a solution to the given instance, algorithm \(\mathsf {B}\) terminates with the same output. In conclusion, we can now efficiently simulate \(\mathsf {A}\)’s behavior to \(\mathsf {R}\), so that the reduction together with this simulation technique yields our efficient algorithm \(\mathsf {B}\) against game \(\mathsf {G}\) (see the right-hand side of Fig. 9).
Let us stress that the impossibility result above does not hold for sequential-OR signatures. The difference lies in the observability of the reduction in both cases. In the parallel-OR case we still need to tell \(\mathsf {R}\) which query \(\mathcal {H}(\mathsf {vk},\mathsf {com}_0^*,\mathsf {com}_1^*,m^*)\) the adversary has made to compute the forgery. But we have already argued that the simulated value \(\mathsf {com}_b^*\) is indistinguishable from the prover’s value \(\mathsf {com}_b^*\) in the forgery, so that this query does not give any additional information to \(\mathsf {R}\). In the sequential-OR case, however, we would need to inform \(\mathsf {R}\) which query \(\mathsf {A}\) makes first, revealing which witness it has computed.
Proof
Consider an efficient reduction \(\mathsf {R}\) interacting with instances of our all-powerful adversary \(\mathsf {A}\). Assume that the reduction calls at most \(q_\mathsf {A}\) instances of \(\mathsf {A}\) and makes at most \(q_\mathcal {H}\) calls to the random oracle. Since \(\mathsf {R}\) is polynomial-time, both parameters are polynomially bounded. We can also assume that \(\mathsf {R}\) never runs an instance for the same key \(\mathsf {vk}\) and then the same signature \(\sigma \) twice, because it will just receive the same answers as before.
We start by making some simplifying assumptions about the reduction. First, we can assume that \(\mathsf {R}\) only provides \(\mathsf {A}\) with a valid signature to some verification key \(\mathsf {vk}=(x_0,x_1)\) if \(x_0\in L_0\) or \(x_1\in L_1\) (or both). Indeed, since \(\varPi _0\) and \(\varPi _1\) are optimally sound, if both values are not in their language, then each commitment \(\mathsf {com}_0\) for \(x_0\) and \(\mathsf {com}_1\) for \(x_1\) only allows for at most one challenge, \(\mathsf {ch}_0\) and \(\mathsf {ch}_1\), to have a valid response. But then, the probability that a random oracle query \(\mathcal {H}(\mathsf {vk},\mathsf {com}_0,\mathsf {com}_1,m_\mathsf {vk})\) matches the unique value \(\mathsf {ch}_0\,\,\oplus \,\,\mathsf {ch}_1\) is at most \(2^{-\ell (\lambda )}\). The probability that such a random oracle query exists at all, either made by \(\mathsf {R}\) or, if not, later made by any instance of the adversary \(\mathsf {A}\) when verifying the signature, is therefore at most \((q_\mathcal {H}(\lambda )+q_\mathsf {A}(\lambda ))\cdot 2^{-\ell (\lambda )}\). Given that \(\mathsf {A}\) aborts if the signature it receives is not valid, we can from now on assume that each public key \(\mathsf {vk}\) for which \(\mathsf {R}\) requests a forgery (and must provide a signature) allows \(\mathsf {A}\) to compute a witness \((b,w)\), and that \(\mathsf {R}\) itself leaves the instance immediately if verification fails.
Second, we may assume that, whenever \(\mathsf {A}\) creates a forgery for \(m^*\), the random oracle has not been queried by any party yet about any value terminating in \(m^*\). Indeed, since \(\mathsf {A}\) applies the internal random function to compute \(m^*\) from \(\mathsf {vk}\) and \(\sigma \), and we assume that the reduction never runs the adversary twice on the same values, this can only happen if two random messages \(m^*\) of the adversary collide, or if the reduction has made such a query by chance. The probability for this is at most \((q_\mathcal {H}(\lambda )+q_\mathsf {A}(\lambda ))^2\cdot 2^{-\lambda }\). Hence, we can from now on assume that this does not happen. In other words, if \(\mathsf {R}\) stumbles upon such a value it immediately aborts.
We now define the algorithm \(\mathsf {B}\) as explained in the overview above. On input \((1^\lambda ;\mathsf {inst})\), \(\mathsf {B}\) runs the reduction on security parameter \(1^\lambda \) and instance \(\mathsf {inst}\) as a subroutine, and simulates to \(\mathsf {R}\) its interaction with \(\mathsf {A}\). The random oracle queries made by \(\mathsf {R}\) are answered via lazy sampling. If on the other hand \(\mathsf {R}\) calls an adversarial instance for a forgery under \(\mathsf {vk}=(x_0,x_1)\), \(\mathsf {B}\) does the following:
-
1.
It first requests a signature of \(m_{\mathsf {vk}}=\mathsf {vk}\) under \(\mathsf {vk}\) to its signature oracle (provided by the reduction), and checks if the corresponding signature is valid. If not, it aborts the simulation of the current instance of \(\mathsf {A}\).
-
2.
Assuming that \(\mathsf {R}\) has provided a valid signature of \(m_\mathsf {vk}\) under \(\mathsf {vk}\), \(\mathsf {B}\) does not compute a witness \((b,w)\) for \(\mathsf {vk}\) (as \(\mathsf {A}\) would do). It still picks a random message \(m^*\in \{0,1\}^\lambda \) and fresh coins for the signing process, though.
-
3.
To compute the forgery for \(m^*\), instead of invoking \({\textsf {P}}_b(1^\lambda ; x_b,w)\) to generate \(\mathsf {com}_b\), \(\mathsf {B}\) now runs the two simulators \(\mathsf {S}_0(1^\lambda ; x_0)\) and \(\mathsf {S}_1(1^\lambda ; x_1)\) to compute simulated views \((\mathsf {com}_0^*,\mathsf {resp}_0^*,\mathsf {ch}_0^*)\) and \((\mathsf {com}_1^*,\mathsf {resp}_1^*,\mathsf {ch}_1^*)\).
-
4.
Algorithm \(\mathsf {B}\) saves \(\mathcal {H}(\mathsf {vk},\mathsf {com}_0^*,\mathsf {com}_1^*,m^*)\,{:}{=}\,\mathsf {ch}_0^*\oplus \mathsf {ch}_1^*\) into the lookup table it keeps to simulate the random oracle to \(\mathsf {R}\), and informs \(\mathsf {R}\) that the adversary \(\mathsf {A}\) it is simulating has made a query \((\mathsf {vk},\mathsf {com}_0^*,\mathsf {com}_1^*,m^*)\) to the random oracle, with answer \(\mathsf {ch}_0^*\oplus \mathsf {ch}_1^*\).
-
5.
Finally, \(\mathsf {B}\) sends \(m^*\) and \(\sigma ^*=(\mathsf {com}_0^*,\mathsf {com}_1^*,\mathsf {resp}_0^*,\mathsf {resp}_1^*)\) to \(\mathsf {R}\) as the forgery computed by the simulated instance of \(\mathsf {A}\).
Note that \(\mathsf {B}\) is now efficient: The only potentially exponential step involving the witness search has been eliminated. We must now argue that \(\mathsf {B}\)’s success probability in the standard model is close to the one of \(\mathsf {C}\) in the ROM. This is done by carrying out a reduction to the pointwise zero-knowledge property of the protocols \(\varPi _0\) and \(\varPi _1\), where zero-knowledge must hold for every \((x,w)\in R\), even in the presence of some auxiliary information \(z\in \{0,1\}^*\) that may contain further information about \((x,w)\). The proof is done via a hybrid argument for hybrids \(\mathsf {Hyb}_0,\dots ,\mathsf {Hyb}_{q_\mathsf {A}}\), where \(\mathsf {Hyb}_i\) answers \(R\)’s forgery requests by running the (unbounded) algorithm \(\mathsf {A}\) up to, and including, the i-th adversarial instance (as \(\mathsf {C}\) would do), and then efficiently simulates \(\mathsf {A}\) for the remaining instances (as \(\mathsf {B}\) would do). Then the extreme hybrid \(\mathsf {Hyb}_{q_\mathsf {A}}\) corresponds to the original inefficient algorithm \(\mathsf {C}\), whereas the extreme hybrid \(\mathsf {Hyb}_0\) coincides with \(\mathsf {B}\)’s simulation.
The jump from hybrid \(\mathsf {Hyb}_{i-1}\) to hybrid \(\mathsf {Hyb}_i\) substitutes the honestly generated proof for \(x_b\) (where \(x_b\) is the instance that \(\mathsf {A}\) finds a witness for) in the i-th adversarial instance with a simulated one, so that we can construct a reduction to the pointwise HVCZK property of \(\varPi _b\). The main idea is to let the reduction interact with the inefficient forger \(\mathsf {A}\) for the first i instances, up to the point where \(\mathsf {A}_i\) has determined the witness \((b,w)\) for \(x_b\), and save all the state information into the auxiliary input z. This allows us to pick up the reduction later. We then leverage the pointwise HVCZK property of \(\varPi _b\), with instance \((x_b,w)\in R_b\): The zero-knowledge distinguisher \(\mathsf {D}_b\) receives a genuine or simulated view for \(x_b\) and the state information z, and continues to run the reduction, but now using \(\mathsf {B}\)’s simulation for the remaining instances (so that \(\mathsf {D}_b\) is efficient).
More formally, we use the pointwise HVCZK property of \(\varPi _b\) for the distinguisher \(\mathsf {D}_b\), the instance \((x_b,w)\in R_b\), and the auxiliary information z defined as follows. We let  generate an instance of \(\mathsf {G}\), pick a random tape r for the reduction and a random index i between 1 and \(q_\mathsf {A}\) for the jump in the hybrids, and then run the reduction (interacting with \(\mathsf {A}\)) on input \(\mathsf {inst}\), up to the point where \(\mathsf {A}\) has computed a witness for one of the two instances in the i-th execution (on input \(\mathsf {vk}=(x_0,x_1)\)) and has generated the message \(m^*\). All random oracle queries are answered via lazy sampling and a table H is maintained to record previously answered queries. Let S store all forgery attempts of \(\mathsf {A}\). Then we let \((x_b,w)\in R_b\) be the instance and the corresponding witness found by \(\mathsf {A}\), and we set \(z=(\mathsf {inst},\mathsf {st},r,i,x_{1-b},b,w,m^*,H,S)\). Note that if no witness can be found by \(\mathsf {A}\), or if \(\mathsf {A}\) has stopped in this instance prematurely, then we simply set \(x_b\) and \(w\) to some fixed elements of the relation \(R_0\) and the output z as before. In any case, z is of polynomial size and can be processed by an efficient distinguisher, because \(q_\mathcal {H}\) and \(q_\mathsf {A}\) are polynomially bounded.
generate an instance of \(\mathsf {G}\), pick a random tape r for the reduction and a random index i between 1 and \(q_\mathsf {A}\) for the jump in the hybrids, and then run the reduction (interacting with \(\mathsf {A}\)) on input \(\mathsf {inst}\), up to the point where \(\mathsf {A}\) has computed a witness for one of the two instances in the i-th execution (on input \(\mathsf {vk}=(x_0,x_1)\)) and has generated the message \(m^*\). All random oracle queries are answered via lazy sampling and a table H is maintained to record previously answered queries. Let S store all forgery attempts of \(\mathsf {A}\). Then we let \((x_b,w)\in R_b\) be the instance and the corresponding witness found by \(\mathsf {A}\), and we set \(z=(\mathsf {inst},\mathsf {st},r,i,x_{1-b},b,w,m^*,H,S)\). Note that if no witness can be found by \(\mathsf {A}\), or if \(\mathsf {A}\) has stopped in this instance prematurely, then we simply set \(x_b\) and \(w\) to some fixed elements of the relation \(R_0\) and the output z as before. In any case, z is of polynomial size and can be processed by an efficient distinguisher, because \(q_\mathcal {H}\) and \(q_\mathsf {A}\) are polynomially bounded.
The (efficient) distinguisher \(\mathsf {D}_b\) against the pointwise HVCZK property of \(\varPi _b\) receives \(x_b\), a real or simulated view \((\mathsf {com}_b^*,\mathsf {resp}_b^*,\mathsf {ch}_b^*)\) for \(x_b\), and the auxiliary information \(z=(\mathsf {inst},\mathsf {st},r,i,x_{1-b},b,w,m^*,H,S)\). With these data \(\mathsf {D}_b\) can re-run the reduction up to the interaction of \(\mathsf {R}\) with the i-th adversarial instance and then inject the given transcript \((\mathsf {com}_b^*,\mathsf {ch}_b^*,\mathsf {resp}_b^*)\) into this instance (the transcript for \(x_{1-b}\) needed to complete the forgery is obtained via the simulator \(\mathsf {S}_{1-b}(1^\lambda ;x_{1-b})\)). Algorithm \(\mathsf {D}_b\) now completes the execution of the reduction, using lazy sampling and the table H to continue the consistent simulation of random oracle queries. In particular, in all subsequent signature forgeries it will use \(\mathsf {B}\)’s efficient simulation technique, calling the simulators \(\mathsf {S}_0\) and \(\mathsf {S}_1\) to create the two transcripts and programming the random oracle accordingly. Note that the order of execution of these two simulators is irrelevant, because \(\mathsf {D}_b\) only needs to inform the reduction about a single random oracle query. Finally, \(\mathsf {D}_b\) takes the reduction’s output \(\mathsf {sol}\) and returns the decision bit \(\mathsf {V}(1^\lambda ;\mathsf {inst},\mathsf {sol},\mathsf {st})\).
Observe that \(\mathsf {D}_b\) runs in polynomial time, because it does not need to invoke any super-polynomial subroutines like \(\mathsf {A}\). If \(\mathsf {D}_b\) receives a real view \((\mathsf {com}_b^*,\mathsf {resp}_b^*,\mathsf {ch}_b^*)\) in the i-th instance, then \(\mathsf {ch}_b^*\) is truly random and independent, and therefore programming the (simulated) random oracle to \(\mathcal {H}(\mathsf {vk},\mathsf {com}_0^*,\mathsf {com}_1^*,m^*)\,{:}{=}\,\mathsf {ch}_0^*\oplus \mathsf {ch}_1^*\) is perfectly sound. Hence, for real transcripts \(\mathsf {D}_b\) simulates the hybrid \(\mathsf {Hyb}_i\) with the first i instances according to \(\mathsf {C}\)’s strategy, and the following instances with the simulated mode of \(\mathsf {B}\).
If on the other hand the transcript is simulated by \(\mathsf {S}_b\), then both parts of the signature are simulated. This means that both \(\mathsf {ch}_0^*\) and \(\mathsf {ch}_1^*\) are indistinguishable from random strings to an efficient adversary, which again implies that programming \(\mathcal {H}(\mathsf {vk},\mathsf {com}_0^*,\mathsf {com}_1^*,m^*)\,{:}{=}\,\mathsf {ch}_0^*\oplus \mathsf {ch}_1^*\) is sound for \(\mathsf {R}\). In this case, only the first \(i-1\) instances follow \(\mathsf {C}\)’s method; starting form the i-th adversarial instance we have two simulated proofs, each simulated individually. Hence, this corresponds to the \((i-1)\)-th hybrid \(\mathsf {Hyb}_{i-1}\).
Let \(\mu _b:\mathbb {N}\rightarrow \mathbb {R}\) be the negligible function bounding the distinguishing advantage of \(\mathsf {D}_b\) in the pointwise HVCZK experiment of \(\varPi _b\). It follows via a standard hybrid argument that any change in the reduction’s behavior translates into a distinguisher against the pointwise HVCZK property of \(\varPi _0\) and \(\varPi _1\) (times the number of queries \(q_\mathsf {A}\)). The advantage of our algorithm \(\mathsf {B}\) in breaking the game is thus at least
where \(\epsilon \) is the advantage of \(\mathsf {C}\). Since \(\epsilon \) is non-negligible by assumption, so must be \(\mathsf {B}\)’s advantage. But this contradicts the presumed hardness of \(\mathsf {G}\). \(\square \)
6 Security in the Quantum Random Oracle Model
In this section we give an outline of the security proof for signatures derived from the sequential-OR construction in the QROM. More details can be found in the full version [34].
While treating quantum random oracles is a clear qualitative extension in terms of the security guarantees (especially if we work with quantum-resistant primitives), we have to sacrifice two important features of our proof in the classical case. One is that the bound we obtain is rather loose. The other point is that we need to program the random oracle in the security reduction. Both properties are currently shared by all proofs in the quantum random oracle model, e.g., programmability appears in form of using pairwise independent hash functions or semi-constant distributions (see [60]). Hopefully, progress in this direction will also carry over to the case of sequential-OR signatures.
Our starting point is the “measure-and-reprogram” technique of Don et al. [27] for Fiat-Shamir protocols in the QROM. They show that it is possible to turn a quantum adversary \(\mathsf {A}\) into an algorithm \(\mathsf {R}^\mathsf {A}\) such that \(\mathsf {R}^\mathsf {A}\) measures one of the \(q_{\mathcal {H}}\) quantum queries of \(\mathsf {A}\) to the random oracle, yielding some classical query \(\mathsf {com}'\). The choice of this query is made at random. Algorithm \(\mathsf {R}^\mathsf {A}\) returns either correctly \(\mathcal {H}(\mathsf {com}')\) or an independent and random value \(\varTheta \) to this now classical query, the choice being made at random. Algorithm \(\mathsf {R}^\mathsf {A}\) continues the execution of \(\mathsf {A}\) but always returns \(\varTheta \) for \(\mathsf {com}'\) from then on. Algorithm \(\mathsf {R}^\mathsf {A}\) eventually returns the output \((\mathsf {com},\mathsf {resp})\) of \(\mathsf {A}\).
Don et al. [27] now show that, for any quantum adversary \(\mathsf {A}\) making at most \(q_{\mathcal {H}}\) quantum random oracle queries, there exists a (quantum) algorithm \(\mathsf {R}^\mathsf {A}\) such that, for every fixed \(\mathsf {com}_0\) and every predicate \(\varLambda \), there exists a negligible function \(\mu _{\mathsf {com}_0}:\mathbb {N}\rightarrow \mathbb {R}\) such that

where \(\sum _{\mathsf {com}_0}\mu _{\mathsf {com}_0}(\lambda )=\frac{1}{q_{\mathcal {H}}(\lambda )\cdot 2^{\ell (\lambda )+1}}\) for the output size \(\ell \) of the random oracle.
We will apply the above measure-and-reprogram technique twice in order to capture the two (classical) queries in which the adversary asks for the two commitments \(\mathsf {com}_0^*\) and \(\mathsf {com}_1^*\) for the forgery. However, we do not know if the strategy can be safely applied multiple times in general. Fortunately, we can apply the technique in our setting once without actually reprogramming the random oracle, only turning one of the queries into a classical one, and then view this as a special adversary \(\mathsf {B}\) which still works with the given random oracle model. In doing so we lose a factor of approximately \(1/q^2\) in the success probability, where \(q(\lambda )=q_{\mathcal {H}}(\lambda )+2+2q_s(\lambda )\) counts the number of hash queries made by both the adversary and the signature scheme. Then we can apply the technique once more to \(\mathsf {B}\), losing another factor \(1/q^2\). Finally, we need to take into account that we actually obtain the matching commitments in the two measured queries, costing us another factor 1/q. Eventually, we get an algorithm \(\mathsf {R}\) which makes two classical queries about the two commitments in the forgery with high probability, but with a loose factor of \(1/q^5\) compared to the original success probability of the forger.
Note that we now have a forger making two classical queries about the commitments \(\mathsf {com}^*_{a^*}\) and \(\mathsf {com}_{1-a^*}^*\) in the forgery in this order, but where we reprogram the random oracle reply in the second query about \(\mathsf {com}_{1-a^*}^*\) to \(\varTheta \). In our sequential-OR construction this value \(\varTheta \) describes the (now reprogrammed) challenge for the first commitment. In particular, the forgery then satisfies \({\textsf {V}}_{a^*}(1^\lambda ;x_{a^*},\mathsf {com}_{a^*}^*,\varTheta ,\mathsf {resp}_{a*}^*)=1\) for the commitment \(\mathsf {com}_{a^*}^*\) chosen before \(\varTheta \) is determined. If \(x_{a^*}\) was a no-instance, this should be infeasible by the optimal soundness property. The last step in the argument is then similar to the classical setting, showing that if \(\mathsf {R}\) is forced to use the “wrong order” and queries about a no-instance first with sufficiently high probability, its success probability will be small by the witness indistinguishability of the protocol and the decisional hardness of the problems (but this time against quantum algorithms).
Overall, we get:
Theorem 10
Let \(R_0\) and \(R_1\) be decisional hard relations against quantum algorithms, and let \(\varPi _0\) and \(\varPi _1\) be two 3PC optimally sound SCZK protocols w.r.t. \(R_0\) and \(R_1\), where zero-knowledge holds with respect to quantum distinguishers, such that the length functions satisfy \(\ell _0=\ell _1\,{=}{:}\,\ell \). Consider the signature scheme \(\varGamma \) obtained from the protocol \(\varPi =\mathsf {seq}\text {-}\mathsf {OR}\mathopen {}\left[ \varPi _0,\varPi _1,\mathsf {S}_0,\mathsf {S}_1,\mathcal {H}\right] \mathclose {}\) as depicted in Fig. 8. Then \(\varGamma \) is an \(\mathsf {UF}\text {-}\mathsf {CMA}\)-secure signature scheme in the quantum random oracle model. More precisely, for any polynomial-time quantum adversary \(\mathsf {A}\) against the \(\mathsf {UF}\text {-}\mathsf {CMA}\)-security of \(\varGamma \) making at most \(q_{\mathcal {H}}\) quantum queries to the random oracle \(\mathcal {H}\) and at most \(q_s\) signature queries, there exist a negligible function \(\mu :\mathbb {N}\rightarrow \mathbb {R}\) and polynomial-time quantum algorithms \(\mathsf {C}\), \({\textsf {V}} ^*\), \(\mathsf {D}_0\) and \(\mathsf {D}_1\) such that

Notes
- 1.
One can think of this as a very lossy mode.
- 2.
One could indeed argue why we are here allowed to program the random oracle in light of the discussion about non-programmability. One may think of this here as a restriction of the reduction, that it needs to be able to cope with such external oracles. Technically, it gives the required advantage over the reduction to make the meta-reduction argument work.
References
Abdalla, M., An, J.H., Bellare, M., Namprempre, C.: From identification to signatures via the Fiat-Shamir transform: minimizing assumptions for security and forward-security. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 418–433. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_28
Abdalla, M., Fouque, P.-A., Lyubashevsky, V., Tibouchi, M.: Tightly secure signatures from lossy identification schemes. J. Cryptol. 29(3), 597–631 (2016). https://doi.org/10.1007/s00145-015-9203-7
Abe, M., Ohkubo, M., Suzuki, K.: 1-out-of-n signatures from a variety of keys. In: Zheng, Y. (ed.) ASIACRYPT 2002. LNCS, vol. 2501, pp. 415–432. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-36178-2_26
Alkim, E., et al.: Revisiting TESLA in the quantum random oracle model. In: Lange, T., Takagi, T. (eds.) PQCrypto 2017. LNCS, vol. 10346, pp. 143–162. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-59879-6_9
Ambainis, A., Rosmanis, A., Unruh, D.: Quantum attacks on classical proof systems: the hardness of quantum rewinding. In: 55th FOCS, pp. 474–483 (2014)
Bader, C., Hofheinz, D., Jager, T., Kiltz, E., Li, Y.: Tightly-secure authenticated key exchange. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 629–658. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_26
Bai, S., Galbraith, S.D.: An improved compression technique for signatures based on learning with errors. In: Benaloh, J. (ed.) CT-RSA 2014. LNCS, vol. 8366, pp. 28–47. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-04852-9_2
Baum, C., Lin, H., Oechsner, S.: Towards practical lattice-based one-time linkable ring signatures. In: Naccache, D., et al. (eds.) ICICS 2018. LNCS, vol. 11149, pp. 303–322. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-01950-1_18
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: ACM CCS, vol. 93, pp. 62–73 (1993)
Boneh, D., Dagdelen, Ö., Fischlin, M., Lehmann, A., Schaffner, C., Zhandry, M.: Random oracles in a quantum world. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 41–69. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_3
Boneh, D., Venkatesan, R.: Breaking RSA may not be equivalent to factoring. In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 59–71. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054117
Bünz, B., Bootle, J., Boneh, D., Poelstra, A., Wuille, P., Maxwell, G.: Bulletproofs: short proofs for confidential transactions and more. In: 2018 IEEE Symposium on Security and Privacy, pp. 315–334 (2018)
Camenisch, J.: Efficient and generalized group signatures. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 465–479. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_32
Camenisch, J., Drijvers, M., Gagliardoni, T., Lehmann, A., Neven, G.: The wonderful world of global random oracles. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part I. LNCS, vol. 10820, pp. 280–312. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_11
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: 42nd FOCS, pp. 136–145 (2001)
Canetti, R., Dodis, Y., Pass, R., Walfish, S.: Universally composable security with global setup. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 61–85. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_4
Canetti, R., Goldreich, O., Halevi, S.: The random oracle methodology, revisited (preliminary version). In: 30th ACM STOC, pp. 209–218 (1998)
Canetti, R., Jain, A., Scafuro, A.: Practical UC security with a global random oracle. In: ACM CCS 2014, pp. 597–608 (2014)
Chaum, D., van Heyst, E.: Group signatures. In: Davies, D.W. (ed.) EUROCRYPT 1991. LNCS, vol. 547, pp. 257–265. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-46416-6_22
Ciampi, M., Persiano, G., Scafuro, A., Siniscalchi, L., Visconti, I.: Improved OR-composition of sigma-protocols. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016, Part II. LNCS, vol. 9563, pp. 112–141. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49099-0_5
Ciampi, M., Persiano, G., Scafuro, A., Siniscalchi, L., Visconti, I.: Online/offline OR composition of sigma protocols. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 63–92. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_3
Cramer, R., Damgård, I.: Fast and secure immunization against adaptive man-in-the-middle impersonation. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 75–87. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_7
Cramer, R., Damgård, I., Schoenmakers, B.: Proofs of partial knowledge and simplified design of witness hiding protocols. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 174–187. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48658-5_19
Dagdelen, Ö., Fischlin, M., Gagliardoni, T.: The Fiat–Shamir transformation in a quantum world. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part II. LNCS, vol. 8270, pp. 62–81. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_4
Damgård, I.: On \(\Sigma \)-protocols. Lecture Notes, Department for Computer Science, University of Aarhus (2002)
Dodis, Y., Shoup, V., Walfish, S.: Efficient constructions of composable commitments and zero-knowledge proofs. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 515–535. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_29
Don, J., Fehr, S., Majenz, C., Schaffner, C.: Security of the Fiat-Shamir transformation in the quantum random-oracle model. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part II. LNCS, vol. 11693, pp. 356–383. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_13
Ducas, E. et al.: CRYSTALS-Dilithium: a lattice-based digital signature scheme. IACR TCHES 2018, vol. 1, pp. 238–268 (2018). https://tches.iacr.org/index.php/TCHES/article/view/839
Ducas, L., et al.: Crystals-Dilithium: algorithm specifications and supporting documentation (2019). https://pq-crystals.org/dilithium/index.shtml
Esgin, M.F., Steinfeld, R., Liu, J.K., Liu, D.: Lattice-based zero-knowledge proofs: new techniques for shorter and faster constructions and applications. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part I. LNCS, vol. 11692, pp. 115–146. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26948-7_5
Feige, U., Shamir, A.: Witness indistinguishable and witness hiding protocols. In: 22nd ACM STOC, pp. 416–426 (1990)
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Fischlin, M., Fleischhacker, N.: Limitations of the meta-reduction technique: the case of Schnorr signatures. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 444–460. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_27
Fischlin, M., Harasser, P., Janson, C.: Signatures from sequential-OR proofs. IACR Cryptology ePrint Archive (2020). https://eprint.iacr.org/2020/271
Fischlin, M., Lehmann, A., Ristenpart, T., Shrimpton, T., Stam, M., Tessaro, S.: Random oracles with(out) Programmability. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 303–320. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_18
Fukumitsu, M., Hasegawa, S.: Impossibility on the provable security of the Fiat-Shamir-Type signatures in the non-programmable random oracle model. In: Bishop, M., Nascimento, A.C.A. (eds.) ISC 2016. LNCS, vol. 9866, pp. 389–407. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45871-7_23
Fukumitsu, M., Hasegawa, S.: Black-box separations on Fiat-Shamir-type signatures in the non-programmable random oracle model. IEICE Trans. 101-A(1), 77–87 (2018)
Garay, J.A., MacKenzie, P., Yang, K.: Strengthening zero-knowledge protocols using signatures. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 177–194. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_11
Gjøsteen, K., Jager, T.: Practical and tightly-secure digital signatures and authenticated key exchange. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part II. LNCS, vol. 10992, pp. 95–125. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_4
Goldwasser, S., Micali, S., Rivest, R.L.: A digital signature scheme secure against adaptive chosen-message attacks. SIAM J. Comput. 17(2), 281–308 (1988)
Guillou, L.C., Quisquater, J.-J.: A practical zero-knowledge protocol fitted to security microprocessor minimizing both transmission and memory. In: Barstow, D., et al. (eds.) EUROCRYPT 1988. LNCS, vol. 330, pp. 123–128. Springer, Heidelberg (1988). https://doi.org/10.1007/3-540-45961-8_11
Hofheinz, D., Jager, T.: Tightly secure signatures and public-key encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 590–607. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_35
Jakobsson, M., Sako, K., Impagliazzo, R.: Designated verifier proofs and their applications. In: Maurer, U. (ed.) EUROCRYPT 1996. LNCS, vol. 1070, pp. 143–154. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68339-9_13
Jedusor, T.E.: MimbleWimble (2016). https://download.wpsoftware.net/bitcoin/wizardry/mimblewimble.txt
Kiltz, E., Lyubashevsky, V., Schaffner, C.: A concrete treatment of Fiat-Shamir signatures in the quantum random-oracle model. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part III. LNCS, vol. 10822, pp. 552–586. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_18
Lindell, Y.: An efficient transform from sigma protocols to NIZK with a CRS and non-programmable random oracle. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 93–109. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_5
Liu, J.K., Wei, V.K., Wong, D.S.: Linkable spontaneous anonymous group signature for ad hoc groups (extended abstract). In: Wang, H., Pieprzyk, J., Varadharajan, V. (eds.) ACISP 2004. LNCS, vol. 3108, pp. 325–335. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-27800-9_28
Liu, Q., Zhandry, M.: Revisiting post-quantum Fiat-Shamir. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part II. LNCS, vol. 11693, pp. 326–355. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_12
Lyubashevsky, V.: Lattice signatures without trapdoors. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 738–755. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_43
Maxwell, G., Poelstra, A.: Borromean ring signatures (2015). https://pdfs.semanticscholar.org/4160/470c7f6cf05ffc81a98e8fd67fb0c84836ea.pdf
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information: 10th Anniversary Edition, 10th edn. Cambridge University Press, New York (2011)
Okamoto, T.: Provably secure and practical identification schemes and corresponding signature schemes. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 31–53. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-48071-4_3
Paillier, P., Vergnaud, D.: Discrete-log-based signatures may not be equivalent to discrete log. In: Roy, B. (ed.) ASIACRYPT 2005. LNCS, vol. 3788, pp. 1–20. Springer, Heidelberg (2005). https://doi.org/10.1007/11593447_1
Poelstra, A.: MimbleWimble (2016). https://download.wpsoftware.net/bitcoin/wizardry/mimblewimble.pdf
Pointcheval, D., Stern, J.: Security arguments for digital signatures and blind signatures. J. Cryptol. 13(3), 361–396 (2000). https://doi.org/10.1007/s001450010003
Rivest, R.L., Shamir, A., Tauman, Y.: How to leak a secret. In: Boyd, C. (ed.) ASIACRYPT 2001. LNCS, vol. 2248, pp. 552–565. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45682-1_32
Schnorr, C.-P.: Efficient signature generation by smart cards. J. Cryptol. 4(3), 161–174 (1991). https://doi.org/10.1007/BF00196725
van Saberhagen, N.: CryptoNote v 2.0 (2013). https://cryptonote.org/whitepaper.pdf
Venturi, D.: Zero-knowledge proofs and applications (2015). http://wwwusers.di.uniroma1.it/~venturi/misc/zero-knowledge.pdf
Zhandry, M.: Secure identity-based encryption in the quantum random oracle model. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 758–775. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_44
Zhang, Z., Chen, Y., Chow, S.S.M., Hanaoka, G., Cao, Z., Zhao, Y.: Black-box separations of hash-and-sign signatures in the non-programmable random oracle model. In: Au, M.-H., Miyaji, A. (eds.) ProvSec 2015. LNCS, vol. 9451, pp. 435–454. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-26059-4_24
Acknowledgments
We thank the anonymous reviewers for valuable comments. We thank Serge Fehr and Tommaso Gagliardoni for helpful discussions. This work was funded by the Deutsche Forschungsgemeinschaft (DFG) – SFB 1119 – 236615297.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Fischlin, M., Harasser, P., Janson, C. (2020). Signatures from Sequential-OR Proofs. In: Canteaut, A., Ishai, Y. (eds) Advances in Cryptology – EUROCRYPT 2020. EUROCRYPT 2020. Lecture Notes in Computer Science(), vol 12107. Springer, Cham. https://doi.org/10.1007/978-3-030-45727-3_8
Download citation
DOI: https://doi.org/10.1007/978-3-030-45727-3_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-45726-6
Online ISBN: 978-3-030-45727-3
eBook Packages: Computer ScienceComputer Science (R0)














 . It then computes the challenge
. It then computes the challenge 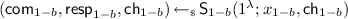 . It then obtains the challenge
. It then obtains the challenge 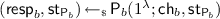 using the witness for
using the witness for 

