Abstract
Simple systems can produce complicated behavior. The reason lies in the structure of space and time. Simple ‘weaving rules’ suffice to determine very complicated motions.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Jacques Hadamard (1865–1963) was a French mathematician who proved an inequality on determinants, leading to the discovery ofHadamard matrices when equality holds. In 1896 he proved the prime number theorem, using complex function theory and published his work on geodesics in the differential geometry of surfaces and dynamical systems. He studied in 1898 geodesics on surfaces of negative curvature, thus introducing symbolic dynamics. He continued his career by working on the problems of mathematical physics, in particular partial differential equations, the calculus of variations and the foundations of functional analysis.
- 2.
George David Birkhoff (1884–1944) proved Poincaré’s “last geometric theorem,” a special case of the three-body problem. In 1923, Birkhoff proved that the Schwarzschild geometry is the unique spherically symmetric solution of the Einstein field equations. Birkhoff discovered in 1931 the ergodic theorem.
- 3.
Pierre Fatou (1878–1929) was a French mathematician working in the field of complex analytic dynamics. In particular, he investigated recursive processes like \(z_{n+1} = z_n^2 + c\), where \(z=x+iy\) is a complex number. Fatou focused his attention to the case where \(z_0 = 0\).
- 4.
Gaston Julia (1893–1978) was a French mathematician who devised the formula for the Julia set. His works were popularized by French mathematician Benoît Mandelbrot; Julia sets and Mandelbrot fractals are thus closely related. Gaston Julia had the unusual habit of wearing a patch to cover the center of his face. The patch was intended to hide extensive disfiguration of his nose and the surrounding region, suffered during Julia’s service in the French Army during World War I.
- 5.
Eberhard Hopf (1902–1983) was a German mathematician and astronomer, one of the founding fathers of the ergodic theory and a pioneer of bifurcation theory. He also made significant contributions to the subjects of partial differential equations and integral equations, fluid dynamics, and differential geometry. Otto met Hopf, speaker of honor at Okan Gurel’s New York chaos conference, in New York (May 1977). Hopf had told the audience that he had lost his memory and that one should tell him if he said the same thing twice in short order. Due to that he therefore unfortunately could no longer do math. While returning at home, Otto traveled with him to Kennedy Airport. When waiting for an hour together before the gate, Otto bridged the time by, on the spur of the moment, drawing for him baker’s transformation onto a tiny little piece of scrap paper: Two squares with an arrow between them and a vertical divided in the left one and a horizontal divide in the right one, and a round-about back arrow. Hopf was excited and told Otto that he remembered distinctly John von Neumann (1903–1957) who was Hungarian and then became an American. Von Neumann was a pure and applied mathematician and physicist. Among others, he contributed to mathematics (functional analysis, ergodic theory, geometry, topology, and numerical analysis), physics (quantum mechanics, hydrodynamics, and fluid dynamics), economics (game theory), computing (Von Neumann architecture, linear programming, self-replicating machines, stochastic computing), and statistics. He was an important member of the Manhattan Project and the Institute for Advanced Study in Princeton. So Hopf remembered von Neumann drawning this very picture on the blackboard in Princeton in 1949, telling the audience that “this has been invented by Eberhard Hopf”.
- 6.
Erich von Holst (1908–1962) was a German behavioral physiologist. Holst worked with the zoologist Konrad Lorenz (1903–1989) concerning the processes of endogenous generation of stimuli and of central coordination as a basis of behavioral physiology. In the 1950s, he founded the Max Planck Institute for Behavioral Physiology at Seewisen (Bavaria) that Otto Rössler visited in 1967 (the center was then directed by Lorenz). From his studies of fish that use rhythmic, synchronized fin motions while maintaining an immobile body, he developed two fundamental principles to describe the coordinative properties of “neural oscillators”: (i) Beharrungstendenz which is a tendency of an oscillator to maintain a steady rhythm (this would include movements such as breathing, chewing and running, which Holst called states of absolute coordination) and (ii) Magneteffekt which describes as an effect that one oscillator exercises over another oscillator of a different frequency so that it appears “magnetically” to draw and couple it to its own frequency. The result of interaction and struggle between Beharrungstendenz and Magneteffekt creates an infinite number of variable couplings, and in essence forms a state of relative coordination. As in his paper published in 1939 [31], he saw chaos produced by periodic forcing of fish fins. The brain was disconnected to let the spinal cord control the motion of the tail fin while a front fin was periodically forced as shown in the figure below.
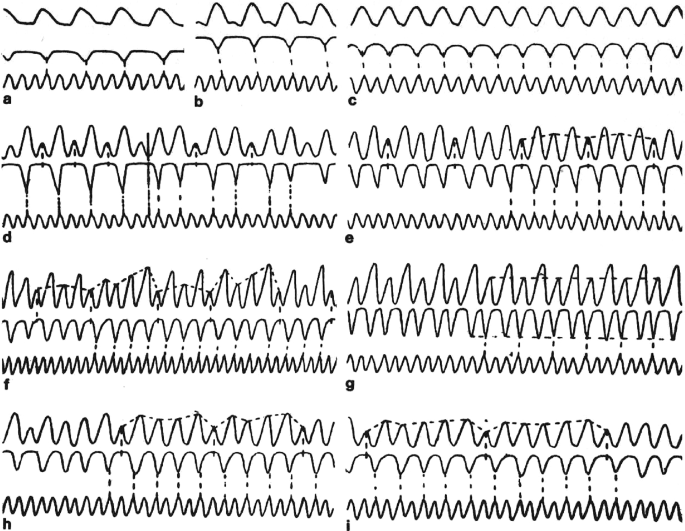
Surgus, pectoral fin (curve 1 and 2), tail fin (curve 3); all segments of curve taken from the same specimen. The nine specimens show ten differently shaped oscillations (in d there is a spontaneous transition from one periodic pattern into another). The different dashed lines are provided to facilitate the overview on the periodic patterns and to point out the relationship between the three rhythms.
- 7.
David Ruelle—who published with Floris Takens an important contribution concerning the turbulence (see Sect. 10.5)—considered that the Lorenz attractor was an example of the “strange attractor” they predicted. He thus popularized the Lorenz system as a benchmark system for studying “turbulent” behaviors [24].
References
V.I. Arnold, A. Avez, Ergodic Problems of Classical Mechanics (Benjamin, New York, 1970); First Edition in French (Théorie Ergodique des systèmes dynamiques, Gauthier-Vilars, Paris, 1967)
G.D. Birkhoff, On the periodic motions of dynamical systems. Acta Math. 50, 359–379 (1927)
M.L. Cartwright, J.E. Littlewood, On nonlinear differential equations of the second order: I. The equation \(\ddot{y}-k(1-y^2)\dot{y}+y=b \lambda k \cos (\lambda t + \alpha )\), \(k\) large. J. Lond. Math. Soc. 20, 160–189 (1945)
A. Christie, Chinese Mythology (Paul Hamlyn, London, 1968), p. 44
P. Fatou, Mémoire sur les équations fonctionnelles. Bulletin de la Société Mathématique de France 47, 161–271 (1919)
I. Gumowski, C. Mira, Dynamique Chaotique (Cepadues Editions, Toulouse, 1980)
J. Hadamard, Les surfaces à courbures opposées et leurs lignes géodésiques. Journal de Mathématiques 5(4), 27–73 (1898)
H. Haken, Analogy between higher instabilities in fluids and lasers. Phys. Lett. A 53(1), 77–78 (1975)
H. Helmholtz, Handbuch der Physiologischen Optik (1866); English translation: Helmholtz’s Treatise on Physiological Optics, vol. 3, ed. by J.P.C. Southall (Optical Society, New York, 1926)
G.W. Hill, Researches in the lunar theory. Am. J. Math. 1, 5–26 (1878)
E. Hopf, Ergodentheorie (Ergodic Theory) (Springer, Berlin, 1937), p. 42
G. Julia, Mémoire sur l’itération des fonctions rationnelles. Journal de Mathématiques Pures et Appliquées, vii 4, 47–245 (1918)
J. LaSalle, Relaxation oscillations. Quaterly Appl. Math. 7, 1–19 (1949)
T.-Y. Li, J.A. Yorke, Period-3 implies chaos. Am. Math. Mon. 82, 985–992 (1975)
A. Liénard, Etudes des oscillations entretenues. Revue Générale de l’Electricité 23, 901–912, 946–954 (1928)
E.N. Lorenz, Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130–141 (1963)
R.M. May, Biological populations with nonoverlapping generations: stable points, limit cycles, and chaos. Science 186, 645–647 (1974)
J.B. McLaughlin, P.C. Martin, Transition to turbulence of a statically stressed fluid system. Phys. Rev. Lett. 33, 1189–1192 (1974)
J. Moser, Stable and Random Motions in Dynamical Systems (Princeton University Press, Princeton, 1973)
P.J. Myrberg, Iteration of the real polynomials of second degree, III. Annales Academiae Scienctiarum Fennicae A, 336(3), 1–18 (1963) (in German)
H. Poincaré, Sur le problème des trois corps et les équations de la dynamique. Acta Math. 13, 1–271 (1890)
O.E. Rössler, Chaos, in Structural Stability in Physics, ed. by W. Güttinger, H. Eikemeier (Springer, Berlin, 1979), pp. 290–309
O.E. Rössler, Chaotic behavior in simple reaction systems. Zeitschrift für Naturforschung A 31, 239–264 (1976)
* D. Ruelle, The Lorenz attractor and the problem of turbulence. Acta Phys. Austriaca (Suppl.) 16, 221–239 (1976)
A.N. Sharkovsky, Coexistence of the cycles of a continuous mapping of the line onto itself. UKrain’kii Matematichnii Zhurnal 16, 61–71 (1964)
S. Smale, Generalized Poincaré’s conjecture in dimensions greater than four. Ann. Math. 74, 391–406 (1961)
S. Smale, Differentiable dynamical system. Bull. Am. Math. Soc. 73, 747–817 (1967)
P.R. Stein, S.M. Ulam, Non-linear transformation studies on electronic computers. Rozprawy Matematyczne 39, 1–65 (1964)
F. Takens, Implicit differential equations: some open problems. Lect. Notes Math. 535, 237–253 (1976)
B. van der Pol, Oscillation hysteresis in a triode generator with two degrees of freedom (in Dutch). Tijdschrift van het Nederlandsch Radiogenootschap 2, 125 (1921); also Philosophical Magazine, vii, 43, 177 (1922)
E. von Holst, Die relative Koordination als Phänomen und als Methode zentral nervöser Funktionsanalyse. Ergebnisse der Physiologie 42, 228–306 (1939)
R.F. Williams, Expanding attractors. Publications Mathématiques de l’Institut des Hautes Etudes Scientifiques 43, 169–203 (1974)
E.C. Zeeman, Differential equations for the heartbeat and nerve impulse, in Towards a Theoretical Biology, vol. 4, ed. by C.H. Waddington. (Edinburgh University Press, Edinburgh, 1972), pp. 8–67
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Rössler, O.E., Letellier, C. (2020). The Phenomenon of Chaos. In: Chaos. Understanding Complex Systems. Springer, Cham. https://doi.org/10.1007/978-3-030-44305-4_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-44305-4_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-44304-7
Online ISBN: 978-3-030-44305-4
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


