Improving GP-UCB Algorithm by Harnessing Decomposed Feedback

Abstract

Gaussian processes (GPs) have been widely applied to machine learning and nonparametric approximation. Given existing observations, a GP allows the decision maker to update a posterior belief over the unknown underlying function. Usually, observations from a complex system come with noise and decomposed feedback from intermediate layers. For example, the decomposed feedback could be the components that constitute the final objective value, or the various feedback gotten from sensors. Previous literature has shown that GPs can successfully deal with noise, but has neglected decomposed feedback. We therefore propose a decomposed GP regression algorithm to incorporate this feedback, leading to less average root-mean-squared error with respect to the target function, especially when the samples are scarce. We also introduce a decomposed GP-UCB algorithm to solve the resulting bandit problem with decomposed feedback. We prove that our algorithm converges to the optimal solution and preserves the no-regret property. To demonstrate the wide applicability of this work, we execute our algorithm on two disparate social problems: infectious disease control and weather monitoring. The numerical results show that our method provides significant improvement against previous methods that do not utilize these feedback, showcasing the advantage of considering decomposed feedback.

1 Introduction

Many challenging sequential decision making problems involve interventions in complex physical or social systems, where the system dynamics must be learned over time. For instance, a challenge commonly faced by policymakers is to control disease outbreaks [16], but the true process by which disease spreads in the population is not known in advance. We study such problems from the perspective of online learning, where a decision maker aims to optimize an unknown expensive objective function [2]. At each step, the decision maker commits to an action and receives the objective value for that action. For instance, a policymaker may implement a disease control policy [9, 12] for a given time period and observe the number of subsequent infections. This information allows the decision maker to update their knowledge of the unknown function. The goal is to obtain low cumulative regret, which measures the difference in objective value between the actions that were taken and the true (unknown) optimum.

This problem has been well-studied in optimization and machine learning. When a parametric form is not available for the objective (as is often the case with complex systems that are difficult to model analytically), a common approach uses a Gaussian process (GP) as a nonparametric prior over smooth functions. This Bayesian approach allows the decision maker to form a posterior distribution over the unknown function’s values. Consequently, the GP-UCB algorithm, which iteratively selects the point with the highest upper confidence bound according to the posterior, achieves a no-regret guarantee [14].

While GP-UCB and similar techniques [3, 17] have seen a great deal of interest in the purely black-box setting, many physical or social systems naturally admit an intermediate level of feedback. This is because the system is composed of multiple interacting components, each of which can be measured individually. For instance, disease spread in a population is a product of the interactions between individuals in different demographic groups or locations [19], and policymakers often have access to estimates of the prevalence of infected individuals within each subgroup [4, 18]. The true objective (total infections) is the sum of infections across the subgroups. Similarly, climate systems involve the interactions of many different variables (heat, wind, humidity, etc.) which can be sensed individually then combined in a nonlinear fashion to produce outputs of interest (e.g., an individual’s risk of heat stroke) [15]. Prior work has studied the benefits of using additive models [6]. However, they only examine the special case where the target function decomposes into a sum of lower-dimensional functions. Motivated by applications such as flu prevention, we consider the more general setting where the subcomponents are full-dimensional and may be composed nonlinearly to produce the target. This general perspective is necessary to capture common policy settings which may involve intermediate observables from simulation or domain knowledge.

However, to our knowledge, no prior work studies the challenge of integrating such decomposed feedback in online decision making. Our first contribution is to remedy this gap by proposing a decomposed GP-UCB algorithm (D-GPUCB). D-GPUCB uses a separate GP to model each individual measurable quantity and then combines the estimates to produce a posterior over the final objective. Our second contribution is a theoretical no-regret guarantee for D-GPUCB, ensuring that its decisions are asymptotically optimal. Third, we prove that the posterior variance at each step must be less than the posterior variance of directly using a GP to model the final objective. This formally demonstrates that more detailed modeling reduces predictive uncertainty. Finally, we conduct experiments in two domains using real-world data: flu prevention and heat sensing. In each case, D-GPUCB achieves substantially lower cumulative regret than previous approaches.

2 Preliminaries

2.1 Noisy Black-Box Optimization

Given an unknown black-box function $f: \mathcal {X} \rightarrow \mathbb {R}$ where $\mathcal {X} \subset \mathbb {R}^n$, a learner is able to select an input $\varvec{x} \in \mathcal {X}$ and access the function to see the outcome $f(\varvec{x})$ – this encompasses one evaluation. Gaussian process regression [11] is a non-parametric method to learn the target function using Bayesian methods [5, 13]. It assumes that the target function is an outcome of a Gaussian process with given kernel $k(\varvec{x},\varvec{x}')$ (covariance function). Gaussian process regression is commonly used and only requires an assumption on the function smoothness. Moreover, Gaussian process regression can handle observation error. It allows the observation at point $\varvec{x}_t$ to be noisy: $y_t = f(\varvec{x}_t) + \epsilon _t$, where $\epsilon _t \sim N(0, \sigma ^2 I)$.

2.2 Decomposition

In this paper, we consider a modification to the Gaussian process regression process. Suppose we have some prior knowledge of the unknown reward function $f(\varvec{x})$ such that we can write the unknown function as a combination of known and unknown subfunctions:

Definition 1 (Linear Decomposition)

$$\begin{aligned} f(\varvec{x}) = \sum \nolimits _{j=1}^J g_j(\varvec{x}) f_j(\varvec{x}) \end{aligned}$$

(1)

where $f_j, g_j: \mathbb {R}^n \rightarrow \mathbb {R}$.

Here $g_j(\varvec{x})$ are known, deterministic functions, but $f_j(\varvec{x})$ are unknown functions that generate noisy observations. For example, in the flu prevention case, the total infected population can be written as the summation of the infected population at each age [4]. Given treatment policy $\varvec{x}$, we can use $f_j(\varvec{x})$ to represent the unknown infected population at age group j with its known, deterministic weighted function $g_j(\varvec{x}) = 1$. Therefore, the total infected population $f(\varvec{x})$ can be simply expressed as $\sum \nolimits _{j=1}^J f_j(\varvec{x})$.

Interestingly, any deterministic linear composition of outcomes of Gaussian processes is still an outcome of Gaussian process. That means if all of the $f_j$ are generated from Gaussian processes, then the entire function f can also be written as an outcome of another Gaussian process.

Next, we generalize this definition to the non-linear case, which we call a general decomposition:

Definition 2 (General Decomposition)

$$\begin{aligned} f(\varvec{x}) = g(f_1(\varvec{x}), f_2(\varvec{x}), ..., f_J(\varvec{x})) \end{aligned}$$

(2)

The function g can be any deterministic function (e.g. polynomial, neural network). Unfortunately, a non-linear composition of Gaussian processes may not be a Gaussian process, so we cannot guarantee function f to be an outcome of a Gaussian process. We will cover the result of linear decomposition first and then generalize it to the cases with general decomposition.

2.3 Gaussian Process Regression

Although Gaussian process regression does not require rigid parametric assumptions, a certain degree of smoothness is still needed to ensure its guarantee of no-regret. We can model f as a sample from a GP: a collection of random variables, one for each $\varvec{x} \in \mathcal {X}$. A GP$(\mu (\varvec{x}), k(\varvec{x},\varvec{x}'))$ is specified by its mean function $\mu (x) = E[f(\varvec{x})]$ and covariance function $k(\varvec{x},\varvec{x}') = E[(f(\varvec{x}) - \mu (\varvec{x}))(f(\varvec{x}') - \mu (\varvec{x}'))]$. For GPs not conditioned on any prior, we assume that $\mu (\varvec{x}) \equiv 0$. We further assume bounded variance $k(\varvec{x},\varvec{x}) \le 1$. This covariance function encodes the smoothness condition of the target function f drawn from the GP.

For a noisy sample $\varvec{y}_T = [y_1, ..., y_T]^\top$ at points $A_T = \{ \varvec{x}_t \}_{t \in [T]}$, $y_t = f(\varvec{x}_t) + \epsilon _t ~\forall t \in [T]$ with $\epsilon _t \sim N(0, \sigma ^2(\varvec{x}_t))$ Gaussian noise with variance $\sigma ^2(\varvec{x}_t)$, the posterior over f is still a Gaussian process with posterior mean $\mu _T(\varvec{x})$, covariance $k_T(\varvec{x},\varvec{x}')$ and variance $\sigma ^2_T(\varvec{x})$:

$$\begin{aligned} \mu _T(\varvec{x})&= \varvec{k}_T(\varvec{x})^\top \varvec{K}_T^{-1} \varvec{k}_T(\varvec{x}'), \end{aligned}$$

(3)

$$\begin{aligned} k_T(\varvec{x}, \varvec{x}')&= k(\varvec{x}, \varvec{x}') - \varvec{k}_T(\varvec{x})^\top \varvec{K}_T^{-1} \varvec{k}(\varvec{x}'), \end{aligned}$$

(4)

$$\begin{aligned} \sigma ^2_T(\varvec{x})&= k_T(\varvec{x},\varvec{x}') \end{aligned}$$

(5)

where $\varvec{k}_T(\varvec{x}) = [k(\varvec{x}_1, \varvec{x}),...,k(\varvec{x}_T, \varvec{x})]^\top$, and $\varvec{K}_T$ is the positive definite kernel matrix $[k(\varvec{x}, \varvec{x}')]_{\varvec{x},\varvec{x}' \in A_T} + \text {diag}([\sigma ^2(\varvec{x}_t)]_{t \in [T]})$.

2.4 Bandit Problem with Decomposed Feedback

Considering the output value of the target function as the learner’s reward (penalty), the goal is to learn the unknown underlying function f while optimizing the cumulative reward. This is usually known as an online learning or multi-arm bandit problem [1]. In this paper, given the knowledge of deterministic decomposition function g (Definition 1 or Definition 2), in each round t, the learner chooses an input $\varvec{x}_t \in \mathcal {X}$ and observes the value of each unknown decomposed function $f_j$ perturbed by a noise: $y_{j,t} = f_j(\varvec{x}_t) + \epsilon _{j,t}, \epsilon _{j,t} \sim N(0, \sigma _j^2)~\forall j \in [J]$. At the same time, the learner receives the composed reward from this input $\varvec{x}_t$, which is $y_t = g(y_{1,t}, y_{2,t}, ..., y_{J,t}) = f(\varvec{x}_t) + \epsilon _t$ where $\epsilon _t$ is an aggregated noise. The goal is to maximize the sum of noise-free rewards $\sum \nolimits _{t=1}^T f(\varvec{x}_t)$, which is equivalent to minimizing the cumulative regret $R_T = \sum \nolimits _{t=1}^T r_t = \sum \nolimits _{t=1}^T f(\varvec{x}^*) - f(\varvec{x}_t)$, where $\varvec{x}^* = \arg \max _{\varvec{x} \in \mathcal {X}} f(\varvec{x})$ and individual regret $r_t = f(\varvec{x}^*) - f(\varvec{x}_t)$.

This decomposed feedback is related to the semi-bandit setting, where a decision is chosen from a combinatorial set and feedback is received about individual elements of the decision [10]. Our work is similar in that we consider an intermediate feedback model which gives the decision maker access to decomposed feedback about the underlying function. However, in our setting a single point is chosen from a continuous set, rather than multiple items from a discrete one. Additional feedback is received about components of the objective function, not the items chosen. Hence, the technical challenges are quite different.

3 Problem Statement and Background

Using the flu prevention as an example, a policymaker will implement a yearly disease control policy and observe the number of subsequent infections. A policy is an input $\varvec{x}_t \in \mathbb {R}^n$, where each entry $x_{t,i}$ denotes the extent to vaccinate the infected people in age group i. For example, if the government spends more effort $x_{t,i}$ in group i, then the people in this group will be more likely to get a flu shot.

Given the decomposition assumption and samples (previous policies) at points $\varvec{x}_t ~\forall t \in [T]$, including all the function values $f(\varvec{x}_t)$ (total infected population) and decomposed function values $f_j(\varvec{x}_t)$ (infected population in group j), the learner attempts to learn the function f while simultaneously minimizing regret. Therefore, we have two main challenges: (i) how best to approximate the reward function using the decomposed feedback and decomposition (non-parametric approximation), and (ii) how to use this estimation to most effectively reduce the average regret (bandit problem).

3.1 Regression: Non-parametric Approximation

Our first aim is to fully utilize the decomposed problem structure to get a better approximation of f(x). The goal is to learn the underlying disease pattern faster by using the decomposed problem structure. Given the linear decomposition assumption that $f(\varvec{x}) = \sum \nolimits _{j=1}^J g_j(\varvec{x}) f_j(\varvec{x})$ and noisy samples at points $\{ \varvec{x}_t\}_{t \in [T]}$, the learner can observe the outcome of each decomposed function $f_j(\varvec{x}_t)$ at each sample point $\varvec{x}_t ~\forall t \in [T]$. Our goal is to provide a Bayesian update to the unknown function which fully utilizes the learner’s knowledge of the decomposition.

3.2 Bandit Problem: Minimizing Regret

In the flu example, each annual flu-awareness campaign is constrained by a budget, and we assume policymaker does not know the underlying disease spread pattern. At the beginning of each year, the policymaker chooses a new campaign policy based on the previous years’ results and observes the outcome of this new policy. The goal is to minimize the cumulative regret (all additional infections in prior years) while learning the underlying unknown function (disease pattern).

We will show how a decomposed GP regression, with a GP-UCB algorithm, can be used to address these challenges.

4 Decomposed Gaussian Process Regression

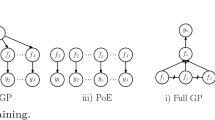
First, we propose a decomposed GP regression (Algorithm 2). The idea behind decomposed GP regression is as follows: given the linear decomposition assumption (Definition 1), run Gaussian process regression for each $f_j(\varvec{x})$ individually, and get the aggregated approximation by $f(\varvec{x}) = \sum \nolimits _{j=1}^J g_j(\varvec{x}) f_j(\varvec{x})$ (illustrated in Fig. 1).

Fig. 1.

Illustration of the comparison between decomposed GP regression (Algorithm 2) and standard GP regression. Decomposed GP regression shows a smaller average variance (0.878 v.s. 0.943) and a better estimate of the target function.

Assuming we have T previous samples with input $\varvec{x}_1, \varvec{x}_2, ..., \varvec{x}_T$ and the noisy outcome of each individual function $\varvec{y}_{j,t} = f_j(\varvec{x}_t) + \epsilon _{j,t} ~\forall j \in [J], t \in [T]$, where $\epsilon _{j,t} \sim N(0, \sigma ^2_j)$, the outcome of the target function f(x) can be computed as $y_t = \sum \nolimits _{j=1}^J g_j(\varvec{x}_t) y_{j,t}$. Further assume the function $f_j(\varvec{x})$ is an outcome of $GP(0, k_j) ~\forall j$. Therefore the entire function f is also an outcome of GP(0, k) where $k(\varvec{x}, \varvec{x}') = \sum \nolimits _{j=1}^J g_j(\varvec{x}) k_j(\varvec{x}, \varvec{x}') g_j(\varvec{x}')$.

We are going to compare two ways to approximate the function $f(\varvec{x})$ using existing samples. (i) Directly use Algorithm 1 with the composed kernel $k(\varvec{x},\varvec{x}')$ and noisy samples $\{(\varvec{x}_t, y_t)\}_{t \in [T]}$ – the typical GP regression process. (ii) For each $j \in [J]$, first run Algorithm 1 with kernel $k_j(\varvec{x},\varvec{x}')$ and noisy samples $\{(\varvec{x}_t, y_{j,t})\}_{t \in [T]}$. Then compose the outcomes with the deterministic weighted function $g_j(\varvec{x})$ to get $f(\varvec{x})$. This is shown in Algorithm 2.

In order to analytically compare Gaussian process regression (Algorithm 1) and decomposed Gaussian process regression (Algorithm 2), we are going to compute the variance (uncertainty) returned by both algorithms. We will show that the latter variance is smaller than the former. Proofs are in the Appendix for brevity.

Proposition 1

The variance returned by Algorithm 1 is

$$\begin{aligned} \sigma _{T,\text {entire}}^2(\varvec{x}) = k(\varvec{x}, \varvec{x}) - \sum \limits _{i,j} \varvec{z}_i^\top (\sum \limits _{l} \varvec{D}_l \varvec{K}_{l,T} \varvec{D}_l)^{-1} \varvec{z}_j \end{aligned}$$

(6)

where $\varvec{D}_j = \text {diag}([g_j(\varvec{x}_1), ..., g_j(\varvec{x}_T)])$ and $\varvec{z}_i = \varvec{D}_i \varvec{k}_{j,T}(\varvec{x}) g_j(\varvec{x}) \in \mathbb {R}^T$.

Proposition 2

The variance returned by Algorithm 2 is

$$\begin{aligned} \sigma ^2_{T, \text {decomp}}(\varvec{x}) = k(\varvec{x},\varvec{x}) - \sum \nolimits _{l} \varvec{z}_l^\top (\varvec{D}_l \varvec{K}_{l,T} \varvec{D}_l)^{-1} \varvec{z}_l \end{aligned}$$

(7)

In order that our approach has lower variance, we first recall the matrix-fractional function and its convex property.

Lemma 1

Matrix-fractional function $h(\varvec{X}, \varvec{y}) \! = \! \varvec{y}^\top \varvec{X}^{-1} \varvec{y}$ is defined and also convex on $\text {dom } f \! = \! \{ (\varvec{X}, \varvec{y}) \in \mathbf {S}^T_+ \times \mathbb {R}^T \}$.

Now we are ready to compare the variance provided by Propositions 1 and 2.

Theorem 1

The variance provided by decomposed Gaussian process regression (Algorithm 2) is less than or equal to the variance provided by Gaussian process regression (Algorithm 1), which implies the uncertainty by using decomposed Gaussian process regression is smaller.

Proof (Proof sketch)

In order to compare the variance given by Propositions 1 and 2, we calculate the difference of Eqs. 6 and 7. Their difference can be rearranged as a Jensen inequality with the form of Matrix-fractional function (Lemma 1), which turns out to be convex. By Jensen inequality, their difference is non-negative, which implies the variance given by decomposed GP regression is no greater than the variance given by GP regression.

Theorem 1 implies that decomposed GP regression provides a posterior with smaller variance, which could be considered the uncertainty of the approximation. In fact, the posterior belief after the GP regression is still a Gaussian process, which implies the underlying target function is characterized by a joint Gaussian distribution, where a smaller variance directly implies a more concentrated Gaussian distribution, leading to less uncertainty and smaller root-mean-squared error. Intuitively, this is due to Algorithm 2 adopts the decomposition knowledge but Algorithm 1 does not. This contribution for handling decomposition in the GP regression context is very general and can be applied to many problems. We will show some applications of this idea in the following sections, focusing first on how a linear and generalized decompositions can be used to augment the GP-UCB algorithm for multi-armed bandit problems.

5 Decomposed GP-UCB Algorithm

The goal of a traditional bandit problem is to optimize the objective function $f(\varvec{x})$ by minimizing the regret. However, in our bandit problem with decomposed feedback, the learner is able to access samples of individual functions $f_j(\varvec{x})$. We first consider a linear decomposition $f(\varvec{x}) = \sum \nolimits _{j=1}^J g_j(\varvec{x}) f_j(\varvec{x})$.

In [14], they proposed the GP-UCB algorithm for classic bandit problems and proved that it is a no-regret algorithm that can efficiently achieve the global optimal objective value. A natural question arises: can we apply our decomposed GP regression (Algorithm 2) and also achieve the no-regret property? This leads to our second contribution: the decomposed GP-UCB algorithm, which uses decomposed GP regression when decomposed feedback is accessible. This algorithm can incorporate the decomposed feedback (the outcomes of decomposed function $f_j$), achieve a better approximation at each iteration while maintaining the no-regret property, and converge to a globally optimal value.

Theorem 2

Let $\delta \in (0,1)$ and $\beta _t = 2 \log (|\mathcal {X}| t^2 \pi ^2 / 6 \delta )$. Running decomposed GP-UCB (Algorithm 3) for a composed sample $f(\varvec{x}) = \sum \nolimits _{j=1} g_j(\varvec{x}) f_j(\varvec{x})$ with bounded variance $k_j(\varvec{x},\varvec{x}) \le 1$ and each $f_j \sim GP(0, k_j(\varvec{x},\varvec{x}'))$, we obtain a regret bound of $\mathcal {O}(\root \of {T \log |\mathcal {X}| \sum _{j=1}^J B_j^2 \gamma _{j,T} })$ with high probability, where $B_j = \max \nolimits _{\varvec{x} \in \mathcal {X}} |g_j(\varvec{x})|$. Precisely,

$$\begin{aligned} \text {Pr}\big \{ R_T \le \root \of {C_1 T \beta _T \sum \nolimits _{j=1}^J B_j^2 \gamma _{j,T} } ~\forall T \! \ge \! 1 \big \} \ge 1 - \delta \end{aligned}$$

(8)

where $C_1 = 8/ \log (1 + \sigma ^{-2})$ with noise variance $\sigma ^{2}$.

We present Algorithm 3, which replaces the Gaussian process regression in GP-UCB with our decomposed Gaussian process regression (Algorithm 2). According to Theorem 1, our algorithm takes advantage of decomposed feedback and provides a more accurate and less uncertain approximation at each iteration. We also provide a regret bound in Theorem 2, which guarantees no-regret property to Algorithm 3.

According to the linear decomposition and the additive and multiplicative properties of kernels, the entire underlying function is still an outcome of GP with a composed kernel $k(\varvec{x},\varvec{x}') = \sum \nolimits _{j=1}^J g_j(\varvec{x}) k_j(\varvec{x},\varvec{x}') g_j(\varvec{x}')$, which implies that GP-UCB algorithm can achieve a similar regret bound by normalizing the kernel $k(\varvec{x},\varvec{x}') \le \sum \nolimits _{j=1}^J B_j^2 = B^2$. The regret bound of GP-UCB can be given by:

$$\begin{aligned} Pr\{ R_T \le \root \of {C_1 T \beta _T B^2 \gamma _{\text {entire}, T}} ~\forall T \ge 1 \} \ge 1 - \delta \end{aligned}$$

(9)

where $\gamma _{\text {enitre}, T}$ is the upper bound on the information gain $I(y_T;f_T)$ of the composed kernel $k(\varvec{x},\varvec{x}')$.

But due to Theorem 1, D-GPUCB can achieve a lower variance and more accurate approximation at each iteration, leading to a smaller regret in the bandit setting, which will be shown to empirically perform better in the experiments.

5.1 No-Regret Property and Benefits of D-GPUCB

Previously, in order to guarantee a sublinear regret bound to GP-UCB, we require an analytical, sublinear bound $\gamma _{\text {entire}, T}$ on the information gain.  [14] provided several elegant upper bounds on the information gain of various kernels. However, in practice, it is hard to give an upper bound to a composed kernel $k(\varvec{x},\varvec{x}')$ and apply the regret bound (Inequality 9) provided by GP-UCB in the decomposed context.

Instead, D-GPUCB and the following generalized D-GPUCB provide a clearer expression to the regret bound, where their bounds (Theorems 2 and 3) only relate to upper bounds $\gamma _{j,T}$ of the information gain of each kernel $k_j(\varvec{x}, \varvec{x}')$. This resolves the problem of computing an upper bound of a composed kernel. We use various sublinear upper bounds of different kernels, which have been widely studied in prior literature [14].

5.2 Generalized Decomposed GP-UCB Algorithm

We now consider the general decomposition (Definition 2):

$$f(\varvec{x}) = g(f_1(\varvec{x}), f_2(\varvec{x}), ..., f_J(\varvec{x}))$$

To achieve the no-regret property, we further require the function g to have bounded partial derivatives $| \nabla _j g(\varvec{x}) | \le B_j ~\forall j \in [J]$. This corresponds to the linear decomposition case, where $| \nabla _j g | = | g_j(\varvec{x}) | \le B_j$.

Since, a non-linear composition of Gaussian processes is no longer a Gaussian process, the standard GP-UCB algorithm does not have any guarantees for this setting. However, we show that our approach, which leverages the special structure of the problem, still enjoys a no-regret guarantee:

Theorem 3

By running generalized decomposed GP-UCB with hyperparameter $\beta _t = 2 \log (|\mathcal {X}| J t^2 \pi ^2 / 6 \delta )$ for a composed sample $f(\varvec{x}) = g(f_1(\varvec{x}), ..., f_J(\varvec{x}))$ of GPs with bounded variance $k_j(\varvec{x},\varvec{x}) \le 1$ and each $f_j \sim GP(0, k_j(\varvec{x},\varvec{x}'))$. we obtain a regret bound of $\mathcal {O}(\root \of {T \log |\mathcal {X}| \sum _{j=1}^J B_j^2 \gamma _{j,T} })$ with high probability, where $B_j = \max \limits _{\varvec{x} \in \mathcal {X}} |\nabla _j g(\varvec{x}) |$. Precisely,

$$\begin{aligned} \text {Pr}\big \{ R_T \le \root \of {C_1 T \beta _T \sum \nolimits _{j=1}^J B_j^2 \gamma _{j,T} } ~ \forall T \ge 1 \big \} \ge 1 - \delta \end{aligned}$$

(10)

where $C_1 = 8/ \log (1 + \sigma ^{-2})$ with noise variance $\sigma ^2$.

The intuition is that so long as each individual function is drawn from a Gaussian process, we can still perform Gaussian process regression on each function individually to get an estimate of each decomposed component. Based on these estimates, we compute the corresponding estimate to the final objective value by combining the decomposed components with the function g. Since the gradient of function g is bounded, we can propagate the uncertainty of each individual approximation to the final objective function, which allows us to get a bound on the total uncertainty. Consequently, we can prove a high-probability bound between our algorithm’s posterior distribution and the target function, which enables us to bound the cumulative regret by a similar technique as Theorem 2.

The major difference for general decomposition is that the usual GP-UCB algorithm no longer works here. The underlying unknown function may not be an outcome of Gaussian process. Therefore the GP-UCB algorithm does not have any guarantees for either convergence or the no-regret property. In contrast, D-GPUCB algorithm still works in this general case if the learner is able to attain the decomposed feedback.

Our result greatly enlarges the feasible functional space where GP-UCB can be applied. We have shown that the generalized D-GPUCB preserves the no-regret property even when the underlying function is a composition of Gaussian processes. Given the knowledge of decomposition and decomposed feedback, based on Theorem 3, the functional space that generalized D-GPUCB algorithm can guarantee no-regret is closed under arbitrary bounded-gradient function composition. This leads to a very general functional space, showcasing the contribution of our algorithm.

5.3 Continuous Sample Space

All the above theorems are for discrete sample spaces $\mathcal {X}$. However, most real-world scenarios have a continuous space. [14] used the discretization technique to reduce the compact and convex continuous sample space to a discrete case by using a larger exploration constant:

$$\begin{aligned} \beta _t = 2 \log (2 t^2 \pi ^2 / (3 \delta )) + 2 d \log (t^2 d b r \root \of {\log (4 d a / \delta )}) \end{aligned}$$

while assuming $\text {Pr}\{ \sup _{\varvec{x} \in \mathcal {X}} |\partial f / \partial \varvec{x}_i | \!>\! L \} \! \le \! a e^{-(L/b)^2}$. (In the general decomposition case, $\beta _t = 2 \log (2 J t^2 \pi ^2 / (3 \delta )) + 2 d \log (t^2 d b r \root \of {\log (4 d a / \delta )})$). All of our proofs directly follow using the same technique. Therefore the no-regret property and regret bound also hold in continuous sample spaces.

6 Experiments

In this section, we run several experiments to compare decomposed Gaussian process regression (Algorithm 2), D-GPUCB (Algorithm 3), and generalized D-GPUCB (Algorithm 4). We also test on both discrete sample space and continuous sample space. All of our examples show a promising convergence rate and also improvement against the GP-UCB algorithm, again demonstrating that more detailed modeling reduces the predictive uncertainty.

6.1 Decomposed Gaussian Process Regression

For the decomposed Gaussian process regression, we compare the average standard deviation (uncertainty) provided by GP regression (Algorithm 1) and decomposed GP regression (Algorithm 2) over varying number of samples and number of decomposed functions. We use the following three common types of stationary kernel [11]:

• Square Exponential kernel is $k(\varvec{x}, \varvec{x}') = \exp (-(2l^2)^{-1} \left\| \varvec{x} - \varvec{x}' \right\| ^2)$, l is a length-scale hyper parameter.

• Matérn kernel is given by $k(\varvec{x}, \varvec{x}') \! = \! (2^{1-\nu } / \varGamma (\nu )) r^\nu B_\nu (r), r \! = \! (\root \of {2 \nu } / l) \left\| \varvec{x} - \varvec{x}' \right\|$, where $\nu$ controls the smoothness of sample functions and $B_\nu$ is a modified Bessel function.

• Rational Quadratic kernel is $k(\varvec{x}, \varvec{x}') = (1 + \left\| \varvec{x} - \varvec{x}' \right\| ^2 / (2 \alpha l^2))^{- \alpha }$. It can be seen as a scale mixture of square exponential kernels with different length-scales.

Fig. 2.

Average improvement for different kernels (with trend line) using decomposed GP regression and GP regression, in RMSE

Fig. 3.

Comparison of cumulative regret: D-GPUCB, GP-UCB, and various heuristics on synthetic (a) and real data (b, c)

For each kernel category, we first draw J kernels with random hyper-parameters. We then generate a random sample function $f_j$ from each corresponding kernel $k_j$ as the target function, combined with the simplest linear decomposition (Definition 1) with $g_j(\varvec{x}) \equiv 1 \forall j$. For each setting and each $T \le 50$, we randomly draw T samples as the previous samples and perform both GP regression and decomposed GP regression. We record the average improvement in terms of root-mean-squared error (RMSE) against the underlying target function over 100 independent runs for each setting. We also run experiments on flu domain with square exponential kernel based on real data and SIR model [4], which is illustrated in Fig. 2(d).

Empirically, our method reduces the RMSE in the model’s predictions by 10–15% compared to standard GP regression (without decomposed feedback). This trend holds across kernels, and includes both synthetic data and the flu domain (which uses a real dataset). Such an improvement in predictive accuracy is significant in many real-world domains. For instance, CDC-reported 95% confidence intervals for vaccination-averted flu illnesses for 2015 range from 3.5M–7M and averted medical visits from 1.7M–3.5M. Reducing average error by 10% corresponds to estimates which are tighter by hundreds of thousands of patients, a significant amount in policy terms. These results confirm our theoretical analysis in showing that incorporating decomposed feedback results in more accurate estimation of the unknown function.

6.2 Comparison Between GP-UCB and D-GPUCB

We now move the online setting, to test whether greater predictive accuracy results in improved decision making. We compare our D-GPUCB algorithm and generalized D-GPUCB with GP-UCB, as well as common heuristics such as Expected Improvement (EI) [8] and Most Probable Improvement (MPI) [7]. For all the experiments, we run 30 trials on all algorithms to find the average regret.

Synthetic Data (Linear Decomposition with Discrete Sample Space): For synthetic data, we randomly draw $J=10$ square exponential kernels with different hyper-parameters and then sample random functions from these kernels to compose the entire target function. The sample noise is set to be $10^{-4}$. The sample space $\mathcal {X} = [0,1]$ is uniformly discretized into 1000 points. We follow the recommendation in [14] to scale down $\beta _t$ by a factor 5 for both GP-UCB and D-GPUCB algorithm. We run each algorithm for 100 iterations with $\delta = 0.05$ for 30 trials (different kernels and target functions each trial), where the cumulative regrets are shown in Fig. 3(a), and average regret in Fig. 4(a).

Fig. 4.

Comparison of average regret: D-GPUCB, GP-UCB, and various heuristics on synthetic (a) and real data (b, c)

Flu Prevention (Linear Decomposition with Continuous Sample Space): We consider a flu age-stratified SIR model [4] as our target function. The population is stratified into several age groups: young (0–19), adult (20–49), middle aged (50–64), senior (65–69), elder (70+). The SIR model allows the contact matrix and susceptibility of each age group to vary. Our input here is the vaccination rate $\varvec{x} \in [0,1]^5$ with respect to each age group. Given a vaccination rate $\varvec{x}$, the SIR model returns the average sick days per person $f(\varvec{x})$ within one year. The model can also return the contribution to the average sick days from each age group j, which we denote as $f_j(\varvec{x})$. Therefore we have $f(\varvec{x}) = \sum \nolimits _{j=1}^5 f_j(\varvec{x})$, a linear decomposition. The goal is to find the optimal vaccination policy which minimizes the average sick days subject to budget constraints. Since we do not know the covariance kernel functions in advance, we randomly draw 1000 samples and fit a composite kernel (composed of square exponential kernel and Matérn kernel) before running UCB algorithms. We run all algorithms and compare their cumulative regret in Fig. 3(b) and average regret in Fig. 4(b).

Perceived Temperature (General Decomposition with Discrete Sample Space): The perceived temperature is a combination of actual temperature, humidity, and wind speed. When the actual temperature is high, higher humidity reduces the body’s ability to cool itself, resulting a higher perceived temperature; when the actual temperature is low, the air motion accelerates the rate of heat transfer from a human body to the surrounding atmosphere, leading to a lower perceived temperature. All of these are nonlinear function compositions. We use the weather data collected from 2906 sensors in United States provided by OpenWeatherMap. Given an input location $\varvec{x} \in \mathcal {X}$, we can access to the actual temperature $f_1(\varvec{x})$, humidity $f_2(\varvec{x})$, and wind speed $f_3(\varvec{x})$. In each test, we randomly draw one third of the entire data to learn the covariance kernel functions. Then we run generalized D-GPUCB and all the other algorithms on the remaining sensors to find the location with highest perceived temperature. The result is averaged over 30 different tests and is also shown in Figs. 3(c) and 4(c).

Discussion: In the bandit setting with decomposed feedback, Fig. 3 shows a $10\%{-}20\%$ improvement in cumulative regret for both synthetic (Fig. 3(a)) and real data (Fig. 3(b), (c)). As in the regression setting, such improvements are highly significant in policy terms; a 10% reduction in sickness due to flu corresponds to hundreds of thousands of infections averted per year. The benefit to incorporating decomposed feedback is particularly large in the general decomposition case (Fig. 3(c)), where a single GP is a poor fit to the nonlinearly composed function. Figure 4 shows the average regret of each algorithm (as opposed to the cumulative regret). Our algorithm’s average regret tends to zero. This allows us to empirically confirm the no-regret guarantee for D-GPUCB in both the linear and general decomposition settings. As with the cumulative regret, D-GPUCB uniformly outperforms the baselines.

7 Conclusions

We propose algorithms for nonparametric regression and online learning which exploit the decomposed feedback common in real world sequential decision problems. In the regression setting, we prove that incorporating decomposed feedback improves predictive accuracy (Theorem 1). In the online learning setting, we introduce the D-GPUCB algorithms (Algorithm 3 and Algorithm 4) and prove corresponding no-regret guarantees. We conduct experiments in both real and synthetic domains to investigate the performance of decomposed GP regression, D-GPUCB, and generalized D-GPUCB. All show significant improvement against GP-UCB and other methods that do not consider decomposed feedback, demonstrating the benefit that decision makers can realize by exploiting such information.